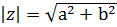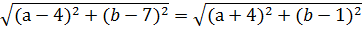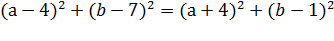Версия для печати и копирования в MS Word
1
Изобразите на чертеже множество точек комплексной плоскости, для которых выполняется условие Среди чисел, удовлетворяющих этому равенству, найдите число с наименьшим модулем. Запишите найденное число в тригонометрической форме.
Загрузка решений доступна для зарегистрировавшихся пользователей
2
Среди комплексных чисел z, удовлетворяющих условию найдите число с наименьшим модулем.
Загрузка решений доступна для зарегистрировавшихся пользователей
3
Среди чисел z, таких, что найдите числа с наименьшим и наибольшим модулем.
Загрузка решений доступна для зарегистрировавшихся пользователей
4
Найдите наибольший модуль комплексного числа z, удовлетворяющего условию
Загрузка решений доступна для зарегистрировавшихся пользователей
5
Загрузка решений доступна для зарегистрировавшихся пользователей
6
Известно, что комплексные числа z и имеют одинаковый модуль. В каких пределах может изменяться значение этого модуля?
Загрузка решений доступна для зарегистрировавшихся пользователей
7
Загрузка решений доступна для зарегистрировавшихся пользователей
8
Множество точек комплексной плоскости определяется условием В каких пределах изменяется
Загрузка решений доступна для зарегистрировавшихся пользователей
9
Загрузка решений доступна для зарегистрировавшихся пользователей
10
Найдите такое мнимое число z, что сумма минимальна.
Загрузка решений доступна для зарегистрировавшихся пользователей
11
Из всех чисел z, удовлетворяющих условию найдите такие, что
принимает наименьшее значение.
Загрузка решений доступна для зарегистрировавшихся пользователей
12
Загрузка решений доступна для зарегистрировавшихся пользователей
Завершить тестирование, свериться с ответами, увидеть решения.
- Авторы
- Файлы
- Ключевые слова
- Литература
Грудинина О.С.
1
1 МБОУ ШР «СОШ №2»
перспективная модель
контрольно-измерительные материалы
единый государственный экзамен
профильный уровень
комплексные числа
1. «Министерство сельского хозяйства Российской Федерации Департамент научно-технологической политики и образования Федеральное государственное бюджетное образовательное учреждение высшего образования «Волгоградский государственный аграрный университет» Комплексные числа 2020.
2. ФГБНУ « Федеральный институт педагогических измерений» [Электронный ресурс]. – Режим доступа: https://fipi.ru/ (дата обращения 22.03.2021).
Введение
В декабре 2020 года Федеральный институт педагогических измерений [2] опубликовал для общественного обсуждения перспективные модели измерительных материалов ЕГЭ на 2022 год, в том числе, по математике профильного уровня. Напомню, что в 2021 году ЕГЭ базового уровня отменен.
Особое волнение среди педагогов и старшеклассников вызывает тот факт, что в предложенной демоверсии три первых базовых задания, позволяющие выпускнику преодолеть минимальный порог на экзамене, заменили более сложными заданиями, в том числе, появилось задание по теме «Комплексные числа».
Мне стало интересно, и я решила сравнить демоверсии измерительных материалов 2021 года и перспективной, которая возможно будет внедрена в 2022 году, когда я буду выпускницей.
Мой вклад в решение проблемы: сравнение демоверсий измерительных материалов, разбор задания по теме «Комплексные числа».
Обзор литературы
Методическое пособие «Министерство сельского хозяйства Российской Федерации Департамент научно- технологической политики и образования Федеральное государственное бюджетное образовательное учреждение высшего образования «Волгоградский государственный аграрный университет». Комплексные числа. Практикум. 2020 год [1].
Цель
Сравнение демоверсий измерительных материалов 2021 года и перспективной модели на 2022 год по математике профильного уровня [2]. Разбор задания по теме «Комплексные числа» из демоверсии перспективной модели измерительных материалов ЕГЭ профильного уровня.
Методы исследования
1.Поисковый.
2. Анализ, синтез (отбор необходимой информации, обобщение)
3.Практический
Результаты исследования
Сейчас измерительные материалы ЕГЭ профильного уровня включают 19 заданий:
-часть 1 содержит 8 заданий базового уровня (задания 1–8);
-часть 2 содержит 9 заданий повышенного уровня (задания 9–17) и 2 задания высокого уровня сложности (задания 18, 19).
Что предлагается изменить?!
Убрать три базовых задания:
1 задание. – Простейшие текстовые задачи;
2 задание. – Чтение графиков и диаграмм;
3 задание. –Квадратная решетка.
Наряду с выше обозначенными изменениями происходит замена нумерации заданий:
№1. Простейшие уравнения;
№2. Начало теории вероятности;
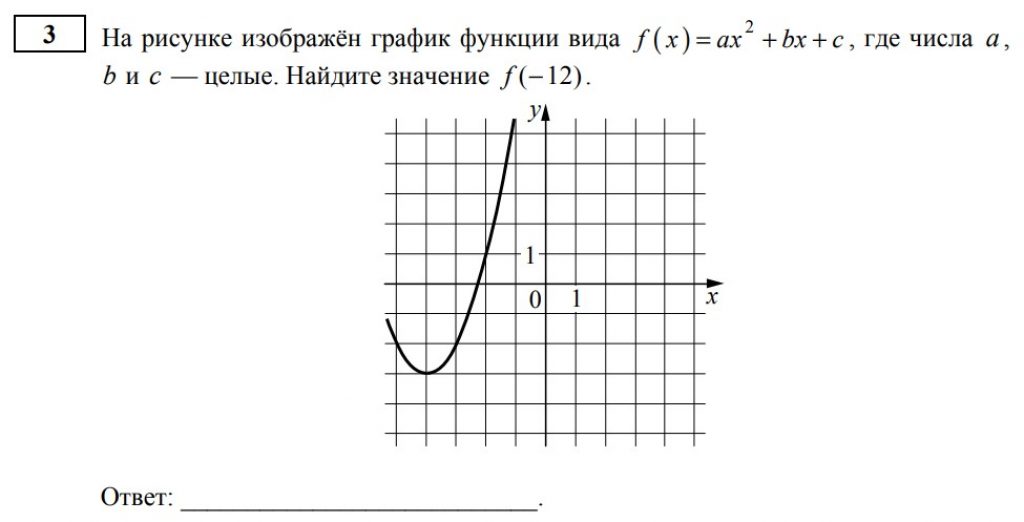
№ 3. Функции, графики функций (новое);
Приведу пример задания №3 из демоверсии измерительных материалов перспективной модели ЕГЭ профильного уровня:
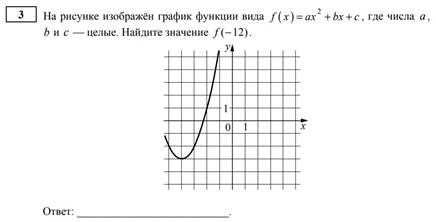
№4. Планиметрия;
№5. Вычисления и преобразования;
№6. Стереометрия;
№7. Производная и первообразная;
№8. Задачи с прикладным содержанием;
№9. Текстовые задачи;
№10. Вероятности повышенного уровня (новое);
№11. Комплексные числа (новое);
№12. Наибольшее и наименьшее значение функций;
№13. Уравнения;
№14. Стереометрическая задача;
№15. Неравенства;
№16. Финансовая математика;
№17. Планиметрия;
№18. Задача с параметром;
№19. Числа и их свойства;
Рассмотрим задание №11 по теме «Комплексные числа».
Для начала приведу основные теоретические сведения по теме «Комплексные числа».
Определение. Комплексным числом z называется упорядоченная пара чисел (а,b), над множеством которых по определенным правилам можно производить следующие операции: сложение , умножение, деление, возведение в степень результаты которых также являются комплексными числами [1, с.2].
Определение. Комплексное число — это упорядоченная пара вещественных, или символ z = а + ib, где i — мнимая единица: i2 = −1; а называется действительной, а b — мнимой частью z [1, с.2].
Понятие комплексного числа имеет геометрическое истолкование. Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Комплексные числа включают в себя все множества чисел, которые изучались ранее. Так натуральные, целые, рациональные, иррациональные, действительные числа являются, вообще говоря, частными случаями комплексных чисел.
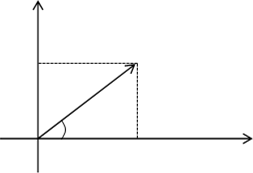
Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, (комплексной плоскости z) координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная — мнимой осью.
Таким образом, на оси ОХ располагаются действительные числа a, а на оси ОY – чисто мнимые-b [1, с.2].
Модулемкомплексного числа называется длина вектора, соответствующего этому числу:
Задание №11:
Про комплексное число z известно, что |z-4-7i|=|z+4-i|. Найдите наименьшее значение |z| [2].
z = а + ib, в свою очередь 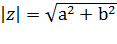
| а + ib-4-7i|=| а + ib+4-i|
Сгруппируем:
|(a-4) +i(b-7) |=|(a+4) +i(b-1) |
Видим, что внутри модуля комплексное число вида z = а + ib. Применим свойство 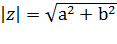
Применим формулы квадратов суммы и разности, упростим:
-16а-12b=-48
4а+3b=12
Выразим b: b=4-
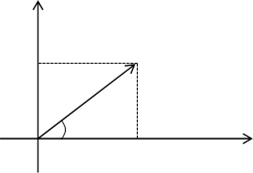
Модулем является расстояниеот начала отсчёта до точки координатной прямой, соответствующейэтомучислу. Кратчайшее (наименьшее) расстояние – перпендикуляр.

Если b=0, то а = 3
Если а=0, то b=4
Рассмотрим прямоугольный треугольник с катетами 3 и 4, гипотенузой 5.
С одной стороны, площадь треугольника равна: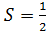
С другой стороны: 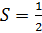
Отсюда следует: 6=0,5·h·5, h=2,4. Высота – перпендикуляр, наименьшее расстояние, которое соответствует |z|.
Ответ: 2,4
Заключение
Я сравнила демоверсии измерительных материалов 2021 года и перспективной модели на 2022 год по математике профильного уровня [2]. Разобрала задание по теме «Комплексные числа» из демоверсии перспективной модели измерительных материалов ЕГЭ профильного уровня. На мой взгляд, уже в следующем учебном году задания по теме «Комплексные числа» необходимо включать в рабочие программы уроков, курсов внеурочной деятельности. И тогда у выпускников не возникнет сложностей с решением этого задания на экзамене.
Библиографическая ссылка
Грудинина О.С. ПЕРСПЕКТИВНАЯ МОДЕЛЬ ЕГЭ ПО МАТЕМАТИКЕ. КОМПЛЕКСНЫЕ ЧИСЛА // Старт в науке. – 2021. – № 2.
;
URL: https://science-start.ru/ru/article/view?id=2027 (дата обращения: 11.03.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Недавно ФИПИ опубликовал новые проекты КИМов ЕГЭ почти по всем предметам. После общественного обсуждения по этим вариантам, возможно, будут сдавать экзамен нынешние 10-классники.
Следует отметить, что, возможно, эта “перспективная модель” ещё очень сильно поменяется, прежде чем стать официальной демоверсией [так и случилось, см. ниже]. Так было, например, при внесении существенных изменений в формат ОГЭ: проект был очень страшным, но в итоговую демоверсию внесли не такие “жесткие” изменения.
Кстати, что изменения ОГЭ, что изменения ЕГЭ свалились на головы именно школьникам 2011 года поступления. Это связано, как я думаю, с введением новых федеральных стандартов – ФГОС. Так что изменения в ЕГЭ – 2022 были для меня вполне ожидаемы.
📌Изменения в ЕГЭ по математике. Новая задача: найдите наименьшее значение модуля комплексного числа.
Основные изменения
В тестовой части ЕГЭ ликвидировали самые простые номера 1-3. Это простейшая текстовая задача, умение находить наименьшую/наибольшую точку на графике и простейшая геометрия как правило на знание формул площадей треугольника, прямоугольника и трапеции. А ещё почти все “старые” номера поменяли местами. Теперь вариант выглядит так:
Часть с кратким ответом:
Новый №1 — это №5 из нынешнего ЕГЭ, простое уравнение: показательное, логарифмическое или иррациональное.
Новый №2 — это “старый” №4, теория вероятностей.
Новый №3 — новое задание, на умение работать с графиком функции
Новый №4 — это “старый” №6, простая задачка по планиметрии.
Новый №5 — это “старый” №9, пример для вычисления с тригонометрией, степенями или логарифмами.
Новый №6 — это “старый” №8, стереометрия.
Новый №7 — без изменений, на производную функции.
Новый №8 — это “старый” №10: вычисления по заранее известной формуле.
Новый №9 — это “старый” №11: сложная текстовая задача.
Новый №10 — опять теория вероятностей, но немного труднее чем №2.
Новый №11 — новое задание, на комплексные числа. Её условие приведём ниже.
Новый №12 — без изменений, нахождение экстремумов функции через производную.
Часть с развернутым ответом:
В 13-ой задаче убрали пункт б) – отбор корней уравнения, принадлежащих промежутку. Оценивается задача по-прежнему в 2 балла.
Задача №15 теперь состоит из трёх пунктов: нужно решить неравенство, уравнение и ещё их систему. Оценивается она теперь в 3 балла, раньше было 2 балла.
В остальном изменений почти нет. Разве что поменяли местами 16 и 17 задачи.
Комплексные числа
Одно из новшеств в “новом” ЕГЭ по математике – задача на комплексные числа. Вот так она выглядит:
Про комплексное число z известно, что |z-4-7ⅈ|=|z+4-ⅈ|. Найдите наименьшее значение |z|.
Решение задачи строится на использовании формулы для модуля комплексного числа :
. Следует представить z в виде
, воспользоваться формулой для модуля, упростить выражение, а затем изобразить решение уравнения на плоскости (a;b) – это будет прямая. Модуль числа z при этом будет иметь смысл рассояния до точки на прямой до начала координат. Наименьшим это расстояние будет в случае перпендикулярности отрезка от точки на прямой до начала координат к этой самой прямой.
Полное решение посмотреть можно тут:
📌Изменения в ЕГЭ по математике. Новая задача: найдите наименьшее значение модуля комплексного числа.
Не стоит бояться необычных формулировок, требующих геометрических построений: рецепт здесь один — тренировки. Чем больше задач вы решите — тем легче вы сможете применять геометрические трюки в необычных ситуациях.
ВНИМАНИЕ! Выше рассмотрена ПЕРСПЕКТИВНАЯ МОДЕЛЬ, от которой все же решили отказаться. Опубликована официальная демоверсия, и она имеет мало общего с перспективной моделью, о которой мы говорили выше.
ЕГЭ-2022 по математике. Профильный уровень. Вероятность и комплексные числа
ФИПИ опубликовал документ с длинным названием Перспективная модель измерительных материалов для государственной итоговой аттестации по программам среднего общего образования по МАТЕМАТИКЕ. Демонстрационный вариант
Matematika_ma-11-ege-pm2022-demo.pdf (userapi.com)
По знакомому оформлению и «ege-pm2022» в адресе сайта узнаётся перспективная демоверсия ЕГЭ для 2022 года. Давайте посмотрим, что ждёт выпускников в перспективе. Сегодня остановлюсь на задачах по вероятности.
Первая задача до боли знакома. не обсуждаем. Вторая задача может поставить в тупик. Здесь надо разобраться, что означает событие А — «мотор проработал более года». Это значит, что произошло одно из двух событий:
B — «мотор проработал более года, но не более двух лет» и
С — «мотор проработал более двух лет».
По условию задачи P (А) = 0,8, P (C) = 0,6.
Событие А произойдёт, если наступит или событие В, или событие С, то есть
A = B + C, P (A) = P (B + C).
А так как события В и С несовместные (не могут произойти одновременно), то
P (B + C) = P (B) + P (C). Окончательно имеем:
0,8 = P (B) + 0,6,
P (B) = 0,2.
Ответ. 0,2.

Обратим внимание на появление в варианте ещё одной задачи на вероятность, её номер 10. Вот два примера.
Разбираем решение первой задачи. После трёх бросков сумма 6 очков могла получиться лишь при таких наборах очков 1 + 1 + 4; 1 + 2 + 3; 2 + 2 + 2 (без учета порядка следования очков в сумме). За счёт перестановок слагаемых получаем:
114, 141, 411 — 3 исхода;
123, 132, 213, 231, 312, 321 — 6 исходов;
222 — 1 исход.
Всех равновозможных исходов для получения в сумме 6 оков — 10, только 6 из них благоприятствуют событию «хотя бы раз выпало 3 очка». Вероятность этого события
6 : 10 = 0,6.
Ответ. 0,6. (В таблице ответ 0,5 — опечатка).
Вторая задача, как мне показалось, к теме «вероятность» притянута за уши, так как ответ к ней получается при решении задачи на проценты. Сформулируем её, заменив «выбрали взрослого мужчину» на «выбрали мужчину», так как взрослые делятся на мужчин и женщин, невзрослых мужчин по смыслу задачи нет. Слово «взрослого» лишнее.
В городе 48 % взрослого населения мужчины. Пенсионеры составляют 12,6 % взрослого населения, причём доля пенсионеров среди женщин составляет 15 %. Какова доля пенсионеров среди мужчин?
Если доля пенсионеров окажется равной m/n, то вероятность случайного выбора пенсионера из мужчин составляет m/n.
Пусть в городе было x взрослых — мужчин и женщин. Тогда в нём 0,48x мужчин, 0,52x женщин, 0,126x пенсионеров,
0,15 * 0,52x = 0,078x женщин-пенсионеров и
0,126x – 0,078x = 0,048x — мужчин-пенсионеров.
Доля мужчин-пенсионеров среди мужчин составляет
0,048x : 0,48x = 0,1.
Ответ. 0,1.
Рассмотрим теперь задачу по комплексным числам, которых до сих пор никогда не было в ЕГЭ, но они всегда присутствовали в выпускном экзамене по программе углубленного изучения математики. На мой взгляд, это ошибка составителей варианта. Нельзя устраивать дискриминацию учащихся, не изучавших математику углублённо. Рассмотрим задачу.
Ученику обычного класса придётся прочитать про комплексные числа, про мнимую единицу i, квадрат которой равен –1. Про то, что комплексным числом называют выражение z, записанное в виде z = a + bi, где a и b — действительные числа, а i — мнимая единица. Комплексное число задаётся парой действительных чисел (a; b), его удобно изображать в системе координат точкой (a; b). Модулем комплексного числа называют расстояние от начала отсчёта системы координат до точки, изображающей число z. Модуль комплексного числа z = a + bi вычисляют по формуле: |z| = 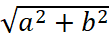
Решаем задачу 11.
Пусть число z = a + bi, тогда число 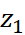
| 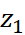
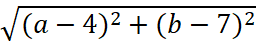
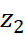
| 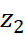
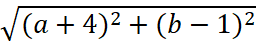
Равенство | 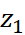
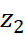

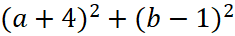
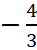
Найдём значение a, при котором величина |z| = 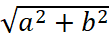
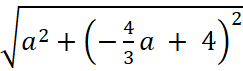
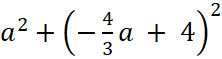
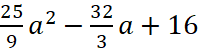
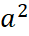
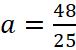
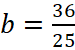
|z| = 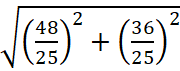
Ответ. 2,4.
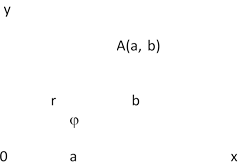
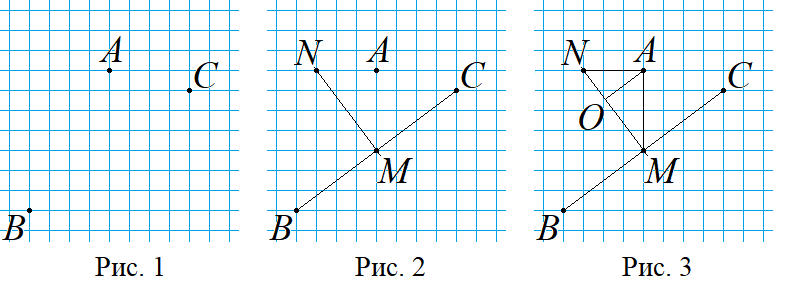
Решим задачу, изображая комплексное число точкой координатной плоскости. Этот способ вполне годится для решения задачи на ЕГЭ, так как там подробное решение не требуется, достаточно привести правильный ответ. Изобразим на клетчатой бумаге точками числа z = a + bi, 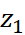
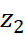
Знать, где находятся оси координат не нужно, главное взаимное расположение точек A (a; b), B (a – 4; b – 7) и С (a + 4; b – 1), соответствующих числам z, 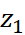
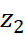
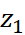
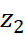
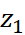
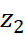
Точка O лежит на прямой MN, а нам нужно, чтобы расстояние AO было наименьшим, это возможно лишь тогда, когда является перпендикуляром к AO. Строим AO и находим его длину как высоту прямоугольного треугольника AMN с гипотенузой MN (рис 3).
Вычислив площадь треугольника AMN двумя способами, выразим длину высоты, проведённой к гипотенузе MN. Получим 2,4.
Шевкин А.В., avshevkin@mail.ru