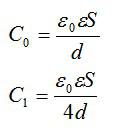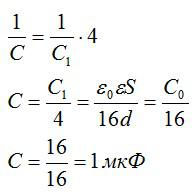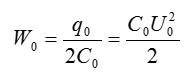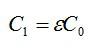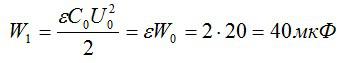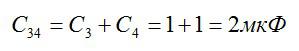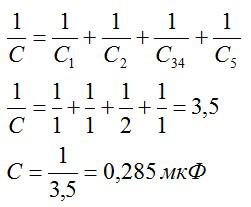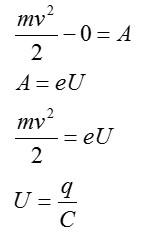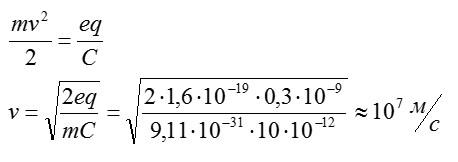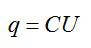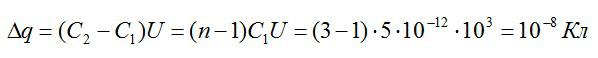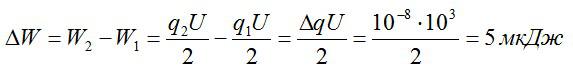Задачи на конденсаторы егэ физика - Помощь в подготовке к экзаменам и поступлению

Каталог заданий.
Электрическая ёмкость

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Конденсатор электроемкостью 0,5 Ф был заряжен до напряжения 4 В. Затем к нему подключили параллельно незаряженный конденсатор электроемкостью 0,5 Ф. Какова энергия системы из двух конденсаторов после их соединения? (Ответ дать в джоулях.)

К источнику тока с ЭДС 2 В подключён конденсатор ёмкостью 1 мкФ. Какую работу совершил источник тока при зарядке конденсатора? (Ответ дайте в микроджоулях.)

К источнику тока с ЭДС 2 В подключен конденсатор емкостью 1 мкФ. Какое тепло выделится в цепи в процессе зарядки конденсатора? (Ответ дайте в микроджоулях.) Эффектами излучения пренебречь.

К идеальному источнику тока с ЭДС 3 В подключили конденсатор ёмкостью 1 мкФ один раз через резистор а второй раз  — через резистор Во сколько раз во втором случае тепло, выделившееся на резисторе, больше по сравнению с первым? Излучением пренебречь.

Плоский воздушный конденсатор изготовлен из квадратных пластин со стороной a, зазор между которым равен d. Другой плоский конденсатор изготовлен из двух одинаковых квадратных пластин со стороной a/2, зазор между которым также равен d, и заполнен непроводящим веществом. Чему равна диэлектрическая проницаемость этого вещества, если электрические ёмкости данных конденсаторов одинаковы?

Пройти тестирование по этим заданиям

Источник

Тема 12.

Электрическое поле. Законы постоянного тока

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

электрическое поле. законы постоянного тока

12.01Электростатика. Закон Кулона

12.02Электростатика. Напряженность и потенциал электрического поля

12.03Конденсаторы

12.04Электрический ток. Закон Ома

12.05Работа тока. Закон Джоуля – Ленца

Решаем задачи

Конденсатор, имеющий заряд 10 нКл, площадь пластин 10 2
см и расстояние между пластинами 17,7 мм, погружают в керосин при
вертикальном положении пластин на 2/3 его объема. Чему равно напряжение (в кВ) на таком конденсаторе? Диэлектрическая
проницаемость керосина 2.

Показать ответ и решение

Рассмотри два параллельно соединенных конденсатора: без диэлектрика(), с диэлектриком ().

S1
C1 = 𝜀0d

C2 =𝜀𝜀0S2,
d

где – площадь конденсатора, – расстояние между обкладками, – диэлектрическая проничаемость диэлектрика, –
диэлектрическая постоянная.

Воздушный плоский конденсатор емкостью 5 мкФ заполняют жидким диэлектриком с диэлектрической проницаемостью 6.
Конденсатор какой емкости (в мкФ) надо соединить последовательно с данным, чтобы такая батарея вновь имела емкость 5
мкФ?

Показать ответ и решение

Емкость конденсатора:

S
C =𝜀𝜀0d-,

При последовательном соединении общее сопротивление находится по формуле::

-1-= -1-+ 1--
C0 C2 C3

-C0C2-- -5 мкФ-⋅30 м-кФ
C3 = C2 − C0 = 30 мкФ − 5 мкФ = 6 мкФ

Если заряженный до напряжения 300 В конденсатор емкостью C1 = 50 мкФ соединить параллельно с незаряженным
конденсатором емкостью мкФ, то на втором конденсаторе появится заряд равный? Ответ дайте в мКл

Показать ответ и решение

Определим первоначальный заряд конденсатора:

При параллельном соединении напряжение на конденсаторах одинаково. При соединении конденсаторов выполняется закон
сохранения заряда:

C U
q0 = q1 +q2 C1U0 = (C1+ C2)U ⇒ U = C-1+-0C-= 100 В
1 2

Тогда заряд на

Показать ответ и решение

После замыкания ключа вся энергия конденсатора выделится на резисторе, то есть

qU 20⋅10− 6
Q = WC = 2--= ---2---= 10 мкД ж

Конденсатор ёмкостью 50 мкФ подключен к источнику постоянного напряжения с ЭДС 100 В. Найдите энергию конденсатора в
установившемся режиме. Ответ дайте в мДж

Показать ответ и решение

Энергия заряженного конденсатора:

CU2
W = -2--,

где – ёмкость конденсатора, – напряжение на конденсаторе.
Так как конденсатор подключен с источнику, то напряжение на конденсаторе равно ЭДС, откуда

2
W = 50 м-кФ⋅10000 В-= 250 мД ж
2

Напряжение на конденсаторе равно 10 В, а его энергия равна 20 мкДж. Найдите ёмкость конденсатора. Ответ дайте в
мкФ.

Показать ответ и решение

Энергия заряженного конденсатора:

CU2
W = -2--,

где – ёмкость конденсатора, – напряжение на конденсаторе.
Выразим ёмкость

На конденсаторе ёмкостью 1 мкФ накоплен заряд 10 мкКл. Найдите напряжение на конденсаторе. Ответ дайте в
В.

Показать ответ и решение

Напряжение на конденсаторе находится по формуле:

q
U = C,

где – заряд конденсатора, – его ёмкость.
Тогда

U = 10-мкКл = 10 В
1 мкФ

К идеальному источнику тока с ЭДС 3 В подключили конденсатор ёмкостью 1 мкФ один раз через резистор 7
10 Ом, а второй раз –
через резистор 2⋅107 Ом. Во сколько раз во втором случае тепло, выделившееся на резисторе, больше по сравнению с первым?
Излучением пренебречь.

Показать ответ и решение

Энергия, запасенная в конденсаторе находится по формуле:

CU2 Cξ2
W = --2- = -2--

Вся энергия, запасенная в конденсаторе выделяется через резисторы в виде тепла. Энергия не зависит от сопротивления
резистора, поэтому при замене резисторов, кол-во выделяемого тепла не изменяется.

ЭДС источника в цепи, изображенной на схеме, равна 12 В, сопротивление источника 1 Ом, сопротивление резистора 2 Ом, ёмкость
конденсатора 100 мкФ. Найдите силу тока в цепи, в установившемся состоянии. Ответ дайте в Амперах.

Показать ответ и решение

В установившемся состоянии ток через конденсатор не течет, следовательно, сила тока через резистор по закону Ома для полной
цепи равна:

ξ 12 В
I = R-+-r = 2-Ом-+-1 Ом-= 4 А

ЭДС источника в цепи, изображенной на схеме, равна 12 В, сопротивление источника 1 Ом, сопротивление резистора 2 Ом,
ёмкость конденсатора 100 мкФ. Найдите напряжение на конденсаторе, при силе тока, равной 2 А. Ответ дайте в
вольтах.

Показать ответ и решение

Из закона сохранения заряда

При силе тока I =2 А, напряжение на источнике и резисторе равны соответственно и .

Откуда напряжение на конденсаторе

ЭДС источника в цепи, изображенной на схеме, равна 12 В, сопротивление источника 1 Ом, сопротивление резистора
2 Ом, ёмкость конденсатора 100 мкФ. Найдите заряд на конденсаторе, при силе тока, равной 2 А. Ответ дайте в
мкКл.

Показать ответ и решение

Из закона сохранения заряда

При силе тока I =2 А, напряжение на источнике и резисторе равн соответственно и .

Откуда напряжение на конденсаторе

А заряд

ЭДС источника в цепи, изображенной на схеме, равна 12 В, сопротивление источника 1 Ом, сопротивление резистора 2
Ом, ёмкость конденсатора 100 мкФ. Найдите заряд на конденсаторе, в установившемся состоянии. Ответ дайте в
мКл.

Показать ответ и решение

В установившемся состоянии конденсатор будет заряжен до напряжения, равного ЭДС, это напряжение равно 12 В. Заряд на
конденсаторе же находится по формуле:

ЭДС источника в цепи, изображенной на схеме, равна 12 В, сопротивление источника 1 Ом, сопротивление резистора 2 Ом, ёмкость
конденсатора 100 мкФ. Найдите напряжение на конденсаторе, в установившемся состоянии.

Показать ответ и решение

В установившемся состоянии конденсатор будет заряжен до напряжения, равного ЭДС, это напряжение равно 12
В

Показать ответ и решение

В установившемся состоянии ток через конденсатор не течет, следовательно, сила тока равна 0

Конденсатор подключен к зажимам батареи. Когда параллельно конденсатору подключили сопротивление 15 Ом, заряд на
конденсаторе уменьшился в 1,2 раза. Определите внутреннее сопротивление батареи. Ответ дайте в Омах

Показать ответ и решение

Связь напряжения и заряда для конденсатора:

q = UC

– емкость, – напряжение. Следовательно,
В первом случае напряжение на конденсаторе равно ЭДС , во втором случае равно напряжению на резисторе

U1 = ξ

ξR
U2 = R-+r-

– ЭДС, – внешнее сопротивление, – внутреннее сопротивление.

ξ = 1,2ξR
R + r

Во сколько раз увеличится электроёмкость плоского воздушного конденсатора, если заряд на его обкладках увеличить в 2 раза, а
расстояние между пластинами уменьшить в 2 раза?

Показать ответ и решение

Ёмкость конденсатора:

S
C =𝜀𝜀0d-,

где – площадь конденсатора, – расстояние между обкладками, – диэлектрическая проничаемость диэлектрика, –
диэлектрическая постоянная. Ёмкость увеличится в 2 раза (Емкость не зависит от заряда).

Во сколько раз нужно уменьшить заряд на обкладках плоского конденсатора, чтобы после увеличения зазора между обкладками в 3
раза, напряженность электрического поля в зазоре уменьшилась в итоге вдвое?

Показать ответ и решение

Емкость конденсатора:

S
C =𝜀𝜀0d-,

C2 = 𝜀𝜀0-S-
3⋅d

U = Ed

– напряженность, – расстояние между обкладками.

U2 = 1 E3d= 1,5Ed
2

Заряд равен:

q = CU

– емкость, – напряжение. Таким образом, заряд необходимо уменьшить в 2 раза.

Плоский воздушный конденсатор имеет емкость C. Во сколько раз увеличится его емкость, если расстояние между его пластинами
уменьшить в 3 раза?

Показать ответ и решение

Ёмкость конденсатора:

S
C =𝜀𝜀0d-,

где – площадь конденсатора, – расстояние между обкладками, – диэлектрическая проничаемость диэлектрика, –
диэлектрическая постоянная. Если расстояние между пластинами уменьшить в 3 раза, то емкость конденсатора увеличится в 3
раза.

При разрядке батареи, состоящей из 20 параллельно включенных конденсаторов одинаковыми емкостями 4 мкФ, выделилось
количество теплоты 10 Дж. До какой разности потенциалов были заряжены конденсаторы?

Показать ответ и решение

При параллельном соединении конденсаторов емкости суммируются.

CU2-
W = 2 ,

где – емкость, – напряжение, тогда напряжение равно

∘ ---- ∘ ----------
U = 2W- = 2-⋅10 Дж−6 Ф =500В
C1 80⋅10

Конденсатору емкостью 2 мкФ сообщен заряд 0,01 Кл. Обкладки конденсатора соединили проводником. Найдите количество
теплоты, выделившееся в проводнике при разрядке конденсатора.

Показать ответ и решение

Энергия конденсатора:

q2
W = 2C,

где – заряд конденсатора, – емкость конденсатора. При соединениии конденсатора проводником, вся энергия выдлеится в
виде теплоты:

2
Q = q--= 25 Дж
2C

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

ЭДС источника в цепи, изображенной на схеме, равна 12 В, сопротивление источника 1 Ом, сопротивление резистора 2 Ом, ёмкость конденсатора 100 мкФ. Найдите силу тока в цепи, в установившемся состоянии.

В установившемся состоянии ток через конденсатор не течет, следовательно, сила тока равна 0

Ответ: 0

Во сколько раз увеличится электроемкость плоского воздушного конденсатора, если заряд на его обкладках увеличить в 2 раза, а расстояние между пластинами уменьшить в 2 раза?

Емкость конденсатора: [C=varepsilon varepsilon_0 dfrac{2S}{d},] где (S) — площадь конденсатора, (d) — расстояние между обкладками, (varepsilon) — диэлектрическая проничаемость диэлектрика, (varepsilon_0) — диэлектрическая постоянная. Емкость увеличится в 2 раза (Емкость не зависит от заряда).

Ответ: 2

Во сколько раз уменьшится емкость плоского воздушного конденсатора, если площадь обкладок уменьшить в 2 раза, а расстояние между ними увеличить в 2 раза?

Емкость конденсатора: [C=varepsilon varepsilon_0 dfrac{S}{d},] где (S) — площадь конденсатора, (d) — расстояние между обкладками, (varepsilon) — диэлектрическая проничаемость воздуха, (varepsilon_0) — диэлектрическая постоянная. [C_2=varepsilon varepsilon_0 dfrac{S}{2cdot2d}] Емкость уменьшится в 4 раза.

Ответ: 4

Емкость конденсатора: [C=varepsilon varepsilon_0 dfrac{S}{d},] где (S) — площадь конденсатора, (d) — расстояние между обкладками, (varepsilon) — диэлектрическая проничаемость диэлектрика, (varepsilon_0) — диэлектрическая постоянная. Если расстояние между пластинами уменьшить в 3 раза, то емкость конденсатора увеличится в 3 раза.

Ответ: 3

При разрядке батареи, состоящей из 20 параллельно включенных конденсаторов одинаковыми емкостями 4 мкФ, выделилось количество теплоты 10 Дж. До какой разности потенциалов были заряжены конденсаторы?

При параллельном соединении конденсаторов емкости суммируются. [C_1=20C_0=80 text{ мкФ}] [W=dfrac{CU^2}{2},] где (C) — емкость, (U) — напряжение, тогда напряжение равно [U=sqrt{dfrac{2W}{C_1}}=sqrt{dfrac{2cdot10text{ Дж}}{80cdot10^{-6}}text{ Ф}}=500 text{В}]

Ответ: 500

Конденсатору емкостью 2 мкФ сообщен заряд 0,01 Кл. Обкладки конденсатора соединили проводником. Найдите количество теплоты, выделившееся в проводнике при разрядке конденсатора.

Энергия конденсатора: [W=dfrac{q^2}{2C},] где (q) — заряд конденсатора, (C) — емкость конденсатора. При соединениии конденсатора проводником, вся энергия выдлеится в виде теплоты: [Q=dfrac{q^2}{2C}=25 text{ Дж}]

Ответ: 25

Конденсатор, имеющий заряд 10 нКл, площадь пластин 10 см(^2) и расстояние между пластинами 17,7 мм, погружают в керосин при вертикальном положении пластин на 2/3 его объема. Чему равно напряжение (в кВ) на таком конденсаторе? Диэлектрическая проницаемость керосина 2.

Рассмотри два параллельно соединенных конденсатора: без диэлектрика((S_1=1/3S_0)), с диэлектриком ((S_2=2/3S_0)). [C_1=varepsilon_0 dfrac{S_1}{d}] [C_2=varepsilon varepsilon_0 frac{S_2}{d},] где (S) — площадь конденсатора, (d) — расстояние между обкладками, (varepsilon) —- диэлектрическая проничаемость диэлектрика, (varepsilon_0) — диэлектрическая постоянная. [C_0=C_1+C_2] [U=dfrac{q}{C_0}=dfrac{q}{C_1+C_2}=dfrac{qd}{varepsilon_0(S_1+S_2varepsilon)}=12 text{ кВ}]

Ответ: 12

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Конденсатор – деталька, без которой не обойдется работа ни одного электронного прибора. Но прежде чем разбираться с основами электроники, нужно научиться решать физические задачи на конденсатор и электроемкость. Именно этим мы и займемся в сегодняшней статье, посвященной подробному разбору решений задач.

Подписывайтесь на наш телеграм: теперь помимо полезных и интересных материалов там можно найти скидки и акции на любые работы.

Задачи на конденсаторы и электроемкость с решением

Если вы не знаете, как решать задачи с конденсаторами, сначала посмотрите теорию и вспомните про памятку по решению задач по физике и полезные формулы.

Задача №1 на электроемкость батареи конденсаторов

Условие

Плоский конденсатор емкостью 16 мкФ разрезают на 4 равные части вдоль плоскостей, перпендикулярных обкладкам. Полученные конденсаторы соединяют последовательно. Чему равна емкость батaреи конденсаторов?

Решение

Из условия следует, что площадь получившихся конденсаторов в 4 раза меньше, чем у исходного. Зная это, можно найти емкость каждого полученного конденсатора:

Соединяя 4 таких конденсатора последовательно, получаем:

Ответ: 1 мкФ.

Задача №2 на энергию плоского конденсатора

Условие

Плоский конденсатор заполнили диэлектриком с диэлектрической проницаемостью, равной 2. Энергия конденсатора без диэлектрика равна 20 мкДж. Чему равна энергия конденсатора после заполнения диэлектриком? Считать, что источник питания отключен от конденсатора.

Решение

Энергия конденсатора до заполнения диэлектриком равна:

После заполнения емкость конденсатора изменится:

Энергия конденсатора после заполнения:

Ответ: 40 мкФ.

Задача №3 на последовательное и параллельное соединение конденсаторов

Условие

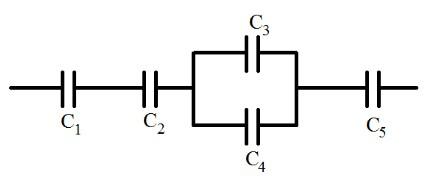
На рисунке изображена батарея конденсаторов. Каждый конденсатор имеет емкость 1 мкФ. Найдите емкость батареи.

Решение

Как видим, часть конденсаторов соединена параллельно, а часть последовательно. Это типичный пример смешанного соединения конденсаторов. Алгоритм решения задач при смешанном соединении конденсаторов сводится к тому, чтобы упростить схему и свести все только к параллельному или последовательному соединению.

Конденсаторы 3 и 4 соединены параллельно. Складывая их емкость, получаем в итоге последовательное соединение четырех конденсаторов: 1, 2, 5 и 3-4. Для параллельного соединения:

Для последовательного соединения:

Ответ: 0,285 мкФ.

Задача №4 на пролет частицы в конденсаторе

Заряд конденсатора равен 0,3 нКл, а емкость – 10 пФ. Какую скорость приобретет электрон, пролетая в конденсаторе от одной пластины к другой. Начальная скорость электрона равна нулю.

Решение

По закону сохранения энергии, разность кинетических энергий электрона в начале и в конце пути будет равна работе поля по его перемещению. По условию, начальная кинетическая энергия электрона равна 0. Запишем:

С учетом этого, получим:

Ответ: 10^7 м/с.

Задача №5 на вычисление энергии электрического поля конденсатора

Условие

Конденсатор подключен к источнику постоянного напряжения U=1 кВ. Емкость конденсатора равна 5 пФ. Как изменяться заряд на обкладках конденсатора и его энергия, если расстояние между обкладками уменьшить в три раза.

Решение

Заряд конденсатора равен:

Изменение заряда будет равно:

Изменение энергии:

Ответ: 5 мкДж.

Вопросы на тему «Конденсатор и электроемкость»

Вопрос 1. Что такое конденсатор?

Ответ. Конденсатор – устройство, имеющее два полюса и предназначенное для накопления электрического заряда.

Простейший тип конденсатора – плоский воздушный конденсатор. Он состоит из двух пластин (обкладок), имеющих разные заряды и разделенных воздухом. В зависимости от диэлектрика, разделяющего обкладки, разделяют:

воздушные конденсаторы;
бумажные конденсаторы;
слюдяные и другие конденсаторы.

Основная роль конденсатора в электронных приборах – накапливать заряд, а потом передавать его дальше в цепь.

Вопрос 2. Что такое электроемкость?

Ответ. Электроемкость – скалярная физическая величина, характеризующая способность накапливать электрический заряд. В системе СИ измеряется в Фарадах.

Вопрос 3. Какие есть способы соединения конденсаторов?

Ответ. Конденсаторы можно соединить последовательно и параллельно.

При параллельном соединении емкость цепи равна сумме емкостей отдельных конденсаторов.

При последовательном соединении величина, обратная общей емкости, равна сумме обратных емкостей каждого конденсатора.

Вопрос 4. Что такое колебательный контур?

Ответ. Это простейшая электрическая цепь, состоящая из конденсатора, катушки индуктивности и источника тока. В колебательном контуре происходят свободные электромагнитные колебания: энергия конденсатора переходит в энергию катушки, и наоборот.

Вопрос 5. Что происходит при отключении источника питания, к которому подключен конденсатор в цепи?

Ответ. В этот момент конденсатор начинает разряжаться, отдавая накопленный заряд другим элементам цепи.

Мы не понасылшке знаем, что от сложных задач на конденсаторы мозги буквально плавятся. Если ваш мозг устал от постоянного решения задач по физике и других заданий, обращайтесь в профессиональный образовательный сервис за консультацией и поддержкой в любое время. У нас есть решение для ваших проблем с учебой!

Источник

В задачах с присутствием конденсаторов очень часто нужно уметь находить емкость последовательного и параллельного соединения емкостей. С параллельным соединением емкостей все просто: при параллельном соединении емкости складываются. Почему это так? Дело в том, что при параллельном соединении на всех конденсаторах одинаковое напряжение, а их заряды пропорциональны емкостям:

и т.д.

Общий заряд на конденсаторах:

Тогда емкость системы конденсаторов: .

С последовательным соединением все сложнее. Кстати, когда готовила эту статью, наткнулась на такой вот перл, который не могла не процитировать:

Заряды при последовательном соединении одинаковы на всех конденсаторах:

и т.д.

Тогда напряжение между крайними точками равно:

$U=U_1+ U_2+... +U_n=q(1/{C_1}+1/{C_2}+...+1/{C_n})$

Емкость всей системы: $C=q/U=1/(1/{C_1}+1/{C_2}+...+1/{C_n})$ , или $1/C=(1/{C_1}+1/{C_2}+...+1/{C_n})$

1. Разность потенциалов между точками А и В U=9 В. Емкость конденсаторов соответственно равна C_1=3 мкФ и C_2=6 мкФ. Определите заряды Q_1 и Q_2 и разности потенциалов U_1 и U_2 на обкладках первого и второго конденсаторов.

Задача 1

Определим общую емкость такого соединения: $1/{C_Sigma}=1/{C_1}+1/{C_2}$ ,

мкФ (сразу считаем в микрофарадах, чтобы не расписывать степени десятки)

Тогда заряд равен:

мкКл.

Заряды при последовательном соединении на всех конденсаторах одинаковые, значит для первого:

, для второго .

Напряжения на конденсаторах:

$U_1=q_1/{C_1}=18*10^{-6}/{3*10^{-6}}=6$ В, $U_2=q_2/{C_2}=18*10^{-6}/{6*10^{-6}}=3$ В.

Ответ: 18 мкКл, 6 В, 3 В.

2. Определите емкость батареи конденсаторов, изображенной на рисунке. Емкость каждого конденсатора C=1 мкФ.

Задача 2

Емкости C_3 и C_4 , поскольку они соединены параллельно, необходимо сложить: мкФ. Тогда получим последовательное соединение трех одинаковых емкостей и C_34 , емкость которой вдвое больше. При последовательном соединении емкостей их эквивалентная емкость вычисляется по формуле: $1/{C_Sigma}=sum{1}{n}{1/{C_i}}$ . Тогда получим: $1/{C_Sigma}=1/1+1/1+1/2+1/1=3,5$ , ${C_Sigma}=1/{3,5}=0,286$ мкФ.

Ответ: 286 нФ

3. Емкость батареи конденсаторов, образованной двумя последовательно включенными конденсаторами, 100 пФ, а заряд 20 нКл. Определите емкость второго конденсатора, а также разность потенциалов на обкладках каждого из них, если C_1=200 пФ.

Воспользуемся . Тогда (считаем в пикофарадах)

Отсюда , , C_2=200 пФ.

При последовательном соединении заряд на конденсаторах равный: нКл.

Напряжения также получатся одинаковыми:

$U_1=q_1/{C_1}=20*10^{-9}/{200*10^{-12}}=100$ В, В.

Ответ: В, нКл.

4. Наибольшая емкость конденсатора 60 мкФ. Какой заряд он накопит при подключении источника постоянного напряжения 60В?

Так как q=C*U , то $q=60*10^{-6}*60=0,36$ мКл.

Ответ: 0,36 мКл

5. При введении в пространство между пластинами воздушного конденсатора твердого диэлектрика напряжение на конденсаторе уменьшилось с 400 до 100 В. Какова диэлектрическая проницаемость диэлектрика?

Рассмотрим сначала конденсатор до введения диэлектрика: q=C_1*U , . Заряд остался тем же при введении диэлектрика, а напряжение изменилось: .

Тогда , или $C_1/{C_2}=1/4$

Емкость конденсатора, как известно, зависит от площади пластин и расстояния между ними, а также от диэлектрика:

$C={varepsilon*varepsilon_0*S}/d$

В первом случае, без диэлектрика: $C_1={varepsilon_0*S}/d$ , а во втором $C_2={varepsilon*varepsilon_0*S}/d$

Найдем и в этом случае отношение емкостей: $C_1/{C_2}=1/varepsilon$ , или $varepsilon=C_2/{C_1}=4$

Ответ: Кл*Кл/Н*м*м

6. Площадь пластин конденсатора равна 520 см кв. На каком расстоянии нужно разместить пластины в воздухе, чтобы емкость конденсатора была равна 50 пФ?

Емкость конденсатора без диэлектрика:

$C={varepsilon_0*S}/d$

Площадь нужно выразить в кв. метрах: $S=520*10^{-4}=0,052$

Электрическая постоянная $varepsilon_0=8,85*10^{-12}$ .

Выразим из первого выражения нужную нам величину: $d={varepsilon_0*S}/C={8,85*10^{-12}*0,052}/{50*10^{-12}}=0,0092$ м, или 9,2 мм.

Ответ: 9,2 мм

7. Конденсатору емкостью 20 мкФ сообщили заряд 5 мкКл. Какова энергия заряженного конденсатора?

Энергию электрического поля, накопленную конденсатором, можно вычислить по формуле:

$W=CU^2/2=q^2/{2C}$ — и в этой задаче как раз хорошо будет воспользоваться второй записью.

Тогда: $W=q^2/{2C}=(5*10^{-6})^2/{2*20*10^{-6}}=25/40=0,625*10^{-6}$ мкДж

8. Расстояние между пластинами плоского конденсатора с диэлектриком из бумаги, пропитанной парафином, равно 2 мм, а напряжение 200 В. Найти плотность энергии поля.

Чтобы найти плотность энергии, нужно сначала определить энергию поля, а потом посчитать, в каком объеме она сосредоточена.

, с другой стороны, емкость $C={varepsilon*varepsilon_0*S}/d$ , тогда $W={{varepsilon*varepsilon_0*S}U^2}/{2d}$ . Объем пространства между пластинами конденсатора — это произведение площади пластин на расстояние между ними: V=Sd . Тогда плотность энергии поля равна $W/V={{varepsilon*varepsilon_0}U^2}/{2d^2}$

Посмотрим в справочнике, какова диэлектрическая проницаемость бумаги с парафином, выразим расстояние между пластинами в метрах, и подставим цифры:

$W/V={{2,2*8,85*10^{-12}}200^2}/{2(0,002)^2}=9,7$ мДж

Источник

Задание 26 № 6096. Два одинаковых незаряженных конденсатора ёмкостью 4 мкФ каждый соединили параллельно и зарядили их до некоторого напряжения. Затем конденсаторы разъединили и замкнули выводы одного из них резистором с сопротивлением 100 кОм. После этого в резисторе за достаточно большое время выделилось количество теплоты, равное 50 мкДж. До какого напряжения были заряжены конденсаторы? Ответ приведите в В.

Решение.

П осле присоединения одного из этих конденсаторов к резистору конденсатор начнёт разряжаться, и, через достаточно большой промежуток времени, вся запасённая в конденсаторе энергия выделится в виде теплоты на резисторе. То есть

Откуда

Ответ: 5 В.

Источник

При подготовке к ЕГЭ по физике и решении задач повышенной сложности очень часто обучающиеся сталкиваются с трудностями анализа физических процессов в конденсаторах. Целью данной работы является некоторая систематизация и выделение ключевых позиций при решении задач повышенной сложности по теме «Конденсаторы и их соединение». Реализовывая системно-деятельностный подход к изучению физики, возможно рассмотрение следующих ситуаций анализа решаемых задач, а также вариативных вопросов к ним.

I. Рассмотрим известную задачу, которая раскрывает взаимосвязь физических характеристик конденсатора и последовательность их изменений [2]:

Плоский конденсатор, между пластинами которого находится воздух, заряжен от источника питания. Как меняются заряд конденсатора, напряженность электрического поля, разность потенциалов между пластинами, энергия и плотность энергии электрического поля, если увеличить в n раз расстояние между пластинами в ситуациях, если а) конденсатор отключить от источника питания и б) с включенным источником питания.

Рассмотрим первую ситуацию: изменяем расстояние между пластинами при отключенном источнике.

В ключевых позициях устанавливаем два опорных положения, которые позволяют анализировать изменения физических характеристик

— Что остается неизменным в данном процессе. (q = const, заряд на пластинах конденсатора при отключении источника тока)

— Что происходит с емкостью конденсатора (Конденсатор плоский: d
увеличивается, C уменьшается)

Анализируем и доказываем, как изменяются физические характеристики и причины их изменения:

1) Напряженность электрического поля конденсатора E = ϭ/(2ε₀) (не изменяется)

2) Разность потенциалов между пластинами C = q/U (С уменьшается, U
увеличивается в n раз)

3) Энергия электрического поля W = qU/2 (U увеличивается в n раз, W
увеличивается в n раз)

4) Плотность энергии ω = ε₀E²/2 (не изменяется)

Рассмотрим вторую ситуацию: изменяем расстояние между пластинами при включенном источнике питания.

— Что остается неизменным в данном процессе. (U = const, напряжение на пластинах конденсатора при включении источнике тока)

— Что происходит с емкостью конденсатора (Конденсатор плоский: d
увеличивается, C уменьшается)

Анализируем и доказываем, как изменяются физические характеристики и причины их изменения:

1) При неизменном напряжении и уменьшении емкости, заряд конденсатора должен уменьшиться в n раз (анализ C = q/U)

2) Напряженность электрического поля конденсатора E = ϭ/(2ε₀) (E
уменьшается в n раз при уменьшении заряда в n раз)

3) Энергия электрического поля W = qU/2 (q уменьшается в n раз, W
уменьшается в n раз)

4) Плотность энергии ω = ε₀E²/2 уменьшается в n² раз (при уменьшении напряженности)

Особое внимание следует обратить на энергетические превращения в конденсаторе. При увеличении расстояния между пластинами совершается положительная механическая работа, но энергия конденсатора уменьшается. Согласно закону сохранения энергии источник должен забирать энергию, равную убыли энергии конденсатора и механической работы внешних сил. Иначе, если источник является аккумулятором, то он будет заряжаться от конденсатора. Если источником является гальванический элемент, то на нем будет выделяться тепло.

Поставленную задачу можно не ограничивать данными изменениями, а можно выполнить анализ при изменении площади пластин конденсатора или замене диэлектрика между пластинами. В результате поможет сформировать у обучающихся целостное и устойчивое представление физических процессов и их характеристик в конденсаторе, варьируя ситуации.

II. Рассмотрим две возможные ситуации при параллельном подключении одного конденсатора к другому, если обкладки конденсаторов соединены одноименными зарядами и разноименными зарядами [2]:

Конденсатор емкостью C₁ заряжен до разности потенциалов U₁. Какой заряд и каково напряжение будет на обкладках конденсатора, если к нему подключить параллельно другой конденсатор емкостью C₂, заряженный до разности потенциалов U₂.

Если обкладки конденсаторов соединены одноименными зарядами, то решение задачи сводится к составлению уравнения закона сохранения заряда до соединения и после соединения конденсаторов. Закон сохранения заряда будет ключевым моментом анализа задачи. Второй момент — равенство напряжений на конденсаторах при параллельном подключении, дает возможность упростить и решить данную задачу.

Иначе дело обстоит, если обкладки конденсаторов соединены разноименными зарядами. При соединении двух конденсаторов возникает ситуация, когда при распределении зарядов после подключения происходит перезарядка одного из конденсаторов и смена знаков зарядов на его обкладках. В этом случае при составлении уравнения закона сохранения заряда как ключевого момента следует не забыть изменить знак заряда на противоположный. Положим, в данном примере U₂ > U₁, то при соединении конденсаторов, первый конденсатор перезарядится, и знаки зарядов на его пластинах сменятся. Поэтому удобно при составлении закона сохранения заряда, принять заряд первого конденсатора, до соединения к нему второго, за отрицательный заряд.

Закон сохранения заряда для данного примера будет выглядеть: -q₁+ q₂
= q₁‘+ q₂‘. Последующее равенство напряжений на конденсаторах при параллельном подключении дает возможность упростить и решить данную задачу.

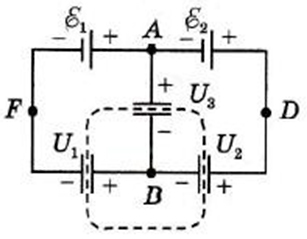
III. Рассмотрим анализ схемы соединения конденсаторов, где их соединения не сводятся к совокупности параллельных и последовательных соединений.

Например, в разветвленной схеме требуется найти напряжения на конденсаторах. Данный пример подробно описан [1]. Из данного примера выделим следующие ключевые моменты:

1) Составляем независимые уравнения, связывающие напряжения на конденсаторах с электродвижущими силами, выбрав точки разности потенциалов.

А) Между точками F и D: Ɛ₁+ Ɛ₂= U₁+ U₂

Б) Между точками F и A: Ɛ₁= U₁+ U₃

2) Составляем уравнение алгебраической суммы зарядов в узле точки B:

q₁— q₂— q₃= 0 или C₁U₁— C₂U₂ — C₃U₃= 0

Система трех независимых уравнений с тремя неизвестными дает их решение. Если схема симметрична (Ɛ₁ = Ɛ₂, C₁ = C₂), то U₃ (Напряжение между точками A и B) равно нулю, а напряжение U₁= U₂.

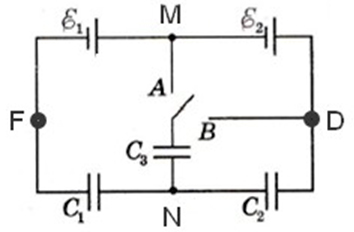
В связи с данным примером, возникает упрощенный анализ схем при переключении в цепи с конденсаторами, например [1]:

Для положения ключа в состоянии A и B между точками F и D выражение Ɛ₁ + Ɛ₂ = U₁ + U₂ справедливо в обоих случаях. Следовательно, U₂не изменяется при переключении.

Для узла N сумма зарядов в узле равна нулю: q₁— q₂± q₃= 0. Следовательно, не изменится заряд третьего конденсатора, а вместе с ним и не изменится напряжение U₃.

После переключения U₂= U₃, конденсаторы соединены параллельно.

В данном примере интересен вывод: точки A и B имеют одинаковый потенциал, следовательно Ɛ₂= 0.

IV. Рассмотрим некоторые варианты изменения энергии конденсатора с точки зрения закона сохранения энергии, подробные объяснения которых обсуждаются в источнике [3].

Изменение энергии конденсатора можно произвести от источника питания или путем совершения механической работы внешними силами.

Увеличение энергии конденсатора при зарядке конденсатора в общем виде можно определить из уравнения закона сохранения:

Aист. = ΔWк + A + Q,

где Aист. – работа источника при зарядке конденсатора, ΔWк – изменение энергии конденсатора, A – механическая работа сил электрического поля, Q – выделяющееся тепло. В идеальном случае, при отсутствии потерь энергии от источника: Aист. = ΔWк

Однако наиболее часто встречаются задания, где изменение энергии заряженного конденсатора происходит путем совершения работы внешней силы в ситуациях с отключенным и подключенным источником тока.

Рассмотрим первую ситуацию: как изменится энергия конденсатора, если вынуть диэлектрическую пластину из заряженного конденсатора или раздвинуть его обкладки при отключенном источнике питания.

— обращаем внимание на то, что в данной ситуации остается неизменным заряд q конденсатора.

— обращаем внимание на то, что емкость при выемке диэлектрика или раздвижении пластин уменьшается емкость конденсатора (C = εε₀S/d)

Формируем вывод исходя из формулы энергии при неизменном заряде: W = q₂/2C – энергия конденсатора увеличивается. Увеличение энергии произошло за счет работы внешней силы. ΔWк = Aвнеш.

Рассмотрим вторую ситуацию: как изменится энергия конденсатора, если вынуть диэлектрическую пластину из заряженного конденсатора или раздвинуть его обкладки при включенном источнике питания.

— обращаем внимание на то, что в данной ситуации остается неизменным напряжение U на обкладках конденсатора.

Формируем вывод исходя из формулы энергии при неизменном напряжении: W = CU²/2 – энергия конденсатора уменьшается. Уменьшение энергии произошло за счет того, что источник совершает отрицательную работу, забирая часть заряда с обкладок конденсатора при положительной работе внешних сил:. ΔWк = Aист. + Aвнеш.

Возможны и другие очевидные вариации изменения энергии конденсатора с помощью работы внешних сил.

В данной работе рассмотрена лишь небольшая часть анализа ключевых ситуаций по данной теме. Но все рассмотренные ситуации являются опорными для формирования разбора задач и их решения.

Литература

1. Е.И.Бутиков, А.А.Быков, А.С.Кондратьев. Физика в примерах и задачах, МЦНМО, Пероглиф, 2019, стр. 297-301.

2. А.С.Кондратьев, В.М.Уздин. Физика. Сборник задач, М., ФИЗМАТЛИТ, 2020, стр.67-69.

3. А.С.Кондратьев, Л.А.Ларченкова, В.А.Ляпцев. Методы решения задач по физике. М., ФИЗМАТЛИТ, 2019, стр.149-154.

Источник