Задачи на куб решу егэ - Помощь в подготовке к экзаменам и поступлению

Каталог заданий.
Куб

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 2 № 27055

Площадь поверхности куба равна 18. Найдите его диагональ.

Аналоги к заданию № 5041: 27055 72585 72539 72541 72543 72545 72547 72549 72551 72553 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность

Классификатор стереометрии: Площадь поверхности куба

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 2 № 27056

Объем куба равен 8. Найдите площадь его поверхности.

Аналоги к заданию № 27056: 5043 72587 72589 72591 72593 72595 72597 72599 Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.3.2 Параллелепипед; куб; симметрии в кубе, в параллелепипеде, 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы

Классификатор стереометрии: Площадь поверхности куба

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 2 № 27061

Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.

Аналоги к заданию № 27061: 5053 72865 520184 520203 27145 72823 72825 72827 72829 72831 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.3.2 Параллелепипед; куб; симметрии в кубе, в параллелепипеде

Классификатор стереометрии: Площадь поверхности куба

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 2 № 27081

Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?

Аналоги к заданию № 27081: 73627 500957 73629 73631 73633 73635 73637 73639 Все

Классификатор планиметрии: Отношение длин, площадей, объемов подобных фигур

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 2 № 27098

Диагональ куба равна Найдите его объем.

Аналоги к заданию № 27098: 74417 74419 74429 505446 74421 74423 74425 74427 Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник

СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика базового уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Справочник

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

10 марта

Как подготовиться к ЕГЭ и ОГЭ за 45 дней

6 марта

Изменения ВПР 2023

3 марта

Разместили утвержденное расписание ЕГЭ

27 января

Вариант экзамена блокадного Ленинграда

23 января

ДДОС-атака на Решу ЕГЭ. Шантаж.

6 января

Открываем новый сервис: «папки в избранном»

22 декабря

Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!

4 ноября

Материалы для подготовки к итоговому сочинению 2022–2023

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

21 марта

Новый сервис: рисование

31 января

Внедрили тёмную тему!

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Каталог заданий.
Куб

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Задания Д13 № 5053

Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.

Аналоги к заданию № 27061: 5053 72865 27145 72823 72825 72827 72829 72831 72833 72835 … Все

Решение

Сообщить об ошибке · Помощь

Задания Д13 № 27055

Площадь поверхности куба равна 18. Найдите его диагональ.

Аналоги к заданию № 27055: 72585 5041 72539 72541 72543 72545 72547 72549 72551 72553 … Все

Решение

Сообщить об ошибке · Помощь

Задания Д13 № 27056

Объем куба равен 8. Найдите площадь его поверхности.

Аналоги к заданию № 27056: 5043 72587 72589 72591 72593 72595 72597 72599 Все

Решение

Сообщить об ошибке · Помощь

Задания Д13 № 27061

Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.

Аналоги к заданию № 27061: 5053 72865 27145 72823 72825 72827 72829 72831 72833 72835 … Все

Решение

Сообщить об ошибке · Помощь

Задания Д13 № 27081

Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?

Аналоги к заданию № 27081: 73627 73629 73631 73633 73635 73637 73639 Все

Решение

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

О проекте · Редакция · Правовая информация · О рекламе

Источник

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 527 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Куб целиком находится в правильной треугольной пирамиде SABC с вершиной S так, что одна грань куба принадлежит основанию, одно ребро целиком принадлежит грани SBC, а грани SAB и SAC содержат по одной вершине куба. Известно, что ребро АВ в 2 раза больше высоты пирамиды.

а)  Докажите, что плоскость, проходящая через вершины куба, принадлежащие граням SAB и SAC, и вершину пирамиды, перпендикулярна плоскости ASD, где D  — середина стороны ВС.

б)  Найдите отношение объемов пирамиды и куба.

Источник: А. Ларин: Тренировочный вариант № 222.

Объем одного куба в 125 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Куб вписан в шар радиуса Найдите объем куба.

Все ребра куба равны

а)  Постройте сечение куба, проходящее через середины ребер AB, BC, CC₁.

б)  Найдите площадь этого сечения.

Источник: А. Ларин: Тренировочный вариант № 134.

Внутри куба расположены два равных шара, касающихся друга. При этом один шар касается трех граней куба, имеющих общую вершину, а другой касается трех оставшихся граней.

а)  Докажите, что центры шаров принадлежат диагонали куба, исходящей из общей для граней вершины.

б)  Найдите радиусы этих шаров, если ребро куба равно 13.

Источник: А. Ларин: Тренировочный вариант № 209.

Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.

Середина ребра куба со стороной 1,9 является центром шара радиуса 0,95. Найдите площадь S части поверхности шара, лежащей внутри куба. В ответе запишите

Объем первого куба в 8 раз больше объема второго куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Если каждое ребро куба увеличить на 5, то его площадь поверхности увеличится на 390. Найдите ребро куба.

Объем одного куба в 729 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Шар, объём которого равен 6π, вписан в куб. Найдите объём куба.

Источник: ЕГЭ 28.04.2014 по математике. Досрочная волна. Вариант 2.

Шар, объём которого равен вписан в куб. Найдите объём куба.

Во сколько раз увеличится объем куба, если все его рёбра увеличить в 5 раз?

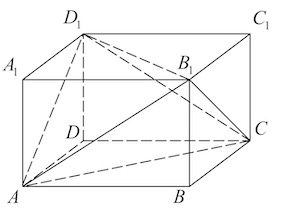
Длина диагонали куба ABCDA₁B₁C₁D₁ равна 3. На луче A₁C отмечена точка P так, что A₁P  =  4.

а)  Докажите, что PBDC₁ — правильный тетраэдр.

б)  Найдите длину отрезка AP.

Источник: ЕГЭ по математике 2017. Досрочная волна, резервная волна. Вариант А. Ларина (часть С)

Если каждое ребро куба увеличить на 5, то его площадь поверхности увеличится на 270. Найдите ребро куба.

Если каждое ребро куба увеличить на 3, то его площадь поверхности увеличится на 162. Найдите ребро куба.

Шар, объём которого равен 28π, вписан в куб. Найдите объём куба.

Шар, объём которого равен 44π, вписан в куб. Найдите объём куба.

Всего: 527 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Задача 1. В прямоугольном параллелепипеде известно, что Найдите длину диагонали

Решение: + показать

Задача 2. Найдите угол прямоугольного параллелепипеда, для которого . Ответ дайте в градусах.

Решение: + показать

Задача 3. В прямоугольном параллелепипеде известны длины рёбер Найдите синус угла между прямыми и

Решение: + показать

Задача 4. Площадь поверхности куба равна Найдите его диагональ.

Решение: + показать

Задача 5. Объем куба равен Найдите площадь его поверхности.

Решение: + показать

Задача 6. Диагональ куба равна . Найдите его объем.

Решение: + показать

Задача 6. Объем куба равна . Найдите его диагональ.

Решение: + показать

Задача 7. Во сколько раз увеличится объем куба, если его ребра увеличить в десять раз?

Решение: + показать

Задача 8. Если каждое ребро куба увеличить на , то его площадь поверхности увеличится на Найдите ребро куба.

Решение: + показать

Задача 9. Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в раза?

Решение: + показать

Задача 10. Объем одного куба в раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Решение: + показать

Задача 11. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны и Площадь поверхности этого параллелепипеда равна Найдите третье ребро, выходящее из той же вершины.

Решение: + показать

Задача 12. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны и Найдите ребро равновеликого ему куба.

Решение: + показать

Задача 13. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны и Диагональ параллелепипеда равна Найдите объем параллелепипеда.

Решение: + показать

Задача 14. Площадь грани прямоугольного параллелепипеда равна Ребро, перпендикулярное этой грани, равно Найдите объем параллелепипеда.

Решение: + показать

Задача 15. В прямоугольном параллелепипеде известны длины рёбер: Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки и

Решение: + показать

Задача 16. Диагональ прямоугольного параллелепипеда равна и образует углы $30^{circ}$ , $30^{circ}$ и $45^{circ}$ с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.

Решение: + показать

Задача 17. В прямоугольном параллелепипеде ребро , ребро , ребро . Точка — середина ребра Найдите площадь сечения, проходящего через точки .

Решение: + показать

Задача 18. Одна из граней прямоугольного параллелепипеда — квадрат. Диагональ параллелепипеда равна и образует с плоскостью этой грани угол °. Найдите объем параллелепипеда.

Решение: + показать

Задача 19. Найдите объем многогранника, вершинами которого являются точки прямоугольного параллелепипеда у которого

Решение: + показать

Задача 20. Найдите объем параллелепипеда , если объем треугольной пирамиды равен

Решение: + показать

Задача 21. Найдите объем многогранника, вершинами которого являются точки прямоугольного параллелепипеда у которого

Решение: + показать

Задача 22. Найдите объем многогранника, вершинами которого являются точки прямоугольного параллелепипеда у которого

Решение: + показать

Задача 23. Объем параллелепипеда равен Найдите объем треугольной пирамиды

Решение: + показать

Задача 24. В кубе точка — середина ребра , точка — середина ребра , точка — середина ребра Найдите угол . Ответ дайте в градусах.

Решение: + показать

Вы можете пройти тест

Источник

8. Геометрия в пространстве (стереометрия)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи по теме «Куб»

Куб – это прямоугольный параллелепипед, все грани которого – равные квадраты.

Следовательно:

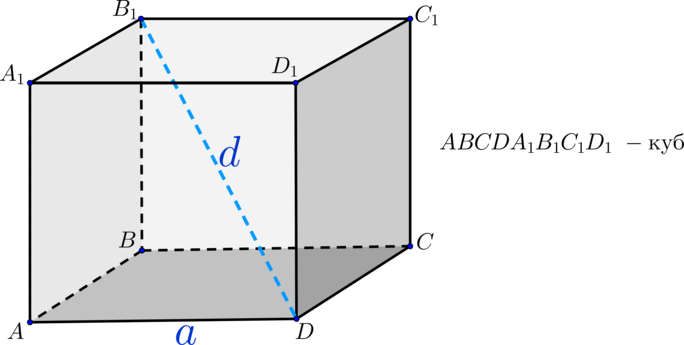
(blacktriangleright) для объема куба верна следующая формула (где (a) – ребро куба): [{Large{V=a^3}}] (blacktriangleright) диагональ куба ({Large{d^{,2}=3a^2}})
(blacktriangleright) площадь поверхности куба равна сумме площадей шести одинаковых квадратов, т.е. ({Large{S_{text{пов.куб}}=6a^2}})

Задание
1

#1874

Уровень задания: Сложнее ЕГЭ

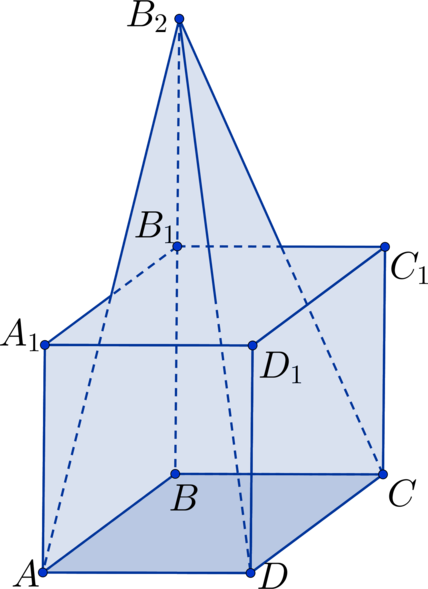
Дан куб (ABCDA_1B_1C_1D_1). Точка (B_2) лежит на продолжении ребра (BB_1) за точку (B_1), (BB_2 = 2cdot BB_1). Во сколько раз объем куба отличается от объема пирамиды (B_2ABCD)?

Отрезок (BB_2) является высотой пирамиды. Если сторону куба обозначить за (x), то (BB_2 = 2x) (Rightarrow) [displaystyle V_{text{пир.}} = frac{1}{3}cdot BB_2 cdot S_{ABCD} = frac{1}{3}cdot 2x cdot x^2 = frac{2}{3}cdot x^3,,,,, V_{text{куб}} = x^3.] Теперь найдем искомую величину: [displaystyle frac{V_{text{куб}}}{V_{text{пир.}}} = frac{x^3}{frac{2}{3}cdot x^3} = 1,5.]

Ответ: 1,5

Задание
2

#960

Уровень задания: Сложнее ЕГЭ

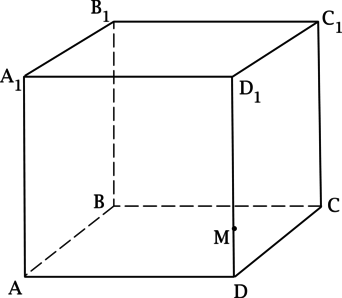
(ABCDA_1B_1C_1D_1) – куб с длиной ребра равной (sqrt[4]{17}). Точка (M) лежит на ребре (DD_1) так, что (MD_1 = 3MD). Найдите площадь сечения куба, проведённого через точку (M) и ребро (AB).

Пусть (N) – точка на (CC_1), такая что (NC_1 = 3NC), тогда (MNparallel CDparallel AB), следовательно, сечение, проходящее через точку (M) и ребро (AB) – четырёхугольник (AMNB), причём ((AA_1D_1D) bot MN), следовательно, (AM bot MN). Аналогично (MNbot BNbot AB), то есть (AMNB) – прямоугольник. [S_{AMNB} = AMcdot MN = AMcdot sqrt[4]{17}.] Найдём (AM) по теореме Пифагора: [AM = sqrt{AD^2 + MD^2} = sqrt{AD^2 + (0,25AD)^2} = sqrt{dfrac{17}{16}AD^2} = dfrac{sqrt{17}}{4}AD = dfrac{sqrt[4]{17^3}}{4}.] Тогда (S_{AMNB} = dfrac{sqrt[4]{17^3}}{4} cdot sqrt[4]{17} = dfrac{17}{4} = 4,25).

Ответ: 4,25

Задание
3

#1873

Уровень задания: Сложнее ЕГЭ

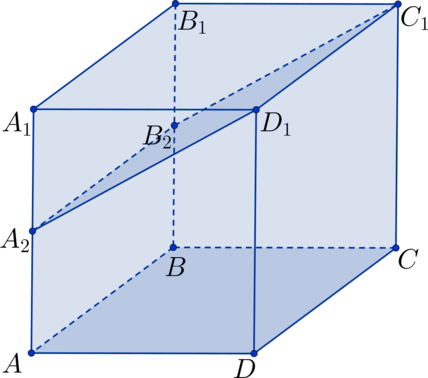
В кубе (ABCDA_1B_1C_1D_1) точки (A_2) и (B_2) – середины соответственно сторон (AA_1) и (BB_1). Найдите площадь поверхности фигуры (ABCDA_2B_2C_1D_1), если ребро куба равно (sqrt{32 — 4sqrt5}).

Площадь поверхности фигуры (ABCDA_2B_2C_1D_1) состоит из суммы следующих площадей: [S_{text{пов.}} = S_{AA_2D_1D} + S_{BB_2C_1C} + S_{DD_1C_1C} + S_{AA_2B_2B} + S_{ABCD} + S_{A_2B_2C_1D_1}.] Обозначим ребро куба за (2x), тогда (AA_2 = BB_2 = x). (AA_2D_1D) и (BB_2C_1C) – равные прямоугольные трапеции, площадь которых равна [displaystyle S_{AA_2D_1D} = S_{BB_2C_1C} = frac{1}{2}cdot(AA_2 + DD_1)cdot AD = frac{(x + 2x)cdot2x}{2} = 3x^2.] Также найдем площади остальных граней: (S_{DD_1C_1C} = 4x^2), (S_{AA_2B_2B} = 2x^2), (S_{ABCD} = 4x^2); для того чтобы найти площадь грани (A_2B_2C_1D_1) нам понадобится сначала найти сторону (A_2D_1). Найдем ее, используя теорему Пифагора в треугольнике (triangle A_2A_1D_1): [A_2D_1^2 = A_2A_1^2 + A_1D_1^2 = x^2 + 4x^2 = 5x^2] (Rightarrow) (A_2D_1 = sqrt5x). Тогда (S_{A_2B_2C_1D_1} = A_2B_2cdot A_2D_1 = 2sqrt5x^2). Теперь сложим все площади граней искомой фигуры: [S_{text{пов.}} = 3x^2 + 3x^2 + 4x^2 + 2x^2 + 4x^2 + 2sqrt5x^2 = (16 + 2sqrt5)cdot x^2.] По условию задачи имеем: (2x = sqrt{32 — 4sqrt5} = 2cdotsqrt{8 — sqrt5}) (Rightarrow) (x = sqrt{8 — sqrt5}). Подставим в формулу площади и получим окончательный результат: [S_{text{пов.}} = (16 + 2sqrt5)cdotleft(sqrt{8 — sqrt5}right)^2 = 2cdot(8 + sqrt5)cdot(8 — sqrt5) = 2cdot59 = 118.]

Ответ: 118

Задание
4

#961

Уровень задания: Сложнее ЕГЭ

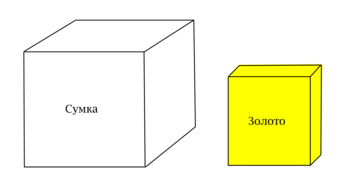
Анатолий грабит банк. Слитки золота имеют форму прямоугольных параллелепипедов с измерениями (4times 4times 2). Сумка, которая есть у Анатолия, имеет форму куба с ребром длины (6). Анатолию нужно уложить как можно больше слитков в сумку так, чтобы она закрылась и с ней можно было выйти, не привлекая к ней внимания. Сколько слитков сможет вынести Анатолий, если будет действовать разумно?

Сначала заметим, что ответ не изменится, если уменьшить масштаб в два раза по каждому направлению. При этом сумка станет кубом с ребром (3), а слитки золота станут прямоугольными параллелепипедами с измерениями (2times 2times 1).

Оценим возможное количество слитков сверху: так как объём сумки равен (3^3 = 27), а объём слитка равен (2cdot 2cdot 1 = 4), то более (6) слитков в сумку не войдут. Но могут ли войти в неё 6?

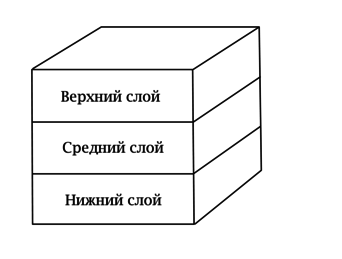
Назовём слиток горизонтальным, если две его грани параллельны дну сумки так, что его высота равна 1. В противном случае назовём слиток вертикальным. Мысленно “расслоим”( )сумку на 3 одинаковых горизонтальных слоя.

Каждый вертикальный слиток занимает в среднем слое по 2 соседних кубика с ребром 1. Средний слой состоит из 9 таких кубиков, следовательно, вертикальных слитков в сумку входит не более 4. При этом горизонтальных слитков в сумку входит не более 3 (в каждый слой входит не более одного горизонтального слитка).

В случае, когда горизонтальных слитков ровно 3, получим, что в среднем слое 4 кубика из 9 заняты горизонтальным слитком, то есть в среднем слое остаётся (9 — 4 = 5) кубиков, но каждый вертикальный слиток должен занимать в среднем слое по 2 кубика, тогда получаем, что вертикальных слитков при этом не более 2 и всего слитков при трёх горизонтальных (leq 2 + 3 = 5).

Таким образом, последний шанс Анатолия унести 6 слитков – это 4 вертикальных слитка и 2 горизонтальных. Возможно ли это? Понятно, что для этого необходимо, чтобы горизонтальные слитки лежали в нижнем и верхнем слоях, но верхний слиток не должен “полностью нависать”( )над нижним. Тогда остаётся всего 2 принципиально различных способа уложить горизонтальные слитки в верхнем и нижнем слоях относительно друг друга.

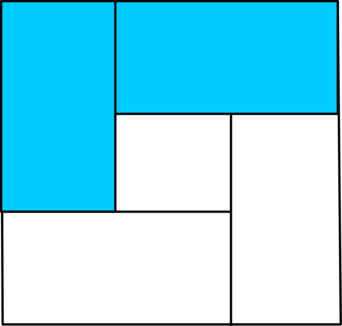
При этом один из них позволяет уложить 6 слитков. Чтобы наглядно проиллюстрировать его сначала поместим в сумку только вертикальные слитки и покажем вид сверху:

здесь голубым отмечены все те вертикальные слитки, которые стоят на дне сумки. Тогда на дно можно подложить ещё 1 горизонтальный слиток под те вертикальные, которые не стоят на дне сумки. Аналогично, в верхний слой можно подложить 1 горизонтальный слиток.

Итого: при разумном подходе Анатолий может вынести 6 слитков.

Ответ: 6

Подготовка к сдаче ЕГЭ по математике, как правило, начинается с повторения полной теории и базовых формул, в том числе и тех, с помощью которых можно найти площадь куба. И хотя эта тема достаточно подробно рассматривается преподавателями в рамках школьной программы, многим старшеклассникам требуется освежить в памяти основной материал.

Поняв, как найти объем куба и других параметров и отлично усвоив алгоритм решения таких задач, учащиеся смогут получить достаточно высокие баллы по итогам сдачи ЕГЭ.

Основные моменты

Чтобы вопрос, как вычислить объем куба, не ставил ученика в тупик, рекомендуем вспомнить основные свойства этой фигуры.

Так как куб представляет собой прямоугольный параллелепипед, все шесть граней которого равны между собой, последние являются квадратами.
Все двугранные углы многогранника прямые.
Противоположные грани куба попарно параллельны.
Диагональ грани многогранника в √3 раза больше длины ребра.
Если все линейные размеры сторон куба увеличиваются в k раз, то площадь его поверхности увеличивается в k2 раз.

Готовьтесь к единому госэкзамену качественно и эффективно вместе с образовательным проектом «Школково»

Занимаясь накануне прохождения аттестационного испытания, многие учащиеся сталкиваются с проблемой поиска базовой информации. Далеко не всегда школьный учебник оказывается под рукой. А на поиск подходящих формул для решения задач по теме «Куб» зачастую уходит большое количество времени.

Регулярные занятия на образовательном сайте «Школково» помогут учащимся избежать типовых ошибок при прохождении аттестационного испытания. Мы предлагаем выстроить процесс подготовки к экзамену по-новому, переходя от простого к сложному. Это позволит учащимся определить непонятные для себя темы и ликвидировать пробелы в знаниях.

Весь базовый материал представлен в разделе «Теоретическая справка». Основные понятия и формулы собраны и изложены нашими специалистами в максимально доступной форме.

Для того чтобы лучше усвоить материал, предлагаем также потренироваться в выполнении задач по темам «Куб», ”Прямоугольный параллелепипед”. Большая подборка упражнений различной степени сложности представлена в разделе «Каталог». Все задания содержат подробный алгоритм нахождения правильного ответа. База упражнений на сайте постоянно дополняется и обновляется.

В случае необходимости любое из представленных заданий можно сохранить в «Избранное». Это позволит в дальнейшем быстро его найти и обсудить алгоритм нахождения правильного ответа с преподавателем в школе или репетитором.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Куб»

Открытый банк заданий по теме куб. Задания B8 из ЕГЭ по математике (профильный уровень)

Производная и первообразная функции

Задание №318

Тип задания: 8
Тема:
Куб

Условие

При увеличении ребра куба на 3 его площадь поверхности увеличивается на 306. Найдите ребро куба.

Показать решение

Решение

Поверхность куба состоит из 6 граней, каждая из которых является квадратом, поэтому площадь поверхности куба S=6a^2, где a — ребро куба.

По условию 6(a+3)^2-6a^2=306,

(a+3)^2-a^2=51,

(a+3-a)(a+3+a)=51,

3cdot(a+3+a)=51,

2a+3=17,

a=7.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №309

Тип задания: 8
Тема:
Куб

Условие

Во сколько раз увеличится объем куба, если все его ребра увеличить в семь раз?

Куб

Показать решение

Решение

Пусть a — ребро исходного куба. Тогда его объем V_1=a^3; После увеличения ребро куба будет равно 7a, а его объем V_2=(7a)^3=343a^3. Тогда frac{V_2}{V_1}=frac{343a^3}{a^3}=343.

Ответ

343

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №112

Тип задания: 8
Тема:
Куб

Условие

Диагональ куба равна sqrt{48}. Найдите объем куба.

Показать решение

Решение

Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. Так как все измерения куба равны a, то

d^2=a^2+a^2+a^2

48 = 3a^2

a^2=16

a = 4

Зная сторону куба, найдем его объем

V = a^3 = 64

Ответ

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник

Практикум №1 по решению стереометрических задач ( базовый уровень )

ЕГЭ — 2020

Задания №13 и №16

базового уровня

с кубом

Содержание

Задача №1
Задача №2
Задача №3
Задача №4
Задача №5
Задача №6
Задача №7

Задача №8
Задача №9
Задача №10
Задача №11
Задача №12
Задача №13
Задача №14

Вспомним!

Куб – прямоугольный параллелепипед, все грани которого – квадраты.
Все грани куба равные квадраты.
S п. пов. = 6а ² ; S осн . = а ²
Объем куба равен : V = a³
Все диагонали куба равны, пересекаются в одной точке и делятся этой точкой пополам.
Боковые рёбра перпендикулярны его основаниям
Диагональ куба равна : d² = 3a²

Задача №1

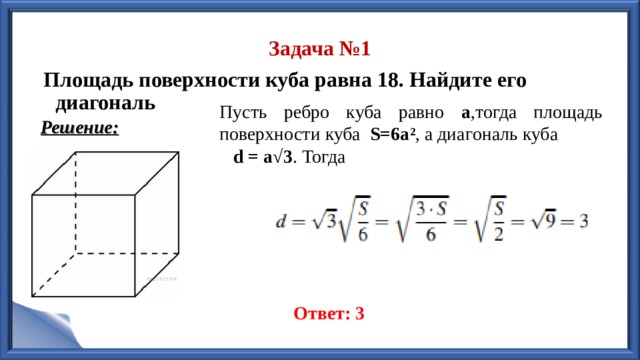
Площадь поверхности куба равна 18. Найдите его диагональ

Пусть ребро куба равно а ,тогда площадь поверхности куба S=6a² , а диагональ куба

d = a√3 . Тогда

Ответ: 3

Решение:

Задача №2

Объем куба равен 8. Найдите площадь его поверхности.

Решение:

Площадь поверхности куба выражается через его ребро а как S=6a² , а объем — как V=a³ . Отсюда видно, что площадь поверхности куба выражается через его объем как .Отсюда находим, что

Задача №3

Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.

Решение:

Площадь поверхности куба выражается через его ребро a

как S=6a² , поэтому при увеличении длины ребра на 1

площадь увеличится н а

Отсюда находим, что ребро

Ответ: 4

Задача №4

Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?

Решение:

Объем куба с ребром а равен V=a³ . Если ребра увеличить в 3 раза , то объем куба увеличится в 3³=27 раз.

Ответ: 27

Задача №5

Объем куба равен 24 √3 . Найдите его диагональ

Решение:

Пусть ребро куба равно а , тогда площадь поверхности куба S=6a² , а диагональ куба d = a√3 . Тогда

Значит d = 6 .

! Можно решить и через…. (рассмотрите самостоятельно)

a=2; a= -3 ( не подходит по условию задачи ) Ответ: 2. » width=»640″

Задача №6

Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.

Решение:

Объем куба с ребром а равен V=a³ .

Увеличение объема равно 19:

Решим уравнение: a² + a — 6 = 0 = a=2; a= -3 ( не подходит

по условию задачи )

Ответ: 2.

Задача №7

Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в три раза?

Решение:

Площади подобных тел относятся как квадрат коэффициента подобия, поэтому при увеличении ребра в 3 раза , площадь поверхности увеличится в 9 раз.

а = d :√3 = 1/√3 , тогда » width=»640″

Задача №8

Диагональ куба равна 1. Найдите площадь его поверхности.

Решение:

Знаем, что d = a√3 = а = d :√3 = 1/√3 , тогда

а ² = S /6 , т.е. а=√ S /6 , тогда » width=»640″

Задача №9

Площадь поверхности куба равна 24. Найдите его объем

Решение:

Объем куба с ребром а равен V=a³ , а S=6a² . = а ² = S /6 , т.е. а=√ S /6 , тогда

Задача №10

Объем одного куба в 8 раз больше объема другого куба.

Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Решение:

Объемы подобных тел относятся как куб коэффициента подобия, поэтому один из кубов в 2 раза больше другого .

Площади поверхностей подобных тел относятся как квадрат коэффициента подобия, поэтому их отношение равно 4.

Ответ:4

Задача №11

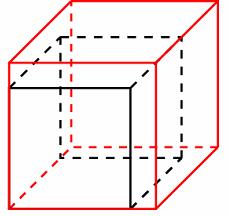
От деревянного кубика отпилили все его вершины (см. рис). Сколько граней у получившегося многогранника (невидимые ребра на рисунке не обозначены)?

Решение.

У кубика 6 граней. В результате отпиливания 8 вершин появились 8 граней. Всего 14 граней.

Ответ: 14

Задача №12

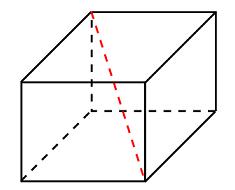
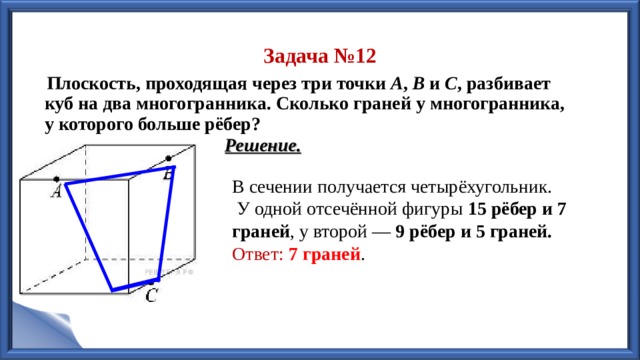
Плоскость, проходящая через три точки A , B и С , разбивает куб на два многогранника. Сколько граней у многогранника, у которого больше рёбер?

Решение.

В сечении получается четырёхугольник.

У одной отсечённой фигуры 15 рёбер и 7 граней , у второй — 9 рёбер и 5 граней.

Ответ: 7 граней .

Задача №13

Ящик, имеющий форму куба с ребром 10 см без одной грани, нужно покрасить со всех сторон снаружи. Найдите площадь поверхности, которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.

Решение:

Площадь одной грани равна 10 · 10 = 100 см ² . В кубе шесть граней , но нам надо найти только площадь пяти граней , следовательно 100 · 5 = 500 см ² .

Ответ: 500

Задача №14

Диагональ куба равна √12 . Найдите его объем.

Решение:

Диагональ куба d = a√3 , т.е. в √3 раз больше его ребра. Получим, что ребро равно

Тогда V=a ³ = 2 ³ = 8

Задачи

для самостоятельного решения

Задача №1 Решите самостоятельно

Площадь поверхности куба равна 2592. Найдите его диагональ.
Площадь поверхности куба равна 1568. Найдите его диагональ.
Площадь п оверхности куба равна 18. Найдите его диагональ.

Задача № 2 Решите самостоятельно

1) Объем куба равен 8. Найдите площадь его поверхности.

2) Объем куба равен 343 . Найдите площадь его поверхности.

3) Объем куба равен 216 . Найдите площадь его поверхности.

4 ) Объем куба равен 125 . Найдите площадь его поверхности.

Задача №3 Решите самостоятельно

Если каждое ребро куба увеличить на 5 , то его площадь поверхности увеличится на 390 . Найдите ребро куба

Если каждое ребро куба увеличить на 2, то его площадь поверхности увеличится на 144. Найдите ребро куба.

Если каждое ребро куба увеличить на 4, то его площадь поверхности увеличится на 240. Найдите ребро куба.

Задача №4 Решите самостоятельно

Во сколько раз увеличится объем куба, если его ребра увеличить в пятнадцать раз?
Во сколько раз увеличится объем куба, если его ребра увеличить в шесть раз?
Во сколько раз увеличится объем куба, если его ребра увеличить в 12 раз?
Во сколько раз увеличится объем куба, если его ребра увеличить в 10 раз?

Задача №5 Решите самостояте льно

Объем куба равен 0,003 √3 . Найдите его диагональ.
Объем куба равен 1536 √3 . Найдите его диагональ.
Объем куба равен 3000 √3 . Найдите его диагональ.
Объем куба равен 81 √3 . Найдите его диагональ.
Объем куба равен 192 √3 . Найдите его диагональ.
Объем куба равен 2187 √3. Найдите его диагональ.

Задача №4 Решите самостоятельно

Если каждое ребро куба увеличить на 2, то его объем увеличится на 728. Найдите ребро куба.
Если каждое ребро куба увеличить на 3, то его объем увеличится на 819. Найдите ребро куба.
Если каждое ребро куба увеличить на 3, то его объем увеличится на 1413. Найдите ребро куба.
Если каждое ребро куба увеличить на 1, то его объем увеличится на 721. Найдите ребро куба.

Задача № 7 Решите самостоятельно

Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в 2 раза?
Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в 24 раза?
Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в 33 раза?

Задача № 8 Решите самостоятельно

Диагональ куба равна 6. Найдите площадь его поверхности.
Диагональ куба равна 34. Найдите площадь его поверхности.
Диагональ куба равна 41. Найдите площадь его поверхности.
Диагональ куба равна 9. Найдите площадь его поверхности.

Задача № 9 Решите самостоятельно

Площадь поверхности куба равна 864. Найдите его объем.
Площадь поверхности куба равна 54. Найдите его объем.
Площадь поверхности куба равна 216. Найдите его объем.
Площадь поверхности куба равна 96. Найдите его объем.

Задача № 10 Решите самостоятельно

Объем одного куба в 125 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Объем одного куба в 64 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Объем одного куба в 729 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Задача №1 3 Решите самостоятельно

Ящик, имеющий форму куба с ребром 3 0 см без одной грани, нужно покрасить со всех сторон снаружи. Найдите площадь поверхности, которую необходимо покрасить. Ответ дайте в квадратных сантиметрах. Ответ: 4500

Задача №14 Решите самостоятельно

Диагональ куба равна √2 43 . Найдите его объем.
Диагональ куба равна √ 588 . Найдите его объем.
Диагональ куба равна √ 48 . Найдите его объем.
Диагональ куба равна √ 300 . Найдите его объем.
Диагональ куба равна √ 27 . Найдите его объем.
Диагональ куба равна √ 675 . Найдите его объем.

Шаблон подготовила учитель русского языка и литературы Тихонова Надежда Андреевна
«Решу ЕГЭ» Образовательный портал для подготовки к ЕГЭ и ОГЭ. Режим доступа: http://mathb.reshuege.ru

http://sch-53.ru/files/director/GIA/2016/%D0%95%D0%93%D0%AD%202016.jpg

http://a550.phobos.apple.com/us/r30/Purple/v4/0c/91/17/0c9117c4-c866-54fc-68ce-0e5aa31f5929/mzl.dfcpkqki.png

Источник