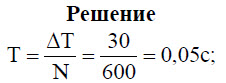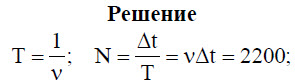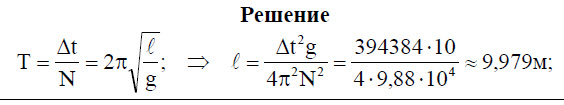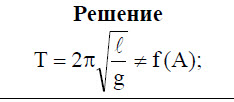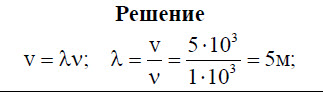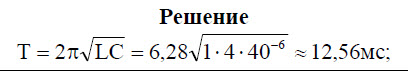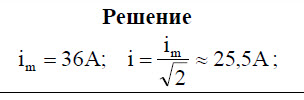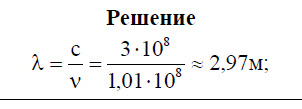Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Период колебаний потенциальной энергии горизонтального пружинного маятника 1 с. Каким будет период ее колебаний, если массу груза маятника увеличить в 2 раза, а жесткость пружины вдвое уменьшить? (Ответ дайте в секундах.)
2
Период колебаний потенциальной энергии пружинного маятника 1 с. Каким будет период ее колебаний, если массу груза маятника и жесткость пружины увеличить в 4 раза? (Ответ дайте в секундах.)
3
На рисунке представлен график зависимости потенциальной энергии математического маятника (относительно положения его равновесия) от времени. Какова полная механическая энергия маятника в момент времени, соответствующий на графике точке D? (Ответ дайте в джоулях.)
4
На рисунке представлен график зависимости потенциальной энергии математического маятника (относительно положения его равновесия) от времени. Какова кинетическая энергия маятника в момент времени
? (Ответ дайте в джоулях.)
5
На рисунке представлен график зависимости потенциальной энергии математического маятника (относительно положения его равновесия) от времени. Какова кинетическая энергия маятника в момент времени
? (Ответ дайте в джоулях.)
Пройти тестирование по этим заданиям
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 556 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Маятник совершает вынужденные колебания под действием внешней силы, изменяющейся по гармоническому закону, причём частота изменения этой силы такова, что наблюдается резонанс. Затем частоту изменения внешней силы уменьшают.
Определите, как изменятся через достаточно продолжительное время следующие физические величины: амплитуда колебаний маятника, частота вынужденных колебаний маятника.
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Амплитуда колебаний маятника | Частота вынужденных колебаний маятника |
Маятник совершает вынужденные колебания под действием внешней силы, изменяющейся по гармоническому закону, причём частота изменения этой силы такова, что наблюдается резонанс. Затем частоту изменения внешней силы увеличивают.
Определите, как изменятся через достаточно продолжительное время следующие физические величины: амплитуда колебаний маятника, частота вынужденных колебаний маятника.
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Амплитуда колебаний маятника | Частота вынужденных колебаний маятника |
Небольшое тело, закреплённое на лёгкой пружине жёсткостью 1 Н/м, совершает гармонические колебания вдоль горизонтальной оси OX.
На рисунке показан график зависимости проекции ускорения ax этого тела на указанную ось от времени t.
Из приведённого ниже списка выберите все верные утверждения, описывающие данное движение тела. Запишите цифры, под которыми они указаны.
1) Период колебаний тела равен 4 с.
2) Амплитуда колебаний тела примерно равна 8 мм.
3) Максимальная потенциальная энергия пружины равна 16 мкДж.
4) Частота ν колебаний тела равна 2 Гц.
5) Масса тела примерно равна 400 г.
В электрической цепи, схема которой изображена на рисунке, конденсатор ёмкостью С = 4 мкФ в начальный момент заряжен до напряжения U = 100 В, а оба ключа разомкнуты. Замкнув ключ К1, к конденсатору подключили цепочку из двух последовательно соединённых катушек с одинаковой индуктивностью L = 20 мГн, в результате чего в цепи возникли гармонические колебания. В момент, когда сила тока в цепи при этих колебаниях обратилась в ноль, замкнули ключ К2. Как и на сколько изменилась после этого амплитуда колебаний силы тока в цепи?
Небольшое тело массой 200 г, закреплённое на лёгкой пружине, совершает гармонические колебания вдоль оси Ox. На рисунке показан график зависимости проекции скорости Vx этого тела на указанную ось от времени t.
Из приведённого ниже списка выберите все верные утверждения, описывающие данное движение тела. Запишите цифры, под которыми они указаны.
1) Период колебаний тела равен 2 с.
2) Частота ν колебаний тела равна 0,25 Гц.
3) Жёсткость пружины примерно равна 0,5 Н/м.
4) Амплитуда колебаний тела примерно равна 13 мм.
5) Максимальная кинетическая энергия тела равна 20 мкДж.
Груз массой m, подвешенный к длинной нерастяжимой нити длиной l, совершает колебания с периодом Угол максимального отклонения равен
Что произойдет с периодом колебаний, максимальной кинетической энергией и частотой колебаний нитяного маятника, если при неизменном максимальном угле отклонения груза уменьшить длину нити?
К каждому элементу первого столбца подберите элемент из второго и внесите в строку ответов выбранные цифры под соответствующими буквами. Цифры могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) Период колебаний
Б) Максимальная кинетическая энергия
В) Частота колебаний
ИЗМЕНЕНИЕ ВЕЛИЧИНЫ
1) Увеличивается
2) Уменьшается
3) Не изменится
Груз, подвешенный к пружине с коэффициентом жесткости k совершает колебания с периодом T и амплитудой Что произойдет с периодом колебаний, максимальной потенциальной энергией пружины и частотой колебаний, если пружину заменить на другую с меньшим коэффициентом жесткости, а амплитуду колебаний оставить прежней?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
4) может измениться любым из выше указанных способов
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Период колебаний | Максимальная потенциальная
энергия пружины |
Частота колебаний |
Пружинный маятник представляет собой груз, прикреплённый к легкой пружине. Он совершает гармонические колебания вдоль поверхности гладкого горизонтального стола. В момент, когда груз находился в крайней точке своей траектории, к нему прилипла тяжелая дробинка, не имевшая в момент перед прилипанием скорости относительно груза. Как изменились в результате этого частота колебаний пружинного маятника, амплитуда колебаний пружинного маятника, максимальная кинетическая энергия пружинного маятника?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) частота колебаний пружинного маятника
Б) амплитуда колебаний пружинного маятника
В) максимальная кинетическая энергия пружинного маятника
ИХ ИЗМЕНЕНИЕ
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Груз массой подвесили на невесомой пружине, и он мог совершать вертикальные гармонические колебания с некоторой частотой. Затем параллельно первой пружине присоединили вторую такую же и подвесили к ним другой груз. Частота колебаний новой системы оказалась вдвое меньше, чем прежней. Чему равна масса М второго груза?
Какие законы Вы используете для описания колебательного движения маятника? Обоснуйте их применение.
На гладкой плоскости, наклонённой под углом
= 30° к горизонту, лежит маленький грузик, привязанный невесомой нерастяжимой нитью длиной l = 40 см к вбитому в плоскость гвоздику (см. рис.). Найдите период малых (угол
<< 1) колебаний грузика после его отклонения от положения равновесия вдоль плоскости в направлении, перпендикулярном нити.
Какие законы Вы используете для описания малых колебаний шарика? Обоснуйте их применение к данному случаю.
Груз, подвешенный к пружине с коэффициентом жесткости k, совершает колебания с периодом T и амплитудой Что произойдет с периодом колебаний, максимальной потенциальной энергией пружины и частотой колебаний, если пружину заменить на другую с большим коэффициентом жесткости, а амплитуду колебаний оставить прежней?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
4) может измениться любым из выше указанных способов
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Период колебаний | Максимальная потенциальная
энергия пружины |
Частота колебаний |
Груз массой m колеблется с периодом T и амплитудой
на гладком горизонтальном столе. Что произойдет с периодом колебаний, максимальной потенциальной энергией пружины и частотой колебаний, если при неизменной амплитуде увеличить массу груза?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Период колебаний | Максимальная потенциальная
энергия пружины |
Частота колебаний |
Груз, подвешенный на лёгкой пружине жёсткостью 200 Н/м, совершает вертикальные колебания. На рисунке изображены графики зависимости смещения груза x и проекции скорости груза Vx от времени t.
На основании анализа приведённых графиков, выберите все верные утверждения и укажите в ответе их номера.
1) Круговая частота ω колебаний груза равна 20 рад/с.
2) Период колебаний груза равен (0,1π) с.
3) Максимальное ускорение груза равно по модулю 800 см/с2.
4) Масса груза равна 1 кг.
5) Максимальная потенциальная энергия упругой деформации пружины равна 4 кДж.
Груз, подвешенный на лёгкой пружине жёсткостью 200 Н/м, совершает вертикальные колебания. На рисунке изображены графики зависимости смещения груза x и проекции скорости груза Vx от времени t.
На основании анализа приведённых графиков, выберите все верные утверждения и укажите в ответе их номера.
1) Круговая частота ω колебаний груза равна 20 рад/с.
2) Период колебаний груза равен (10/π) с.
3) Максимальное ускорение груза равно по модулю 80 см/с2.
4) Масса груза равна 1 кг.
5) Максимальная потенциальная энергия упругой деформации пружины равна 202,5 мДж.
Равносторонний треугольник, состоящий из трёх жёстких лёгких стержней, может вращаться без трения вокруг горизонтальной оси, совпадающей с одной из его сторон. В точке пересечения двух других его сторон к треугольнику прикреплён массивный грузик (см. рисунок). Как и во сколько раз изменится период малых колебаний грузика около его положения равновесия, если ось вращения наклонить под углом
к горизонту?
Какие законы Вы используете для описания движения маятника? Обоснуйте их применение.
Равносторонний треугольник, состоящий из трех жёстких лёгких стержней, может вращаться без трения вокруг горизонтальной оси, совпадающей с одной из его сторон. В точке пересечения двух других его сторон к треугольнику прикреплен массивный грузик (см. рис.). Как и во сколько раз изменится период малых колебаний грузика около его положения равновесия, если ось вращения наклонить под углом
к горизонту?
Какие законы Вы используете для описания движения маятника? Обоснуйте их применение.
В колебательном контуре из конденсатора электроемкостью 2 мкФ и катушки происходят свободные электромагнитные колебания с циклической частотой Амплитуда колебаний силы тока в контуре 0,01 А. Чему равна амплитуда колебаний напряжения на конденсаторе? Ответ приведите в вольтах.
В колебательном контуре из конденсатора и катушки индуктивностью 0,5 Гн происходят свободные электромагнитные колебания с циклической частотой Амплитуда колебаний силы тока в контуре 0,01 А. Чему равна амплитуда колебаний напряжения на катушке? Ответ приведите в вольтах.
Груз массой m, подвешенный к пружине, совершает колебания с периодом T и амплитудой Что произойдет с периодом колебаний, максимальной потенциальной энергией пружины и частотой колебаний, если при неизменной амплитуде уменьшить массу груза?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Период колебаний | Максимальная потенциальная
энергия пружины |
Частота колебаний |
Груз массой m, подвешенный к пружине, совершает колебания с периодом T и амплитудой Что произойдет с периодом колебаний, максимальной потенциальной энергией пружины и частотой колебаний, если при неизменной амплитуде увеличить массу груза?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Период колебаний | Максимальная потенциальная
энергия пружины |
Частота колебаний |
Всего: 556 1–20 | 21–40 | 41–60 | 61–80 …
Тема 3.
Статика. Гидростатика. Механические колебания и волны. Импульс. Законы сохранения в механике
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
статика. гидростатика. механические колебания и волны. импульс. законы сохранения в механике
3.01Давление
3.02Гидростатика. Сила Архимеда
3.03Момент силы, механическое равновесие тела
3.04Механические колебания
3.05Волны
3.06Импульс
3.07Закон сохранения импульса и изменения импульса
3.08Работа силы
3.09Кинетическая энергия
3.10Потенциальная энергия силы тяжести и пружины
3.11Закон сохранения энергии и изменения энергии
3.12Мощность. КПД. Энергия
Решаем задачи
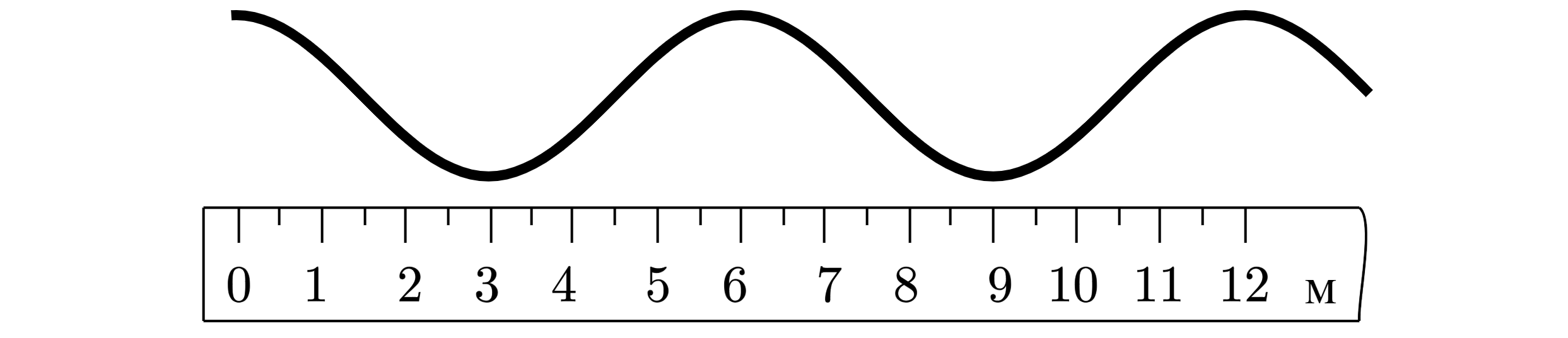
На рисунке представлена фотография шнура, по которому распространяется поперечная
волна.
Скорость распространения волны по шнуру равна 24 м/c. Определите частоту колебаний источника
волны (в Гц).
Показать ответ и решение
Формула для расчета частоты:
где
– скорость распространения,
– длина волны.
По рисунку длина волны равна 6 м (9 м — 3 м). Тогда
Колеблющаяся струна издает звук с длиной волны м. Найдите период колебания, если
скорость звука м/с. Ответ дайте в секундах.
Показать ответ и решение
Период колебания волн вычисляется по формуле:
Где – это частота колебаний
Формула для расчета частоты:
Подставим (2) в (1)
Показать ответ и решение
Формула для расчета частоты:
Где – частота колебаний
Выразим скорость
Частота и период связаны формулой:
Подставим (2) в (1)
Показать ответ и решение
Формула для расчета частоты:
Выразим скорость и подставим числа из условия
Петя стоит на расстоянии м от горы и говорит в громкоговоритель. Найдите время,
через которое Петя вновь услышит себя. Скорость звука принять 330 м/c. (Ответ дайте в
секундах.)
Показать ответ и решение
Звук сначала дойдет до горы, потом отразится от горы и вновь дойдет до Пети. Значит он пройдет ,
обозначим это расстояние , а двигаться будет равномерно. Чтобы посчитать время будем
использовать формулу
Где – скорость звука
Колеблющаяся струна издает звук с длиной волны м. Найдите частоту колебаний, если
скорость звука м/с. (Ответ дайте в Гц)
Показать ответ и решение
Формула для расчета частоты
Муха крыльями совершает 300 колебаний за 2 минуты. Найдите частоту колебания крыльев. (Ответ
дайте в Гц)
Показать ответ и решение
Формула для расчета частоты:
Где – количество колебаний, а
– время за которое совершили данное количество
колебаний.
Переведем время в СИ: 2 минуты=120 секунд.
Посчитаем частоту:
Показать ответ и решение
Время рассчитыватся по формуле , где
– скорость. Значит:
Формула для нахождение скорости:
Значит,
Подставим (2) и (3) в (1)
Пчела совершает 600 взмахов крыльев в минуту. Найдите период колебания крыльев. (Ответ дайте в
секундах)
Показать ответ и решение
Период найдем по формуле:
Где — частота колебаний.
Частоту колебаний найдем по формуле:
где – количество взмахов,
– время, за которое совершается данное количество
взмахов.
Переведем взмахи/минуту в взмахи/секунду
Частота колебаний равна 10 Гц. Найдем период:
Показать ответ и решение
Частота находится по формуле:
Выразим :
Значит,
Так как звук в одной среде распространяется с одинаковой скоростью, то , следовательно
Показать ответ и решение
Частота находится по формуле
Значит
Так как звук в одной среде распространяется с одинаковой скоростью, то , следовательно
Канатоходец заметил, что, когда он наступает на канат, то он выглядит так, как показано на
рисунке, а скорость распространения волны 3 м/с. Найдите частоту колебаний. Ответ дайте в
Гц.
Показать ответ и решение
По рисунку видно, что половина длины волны равна 3 метра, значит длина волны равна 6
м.
По формуле найдем частоту:
Задачи на Механические волны с решениями
Формулы, используемые на уроках «Задачи на Механические волны».
Название величины |
Обозначение |
Единица измерения |
Формула |
Длина волны |
λ |
м |
λ = vT ;λ = v / v |
Скорость волны |
v |
м/с |
v = λ / T ;v = λv |
Период колебаний |
T |
с |
T = λ / v ;T = t / N |
Частота колебаний |
v |
Гц |
v = v / λ ;v = N / t |
Число колебаний |
N |
N = t / T ;N = vt |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Лодка качается на волнах, распространяющихся со скоростью 4 м/с, и за 10 с совершает 20 колебаний. Каково расстояние между соседними гребнями волн?
Задача № 2.
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.
Задача № 3.
Скорость звука в эбоните 2400 м/с, а в кирпиче — 3600 м/с. В каком веществе звуковому сигналу требуется большее время для распространения? Во сколько раз?
Задача № 4.
Расстояние между ближайшими гребнями волн в море 6 м. Лодка качается на волнах, распространяющихся со скоростью 2 м/с. Какова частота ударов волн о корпус лодки?
Задача № 5.
Наблюдатель, находящийся на расстоянии 2 км 150 м от источника звука, слышит звук, пришедший по воздуху, на 4,8 с позднее, чем звук от того же источника, пришедший по воде. Определите скорость звука в воде, если скорость звука в воздухе равна 345 м/с.
Задача № 6.
Охотник выстрелил, находясь на расстоянии 170 м от лесного массива. Через сколько времени после выстрела охотник услышит эхо?
Задача № 7.
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.
Задача № 8.
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?
Задача № 9.
Длина волны в воздухе 17 см (при скорости 340 м/с). Найти скорость распространения звука в теле, в котором при той же частоте колебаний длина волны равна 1,02 м.
Задача № 10.
ОГЭ
Расстояние между гребнями волн в море λ = 5 м. При встречном движении катера волна за t = 1 с ударяет о корпус катера N1 = 4 раза, а при попутном — N2 = 2 раза. Найти скорость катера и волны.
Задача № 11.
ОГЭ
Звуковые колебания, имеющие частоту v = 500 Гц и амплитуду А = 0,25 мм, распространяются в воздухе. Длина волны λ = 70 см. Найти скорость распространения колебаний v и максимальную скорость частиц среды.
Краткая теория для решения Задачи на Механические волны.
Это конспект по теме «ЗАДАЧИ на Механические волны». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на
- Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
По теме: методические разработки, презентации и конспекты
Механические колебания м волны .Тест
тест по теме «Механические колебания м волны » поможет проверить и оценить знания учащихся по данной теме…
Механические колебания и волны
презентация урока по физике 8 класса. С помощью данной презентации можно повторить теоретические сведения данной темы и провести контроль знаний. Задания для проверки подобраны нестандартные….
Обобщение и систематизация знаний по теме: «Механические колебания и волны»
Урок повторения материала по главе «Механические колебания и волны», подготовка к контрольной работе…
Решение задач по теме «Механические колебания и волны. Звук».
Урок физики в 9 классе. Урок обобщения, закрепления и комплексного применения знаний. На данном уроке отрабатываются навыки решения качественных и количественных задач. Расширяется кругозор обучающихс…
Вопросы к зачёту по темам: «Механические колебания и волны» и «Электростатика»
Зачёты сдаются письменно в формате проверочных работ…
Проверочная работа по теме «Механические колебания и волны. Звук» Физика 9 кл. УМК Пёрышкин А.В.
Тестовые задания «Механические колебания и волны. Звук» по физике 9 кл…
Повторительно-обобщающий урок «Механические колебания и волны. Звук».
Тема урока — Повторительно-обобщающий урок «Механические колебания и волны. Звук».План урокаI. Организационный моментII. Повторение темы «Механические колебания» 1. Разми…
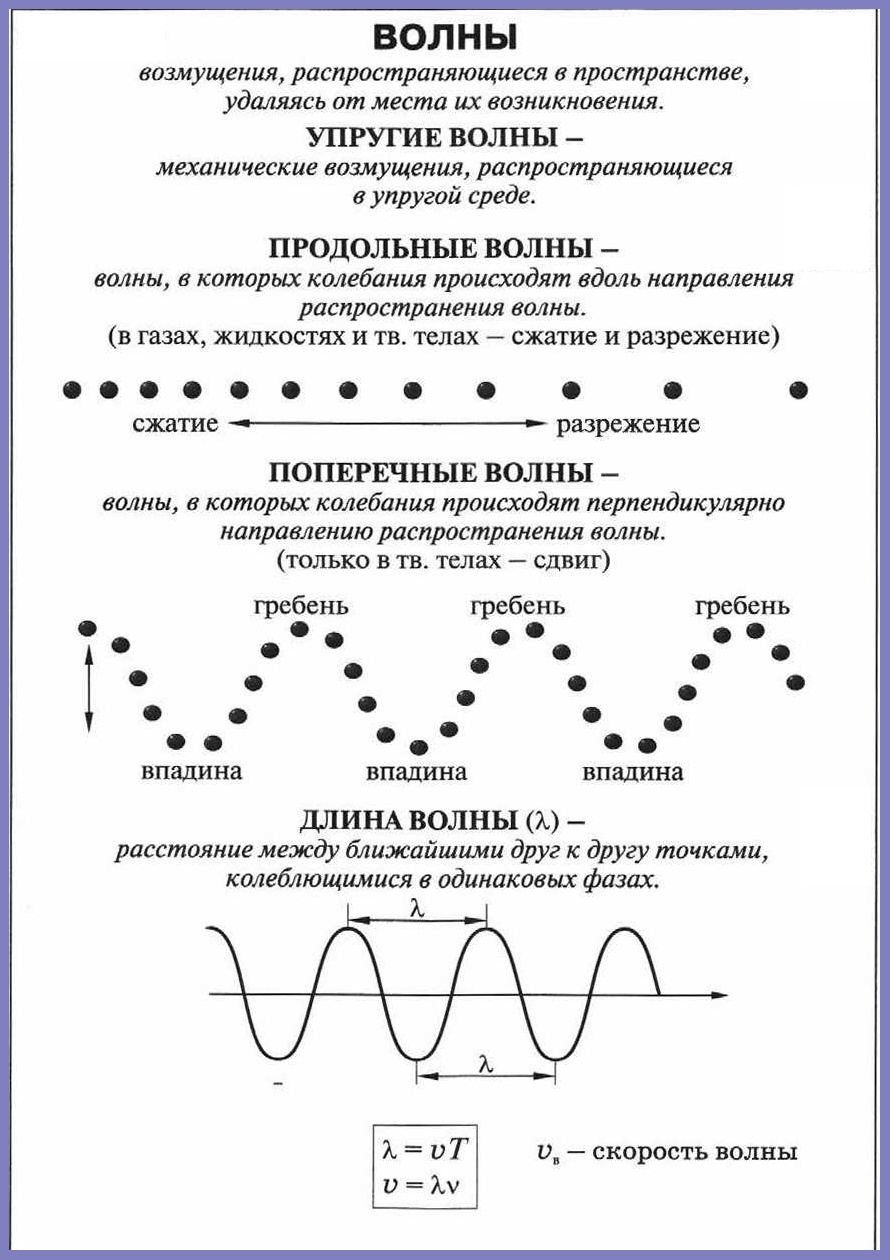
Волновой процесс — любое изменение состояния сплошной среды, распространяющееся со скоростью и несущее энергию.
Поперечные волны — волны, при распространении которых смещение частиц среды происходит в направлении, перпендикулярном распространению волны.
— волна, при распространении которой смещение частиц среды происходит в направлении распространения волны.
Длина волны (lambda) — расстояние между двумя ближайшими друг другу точками в пространстве, в которых колебания происходят в одинаковой фазе.
Единицы измерения: (displaystyle [text{м}])
Скорость распространения волны
[displaystyle v=dfrac{lambda}{T}=hnu]
где (T) — период колебаний, (nu) — частота колебаний.
Поскольку для всех электромагнитных волн скорость в вакууме ((c)) одинакова, по частоте легко определить длину волны (lambda):
[lambda=dfrac{c}{nu}]
Какова скорость звуковых волн в среде (upsilon), если при частоте (nu=500) Гц длина волны (lambda=2) м?
Формула для расчета частоты: [nu=frac{upsilon}{lambda}]
Выразим скорость и подставим числа из условия [upsilon=nucdotlambda=500text{ Гц}cdot2text{ м}=1000text{ м/с}]
Ответ: 1000
Какова скорость звуковых волн в среде (upsilon), если период (T=0,025) с, а длина волны (lambda=3) м?
Формула для расчета частоты: [nu=frac{upsilon}{lambda}]
Где (nu) – частота колебаний
Выразим скорость [upsilon=nu cdot lambda quad (1)]
Частота и период связаны формулой: [nu=frac{1}{T} quad (2)]
Подставим (2) в (1) [upsilon=frac{lambda}{T}=frac{3text{ м}}{0,025text{ с}}=120 text{ м/с}]
Ответ: 120
Колеблющаяся струна издает звук с длиной волны (lambda=1,36) м. Найдите период колебания, если скорость звука (upsilon=340) м/с. Ответ дайте в секундах.
Период колебания волн вычисляется по формуле: [T=frac{1}{nu}quad (1)]
Где (nu) – это частота колебаний
Формула для расчета частоты: [nu=frac{upsilon}{lambda}quad (2)]
Подставим (2) в (1) [T=frac{lambda}{upsilon}=frac{1,36text{ м}}{340text{ м/c}}=0,004text{ с}]
Ответ: 0,004
Струна гитары издает звуковые волны с максимальной длиной волны (lambda_1=3) м, а струна балалайки (lambda_2=12) м. Найдите отношение частот (dfrac{nu_1}{nu_2}).
Частота находится по формуле [nu=dfrac{upsilon}{lambda}]
Значит [dfrac{nu_1}{nu_2}=dfrac{dfrac{upsilon_1}{lambda_1}}{dfrac{upsilon_2}{lambda_2}}]
Так как звук в одной среде распространяется с одинаковой скоростью, то (upsilon_1=upsilon_2), следовательно [dfrac{nu_1}{nu_2}=dfrac{lambda_2}{lambda_1}=dfrac{12text{ м}}{3text{ м}}=4]
Ответ: 4
Колебания и волны.
Задачи ЕГЭ с решениями
Формулы для решения задач по теме «Колебания и волны. Задачи ЕГЭ».
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1.[/su_highlight] При измерении пульса человека было зафиксировано 75 пульсаций крови за 1 мин. Определите частоту сокращения сердечной мышцы.
Задача 2.[/su_highlight] Каков период колебаний поршня двигателя автомобиля, если за 30 с поршень совершает 600 колебаний?
Задача 3.[/su_highlight] Сколько полных колебаний совершит материальная точка за 5 с, если частота колебаний 440 Гц?
Задача 4.[/su_highlight] Тело совершает гармонические колебания по закону х = 0,2sin(4πt). Определите амплитуду колебаний.
Задача 5.[/su_highlight] Математический маятник совершил 100 колебаний за 628 с. Чему равна длина нити маятника?
Задача 6.[/su_highlight] Амплитуду колебаний математического маятника уменьшили в 2 раза. Как при этом изменился период колебаний маятника?
Задача 7.[/su_highlight] К пружине жесткостью 200 Н/м подвешен груз массой 0,4 кг. Определите частоту свободных колебаний этого пружинного маятника.
Задача 8.[/su_highlight] Груз, подвешенный на пружине жесткостью 250 Н/м, совершает свободные колебания с циклической частотой 50 с–1. Найдите массу груза.
Задача 9.[/su_highlight] Груз, подвешенный на лёгкой пружине жесткостью 100 Н/м, совершает свободные гармонические колебания. Какой должна быть жесткость пружины, чтобы частота колебаний этого же груза увеличилась в 4 раза?
Задача 10.[/su_highlight] Расстояние между ближайшими гребнями волн в море 4 м. Лодка качается на волнах, распространяющихся со скоростью 3 м/с. С какой частотой волны ударяют о корпус лодки?
Задача 11.[/su_highlight] Источник колебаний с периодом 5 мс вызывает в воде звуковую волну с длиной волны 7,175 м. Определите скорость звука в воде.
Задача 12.[/su_highlight] Звуковая волна частотой 1 кГц распространяется в стальном стержне со скоростью 5 км/с. Определите длину этой волны.
Задача 13.[/su_highlight] Скорость звука в воздухе 340 м/с. Длина звуковой волны в воздухе для самого низкого мужского голоса достигает 4,3 м. Определите частоту колебаний этого голоса.
Задача 14.[/su_highlight] Колебания напряжения на конденсаторе в цепи переменного тока описываются уравнением: u = 50соs(100πt), где все величины выражены в единицах СИ. Чему равна циклическая частота колебаний напряжения?
Задача 15.[/su_highlight] Чему равен период колебаний в колебательном контуре, состоящем из конденсатора емкостью 4 мкФ и катушки индуктивности 1 Гн? Ответ выразите в миллисекундах, округлив его до целых.
Задача 16.[/su_highlight] Колебательный контур состоит из конденсатора электроемкостью С и катушки индуктивности L. Как изменится период электромагнитных колебаний в этом контуре, если электроемкость конденсатора увеличить в 4 раза?
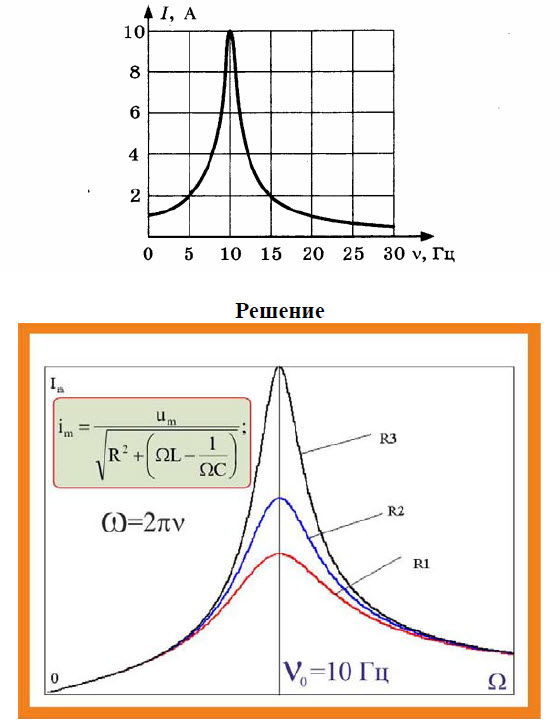
Задача 17.[/su_highlight] На рисунке представлен график зависимости амплитуды силы тока вынужденных колебаний от частоты v вынуждающей ЭДС. При какой частоте происходит резонанс?
Задача 18.[/su_highlight] Амплитуда колебаний напряжения на участке цепи переменного тока равна 50 В. Чему равно действующее значение напряжения на этом участке цепи?
Задача 19.[/su_highlight] Действующее значение силы тока в цепи переменного то ка равно 5 А. Чему равна амплитуда колебаний силы тока в цепи?
Задача 20.[/su_highlight] Сила тока через резистор меняется по закону i = 36sin(128t). Определите действующее значение силы тока в цепи.
Задача 21.[/su_highlight] Емкость конденсатора, включенного в цепь переменного тока, равна 2 мкФ. Уравнение колебаний напряжения на конденсаторе имеет вид: u = 75cos(2•103t), где все величины выражены в СИ. Определите амплитуду силы тока.
Задача 22.[/su_highlight] Чему равна длина электромагнитной волны, распространяющейся в воздухе, если период колебаний 0,01 мкс? Скорость распространения электромагнитных волн с = 3 10* м/с .
Задача 23.[/su_highlight] На какую длину волны нужно настроить радиоприёмник, чтобы слушать радиостанцию «Наше радио», которая вещает на частоте 101,7 МГц? Скорость распространения электромагнитных волн с = 3 • 108 м/с.
Задача 24.[/su_highlight] Длина электромагнитной волны в воздухе равна 0,6 мкм. Чему равна частота колебаний вектора напряженности электрического поля в этой волне? Скорость распространения электромагнитных волн с = 3 • 108 м/с.
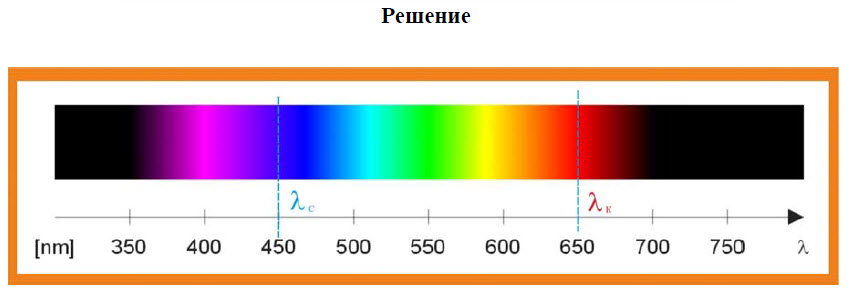
Задача 25.[/su_highlight] У какого света больше длина волны у красного или синего?
Задача 26.[/su_highlight] Земля удалена от Солнца на расстояние 150 млн км. Сколько времени идет свет от Солнца к Земле? Скорость распространения электромагнитных волн с = 3 • 108 м/с.
Вы смотрели конспект по теме «Колебания и волны. Задачи ЕГЭ». Ключевые слова конспекта: Кинематика гармонических колебаний. Математический маятник. Пружинный маятник. Энергия колебаний. Волны. Электрический контур. Переменный ток. Трансформаторы. Автор задач и решений: Исаков Александр Яковлевич (КамчатГТУ). Выберите дальнейшие действия:
- Перейти к теме:
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Колебания — сложные задачи.
Задачи на малые колебания – всегда не самые простые, а эти предлагают учащимся СУНЦ МГУ в качестве домашнего задания. Начнем с самых простых, затем перейдем к тем, что сложнее. Порешаем?
Задача 1.
Определите период малых колебаний математического маятника длиной
, точка подвеса которого закреплена в кабине лифта, движущегося с постоянным ускорением
а)вниз, б) вверх.
Решение. Показать
Задача 2.
Определите период малых колебаний и положение равновесия математического маятника длиной
, находящегося в вагоне, движущемся с постоянным горизонтальным ускорением
.
Решение.Показать
Задача 3.
Груз колеблется по вертикали на резиновом шнуре с частотой . Какой будет частота
колебаний груза на этом шнуре, если его сложить вдвое?
Решение.Показать
Задача 4.
Определите период малых колебаний математического маятника длиной
см, если он находится в жидкости, плотность которой в 3 раза меньше плотности материала тела. Сопротивление жидкости пренебрежимо мало.
Решение. Показать
Задача 5.
По гладкой горизонтальной направляющей длины скользит бусинка с отрицательным зарядом
и массой
. На концах направляющей находятся отрицательные заряды
. Бусинка совершает малые колебания с периодом
. Чему будет равен период колебаний бусинки, если ее заряд увеличить в 4 раза?
Решение.Показать
Статьи
Подготовка к ОГЭ и ЕГЭ
Среднее общее образование
Линия УМК А. В. Грачева. Физика (10-11) (БУ)
Физика
ЕГЭ по физике: решение задач о колебаниях
Александр Грачев, кандидат физико-математических наук, доцент МГУ, автор УМК по физике, рассказал о едином подходе к решению задач о колебаниях.
27 июня 2017
Материал подготовлен на основе вебинара «Трудные вопросы ЕГЭ по физике: Методика решения задач по механическим и электромагнитным колебаниям».
Как достичь успеха в обучении физике? Либо заставлять учить, либо помогать понимать. Выбор только между этими плоскостями. Учить — это запоминать и подставлять числа в формулы. А как учить понимать?
Это надо делать серьезно с самого начала — давать более широкий взгляд на явления, опираться на аналогии. Пока люди не прочувствуют закономерности — ничего не поймут. На этих принципах построен учебник физики (Линия УМК А. В. Грачева. Физика, 10-11), а теперь к ним вышли и рабочие тетради. Задания из них уже вошли в ЕГЭ.
Так, в учебнике для 11 класса идет разговор о гармонических механических колебаниях, и дается два способа решения — динамический и энергетический — представлены соположено. Значит ли это, что выбор равноправный и произвольный? От чего зависит? А теперь смотрим на электромагнитные — насколько симметрична ситуация для механических и электромагнитных колебаний? И оказывается, тут тоже два способа, и первый похож на динамический, но с некоторой разницей, и мы решаем и опять приходим к ситуации, как в механике. Полезно обдумывать эти аналогии с учениками, они должны прочувствовать эти замены, ведь математические истории, которые стоят за ними, одни и те же.
Таким же естественным должен стать графический подход для понимания процессов колебания. Сначала придется обстоятельно поговорить о первой четверти периода — что происходит при замене электрической энергии на потенциальную, магнитную на кинетическую? Надо, чтобы график помогал ученикам описывать разные истории. И тогда задача №18 из ЕГЭ не вызовет проблем. Тут речь об одной из энергий, а не о чем-либо другом, и надо смотреть, с чего задача (график) начинается.
Есть по теме и «волшебная» формула — формула изменения энергии в зависимости от работы внешних сил и сил трения. Проникнуться ей, понять ее — значит, суметь вывести все формулы колебания и свободно думать во многих ситуациях (задачи №№5, 16, 30).
Полезно придумывать задачи для одного вида колебаний по поводу уже существующих для другого. В рабочей тетради есть такие задачи, но всегда интересно попробовать самому. И так на любой теме: мыслим глобально, чтобы хорошо решать локально.
Решение задач о гармонических механических колебаниях:

Решение задач о свободных гармонических электромагнитных колебаниях двумя способами:

Записала Людмила Кожурина