Задачи на механическое движение егэ - Помощь в подготовке к экзаменам и поступлению

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 36 1–20 | 21–36

Добавить в вариант

На гладком горизонтальном столе покоится брусок с прикреплённой к нему гладкой изогнутой в вертикальной плоскости тонкой жёсткой трубкой (см. рис.). Общая масса бруска с трубкой равна M = 0,8 кг. В верхний конец вертикальной части трубки, находящийся на высоте H = 70 см над бруском, опускают без начальной скорости маленький шарик массой m = 50 г. Другой конец трубки наклонён к горизонту под углом α = 30° и находится на высоте h = 20 см над бруском. Найдите модуль скорости, с которой будет двигаться брусок после того, как шарик вылетит из трубки.

Какие законы Вы используете для описания движения и взаимодействия трубки и шарика? Обоснуйте их применение к данному случаю.

Источник: Тренировочная работа по физике 28.04.2017, вариант ФИ10503

Задания Д1 B1 № 131

Лодка должна попасть на противоположный берег реки по кратчайшему пути в системе отсчета, связанной с берегом. Скорость течения реки u, а скорость лодки относительно воды v . Чему должен быть равен модуль скорости лодки относительно берега?

Автобус везёт пассажиров по прямой дороге со скоростью 10 м/с. Пассажир равномерно идёт по салону автобуса со скоростью 1 м/с относительно автобуса, двигаясь от задней двери к кабине водителя. Чему равен модуль скорости пассажира относительно дороги? (Ответ дайте в метрах в секунду.)

Задания Д29 C2 № 9072

Задания Д1 B1 № 5952

Два камня одновременно бросили из одной точки: первый  — вертикально вверх, второй  — под углом 45° к горизонту. Сопротивление воздуха пренебрежимо мало. Как движется первый камень в системе отсчёта, связанной со вторым камнем?

1)  покоится

2)  движется по параболе

3)  движется равномерно и прямолинейно

4)  движется по дуге окружности

Задания Д1 B1 № 5987

Два камня одновременно бросили из одной точки: первый  — вертикально вверх, второй  — под углом 30° к горизонту. Сопротивление воздуха пренебрежимо мало. Как движется второй камень в системе отсчёта, связанной с первым камнем?

1)  покоится

2)  движется по параболе

3)  движется равномерно и прямолинейно

4)  движется по дуге окружности

Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге навстречу ему едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)

Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге в том же направлении едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)

Задания Д2 B2 № 6637

Маша взяла в руку монету и, стоя в комнате своей квартиры, выпустила её из пальцев без начальной скорости. Монета полетела вдоль вертикали и упала на пол комнаты. Затем Маша вышла из дома, села в подъехавший автобус и, дождавшись, пока он начнёт двигаться равномерно и прямолинейно по горизонтальной дороге, повторила опыт с бросанием монеты. Оказалось, что монета в равномерно движущемся автобусе падает точно так же, как и в квартире. Иллюстрацией какого закона или принципа может служить этот опыт?

1)  первого закона Ньютона

2)  второго закона Ньютона

3)  третьего закона Ньютона

4)  принципа относительности Галилея

Задания Д2 B2 № 6676

Саша взял в руку монету и, стоя в равномерно движущемся вниз лифте, выпустил её из пальцев без начальной скорости. Монета полетела вдоль вертикали и упала на пол лифта. Затем Саша вышел из дома, сел в подъехавший автобус и, дождавшись, пока он начнёт двигаться равномерно и прямолинейно по горизонтальной дороге, повторил опыт с бросанием монеты. Оказалось, что монета в равномерно движущемся автобусе падает точно так же, как и в равномерно опускающемся лифте. Иллюстрацией какого закона или принципа может служить этот опыт?

1)  Первого закона Ньютона

2)  Второго закона Ньютона

3)  Третьего закона Ньютона

4)  принципа относительности Галилея

Задания Д1 B1 № 125

Вертолет поднимается вертикально вверх. Какова траектория движения точки на конце лопасти винта вертолета в системе отсчета, связанной с винтом?

1)  точка

2)  прямая

3)  окружность

4)  винтовая линия

Задания Д3 B3 № 4412

Два бруска массой m и равномерно движутся вдоль прямой OX (см. рис.). В системе отсчёта, связанной с бруском модуль импульса второго бруска равен

1)   6mV

2)   4mV

3)   3mV

4)   2mV

Задания Д3 B3 № 4447

Два бруска массой m и равномерно движутся вдоль прямой OX (см. рис.). В системе отсчёта, связанной с бруском модуль импульса первого бруска равен

1)  mV

2)   2mV

3)   3mV

4)   4mV

Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показано изменение расстояния между автомобилями с течением времени. Каков модуль скорости первого автомобиля в системе отсчёта, связанной со вторым автомобилем? Ответ приведите в метрах в секунду.

Источник: Демонстрационная версия ЕГЭ—2020 по физике.

Задания Д1 B1 № 3357

Вертолет равномерно поднимается вертикально вверх. Какова траектория крайней точки лопасти вертолета в системе отсчета, связанной с корпусом вертолета?

1)  прямая линия

2)  винтовая линия

3)  окружность

4)  эллипс

Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с. (Ответ дайте в метрах в секунду.)

Из незакреплённой пушки стреляют снарядом массой 20 кг, который вылетает из ствола в горизонтальном направлении со скоростью 102 м/с относительно пушки. Пушка при этом откатывается, приобретая относительно земли скорость 2 м/с. Чему равна масса пушки, если массой сгоревшего порохового заряда можно пренебречь? Ответ дайте в килограммах.

Из незакреплённой пушки массой 800 кг стреляют снарядом, который вылетает из ствола в горизонтальном направлении со скоростью 102 м/с относительно пушки. Пушка при этом откатывается, приобретая относительно земли скорость 2 м/с. Чему равна масса снаряда, если массой сгоревшего порохового заряда можно пренебречь? Ответ дайте в килограммах.

Пароход движется по реке против течения со скоростью 5 м/с относительно берега. Определите скорость течения реки, если скорость парохода относительно берега при движении в обратном направлении равна 8 м/с. (Ответ дайте в метрах в секунду.)

Всего: 36 1–20 | 21–36

Источник

Механическое движение.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: механическое движение и его виды, относительность механического движения, скорость, ускорение.

Понятие движения является чрезвычайно общим и охватывает самый широкий круг явлений. В физике изучают различные виды движения. Простейшим из них является механическое движение. Оно изучается в механике.
Механическое движение — это изменение положение тела (или его частей) в пространстве относительно других тел с течением времени.

Если тело A меняет своё положение относительно тела B, то и тело B меняет своё положение относительно тела A. Иначе говоря, если тело A движется относительно тела B, то и тело B движется относительно тела A. Механическое движение является относительным — для описания движения необходимо указать, относительно какого тела оно рассматривается.

Так, например, можно говорить о движении поезда относительно земли, пассажира относительно поезда, мухи относительно пассажира и т. д. Понятия абсолютного движения и абсолютного покоя не имеют смысла: пассажир, покоящийся относительно поезда, будет двигаться с ним относительно столба на дороге, совершать вместе с Землёй суточное вращение и двигаться вокруг Солнца.
Тело, относительно которого рассматривается движение, называется телом отсчёта.

Основной задачей механики является определение положения движущегося тела в любой момент времени. Для решения этой задачи удобно представить движение тела как изменение координат его точек с течением времени. Чтобы измерить координаты, нужна система координат. Чтобы измерять время, нужны часы. Всё это вместе образует систему отсчёта.

Система отсчёта — это тело отсчёта вместе с жёстко связанной с ним («вмороженной»» в него) системой координат и часами.
Система отсчёта показана на рис. 1. Движение точки рассматривается в системе координат OXYZ . Начало координат является телом отсчёта.

Рисунок 1.

Вектор называется радиус-вектором точки . Координаты x, y, z точки являются в то же время координатами её радиус-вектора .
Решение основной задачи механики для точки состоит в нахождении её координат как функций времени: .
В ряде случаев можно отвлечься от формы и размеров изучаемого объекта и рассматривать его просто как движущуюся точку.

Материальная точка — это тело, размерами которого можно пренебречь в условиях данной задачи.
Так, поезд можно считать материальной точкой при его движении из Москвы в Саратов, но не при посадке в него пассажиров. Землю можно считать материальной точкой при описании её движения вокруг Солнца, но не её суточного вращения вокруг собственной оси.

К характеристикам механического движения относятся траектория, путь, перемещение, скoрость и ускорение.

Траектория, путь, перемещение.

В дальнейшем, говоря о движущемся (или покоящемся) теле, мы всегда полагаем, что тело можно принять за материальную точку. Случаи, когда идеализацией материальной точки пользоваться нельзя, будут специально оговариваться.

Траектория — это линия, вдоль которой движется тело. На рис. 1 траекторией точки является синяя дуга, которую описывает в пространстве конец радиус-вектора .
Путь — это длина участка траектории, пройденного телом за данный промежуток времени.
Перемещение — это вектор, соединяющий начальное и конечное положение тела.
Предположим, что тело начало движение в точке и закончило движение в точке (рис. 2). Тогда путь, пройденный телом, это длина траектории ACB . Перемещение тела — это вектор .

Рисунок 2.

Скорость и ускорение.

Рассмотрим движение тела в прямоугольной системе координат с базисом (рис. 3).

Рисунок 3.

Пусть в момент времени тело находилось в точке с радиус-вектором

Спустя малый промежуток времени Delta t тело оказалось в точке с
радиус-вектором

Перемещение тела:

(1)

Мгновенная скорость Delta v в момент времени — это предел отношения перемещения к интервалу времени Delta t , когда величина этого интервала стремится к нулю; иными словами, скорость точки — это производная её радиус-вектора:

$vec{v}=frac{displaystyle Delta vec{displaystyle r}}{displaystyle Delta displaystyle t}=frac{displaystyle dvec{r}}{displaystyle dt}$ (2)

Из (2) и (1) получаем:

$vec{v}=lim_{Delta trightarrow 0}left ( frac{displaystyle Delta displaystyle x}{displaystyle Delta displaystyle t}vec{displaystyle i}+frac{displaystyle Delta displaystyle y}{displaystyle Delta displaystyle t}vec{displaystyle j}+frac{displaystyle Delta displaystyle z}{displaystyle Delta displaystyle t}vec{displaystyle k} right )$

Коэффициенты при базисных векторах в пределе дают производные:

$dot{x}=lim_{Delta trightarrow 0}frac{displaystyle Delta displaystyle x}{displaystyle Delta displaystyle t}, dot{y}=lim_{Delta trightarrow 0}frac{displaystyle Delta displaystyle y}{displaystyle Delta displaystyle t}, dot{z}=lim_{Delta trightarrow 0}frac{displaystyle Delta displaystyle z}{displaystyle Delta displaystyle t}$

(Производная по времени традиционно обозначается точкой над буквой.) Итак,

Мы видим, что проекции вектора скорости на координатные оси являются производными координат точки:

$displaystyle v_{displaystyle x}=dot{x}, displaystyle v_{displaystyle y}=dot{y}, displaystyle v_{displaystyle z}=dot{z}.$

Когда Delta t стремится к нулю, точка приближается к точке и вектор перемещения разворачивается в направлении касательной. Оказывается, что в пределе вектор направлен точно по касательной к траектории в точке . Это и показано на рис. 3.

Понятие ускорения вводится похожит образом. Пусть в момент времени скорость тела равна vec{v} , а спустя малый интервал Delta t скорость стала равна .
Ускорение vec{a} — это предел отношения изменения скорости к интервалу , когда этот интервал стремится к нулю; иначе говоря, ускорение — это производная скорости:
$vec{a}=lim_{Delta trightarrow 0}frac{displaystyle Delta vec{displaystyle v}}{displaystyle Delta displaystyle t}=frac{displaystyle dvec{displaystyle a}}{displaystyle dt}.$

Ускорение, таким образом, есть «cкорость изменения скорости». Имеем:

$vec{a}=frac{displaystyle d}{displaystyle dt}(displaystyle v_{displaystyle x}vec{displaystyle i}+displaystyle v_{displaystyle y}vec{displaystyle j}+displaystyle v_{displaystyle z}vec{displaystyle k})=dot{displaystyle v_{displaystyle x}}vec{displaystyle i}+dot{displaystyle v_{displaystyle y}}vec{displaystyle j}+dot{v_{displaystyle z}}vec{displaystyle k}.$

Следовательно, проекции ускорения являются производными проекций скорости (и, стало быть, вторыми производными координат):

$displaystyle a_{displaystyle x}=dot{displaystyle v_{displaystyle x}}=ddot{displaystyle x}, displaystyle a_{displaystyle y}=dot{displaystyle v_{displaystyle y}}=ddot{displaystyle y}, displaystyle a_{displaystyle z}=dot{displaystyle v_{displaystyle z}}=ddot{displaystyle z}.$

Закон сложения скоростей.

Пусть имеются две системы отсчёта. Одна из них связана с неподвижным телом отсчёта . Эту систему отсчёта обозначим и будем называть неподвижной.
Вторая система отсчёта, обозначаемая {K} , связана с телом отсчёта {O} , которое движется относительно тела со скоростью vec{u} . Эту систему отсчёта называем движущейся. Дополнительно предполагаем, что координатные оси системы {K} перемещаются параллельно самим себе (нет вращения системы координат), так что вектор vec{u} можно считать скоростью движущейся системы относительно неподвижной.

Неподвижная система отсчёта обычно связана с землёй. Если поезд плавно едет по рельсам со скоростью vec{u} , это система отсчёта, связанная с вагоном поезда, будет движущейся системой отсчёта {K} .

Заметим, что скорость любой точки вагона (кроме вращающихся колёс!) равна vec{u} . Если муха неподвижно сидит в некоторой точке вагона, то относительно земли муха движется со скоростью vec{u} . Муха переносится вагоном, и потому скорость vec{u} движущейся системы относительно неподвижной называется переносной скоростью.

Предположим теперь, что муха поползла по вагону. Скорость мухи относительно вагона (то есть в движущейся системе {K} ) обозначается и называется относительной скоростью. Скорость мухи относительно земли (то есть в неподвижной системе ) обозначается vec{v} и называется абсолютной скоростью.

Выясним, как связаны друг с другом эти три скорости — абсолютная, относительная и переносная.
На рис. 4 муха обозначена точкой .Далее:
vec{r} — радиус-вектор точки в неподвижной системе ;
— радиус-вектор точки в движущейся системе {K} ;
vec{R} — радиус-вектор тела отсчёта {O} в неподвижной системе .

Рисунок 4.

Как видно из рисунка,

Дифференцируя это равенство, получим:

$frac{displaystyle dvec{displaystyle r}}{displaystyle dt}=frac{displaystyle dvec{displaystyle R}}{displaystyle dt}+frac{displaystyle d{vec{displaystyle r}}$ (3)

(производная суммы равна сумме производных не только для случая скалярных функций, но и для векторов тоже).
Производная есть скорость точки в системе , то есть абсолютная скорость:

$frac{displaystyle dvec{displaystyle r}}{displaystyle dt}=vec{v}$ .

Аналогично, производная есть скорость точки в системе {K} , то есть относительная скорость:

$frac{displaystyle d{vec{displaystyle r}}$
А что такое ? Это скорость точки {O} в неподвижной системе, то есть — переносная скорость vec{u} движущейся системы относительно неподвижной:

$frac{displaystyle dvec{displaystyle R}}{displaystyle dt}=vec{u}$

В результате из (3) получаем:

Закон сложения скоростей. Скорость точки относительно неподвижной системы отсчёта равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы. Иными словами, абсолютная скорость есть сумма переносной и относительной скоростей.

Таким образом, если муха ползёт по движущемуся вагону, то скорость мухи относительно земли равна векторной сумме скорости вагона и скорости мухи относительно вагона. Интуитивно очевидный результат!

Виды механического движения.

Простейшими видами механического движения материальной точки являются равномерное и прямолинейное движения.
Движение называется равномерным, если модуль вектора скорости остаётся постоянным (направление скорости при этом может меняться).

Движение называется прямолинейным, если направление вектора скорости остаётся постоянным (а величина скорости при этом может меняться). Траекторией прямолинейного движения служит прямая линия, на которой лежит вектор скорости.
Например, автомобиль, который едет с постоянной скоростью по извилистой дороге, совершает равномерное (но не прямолинейное) движение. Автомобиль, разгоняющийся на прямом участке шоссе, совершает прямолинейное (но не равномерное) движение.

А вот если при движении тела остаются постоянными как модуль скорости, так и его направление, то движение называется равномерным прямолинейным.

В терминах вектора скорости можно дать более короткие определения данным типам движения:

Важнейшим частным случаем неравномерного движения является равноускоренное движение, при котором остаются постоянными модуль и направление вектора ускорения:

равноускоренное движение

Наряду с материальной точкой в механике рассматривается ещё одна идеализация — твёрдое тело.
Твёрдое тело — это система материальных точек, расстояния между которыми не меняются со временем. Модель твёрдого тела применяется в тех случаях, когда мы не можем пренебречь размерами тела, но можем не принимать во внимание изменение размеров и формы тела в процессе движения.

Простейшими видами механического движения твёрдого тела являются поступательное и вращательное движения.
Движение тела называется поступательным, если всякая прямая, соединяющая две какие-либо точки тела, перемещается параллельно своему первоначальному направлению. При поступательном движении траектории всех точек тела идентичны: они получаются друг из друга параллельным сдвигом (рис. 5).

Рисунок 5.

Движение тела называется вращательным, если все его точки описывают окружности, лежащие в параллельных плоскостях. При этом центры данных окружностей лежат на одной прямой, которая перпендикулярна всем этим плоскостям и называется осью вращения.

На рис. 6 изображён шар, вращающийся вокруг вертикальной оси. Так обычно рисуют земной шар в соответствующих задачах динамики.

Рисунок 6.

Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Механическое движение.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

1.
Чему
равны перемещение и путь точки, расположенной на краю диска радиусом R, при его
повороте на ; 480⁰? (R, R;, )

2.
Катер
прошел по озеру в направлении строго на северо – восток 2
км, а затем в направлении на север 1
км. Найти величину и направление перемещения (угол к меридиану). (2,8
км; 30⁰)

3.
Тело
переместилось из т. А (-1; 2) в т. В (5; 3). Определите
радиус – вектор т. А и т. В, изменение радиус – вектора. (; 116,6⁰; ; 31⁰; )

4.
Радиус
– вектор т. А имеет модуль и угол наклона α =
45⁰ к оси ОХ. Материальная точка перемещается из т. А
в т. В (5; -1). Определите угол поворота радиус – вектора и его
изменение. (303,7; )

5.
Автоинспектор
ГАИ замечает радаром в 10 ч 46 мин, что скорость автомобиля,
находящегося в 100 м от поста ГАИ составляет 10 м/с. Какова
координата автомобиля через 1 мин? (500 м)

6.
Автобус
выезжает из п. А в п. В, находящимися друг от друга на расстоянии
70 км, в 8 ч 30 мин по московскому времени. Когда он
прибудет в пункт назначения, если скорость его движения 20 м/с? (9
ч 28 мин)

7.
Тело,
двигаясь прямолинейно и равномерно в плоскости XOY,
перемещается из точки А с координатами (1;2) в точку В с
координатами (4; -2) за время равное 10 с. Определите модуль
скорости тела, ее направление по отношению к оси ОХ. (0,5 м/с; -53⁰)

8.
Точка
А располагается на краю диска радиусом 3 см. За время 3,14 с
диск поворачивается на рад. Определите
скорость точки. (0,02 м/с; 0,0165 м/с)

9.
В
осях (t – v), где t – время в
секундах, v – скорость
в метрах в секунду, зависимость модуля скорости тела от времени имеет вид
прямой, соединяющей точки (0; 3) и (2; 9). Какой путь проходит
тело за промежуток времени от t₁ = 0 до t₂ =2 с? (12
м)

10.
По
заданным графикам x(t) на рис.
1.1. запишите уравнения движения тел. Из уравнений найдите место и время
встречи тел. Постройте зависимости S(t) и v(t).

11.
В
момент времени t = -2 с автомобиль
начал движение из точки х = 50 м с постоянной скоростью v = -10 м/с. Постройте
кривую зависимости x(t). В какой
момент времени автомобиль будет в точке 0? Запишите закон движения тела.
(3 с; х = 30 – 10t)

12.
Построить
график зависимости v (t) для движения
x = 15t + 2t² и
определить мгновенную скорость в момент времени t₁ = 10 с. (55
м/с)

13.
Тело
движется в плоскости XOY
прямолинейно по закону x = 2·t – 3; y = 5 – 0,5·t.
Определите скорость движения, её направление, путь и перемещение за 5 с.
Определите конечное положение тела. Запишите уравнение траектории данного
движения. (2,06 м/с; -14⁰; 10,3 м; 10,3 м; х = 7; y =
2,5; y = 4,25 – 0,25x)

14.
Два
тела А и С движутся в плоскости XOY. Их
координаты изменяются со временем по законам x_A = 2t, y_A = 5t и x_C = t + 1, y_C = t + 4.
Встретятся ли эти тела, и если да, то каковы координаты точки встречи? Задачу
решить аналитически и графически. (2;5)

15.
Расстояние
между городами А и В равно 300 км. Из этих городов
одновременно выезжают две машины. Машина, выехавшая из города А,
движется в город В со скоростью 60 км/ч, а другая – со скоростью 40
км/ч. Определить координатным методом место и время встречи машин. (3 ч, 180 км; 15 ч,
900 км)

16. Из пункта А
в 10 часов утра выходит поезд со скоростью 80 км/ч, а
навстречу ему из пункта В, находящегося на расстоянии 600 км, в два
часа дня другой поезд со скоростью 60 км/ч. Через какое время после
выхода второго поезда они встретятся? (2 часа)

Источник

Чему равны перемещение и путь точки, расположенной на краю диска радиусом R, при его повороте на ; 480⁰? (R, R;, )

Катер прошел по озеру в направлении строго на северо – восток 2 км, а затем в направлении на север 1 км. Найти величину и направление перемещения (угол к меридиану). (2,8 км; 30⁰)

Тело переместилось из т. А (-1; 2) в т. В (5; 3). Определите радиус – вектор т. А и т. В, изменение радиус – вектора. (; 116,6⁰; ; 31⁰; )

Радиус – вектор т. А имеет модуль и угол наклона α = 45⁰ к оси ОХ. Материальная точка перемещается из т. А в т. В (5; -1). Определите угол поворота радиус – вектора и его изменение. (303,7; )

Автоинспектор ГАИ замечает радаром в 10 ч 46 мин, что скорость автомобиля, находящегося в 100 м от поста ГАИ составляет 10 м/с. Какова координата автомобиля через 1 мин? (500 м)

Автобус выезжает из п. А в п. В, находящимися друг от друга на расстоянии 70 км, в 8 ч 30 мин по московскому времени. Когда он прибудет в пункт назначения, если скорость его движения 20 м/с? (9 ч 28 мин)

Тело, двигаясь прямолинейно и равномерно в плоскости XOY, перемещается из точки А с координатами (1;2) в точку В с координатами (4; -2) за время равное 10 с. Определите модуль скорости тела, ее направление по отношению к оси ОХ. (0,5 м/с; -53⁰)

Точка А располагается на краю диска радиусом 3 см. За время 3,14 с диск поворачивается на рад. Определите скорость точки. (0,02 м/с; 0,0165 м/с)

В осях (t – v), где t – время в секундах, v – скорость в метрах в секунду, зависимость модуля скорости тела от времени имеет вид прямой, соединяющей точки (0; 3) и (2; 9). Какой путь проходит тело за промежуток времени от t₁ = 0 до t₂ =2 с? (12 м)

По заданным графикам x(t) на рис. 1.1. запишите уравнения движения тел. Из уравнений найдите место и время встречи тел. Постройте зависимости S(t) и v(t).

В момент времени t = -2 с автомобиль начал движение из точки х = 50 м с постоянной скоростью v = -10 м/с. Постройте кривую зависимости x(t). В какой момент времени автомобиль будет в точке 0? Запишите закон движения тела. (3 с; х = 30 – 10t)

Построить график зависимости v (t) для движения x = 15t + 2t² и определить мгновенную скорость в момент времени t₁ = 10 с. (55 м/с)

Тело движется в плоскости XOY прямолинейно по закону x = 2·t – 3; y = 5 – 0,5·t. Определите скорость движения, её направление, путь и перемещение за 5 с. Определите конечное положение тела. Запишите уравнение траектории данного движения. (2,06 м/с; -14⁰; 10,3 м; 10,3 м; х = 7; y = 2,5; y = 4,25 – 0,25x)

Два тела А и С движутся в плоскости XOY. Их координаты изменяются со временем по законам x_A = 2t, y_A = 5t и x_C = t + 1, y_C = t + 4. Встретятся ли эти тела, и если да, то каковы координаты точки встречи? Задачу решить аналитически и графически. (2;5)

Расстояние между городами А и В равно 300 км. Из этих городов одновременно выезжают две машины. Машина, выехавшая из города А, движется в город В со скоростью 60 км/ч, а другая – со скоростью 40 км/ч. Определить координатным методом место и время встречи машин. (3 ч, 180 км; 15 ч, 900 км)

Из пункта А в 10 часов утра выходит поезд со скоростью 80 км/ч, а навстречу ему из пункта В, находящегося на расстоянии 600 км, в два часа дня другой поезд со скоростью 60 км/ч. Через какое время после выхода второго поезда они встретятся? (2 часа)

Источник

: ЕГЭ по физике

Подборка заданий по кинематике для подготовки к ЕГЭ по физике в 11 классе.

→ Скачать задания

→ Скачать ответы

Данный тренинг соответствует разделу кодификатора 1. 1 — кинематика.

Этот раздел содержит 8 различных типов задач на разные темы. (1. 1. 1 — 1. 1.

В тренинге задачи подобраны в соответствие с кодификатором.

Пример заданий:

Камень падает с высокого обрыва, двигаясь по вертикали. Сопротивление воздуха пренебрежимо мало. Модуль средней скорости камня с течением времени

1) увеличивается

2) уменьшается

3) не изменяется

4) сначала увеличивается, а затем начинает уменьшаться

Ответ: _____.

Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге навстречу ему едет автомобиль с постоянной скоростью 70 км/ч. Модуль скорости движения мотоцикла относительно автомобиля равен

1) 20 км/ч

2) 20 км/ч

3) 120 км/ч

4) 50 км/ч

Ответ: _____.

Связанные страницы:

Источник

Решение текстовых задач на движение подчиняется четкому алгоритму, который состоит из нескольких этапов:

Анализ данных.
Составление таблицы.
Составление уравнения.
Решение уравнения.

Остановимся подробно на каждом пункте:

1. Первое, с чего нужно начать — медленно и вдумчиво прочитать условие задачи, то есть проанализировать данные.

Чтобы наглядно представить задачу, необходимо сделать рисунок и отобразить на нем все известные по условию задачи величины.

2. Второй шаг — составить таблицу по условию задачи, внести в таблицу известные величины и ввести неизвестные.

Таблица состоит из трех столбцов S, v и t (путь, скорость и время) и нескольких строк. При заполнении каждой строки сначала выбираем и заполняем тот столбец, информация о котором дана в задаче. Еще один столбец записываем в роли неизвестного (чаще всего, это то, что требуется найти в задаче). В третью, оставшуюся колонку вписываем связь характеристик из двух уже заполненных столбцов по формуле:

S = v · t.

В таблице получается столько строчек, сколько каждый из объектов задачи действовал (то есть, перемещался) или мог бы действовать.

3. Следующий шаг — при помощи сделанного рисунка и заполненной таблицы составить уравнение или систему уравнений.

По окончании заполнения таблицы оказывается, что есть часть информации, которая не вошла в таблицу. Эта информация характеризует те значения величин в колонках, которые вычисляются в третью очередь, то есть по формуле. На основании этой информации и данных из третьей колонки составляем уравнение.

4. Решить полученное уравнение и прийти к ответу.

Когда уравнение составлено, последний шаг — это решить его, и, в конце концов, получить ответ.

Будьте внимательны, если за неизвестное вы приняли не то, что требуется найти в задаче. В этом случае следует выразить то, что нужно найти через полученное решение уравнения.
Если, решив уравнение, вы получили несколько ответов, то следует отобрать только имеющие смысл решения. Помните, что путь, скорость и время не могут быть отрицательными.

Пример:

Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.

Решение:

В задаче требуется найти скорость второго, более медленного, велосипедиста. Примем его скорость за x. Заполним таблицу:

	v, км/ч	t, ч	S, км
Первый велосипедист	x + 10	$ frac{60}{x+10} $	60
Второй велосипедист	x	$ frac{60}{x} $	60

В условии задачи сказано, что первый велосипедист прибыл к финишу на 3 часа раньше второго. На основании этого составим уравнение:

$ frac{60}{x+10}+3=frac{60}{x} $

$ frac{60+3x+30}{x+10}=frac{60}{x} $

3x² + 90x = 600 + 60x;

x² + 10x – 200 = 0.

Получаем два корня, x₁ = 10 и x₂ = –20. Второй корень не подходит, так как скорость не может быть отрицательной.

Ответ: 10 км/ч.

Виды задач на движение:

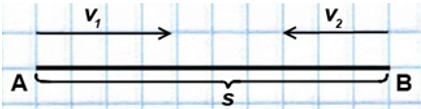
1. Движение навстречу друг другу, движениев противоположных направлениях:

Если два объекта движутся навстречу друг другу, то они сближаются:

При объекты удаляются:

В обоих случаях объекты как бы «помогают» друг другу преодолеть общее для них расстояние, «действуют сообща». Поэтому чтобы найти их совместную скорость (это и будет скорость сближения или удаления), нужно складывать скорости объектов:

v = v₁ + v₂.

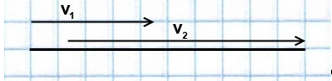
2. Движение друг за другом (вдогонку):

При движении в одном направлении объекты также могут как сближаться, так и удаляться. В этом случае они как бы «соревнуются» в преодолении общего расстояния, «действуют друг против друга». Поэтому их совместная скорость будет равна разности скоростей.

Если скорость идущего впереди объекта меньше скорости объекта, следующего за ним, то они сближаются. Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:

$ {upsilon_{c}=upsilon_{1}-upsilon_{2};\ upsilon_{1}>upsilon_{2}.} $

Если объект, идущий впереди, движется с большей скоростью, чем идущий следом за ним, то они удаляются. Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:

$ {upsilon_{y}=upsilon_{2}-upsilon_{1};\ upsilon_{2}>upsilon_{1}.} $

Таким образом:

При движении навстречу друг другу и движении в противоположных направлениях скорости складываем.
При движении в одном направлении скорости вычитаем.

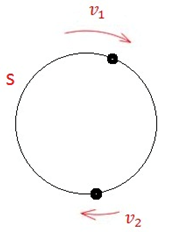
3. Движение по кругу:

При движении по кругу объекты могут:

сближаться, если скорость догоняющего больше скорости догоняемого. Скорость сближения будет равна $ upsilon_{c}=upsilon_{1}-upsilon_{2}; $
отдаляться, если скорость догоняющего меньше скорости догоняемого. Скорость удаления будет равна $ upsilon_{y}=upsilon_{2}-upsilon_{1}. $

При этом пройденные расстояния измеряются длиной круговой трассы, равной S.

Если два объекта начинают движение по кругу из одной и той же точки, то в момент первой встречи более быстрый объект пройдет расстояние на один круг больше.
Если два объекта начинают движение по кругу из разных точек, расстояние между которыми равно S₀, то в момент первой встречи догоняющий объект пройдет на S₀км большее расстояние, чем догоняемый.
Если через определенное время t первый объект опережает второй на m кругов, то разница пройденных объектами расстояний будет равна m · S:

S₁ – S₂ = m · S.

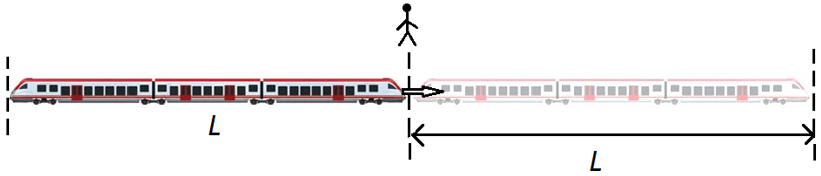
4. Движение мимо объекта:

В задачах на движение мимо объекта обязательно присутствуют протяженные тела — поезда, туннели, корабли и т. п. Зачастую движущимся объектом является поезд.

Если поезд длиной L движется мимо точечного объекта (столба, светофора, человека), то он проходит расстояние, равное его длине L:

S = L = v₀ · t.

При этом, если точечный объект (пешеход, велосипедист) тоже движется, то совместная скорость равна сумме скоростей, если поезд и объект двигаются в разных направлениях (как в пункте 1), и равна разности скоростей, если они двигаются в одном направлении (как в пункте 2).

Если поезд длиной L₁ движется мимо протяженного объекта (туннеля, лесополосы) длиной L₂, то он проходит расстояние, равное сумме длин самого поезда и протяженного объекта:

S = L₁ + L₂ = v₀ · t.

При этом, если протяженный объект (например, другой поезд) тоже движется, то совместная скорость равна сумме скоростей, если оба объекта двигаются в разных направлениях, и равна разности скоростей (из большей вычитается меньшая), если они двигаются в одном направлении.

5. Движение по воде:

В задачах на движение помимо собственной скорости плывущего тела нужно учитывать скорость течения.

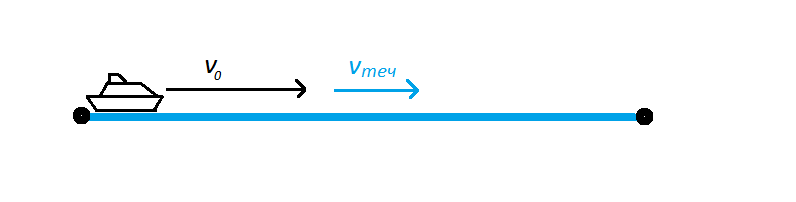
При движении по течению скорость течения прибавляется к скорости плывущего тела: v = v₀ + v_теч.

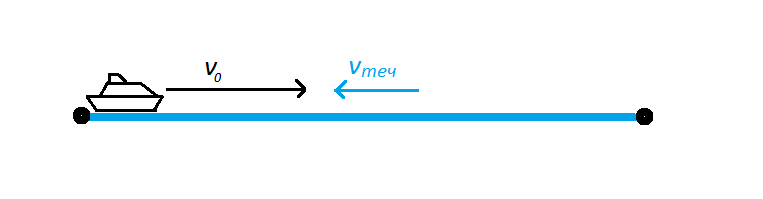
При движении против течения скорость течения отнимается от скорости плывущего тела: v = v₀ – v_теч.

Скорость плота считается равной скорости течения.

Источник