Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Элементами множеств А, P, Q являются натуральные числа, причём P = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}. Известно, что выражение
( (x ∈ A) → (x ∈ P) ) ∧ ( (x ∈ Q) → ¬(x ∈ A) )
истинно (то есть принимает значение 1) при любом значении переменной х. Определите наибольшее возможное количество элементов в множестве A.
2
Элементами множества А являются натуральные числа. Известно, что выражение
(x ∈ {2, 4, 6, 8, 10, 12}) → (((x ∈ {3, 6, 9, 12, 15}) ∧ ¬(x ∈ A)) → ¬(x ∈ {2, 4, 6, 8, 10, 12}))
истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.
3
Элементами множеств А, P, Q являются натуральные числа, причём P = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}.
Известно, что выражение
((x ∈ P) → (x ∈ A)) ∨ (¬(x ∈ A) → ¬(x ∈ Q))
истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 18 января 2017 года Вариант ИН10304
4
Элементами множеств А, P, Q являются натуральные числа, причём P = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}.
Известно, что выражение
((x 
A) → (x P)) ∨ (¬(x Q) → ¬(x A))
истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наибольшее возможное количество элементов в множестве A.
5
Элементами множеств А, P, Q являются натуральные числа, причём P = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21}, Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}. Известно, что выражение
((x ∈ P) → (x ∈ A)) ∨ (¬(x ∈ A) → ¬(x ∈ Q))
истинно ( т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 18 января 2017 года Вариант ИН10303
Пройти тестирование по этим заданиям
Тема 15.
Преобразование логических выражений
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
преобразование логических выражений
15.01Смешанное
15.02Отрезки
15.03Побитовая конъюнкция
15.04Деление без остатка
15.05Неравенства
15.06Множества
15.07Другое
Решаем задачи
Элементами множества 
являются натуральные числа, причем
Известно, что выражение
истинно (т.е. принимает значение 
) для всех 
Определите минимальную сумму элементов множества 
.
Показать ответ и решение
Максимальный размер множества 
: 
. Будем выкидывать из него элементы, чтобы найти
минимальную сумму.
Очевидно, что при любом чётном 
первая скобка всегда будет истинной, и неважно, входит 
в множество 
или
нет. Значит, из множества 
можно убрать все чётные элементы, то есть 
При 
или 
в качестве 
можно взять число 
, тогда будет верна третья скобка, и неважно,
входит 
в множество 
или нет. Значит, из множества 
можно убрать элементы 
и 
, то есть
Тогда минимальная сумма элементов 
равна: 
.
Неверное решение программой:
a = [] for x in range(1, 10): if ((x % 2 == 0) or (x in a) or (any(y*x % 15 == 0 for y in a))) == 0: a.append(x) print(a)
В данной задаче стандартное решение программой ошибочно, поскольку оно не учитывает, что, если в множестве 
будет элемент 
, то элементы 
и 
можно не добавлять в множество, поскольку они оба в произведении с 
кратны
. Тогда итоговая сумма будет меньше той, что получила программа.
Показать ответ и решение
Система для врагов:
Враги мечтают чтобы 
были в 
и в 
, то есть 
, и они не были в A.
Друзья хотят чтобы эти иксы были в A и хотят сделать A с минимальной суммой элементов, тогда они возьмут все
элементы из пересечения 
и 
, тогда ответ 
.
Показать ответ и решение
Система для врагов:
Враги мечтают чтобы 
были в 
и в 
и они не были в A.
Друзья хотят чтобы эти иксы были в A и хотят сделать A с минимальным произведением элементов, тогда они возьмут
все элементы из пересечения 
и 
, тогда ответ 
.
Элементами множества А являются натуральные числа. Известно, что выражение
истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное количество
элементов множества A.
Показать ответ и решение
def f(x, A):
first = [2, 4, 6, 8, 10, 12]
second = [3, 6, 9, 12, 15]
return (x not in first) <= (((x in second) and (x not in A)) <= (x in first))
def podh(A):
for x in range(1, 100):
if not f(x, A):
return False
return True
arr = [2, 3, 4, 6, 8, 9, 10, 12, 15]
ans = 100
for i in range(2 ** len(arr)):
A = []
t = i
for j in range(len(arr)):
if t % 2 == 1:
A.append(arr[j])
t //= 2
if podh(A):
if ans > len(A):
print(A)
ans = min(ans, len(A))
print(ans)
Элементами множества А являются натуральные числа. Известно, что выражение
истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное количество
элементов множества A.
Показать ответ и решение
def f(x, A):
first = [2, 4, 6, 8, 10, 12]
second = [3, 6, 9, 12, 15]
return (x not in first) or (((x in second) and (x not in A)) <= (x not in first))
def podh(A):
for x in range(1, 100):
if not f(x, A):
return False
return True
arr = [2, 4, 6, 8, 10, 12, 15, 9, 3]
minim = 100
for i in range(2 ** len(arr)):
A = []
t = i
for j in range(len(arr)):
if t % 2 == 1:
A.append(arr[j])
t //= 2
if podh(A):
minim = min(minim, len(A))
print(minim)
Элементами множеств A, P, Q являются натуральные числа, причем
Известно, что выражение
истинно (т.е. принимает значение 1) при любом значении переменной х.
Определите наибольшее возможное количество элементов в множестве 
.
Показать ответ и решение
Решение 
(ручками):
Запишем, чего хотят враги:
Максимальное 
. Это множество содержит 
элементов, запишем это значение в ответ.
Решение 
(прогой):
p = [i for i in range(2, 21, 2)] q = [i for i in range(5, 51, 5)] a = [i for i in range(100)] for i in range(100): for x in range(1000): if (((x == i) <= (x in p)) or ((x not in q) <= (x != i))) == 0: a.remove(i) print(len(a))
Элементами множеств A, P, Q являются натуральные числа, причем
Известно, что выражение
истинно (т.е. принимает значение 1) при любом значении переменной х.
Определите наименьшее возможное количество элементов в множестве 
.
Показать ответ и решение
def f(x, a):
P = set([i * 2 for i in range(1, 6)])
Q = set([i * 3 for i in range(1, 6)])
return ((not(x in a)) <= (x in P)) or ((x in Q) <= (x in a))
a = set()
for x in range(20):
if not(f(x, a)):
a.add(x)
print(len(a))
Элементами множества А являются натуральные числа. Известно, что выражение
истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное количество
элементов множества A.
Показать ответ и решение
def f(x, A):
first = [2, 4, 6, 8, 10, 12]
second = [3, 6, 9, 12, 15]
return (x not in first) or (((x in second) and (x not in A)) <= (x not in first))
def podh(A):
for x in range(1, 100):
if not f(x, A):
return False
return True
arr = [2, 4, 6, 8, 10, 12, 15, 9, 3]
minim = 100
for i in range(2 ** len(arr)):
A = []
t = i
for j in range(len(arr)):
if t % 2 == 1:
A.append(arr[j])
t //= 2
if podh(A):
minim = min(minim, len(A))
print(minim)
На числовой прямой даны два отрезка:
Элементами множеств A, P, Q являются натуральные числа, причем
Известно, что выражение
истинно (т.е. принимает значение 1) при любом значении переменной х.
Определите наибольшее возможное количество элементов в множестве 
.
Показать ответ и решение
def f(x, P, Q, A):
return ((x in A) <= (x in P)) or ((not (x in Q)) <= (not (x in A)))
P = set([x for x in range(2, 21, 2)])
Q = set([x for x in range(3, 31, 3)])
A = set(x for x in range(40))
for x in range(40):
if not f(x, P, Q, A):
A.remove(x)
print(len(A))
Элементами множеств A, P, Q являются натуральные числа, причем
Известно, что выражение
истинно (т.е. принимает значение 1) при любом значении переменной х.
Определите наименьшее возможное количество элементов в множестве 
.
Показать ответ и решение
def f(x, P, Q, A):
return ((x in A) <= (x in P)) or ((not (x in Q)) <= (not (x in A)))
P = set([x for x in range(1, 22, 2)])
Q = set([x for x in range(3, 31, 3)])
A = set()
for x in range(40):
if not f(x, P, Q, A):
A.add(x)
print(len(A))
Элементами множеств A, P, Q являются натуральные числа, причем
Известно, что выражение
истинно (т.е. принимает значение 1) при любом значении переменной х.
Определите наименьшее возможное количество элементов в множестве 
.
Показать ответ и решение
def f(x, P, Q, A):
return ((not(x in A)) <= (x in P)) or ((x in Q) <= (x in A))
P = set([x for x in range(2, 21, 2)])
Q = set([x for x in range(3, 31, 3)])
A = set()
for x in range(40):
if not f(x, P, Q, A):
A.add(x)
print(len(A))
Элементами множеств 
являются натуральные числа, причём 
,
. Известно, что выражение
истинно (т.е. принимает значение 
при любом значении переменной 
. Определите наименьшее возможное
количество элементов в множестве 
.
Элементами множеств 
являются натуральные числа, причём 
, 
. Известно, что
выражение
истинно (т.е. принимает значение 1 при любом значении переменной 
. Определите наименьшее возможное количество
элементов в множестве 
.
Элементами множеств 
являются натуральные числа, причём 
, 
. Известно, что
выражение
истинно (т.е. принимает значение 1 при любом значении переменной 
. Определите наименьшее возможное количество
элементов в множестве 
.
Элементами множеств 
, 
и 
являются натуральные числа, причём 
и 
. Известно, что выражение
истинно (т.е. принимает значение 
при любом значении переменной 
. Определите наименьшее возможное
количество элементов в множестве 
.
Элементами множеств 
, 
и 
являются натуральные числа, причём 
и 
. Известно, что выражение
истинно (т.е. принимает значение 
при любом значении переменной 
. Определите наибольшее возможное
количество элементов в множестве 
.
МБОО «Лицей села Верхний Мамон»
Теория и практика решения задания 18 ЕГЭ по информатике
Автор:
учитель информатики МБОО «Лицей села Верхний Мамон»
ВКК Мирошников Роман Сергеевич
Мнемоническое правило
Соционика – это информационная психология
Один из ее главных принципов – дополнение до целого ( дополнение противоположностью )
Решающая формула
В алгебре логики есть формула дополнения до целого:
А ¬А = 1
В некоторых задачах мы будем использовать вместо этой формулы умножение противоположностей:
А ¬А = 0
Типы задания 18
- Задания на отрезки
- Задания на множества
- Задания на поразрядную конъюнкцию
- Задания на условие делимости
![Задания на отрезки ( № 376 ) На числовой прямой даны два отрезка: P=[4,15] и Q=[12,20]. Укажите наименьшую возможную длину такого отрезка A, что формула ((x ∈ P) ∧ (x ∈ Q)) → (x ∈ A) тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Источник - сайт Полякова К.Ю.](https://fsd.multiurok.ru/html/2023/02/13/s_63ea739f78aef/img5.jpg)
Задания на отрезки
( № 376 ) На числовой прямой даны два отрезка: P=[4,15] и Q=[12,20]. Укажите наименьшую возможную длину такого отрезка A, что формула ((x ∈ P) ∧ (x ∈ Q)) → (x ∈ A)
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
Источник — сайт Полякова К.Ю.
Решающая формула
Для выбора решающей формулы важно внимательно прочитать требование задачи.
В нашей задаче в требовании сказано:
принимает значение 1 при любом значении переменной х.
Выбор решающей формулы очевиден:
А ¬А = 1
Решение задачи на отрезки
Разделим решение задачи на этапы:
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи на отрезки
- Легенда – это удобные нам условные обозначения, которые мы будем использовать при решении.
Введем следующие обозначения:
P = x P
Q = x Q
A = x A
Решение задачи на отрезки
2) Формализация условия – перепишем формулу из условия задачи в соответствие с легендой.
Было:
((x ∈ P) ∧ (x ∈ Q)) → (x ∈ A) = 1
Стало:
(P ∧ Q) → A = 1
Решение задачи на отрезки
3) Решение логического уравнения – вначале это, возможно, самый сложный этап в решении задачи. Но позже, при накоплении опыта, он уже не будет казаться таким уж сложным
Рассмотрим решение логического уравнения по шагам.
Решение задачи на отрезки
3.1. Представим логическое следование в базовых логических операциях по формуле: А → В = ¬А В :
(P ∧ Q) → A = 1
¬ (P ∧ Q) A = 1
Решение задачи на отрезки
3.2. Сведем получившееся выражение к решающей формуле: А ¬А = 1 (в алгебре логики справедлив закон коммутативности, т.е. А ¬А = ¬А А) :
¬(P ∧ Q) A = 1, отсюда
¬А = ¬(P ∧ Q)
Ответом в логическом уравнении будет:
А = P ∧ Q.
Решение задачи на отрезки
4) Интерпретация полученного результата .
Наш ответ: А = P ∧ Q .
В алгебре логики это выражение означает пересечение объемов двух логических объектов. По условию нашей задачи – это пересечение отрезков P и Q .
![Решение задачи на отрезки Пересечение отрезков P и Q можно визуализировать: P=[4,15] и Q=[12,20]. 15 12 20 4 По условию нашей задачи, нам нужна минимальная длина отрезка А . Находим ее: 15 – 12 = 3 . Ответ: 3 . Ответ на сайте Полякова К.Ю.: 3](https://fsd.multiurok.ru/html/2023/02/13/s_63ea739f78aef/img14.jpg)
Решение задачи на отрезки
Пересечение отрезков P и Q можно визуализировать: P=[4,15] и Q=[12,20].
15
12
20
4
По условию нашей задачи, нам нужна минимальная длина отрезка А . Находим ее: 15 – 12 = 3 .
Ответ: 3 .
Ответ на сайте Полякова К.Ю.: 3
![Задания на отрезки (№ 360) На числовой прямой даны три отрезка: P=[10,25], Q=[15,30] и R=[25,40]. Какова максимальная длина отрезка A, при котором формула ((x ∈ Q) → (x ∉ R) ) ∧ (x ∈ A) ∧ (x ∉ P) тождественно ложна, то есть принимает значение 0 при любом значении переменной х? Источник - сайт Полякова К.Ю.](https://fsd.multiurok.ru/html/2023/02/13/s_63ea739f78aef/img15.jpg)
Задания на отрезки
(№ 360) На числовой прямой даны три отрезка: P=[10,25], Q=[15,30] и R=[25,40]. Какова максимальная длина отрезка A, при котором формула ((x ∈ Q) → (x ∉ R) ) ∧ (x ∈ A) ∧ (x ∉ P)
тождественно ложна, то есть принимает значение 0 при любом значении переменной х?
Источник — сайт Полякова К.Ю.
Решающая формула
Для выбора решающей формулы важно внимательно прочитать требование задачи.
В нашей задаче в требовании сказано:
принимает значение 0 при любом значении переменной х.
Выбор решающей формулы очевиден:
А ¬А = 0
Решение задачи на отрезки
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи на отрезки
- Легенда
R = x R
Q = x Q
A = x A
P = x P
Решение задачи на отрезки
2) Формализация условия
Было:
((x ∈ Q) → (x ∉ R) ) ∧ (x ∈ A) ∧ (x ∉ P) = 0
Стало:
( Q → ¬R ) ∧ A ∧ ¬ P = 0
Решение задачи на отрезки
3) Решение логического уравнения
( Q → ¬R ) ∧ A ∧ ¬ P = 0
3.1. Представим логическое следование в базовых логических операциях по формуле: А → В = ¬А В , и переставим множители согласно закону коммутативности умножения:
A ∧ (¬ Q ¬R ) ∧ ¬ P = 0
Решение задачи на отрезки
3) Решение логического уравнения
A ∧ ( ¬ Q ¬R ) ∧ ¬ P = 0
3.2. Сведем получившееся выражение к решающей формуле: А ¬А = 0 и найдем, чему равно ¬А :
¬А = (¬ Q ¬R ) ∧ ¬ P
Решение задачи на отрезки
3) Решение логического уравнения
¬А = (¬ Q ¬R ) ∧ ¬ P
3.3. Упростим выражение для ¬А по закону де Моргана ¬А ¬В=¬(А В) :
¬А = ¬ (Q R ) ∧ ¬ P,
и по другому закону де Моргана ¬А ¬В =¬(А В ) :
¬А = ¬ (Q R P)
Решение задачи на отрезки
3) Решение логического уравнения
¬А = ¬ (Q R P)
3.4. Очевидно, что
А = Q R P
Решение задачи на отрезки
4) Интерпретация полученного результата
А = Q R P
Отрезок А – это пересечение отрезков Q и R и его объединение с отрезком Р .
![Решение задачи на отрезки Пересечение отрезков R и Q можно визуализировать: Q=[15,30] и R=[25,40]. 30 25 40 15 Отрезок P=[10,25] нанесем на наш чертеж и объединим с пересечением: 25 30 15 40 10](https://fsd.multiurok.ru/html/2023/02/13/s_63ea739f78aef/img25.jpg)
Решение задачи на отрезки
Пересечение отрезков R и Q можно визуализировать: Q=[15,30] и R=[25,40].
30
25
40
15
Отрезок P=[10,25] нанесем на наш чертеж и объединим с пересечением:
25
30
15
40
10
Решение задачи на отрезки
А = Q R P
40
25
30
10
15
По условию нашей задачи, нам нужна максимальная длина отрезка А . Находим ее: 30 – 10 = 20 .
Ответ: 20 .
Ответ на сайте Полякова К.Ю.: 20
27
2. Задания на множества
(№ 386) Элементами множеств А, P, Q являются натуральные числа, причём P={1,2,3,4,5,6}, Q={3,5,15}. Известно, что выражение (x ∉ A) → ((x ∉ P) ∧ (x ∈ Q)) ∨ (x ∉ Q)
истинно (т.е. принимает значение 1 при любом значении переменной х. Определите наименьшее возможное количество элементов в множестве A.
Источник — сайт Полякова К.Ю.
Решение задачи на множества
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи на множества
- Легенда
A = x ∈ A
P = x ∈ P
Q = x ∈ Q
Решение задачи на множества
2) Формализация условия
Было:
(x ∉ A) → ((x ∉ P) ∧ (x ∈ Q)) ∨ (x ∉ Q) = 1
Стало:
¬ A → (¬P ∧ Q) ¬ Q = 1
Решение задачи на множества
3) Решение логического уравнения
¬ A → (¬P ∧ Q) ¬ Q = 1
3.1. Представим логическое следование в базовых логических операциях и сгруппируем:
A ((¬P ∧ Q) ¬ Q) = 1
Решение задачи на множества
A (( ¬P ∧ Q) ¬Q) = 1
3.2. Сведем получившееся выражение к решающей формуле:
А ¬А = 1
и найдем, чему равно ¬А :
¬А = (¬P ∧ Q) ¬Q
Решение задачи на множества
¬А = (¬P ∧ Q) ¬Q
3.3. Упростим выражение для ¬А, раскрыв скобки по закону дистрибутивности сложения:
¬А = ( ¬P ¬Q) (Q ¬Q)
Q ¬Q = 1
¬А = ( ¬P ¬Q)
Решение задачи на множества
¬А = ( ¬P ¬Q)
По закону де Моргана:
¬А = ¬(P Q)
3.4. Очевидно, что
А = P Q
Решение задачи на множества
А = P Q
4) Интерпретация полученного результата
Искомое множество А представляет собой пересечение множеств P и Q.
Решение задачи на множества
Искомое множество А есть пересечение множеств
P = 1, 2, 3 , 4, 5 , 6 и Q = { 3 , 5 ,15}, таким образом A = { 3 , 5 }
и содержит только 2 элемента.
Ответ: 2
Ответ на сайте Полякова: 2
2. Задания на множества
(№ 368) Элементами множеств А, P, Q являются натуральные числа, причём P={2,4,6,8,10,12} и Q={4,8,12,116}. Известно, что выражение (x ∈ P) → (((x ∈ Q) ∧ (x ∉ A)) → (x ∉ P))
истинно (т. е. принимает значение 1 ) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.
Источник — сайт Полякова К.Ю.
Решение задачи на множества
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи на множества
- Легенда
A = x ∈ A
P = x ∈ P
Q = x ∈ Q
Решение задачи на множества
2) Формализация условия
Было:
(x ∈ P)→(((x ∈ Q) ∧ (x ∉ A))→(x ∉ P)) = 1
Стало:
P → ((Q ∧ ¬ A) → ¬ P) = 1
Решение задачи на множества
3) Решение логического уравнения
P → ((Q ∧ ¬ A) → ¬ P) = 1
3.1. Представим первое логическое следование (в скобках) в базовых логических операциях :
P → ( ¬ (Q ∧ ¬ A) ¬ P) = 1
Решение задачи на множества
P → ( ¬ (Q ∧ ¬ A) ¬ P) = 1
Представим второе логическое следование в базовых логических операциях, применим закон де Моргана и перегруппируем:
¬ P ( ¬ (Q ∧ ¬ A) ¬ P) = 1
¬ P ¬ Q A ¬ P = 1
Решение задачи на множества
A ( ¬ P ¬ Q ¬ P) = 1
3.2. Сведем получившееся выражение к решающей формуле:
А ¬А = 1
и найдем, чему равно ¬А :
¬А = ( ¬ P ¬ Q ¬ P)
Решение задачи на множества
¬А = ¬ P ¬ Q ¬ P
3.3. Упростим выражение для ¬А по формуле А А = А :
¬А = ¬ P ¬ Q
Далее, по закону де Моргана получаем:
¬А = ¬( P Q)
Решение задачи на множества
¬А = ¬(P Q)
3.4. Очевидно, что
А = P Q
4) Интерпретация полученного результата
Искомое множество А представляет собой пересечение множеств P и Q.
Решение задачи на множества
Искомое множество А есть пересечение множеств
P = 2, 4 , 6, 8 , 10, 12 и
Q = { 4 , 8 , 12 , 16}, таким образом
A = { 4 , 8 , 12 }
и содержит только 3 элемента, сумма которых 4+8+12=24 .
Ответ: 24
Ответ на сайте Полякова: 24
3. Задания на поразрядную конъюнкцию
(№ 379) Обозначим через m & n пораз-рядную конъюнкцию неотрицательных целых чисел m и n . Так, например, 14 & 5 = 1110 2 & 0101 2 = 0100 2 = 4. Для какого наименьшего неотрицательного целого числа А формула (x & 29 ≠ 0) → ((x & 12 = 0) → (x & А ≠ 0))
тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?
Решение задачи на поразрядную конъюнкцию
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи на поразрядную конъюнкцию
- Легенда
Легенда для задач на поразрядную конъюнкцию отличается от всех остальных случаев:
B = (x & 29 ≠ 0)
C = (x & 12 ≠ 0)
A = (x & А ≠ 0)
Решение задачи на поразрядную конъюнкцию
Мы принимаем за истинное высказывание поразрядную конъюнкцию, отличную от нуля, иначе поразрядная конъюнкция теряет свой логический смысл, т.к. всегда можно представить Х всеми нулями.
Решение задачи на поразрядную конъюнкцию
2) Формализация условия
Было:
(x & 29 ≠ 0)→((x & 12 = 0)→(x & А ≠ 0))=1
Стало:
В → ( ¬С → А) = 1
Решение задачи на поразрядную конъюнкцию
3) Решение логического уравнения
В → ( ¬С → А) = 1
В → (С А) = 1
(¬В С) А = 1
¬А = ¬В С
¬А = ¬(В ¬ С)
Очевидно, что
А = В ¬ С
Решение задачи на поразрядную конъюнкцию
4) Интерпретация полученного результата
Искомое двоичное значение поразрядной конъюнкции А – это двоичное значение поразрядной конъюнкции значения В и инверсии двоичного значения С .
Решение задачи на поразрядную конъюнкцию
B = (x & 29 ≠ 0)
В или 29 = 11101 2
C = (x & 12 ≠ 0)
12 = 1100 2
¬С или инверсия 12 = 0011 2
Решение задачи на поразрядную конъюнкцию
В или 29 = 11101 2
¬С или инверсия 12 = 0011 2
А = В ¬ С
х 11101 2
0011 2
10001 2
А = 1 0001 2 = 17
Ответ на сайте Полякова: 17
27
3. Задания на поразрядную конъюнкцию
(№ 375) Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K (логическое «И» между соответ-ствующими битами двоичной записи). Определите наименьшее натуральное число A, такое что выражение (X & 49 ≠ 0) → ((X & 33 = 0) → (X & A ≠ 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?
Решение задачи на поразрядную конъюнкцию
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи на поразрядную конъюнкцию
- Легенда
Легенда для задач на поразрядную конъюнкцию отличается от всех остальных случаев:
B = (x & 49 ≠ 0)
C = (x & 33 ≠ 0)
A = (x & А ≠ 0)
Решение задачи на поразрядную конъюнкцию
2) Формализация условия
Было:
(X & 49 ≠ 0) → ((X & 33 = 0) → (X & A ≠ 0))=1
Стало:
В → ( ¬С → А) = 1
Решение задачи на поразрядную конъюнкцию
3) Решение логического уравнения
В → ( ¬С → А) = 1
В → (С А) = 1
(¬В С) А = 1
¬А = (¬В С)
Очевидно:
А = В ¬С
Решение задачи на поразрядную конъюнкцию
4) Интерпретация полученного результата
Искомое двоичное значение поразрядной конъюнкции А – это двоичное значение поразрядной конъюнкции значения В и инверсии двоичного значения С .
Решение задачи на поразрядную конъюнкцию
B = (x & 49 ≠ 0)
В или 49 = 110001 2
C = (x & 33 ≠ 0)
33 = 100001 2
¬С или инверсия 33 = 011110 2
Решение задачи на поразрядную конъюнкцию
В или 49 = 110001 2
¬С или инверсия 33 = 011110 2
А = В ¬ С
х 110001 2
011110 2
010000 2
А = 1 0000 2 = 16
Ответ на сайте Полякова: 16
27
4. Задания на условие делимости
(№ 372) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула ¬ДЕЛ(x,А) → (¬ДЕЛ(x,21) ∧ ¬ДЕЛ(x,35))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Источник — сайт Полякова К.Ю.
Решение задачи
на условие делимости
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи
на условие делимости
- Легенда
Легенда простая: А = ДЕЛ(x,А)
21 = ДЕЛ(х,21)
35 = ДЕЛ(x,35)
Решение задачи
на условие делимости
2) Формализация условия
Было:
¬ДЕЛ(x,А) → (¬ДЕЛ(x,21) ∧ ¬ДЕЛ(x,35))
тождественно истинна (то есть принимает значение 1)
Стало:
¬А → (¬21 ∧ ¬35) = 1
Решение задачи
на условие делимости
3) Решение логического уравнения
¬А → (¬21 ∧ ¬35) = 1
А (¬21 ∧ ¬35) = 1
¬А = ¬21 ∧ ¬35
Очевидно, что
А = 21 35
Решение задачи
на условие делимости
4) Интерпретация полученного результата
А = 21 35
В данной задаче это самый сложный этап решения. Нужно понять, что же представляет из себя число А – НОК или НОД или …
Решение задачи
на условие делимости
4) Интерпретация полученного результата
А = 21 35
Итак, наше число А таково, что Х делится на него без остатка, тогда и только тогда, когда Х делится без остатка на 21 или на 35. В этом случае ищем
А = НОД (21, 35) = 7
Ответ на сайте Полякова: 7
4. Задания на условие делимости
(№ 370) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула ¬ДЕЛ(x,А) → ((ДЕЛ(x,6) → ¬ДЕЛ(x,4))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Источник — сайт Полякова К.Ю.
Решение задачи
на условие делимости
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи
на условие делимости
- Легенда
А = ДЕЛ(x,А)
6 = ДЕЛ(x,6)
4 = ДЕЛ(x,4)
Решение задачи
на условие делимости
2) Формализация условия
Было:
¬ДЕЛ(x,А) → ((ДЕЛ(x,6) → ¬ДЕЛ(x,4))
тождественно истинна (то есть принимает значение 1
Стало:
¬А → (6 → ¬4) = 1
Решение задачи
на условие делимости
3) Решение логического уравнения
¬А → (6 → ¬4) = 1
¬А → (¬ 6 ¬4) = 1
А (¬ 6 ¬4) = 1
¬А = ¬ 6 ¬4
Очевидно:
А = 6 4
Решение задачи
на условие делимости
4) Интерпретация полученного результата
А = 6 4
Итак, А таково, что Х делится на него без остатка тогда и только тогда, когда Х делится без остатка и на 6, и на 4. Т.е. А = НОК(6, 4) = 12
Ответ на сайте Полякова: 12
Рефлексия
Оцените, пожалуйста, свой уровень понимания, достигнутый на занятии, по шкале от 0 до 10.
Сможете ли Вы теперь объяснить решение задания 18 своим ученикам или друзьям?
(да, нет, не знаю).
Спасибо за внимание!
Муниципальное бюджетное общеобразовательное
учреждение средняя общеобразовательная школа с. Никифарово МР Альшеевский район
Инновации в образовании
(опыт удачных наработок).
учитель информатики и математики
Абдуллина Л.Т.
Аннотация
В декабре прошел районный семинар
учителей информатики средних общеобразовательных школ
«Подготовка учащихся к единому государственному экзамену по информатике и ИКТ».
В рамках семинара прошли открытые уроки.
1.
Урок информатики в 11 классе по теме: «Множества и логика в
задачах ЕГЭ по информатике».
2.
Урок информатики в 7 классе по теме: «Робототехника. Линейный алгоритм
– следование в визуальной среде программирования ТРИК студио».
Уроки получили высокую оценку от
коллег. На уроке в 11 классе рассматриваются задачи, входящие в ЕГЭ по информатике по теме «Логика».
Изучение робототехники в школе –
это новое перспективное направление в изучении информатики В настоящий момент
проводятся олимпиады по робототехнике не только на региональном уровне, но уже
на федеральном. Данная разработка будет являться хорошей помощью учителям
информатики в изучении робототехники.
Затем был проведён круглый стол по
теме «Проблемные задания на ЕГЭ и ГИА». Анализ результатов ГИА
и ЕГЭ учащихся школ района за прошлый учебный год». Затем учителя
разбирали сложные задания ЕГЭ по информатике.
Особое внимание
уделялось на семинаре теме формирования ИКТ-
компетентности учащихся учителей
своих школ. Всех волновал вопрос: На ком лежит задача формирования ИКТ
— компетентности учащихся и учителей?
В ходе обсуждения
проблемных вопросов было принято решение, что учителя информатики должны
активно пропагандировать в своих школах необходимость развития
ИКТ-компетентность у всех участников образовательного процесса. И начинать это
надо с учителей, для которых в каждой школе должна быть составлена программа
информатизации образования.
Урок информатики по теме: «Множества и
логика
в задачах ЕГЭ по информатике».
План урока.
1. Организационный
момент.
Учитель:
здравствуйте, ребята! В настоящее время в ЕГЭ по информатике есть много заданий
по теме «алгебра логики». Цель данного урока — закрепление навыков решения
задач ЕГЭ по информатике с использованием элементов алгебры логики.
Цель урока:
•
Формировать умения применять полученные знания
на практике;
•
Развивать умения решать задачи ЕГЭ с
использованием законов логики;
•
Способствовать подготовке к ЕГЭ.
Задачи урока:
•
Воспитательная –
развитие познавательного интереса, логического мышления.
•
Образовательная – повторение основ математической логики, выполнение практических
заданий.
•
Развивающая –
развитие логического мышления, внимательности.
Ход
урока
1.
Повторение логических операций и законов и множеств.
2.
Проверка домашнего задания.
2.
Применение логических операций и законов на практике.
3. Объяснение домашнего задания.
4. Оценивание.
5. Рефлексия.
Сегодня мы с вами завершаем тему «Основы логики» и применим
основные логические операции, законы преобразования для решения задач ЕГЭ по
информатике.
Урок идет параллельно с презентацией.
- Повторение
логических операций и законов.
|
Закон |
Для И |
Для ИЛИ |
|
двойного отрицания |
|
|
|
исключения |
|
|
|
исключения констант |
A |
A |
|
повторения |
A |
A |
|
поглощения |
A |
A |
|
переместительный |
A |
A |
|
сочетательный |
A |
A |
|
распределительный |
A |
A |
|
де Моргана |
|
|
Презентация
к уроку:
Общий
подход к решению
1. 
Свести задачу к одной из
базовых задач
Задача 1.
 |
Задача 2.
2. 
Использовать готовое
решение:
Задача 1.
Задача 2
- Проверка
домашнего задания. (по презентации) - Применение
логических операций и законов на практике. 
Задачи
1) На числовой прямой даны два
отрезка:
P
= [37; 60] и Q = [40; 77]. Укажите
наименьшую возможную длину такого отрезка A, что выражение (x
Î P) → (((x Î
Q) Ù ¬(x Î
A)) → ¬(x Î P))
истинно при любом значении переменной х.
2)На числовой прямой даны два
отрезка:
P
= [10; 20] и Q = [25; 55]. Укажите наибольшую возможную
длину такого отрезка A, что выражение (x Î
A) → ((x Î P)
Ú (x Î
Q))
истинно при любом значении переменной х.
3) Элементами множеств А, P и Q
являются натуральные числа, причём
P =
{2, 4, 6, 8, 10, 12} и Q = {4, 8, 12, 116}.
Известно, что выражение
(x Î
P) → (((x Î Q)
Ù ¬(x Î
A)) → ¬(x Î P))
истинно при любом значении переменной х.
Определите наименьшее возможное значение суммы элементов множества A.
4)Элементами множеств А, P и Q являются
натуральные числа, причём
P
= { 2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
Q
= { 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 }.
Известно, что выражение
((x Î
A) → ¬(x Î P))
Ù (¬(x Î
Q) → ¬(x Î A))
истинно при любом значении переменной х.
Определите наибольшее возможное количество элементов множества A.
5) Для какого наибольшего натурального
числа А выражение
¬ДЕЛ(x,
А) ® (ДЕЛ(x, 6)
® ¬ДЕЛ(x,
4))
тождественно истинно (то есть принимает
значение 1 при любом натуральном значении
переменной х)?
6) Для какого наибольшего натурального
числа А выражение
¬ДЕЛ(x,
А) ® (¬ ДЕЛ(x, 21)
Ù ¬ДЕЛ(x,
35))
тождественно истинно?
7) Для какого наименьшего натурального
числа А выражение
ДЕЛ(x, А) ®
(¬ ДЕЛ(x, 21) Ú
ДЕЛ(x, 35))
тождественно истинно?
Определите наименьшее натуральное число
A, такое что выражение
(x
& 53 ¹ 0) ®
((x & 41 = 0) ®
(x
& A ¹ 0))
тождественно истинно?
9) Определите
наибольшее натуральное число A, такое что выражение
(x
& A ¹
0) ® ((x & 20 = 0) ®
(x
& 5 ¹ 0))
тождественно истинно?
Домашнее задание.
1) Введём
выражение M & K, обозначающее
поразрядную конъюнкцию M и K
(логическое «И» между соответствующими битами двоичной записи). Определите
наименьшее натуральное число A,
такое что выражение
(X & 102 ¹ 0) ® ((X & 36 = 0) ® (X & A ¹ 0))
тождественно истинно (то
есть принимает значение 1 при любом натуральном значении переменной X)?
2) Обозначим
через ДЕЛ(n, m) утверждение «натуральное число n делится
без остатка на натуральное число m». Для какого наименьшего натурального
числа А формула
(ДЕЛ(x,
A)
Ù
ДЕЛ(x, 24) Ù ¬ДЕЛ(x, 16)) ®
¬ДЕЛ(x, A)
тождественно
истинна (то есть принимает значение 1 при любом натуральном значении переменной
х)?
3)
Элементами множества А являются
натуральные числа. Известно, что выражение
¬(x ÎA)
→¬((x Î{1, 2, 4, 8}) Ú
(xÎ {1,
2, 3, 4, 5, 6}))
истинно
(т. е. принимает значение 1) при любом значении переменной х.
Определите
наименьшее возможное количество элементов множества A.
4) На
числовой прямой даны два отрезка: P = [43; 49] и Q = [44; 53]. Укажите
наибольшую возможную длину такого отрезка A, что формула
тождественно
истинна, то есть принимает значение 1 при любом значении переменной х.
Оценки за
урок.
Рефлексия. Как вы считаете, сможете на ЕГЭ решать задачи такого
типа? Все задачи были понятны? Удовлетворены ли вы уроком?
Литература:
— Информатика и
ИКТ. Профильный уровень. Учебник для 10 -11 класса/ Поляков К.Ю. – М: БИНОМ.
Лаборатория знаний, 2015.
— Сборник заданий
по информатике/ Е. М. Зорина, М. В. Зорин.- Эксмо, 2015 Информатика и ИКТ.
— Подготовка к
ЕГЭ/Н. В Макарова — М: БИНОМ. Лаборатория знаний, 2015
http://4ege.
ru/
http://www. fipi. ru
http://www.inksystem-az.com/konspekt-uroka-reshenie-logicheskix-zadach-10-klass/
http://kpolyakov.spb.ru/school/basebook.htm
Теория и практика решения задания 15 ЕГЭ по информатике
Мнемоническое правило
Соционика – это информационная психология
Один из ее главных принципов – дополнение до целого ( дополнение противоположностью )
Решающая формула
В алгебре логики есть формула дополнения до целого:
А ¬А = 1
В некоторых задачах мы будем использовать вместо этой формулы умножение противоположностей:
А ¬А = 0
Типы задания 15
- Задания на отрезки
- Задания на множества
- Задания на поразрядную конъюнкцию
- Задания на условие делимости
- Задания на функции
![Задания на отрезки ( № 376 ) На числовой прямой даны два отрезка: P=[4,15] и Q=[12,20]. Укажите наименьшую возможную длину такого отрезка A, что формула ((x ∈ P) ∧ (x ∈ Q)) → (x ∈ A) тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Источник - сайт Полякова К.Ю.](https://fsd.videouroki.net/html/2023/01/26/v_63d249777a998/img5.jpg)
Задания на отрезки
( № 376 ) На числовой прямой даны два отрезка: P=[4,15] и Q=[12,20]. Укажите наименьшую возможную длину такого отрезка A, что формула ((x ∈ P) ∧ (x ∈ Q)) → (x ∈ A)
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
Источник — сайт Полякова К.Ю.
Решающая формула
Для выбора решающей формулы важно внимательно прочитать требование задачи.
В нашей задаче в требовании сказано:
принимает значение 1 при любом значении переменной х.
Выбор решающей формулы очевиден:
А ¬А = 1
Решение задачи на отрезки
Разделим решение задачи на этапы:
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи на отрезки
- Легенда – это удобные нам условные обозначения, которые мы будем использовать при решении.
Введем следующие обозначения:
P = x P
Q = x Q
A = x A
Решение задачи на отрезки
2) Формализация условия – перепишем формулу из условия задачи в соответствие с легендой.
Было:
((x ∈ P) ∧ (x ∈ Q)) → (x ∈ A) = 1
Стало:
(P ∧ Q) → A = 1
Решение задачи на отрезки
3) Решение логического уравнения – вначале это, возможно, самый сложный этап в решении задачи. Но позже, при накоплении опыта, он уже не будет казаться таким уж сложным
Рассмотрим решение логического уравнения по шагам.
Решение задачи на отрезки
3.1. Представим логическое следование в базовых логических операциях по формуле: А → В = ¬А В :
(P ∧ Q) → A = 1
¬ (P ∧ Q) A = 1
Решение задачи на отрезки
3.2. Сведем получившееся выражение к решающей формуле: А ¬А = 1 (в алгебре логики справедлив закон коммутативности, т.е. А ¬А = ¬А А) :
¬(P ∧ Q) A = 1, отсюда
¬А = ¬(P ∧ Q)
Ответом в логическом уравнении будет:
А = P ∧ Q.
Решение задачи на отрезки
4) Интерпретация полученного результата .
Наш ответ: А = P ∧ Q .
В алгебре логики это выражение означает пересечение объемов двух логических объектов. По условию нашей задачи – это пересечение отрезков P и Q .
![Решение задачи на отрезки Пересечение отрезков P и Q можно визуализировать: P=[4,15] и Q=[12,20]. 15 12 20 4 По условию нашей задачи, нам нужна минимальная длина отрезка А . Находим ее: 15 – 12 = 3 . Ответ: 3 . Ответ на сайте Полякова К.Ю.: 3](https://fsd.videouroki.net/html/2023/01/26/v_63d249777a998/img14.jpg)
Решение задачи на отрезки
Пересечение отрезков P и Q можно визуализировать: P=[4,15] и Q=[12,20].
15
12
20
4
По условию нашей задачи, нам нужна минимальная длина отрезка А . Находим ее: 15 – 12 = 3 .
Ответ: 3 .
Ответ на сайте Полякова К.Ю.: 3
![Задания на отрезки (№ 360) На числовой прямой даны три отрезка: P=[10,25], Q=[15,30] и R=[25,40]. Какова максимальная длина отрезка A, при котором формула ((x ∈ Q) → (x ∉ R) ) ∧ (x ∈ A) ∧ (x ∉ P) тождественно ложна, то есть принимает значение 0 при любом значении переменной х? Источник - сайт Полякова К.Ю.](https://fsd.videouroki.net/html/2023/01/26/v_63d249777a998/img15.jpg)
Задания на отрезки
(№ 360) На числовой прямой даны три отрезка: P=[10,25], Q=[15,30] и R=[25,40]. Какова максимальная длина отрезка A, при котором формула ((x ∈ Q) → (x ∉ R) ) ∧ (x ∈ A) ∧ (x ∉ P)
тождественно ложна, то есть принимает значение 0 при любом значении переменной х?
Источник — сайт Полякова К.Ю.
Решающая формула
Для выбора решающей формулы важно внимательно прочитать требование задачи.
В нашей задаче в требовании сказано:
принимает значение 0 при любом значении переменной х.
Выбор решающей формулы очевиден:
А ¬А = 0
Решение задачи на отрезки
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи на отрезки
- Легенда
R = x R
Q = x Q
A = x A
P = x P
Решение задачи на отрезки
2) Формализация условия
Было:
((x ∈ Q) → (x ∉ R) ) ∧ (x ∈ A) ∧ (x ∉ P) = 0
Стало:
( Q → ¬R ) ∧ A ∧ ¬ P = 0
Решение задачи на отрезки
3) Решение логического уравнения
( Q → ¬R ) ∧ A ∧ ¬ P = 0
3.1. Представим логическое следование в базовых логических операциях по формуле: А → В = ¬А В , и переставим множители согласно закону коммутативности умножения:
A ∧ (¬ Q ¬R ) ∧ ¬ P = 0
Решение задачи на отрезки
3) Решение логического уравнения
A ∧ ( ¬ Q ¬R ) ∧ ¬ P = 0
3.2. Сведем получившееся выражение к решающей формуле: А ¬А = 0 и найдем, чему равно ¬А :
¬А = (¬ Q ¬R ) ∧ ¬ P
Решение задачи на отрезки
3) Решение логического уравнения
¬А = (¬ Q ¬R ) ∧ ¬ P
3.3. Упростим выражение для ¬А по закону де Моргана ¬А ¬В=¬(А В) :
¬А = ¬ (Q R ) ∧ ¬ P,
и по другому закону де Моргана ¬А ¬В =¬(А В ) :
¬А = ¬ (Q R P)
Решение задачи на отрезки
3) Решение логического уравнения
¬А = ¬ (Q R P)
3.4. Очевидно, что
А = Q R P
Решение задачи на отрезки
4) Интерпретация полученного результата
А = Q R P
Отрезок А – это пересечение отрезков Q и R и его объединение с отрезком Р .
![Решение задачи на отрезки Пересечение отрезков R и Q можно визуализировать: Q=[15,30] и R=[25,40]. 30 25 40 15 Отрезок P=[10,25] нанесем на наш чертеж и объединим с пересечением: 25 30 15 40 10](https://fsd.videouroki.net/html/2023/01/26/v_63d249777a998/img25.jpg)
Решение задачи на отрезки
Пересечение отрезков R и Q можно визуализировать: Q=[15,30] и R=[25,40].
30
25
40
15
Отрезок P=[10,25] нанесем на наш чертеж и объединим с пересечением:
25
30
15
40
10
Решение задачи на отрезки
А = Q R P
40
25
30
10
15
По условию нашей задачи, нам нужна максимальная длина отрезка А . Находим ее: 30 – 10 = 20 .
Ответ: 20 .
Ответ на сайте Полякова К.Ю.: 20
27
2. Задания на множества
(№ 386) Элементами множеств А, P, Q являются натуральные числа, причём P={1,2,3,4,5,6}, Q={3,5,15}. Известно, что выражение (x ∉ A) → ((x ∉ P) ∧ (x ∈ Q)) ∨ (x ∉ Q)
истинно (т.е. принимает значение 1 при любом значении переменной х. Определите наименьшее возможное количество элементов в множестве A.
Источник — сайт Полякова К.Ю.
Решение задачи на множества
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи на множества
- Легенда
A = x ∈ A
P = x ∈ P
Q = x ∈ Q
Решение задачи на множества
2) Формализация условия
Было:
(x ∉ A) → ((x ∉ P) ∧ (x ∈ Q)) ∨ (x ∉ Q) = 1
Стало:
¬ A → (¬P ∧ Q) ¬ Q = 1
Решение задачи на множества
3) Решение логического уравнения
¬ A → (¬P ∧ Q) ¬ Q = 1
3.1. Представим логическое следование в базовых логических операциях и сгруппируем:
A ((¬P ∧ Q) ¬ Q) = 1
Решение задачи на множества
A (( ¬P ∧ Q) ¬Q) = 1
3.2. Сведем получившееся выражение к решающей формуле:
А ¬А = 1
и найдем, чему равно ¬А :
¬А = (¬P ∧ Q) ¬Q
Решение задачи на множества
¬А = (¬P ∧ Q) ¬Q
3.3. Упростим выражение для ¬А, раскрыв скобки по закону дистрибутивности сложения:
¬А = ( ¬P ¬Q) (Q ¬Q)
Q ¬Q = 1
¬А = ( ¬P ¬Q)
Решение задачи на множества
¬А = ( ¬P ¬Q)
По закону де Моргана:
¬А = ¬(P Q)
3.4. Очевидно, что
А = P Q
Решение задачи на множества
А = P Q
4) Интерпретация полученного результата
Искомое множество А представляет собой пересечение множеств P и Q.
Решение задачи на множества
Искомое множество А есть пересечение множеств
P = 1, 2, 3 , 4, 5 , 6 и Q = { 3 , 5 ,15}, таким образом A = { 3 , 5 }
и содержит только 2 элемента.
Ответ: 2
Ответ на сайте Полякова: 2
2. Задания на множества
(№ 368) Элементами множеств А, P, Q являются натуральные числа, причём P={2,4,6,8,10,12} и Q={4,8,12,116}. Известно, что выражение (x ∈ P) → (((x ∈ Q) ∧ (x ∉ A)) → (x ∉ P))
истинно (т. е. принимает значение 1 ) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.
Источник — сайт Полякова К.Ю.
Решение задачи на множества
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи на множества
- Легенда
A = x ∈ A
P = x ∈ P
Q = x ∈ Q
Решение задачи на множества
2) Формализация условия
Было:
(x ∈ P)→(((x ∈ Q) ∧ (x ∉ A))→(x ∉ P)) = 1
Стало:
P → ((Q ∧ ¬ A) → ¬ P) = 1
Решение задачи на множества
3) Решение логического уравнения
P → ((Q ∧ ¬ A) → ¬ P) = 1
3.1. Представим первое логическое следование (в скобках) в базовых логических операциях :
P → ( ¬ (Q ∧ ¬ A) ¬ P) = 1
Решение задачи на множества
P → ( ¬ (Q ∧ ¬ A) ¬ P) = 1
Представим второе логическое следование в базовых логических операциях, применим закон де Моргана и перегруппируем:
¬ P ( ¬ (Q ∧ ¬ A) ¬ P) = 1
¬ P ¬ Q A ¬ P = 1
Решение задачи на множества
A ( ¬ P ¬ Q ¬ P) = 1
3.2. Сведем получившееся выражение к решающей формуле:
А ¬А = 1
и найдем, чему равно ¬А :
¬А = ( ¬ P ¬ Q ¬ P)
Решение задачи на множества
¬А = ¬ P ¬ Q ¬ P
3.3. Упростим выражение для ¬А по формуле А А = А :
¬А = ¬ P ¬ Q
Далее, по закону де Моргана получаем:
¬А = ¬( P Q)
Решение задачи на множества
¬А = ¬(P Q)
3.4. Очевидно, что
А = P Q
4) Интерпретация полученного результата
Искомое множество А представляет собой пересечение множеств P и Q.
Решение задачи на множества
Искомое множество А есть пересечение множеств
P = 2, 4 , 6, 8 , 10, 12 и
Q = { 4 , 8 , 12 , 16}, таким образом
A = { 4 , 8 , 12 }
и содержит только 3 элемента, сумма которых 4+8+12=24 .
Ответ: 24
Ответ на сайте Полякова: 24
3. Задания на поразрядную конъюнкцию
(№ 379) Обозначим через m & n пораз-рядную конъюнкцию неотрицательных целых чисел m и n . Так, например, 14 & 5 = 1110 2 & 0101 2 = 0100 2 = 4. Для какого наименьшего неотрицательного целого числа А формула (x & 29 ≠ 0) → ((x & 12 = 0) → (x & А ≠ 0))
тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?
Решение задачи на поразрядную конъюнкцию
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи на поразрядную конъюнкцию
- Легенда
Легенда для задач на поразрядную конъюнкцию отличается от всех остальных случаев:
B = (x & 29 ≠ 0)
C = (x & 12 ≠ 0)
A = (x & А ≠ 0)
Решение задачи на поразрядную конъюнкцию
Мы принимаем за истинное высказывание поразрядную конъюнкцию, отличную от нуля, иначе поразрядная конъюнкция теряет свой логический смысл, т.к. всегда можно представить Х всеми нулями.
Решение задачи на поразрядную конъюнкцию
2) Формализация условия
Было:
(x & 29 ≠ 0)→((x & 12 = 0)→(x & А ≠ 0))=1
Стало:
В → ( ¬С → А) = 1
Решение задачи на поразрядную конъюнкцию
3) Решение логического уравнения
В → ( ¬С → А) = 1
В → (С А) = 1
(¬В С) А = 1
¬А = ¬В С
¬А = ¬(В ¬ С)
Очевидно, что
А = В ¬ С
Решение задачи на поразрядную конъюнкцию
4) Интерпретация полученного результата
Искомое двоичное значение поразрядной конъюнкции А – это двоичное значение поразрядной конъюнкции значения В и инверсии двоичного значения С .
Решение задачи на поразрядную конъюнкцию
B = (x & 29 ≠ 0)
В или 29 = 11101 2
C = (x & 12 ≠ 0)
12 = 1100 2
¬С или инверсия 12 = 0011 2
Решение задачи на поразрядную конъюнкцию
В или 29 = 11101 2
¬С или инверсия 12 = 0011 2
А = В ¬ С
х 11101 2
0011 2
10001 2
А = 1 0001 2 = 17
Ответ на сайте Полякова: 17
27
3. Задания на поразрядную конъюнкцию
(№ 375) Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K (логическое «И» между соответ-ствующими битами двоичной записи). Определите наименьшее натуральное число A, такое что выражение (X & 49 ≠ 0) → ((X & 33 = 0) → (X & A ≠ 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?
Решение задачи на поразрядную конъюнкцию
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи на поразрядную конъюнкцию
- Легенда
Легенда для задач на поразрядную конъюнкцию отличается от всех остальных случаев:
B = (x & 49 ≠ 0)
C = (x & 33 ≠ 0)
A = (x & А ≠ 0)
Решение задачи на поразрядную конъюнкцию
2) Формализация условия
Было:
(X & 49 ≠ 0) → ((X & 33 = 0) → (X & A ≠ 0))=1
Стало:
В → ( ¬С → А) = 1
Решение задачи на поразрядную конъюнкцию
3) Решение логического уравнения
В → ( ¬С → А) = 1
В → (С А) = 1
(¬В С) А = 1
¬А = (¬В С)
Очевидно:
А = В ¬С
Решение задачи на поразрядную конъюнкцию
4) Интерпретация полученного результата
Искомое двоичное значение поразрядной конъюнкции А – это двоичное значение поразрядной конъюнкции значения В и инверсии двоичного значения С .
Решение задачи на поразрядную конъюнкцию
B = (x & 49 ≠ 0)
В или 49 = 110001 2
C = (x & 33 ≠ 0)
33 = 100001 2
¬С или инверсия 33 = 011110 2
Решение задачи на поразрядную конъюнкцию
В или 49 = 110001 2
¬С или инверсия 33 = 011110 2
А = В ¬ С
х 110001 2
011110 2
010000 2
А = 1 0000 2 = 16
Ответ на сайте Полякова: 16
27
4. Задания на условие делимости
(№ 372) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула ¬ДЕЛ(x,А) → (¬ДЕЛ(x,21) ∧ ¬ДЕЛ(x,35))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Источник — сайт Полякова К.Ю.
Решение задачи
на условие делимости
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи
на условие делимости
- Легенда
Легенда простая: А = ДЕЛ(x,А)
21 = ДЕЛ(х,21)
35 = ДЕЛ(x,35)
Решение задачи
на условие делимости
2) Формализация условия
Было:
¬ДЕЛ(x,А) → (¬ДЕЛ(x,21) ∧ ¬ДЕЛ(x,35))
тождественно истинна (то есть принимает значение 1)
Стало:
¬А → (¬21 ∧ ¬35) = 1
Решение задачи
на условие делимости
3) Решение логического уравнения
¬А → (¬21 ∧ ¬35) = 1
А (¬21 ∧ ¬35) = 1
¬А = ¬21 ∧ ¬35
Очевидно, что
А = 21 35
Решение задачи
на условие делимости
4) Интерпретация полученного результата
А = 21 35
В данной задаче это самый сложный этап решения. Нужно понять, что же представляет из себя число А – НОК или НОД или …
Решение задачи
на условие делимости
4) Интерпретация полученного результата
А = 21 35
Итак, наше число А таково, что Х делится на него без остатка, тогда и только тогда, когда Х делится без остатка на 21 или на 35. В этом случае ищем
А = НОД (21, 35) = 7
Ответ на сайте Полякова: 7
4. Задания на условие делимости
(№ 370) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула ¬ДЕЛ(x,А) → ((ДЕЛ(x,6) → ¬ДЕЛ(x,4))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Источник — сайт Полякова К.Ю.
Решение задачи
на условие делимости
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи
на условие делимости
- Легенда
А = ДЕЛ(x,А)
6 = ДЕЛ(x,6)
4 = ДЕЛ(x,4)
Решение задачи
на условие делимости
2) Формализация условия
Было:
¬ДЕЛ(x,А) → ((ДЕЛ(x,6) → ¬ДЕЛ(x,4))
тождественно истинна (то есть принимает значение 1
Стало:
¬А → (6 → ¬4) = 1
Решение задачи
на условие делимости
3) Решение логического уравнения
¬А → (6 → ¬4) = 1
¬А → (¬ 6 ¬4) = 1
А (¬ 6 ¬4) = 1
¬А = ¬ 6 ¬4
Очевидно:
А = 6 4
Решение задачи
на условие делимости
4) Интерпретация полученного результата
А = 6 4
Итак, А таково, что Х делится на него без остатка тогда и только тогда, когда Х делится без остатка и на 6, и на 4. Т.е. А = НОК(6, 4) = 12
Ответ на сайте Полякова: 12
A ) ∨ ( x A ) истинно для любых целых положительных значений x и y . » width=»640″
5. Задания на функции
Укажите наибольшее целое значение А, при котором выражение
( y + 2 x 99) ∨ ( y A ) ∨ ( x A )
истинно для любых целых положительных значений x и y .
A ) or ( x A ) выполнялось при всех x и y , для которых ложно ( y + 2 x 99) , то есть истинно ( y + 2 x = 99) или y = –2 x + 99 » width=»640″
Решение задачи
на функции
1) первое выражение не зависит от выбора A :
( y + 2 x 99)
2) таким образом, нам нужно выбрать значение A так, чтобы условие ( y A ) or ( x A ) выполнялось при всех x и y , для которых ложно ( y + 2 x 99) , то есть истинно ( y + 2 x = 99) или y = –2 x + 99
A ) or ( x A ) для некоторого значения A , например, для A = 50 (конечно, нужно учесть, что x и y положительны и добавить ещё два ограничения: ( x 0) and ( y 0) ): » width=»640″
Решение задачи
на функции
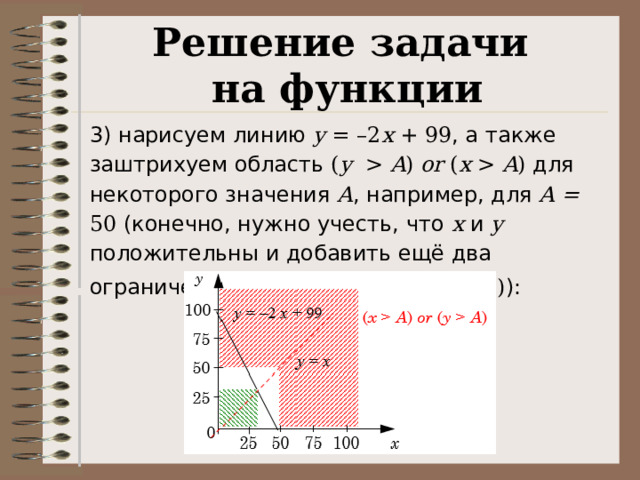
3) нарисуем линию y = –2 x + 99 , а также заштрихуем область ( y A ) or ( x A ) для некоторого значения A , например, для A = 50 (конечно, нужно учесть, что x и y положительны и добавить ещё два ограничения: ( x 0) and ( y 0) ):
Решение задачи
на функции
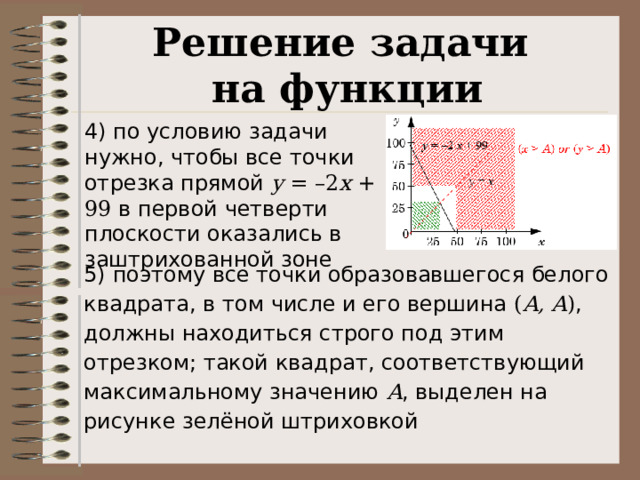
4) по условию задачи нужно, чтобы все точки отрезка прямой y = –2 x + 99 в первой четверти плоскости оказались в заштрихованной зоне
5) поэтому все точки образовавшегося белого квадрата, в том числе и его вершина ( A, A ) , должны находиться строго под этим отрезком; такой квадрат, соответствующий максимальному значению A , выделен на рисунке зелёной штриховкой
Решение задачи
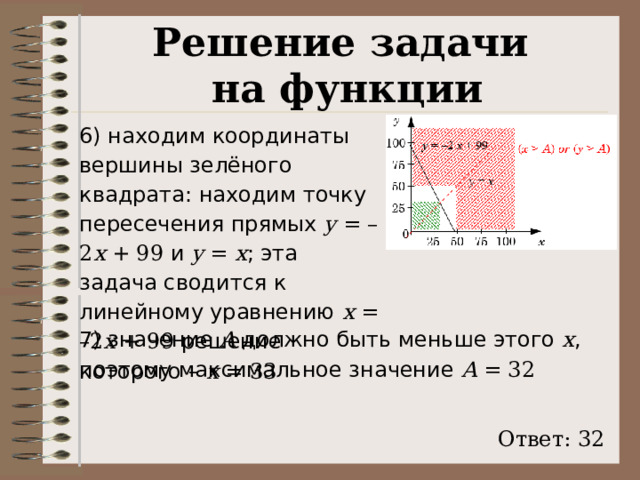
на функции
6) находим координаты вершины зелёного квадрата: находим точку пересечения прямых y = –2 x + 99 и y = x ; эта задача сводится к линейному уравнению x = –2 x + 99 решение которого – x = 33
7) значение A должно быть меньше этого x , поэтому максимальное значение A = 32
Ответ: 32
50) ∨ (4 y – x истинно для любых целых положительных значений x и y . » width=»640″
5. Задания на функции
Укажите наименьшее целое значение А, при котором выражение
( y + 3 x A ) ∨ (2 y +x 50) ∨ (4 y – x
истинно для любых целых положительных значений x и y .
50) or (4 y – x 2) таким образом, нам нужно выбрать значение A так, чтобы условие ( y + 3 x A ) выполнялось при всех x и y , для которых ложно (2 y +x 50) or (4 y – x y +x 50) and (4 y – x 40) 3) последние два условия можно переписать в виде ( y – x /2 + 25) and ( y x /4 + 10) » width=»640″
Решение задачи
на функции
1) второе и третье выражения не зависят от выбора A : (2 y +x 50) or (4 y – x
2) таким образом, нам нужно выбрать значение A так, чтобы условие ( y + 3 x A ) выполнялось при всех x и y , для которых ложно (2 y +x 50) or (4 y – x y +x 50) and (4 y – x 40)
3) последние два условия можно переписать в виде
( y – x /2 + 25) and ( y x /4 + 10)
0) and ( y 0) 5) изобразим схематично на плоскости x – y эту область (она заштрихована): » width=»640″
Решение задачи
на функции
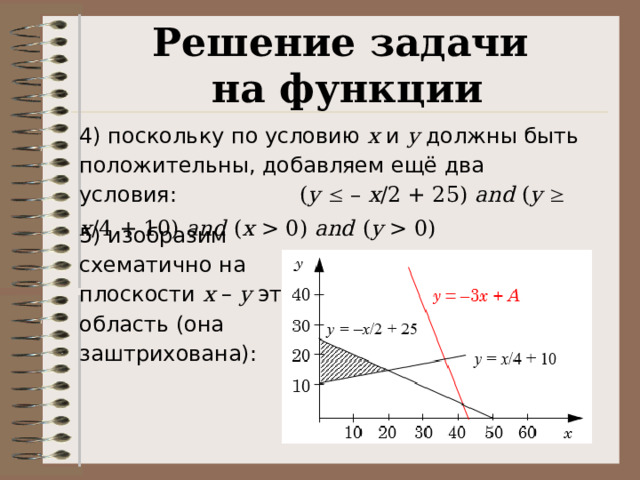
4) поскольку по условию x и y должны быть положительны, добавляем ещё два условия: ( y – x /2 + 25) and ( y x /4 + 10) and ( x 0) and ( y 0)
5) изобразим схематично на плоскости x – y эту область (она заштрихована):
Решение задачи
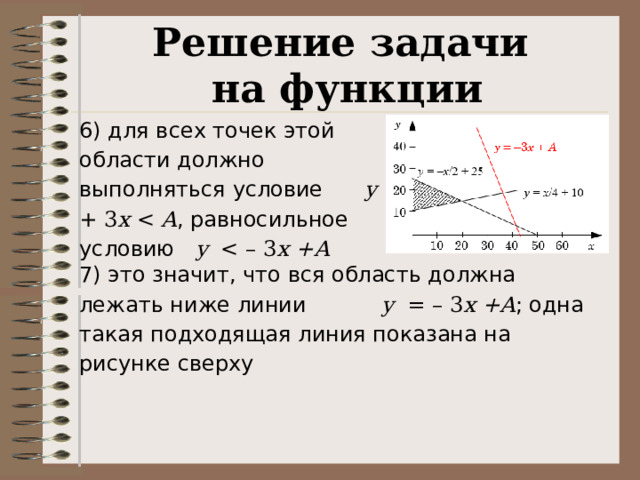
на функции
6) для всех точек этой области должно выполняться условие y + 3 x A , равносильное условию y x +A
7) это значит, что вся область должна лежать ниже линии y = – 3 x +A ; одна такая подходящая линия показана на рисунке сверху
75 откуда следует, что A min = 76. Ответ: 76 » width=»640″
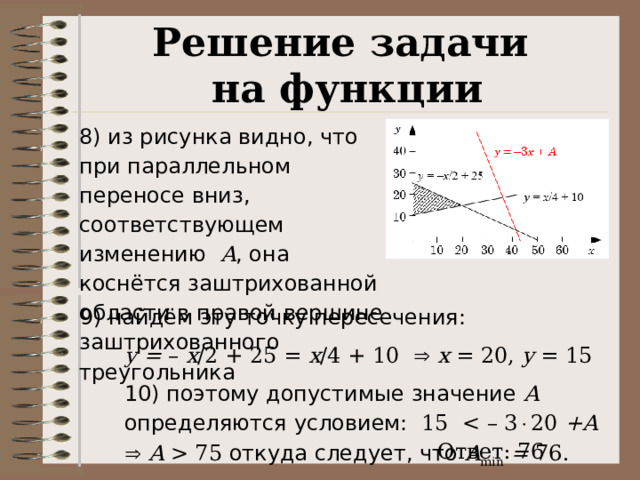
Решение задачи
на функции
из рисунка видно, что при параллельном переносе вниз, соответствующем изменению A , она коснётся заштрихованной области в правой вершине заштрихованного треугольника
9) найдём эту точку пересечения:
y = – x /2 + 25 = x /4 + 10 x = 20, y = 15
10) поэтому допустимые значение A определяются условием: 15 +A A 75 откуда следует, что A min = 76.
Ответ: 76