Задачи на нахождение объемов тел егэ по математике

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 129    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 129    1–20 | 21–40 | 41–60 | 61–80 …

11 февраля 2016

В закладки

Обсудить

Жалоба

Задачи на нахождение объёмов тел

Задание №8 профильного уровня ЕГЭ по математике (бывшее B11).

В данной разработке представлены задачи от самых простых до более сложных. К задачам представлено подробное решение.

Задание 8. Из спецификации к демоверсии:

Уметь выполнять действия с геометрическими фигурами, координатами и векторами.

Автор: Тихончук Людмила Юрьевна, учитель математики.

8obemi.docx

1)Аквариум имеет форму прямоугольного параллелепипеда с размерами 80 см × 30 см ×  40 см. Сколько литров составляет объём аквариума? В одном литре 1000 кубических сантиметров.

2)Через точку, делящую высоту конуса в отношении 1:3, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём этого конуса, если объём конуса, отсекаемого от данного конуса проведённой плоскостью, равен 5.

3)Два ребра прямоугольного параллелепипеда равны 8 и 5,
а объём параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.

4)Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка

в четыре раза ниже второй, а вторая

в полтора раза шире первой. Во сколько раз объём второй коробки больше объёма первой?

5)Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а высота этой призмы равна 4. Найдите объём призмы АВСА1В1С1

6)Объём  конуса равен  24π, а  его  высота равна 8. Найдите радиус основания конуса.

7)Вода в сосуде цилиндрической формы находится на уровне h= 80 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте

в сантиметрах.

8)В бак, имеющий форму прямой призмы, налито 12 л воды. После полного погружения в воду детали уровень воды

в баке увеличился в 1,5 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.

9)Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6,

а второго — 6 и 4. Во сколько раз объём второго цилиндра больше объёма первого?

10)Даны два конуса. Радиус основания и высота первого конуса равны соответственно 3 и 2, а второго — 2 и 3. Во сколько раз объём первого конуса больше объёма второго?

11)В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды

в баке поднялся в 1,4 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре

1000 кубических сантиметров.

12)Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 2 и 5,

а второго — 5 и 6. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого

13)Даны два шара с радиусами 5 и 1. Во сколько раз объём большего шара больше объёма меньшего?

14)В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём сосуда 120 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.

15)

15)Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.

16)Объём конуса равен 25π, а его высота равна 3. Найдите радиус основания конуса

Данное занятие может быть проведено после изучения формул объемов многогранников на уроках геометрии в 11-м классе или в рамках элективного курса по подготовке к ЕГЭ. Материал также доступен и учащимся 10-го класса (во 2-м полугодии).

Цели занятия:

• показать примеры задач, аналогичных заданиям ЕГЭ по математике базового уровня и первой части профильного уровня;
• повторить теоретический материал, связанный с площадями фигур, со свойствами многогранников;
• отработка навыков самоконтроля;
• отработка навыков сотрудничества между учащимися.

Оборудование:

• оборудование для демонстрации презентации Microsoft PowerPoint (компьютер, проектор, экран или доска);
• раздаточный материал (тексты задач с чертежами);
• таблица квадратов натуральных чисел.

План занятия

1. Организационный момент
2. Устная работа
3. Решение задач
4. Работа в группах
5. Подведение итогов

Ход занятия

Занятие сопровождается демонстрацией презентации.

1. Организационный момент

Cообщение целей занятия, деление класса на группы по 4 человека (можно объединить учащихся, сидящих за соседними партами).

2. Устная работа

Условия задач и правильные ответы демонстрируются на слайдах. Задачи решаются устно, ответы можно спросить у нескольких учащихся, один из них коротко рассказывает путь решения.

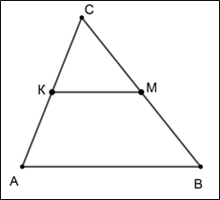
Задача 1. (Слайд №4) Площадь треугольника АВС равна 120. КМ – средняя линия, параллельная стороне АВ. Найти площадь четырехугольника АКМВ. (Ответ: 90)

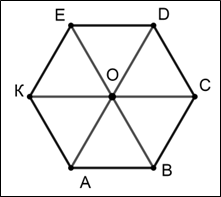
Задача 2. (Слайды №5,6) Площадь правильного шестиугольника АВСДЕК равна 60, О – центр шестиугольника. Найти площади треугольника АОВ, треугольника  АВС, треугольника АВЕ, четырехугольника ВСДЕ. (Ответ: 10; 10; 20; 30)

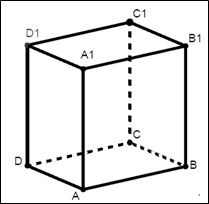
Задача 3. (Слайд №7) Площадь грани прямоугольного параллелепипеда равна 15. Ребро, перпендикулярное этой грани, равно 6. Найти объем параллелепипеда. (Ответ: 90)

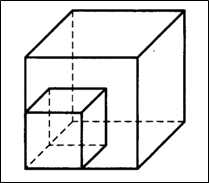
Задача 4. (Слайд №8) Во сколько раз увеличится объем куба, если его ребро увеличить в 5 раз? (Ответ:  125)

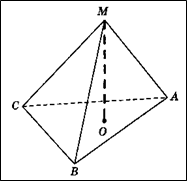
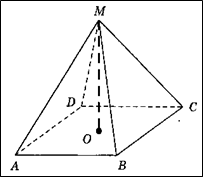
Задача 5. (Слайд №9) В правильной треугольной пирамиде МАВС О – точка пересечения медиан основания. Площадь треугольника АВС равна 5, а объем пирамиды – 35. Найти длину отрезка МО. (Ответ: 21)

Задача 6. (Слайд №10) Как изменится объем пятиугольной пирамиды, если её высоту увеличить в 4 раза? (Ответ: увеличится в 4 раза)

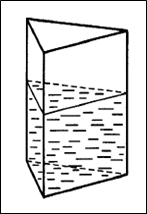
Задача 7. (Слайд №11) В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды составил 20 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд такой же формы, у которого сторона основания в 2 раза больше, чем у первого? (Ответ: 5 см)

При подведении итогов устной работы необходимо обратить внимание на формулы для вычисления объемов призмы и пирамиды.

3. Решение задач

Чертежи заранее сделаны на доске, каждый ученик получает заготовку с чертежами (Приложение 1). Учащиеся у доски записывают краткие решения, сопровождая их устными пояснениями. Также можно использовать слайды №13, 14, 15.

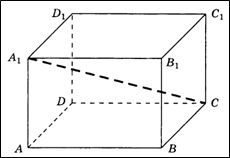
Задача 8. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 6 и 3. Объем параллелепипеда равен 108. Найти его диагональ.

Задача 9. В сосуд, имеющий форму правильной треугольной призмы, налили 1000 см³ воды и погрузили в воду деталь. При этом  уровень воды поднялся с отметки 25 см до отметки 27 см. Найти объем детали. Ответ выразить в см³.

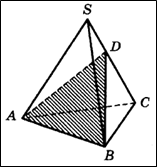
Задача 10. Объем треугольной пирамиды SABC равен 15. Плоскость проходит через сторону АВ основания этой пирамиды и пересекает противоположное боковое ребро в точке D, делящей ребро SC в отношении 1 : 2, считая от вершины S. Найти объем пирамиды DABC.

4. Работа в группах

Каждая группа получает набор задач (Приложение 2), к которым надо записать краткие решения. После истечения отведенного времени проверяются ответы, представители групп могут прокомментировать ход решения задач. В это время чертежи демонстрируются на слайдах №17, 18, 19. Для быстрой проверки можно использовать слайд №20. После этого листы с решениями сдаются учителю.

5. Подведение итогов

При подведении итогов следует обратить внимание на две основные формулы объемов и их частные случаи, а также на отношение объемов подобных тел (слайд 22).

Задача. (Слайд №23) Боковые ребра правильной треугольной пирамиды взаимно перпендикулярны и равны 6. Найти объем пирамиды. (Ответ: 36)

При решении этой задачи очень важно обратить внимание на метод решения. Если тетраэдр перевернуть, то задачу можно решить устно.

Задача. (Слайды №24, 25) Объем тетраэдра равен 12. Найти объем многогранника, вершинами которого являются середины сторон данного тетраэдра. (Ответ: 6)

6. Домашнее задание (Приложение 3)

Литература

1. Ященко И. В. ЕГЭ: 4000 задач с ответами по математике. Все задания «Закрытый сегмент». Базовый и профильный уровни. – М: Издательство «Экзамен», 2020.
2. Балаян Э. Н. Геометрия: задачи на готовых чертежах для подготовки к ЕГЭ: 10-11 классы. – Ростов н/Д: Феникс, 2018.
3. Материалы сайта: https://math-ege.sdamgia.ru/

Список приложений

• Приложение 1 – задачи для работы в классе
• Приложение 2 – задачи для работы в группах
• Приложение 3 – домашнее задание
• Приложение 4 – ПРЕЗЕНТАЦИЯ