в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 135 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Небольшая шайба после удара скользит вверх по наклонной плоскости из точки А (см. рис.).
В точке В наклонная плоскость без излома переходит в наружную поверхность горизонтальной трубы радиусом R. Если в точке А скорость шайбы превосходит то в точке В шайба отрывается от опоры. Длина наклонной плоскости
угол
Коэффициент трения между наклонной плоскостью и шайбой
Найдите внешний радиус трубы R.
Какие законы Вы использовали для описания движения тела? Обоснуйте их применимость к данному случаю.
Задания Д29 C2 № 2952
Небольшая шайба после удара скользит вверх по наклонной плоскости из точки А (см. рис.).
В точке В наклонная плоскость без излома переходит в наружную поверхность горизонтальной трубы радиусом R. Если в точке А скорость шайбы превосходит то в точке В шайба отрывается от опоры. Длина наклонной плоскости
угол
Коэффициент трения между наклонной плоскостью и шайбой
Найдите внешний радиус трубы R.
Гоночный автомобиль едет по треку, имеющему на повороте радиусом R = 50 м угол наклона полотна дороги к горизонту α = 30° внутрь поворота. С какой максимальной скоростью V может двигаться автомобиль, чтобы не заскользить и не вылететь с трека? Коэффициент трения колёс автомобиля о дорогу μ = 0,8. Ответ выразите в км/ч.
Какие законы Вы используете для описания движения автомобиля? Обоснуйте их применение к данному случаю.
Источник: Тренировочная работа по физике 18.09.2018, вариант ФИ10101
Задания Д29 C2 № 3070
Наклонная плоскость пересекается с горизонтальной плоскостью по прямой AB. Угол между плоскостями Маленькая шайба начинает движение вверх по наклонной плоскости из точки A с начальной скоростью
под углом
к прямой AB. В ходе движения шайба съезжает на прямую AB в точке B. Пренебрегая трением между шайбой и наклонной плоскостью, найдите расстояние AB.
Брусок скользит по наклонной плоскости вниз без трения. Что происходит при этом с его скоростью, потенциальной энергией, силой реакции наклонной плоскости?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Скорость бруска | Потенциальная энергия
бруска |
Сила реакции наклонной
плоскости |
Небольшой брусок соскальзывает без начальной скорости с наклонной плоскости длиной L. Наклонная плоскость составляет с горизонтом угол α. В процессе движения на брусок со стороны плоскости действует сила нормальной реакции, модуль которой равен N, а модуль силы трения скольжения при этом равен F. Установите соответствие между физическими величинами, характеризующими движение бруска, и формулами, выражающими эти величины в рассматриваемой задаче. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) кинетическая энергия бруска в конце движения по наклонной плоскости
Б) время движения бруска до основания наклонной плоскости
Ответ:
Задания Д29 C2 № 2947
Брусок массой соскальзывает по наклонной плоскости с высоты h и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой
В результате абсолютно неупругого соударения общая кинетическая энергия брусков становится равной 2,5 Дж. Определите высоту наклонной плоскости h. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.
Задания Д29 C2 № 2948
Брусок массой соскальзывает по наклонной плоскости с высоты
и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой
Считая столкновение абсолютно неупругим, определите общую кинетическую энергию брусков после столкновения. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.
Задания Д29 C2 № 7160
Брусок массой m1 = 500 г соскальзывает по наклонной плоскости с некоторой высоты h и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой m2 = 300 г. Считая столкновение абсолютно неупругим, определите высоту h, если общая кинетическая энергия брусков после столкновения равна 2,5 Дж. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.
Брусок массой m1 = 500 г соскальзывает по наклонной плоскости с некоторой высоты h и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой m2 = 300 г. Считая столкновение абсолютно неупругим, определите высоту h, если общая кинетическая энергия брусков после столкновения равна 2,5 Дж. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.
Какие законы Вы используете для описания неупругого столкновения брусков? Обоснуйте их применение к данному случаю.
Небольшую шайбу массой 100 г, покоящуюся у основания наклонной плоскости, толкают вдоль неё вверх. В результате шайба поднимается по наклонной плоскости на некоторую высоту. На рисунке показан график зависимости максимальной высоты подъёма h шайбы от начальной кинетической энергии E, которую сообщили шайбе при её толкании. Угол наклона плоскости к горизонту равен 45°.
Из приведённого ниже списка выберите все правильные утверждения.
1) Если сообщить шайбе начальную скорость 6 м/с, то шайба поднимется по наклонной плоскости на высоту более 2 м.
2) Для того, чтобы шайба поднялась по наклонной плоскости на высоту 3 м, надо сообщить шайбе начальную кинетическую энергию 4,5 Дж.
3) Наклонная плоскость гладкая.
4) Коэффициент трения шайбы о наклонную плоскость равен 0,5.
5) После подъёма по наклонной плоскости на максимальную высоту шайба остановится.
Небольшую шайбу массой 100 г, покоящуюся у основания наклонной плоскости, толкают вдоль неё вверх. В результате шайба поднимается по наклонной плоскости на некоторую высоту. На рисунке показан график зависимости максимальной высоты подъёма h шайбы от начальной кинетической энергии E, которую сообщили шайбе при её толкании. Угол наклона плоскости к горизонту равен 45°.
Из приведённого ниже списка выберите все правильные утверждения.
1) Для того чтобы шайба поднялась по наклонной плоскости на высоту 1 м, надо сообщить шайбе начальную кинетическую энергию 1,5 Дж.
2) Если сообщить шайбе начальную скорость 6 м/с, то шайба поднимется по наклонной плоскости на высоту более 1,5 м.
3) Коэффициент трения шайбы о наклонную плоскость равен 0,5.
4) Наклонная плоскость гладкая.
5) После подъёма по наклонной плоскости на максимальную высоту шайба остановится.
Источник: ЕГЭ по физике 06.06.2022. Основная волна. Разные задачи
Всего: 135 1–20 | 21–40 | 41–60 | 61–80 …
- Подробности
- Обновлено 30.05.2018 23:11
- Просмотров: 1097
Задачи по физике — это просто!
Не забываем
Решать задачи надо всегда в системе СИ!
А теперь к задачам!
Типовые задачи из курса школьной физики по динамике на движение тела по наклонной плоскости под действием нескольких сил.
Задача 1
Сани спускаются с горы высотой 20 метров и длиной 100 метров с ускорением 1 м/с. Определить коэффициент трения.
Задача 2
C каким ускорением будет скользить вниз ящик по наклонной плоскости, если коэффициент трения равен 0,9, а угол наклонной плоскости относительно горизонтали составляет 60o?
Задача 3
Какую силу надо приложить к тележке массой 200 кг, чтобы она двигалась вверх по наклонной плоскости с ускорением 0,5 м/с2, если коэффициент трения равен 0,2, а наклонная плоскость составляет с горизонталью угол 30o?
Движение тела по наклонной плоскости
Репетитор по физике
8 916 478 10 32
Пройти тест на эту тему
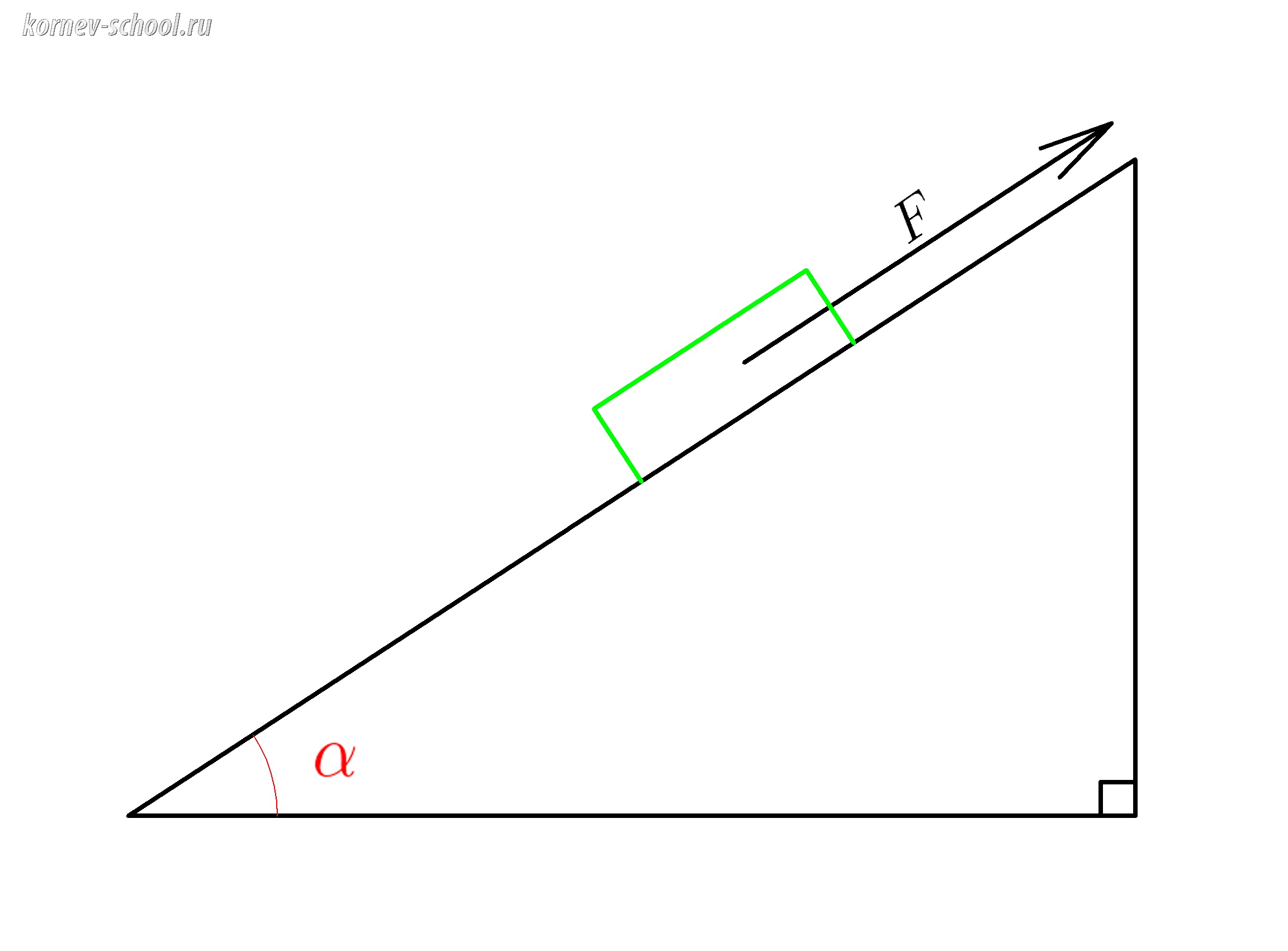
Тело на наклонной плоскости с углом наклона ( alpha )
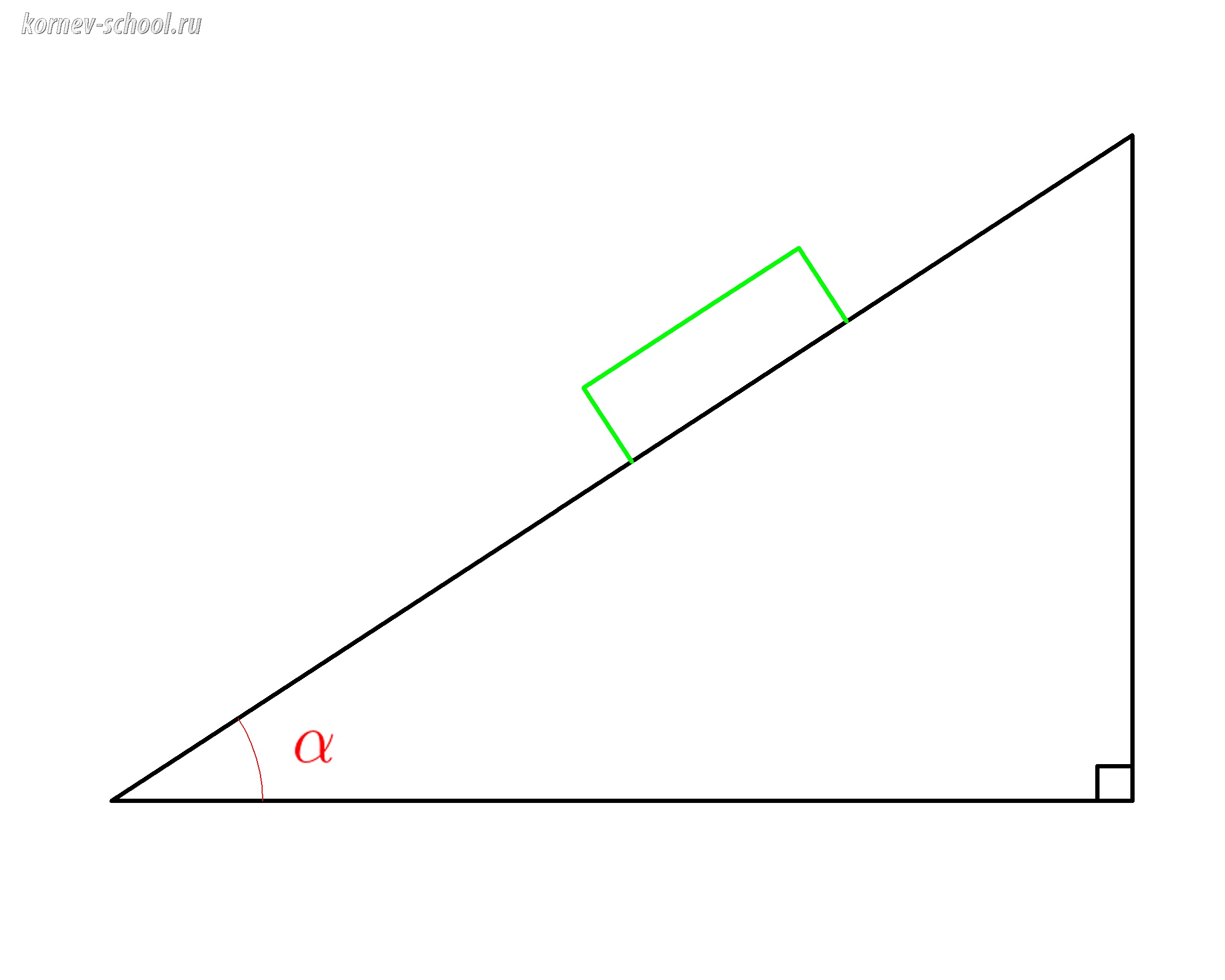
Уменьшим размеры тела для того, чтобы его габариты не мешали разбираться построении векторов и их проекций.
Жирная зеленая точка это и есть наше тело.
Проведем из нее вектор силы тяжести (mg).
При решении задач на движение тела по наклонной плоскости мы направляем ось ( x ) вдоль гипотенузы,а ось ( y )
перпендикулярно ей
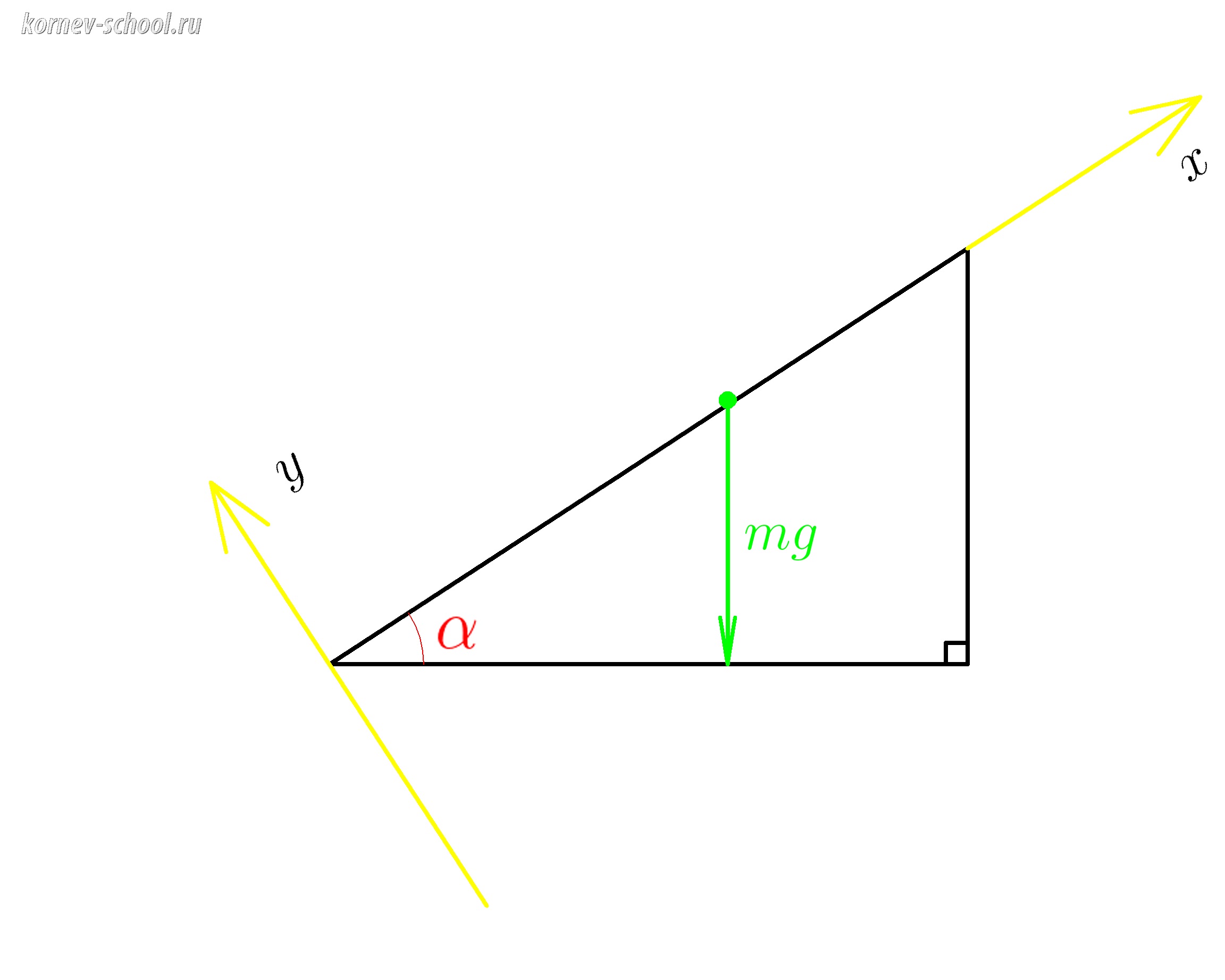
Проведем перпендикуляр из конца вектора силы тяжести на ось ( x )
(F_{тx} ; ) это проекция силы тяжести на ось x
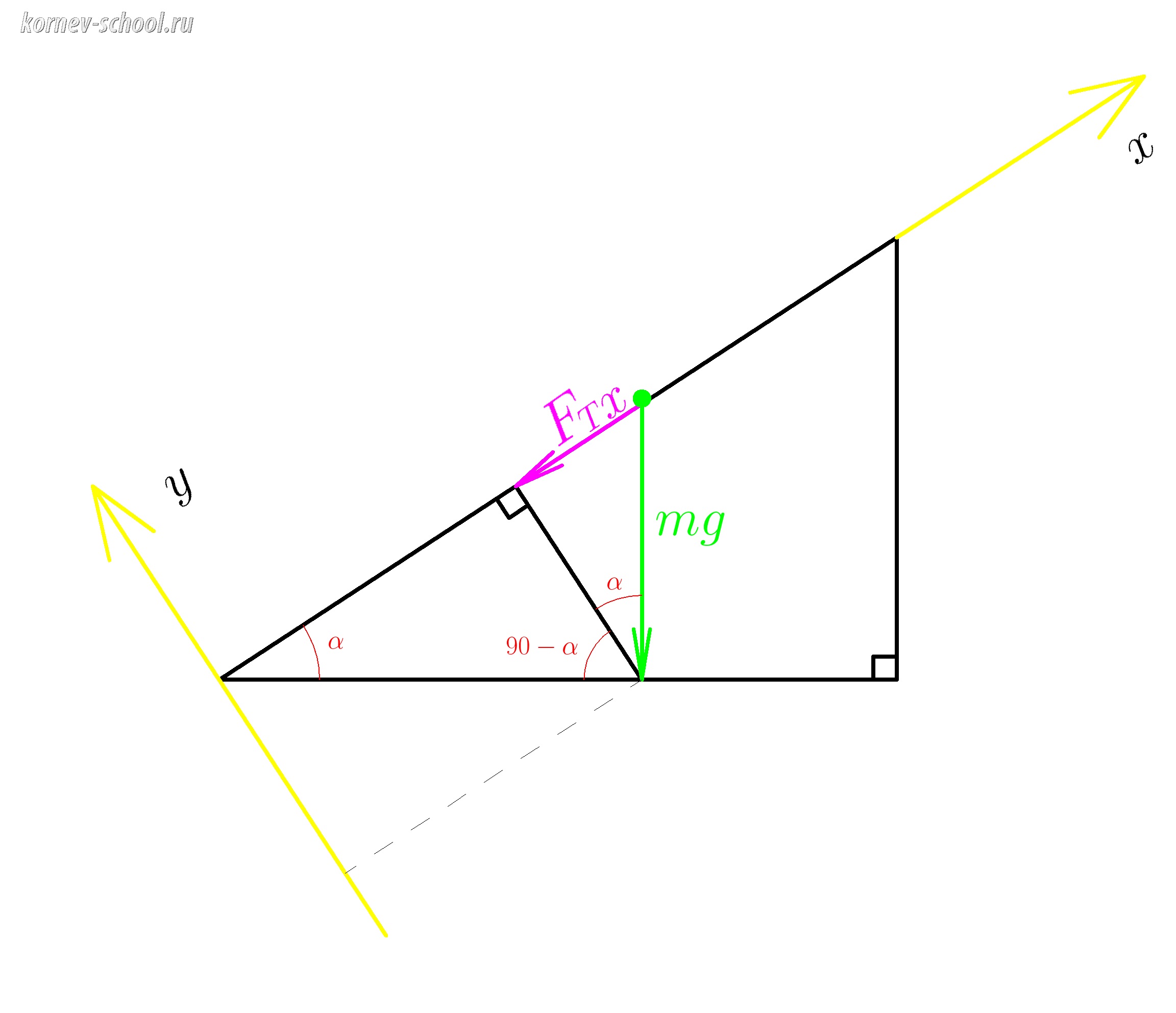
Сфокусируем все свое внимание на прямоугольный треугольничек с зелененькой гипотенузой
(mg )
и фиолетовым катетом (F_{тx} ; )
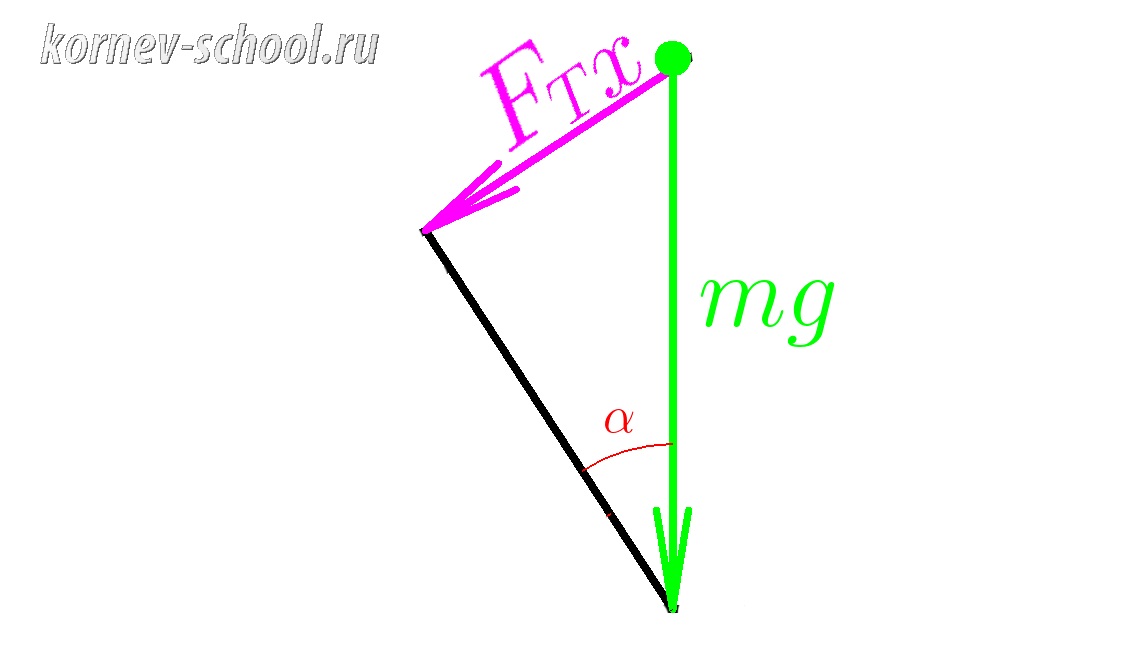
(sin ; alpha=dfrac{F_{Тx}}{mg} )
( F_{Тx}= mg cdot sin ; alpha ;;;;; ) это мы нашли проекцию силы тяжести на ось (x)
Задача 1.
К телу массой (m=1 кг ), покоящемуся на гладкой наклонной плоскости с углом наклона ( alpha=30^0 ), приложена сила (F),
направленная вдоль наклонной плоскости, поэтому тело не соскальзывает, а покоится.
Найти значение этой силы (F)
Показать ответ
Показать решение
Видеорешение
Задача 2.
К телу массой (m=2 кг ), покоящемуся на гладкой наклонной плоскости с углом наклона ( alpha=30^0 ), приложена сила (F),
направленная вдоль наклонной плоскости, поэтому тело не соскальзывает, а покоится.
Найти значение этой силы (F)

Показать ответ
Показать решение
Видеорешение
Задача 3.
К телу массой (m=sqrt{2} кг ), покоящемуся на гладкой наклонной плоскости с углом наклона ( alpha=45^0 ), приложена сила (F),
направленная вдоль наклонной плоскости, поэтому тело не соскальзывает, а покоится.
Найти значение этой силы (F)

Показать ответ
Показать решение
Видеорешение
Задача 4.
К телу массой (m=sqrt{27} кг ), покоящемуся на гладкой наклонной плоскости с углом наклона ( alpha=60^0 ), приложена сила (F),
направленная вдоль наклонной плоскости, поэтому тело не соскальзывает, а покоится.
Найти значение этой силы (F)

Показать ответ
Показать решение
Видеорешение
Пройти тест на эту тему
Задача 6.
С каким ускорением (a ) движется тело по гладкой наклонной плоскости с углом наклона ( alpha=45^0 ; ? )
Ускорение свободного падения ( g=10м/с^2 ; )
Ответ округлить до сотых

Показать ответ
Показать решение
Видеорешение
Пройти тест на эту тему
Проецирование сил. Движение по наклонной плоскости
Задачи по динамике.
I и II закон Ньютона.
Ввод и направление осей.
Неколлинеарные силы.
Проецирование сил на оси.
Решение систем уравнений.
Самые типовые задачи по динамике
Начнем с I и II законов Ньютона.
Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых… Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.
I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.
Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.
II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.
Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.
При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.
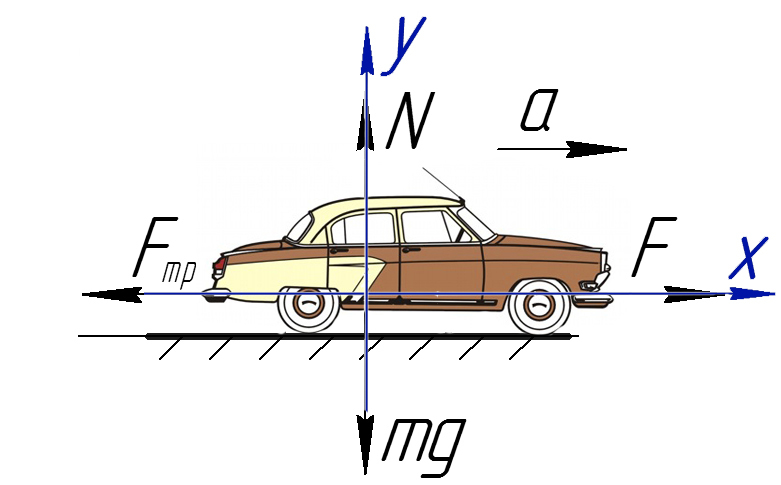
Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².
Обязательно в таких задачах делать рисунок, и показывать силы, которые дествуют на машину:
На Ось Х: движение с ускорением
На Ось Y: нет движения (здесь координата, как была ноль так и останется, машина не поднимает в горы или спускается вниз)
Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.
По оси X: сила тяги направлена вправо, так же как и ось X, ускорение так же направлено вправо.
Fтр = μN, где N — сила реакции опоры. На оси Y: N = mg, тогда в данной задаче Fтр = μmg.
Получаем, что:
Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.
Ответ: 0,25
Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.
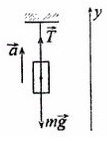
Сделаем рисунок, покажем силы, которые дествуют на груз
T — сила натяжения нити
На ось X: нет сил
Разберемся с направлением сил на ось Y:
Выразим T (силу натяжения) и подставим числительные значения:
Ответ: 65 Н
Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.
Далеко не всегда все силы, действующие на тело, направлены вдоль осей.
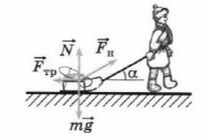
Простой пример: мальчик тянет санки
Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей.
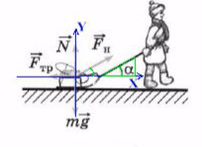
Отношение противолежащего катета к гипотенузе — это синус.
Отношение прилежащего катета к гипотенузе — это косинус.
Сила тяги на ось Y — отрезок (вектор) BC.
Сила тяги на ось X — отрезок (вектор) AC.
Если это непонятно, посмотрите задачу №4.
Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле, ведь сила, которая действуют на ось X— это Fнcosα. При каком угле косинус максимален? Чем больше будет этот катет, тем сильнее горизонтальная сила.
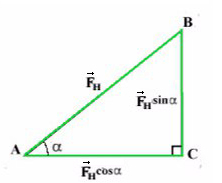
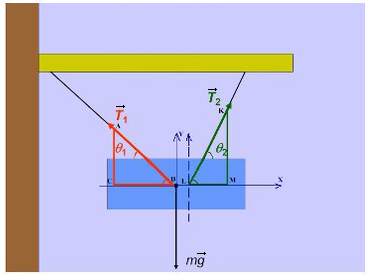
Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34 Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.
Введем оси и спроецируем силы:
Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — проекции на ось X, AC и KM — на ось Y.
Ответ: 4,22 кг
Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска?
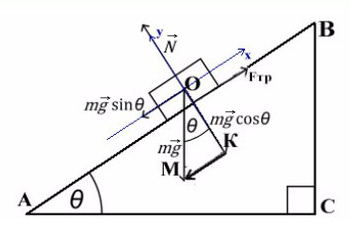
Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).
Рассмотрим поподробнее ΔKOM:
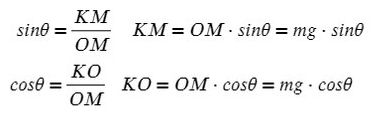
Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!
Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:
Ответ: 6,36 м/с²
Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время.
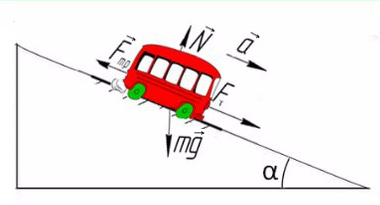
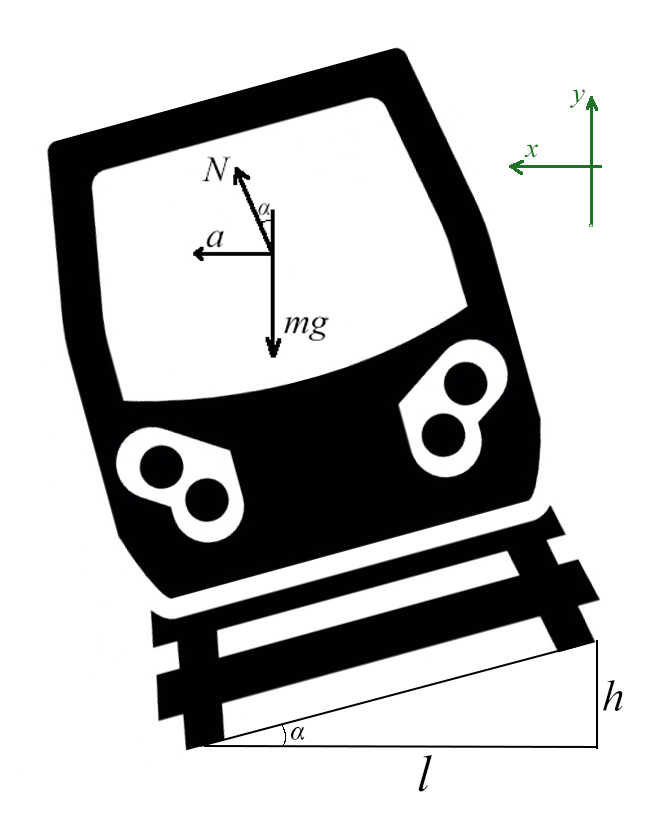
Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с² и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.
Сделаем рисунок с силами:
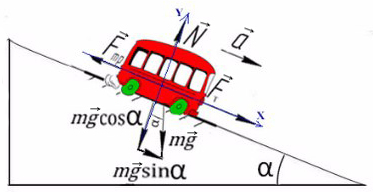
Введем оси X и Y. Спроецируем mg на оси:
Запишем второй закон Ньютона на X и Y:
Ответ: 6000 кг
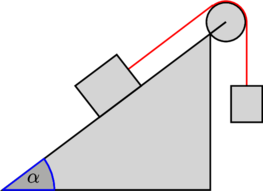
Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.
Самое сложное — понять, какие силы куда действуют, и как угол влияет на них.
Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!
Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)
Запишем какие силы действуют на оси:
Ускорение в данной задачи центростремительное!
Поделим одно уравнение на другое:
Тангенс — это отношение противолежащего катета к прилежащему:
Ответ: 7,5 см
Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.
В качестве закрепления материала решите несколько похожих задач с подсказками и ответами.
Будь в курсе новых статеек, видео и легкого технического юмора.
В данной статье рассказывается о том, как решать задачи про движение по наклонной плоскости. Рассмотрено подробное решение задачи о движении связанных тел по наклонной плоскости из ЕГЭ по физике.
Решение задачи о движении по наклонной плоскости
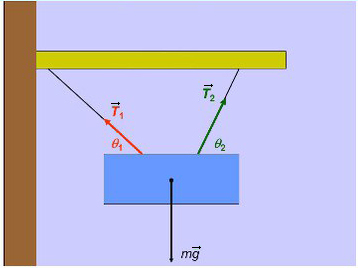
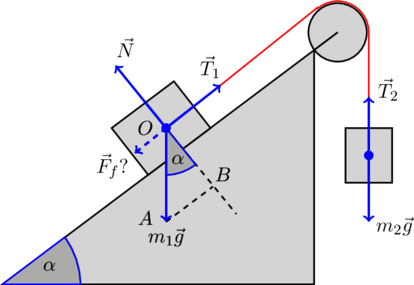
Прежде чем перейти непосредственно к решению задачи, как репетитор по математике и физике, рекомендую тщательно проанализировать ее условие. Начать нужно с изображения сил, которые действуют на связанные тела:
Здесь и
— силы натяжения нити, действующие на левое и правое тело, соответственно,
— сила реакции опоры, действующая на левое тело,
и
— силы тяжести, действующие на левое и правое тело, соответственно. С направлением этих сил все понятно. Сила натяжения направлена вдоль нити, сила тяжести вертикально вниз, а сила реакции опоры перпендикулярно наклонной плоскости.
А вот с направлением силы трения придется разбираться отдельно. Поэтому на рисунке она изображена пунктирной линией и подписана со знаком вопроса. Интуитивно понятно, что если правый груз будет «перевешивать» левый, то сила трения будет направлена противоположно вектору
. Наоборот, если левый груз будет «перевешивать» правый, то сила трения будет сонаправлена с вектором
.
Правый груз тянет вниз сила Н. Здесь мы взяли ускорение свободного падения
м/с2. Левый груз вниз тоже тянет сила тяжести, но не вся целиком, а только ее «часть», поскольку груз лежит на наклонной плоскости. Эта «часть» равна проекции силы тяжести на наклонную плоскости, то есть катету
в прямоугольном треугольнике
, изображенном на рисунке, то есть равна
Н.
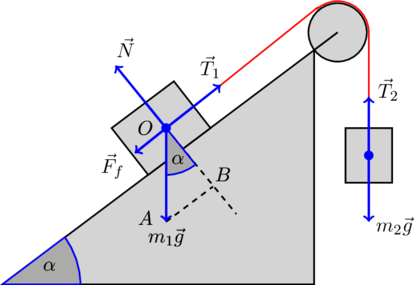
То есть «перевешивает» все-таки правый груз. Следовательно, сила трения направлена так, как показано на рисунке (мы ее нарисовали от центра масс тела, что возможно в случае, когда тело можно моделировать материальной точкой):
Второй важный вопрос, с которым нужно разобраться, будет ли вообще двигаться эта связанная система? Вдруг окажется так, что сила трения между левым грузом и наклонной плоскостью будет настолько велика, что не даст ему сдвинуться с места?
Такая ситуация будет возможна в том случае, когда максимальная сила трения, модуль которой определяется по формуле (здесь
— коэффициент трения между грузом и наклонной плоскостью,
— сила реакции опоры, действующая на груз со стороны наклонной плоскости), окажется больше той силы, которая старается привести систему с движение. То есть той самой «перевешивающей» силы, которая равна
Н.
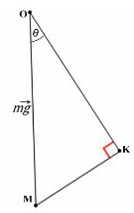
Модуль силы реакции опоры равен длине катета
в треугольнике
по 3-музакону Ньютона (с какой по величине силой груз давит на наклонную плоскость, с такой же по величине силой наклонная плоскость действует на груз). То есть сила реакции опоры равна
Н. Тогда максимальная величина силы трения составляет
Н, что меньше, чем величина «перевешивающей силы».
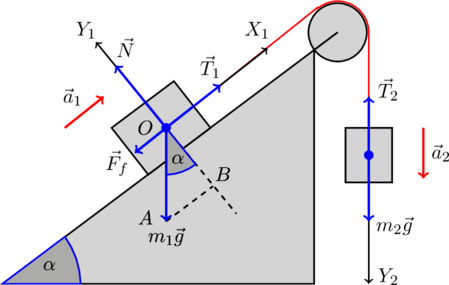
Следовательно, система будет двигаться, причем двигаться с ускорением. Изобразим на рисунке эти ускорения и оси координат, которые нам понадобятся далее при решении задачи:
Теперь, после тщательного анализа условия задачи, мы готовы приступить к ее решению.
Запишем 2-ой закон Ньютона для левого тела:
А в проекции на оси координатной системы получаем:
Здесь с минусом взяты проекции, векторы которых направлен против направления соответствующей оси координат. С плюсом взяты проекции, векторы которых сонаправлен с соответствующей осью координат.
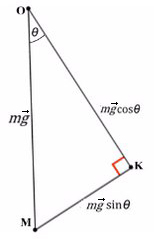
Еще раз подробно объясним, как находить проекции и
. Для этого рассмотрим прямоугольный треугольник
, изображенный на рисунке. В этом треугольнике
и
. Также известно, что в этом прямоугольном треугольнике
. Тогда
и
.
Вектор ускорения целиком лежит на оси
, поэтому
и
. Как мы уже вспоминали выше, по определению модуль силы трения равен произведению коэффициента трения на модуль силы реакции опоры. Следовательно,
. Тогда исходная система уравнений принимает вид:
Запишем теперь 2-ой закон Ньютона для правого тела:
В проекции на ось получаем:
Здесь, как и в предыдущем пункте, с минусом взяты проекции, векторы которых противоположно направлены оси , а с плюсом взяты проекции, векторы которых сонаправлены с осью
.
В условии сказано, что нить невесомая, то есть не требуется усилий, чтобы привести ее в движение. Следовательно, . Кроме того, по условию нить нерастяжимая, следовательно левый груз движется синхронно с правым, то есть
.
Тогда система уравнений окончательно принимает вид:
Из уравнения (2) выражаем , из уравнения (3) выражаем
:
Теперь все это подставляем в уравнение (1) и выражаем из него искомое ускорение :
После подстановки численных значений получаем м/с2.
Задачи на движением по наклонной плоскости встречаются в той или иной форме практически в каждом варианте ЕГЭ по физике. Научиться их решать должен каждый школьник. Они являются своеобразным индикатором умения ученика использовать законы Ньютона для решения задач по механике. Удачи вам в подготовке к ЕГЭ по физике!
Репетитор по физике на Юго-Западной
Сергей Валерьевич







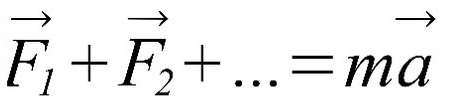
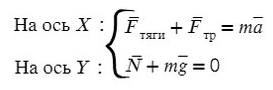
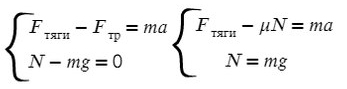
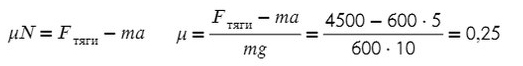
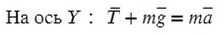
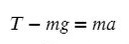
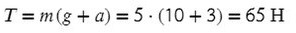
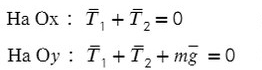
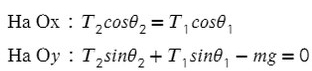
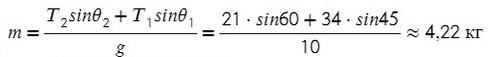
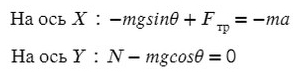
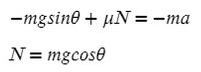
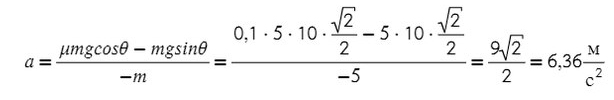
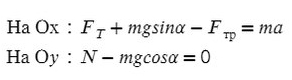
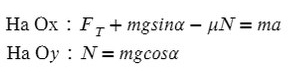

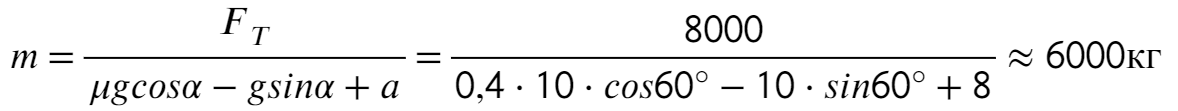
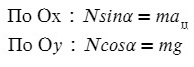
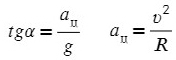
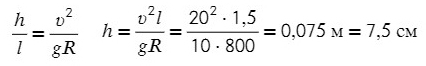
![Rendered by QuickLaTeX.com [ left{begin{array}{lc} T - mu N - m_1gsinalpha = m_1a, & (1)\ N - m_1gcosalpha = 0, & (2)\ m_2g - T = m_2a. & (3)\ end{array} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-1038d09dccecc453a537ee1b81812105_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} N = m_1gcosalpha, \ T = m_2g - m_2a. \ end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-7980b38eaeadb050deccf4e779f136c5_l3.png)