в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 129 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 57.
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 114.
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 138.
Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.
Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 2.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.
Цилиндр описан около шара. Объем шара равен 38. Найдите объем цилиндра.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 116. Найдите объем конуса.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Сибирь
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 42. Найдите объём цилиндра.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
Источник: ЕГЭ по математике. Основная волна 07.06.2021. Урал
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 156. Найдите объём конуса.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 112. Найдите объём конуса.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 36. Найдите объём цилиндра.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 63. Найдите объём цилиндра.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
Источник: Основная волна ЕГЭ по математике 29.05.2019. Центр
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Подмосковье
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 2. Найдите объем шара.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Санкт-Петербург
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём конуса равен 47. Найдите объём шара.
Источник: ЕГЭ по математике 28.03.2016. Досрочная волна, вариант 3
Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.
Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 1.
Всего: 129 1–20 | 21–40 | 41–60 | 61–80 …
1)Аквариум имеет форму прямоугольного параллелепипеда с размерами 80 см × 30 см × 40 см. Сколько литров составляет объём аквариума? В одном литре 1000 кубических сантиметров.
2)Через точку, делящую высоту конуса в отношении 1:3, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём этого конуса, если объём конуса, отсекаемого от данного конуса проведённой плоскостью, равен 5.
3)Два ребра прямоугольного параллелепипеда равны 8 и 5,
а объём параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.
4)Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка
в четыре раза ниже второй, а вторая
в полтора раза шире первой. Во сколько раз объём второй коробки больше объёма первой?
5)Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а высота этой призмы равна 4. Найдите объём призмы АВСА1В1С1
6)Объём конуса равен 24π, а его высота равна 8. Найдите радиус основания конуса.
7)Вода в сосуде цилиндрической формы находится на уровне h= 80 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте
в сантиметрах.
8)В бак, имеющий форму прямой призмы, налито 12 л воды. После полного погружения в воду детали уровень воды
в баке увеличился в 1,5 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
9)Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6,
а второго — 6 и 4. Во сколько раз объём второго цилиндра больше объёма первого?
10)Даны два конуса. Радиус основания и высота первого конуса равны соответственно 3 и 2, а второго — 2 и 3. Во сколько раз объём первого конуса больше объёма второго?
11)В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды
в баке поднялся в 1,4 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре
1000 кубических сантиметров.
12)Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 2 и 5,
а второго — 5 и 6. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого
13)Даны два шара с радиусами 5 и 1. Во сколько раз объём большего шара больше объёма меньшего?
14)В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём сосуда 120 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
15)
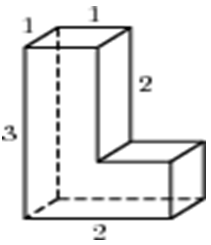
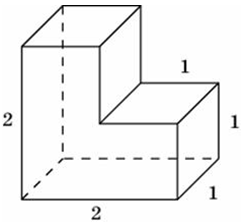
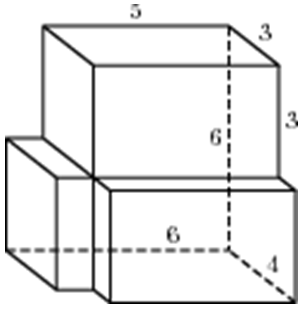
15)Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
16)Объём конуса равен 25π, а его высота равна 3. Найдите радиус основания конуса
10
Сен 2013
Категория: 02 Стереометрия
02. Цилиндр.
2013-09-10
2022-09-11
Задача 1. Радиус основания цилиндра равен высота равна
Найдите площадь боковой поверхности цилиндра, деленную на
.
Решение: + показать
Задача 2. Площадь боковой поверхности цилиндра равна а диаметр основания равен
Найдите высоту цилиндра.
Решение: + показать
Задача 3. Длина окружности основания цилиндра равна высота равна
Найдите площадь боковой поверхности цилиндра.
Решение: + показать
Задача 4. Площадь осевого сечения цилиндра равна Найдите площадь боковой поверхности цилиндра, деленную на
.
Решение: + показать
Задача 5. Объём первого цилиндра равен 48 м У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра (в м
).
Решение: + показать
Задача 6. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
Решение: + показать
Задача 7. В цилиндрический сосуд налили см
воды. Уровень воды при этом достигает высоты
см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на
см. Чему равен объем детали? Ответ выразите в см
Решение: + показать
Задача 8. В цилиндрический сосуд налили см
воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в
раза. Найдите объем детали.
Ответ выразите в см
Решение: + показать
Задача 9. В цилиндрическом сосуде уровень жидкости достигает см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в
раза больше первого? Ответ выразите в сантиметрах.
Решение: + показать
Задача 10. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Задача 11. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Задача 12. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Задача 13. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Вы можете пройти тест “Цилиндр”
Автор: egeMax |
комментария 3
Печать страницы
Тренажер задания 5 профильного ЕГЭ по математике-2022 (с ответами). Здесь приведены прототипы задания 5 — задачи на определение объемов. Это задание на стереометрию. Номер заданий соответствует номеру заданий в базе mathege.ru.
ОБЪЕМ
Параллелепипед
27041. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
27042. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
27079. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
27074. Объем параллелепипеда ABCDA1B1C1D1 равен 9. Найдите объем треугольной пирамиды ABDA1.
77154. Найдите объем параллелепипеда ABCDA1B1C1D1, если объем треугольной пирамиды ABDA1 равен 3.
Куб
27043. Куб описан около сферы радиуса 1. Найдите объём куба.
27105. Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.
324449. Шар, объём которого равен 6π, вписан в куб. Найдите объём куба.
27141. Площадь поверхности куба равна 24. Найдите его объем.
27099. Объем куба равен Найдите его диагональ.
27081. Во сколько раз увеличится объем куба, если все его ребра увеличить в три раза?
27102. Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.
27075. Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.
324459. Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 2. Найдите объём куба.
Многогранник
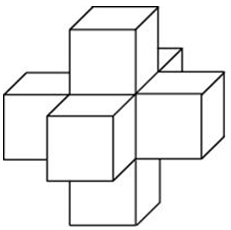
27117. Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
27214. Объём тетраэдра равен 19. Найдите объём многогранника, вершинами которого являются середины рёбер данного тетраэдра.
Цилиндр
27045. В цилиндрический сосуд налили 2000см3 воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в cм3.
27118. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
27053. Дано два цилиндра. Объём первого цилиндра равен 12. У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра.
27050. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра призмы равны 2/π. Найдите объём цилиндра, описанного около этой призмы.
Призма
27047. В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в см3.
27106. Через среднюю линию основания треугольной призмы, объём которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объём отсеченной треугольной призмы.
27107. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если объём отсеченной треугольной призмы равен 5.
27082. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 6 и 8, боковое ребро призмы равно 5. Найдите объём призмы.
27083. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5, объём призмы равен 30. Найдите боковое ребро призмы.
27112. От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.
Пирамида
27086. Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.
27087. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна
27088. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен
27085. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?
27089. Во сколько раз увеличится объем шестиугольной пирамиды, если ее высоту увеличить в четыре раза?
27113. Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 1. Найдите объем шестиугольной пирамиды.
27114. Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.
27115. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
27182. Объем параллелепипеда ABCDA1B1C1D1 равен 12. Найдите объем треугольной пирамиды B1ABC.
27209. Объем параллелепипеда ABCDA1B1C1D1 равен 4.5. Найдите объем треугольной пирамиды AD1CB1.
27184. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
27109. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
27181. Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45º. Найдите объем пирамиды.
Конус
27052. Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Шар
27097. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
27162. Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
1)Аквариум имеет форму прямоугольного
параллелепипеда с размерами 80 см × 30 см ×
40 см. Сколько литров составляет объём
аквариума? В одном литре 1000 кубических
сантиметров.
2)Через точку, делящую высоту конуса в
отношении 1:3, считая от вершины, проведена
плоскость, параллельная основанию. Найдите
объём этого конуса, если объём конуса,
отсекаемого от данного конуса проведённой
плоскостью, равен 5.
3)Два ребра прямоугольного
параллелепипеда равны 8 и 5,
а объём параллелепипеда равен 280.
Найдите площадь поверхности этого
параллелепипеда.
4)Даны две коробки, имеющие форму
правильной четырёхугольной призмы,
стоящей на основании. Первая коробка
в четыре раза ниже второй, а вторая
в полтора раза шире первой. Во сколько раз
объём второй коробки больше объёма
первой?
5)Сторона основания правильной треугольной
призмы ABCA1B1C1 равна 2, а высота этой
призмы равна 4
√
3. Найдите объём призмы
АВСА
1
В
1
С
1
6)Объём конуса равен 24π, а его высота
равна 8. Найдите радиус основания конуса.
7)Вода в сосуде цилиндрической формы
находится на уровне h= 80 см. На каком
уровне окажется вода, если её перелить в
другой цилиндрический сосуд, у которого
радиус основания вдвое больше, чем у
первого? Ответ дайте
в сантиметрах.

налито 12 л воды. После полного погружения в
воду детали уровень воды
в баке увеличился в 1,5 раза. Найдите объём
детали. Ответ дайте в кубических сантиметрах,
зная, что в одном литре 1000 кубических
сантиметров.
9)Даны два цилиндра. Радиус основания и
высота первого цилиндра равны
соответственно 2 и 6,
а второго — 6 и 4. Во сколько раз объём
второго цилиндра больше объёма первого?
10)Даны два конуса. Радиус основания и
высота первого конуса равны соответственно 3
и 2, а второго — 2 и 3. Во сколько раз объём
первого конуса больше объёма второго?
11)В бак, имеющий форму прямой призмы,
налито 5 л воды. После полного погружения в
воду детали уровень воды
в баке поднялся в 1,4 раза. Найдите объём
детали. Ответ дайте в кубических сантиметрах,
зная, что в одном литре
1000 кубических сантиметров.
12)Даны два конуса. Радиус основания и
образующая первого конуса равны
соответственно 2 и 5,
а второго — 5 и 6. Во сколько раз площадь
боковой поверхности второго конуса больше
площади боковой поверхности первого
13)Даны два шара с радиусами 5 и 1. Во
сколько раз объём большего шара больше
объёма меньшего?
14)В сосуде, имеющем форму конуса, уровень
жидкости достигает 1/2 высоты. Объём сосуда
120 мл. Чему равен объём налитой жидкости?
Ответ дайте в миллилитрах.
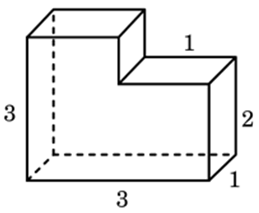
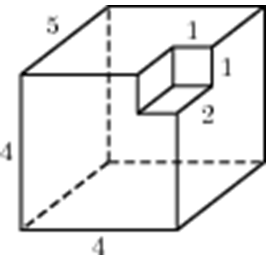
15)Деталь имеет форму изображённого на
рисунке многогранника (все двугранные углы
прямые). Числа на рисунке обозначают длины
рёбер в сантиметрах. Найдите объём этой
детали. Ответ дайте в кубических сантиметрах.
16)Объём конуса равен 25π, а его высота
равна 3. Найдите радиус основания конуса
ЕГЭ Профиль №5. Площадь поверхности и объем составного многогранника
Скачать файл в формате pdf.
ЕГЭ Профиль №5. Площадь поверхности и объем составного многогранника
| Задача 1. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 18. |
 |
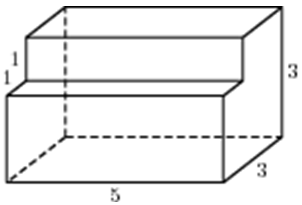
| Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 76. |
 |
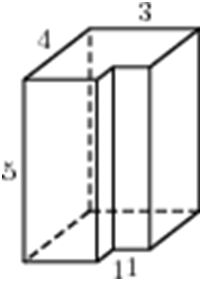
| Задача 3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 92. |
 |
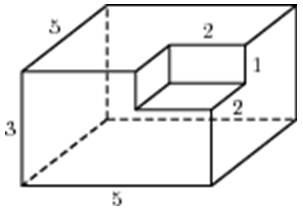
| Задача 4. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 110. |
 |
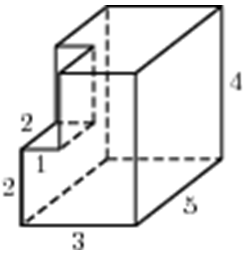
| Задача 5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 94. |
 |
| Задача 6. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 132. |
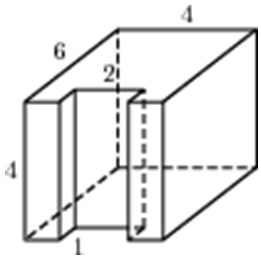 |
| Задача 7. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 114. |
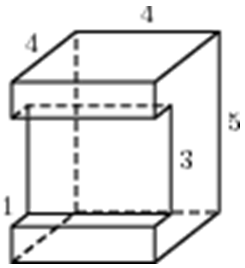 |
| Задача 8. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 48. |
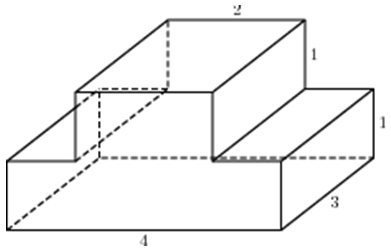 |
| Задача 9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 84. |
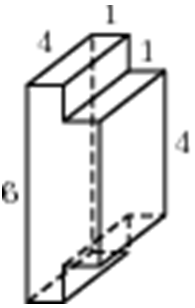 |
| Задача 10. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 96. |
 |
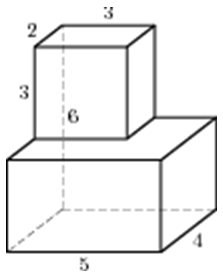
| Задача 11. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 124. |
 |
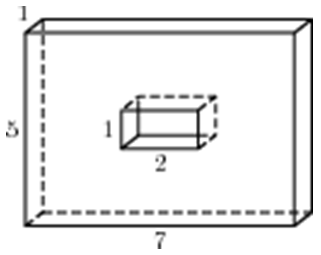
| Задача 12. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Ответ
ОТВЕТ: 14. |
 |
| Задача 13. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
Ответ
ОТВЕТ: 30. |
 |
| Задача 14. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 162. |
 |
| Задача 15. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
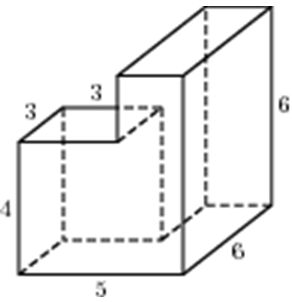
ОТВЕТ: 156. |
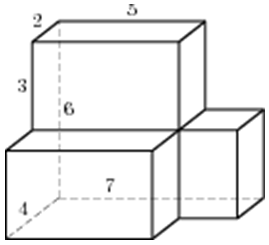 |
| Задача 16. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 152. |
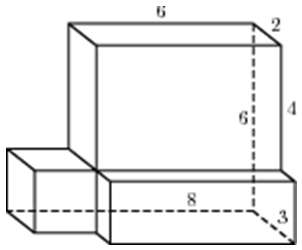 |
| Задача 17. Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Ответ
ОТВЕТ: 8. |
 |
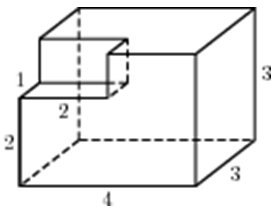
| Задача 18. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 56. |
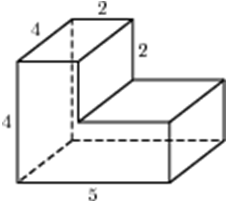 |
| Задача 19. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 7. |
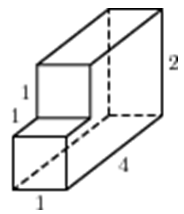 |
| Задача 20. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 40. |
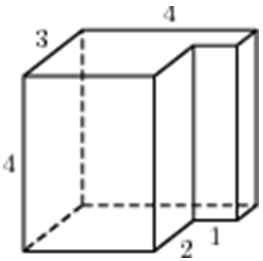 |
| Задача 21. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 34. |
 |
| Задача 22. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 36. |
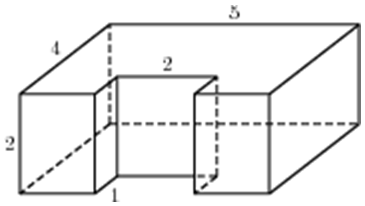 |
| Задача 23. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 90. |
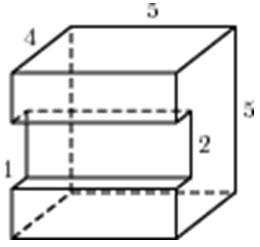 |
| Задача 24. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 18. |
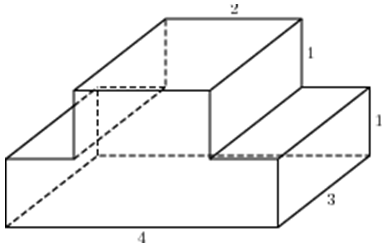 |
| Задача 25. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 24. |
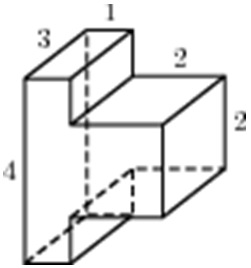 |
| Задача 26. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 45. |
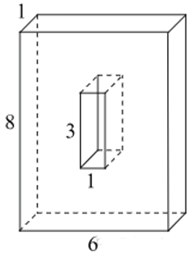 |
| Задача 27. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 78. |
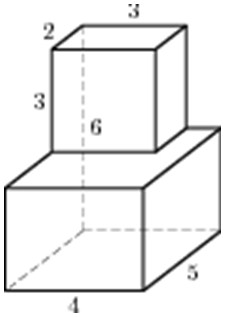 |
| Задача 28. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 104. |
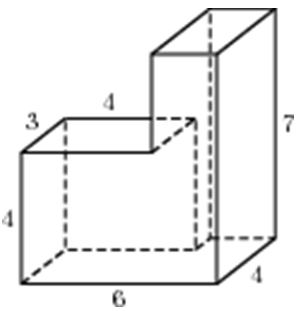 |
| Задача 29. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 87. |
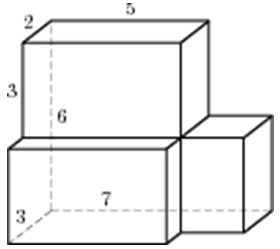 |
| Задача 30. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 114. |
 |
| Задача 31. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 78. |
 |
14. Задачи по стереометрии
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение объемов и площадей
Напомним объемы некоторых пространственных фигур:
(blacktriangleright) Объем пирамиды ({large{V=dfrac{1}{3}S_{text{осн}}h}}) , где (S_{text{осн}}) – площадь основания, (h) – высота.
(blacktriangleright) Объем призмы ({large{V=S_{text{осн}}cdot
h}}), где (S_{text{осн}}) – площадь основания, (h) – высота.
Т.к. параллелепипед — частный случай призмы, то его объем ищется по той же формуле.
(blacktriangleright) Объем прямоугольного параллелепипеда ({large{V=abc}}), где (a, b, c) – три различных боковых ребра.
(blacktriangleright) Объем куба ({large{V=a^3}}), где (a) – ребро куба.
(blacktriangleright) Объем конуса ({large{V=dfrac{1}{3}pi
r^2h}}), где (r) – радиус основания, (h) – высота конуса.
(blacktriangleright) Объем цилиндра ({large{V=pi r^2h}}), где (r) – радиус основания, (h) – высота цилиндра.
(blacktriangleright) Объем шара ({large{V=dfrac{4}{3}pi R^3}}), где (R) — радиус шара.
Задание
1
#2885
Уровень задания: Легче ЕГЭ
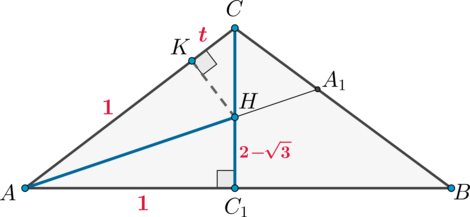
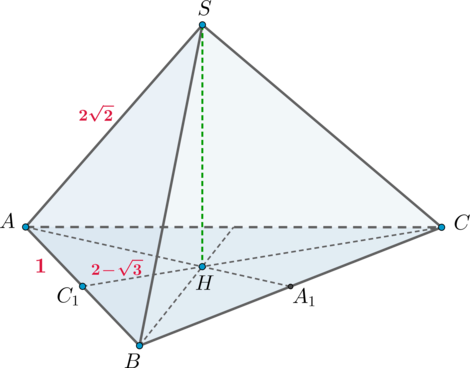
Дана пирамида (SABC) с вершиной (S), высота которой падает в точку пересечения биссектрис основания, являющегося равнобедренным треугольником с (AC=CB). Известно, что радиус вписанной в треугольник (ABC) окружности равен (2-sqrt3), (AB=2), (AS=2sqrt2). Найдите объем пирамиды.
1)
Пусть (SH) – высота пирамиды, то есть (H) – точка пересечения биссектрис основания. Рассмотрим основание (ABC). Так как центр вписанной в треугольник окружности лежит на пересечении биссектрис, то (H) – центр вписанной окружности. Пусть (AA_1, CC_1) – биссектрисы, тогда (CC_1) также медиана и высота, так как (AC=CB). Следовательно, (HC_1perp AB), следовательно, (HC_1=r) и есть радиус вписанной окружности.
Проведем (HK=rperp AC). Тогда (AK=AC_1=1). Пусть (CK=t). Тогда (CC_1=sqrt{AC^2-AC_1^2}=sqrt{t(t+2)}). Тогда из подобия (triangle
KCHsim triangle ACC_1): [dfrac{HK}{AC_1}=dfrac{CK}{CC_1} quadRightarrowquad
dfrac{2-sqrt3}1=dfrac t{sqrt{t(t+2)}} quadRightarrowquad
t=dfrac2{sqrt3}-1] Следовательно, (AC=t+1=dfrac2{sqrt3}). Тогда (CC_1=dfrac1{sqrt3}).
Значит, площадь основания [S_{ABC}=dfrac12cdot ABcdot CC_1=dfrac1{sqrt3}.]
2)
Заметим, что (triangle ASH) прямоугольный, следовательно, для того, чтобы найти высоту пирамиды, нужно найти (AH). Из прямоугольного (AC_1H): [AH^2=AC_1^2+C_1H^2=1+(2-sqrt3)^2=4(2-sqrt3).] Следовательно, [SH=sqrt{AS^2-AH^2}=sqrt{8-4(2-sqrt3)}=sqrt{4sqrt3}=2sqrt[4]3.]
Следовательно, объем пирамиды равен [V=dfrac13cdot SHcdot
S_{ABC}=dfrac2{3sqrt[4]3}.]
Ответ:
(dfrac2{3sqrt[4]3})
Задание
2
#2291
Уровень задания: Равен ЕГЭ
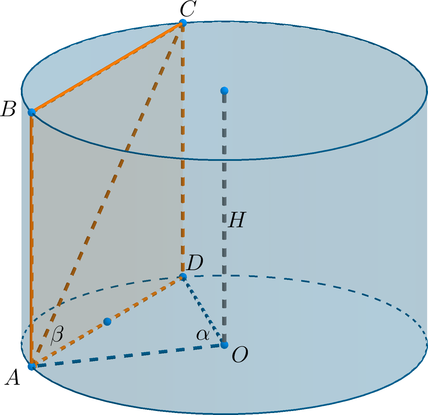
Параллельно оси цилиндра проведена плоскость, отсекающая от окружности основания дугу, градусная мера которой равна (alpha). Диагональ сечения наклонена под углом (beta) к основанию цилиндра.
а) Найдите объем цилиндра, если высота цилиндра равна (H).
б) Вычислите объем цилиндра, если (H=dfrac2{sqrt[3]{pi}}), (alpha=60^circ), (beta=30^circ).
а) Сечение цилиндра данной плоскостью – это прямоугольник (ABCD), где (AB=CD=H).
Дуга (buildrelsmileover{AD}=alpha), следовательно, центральный угол (angle AOD=alpha).
Объем цилиндра равен [V=pi R^2cdot H]
где (R=AO); следовательно, необходимо найти (R^2).
Рассмотрим прямоугольный треугольник (ACD). Из него [mathrm{ctg},beta=dfrac{AD}{CD} quad Rightarrow quad
AD=CDcdot mathrm{ctg},beta=Hcdot mathrm{ctg},beta]
Заметим, что (triangle AOD) – равнобедренный. Тогда по теореме косинусов [AD^2=AO^2+DO^2-2cdot AOcdot DOcdot cosalpha quad
Rightarrow quad (Hmathrm{ctg},beta)^2=2R^2(1-cosalpha)]
Отсюда [R^2=dfrac{H^2mathrm{ctg}^2,beta}{2(1-cosalpha)}]
Следовательно, [V=dfrac{pi
H^3mathrm{ctg}^2,beta}{2(1-cosalpha)}]
б) Подставляя значения из условия, получаем:
[V=dfrac{picdot frac8{pi}cdot (sqrt3)^2}{2left(1-frac12right)}=24.]
Ответ:
б) (24)
Задание
3
#3142
Уровень задания: Сложнее ЕГЭ
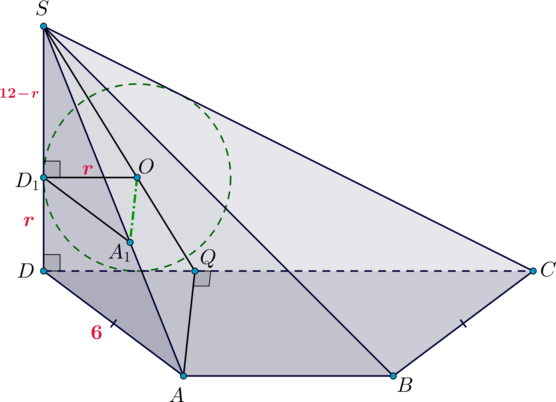
В основании четырехугольной пирамиды (SABCD) лежит равнобедренная трапеция (ABCD), причем (AD=BC=6), (CD>AB). Угол между прямыми (AD) и (BC) равен (60^circ). Известно, что (SD=12) – высота пирамиды.
Внутри пирамиды расположен конус так, что основание конуса – вписанная в треугольник (SCD) окружность, а вершина конуса принадлежит ребру (AS). Найдите объем конуса.
Если (E) – точка пересечения прямых (AD) и (BC), то (angle
AEB=60^circ). Так как также (angle BAE=angle ABE) (так как трапеция равнобедренная), то (triangle AEB) равносторонний и (angle BAE=60^circ). Следовательно, и (angle ADC=angle
BCD=60^circ).
Пусть (O) – центр основания конуса, (A_1) – вершина. Тогда (A_1Operp (SCD)).
Заметим, что если в плоскости (ABC) провести (AQperp CD), то (AQperp (SCD)) (так как (AQperp CD) и (AQperp SD)). Следовательно, прямые (A_1O) и (AQ) параллельны, следовательно, лежат в одной плоскости, причем это плоскость (SAQ) (так как (A_1in SA)).
Рассмотрим грань (SCD). Пусть (OD_1perp SD) – радиус вписанной окружности. Тогда (DD_1=r) по свойству прямоугольного треугольника.
(triangle SD_1Osim triangle SDQ), следовательно, [dfrac{SD_1}{SD}=dfrac{D_1O}{DQ} quadRightarrowquad
dfrac{12-r}{12}=dfrac r{DQ}] (DQ) можно найти из прямоугольного (triangle DQA): (DQ) лежит против угла (angle DAQ=30^circ), значит, (DQ=frac12DA=3). Также по теореме Пифагора можно найти (AQ=3sqrt3).
Следовательно, [dfrac{12-r}{12}=dfrac r3 quadRightarrowquad r=dfrac{12}5] Рассмотрим (triangle ASQ): он подобен (triangle A_1SO), значит, [dfrac{A_1O}{AQ}=dfrac{SO}{SQ}=dfrac{SD_1}{SD}=dfrac{frac{48}5}{12}=
dfrac45] Следовательно, (A_1O=frac45AQ=frac{12sqrt3}5).
Тогда объем конуса равен: [V=dfrac13cdot picdot r^2cdot A_1O=dfrac13cdot picdot
left(dfrac{12}5right)^2cdot
dfrac{12sqrt3}5=dfrac{576}{125}sqrt3pi]
Ответ:
(dfrac{576}{125}sqrt3pi)
Задание
4
#2455
Уровень задания: Сложнее ЕГЭ
Найдите площадь боковой поверхности правильной четырехугольной пирамиды, высота которой равна (H), а величина плоского угла при вершине равна (alpha). Вычислите эту площадь, если (H=3), (alpha=30^circ).
1) Рассмотрим правильную пирамиду (SABCD), (SO=H) – высота (которая падает в точку пересечения диагоналей основания), (angle
CSD=alpha).
Напомним, что у правильной пирамиды все боковые грани представляют собой равные равнобедренные треугольники.
Введем вспомогательный угол между боковым ребром и основанием: (angle SOD=phi).
Тогда (sinphi=dfrac{SO}{SD}), следовательно, (SD=dfrac{H}{sinphi}=SC).
Тогда, т.к. площадь треугольника равна полупроизведению сторон на синус угла между ними,
[S_{text{бок.пов.}}=4cdot dfrac12SDcdot SCcdot sinalpha=
dfrac{2H^2cdot sinalpha}{sin^2phi}]
2) Теперь необходимо выразить (sinphi) через данные в условии величины.
Проведем (SK) – медиану и высоту в равнобедренном (triangle SCD). Тогда [sinangle
DSK=sindfrac{alpha}2=dfrac{DK}{SD}=dfrac{CD}{2SD} qquad (1)]
(BD=sqrt2cdot CD) как диагональ квадрата, следовательно, (OD=frac{sqrt2}2CD). В (triangle SOD):
[cosphi=dfrac{OD}{SD}=dfrac{CD}{sqrt2SD} qquad (2)]
Разделим равенство ((1)) на равенство ((2)) и получим:
[dfrac{sindfrac{alpha}2}{cosphi}=dfrac1{sqrt2} quad Rightarrow
quad cosphi=sqrt2sindfrac{alpha}2]
Тогда (sin^2phi=1-cos^2phi=1-2sin^2dfrac{alpha}2=cosalpha).
3) Таким образом, [S_{text{бок.пов.}}=dfrac{2H^2sinalpha}{cosalpha}=
2H^2cdot mathrm{tg},alpha.]
4) Подставляя значения из условия, находим, что
[S_{text{бок.пов.}}=6sqrt3.]
Ответ:
(2H^2cdot mathrm{tg},alpha;quad 6sqrt3)
Задание
5
#2454
Уровень задания: Сложнее ЕГЭ
Площадь полной поверхности тетраэдра равна (9). Найдите площадь полной поверхности пирамиды, вершинами которой являются точки пересечения медиан граней данного тетраэдра.
Пусть (DABC) – тетраэдр, точки (A_1, B_1, C_1, D_1) — точки пересечения медиан в гранях (DBC, DAC, DAB, ABC) соответственно.
1) Т.к. медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то (DA_1:A_1M=AD_1:D_1M=2:1). Следовательно, (triangle
MADsim triangle MA_1D_1) по углу и двум прилежащим пропорциональным сторонам. Таким образом, (D_1A_1parallel DA) ((angle MA_1D_1=angle MDA) как соответственные) и (D_1A_1=frac13DA).
Аналогичным образом можно доказать, что (D_1B_1=frac13DB), (D_1C_1=frac13DC).
2) (triangle DC_1A_1sim triangle DKM) с коэффициентом (frac23), то есть (C_1A_1=frac23KM). А вот (triangle BKMsim triangle BAC) с коэффициентом (frac12) (т.к. (KM) – средняя линия), то есть (KM=frac12AC).
Следовательно, (C_1A_1=frac23KM=frac23cdot
frac12AC=frac13AC).
Аналогично доказывается, что (A_1B_1=frac13AB), (B_1C_1=frac13BC).
3) Таким образом, все ребра тетраэдра (A_1B_1C_1D_1) в три раза меньше соответствующих ребер тетраэдра (ABCD), а это значит, что каждая грань тетраэдра (A_1B_1C_1D_1) подобна с коэффициентом (frac13) соответствующей грани тетраэдра (ABCD).
4) Т.к. площади подобных треугольников относятся как квадрат коэффициента подобия, то площадь каждой грани тетраэдра (A_1B_1C_1D_1) равна (frac19) от площади соответствующей грани тетраэдра (ABCD). Следовательно,
[S_{A_1B_1C_1D_1}=dfrac19S_{ABCD}=frac19cdot 9=1.]
Ответ: 1
Задание
6
#2292
Уровень задания: Сложнее ЕГЭ
Образующая усеченного конуса составляет с плоскостью нижнего основания угол (phi). Диагональ его осевого сечения перпендикулярна образующей конуса. Сумма длин окружностей оснований равна (2pi
m).
а) Найдите площадь боковой поверхности усеченного конуса.
б) Вычислите эту площадь, если (m=3sqrt2), (phi=arccosfrac15).
а)
1) Достроим усеченный конус до целого конуса. Тогда (EH) – высота, (ED) – образующая всего конуса; (CD) – образующая усеченного конуса, (ABCD) – осевое сечение усеченного конуса, (AC) – диагональ этого сечения, которая перпендикулярна (CD).
(angle EDH=phi) – угол между образующей и плоскостью нижнего основания.
Обозначим за (R) и (r) – радиусы нижнего и верхнего оснований усеченного конуса соответственно. Тогда из условия сумма длин окружностей оснований равна
[2pi m=2pi r+2pi R quad Rightarrow quad R+r=m]
2) Для того, чтобы найти площадь боковой поверхности усеченного конуса, нужно из площади боковой поверхности всего конуса вычесть площадь боковой поверхности маленького конуса:
[S=pi Rcdot ED-pi rcdot EC=pi (Rcdot ED-rcdot EC)]
Заметим, что (triangle EKC) и (triangle EHD) – прямоугольные, следовательно, [cos phi=dfrac{KC}{EC}=dfrac{HD}{ED} quad
Rightarrow quad EC=dfrac{KC}{cos phi}=dfrac{r}{cos phi}
quadtext{ и }quad ED=dfrac{HD}{cos phi}=dfrac{R}{cos phi}]
Значит, площадь боковой поверхности уже приобретает вид:
[S=pileft(dfrac{R^2}{cosphi}-dfrac{r^2}{cosphi}right)=
dfrac{pi}{cosphi}cdot (R-r)(R+r)= dfrac{pi}{cosphi}cdot
mcdot (R-r)]
Необходимо найти (R-r).
3) Т.к. (ACperp CD), то (triangle ACD) – прямоугольный, следовательно, [cos phi=dfrac{CD}{AD} quad Rightarrow quad
CD=ADcdot cos phi=2Rcdot cos phi]
Из данных второго пункта мы можем сказать, что [CD=ED-EC=dfrac{R}{cos phi}-dfrac{r}{cos phi}=dfrac{R-r}{cos phi}]
Таким образом, имеем: [2Rcdot cos phi=dfrac{R-r}{cos phi}
quad Rightarrow quad R(1-2cos^2phi)=r quad Leftrightarrow
quad r=-Rcdot cos2phi]
Но (R+r=m), следовательно, (R-Rcdot cos2phi=m), следовательно, [R=dfrac{m}{1-cos 2phi}]
Подставляя это значение для (R) в (r=-Rcdot cos2phi), находим, что [r=dfrac{mcdot cos 2phi}{cos2phi-1}]
Таким образом, [R-r=dfrac{m(1+cos2phi)}{1-cos2phi}]
4) Значит, площадь боковой поверхности равна
[S=dfrac{pi}{cosphi}cdot
mcdotdfrac{m(1+cos2phi)}{1-cos2phi}=pi m^2cdot
dfrac{1+2cos^2phi-1}{cosphi(1-1+2sin^2phi)}=pi m^2cdot
dfrac{cosphi}{sin^2phi}]
б) Подставляя значения из условия и помня, что (sin^2phi=1-cos^2phi), найдем площадь боковой поверхности:
[S=picdot (3sqrt2)^2cdot
dfrac{cosleft(arccosfrac15right)}{1-cos^2left(arccosfrac15right)}=
dfrac{15}4pi=3,75pi]
Ответ:
а) (pi m^2cdot
dfrac{cosphi}{sin^2phi})
б) (3,75pi)

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ