Каталог заданий.
Шар
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 2 № 27059
Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
Аналоги к заданию № 27059: 5049 27185 72765 72719 72721 72723 72725 72727 72729 72731 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
2
Тип 2 № 27072
Даны два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Аналоги к заданию № 27072: 5075 73287 520653 520694 26551 73243 73245 73247 73249 73251 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор планиметрии: Отношение длин, площадей, объемов подобных фигур
Классификатор стереометрии: Площадь сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
3
Тип 2 № 27097
Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
Аналоги к заданию № 27097: 74403 74405 74407 74409 74411 74413 74415 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор планиметрии: Отношение длин, площадей, объемов подобных фигур, Подобие
Классификатор стереометрии: Площадь сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
4
Тип 2 № 27125
Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Аналоги к заданию № 27125: 75307 75309 75311 75313 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор стереометрии: Объём цилиндра, конуса, шара
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
5
Тип 2 № 27162
Объем первого шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Аналоги к заданию № 27162: 76349 76355 505443 76351 76353 76357 76359 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор планиметрии: Отношение длин, площадей, объемов подобных фигур, Подобие
Классификатор стереометрии: Объём цилиндра, конуса, шара, Площадь сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
08
Сен 2013
Категория: 02 Стереометрия
02. Шар
2013-09-08
2022-09-11
Задача 1. Объем шара равен 12348. Найдите площадь его поверхности, деленную на
Решение: + показать
Задача 2. Площадь большого круга шара равна Найдите площадь поверхности шара.
Решение: + показать
Задача 3. Площадь поверхности шара равна Найдите площадь большого круга шара.
Решение: + показать
Задача 4. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в раз?
Решение: + показать
Задача 5. Во сколько раз увеличится объем шара, если его радиус увеличить в пять раз?
Решение: + показать
Задача 6. Объем первого шара в раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Решение: + показать
Задача 7. Радиусы двух шаров равны и
Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Решение: + показать
Задача 8. Радиусы трех шаров равны ,
и
Найдите радиус шара, объем которого равен сумме их объемов.
Решение: + показать
Вы можете пройти тест
Автор: egeMax |
комментариев 7
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи по теме «Сфера и шар»
(blacktriangleright) Сфера – это множество точек пространства, находящихся на одинаковом расстоянии от заданной точки (O) (называемой центром сферы).
(blacktriangleright) Шар – это сфера вместе со своей внутренностью.
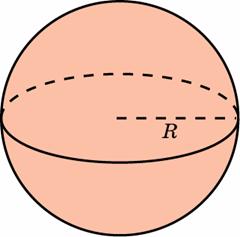
Основные формулы (где (R) – радиус сферы или шара):
(blacktriangleright) площадь сферы ({large{S=4pi R^2}})
(blacktriangleright) объем шара ({large{V=dfrac{4}{3}pi R^3}})
Задание
1
#1878
Уровень задания: Равен ЕГЭ
Объем шара равен (displaystyle frac{36}{sqrtpi}). Чему будет равна площадь поверхности шара, если его радиус увеличить на (displaystyle frac{6}{sqrtpi})?
(displaystyle V_{text{шара}} = frac{4}{3}pi R^3 = frac{36}{sqrtpi}) (Rightarrow) (displaystyle R = frac{3}{sqrtpi}). Радиус нового шара равен: (displaystyle R_{text{нов.}} = R + frac{6}{sqrtpi} = frac{9}{sqrtpi}). Тогда найдем площадь поверхности: (displaystyle {S_{text{пов.}} = 4pi R_{text{нов.}}^2 = 4pi left(frac{9}{sqrtpi}right)^2 = 4pifrac{81}{pi} = 324}.)
Ответ: 324
Задание
2
#1877
Уровень задания: Равен ЕГЭ
Во сколько раз объем шара больше объема сегмента, высота которого равна половине радиуса?
Необходимо объем шара разделить на объем соответствующего сегмента, высота которого равна (H = frac{1}{2}R)
[frac{V_{text{шара}}}{V_{text{сегм.}}} = frac{frac{4}{3}pi R^3}{pi left(frac{1}{2}Rright)^2left(R — frac{1}{3}left(frac{1}{2}Rright)right)} = frac{frac{4}{3}pi R^3}{frac{5}{24}pi R^3} = frac{4}{3} cdot frac{24}{5} = frac{32}{5} = 6,4.]
Ответ: 6,4
Задание
3
#2674
Уровень задания: Сложнее ЕГЭ
Имеются две сферы (S_1) и (S_2), про которые известно, что радиус первой сферы в (2) раза больше, чем радиус второй сферы. Кроме того, сфера (S_2) целиком находится внутри сферы (S_1). Пусть объём шара, ограниченного второй сферой, равен (V_2), а объём тела, заключённого между сферами, равен (V). Найдите (V : V_2).
Пусть (V_1) – объём шара, ограниченного первой сферой. Так как радиус (S_1) в два раза больше, чем радиус (S_2), то (V_1 : V_2 = 
[V = V_1 — V_2 = 8V_2 — V_2 = 7V_2,,] следовательно, (V : V_2 = 7).
Ответ: 7
Задание
4
#2306
Уровень задания: Сложнее ЕГЭ
Площадь поверхности шара равна (frac{37}{pi}). На расстоянии (frac1{2pi}) от центра шара проведена плоскость. Найдите длину полученной в сечении окружности.
Т.к. площадь поверхности сферы ищется по формуле (S=4pi R^2), то
[4pi R^2=dfrac{37}{pi} quad Rightarrow quad R^2=dfrac{37}{4pi^2}]
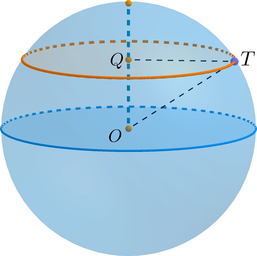
По условию задачи (OQ=frac1{2pi}). Рассмотрим (triangle OQT): он прямоугольный ((angle OQT=90^circ)), гипотенуза (OT=R), катет (QT) равен радиусу (r) окружности сечения.
Таким образом, по теореме Пифагора [QT^2=r^2=OT^2-OQ^2=dfrac{37}{4pi^2}-dfrac1{4pi^2}=dfrac{9}{pi^2}
quad Rightarrow quad r=dfrac3{pi}]
Таким образом, длина окружности сечения равна [C=2pi
r=2picdotfrac3{pi}=6.]
Ответ: 6
Задание
5
#2307
Уровень задания: Сложнее ЕГЭ
Площадь поверхности шара равна (64). На расстоянии (frac3{2sqrt{pi}}) от центра шара проведена плоскость. Найдите площадь полученного сечения.
Т.к. площадь поверхности сферы ищется по формуле (S=4pi R^2), то
[4pi R^2=64 quad Rightarrow quad R^2=dfrac{64}{4pi}]
По условию задачи (OQ=frac3{2sqrt{pi}}). Рассмотрим (triangle
OQT): он прямоугольный ((angle OQT=90^circ)), гипотенуза (OT=R), катет (QT) равен радиусу (r) окружности сечения.
Таким образом, по теореме Пифагора [QT^2=r^2=OT^2-OQ^2=dfrac{64}{4pi}-dfrac9{4pi}=dfrac{55}{4pi}]
Таким образом, площадь сечения равна
[S=picdot r^2=picdot dfrac{55}{4pi}=dfrac{55}4=13,75.]
Ответ: 13,75
Задание
6
#951
Уровень задания: Сложнее ЕГЭ
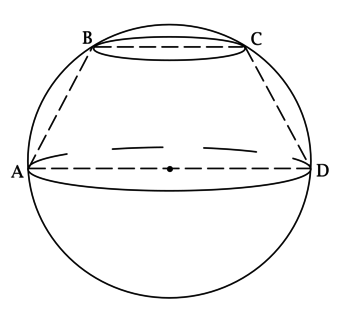
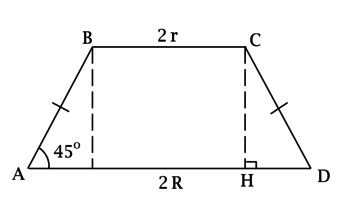
Центр большего основания усечённого конуса совпадает с центром сферы, а окружность его меньшего основания лежит на сфере. Отрезки (BC) и (AD) – диаметры меньшего и большего оснований этого усечённого конуса соответственно, (BCparallel AD), [S_{ABCD} = dfrac{210}{sqrt[3]{pi^2}},qquadqquad dfrac{r}{R} = dfrac{1}{sqrt{15}},] где (R) и (r) – радиусы большего и меньшего оснований усечённого конуса соответственно, (angle ADC = 45^circ). Найдите объём шара, ограниченного данной сферой.
Рассмотрим (ABCD): т.к. (BCparallel AD), то (ABCD) – трапеция. Так как (AB) и (CD) – образующие усечённого конуса, то (AB = CD) и трапеция (ABCD) – равнобедренная.
Построим (CHperp AD). Так как (angle ADC = 45^circ), то (triangle CHD) – равнобедренный и (CH = HD).
[HD = dfrac{AD — BC}{2} = R — r,qquadqquad S_{ABCD} = dfrac{BC + AD}{2}cdot CH = (R + r)(R — r) = R^2 — r^2 = dfrac{210}{sqrt[3]{pi^2}},] но (r = dfrac{R}{sqrt{15}}), тогда [R^2left(1-dfrac{1}{15}right) = dfrac{210}{sqrt[3]{pi^2}}qquadRightarrowqquad R = dfrac{15}{sqrt[3]{pi}}qquadRightarrowqquad V_{text{шара}} = dfrac{4}{3}pi R^3 = dfrac{4}{3}cdotpicdotdfrac{15^3}{pi} = 4500.]
Ответ: 4500
Задание
7
#3114
Уровень задания: Сложнее ЕГЭ
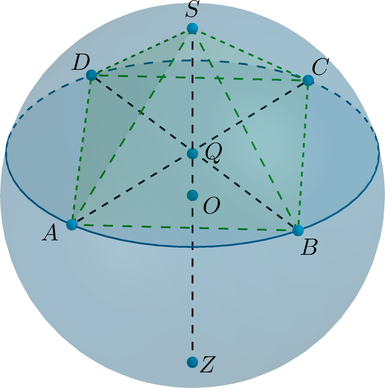
Дан шар, диаметр которого равен (9). Плоскость (alpha) пересекает диаметр (SZ) шара под углом (90^circ) и делит его точкой пересечения в отношении (1:2), считая от вершины (S). Найдите объем пирамиды с вершиной в точке (S), в основании которой лежит квадрат, вписанный в сечение шара плоскостью (alpha).
Пусть (O) – центр шара, (Q) – точка пересечения (SZ) и плоскости (alpha). Пусть (SABCD) – пирамида, объем которой нужно найти.
Рассмотрим сечение шара плоскостью (ASC).
Так как (SQ:QZ=1:2), то (SQ:SZ=1:3), следовательно, (SQ:SO=2:3), следовательно, (OQ:SO=1:3). Тогда [AQ=sqrt{AO^2-OQ^2}=sqrt{AO^2-left(dfrac13AOright)^2}=dfrac{2sqrt2}3AO
=dfrac{2sqrt2}3cdot dfrac92=3sqrt2] Следовательно, (AC=6sqrt2). Следовательно, (AB=AC:sqrt2=6).
Также [SQ=dfrac23SO=dfrac23cdot dfrac92=3] Заметим, что (SQ) – высота пирамиды, так как (SQperp alpha). Следовательно, [V=dfrac13cdot SQcdot AB^2=36.]
Ответ: 36
Задачи по стереометрии, в которых требуется произвести расчет объема сферы и измерение других неизвестных параметров, встречаются в ЕГЭ каждый год. Это означает, что знать основные формулы и уметь оперативно находить правильный ответ должны выпускники с разным уровнем подготовки. Понимая принцип решения задач ЕГЭ, в которых требуется вычислить объем или, к примеру, площадь сферы, старшеклассники смогут выполнять упражнения с любым количеством действий и при этом получить достаточно высокие баллы по итогам прохождения экзаменационного испытания.
Базовая информация
- Сферой называется поверхность, которая состоит из множества точек пространства. Все они располагаются на одинаковом расстоянии от точки О. Она является центром сферы.
- Геометрическое тело, которое ограничено сферой, называется шаром. Его осевое сечение представляет собой круг. Радиус последнего равен радиусу шара.
- Если радиус или диаметр шара увеличить в n раз, то площадь поверхности увеличится в n2 раз, а объем — в n3 раз.
Занимайтесь с образовательным порталом «Школково» для качественной подготовки к экзамену!
Проблема поиска необходимой информации встает перед старшеклассниками достаточно остро. Не всегда школьный учебник оказывается под рукой. А поиск базовых формул для вычисления площади, объема шара и других неизвестных параметров бывает достаточно трудоемким даже в онлайн-режиме.
Наш образовательный проект поможет сэкономить время и эффективно подготовиться к сдаче экзаменационного испытания. Мы предлагаем учащимся и их преподавателям выстроить процесс подготовки к ЕГЭ от простого к сложному. Такой подход позволит старшеклассникам понять, какие темы требуют более детального изучения, и улучшить имеющиеся знания.
Базовая информация, которую стоит повторить еще до выполнения задач на нахождение объема шара, представлена в разделе «Теоретическая справка». Материал, подготовленный опытными преподавателями «Школково», поможет вам восполнить пробелы в знаниях без помощи репетитора.
Чтобы задачи ЕГЭ по теме «Шар» или, например, по теме «Цилиндр», не вызывали затруднений, мы предлагаем также потренироваться в выполнении соответствующих упражнений. Множество заданий разной степени сложности вы найдете в разделе «Каталог». Каждое упражнение содержит подробный алгоритм решения. Попрактиковавшись в режиме онлайн и поняв принцип нахождения правильного ответа, школьники смогут без труда вычислить объем сферы.
При необходимости любое задание можно сохранить в разделе «Избранное». Это позволит в дальнейшем вернуться к нему.
Выполнять онлайн-задания на нахождение площади боковой сферы могут не только школьники из столицы, но и выпускники из других российских городов.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Зачет по теме «Объем шара» Вариант1
1. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
Зачет по теме «Объем шара» Вариант2
1.Во сколько раз увеличится объем шара, если его радиус увеличить в пять раз?
2. Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
2. Радиусы трех шаров равны 1, 6 и 8. Найдите радиус шара, объем которого равен сумме их объемов.
3. В куб с ребром 18 вписан шар. Найдите объем этого шара, деленный на π.
3. В куб с ребром 21 вписан шар. Найдите объем этого шара, деленный на π.
4. Около куба с ребром описан шар. Найдите объем этого шара, деленный на π.
4Около куба с ребром описан шар. Найдите объем этого шара, деленный на π.
5. Объем одного шара в 1331 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
5. Объем одного шара в 2197 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
6. Объем шара равен 288 . Найдите площадь его поверхности, деленную на π.
6. Объем шара равен 972 . Найдите площадь его поверхности, деленную на π.
7. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 27. Найдите объем шара.
7. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 12. Найдите объем шара.
8.Две параллельные плоскости, расстояние между которыми 2, пересекают шар. Одна из плоскостей проходит через центр шара. Отношение площадей сечений шара этими плоскостями равно 0,84. Найдите объем шара.
8. Две параллельные плоскости, расстояние между которыми 4, пересекают шар. Одна из плоскостей проходит через центр шара. Отношение площадей сечений шара этими плоскостями равно 0,44. Найдите объем шара.
ЕГЭ Профиль №5. Цилиндр, конус, шар
Скачать файл в формате pdf.
ЕГЭ Профиль №5. Цилиндр, конус, шар
| Задача 1. В цилиндрический сосуд налили 2000 см3 воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см3.
Ответ
ОТВЕТ: 1500. |
 |
| Задача 2. В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
Ответ
ОТВЕТ: 4. |
|
| Задача 3. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на (pi ).
Ответ
ОТВЕТ: 12. |
|
| Задача 4. В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.
Ответ
ОТВЕТ: 3. |
|
| Задача 5. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
Ответ
ОТВЕТ: 1,125. |
|
| Задача 6. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
Ответ
ОТВЕТ: 6. |
|
| Задача 7. Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
Ответ
ОТВЕТ: 2. |
|
| Задача 8. Площадь боковой поверхности цилиндра равна (72pi ), а диаметр основания — 9. Найдите высоту цилиндра.
Ответ
ОТВЕТ: 8. |
|
| Задача 9. Площадь боковой поверхности цилиндра равна (2pi ), а высота — 1. Найдите диаметр основания.
Ответ
ОТВЕТ: 2. |
|
| Задача 10. Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на (pi ).
Ответ
ОТВЕТ: 4. |
|
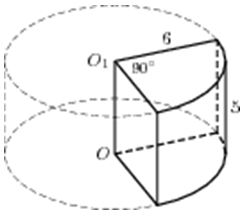
| Задача 11. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 45. |
 |
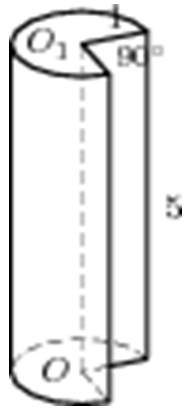
| Задача 12. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 3,75. |
 |
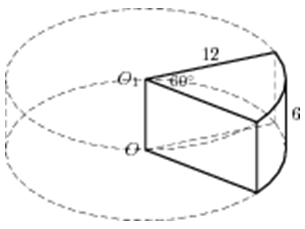
| Задача 13. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 144. |
 |
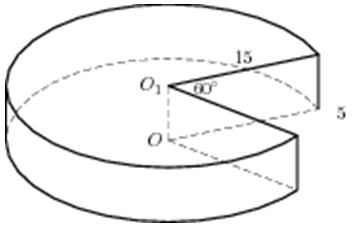
| Задача 14. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 937,5. |
 |
| Задача 15. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 14. |
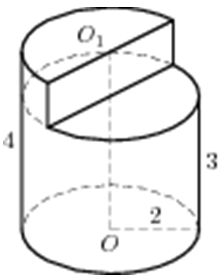 |
| Задача 16. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 105. |
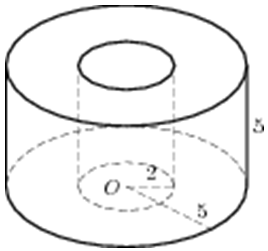 |
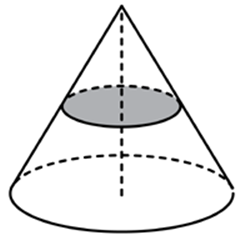
| Задача 17. Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Ответ
ОТВЕТ: 2. |
 |
| Задача 18. Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30o. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 1. |
|
| Задача 19. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 3 раза, а радиус основания останется прежним?
Ответ
ОТВЕТ: 3. |
|
| Задача 20. Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза, а высота останется прежней?
Ответ
ОТВЕТ: 2,25. |
|
| Задача 21. Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на (pi )
Ответ
ОТВЕТ: 128. |
|
| Задача 22. Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на (pi ).
Ответ
ОТВЕТ: 9. |
|
| Задача 23. Конус получается при вращении равнобедренного прямоугольного треугольника ABC вокруг катета, равного 6. Найдите его объем, деленный на (pi ).
Ответ
ОТВЕТ: 72. |
|
| Задача 24. Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на (pi )
Ответ
ОТВЕТ: 16. |
|
| Задача 25. Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.
Ответ
ОТВЕТ: 3. |
| Задача 26. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза, а радиус основания останется прежним?
Ответ
ОТВЕТ: 3. |
|
| Задача 27. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 1,5 раза, а образующая останется прежней?
Ответ
ОТВЕТ: 1,5. |
|
| Задача 28. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
Ответ
ОТВЕТ: 60. |
|
| Задача 29. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Ответ
ОТВЕТ: 3. |
|
| Задача 30. Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на (pi )
Ответ
ОТВЕТ: 24. |
|
| Задача 31. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 87,75. |
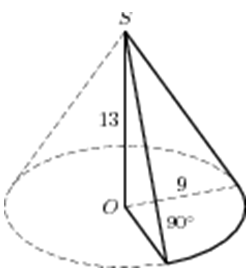 |
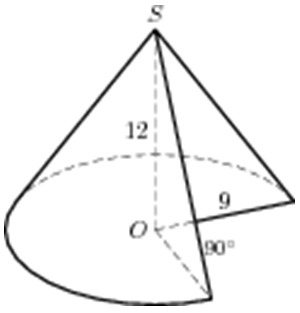
| Задача 32. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 243. |
 |
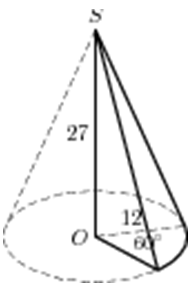
| Задача 33. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 216. |
 |
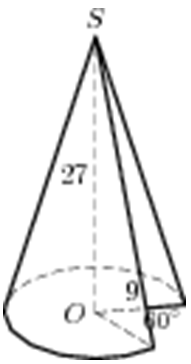
| Задача 34. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите (frac{V}{pi }).
Ответ
ОТВЕТ: 607,5. |
 |
| Задача 35. Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
Ответ
ОТВЕТ: 5. |
|
| Задача 36. Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
Ответ
ОТВЕТ: 6. |
|
| Задача 37. Диаметр основания конуса равен 6, а длина образующей — 5. Найдите высоту конуса.
Ответ
ОТВЕТ: 4. |
|
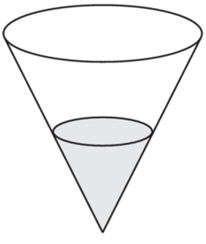
| Задача 38. В сосуде, имеющем форму конуса, уровень жидкости достигает (frac{1}{2}) высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Ответ
ОТВЕТ: 490. |
 |
| Задача 39. Площадь основания конуса равна (16pi ), высота – 6. Найдите площадь осевого сечения конуса.
Ответ
ОТВЕТ: 24. |
|
| Задача 40. Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.
Ответ
ОТВЕТ: 2. |
|
| Задача 41. Высота конуса равна 8, а длина образующей – 10. Найдите площадь осевого сечения этого конуса.
Ответ
ОТВЕТ: 48. |
|
| Задача 42. Диаметр основания конуса равен 12, а длина образующей – 10. Найдите площадь осевого сечения этого конуса.
Ответ
ОТВЕТ: 48. |
|
| Задача 43. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?
Ответ
ОТВЕТ: 4. |
|
| Задача 44. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
Ответ
ОТВЕТ: 27. |
|
| Задача 45. Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Ответ
ОТВЕТ: 12. |
|
| Задача 46. Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Ответ
ОТВЕТ: 9. |
|
| Задача 47. Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Ответ
ОТВЕТ: 10. |
|
| Задача 48. Объем шара равен (288pi ). Найдите площадь его поверхности, деленную на (pi ).
Ответ
ОТВЕТ: 144. |
|
| Задача 49. Площадь поверхности шара равна 12. Найдите площадь большого круга шара.
Ответ
ОТВЕТ: 3. |
20 февраля 2022
В закладки
Обсудить
Жалоба
Объёмы тел вращения
В данной методической разработке приведены формулы и разобраны примеры решения традиционных задач на вычисление объёмов тел вращения.
obemy-tel-vraschenija.docx
obemy-tel-vraschenija.pdf
Задача №1
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 36 см3.
Задача №2
Высота одного цилиндра вдвое больше высоты второго цилиндра, но его радиус в два раза меньше радиуса второго цилиндра. Найти отношение их объёмов
Задача №3
Найти объем 25м цилиндрической трубы (полого цилиндра), если внешний радиус равен 50см, диаметр стенок равен 10см.
Задача №4
Объём конуса равен 36, а его высота равна 12. Найдите радиус основания конуса.
Задача №5
Объём конуса равен 24 см3. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объём меньшего конуса.
Задача №6
Диаметр основания конуса равен 16, а длина образующей — 17. Найдите объем конуса.
Задача №7
Радиусы оснований усечённого конуса равны 4 и 12, а образующая равна 10. Вычислить объем усечённого конуса.
Задача №8
Внутренний диаметр полого шара равен 8 см, а толщина стенок равна 2 см. Найдите объем материала, из которого сделан шар.
Задача №9
Прямоугольная трапеция с основаниями 11см и 17 см и высотой 12 см вращается около прямой, проходящей через вершину острого угла перпендикулярно основаниям. Hайдите объем полученного тела вращения.
Задача №10
Прямоугольный треугольник с катетами 20 см и 15 см вращается вокруг гипотенузы . Найти объём полученного тела вращения.
Задания для самостоятельного решения.
1. Даны две кружки цилиндрической формы. Первая кружка в полтора раза ниже второй, а вторая вдвое шире первой. Во сколько раз объём второй кружки больше объёма первой?
2. Однородный шар диаметром 3 см имеет массу 162 грамма. Чему равна масса шара, изготовленного из того же материала, с диаметром 2 см? Ответ дайте в граммах.
3. Осевое сечение конуса равносторонний треугольник, сторона которого равна 12 см. Найдите объём конуса.
4. Найти объем тела, полученного в результате вращения прямоугольного треугольника вокруг гипотенузы, если катеты равны 3см и 4 см.
5. Прямоугольная трапеция с основанием 5 см и 8 см и высотой 4 см вращается около большего основания. Найдите объем тела вращения.
Автор: Барсукова Наталья Александровна.
Задание 1237
Площадь поверхности шара равна $$24sqrt[3]{frac{pi }{6}}$$. Найдите объем шара.
Ответ: 8
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Площадь поверхности сферы вычисляется по формуле: $$S=4pi R^{2}$$ Объем шара вычисляется по формуле: $$V=frac{4}{3}pi R^{3}$$ Найдем сначала радиус сферы, зная площадь ее поверхности: $$4pi R^{2} =24sqrt[3]{frac{pi }{6}} $$ $$R^{2} =6frac{sqrt[3]{frac{pi }{6}}}{pi} $$ $$R=sqrt[3]{frac{6}{pi}} $$ Тогда объем шара будет равен: $$V=frac{4}{3}pi (sqrt[3]{frac{6}{pi}})^{3}=8$$
Задание 1291
Цилиндр описан около шара. Найдите объем шара, если известно, что объем цилиндра равен 60.
Ответ: 40
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Высота цилиндра у нас равна двум радиусам вписанного шара. Обозначим радиус шара ( в таком случае и радиус основания цилиндра ) за R, объем цилиндра $$V_{1}$$, а объем шара V. Тогда :
$$V_{1}=Sh=pi R^{2}*2R=2pi R^{3}=60$$
$$R^{3}=frac{30}{pi} $$
Тогда объем шара будет:
$$V=frac{4}{3}pi R^{3}=frac{4}{3}pi * frac{30}{pi}=40$$
Задание 3243
Площадь поверхности шара равна 60. Найдите площадь большого круга шара.
Ответ: 15
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Sкруга$$=pi R^{2}$$
Sшара$$=4pi R^{2}$$=4Sкруга $$Rightarrow$$
Sкруга$$=frac{60}{4}=15$$
Задание 3946
Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
Ответ: 12
Задание 3947
Дано два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Ответ: 4
Задание 3948
Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
Ответ: 27
Задание 3949
Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Ответ: 12
Задание 3950
Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Ответ: 9
Задание 3951
Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.
Ответ: 10
Задание 3952
Объем шара равен $$288pi$$. Найдите площадь его поверхности, деленную на $$pi$$.
Ответ: 144
Задание 4012
Радиусы трех шаров равны 3, 4 и 5. Найдите радиус шара, объем которого равен сумме их объемов.
Ответ: 6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$V=V_{1}+V_{2}+V_{3}$$
$$frac{4}{3}pi R^{3}=frac{4}{3}pi R_{1}^{3}+frac{4}{3}pi R_{2}^{3}+frac{4}{3}pi R_{3}^{3}$$
$$R^{3}=R_{1}^{3}+R_{3}^{3}+R_{3}^{3}$$
$$R^{3}=3^{3}+4^{3}+5^{3}=216$$
$$R=6$$
Задание 4663
Площадь сечения шара плоскостью, проходящей через его центр, равна 16. Найдите площадь сечения этого шара плоскостью, отстоящей от его центра на расстояние, равное половине радиуса.
Ответ: 12
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
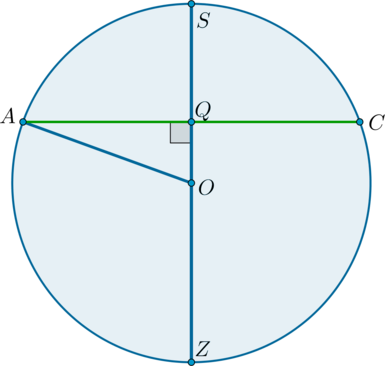
Построим чертеж:
Пусть O — центр большего сечения, А — центр меньшего, АС — его радиус, тогда ОС — радиус сферы. Пусть OC = R, тогда AO = 0,5R
Из треугольника AOC по т. Пифагора: $$AC=sqrt{R^{2}-(0,5R)^{2}}=frac{sqrt{3}*R}{2}$$
Тогда площади сечений относятся как квадрта их коэффеициента подобия, или как отношение их радиусов, возведенное в квадрат:
$$(frac{AC}{OC})^{2}=(frac{frac{sqrt{3}*R}{2}}{R})^{2}=frac{3}{4}$$
Тогда площадь меньшего составляет 3/4 площади большего, то есть 12
Задание 5051
Во сколько раз площадь поверхности шара, описанного около куба, больше площади поверхности шара, вписанного в этот же куб?
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$R=frac{1}{2}d$$; $$r=frac{1}{2}a$$; $$R=frac{1}{2}sqrt{3}a=frac{sqrt{3}a}{2}$$; $$r=frac{a}{2}$$; $$frac{S_{1}}{S_{2}}=(frac{R}{r})^{2}=(sqrt{3})^{2}=3$$
Задание 9059
Шар, объём которого равен 64, вписан в цилиндр. Найдите объём цилиндра.
Ответ: 96
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 9105
Шар вписан в цилиндр. Площадь поверхности шара равна 74. Найдите площадь полной поверхности цилиндра.
Ответ: 111
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!