Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
В 1-е классы поступает 45 человек: 20 мальчиков и 25 девочек. Их распределили по двум классам: в одном должно получиться 22 человека, а в другом ― 23. После распределения посчитали процент девочек в каждом классе и полученные числа сложили. Каким должно быть распределение по классам, чтобы полученная сумма была наибольшей?
Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 1., Пробный экзамен по математике Санкт-Петербург 2015. Вариант 1.
2
В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4t2 у. е. Если на втором объекте работает t человек, то их суточная зарплата составляет t2 у. е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у. е. в этом случае придется заплатить рабочим?
Источник: А. Ларин: Тренировочный вариант № 123.
3
Два велосипедиста равномерно движутся по взаимно перпендикулярным дорогам по направлению к перекрестку этих дорог. Один из них движется со скоростью 40 км/ч и находится на расстоянии 5 км от перекрестка, второй движется со скоростью 30 км/ч и находится на расстоянии 3 км от перекрестка. Через сколько минут расстояние между велосипедистами станет наименьшим? Каково будет это наименьшее расстояние? Считайте, что перекресток не T-образный, обе дороги продолжаются за перекрестком.
Источник: А. Ларин: Тренировочный вариант № 124.
4
Алексей вышел из дома на прогулку со скоростью υ км/ч. После того, как он прошел 6 км, из дома следом за ним выбежала собака Жучка, скорость которой была на 9 км/ч больше скорости Алексея. Когда Жучка догнала хозяина, они повернули назад и вместе возвратились домой со скоростью 4 км/ч. Найдите значение υ, при котором время прогулки Алексея окажется наименьшим. Сколько при этом составит время его прогулки?
Источник: А. Ларин: Тренировочный вариант № 116.
5
В бассейн проведены три трубы. Первая труба наливает 30 м3 воды в час. Вторая труба наливает в час на 3V м3 меньше, чем первая (0 < V < 10), а третья труба наливает в час на 10V м3 больше первой. Сначала первая и вторая трубы, работая вместе, наливают 30% бассейна, а затем все три трубы, работая вместе, наливают оставшиеся 0,7 бассейна. При каком значении V бассейн быстрее всего наполнится указанным способом?
Источник: А. Ларин: Тренировочный вариант № 117.
Пройти тестирование по этим заданиям
В задании №17 в ЕГЭ по профильной математике, вместо ожидаемой текстовой задачи на кредиты, иногда встречаются оптимальный выбор. Этот вид задач считается более сложным по сравнению с кредитами. Чтобы хорошо подготовиться к экзамену, нужно научиться их решать.
Тут требуется умение искать наибольшие и наименьшие значения функции, обычно зависящей от нескольких переменных. Эти переменные, как правило, связаны дополнительными условиями.
Вам обязательно понадобится умение искать производные и исследовать функции на экстремумы. Нужно знать, что такое ограниченные, возрастающие и убывающие функции. Если вы умеете решать 12-й и 7-й номера из ЕГЭ, то вам повезло – все необходимое для решения инструменты уже у вас в руках. А те, кто не умеет считать производные, то настоятельно рекомендуем сначала разобраться с первой частью экзамена и только потом переходить на более сложные задачи, такие, как №17.
Основной подход к решению заключается в следующем. Необходимо составить функцию, задающую нужную зависимость – если нужно найти максимальную или минимальную прибыль, значит это должна быть функция, описывающая прибыль, если нужен максимальный выпуск продукции на заводе, значит функция должна задавать количество продукции выпускаемой заводом, нужно найти оптимальное расстояние – наша функция будет описывать расстояние. Внимательно, функция может зависеть сразу от нескольких переменных. После того, как вы смогли записать функцию, нам предстоит ее исследовать.
На самом деле, тут нет какой-то сухой теории, которую можно прочить и научиться решать задачи на оптимальный выбор. Поэтому давайте учиться на примерах. Сначала разберем простые, поймем алгоритм решения, а потом перейдем к более сложным, которые могут встретиться на экзамене.
Пример 1
Пусть у Василия есть завод, который выпускает спичечные коробки. Расходы на производство одного коробка 1 руб, а продает он их за 5 руб. В итоге с каждого коробка Василий получает прибыль 4 руб. Давайте разберемся, сколько нужно производить коробков, чтобы прибыль была наибольшей, если (Х) работников завода может производить в месяц ( N=-left(x-10right)^{2}+500) коробков.
И так, согласно условию задачи, если на заводе Х работников, то они производят ( N=-left(x-10right)^{2}+500) коробков.
А какая прибыль (P) с такого количества? Ответ очевиден, нужно просто прибыль (4 руб) с одного коробка умножить на количество произведенных коробков: ( P=4*(-left(x-10right)^{2}+500)).
Давайте посмотрим при каком количестве работников прибыль Василия будет максимальна. Или другими словами при каком (Х) будет наибольшим (Р). Такое задание часто встречается в 12-м номере ЕГЭ, нужно просто исследовать нашу зависимость прибыли ( P=4*(-left(x-10right)^{2}+500)) от (Х) и найти экстремумы.
Напомню, что функция принимает наибольшее или наименьшее значения в точках, где ее производная равна 0. Значит ищем производную от (Р) и приравниваем к 0.
$${P}^{’}=(4*(-left(x-10right)^{2}+500))^{‘}= 4cdotleft(-2right)cdotleft(x-10right)$$
Приравниваем (0):
$$4cdotleft(-2right)cdotleft(x-10right)=0$$
И ищем (Х), при котором производная равна (0):
$$ X=10.$$
Что мы такое нашли? При этом значении (Х) (количестве рабочих) прибыль будет либо максимальна, либо минимальна. Это точка экстремума, а какая именно, мы пока не знаем.
Давайте это определим. Напоминаю, если производная отрицательная, то функция убывает, если положительна, то возрастает. Если подставить значения меньшее (10) в нашу производную, например (1):
$$ 4cdotleft(-2right)cdotleft(x-10right) = 4cdotleft(-2right)cdotleft(1-10right)=4*18=72$$
Значение производной получилось больше 0:
$$ {P(x<10)}^{‘}>0$$
Значит при (Х<10) функция возрастает, а при (Х>10) убывает. А значит (Х=10) – это максимум. Мы получили, что максимальная прибыль будет, если на производстве будет задействовано всего 10 рабочих. Как так может быть? Казалось бы, чем больше рабочих, тем больше продукции выпускает завод, а значит и больше прибыль. Но в реальной жизни все не так просто – размеры завода ограничены, и если там будет слишком много людей, то они просто будут мешать друг другу делать свою работу, в результате выпуск продукции начнет снижаться или поднимутся расходы на производство.
Вернемся к задаче, а какая будет максимальная прибыль? Просто подставим (Х=10) в функцию для прибыли:
$$ P=4*(-left(x-10right)^{2}+500)= 4*(-left(10-10right)^{2}+500)=4*500=2000 руб. $$
Только что мы решили первую задачу на оптимальный выбор.
Разберем следующий пример:
Пример 2
Пусть опять у нас есть завод, на котором расходы на производство (y) автомобилей составляет (Q=0,5y^2+y+7) миллионов рублей в месяц. Если продавать каждый автомобиль за (S) тысяч рублей, то при продаже всех произведенных за месяц автомобилей завод получит доход (S*y), а заработает на этом прибыль (доходы минус расходы) — (S*y-Q). Какую наименьшую цену продажи (S) нужно установить, чтобы за 3 месяца завод получил прибыль 75 миллионов рублей?
Первым делом давайте составим функцию, описывающую зависимость прибыли от количества произведенной продукции и цены продажи, которую мы должны установить. Сразу 2 неизвестные!
И так, чтобы посчитать прибыль (P(y,S)), зависящую от (у) и (S), нам нужно стоимость продажи одного автомобиля (S) умножить на количество проданных машин (у), получим общий доход, и вычесть все расходы (Q), которые мы понесли при производстве (в условии, кстати, это написано — подсказка):
$$P(x,S)=S*y-Q=S*y-(0,5*y^2+y+7)=-0,5y^2+(S-1)y-7$$
Проанализируем полученное выражение. Это квадратный многочлен. Если построить график относительно (у), то это уравнение параболы. Как анализировать квадратные многочлены, можно посмотреть тут.
Так как коэффициент перед (y^2) отрицательный, то ветки параболы направлены вниз. То есть, наибольшее значение нашей функции будет в вершине параболы. Можно по известным формулам найти вершину и значение функции и в ней, это и будет максимальное значение. А можно пойти по старому пути, как в примере 1, и посчитать производную. Число (S) будем считать просто за константу, то есть берем производную относительно (у):
$$ {P(x,S)}^{’}={(-0,5y^2+(S-1)y-7)}^{’}=-y+S-1; $$
Приравниваем производную нулю, чтобы найти точки экстремума:
$$-y+S-1=0;$$
$$y=S-1;$$
Так как график исходной функции парабола с ветками вниз, то это точка максимума функции (P(x,S)). Подставим (y=S-1) в нашу функцию:
$$ P(x,S)=-0,5*y^2+(S-1)y-7=-0,5(S-1)^2+(S-1)(S-1)-7=frac{(S-1)^2}{2}-7; $$
Мы получили — какую максимальную прибыль мы можем заработать в зависимости от (S). Другими словами, подставляя различные значения стоимости автомобиля в нашу функцию, получим максимальную прибыль при данной стоимости продажи.
По условию задачи общая прибыль за 3 месяца должна быть не меньше чем 75 миллионов рублей. Запишем это в виде неравенства:
$$ {3*P(S)}_{max}=3*frac{(S-1)^2}{2}-7 ge 75; $$
Осталось только решить это неравенство:
$$(S-1)^2ge64;$$
$$(S-9)(S+7)ge0;$$
(S) отрицательным быть не может, что это тогда за бизнес, где цена продаваемой продукции отрицательна. А значит при (S ge9) прибыль завода будет больше 75 миллионов рублей.
Пример 3
Решим задачу на оптимизацию расстояния:
Два мотоциклиста подъезжают к перекрестку по двум перпендикулярным дорогам. Первый едет со скоростью 40 км/ч и до перекрестка ему осталось ехать 5 км, а скорость второго 30км/ч и ехать до перекрестка 3 км. Через какое время расстояние между мотоциклистами будет наименьшим?
Для решения задачи нам понадобится теорема Пифагора, ведь мотоциклисты едут по взаимно перпендикулярным дорогам, а значит расстояние между ними — это гипотенуза прямоугольного треугольника, а катеты – это расстояния от каждого мотоциклиста до перекрестка.
Пусть мотоциклисты уже находятся в пути (t) часов. Тогда первый проедет расстояние:
$$S=v*t=40t;$$
До перекрестка осталось ехать
$$S_1=5-40t;$$
А второму:
$$S_2=3-30t;$$
Мы получили прямоугольный треугольник с катетами (S_1) и (S_2). По теореме Пифагора выведем функцию, задающую расстояние между мотоциклистами:
$$L=sqrt{(5-40t)^2+(3-30t)^2}=sqrt{25-400t+1600t^2+9-180t+900t^2}=sqrt{2500t^2-580t+34};$$
Согласно условию задачи, нужно найти такое время (t), чтобы расстояние (L) было наименьшим. Для этого опять возьмем производную и исследуем функцию (L) на экстремум:
$$ {L}^{’}=frac{1}{2*sqrt{2500t^2-580t+34}}*(5000*t-580); $$
Приравниваем нулю:
$$5000*t-580=0;$$
$$t=frac{580}{5000}=frac{29}{250} часа;$$
Так как при (t) меньшем этого числа производная функции отрицательна, а при большем – положительна, то получаем точку минимума и, что расстояние между мотоциклистами будет наименьшим через (frac{29}{250}) часа, это и требовалось найти.
Если бы в задаче нас попросили еще найти это расстояние, то нужно подставить (t=frac{29}{250}) в функцию расстояния (L):
$$L(t=frac{29}{250})=sqrt{(5-40*frac{29}{250})^2+(3-30*frac{29}{250})^2}=(frac{3}{5})км$$
Что такое задачи на оптимизацию?
Задача на оптимизацию — в математике задача
нахождения экстремума(минимума или максимума)целевой функции вне которой
области определения. В самых простых задачах на оптимизацию мы имеем дело с
двумя величинами, одна из которых зависит от другой, причем надо найти такое
значение 2-ой величины, при котором первая принимает свое наилучшее в данных
условиях значение.
Как решать задачи на оптимизацию?
Задачи на оптимизацию решают по обычной схеме
из трех этапов математического моделирования:
1) составление
математической модели;
2) работа с
математической моделью;
3) ответ на вопрос
задачи.
Первый этап.
Составление математической модели.
1) Проанализировав
условия задачи, выделите оптимизируемую величину (О.В.),
т. е. величину, о наибольшем или наименьшем значении которой идет речь.
Обозначьте ее буквой y.
2) Одну из
участвующих в задаче неизвестных величин, через которую сравнительно нетрудно
выразить О.В.,примите ее за независимую переменную (Н.П.)
и обозначьте ее буквой x. Установите реальные границы изменения Н.П.,
т. е. область определения для искомой О.В.
3) Исходя из
условий задачи, выразите y через x. Математическая модель задачи
представляет собой функцию y = f(x) с областью определения X,
которую нашли на втором шаге.
Второй этап. Работа
с математической моделью
На втором этапе для функции y=f(x), x ϵ X
найдите yнаим. или yнаиб.в зависимости от того, что
требуется найти в условии задачи.
Третий этап. Ответ
на вопрос задачи. Здесь следует дать
конкретный ответ на вопрос задачи, опираясь на результаты, полученные на этапе
работы с моделью
Задание 17 № 508236. В 1-е классы поступает 45 человек: 20 мальчиков и 25 девочек.
Их распределили по двум классам: в одном должно получиться 22 человека,
а в другом ― 23. После распределения посчитали процент девочек в каждом
классе и полученные числа сложили. Каким должно быть распределение
по классам, чтобы полученная сумма была наибольшей?
Задание
17 № 513301. В двух областях есть по 160 рабочих,
каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия
или никеля. В первой области один рабочий за час добывает 0,1 кг алюминия
или 0,1 кг никеля. Во второй области для добычи x кг алюминия в
день требуется x2 человеко-часов труда, а для добычи у
кг никеля в день требуется у2 человеко-часов труда.
Для нужд промышленности можно
использовать или алюминий, или никель, причём 1 кг алюминия можно заменить
1 кг никеля. Какую наибольшую массу металлов можно за сутки суммарно добыть
в двух областях?
ЕГЭ Профиль №15. Экономические задачи на оптимизацию
Скачать файл в формате pdf.
ЕГЭ Профиль №15. Экономические задачи на оптимизацию
1В. В 1-е классы поступает 45 человек: 20 мальчиков и 25 девочек. Их распределили по двум классам: в одном должно получиться 22 человека, а в другом ? 23. После распределения посчитали процент девочек в каждом классе и полученные числа сложили. Каким должно быть распределение по классам, чтобы полученная сумма была наибольшей?
ОТВЕТ: В одном классе ― 22 девочки, в другом ― 3 девочки и 20 мальчиков.
2В. В 1-е классы поступает 43 человека: 23 мальчика и 20 девочек. Их распределили по двум классам: в одном должно получиться 22 человека, а в другом ? 21. После распределения посчитали процент мальчиков в каждом классе и полученные числа сложили. Каким должно быть распределение по классам, чтобы полученная сумма была наибольшей?
ОТВЕТ: В одном классе ― 21 мальчик, в другом ― 20 девочек и 2 мальчика.
3В. У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 400 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором — 400 ц/га. Фермер может продавать картофель по цене 10 000 руб. за центнер, а свёклу — по цене 11 000 руб. за центнер. Какой наибольший доход может получить фермер?
4В. У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 500 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором – 500 ц/га. Фермер может продать картофель по цене 5 000 руб. за центнер, а свёклу — по цене 8 000 руб. за центнер. Какой наибольший доход может получить фермер?
5В. В двух шахтах добывают алюминий и никель. На первой шахте имеется 50 рабочих, каждый из которых готов трудиться 6 часов в день. При этом один рабочий за час добывает 1 кг алюминия или 3 кг никеля. На второй шахте имеется 180 рабочих, каждый из которых готов трудиться 6 часов в день. При этом один рабочий за час добывает 3 кг алюминия или 1 кг никеля. Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 3 кг алюминия приходится 2 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
6В. В двух шахтах добывают алюминий и никель. На первой шахте имеется 60 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 2 кг алюминия или 3 кг никеля. На второй шахте имеется 260 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 3 кг алюминия или 2 кг никеля. Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
7В. Фабрика, производящая пищевые полуфабрикаты, выпускает блинчики со следующими видами начинки: ягодная и творожная. В данной ниже таблице приведены себестоимость и отпускная цена, а также производственные возможности фабрики по каждому виду продукта при полной загрузке всех мощностей только данным видом продукта.
Для выполнения условий ассортимента, которые предъявляются торговыми сетями, продукции каждого вида должно быть выпущено не менее 15 тонн. Предполагая, что вся продукция фабрики находит спрос (реализуется без остатка), найдите максимально возможную прибыль, которую может получить фабрика от производства блинчиков за 1 месяц (прибылью называется разница между отпускной стоимостью всей продукции и её себестоимостью).
8В. Завод выпускает фруктовые компоты в двух видах тары—стеклянной и жестяной. Производственные мощности завода позволяют выпускать в день 90 центнеров компотов в стеклянной таре или 80 центнеров в жестяной таре. Для выполнения условий ассортимента, которые предъявляются торговыми сетями, продукции в каждом из видов тары должно быть выпущено не менее 20 центнеров. В таблице приведены себестоимость и отпускная цена завода за 1 центнер продукции для обоих видов тары.
Предполагая, что вся продукция завода находит спрос (реализуется без остатка), найдите максимально возможную прибыль завода за один день (прибылью называется разница между отпускной стоимостью всей продукции и её себестоимостью).
9В. Предприятие непрерывного цикла выпускает изделия двух типов. Для изготовления изделия первого типа требуется 15 часов работы цеха А и 10 часов работы цеха Б, а для изготовления изделия второго типа требуется 5 часов работы цеха А и 20 часов работы цеха Б (цеха могут работать над изделием в любой последовательности). По техническим причинам цех А может работать не более 150 часов в неделю, а цех Б — не более 100 часов в неделю. Каждое изделие первого типа приносит предприятию 5 000 д. е. прибыли, а каждое изделие второго типа — 4 000 д. е. прибыли. Найдите наибольшую возможную еженедельную прибыль предприятия и определите, сколько изделий первого типа и сколько изделий второго типа следует еженедельно выпускать для получения этой прибыли.
ОТВЕТ: 10 изделий первого типа; 0 изделий второго типа; максимальная прибыль равна 50 000 д.е.
10В. Предприятие непрерывного цикла выпускает изделия двух типов. Для изготовления изделия первого типа требуется 30 часов работы цеха А и 20 часов работы цеха Б, а для изготовления изделия второго типа требуется 10 часов работы цеха А и 40 часов работы цеха Б (цеха могут работать над изделием в любой последовательности). По техническим причинам цех А может работать не более 600 часов в месяц, а цех Б — не более 400 часов в месяц. Каждое изделие первого типа приносит предприятию 15 000 д. е. прибыли, а каждое изделие второго типа—12 000 д. е. прибыли. Найдите наибольшую возможную ежемесячную прибыль предприятия и определите, сколько изделий первого типа и сколько изделий второго типа следует ежемесячно выпускать для получения этой прибыли.
ОТВЕТ: 20 изделий первого типа; 0 изделий второго типа; максимальная прибыль равна 300 000 д.е.
11В. Предприниматель купил здание и собирается открыть в нём отель. В отеле могут быть стандартные номера площадью 30 квадратных метров и номера «люкс» площадью 40 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 940 квадратных метров. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 4 000 рублей в сутки, а номер «люкс» — 5 000 рублей в сутки. Какую наибольшую сумму (в рублях) сможет заработать в сутки на своём отеле предприниматель?
12В. Предприниматель купил здание и собирается открыть в нём отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера «люкс» площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 981 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2 000 рублей в сутки, а номер «люкс» — 4 000 рублей в сутки. Какую наибольшую сумму (в рублях) сможет заработать в сутки на своём отеле предприниматель?
13В. Предприниматель купил здание и собирается открыть в нём отель. В отеле могут быть номера категории Б площадью 20 квадратных метров и номера категории А площадью 25 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 1 015 квадратных метров. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Номер категории Б будет приносить отелю 3 000 рублей в сутки, а номер категории А — 4 000 рублей в сутки. Какую наибольшую сумму (в рублях) сможет заработать в сутки на своём отеле предприниматель? Сколько номеров категории Б и сколько номеров категории А будет в таком отеле?
ОТВЕТ: 162 000 рублей; номеров категории А – 39, категории Б — 2.
14В. Предприниматель купил здание и собирается открыть в нём отель. В отеле могут быть номера категории Б площадью 15 квадратных метров и номера категории А площадью 18 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 732 квадратных метра. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Номер категории Б будет приносить отелю 4 000 рублей в сутки, а номер категории А — 5000 рублей в сутки. Какую наибольшую сумму (в рублях) сможет заработать в сутки на своём отеле предприниматель? Сколько номеров категории Б и сколько номеров категории А будет в таком отеле?
ОТВЕТ: 203 000 рублей; номеров категории А – 39, категории Б — 2
15В. Баржу грузоподъёмностью 134 тонны используют для перевозки контейнеров типов А и В. По условиям договора количество перевозимых контейнеров типа А должно составлять не более 80% количества перевозимых контейнеров типа В. Вес и стоимость одного контейнера типа А составляет 2 тонны и 5 млн руб., контейнера типа В — 5 тонн и 7 млн руб. соответственно. Найдите наибольшую возможную суммарную стоимость (в млн руб.) всех контейнеров, которые можно перевезти при данных условиях. Укажите число контейнеров типа А и число контейнеров типа В, которые нужно перевезти для получения наибольшей возможной суммарной стоимости.
ОТВЕТ: 220; 16 контейнеров типа А; 20 контейнеров типа В.
16В. Баржу грузоподъёмностью 180 тонн используют для перевозки контейнеров типов А и В. По условиям договора количество перевозимых контейнеров типа А должно составлять не более 75% количества перевозимых контейнеров типа В. Вес и стоимость одного контейнера типа А составляет 3 тонны и 3 млн руб., контейнера типа В — 7 тонн и 5 млн руб. соответственно. Найдите наибольшую возможную суммарную стоимость (в млн руб.) всех контейнеров, которые можно перевезти при данных условиях. Укажите число контейнеров типа А и число контейнеров типа В, которые нужно перевезти для получения наибольшей возможной суммарной стоимости.
ОТВЕТ: 139; 13 контейнеров типа А; 20 контейнеров типа В.
17В. Сергей является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 5 t единиц товара, а если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 12 t единиц товара. За каждый час работы (на каждом из заводов) Сергей платит рабочему 400 рублей. Сергей готов выделять 608 400 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
18В. Владлен является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 6t единиц товара, а если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 8t единиц товара. За каждый час работы (на каждом из заводов) Владлен платит рабочему 300 рублей. Владлен готов выделять 1 920 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
19В. Зинаида является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 8t единиц товара, а если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 15t единиц товара. За каждый час работы (на каждом из заводов) Зинаида платит рабочему 600 рублей. Зинаиде нужно каждую неделю производить 578 единиц товара. Какую наименьшую сумму придётся тратить еженедельно на оплату труда рабочих?
20В. Федор является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 3t единиц товара, а если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 4t единиц товара. За каждый час работы (на каждом из заводов) Федор платит рабочему 400 рублей. Федору нужно каждую неделю производить 225 единиц товара. Какую наименьшую сумму придётся тратить еженедельно на оплату труда рабочих?
21В. Производство x тыс. единиц продукции обходится в (q = 0,5{x^2} + x + 7) млн. рублей в год. При цене p тыс. рублей за единицу продукции годовая прибыль от продажи этой продукции (в млн рублей) составляет (p,x — q). Завод выпускает продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p через три года суммарная прибыль составит не менее 75 млн рублей?
22В. Производство x тыс. единиц продукции обходится в (q = 0,5{x^2} + 2x + 5) млн. рублей в год. При цене p тыс. рублей за единицу продукции годовая прибыль от продажи этой продукции (в млн рублей) составляет (p,x — q). Завод выпускает продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p через четыре года суммарная прибыль составит не менее 52 млн рублей?
23В. Макар является владельцем двух заводов в разных городах. На заводах производится абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе, Макар платит рабочему 300 рублей, а на заводе, расположенном во втором городе,—200 рублей. Макар готов выделять 30 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
24В. Станислав является владельцем двух заводов в разных городах. На заводах производится абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе, Станислав платит рабочему 400 рублей, а на заводе, расположенном во втором городе,—300 рублей. Станислав готов выделять 84 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
25В. В двух областях есть по 160 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,1 кг алюминия или 0,3 кг никеля. Во второй области для добычи x кг алюминия в день требуется x2 человеко-часов труда, а для добычи y кг никеля в день требуется y2 человеко-часов труда. Для нужд промышленности можно использовать или алюминий, или никель, причём 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно за сутки суммарно добыть в двух областях?
26В. В двух областях есть по 100 рабочих, каждый из которых готов трудиться по 10 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,3 кг алюминия или 0,1 кг никеля. Во второй области для добычи x кг алюминия в день требуется x2 человеко-часов труда, а для добычи y кг никеля в день требуется y2 человеко-часов труда. Обе области поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 1 кг алюминия приходится 1 кг никеля. При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
27В. Фёдор является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые изделия, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате если рабочие на заводе, расположенном в первом городе, трудятся суммарно 25t3 часов в неделю, то за эту неделю они производят t изделий, и если рабочие на заводе, расположенном во втором городе, трудятся суммарно t3 часов в неделю, то они производят t изделий. За каждый час работы (на каждом из заводов) Фёдор платит рабочему 360 рублей. Необходимо, чтобы за неделю суммарно производилось 30 изделий. Какую наименьшую сумму (в млн рублей) придётся тратить владельцу заводов еженедельно на оплату труда рабочих?
28В. Василий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые изделия, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате если рабочие на заводе, расположенном в первом городе, трудятся суммарно 16t3 часов в неделю, то за эту неделю они производят t изделий, и если рабочие на заводе, расположенном во втором городе, трудятся суммарно t3 часов в неделю, то они производят t изделий. За каждый час работы (на каждом из заводов) Василий платит рабочему 250 рублей. Необходимо, чтобы за неделю суммарно производилось 20 изделий. Какую наименьшую сумму (в млн рублей) придётся тратить владельцу заводов еженедельно на оплату труда рабочих?
29В. В распоряжении прораба имеется бригада рабочих в составе 25 человек. Их нужно распределить на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 3t2 д. е. Если на втором объекте работает t человек, то их суточная зарплата составляет t2 д. е. Как нужно распределить на эти объекты рабочих бригады, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько д. е. при таком распределении придётся выплатить рабочим?
ОТВЕТ: 6 рабочих на 1-й объект, 19 рабочих на 2-й объект, зарплата 469 д е.
30В. В распоряжении прораба имеется бригада рабочих в составе 22 человек. Их нужно распределить на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4t2 д. е. Если на втором объекте работает t человек, то их суточная зарплата составляет t2 д. е. Как нужно распределить на эти объекты рабочих бригады, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько д. е. при таком распределении придётся выплатить рабочим?
ОТВЕТ: 4 рабочих на 1-й объект, 18 рабочих на 2-й объект, зарплата 388 д е.
31В. Строительство нового завода стоит 78 млн рублей. Затраты на производство x тыс. ед. продукции на таком заводе равны (0,5{x^2} + 2x + 6) млн рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит (p,x — left( {0,5{x^2} + 2x + 6} right)). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 3 года?
32В. Строительство нового завода стоит 140 млн рублей. Затраты на производство x тыс. ед. продукции на таком заводе равны (0,4{x^2} + x + 5) млн рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит (p,x — left( {0,4{x^2} + x + 5} right)). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 4 года?
33В. Производство некоторого товара облагалось налогом в размере t0 рублей за единицу товара. После того как государство, стремясь нарастить сумму налоговых поступлений, увеличило налог вдвое (до 2 t0 рублей за единицу товара), сумма налоговых поступлений не изменилась. На сколько процентов государству следует изменить налог после такого увеличения, чтобы добиться максимальных налоговых поступлений, если известно, что при налоге, равном t рублей за единицу товара, объём производства составляет 10 000 – 2 t единиц и это число положительно?
34В. Производство некоторого товара облагалось налогом в размере t0 рублей за единицу товара. После того как государство, стремясь нарастить сумму налоговых поступлений за счёт увеличения производства товара, уменьшило налог вдвое (до (frac{{{t_0}}}{2}) рублей за единицу товара), сумма налоговых поступлений не изменилась. На сколько процентов государству следует изменить налог после такого уменьшения, чтобы добиться максимальных налоговых поступлений, если известно, что при налоге, равном t рублей за единицу товара, объём производства составляет 10 000 – 2 t единиц и это число положительно?
35В. Пенсионный фонд владеет акциями, цена которых к концу года t становится равной t2 тыс. руб. (т. е. к концу первого года они стоят 1 тыс. руб., к концу второго — 4 тыс. руб. и т. д.), в течение 20 лет. В конце любого года можно продать акции по их рыночной цене на конец года и положить вырученные деньги в банк под 25% годовых. В конце какого года нужно продать акции, чтобы прибыль была максимальной?
36В. Пенсионный фонд владеет акциями, цена которых к концу года t становится равной t2 тыс. руб. (т. е. к концу первого года они стоят 1 тыс. руб., к концу второго — 4 тыс. руб. и т. д.), в течение 30 лет. В конце любого года можно продать акции по их рыночной цене на конец года и положить вырученные деньги в банк под 20% годовых. В конце какого года нужно продать акции, чтобы прибыль была максимальной?
37В. Пенсионный фонд владеет ценными бумагами, которые стоят t2 тыс. рублей в конце года (t;;left( {t = 1,;2,;3…} right)). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться в (1 + r) раз. Пенсионный фонд хочет продать ценные бумаги в конце такого года, чтобы в конце двадцать пятого года сумма на его счёте была наибольшей. Расчёты показали, что для этого ценные бумаги нужно продавать строго в конце двадцать первого года. При каких положительных значениях r это возможно?
ОТВЕТ: (left( {frac{{43}}{{441}};frac{{41}}{{400}}} right))
38В. Пенсионный фонд владеет ценными бумагами, которые стоят 10 t тыс. рублей в конце года (t;;left( {t = 1,;2,;3…} right)). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться в (1 + r) раз. Пенсионный фонд хочет продать ценные бумаги в конце такого года, чтобы в конце двадцать пятого года сумма на его счёте была наибольшей. Расчёты показали, что для этого ценные бумаги нужно продавать строго в конце одиннадцатого года. При каких положительных значениях r это возможно?
ОТВЕТ: (left( {frac{1}{{11}};frac{1}{{10}}} right)).
39В. Зависимость количества Q (в шт., (0 leqslant Q leqslant 20;000)) купленного у фирмы товара от цены P (в руб. за шт.) выражается формулой (Q = 20;000 — P). Затраты на производство Q единиц товара составляют (6;000Q + 4;000;000) рублей. Кроме затрат на производство, фирма должна платить налог t рублей (left( {0 < t < 10;000} right)) с каждой произведённой единицы товара. Таким образом, прибыль фирмы составляет (PQ — 6;000Q — 4;000;000 — t,Q) рублей, а общая сумма налогов, собранных государством, равна (t,Q) рублей. Фирма производит такое количество товара, при котором её прибыль максимальна. При каком значении t общая сумма налогов, собранных государством, будет максимальной?
40В. Зависимость количества Q (в шт., (0 leqslant Q leqslant 15;000)) купленного у фирмы товара от цены P (в руб. за шт.) выражается формулой (Q = 15;000 — P). Затраты на производство Q единиц товара составляют (3;000Q + 1;000;000) рублей. Кроме затрат на производство, фирма должна платить налог t рублей (left( {0 < t < 10;000} right)) с каждой произведённой единицы товара. Таким образом, прибыль фирмы составляет (PQ — 3;000Q — 1;000;000 — t,Q) рублей, а общая сумма налогов, собранных государством, равна (t,Q) рублей. Фирма производит такое количество товара, при котором её прибыль максимальна. При каком значении t общая сумма налогов, собранных государством, будет максимальной?
41В. Зависимость объёма Q (в шт.) купленного у фирмы товара от цены Р (в руб. за шт.) выражается формулой (Q = 15;000 — P,quad 1;000 leqslant P leqslant 15;000). Доход от продажи товара составляет РQ рублей. Затраты на производство Q единиц товара составляют (3;000Q + 5;000;000) рублей. Прибыль равна разности дохода от продажи товара и затрат на его производство. Стремясь привлечь внимание покупателей, фирма уменьшила цену товара на 20%, однако её прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?
42В. На счет, который Кирилл Николаевич имел в начале 1-го года, начисляется в конце этого года x процентов, а на тот счет, который Кирилл Николаевич имел в конце 2-го года y процентов, причем (x + y = 50% ). Кирилл Николаевич положил на счет в начале 1-го года некоторую сумму и добавил в конце 1-го года после начисления процентов десятую часть этой суммы. При каком значении x счет в конце 2-го года окажется максимальным?
43В. Лодка находится в точке Q озера, отстоящей от ближайшей точки A на берегу на 6 км. Лодочник должен попасть в точку B, находящуюся на берегу на расстоянии 11 км от A. Скорость лодки 3 км/ч, скорость ходьбы лодочника по берегу 5 км/ч. Лодочник подсчитал, что если он сперва доплывет до точки C, которая находится между A и B, а затем сразу же пешком направится в точку B, то на путь от Q до B он потратит наименьшее время. Найдите это время и расстояние от A до C, считая, что лодка движется прямолинейно и берег озера – прямая линия.
44В. Два велосипедиста равномерно движутся по взаимно перпендикулярным дорогам по направлению к перекрестку этих дорог. Один из них движется со скоростью 40 км/ч и находится на расстоянии 5 км от перекрестка, второй движется со скоростью 30 км/ч и находится на расстоянии 3 км от перекрестка. через сколько минут расстояние между велосипедистами станет наименьшим? Каково будет это наименьшее расстояние.
ОТВЕТ: (6frac{{24}}{{25}};) мин; (frac{3}{5};) км.
45В. (ЕГЭ 2019) Строительство нового завода стоит 159 млн. рублей. Затраты на производство x тыс. ед. продукции на таком заводе равны (0,5{x^2} + 2x + 6) млн. рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн. рублей) за один год составит (p,x — left( {0,5{x^2} + 2x + 6} right)). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. Цена продукции в первый год 10 тыс. рублей, а каждый следующий год увеличивается на 1 тыс. рублей. Через сколько лет окупится строительство завода?
46В. Евгений хочет купить пакет акций компании. 15 февраля он отложил определённую сумму денег и планирует откладывать такую же сумму денег 15 числа каждого месяца. Первого февраля пакет акций стоил 195 000 рублей. Первого числа каждого месяца пакет акций дорожает на 40 %. Какую наименьшую сумму нужно Евгению откладывать каждый месяц, чтобы через некоторое время купить желаемый пакет акций?
47В. Михаил хочет купить пакет акций компании. 15 февраля он отложил определённую сумму денег и планирует откладывать такую же сумму денег 15 числа каждого месяца. Первого февраля пакет акций стоил 160 000 рублей. Первого числа каждого месяца пакет акций дорожает на 25 %. Какую наименьшую сумму нужно Михаилу откладывать каждый месяц, чтобы через некоторое время купить желаемый пакет акций?
Текстовое решение задач:
| 1B | 2B | 3B | 4B | 5B | 6B | 7B | 8B | 9B | 10B |
| 11B | 12B | 13B | 14B | 15B | 16B | 17B | 18B | 19B | 20B |
| 21B | 22B | 23B | 24B | 25B | 26B | 27B | 28B | 29B | 30B |
| 31B | 32B | 33B | 34B | 35B | 36B | 37B | 38B | 39B | 40B |
| 41B | 42B | 43B | 44B | 45B | 46B | 47B |
15 февраля 2023
В закладки
Обсудить
Жалоба
Задачи на оптимизацию
№15 профильного ЕГЭ по математике.
zadachi_na_optimizatsiyu.pdf
Задачи из видео
1. К 800-летию Нижнего Новгорода идёт активное облагораживание города. На обновление брусчатки одной из пешеходных улиц было выделено 412 500 рублей. К выполнению работ было приглашено две бригады. Один день работы каждой из бригад стоит 3300 рублей. Известно, что первая бригада за x дней выкладывает 60√x м2 брусчатки, а вторая бригада выкладывает 120√x м2. Какое наибольшее количество брусчатки удастся выложить при оптимальном распределении бюджета?
2. Строительство нового завода стоит 78 млн рублей. Затраты на производство x тыс. ед. продукции на таком заводе равны 0,5x2 + 2x + б млн рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит px — (0,5x2 + 2x + б). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 3 года?
3. На счёт, который вкладчик имел в начале первого квартала, начисляется в конце этого квартала r1 процентов, а на тот счёт, который вкладчик имел в конце второго квартала, начисляется в конце этого квартала Т2 процентов, причём r1 + r2 = 150. Вкладчик положил на счёт в начале первого квартала некоторую сумму и снял в конце того же квартала половину этой суммы. При каком значении r1 счёт вкладчика в конце второго квартала окажется максимально возможным?
Задачи для самостоятельного решения
1. Произведение двух положительных чисел равно 484. Найдите эти числа, если известно, что их сумма принимает наименьшее значение.
2. Записать число 625 в виде произведения двух положительных чисел так, чтобы сумма их квадратов была наименьшей.
3. Строительство нового завода стоит 132 млн рублей. Затраты на производство x тыс. ед. продукции на таком заводе равны 0,5x2 + 5x + 17 млн рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит px(0,5x2+5x+17). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 4 года?
4. Зависимость количества Q (в шт 0 ≤ Q ≤ 20000) купленного у фирмы товара от цены P (в руб. за шт.) выражается формулой Q = 20000 — P. Затраты на производство Q единиц товара составляют 6000Q + 4000000 рублей. Кроме затрат на производство, фирма должна платить налог t рублей (0 < t < 10000) с каждой произведённой единицы товара. Таким образом, прибыль фирмы составляет PQ — 6000Q — 4000000 — tQ рублей, а общая сумма налогов, собранных государством, равна tQ рублей.
Фирма производит такое количество товара, при котором её прибыль максимальна. При каком значении t общая сумма налогов, собранных государством, будет максимальной?
Источник: vk.com/j_math
В задании №17 в ЕГЭ по профильной математике, вместо ожидаемой текстовой задачи на кредиты, иногда встречаются оптимальный выбор. Этот вид задач считается более сложным по сравнению с кредитами. Чтобы хорошо подготовиться к экзамену, нужно научиться их решать.
Тут требуется умение искать наибольшие и наименьшие значения функции, обычно зависящей от нескольких переменных. Эти переменные, как правило, связаны дополнительными условиями.
Вам обязательно понадобится умение искать производные и исследовать функции на экстремумы. Нужно знать, что такое ограниченные, возрастающие и убывающие функции. Если вы умеете решать 12-й и 7-й номера из ЕГЭ, то вам повезло – все необходимое для решения инструменты уже у вас в руках. А те, кто не умеет считать производные, то настоятельно рекомендуем сначала разобраться с первой частью экзамена и только потом переходить на более сложные задачи, такие, как №17.
Основной подход к решению заключается в следующем. Необходимо составить функцию, задающую нужную зависимость – если нужно найти максимальную или минимальную прибыль, значит это должна быть функция, описывающая прибыль, если нужен максимальный выпуск продукции на заводе, значит функция должна задавать количество продукции выпускаемой заводом, нужно найти оптимальное расстояние – наша функция будет описывать расстояние. Внимательно, функция может зависеть сразу от нескольких переменных. После того, как вы смогли записать функцию, нам предстоит ее исследовать.
На самом деле, тут нет какой-то сухой теории, которую можно прочить и научиться решать задачи на оптимальный выбор. Поэтому давайте учиться на примерах. Сначала разберем простые, поймем алгоритм решения, а потом перейдем к более сложным, которые могут встретиться на экзамене.
Пример 1
Пусть у Василия есть завод, который выпускает спичечные коробки. Расходы на производство одного коробка 1 руб, а продает он их за 5 руб. В итоге с каждого коробка Василий получает прибыль 4 руб. Давайте разберемся, сколько нужно производить коробков, чтобы прибыль была наибольшей, если (Х) работников завода может производить в месяц ( N=-left(x-10right)^{2}+500) коробков.
И так, согласно условию задачи, если на заводе Х работников, то они производят ( N=-left(x-10right)^{2}+500) коробков.
А какая прибыль (P) с такого количества? Ответ очевиден, нужно просто прибыль (4 руб) с одного коробка умножить на количество произведенных коробков: ( P=4*(-left(x-10right)^{2}+500)).
Давайте посмотрим при каком количестве работников прибыль Василия будет максимальна. Или другими словами при каком (Х) будет наибольшим (Р). Такое задание часто встречается в 12-м номере ЕГЭ, нужно просто исследовать нашу зависимость прибыли ( P=4*(-left(x-10right)^{2}+500)) от (Х) и найти экстремумы.
Напомню, что функция принимает наибольшее или наименьшее значения в точках, где ее производная равна 0. Значит ищем производную от (Р) и приравниваем к 0.
$${P}^{’}=(4*(-left(x-10right)^{2}+500))^{‘}= 4cdotleft(-2right)cdotleft(x-10right)$$
Приравниваем (0):
$$4cdotleft(-2right)cdotleft(x-10right)=0$$
И ищем (Х), при котором производная равна (0):
$$ X=10.$$
Что мы такое нашли? При этом значении (Х) (количестве рабочих) прибыль будет либо максимальна, либо минимальна. Это точка экстремума, а какая именно, мы пока не знаем.
Давайте это определим. Напоминаю, если производная отрицательная, то функция убывает, если положительна, то возрастает. Если подставить значения меньшее (10) в нашу производную, например (1):
$$ 4cdotleft(-2right)cdotleft(x-10right) = 4cdotleft(-2right)cdotleft(1-10right)=4*18=72$$
Значение производной получилось больше 0:
$$ {P(x<10)}^{‘}>0$$
Значит при (Х<10) функция возрастает, а при (Х>10) убывает. А значит (Х=10) – это максимум. Мы получили, что максимальная прибыль будет, если на производстве будет задействовано всего 10 рабочих. Как так может быть? Казалось бы, чем больше рабочих, тем больше продукции выпускает завод, а значит и больше прибыль. Но в реальной жизни все не так просто – размеры завода ограничены, и если там будет слишком много людей, то они просто будут мешать друг другу делать свою работу, в результате выпуск продукции начнет снижаться или поднимутся расходы на производство.
Вернемся к задаче, а какая будет максимальная прибыль? Просто подставим (Х=10) в функцию для прибыли:
$$ P=4*(-left(x-10right)^{2}+500)= 4*(-left(10-10right)^{2}+500)=4*500=2000 руб. $$
Только что мы решили первую задачу на оптимальный выбор.
Разберем следующий пример:
Пример 2
Пусть опять у нас есть завод, на котором расходы на производство (y) автомобилей составляет (Q=0,5y^2+y+7) миллионов рублей в месяц. Если продавать каждый автомобиль за (S) тысяч рублей, то при продаже всех произведенных за месяц автомобилей завод получит доход (S*y), а заработает на этом прибыль (доходы минус расходы) — (S*y-Q). Какую наименьшую цену продажи (S) нужно установить, чтобы за 3 месяца завод получил прибыль 75 миллионов рублей?
Первым делом давайте составим функцию, описывающую зависимость прибыли от количества произведенной продукции и цены продажи, которую мы должны установить. Сразу 2 неизвестные!
И так, чтобы посчитать прибыль (P(y,S)), зависящую от (у) и (S), нам нужно стоимость продажи одного автомобиля (S) умножить на количество проданных машин (у), получим общий доход, и вычесть все расходы (Q), которые мы понесли при производстве (в условии, кстати, это написано — подсказка):
$$P(x,S)=S*y-Q=S*y-(0,5*y^2+y+7)=-0,5y^2+(S-1)y-7$$
Проанализируем полученное выражение. Это квадратный многочлен. Если построить график относительно (у), то это уравнение параболы. Как анализировать квадратные многочлены, можно посмотреть тут.
Так как коэффициент перед (y^2) отрицательный, то ветки параболы направлены вниз. То есть, наибольшее значение нашей функции будет в вершине параболы. Можно по известным формулам найти вершину и значение функции и в ней, это и будет максимальное значение. А можно пойти по старому пути, как в примере 1, и посчитать производную. Число (S) будем считать просто за константу, то есть берем производную относительно (у):
$$ {P(x,S)}^{’}={(-0,5y^2+(S-1)y-7)}^{’}=-y+S-1; $$
Приравниваем производную нулю, чтобы найти точки экстремума:
$$-y+S-1=0;$$
$$y=S-1;$$
Так как график исходной функции парабола с ветками вниз, то это точка максимума функции (P(x,S)). Подставим (y=S-1) в нашу функцию:
$$ P(x,S)=-0,5*y^2+(S-1)y-7=-0,5(S-1)^2+(S-1)(S-1)-7=frac{(S-1)^2}{2}-7; $$
Мы получили — какую максимальную прибыль мы можем заработать в зависимости от (S). Другими словами, подставляя различные значения стоимости автомобиля в нашу функцию, получим максимальную прибыль при данной стоимости продажи.
По условию задачи общая прибыль за 3 месяца должна быть не меньше чем 75 миллионов рублей. Запишем это в виде неравенства:
$$ {3*P(S)}_{max}=3*frac{(S-1)^2}{2}-7 ge 75; $$
Осталось только решить это неравенство:
$$(S-1)^2ge64;$$
$$(S-9)(S+7)ge0;$$
(S) отрицательным быть не может, что это тогда за бизнес, где цена продаваемой продукции отрицательна. А значит при (S ge9) прибыль завода будет больше 75 миллионов рублей.
Пример 3
Решим задачу на оптимизацию расстояния:
Два мотоциклиста подъезжают к перекрестку по двум перпендикулярным дорогам. Первый едет со скоростью 40 км/ч и до перекрестка ему осталось ехать 5 км, а скорость второго 30км/ч и ехать до перекрестка 3 км. Через какое время расстояние между мотоциклистами будет наименьшим?
Для решения задачи нам понадобится теорема Пифагора, ведь мотоциклисты едут по взаимно перпендикулярным дорогам, а значит расстояние между ними — это гипотенуза прямоугольного треугольника, а катеты – это расстояния от каждого мотоциклиста до перекрестка.
Пусть мотоциклисты уже находятся в пути (t) часов. Тогда первый проедет расстояние:
$$S=v*t=40t;$$
До перекрестка осталось ехать
$$S_1=5-40t;$$
А второму:
$$S_2=3-30t;$$
Мы получили прямоугольный треугольник с катетами (S_1) и (S_2). По теореме Пифагора выведем функцию, задающую расстояние между мотоциклистами:
$$L=sqrt{(5-40t)^2+(3-30t)^2}=sqrt{25-400t+1600t^2+9-180t+900t^2}=sqrt{2500t^2-580t+34};$$
Согласно условию задачи, нужно найти такое время (t), чтобы расстояние (L) было наименьшим. Для этого опять возьмем производную и исследуем функцию (L) на экстремум:
$$ {L}^{’}=frac{1}{2*sqrt{2500t^2-580t+34}}*(5000*t-580); $$
Приравниваем нулю:
$$5000*t-580=0;$$
$$t=frac{580}{5000}=frac{29}{250} часа;$$
Так как при (t) меньшем этого числа производная функции отрицательна, а при большем – положительна, то получаем точку минимума и, что расстояние между мотоциклистами будет наименьшим через (frac{29}{250}) часа, это и требовалось найти.
Если бы в задаче нас попросили еще найти это расстояние, то нужно подставить (t=frac{29}{250}) в функцию расстояния (L):
$$L(t=frac{29}{250})=sqrt{(5-40*frac{29}{250})^2+(3-30*frac{29}{250})^2}=(frac{3}{5})км$$
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 г. (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
Муниципальное бюджетное общеобразовательное учреждение
«Средняя школа №23 города Димитровграда Ульяновской области»
Задачи на оптимизацию
Автор разработки : учитель высшей категории
Авакян Л.Р
Димитровград,2021г
- Задачи на оптимизацию – это уже настоящие исследовательские задачи, очень близкие по смыслу (но не по методам решения) к задачам с параметром. Сложность таких задач в том, что не всегда есть готовые методы решения и задача может потребовать своего подхода. Успех в решении таких задач заключается в систематическом тренинге. Решение любой текстовой задачи складывается из нескольких основных этапов:
- 1. подробный разбор условия задачи для четкого понимания сути описанного в задаче процесса;
- 2. выбор переменных, количество которых должно быть достаточным для того, чтобы составить уравнения и неравенства. Если переменных оказалось больше, чем число уравнений, но при этом все было сделано верно, то «лишние» переменные взаимно уничтожатся или сократятся. Иногда в процессе решения требуется найти не сами переменные по отдельности, а их комбинацию;
- 3. формализация или составление уравнений и неравенств. При этом важно обращать внимание на единицы измерения – они должны быть одинаковыми для всех одноименных величин;
- 4.решение полученного уравнения, неравенства или системы;
- 5. интерпретация полученного результата и непосредственно сам ответ на вопрос задачи.
09.04.21
- В задачах оптимизации обычно заданы определённые условия производства какой-либо продукции или услуги и требуется найти значения некоторых величин с целью максимизации прибыли или минимизации расходов.
- Математическая модель (т.е. формализация условия задачи посредством неравенств и уравнений, задающих связи между данными величинами) любой из таких задач обычно приводит к одному-двум линейным уравнениям (неравенствам) относительно двух данных неизвестных и к одному линейному или простейшему нелинейному уравнению, которое связывает данные неизвестные и величину, максимум или минимум которой надо определить.
- После введения в качестве новой неизвестной (параметра) этой величины (её обычно называют целевой функцией ) задача сводится к определению наибольшего (наименьшего) значения параметра, при котором полученное уравнение имеет хотя бы один корень на множестве неотрицательных чисел, удовлетворяющий данным ограничениям.
09.04.21
- Что можно ожидать в качестве задания 17 на экзамене?
09.04.21
09.04.21
Задание №17 (задача на оптимизацию ) Владимир является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t 2 часов в неделю, то за эту неделю они производят t единиц товара.За каждый час работы на заводе, расположенном в первом городе Владимир платит рабочему 500 рублей, а на заводе расположенном во втором городе-300 рублей Владимир готов выделять 1200000 рублей на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах
.
(
—
.
1
й
способ
введение
параметра)
Решение
09.04.21
09.04.21
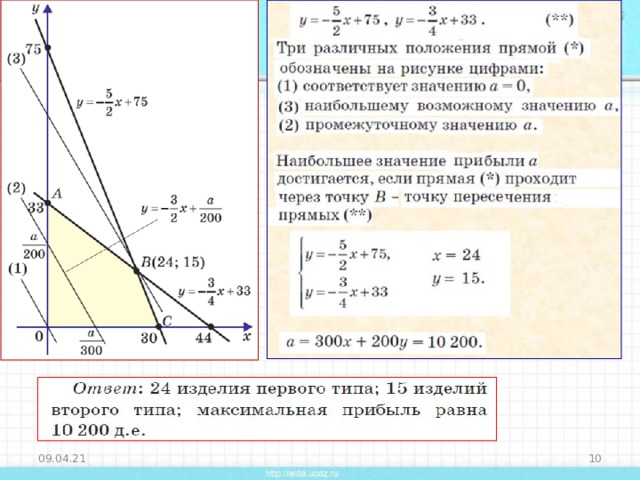
Задание 17 на ЕГЭ 2015 года
09.04.21
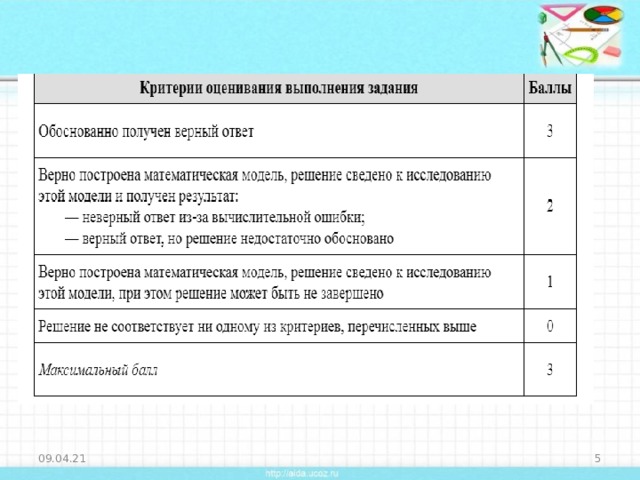
Линейная целевая функция
09.04.21
8
09.04.21
09.04.21
А.Ларин. Тренировочный вариант №123 В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4 t 2 у. е. Если на втором объекте работает t человек, то их суточная зарплата составляет t 2 у. е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у. е. в этом случае придется заплатить рабочим?
09.04.21
09.04.21
09.04.21
09.04.21
09.04.21
Литература
- Образовательный портал для подготовки к ЕГЭ -Решу ЕГЭ(задание17)
- ALEXLARIN.NET. Тесты для подготовки к ЕГЭ.
- Прокофьев А.А. Рекомендации по выполнению 17 задания
- Гущин Д.Д. Встречи с финансовой математикой
09.04.21
09.04.21