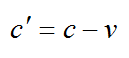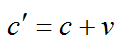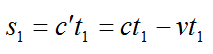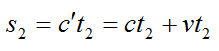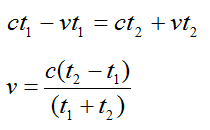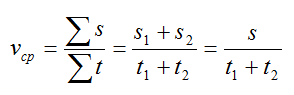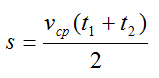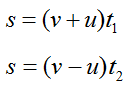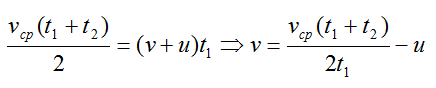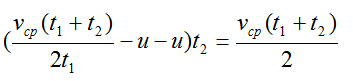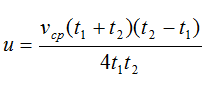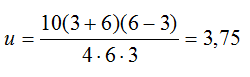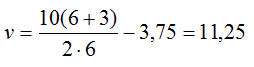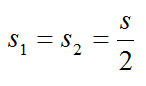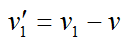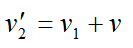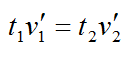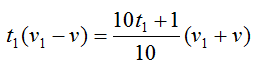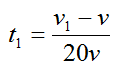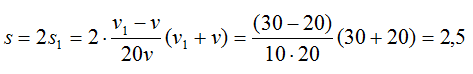в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 36 1–20 | 21–36
Добавить в вариант
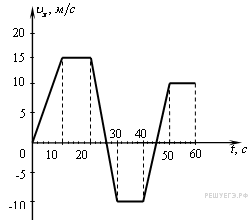
На гладком горизонтальном столе покоится брусок с прикреплённой к нему гладкой изогнутой в вертикальной плоскости тонкой жёсткой трубкой (см. рис.). Общая масса бруска с трубкой равна M = 0,8 кг. В верхний конец вертикальной части трубки, находящийся на высоте H = 70 см над бруском, опускают без начальной скорости маленький шарик массой m = 50 г. Другой конец трубки наклонён к горизонту под углом α = 30° и находится на высоте h = 20 см над бруском. Найдите модуль скорости, с которой будет двигаться брусок после того, как шарик вылетит из трубки.
Какие законы Вы используете для описания движения и взаимодействия трубки и шарика? Обоснуйте их применение к данному случаю.
Источник: Тренировочная работа по физике 28.04.2017, вариант ФИ10503
Задания Д1 B1 № 131
Лодка должна попасть на противоположный берег реки по кратчайшему пути в системе отсчета, связанной с берегом. Скорость течения реки u, а скорость лодки относительно воды Чему должен быть равен модуль скорости лодки относительно берега?
1)
2)
3)
4)
Автобус везёт пассажиров по прямой дороге со скоростью 10 м/с. Пассажир равномерно идёт по салону автобуса со скоростью 1 м/с относительно автобуса, двигаясь от задней двери к кабине водителя. Чему равен модуль скорости пассажира относительно дороги? (Ответ дайте в метрах в секунду.)
Задания Д29 C2 № 9072
На гладком горизонтальном столе покоится брусок с прикреплённой к нему гладкой изогнутой в вертикальной плоскости тонкой жёсткой трубкой (см. рис.). Общая масса бруска с трубкой равна M = 0,8 кг. В верхний конец вертикальной части трубки, находящийся на высоте H = 70 см над бруском, опускают без начальной скорости маленький шарик массой m = 50 г. Другой конец трубки наклонён к горизонту под углом α = 30° и находится на высоте h = 20 см над бруском. Найдите модуль скорости, с которой будет двигаться брусок после того, как шарик вылетит из трубки.
Задания Д1 B1 № 5952
Два камня одновременно бросили из одной точки: первый — вертикально вверх, второй — под углом 45° к горизонту. Сопротивление воздуха пренебрежимо мало. Как движется первый камень в системе отсчёта, связанной со вторым камнем?
1) покоится
2) движется по параболе
3) движется равномерно и прямолинейно
4) движется по дуге окружности
Задания Д1 B1 № 5987
Два камня одновременно бросили из одной точки: первый — вертикально вверх, второй — под углом 30° к горизонту. Сопротивление воздуха пренебрежимо мало. Как движется второй камень в системе отсчёта, связанной с первым камнем?
1) покоится
2) движется по параболе
3) движется равномерно и прямолинейно
4) движется по дуге окружности
Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге навстречу ему едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)
Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге в том же направлении едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)
Задания Д2 B2 № 6637
Маша взяла в руку монету и, стоя в комнате своей квартиры, выпустила её из пальцев без начальной скорости. Монета полетела вдоль вертикали и упала на пол комнаты. Затем Маша вышла из дома, села в подъехавший автобус и, дождавшись, пока он начнёт двигаться равномерно и прямолинейно по горизонтальной дороге, повторила опыт с бросанием монеты. Оказалось, что монета в равномерно движущемся автобусе падает точно так же, как и в квартире. Иллюстрацией какого закона или принципа может служить этот опыт?
1) первого закона Ньютона
2) второго закона Ньютона
3) третьего закона Ньютона
4) принципа относительности Галилея
Задания Д2 B2 № 6676
Саша взял в руку монету и, стоя в равномерно движущемся вниз лифте, выпустил её из пальцев без начальной скорости. Монета полетела вдоль вертикали и упала на пол лифта. Затем Саша вышел из дома, сел в подъехавший автобус и, дождавшись, пока он начнёт двигаться равномерно и прямолинейно по горизонтальной дороге, повторил опыт с бросанием монеты. Оказалось, что монета в равномерно движущемся автобусе падает точно так же, как и в равномерно опускающемся лифте. Иллюстрацией какого закона или принципа может служить этот опыт?
1) Первого закона Ньютона
2) Второго закона Ньютона
3) Третьего закона Ньютона
4) принципа относительности Галилея
Задания Д1 B1 № 125
Вертолет поднимается вертикально вверх. Какова траектория движения точки на конце лопасти винта вертолета в системе отсчета, связанной с винтом?
1) точка
2) прямая
3) окружность
4) винтовая линия
Задания Д3 B3 № 4412
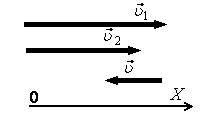
Два бруска массой m и
равномерно движутся вдоль прямой OX (см. рис.). В системе отсчёта, связанной с бруском
модуль импульса второго бруска равен
1)
2)
3)
4)
Задания Д3 B3 № 4447
Два бруска массой m и
равномерно движутся вдоль прямой OX (см. рис.). В системе отсчёта, связанной с бруском
модуль импульса первого бруска равен
1) mV
2)
3)
4)
Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показано изменение расстояния между автомобилями с течением времени. Каков модуль скорости первого автомобиля в системе отсчёта, связанной со вторым автомобилем? Ответ приведите в метрах в секунду.
Источник: Демонстрационная версия ЕГЭ—2020 по физике.
Задания Д1 B1 № 3357
Вертолет равномерно поднимается вертикально вверх. Какова траектория крайней точки лопасти вертолета в системе отсчета, связанной с корпусом вертолета?
1) прямая линия
2) винтовая линия
3) окружность
4) эллипс
Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с. (Ответ дайте в метрах в секунду.)
Из незакреплённой пушки стреляют снарядом массой 20 кг, который вылетает из ствола в горизонтальном направлении со скоростью 102 м/с относительно пушки. Пушка при этом откатывается, приобретая относительно земли скорость 2 м/с. Чему равна масса пушки, если массой сгоревшего порохового заряда можно пренебречь? Ответ дайте в килограммах.
Из незакреплённой пушки массой 800 кг стреляют снарядом, который вылетает из ствола в горизонтальном направлении со скоростью 102 м/с относительно пушки. Пушка при этом откатывается, приобретая относительно земли скорость 2 м/с. Чему равна масса снаряда, если массой сгоревшего порохового заряда можно пренебречь? Ответ дайте в килограммах.
Пароход движется по реке против течения со скоростью 5 м/с относительно берега. Определите скорость течения реки, если скорость парохода относительно берега при движении в обратном направлении равна 8 м/с. (Ответ дайте в метрах в секунду.)
Всего: 36 1–20 | 21–36
Задачи ЕГЭ на относительность движения
Задачи на относительность движения — пожалуй, самые сложные из задач кинематики. Здесь надо очень хорошо представлять себе, как будет выглядеть картина движения, если ты находишься на этом самом корабле и ощущаешь ветер на своем лице, или ты едешь на конце движущегося стержня и можешь видеть второй его конец. То есть нужно уметь поставить себя на место другого, и вообразить, что он ощущает или видит — это всегда сложно, и в задаче, и в жизни.
Задача 1.
Один корабль идет по морю на север с постоянной скоростью 20 узлов, а другой – навстречу ему, на юг, с такой же скоростью. Корабли проходят на малом расстоянии друг от друга. Шлейф дыма от первого корабля вытянулся в направлении на запад, а от второго – на северо-запад. Определите модуль скорости ветра. 1 узел – 1 морская миля в час, 1 морская миля – 1852 м. Ответ выразить в км/ч и округлить до целых. Для начала переведем скорость судов в км/ч:
узлов/ час
км/ч
км/ч.
К задаче 1. Корабли и ветер
Пусть ветер дует под углом по отношению к направлению на север. Так как первый корабль оставляет дым строго слева от себя, то это означает, что его скорость равна проекции скорости ветра на северное направление. Таким образом, корабль и ветер в этом направлении двигаются с одинаковой скоростью и скорость корабля «гасит» скорость ветра. Поэтому можем записать:
Скорость второго корабля, наоборот, накладывается на скорость ветра, на его борту «ветер сильнее». Результатом сложения скоростей ветра и корабля является направление сноса дыма. Чтобы найти скорость ветра в неподвижной системе, нужно из скорости дыма вычесть скорость корабля, который здесь – подвижная система отсчета. Тогда:
Вектора дымов и кораблей
Проекция скорости ветра на северное направление тогда равна Проекция скорости ветра на западное направление равна
, и, следовательно,
Тогда скорость ветра равна:
Ответ: 83 км/ч
Задача 2.
Стержень скользит по инерции по гладкому горизонтальному столу. В некоторый момент времени в неподвижной системе отсчета скорости концов стержня составляют с направлением стержня углы и
. Какой угол
образует со стержнем в этот момент скорость его центра? Пусть скорость одного конца стержня равна
, а второго
. Стержень участвует в двух движениях: в поступательном и вращательном. Если спроецировать скорости концов на направление стержня, то можно определить скорость поступательного движения, а проекции скорости, перпендикулярные направлению стержня, дадут возможность найти мгновенный центр вращения.
К задаче 2. Стержень
Проекции скорости на направление стержня обязаны быть равными, так как стержень не претерпевает растяжения: Проекции скоростей на перпендикулярное стержню направление относятся так же, как расстояния концов стержня до мгновенного центра вращения:
Отсюда
Теперь можем найти скорость середины стержня, и угол, под которым она направлена к стержню. Проекция скорости центра на направление стержня такая же, как и у концов:
. Найдем перпендикулярную составляющую. Для этого составим пропорцию:
Проекция скорости центра стержня на направление стержня такая же, как у концов:
Сам угол равен
Ответ:
.
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Относительное движение
Скорость точки относительно неподвижной системы отсчета равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы.
(v) — абсолютная скорость
(vec{u}) — переносная скорость
(v’) — относительная скорость
[vec{v}=vec{u}+vec{v} ‘]
Автобус везёт пассажиров по прямой дороге со скоростью 10 м/с. Пассажир равномерно идёт по салону автобуса со скоростью 1 м/с относительно автобуса, двигаясь от задней двери к кабине водителя. Чему равен модуль скорости пассажира относительно дороги? (Ответ дайте в метрах в секунду.)
Так как пассажир идет в том же направлении, что и автобус, то вектора их скоростей складываются, поэтому абсолютная скорость равна [upsilon_{text{абс}}=upsilon_{text{пер}}+upsilon_{text{отн}}=10text{ м/с}+1text{ м/с}=11text{ м/с}]
Ответ: 11
По прямой дороге с постоянной скоростью 100 км/ч едет мотоциклист и в том же направлении едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)
[upsilon_{text{отн}}=upsilon_{text{абс}}-upsilon_{text{пер}}=100text{ км/ч}-70text{ км/ч}=30text{ км/ч}]
Ответ: 30
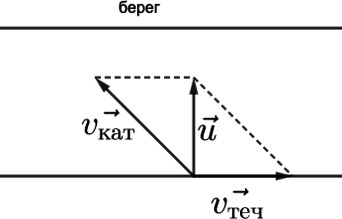
Катер плывёт по прямой реке, двигаясь относительно берега перпендикулярно береговой линии. Модуль скорости катера относительно берега равен 8 км/ч. Река течёт со скоростью 6 км/ч. Чему равен модуль скорости катера относительно воды? Ответ выразите в км/ч.
Чтобы катер двигался перпендикулярно относительно берега, относительно воды ему надо двигаться под углом. По закону сложения скоростей: [vec{v_{text{абс}}}=vec{v_{text{пер}}}+vec{v_{text{отн}}}] [vec{u}=vec{v_{text{теч}}}+vec{v_{text{кат}}}]
По теореме Пифагора найдем скорость катера относительно воды: [v_{text{кат}}=sqrt{u^2+v_{text{теч}}^2}=sqrt{8^2+6^2}=10 text{ км/ч}]
Ответ: 10
Пассажир зашел в автобус через заднюю дверь. Автобус поехал с постоянной скоростью (upsilon_1=25) м/с, а пассажир пошел к передней части автобуса. Скорость пассажира относительно автобуса равна (upsilon_{2}=3) м/с. С какой скоростью едет автобус относительно пассажира?
Скорость первого тела относительного второго равна скорости второго тела относительно первого и направлена в противоположную сторону. [vec{v}_{text{абс}}=vec{v}_{text{отн}}+vec{v}_{text{пер}}] [vec{v}_{text{1}}=vec{v}_{text{12}}+vec{v}_{text{2}}] [vec{v}_{text{2}}=vec{v}_{text{21}}+vec{v}_{text{1}}] [vec{v}_{text{12}}=-vec{v}_{text{21}}] Таким образом, автобус относительно пассажира едет со скоростью 3 м/с в обратную сторону.
Ответ: 3
Вася идет по прямой дороге со скоростью (upsilon_1=3text{ км/ч}.) Навстречу ему движется грузовик со скоростью (upsilon_2=30text{ км/ч}). С какой скоростью (upsilon_3) (по модулю) должен двигаться велосипедист навстречу Васе, чтобы модули его скорости относительно автомобиля и относительно Васи были одинаковы? Ответ дайте в км/ч.
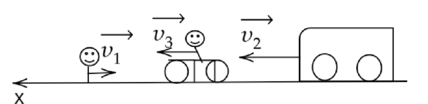
Ответ: 13,5
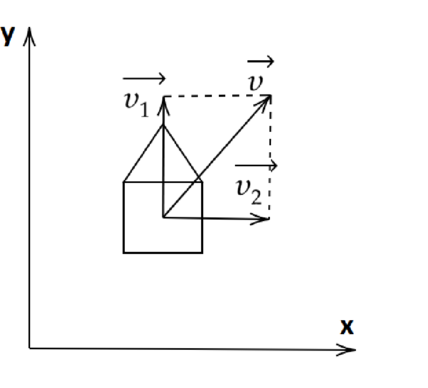
Пароход плывет по прямой реке. Его скорость относительно реки равна (v_1=5) км/ч и направлена перпендикулярно береговой линии. Река течет со скоростью (v_2=4) км/ч. Чему равен модуль скорости (v) (в км/ч) парохода относительно Земли? Ответ округлите до десятых.
Рассмотрим рисунок: векторы cкорости (v_1) и (v_2) составляют друг с другом угол (90^{circ}). Значит (v) можно найти по теореме Пифагора: [v^2=v_1^2+v_2^2] Отсюда: [v=sqrt{v_1^2+v_2^2}=sqrt{(5text{ км/ч})^2+4text{ км/ч})^2}approx6,4text{ км/ч}]
Ответ: 6,4
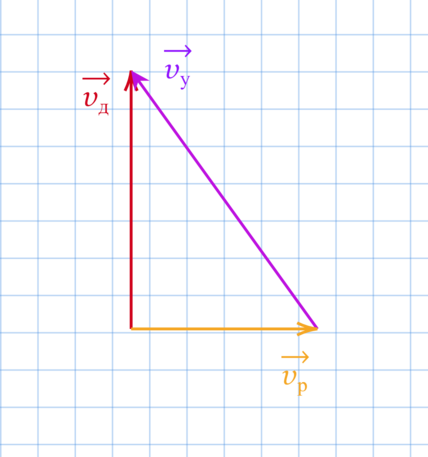
Дейнерис вылетела на драконе Дрогоне из Королевской Гавани в Браавос со скоростью (upsilon_text{д}=43,2) км/ч. Перпендикулярной Ее Величеству Джон Сноу вылетел в Винтерфелл на драконе Рейгале со скоростью (upsilon_text{р}=3,5) м/с. С какой скоростью в м/с они удаляются друг от друга?
Переведем скорость Дрогона в м/с: [upsilon_text{д}=frac{43,2text{ км/ч}cdot1000}{3600}=12text{ м/с}]
Изобразим:
Отсюда видно, что скорость удаления двух драконов (тел) друг от друга — это модуль относительной скорости: [|vec{upsilon}_text{у}|=|vec{upsilon_text{д}}-vec{upsilon_text{р}}|=sqrt{upsilon_text{д}^2+upsilon_text{р}^2}]
Подставим исходные данные: [upsilon_y=sqrt{3,5^2+12^2}=sqrt{156,25}=12,5text{ м/с}]
Ответ: 12,5

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Уровень B
1. Приведите примеры относительно каких тел покоится плот, плывущий по течению? Относительно каких тел движется?
Решение
2. Может ли человек, находясь на движущемся эскалаторе метро, быть в покое в системе отсчета, связанной с землей?
Решение
3. Почему нельзя применять паруса для управления полетом воздушного шара?
Решение
4. Туристы плывут на плоту по реке, и один из них плавает вокруг плота. Изобразите траекторию движения пловца относительно:
а) наблюдателя на плоту,
б) наблюдателя, который находится на высоком обрыве около реки.
Решение
5. Изобразите траекторию движения точки обода велосипедного колеса при прямолинейном движении велосипеда по дороге в системах отсчета, жестко связанных:
а) с велосипедистом;
б) с наблюдателем, стоящим сбоку.
Решение
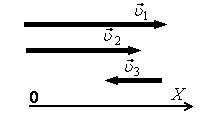
6. На рисунке 1 даны направления движения трех тел. Модули их скоростей относительно неподвижного наблюдателя соответственно равны: υ1 = 5 м/с, υ2 = 4 м/с, υ3 = 2 м/с. Применяя закон сложения скоростей, определите скорости движения тел относительно:
а) первого тела;
б) третьего тела.
Соответствует ли полученный ответ вашей интуиции?
Рис. 1
Решение
7. На рисунке 2 даны направления движения трех тел. Модули скоростей первого и второго тела относительно неподвижного наблюдателя соответственно равны: υ1 = 5 м/с, υ2 = 4 м/с. Скорость третьего тела относительно второго по модулю равна υ3 = 3 м/с. Определите скорость третьего тела относительно:
а) неподвижного наблюдателя;
б) первого тела.
Рис. 2
Решение
8. Скорость пловца относительно воды 1,2 м/с. Скорость течения 0,8 м/с. Определите скорость пловца относительно берега, если пловец плывет по течению реки.
Решение
9. Скорость велосипедиста 36 км/ч, а скорость встречного ветра 4 м/с. Какова скорость ветра в системе отсчета, связанной с велосипедистом?
Решение
10. Определите скорость ветра, если двигатель самолета сообщает ему в безветренную погоду скорость равную 900 км/ч, а при встречном ветре 850 км/ч.
Решение
11. По дороге движутся автомобиль со скоростью 15 м/с и велосипедист со скоростью 5 м/с. Определите скорость их сближения, если:
а) автомобиль догоняет велосипедиста;
б) они движутся навстречу друг другу.
Решение
12. Эскалатор метро движется со скоростью 0,75 м/с. Найдите время, за которое пассажир переместится на 20 м относительно земли, если он сам идет в направлении движения эскалатора со скоростью 0,25 м/с в системе отсчета, связанной с эскалатором.
Решение
13. Два автомобиля движутся навстречу друг другу с равными скоростями по 80 км/ч каждая. За какое время расстояние между ними уменьшится на 10 км?
Решение
14. По двум параллельным железнодорожным линиям равномерно движутся два поезда: грузовой длиной 630 м со скоростью 48 км/ч и пассажирский длиной 120 м со скоростью 102 км/ч. В течение какого времени пассажирский поезд проходит мимо машиниста грузового, если поезда движутся:
а) в одном направлении;
б) навстречу друг другу?
Решение
15. Пассажир, сидящий у окна поезда, идущего со скоростью 72 км/ч, видит в течение 10 с встречный поезд. Длина встречного поезда 290 м. Определите его скорость.
Решение
16. Скорость течения 3 м/с, а рыбак может грести со скоростью 5 м/с при неподвижной воде. Определите время, необходимое рыбаку, чтобы спуститься на 40 м вниз по течению и на столько же подняться вверх.
Решение
Уровень C
1. Скорость движения теплохода относительно берега вниз по реке 20 км/ч, а вверх – 18 км/ч. Определите скорость течения относительно берега и скорость теплохода относительно воды.
Решение
2. Автоколонна длиной 1,2 км движется со скоростью 36 км/ч. Мотоциклист выезжает из головы колонны, доезжает до ее хвоста и возвращается обратно. Определите время, за которое мотоциклист преодолеет данное расстояние, если его скорость равна 72 км/ч.
Решение
3. Пловец, двигаясь относительно воды перпендикулярно течению со скоростью 5 км/ч, переплывает реку шириной 120 м. Скорость течения 3,24 км/ч. Определите:
а) скорость пловца относительно берега;
б) время, которое требуется пловцу, чтобы переплыть реку;
в) перемещение пловца относительно берега;
г) под каким углом к берегу плывет пловец?
Решение
4. Вертолет летел в безветренную погоду на север со скоростью 20 м/с. С какой скоростью и под каким углом к первоначальному направлению будет лететь вертолет, если подует западный ветер со скоростью 10 м/с?
Решение
5. На катере необходимо переплыть реку перпендикулярно берега. Какую скорость должен сообщить мотор катеру, чтобы при скорости течения реки, равной 1,2 м/с, катер двигался относительно берега со скоростью 3,2 м/с?
Решение
6. Пловец желает переплыть реку перпендикулярно берега. Под каким углом к течению он должен плыть, если скорость пловца относительно воды 1 м/с, скорость течения 0,8 м/с?
Решение
7. Скорость течения реки 4 км/ч, ширина ее 240 м. С какой скоростью относительно берега должен плыть пловец, чтобы переплыть реку за 15 мин, если его скорость относительно воды перпендикулярна берегу?
Решение
8. По двум взаимно перпендикулярным дорогам движутся равномерно грузовая и легковая машины со скоростями 36 км/ч и 72 км/ч соответственно. На каком расстоянии окажутся друг от друга машины через 10 мин после встречи у перекрестка?
Решение
9. В безветренную погоду вертолет двигался со скоростью 90 км/ч точно на север. Найдите скорость вертолета, если подул северо-западный ветер под углом 45° к направлению движения. Скорость ветра 10 м/с.
Решение
10. Наблюдатель на берегу определил значение скорости пловца, переплывающего реку, 2,0 м/с. Скорость была направлена под углом 60° к линии берега. Какова скорость пловца относительно воды, если скорость течения реки 1,0 м/с?
Решение
11. По двум пересекающимся под углом 60° дорогам движутся два автомобиля с одинаковыми скоростями, равными 72 км/ч. Через какое время после встречи у перекрестка расстояние между ними станет равным 3 км?
Решение
Как понимать относительность движения? Еще Галилей задумался над этим вопросом в 16 веке и дал на него ответ. Кстати, если вам нужно вспомнить основные понятия из кинематики, то вот отдельный материал на эту тему.
Больше ответов и актуальных студенческих вопросов – на нашем телеграм-канале.
Относительность движения: объяснение, примеры
Конечно, Галилей был не первым, кто размышлял на эту тему. Вот, что думал об относительности движения другой великий ум эпохи Возрождения – Джордано Бруно:
Как это заметили древние и современные истинные наблюдатели природы, и как это показывает тысячью способами чувственный опыт, мы можем заметить движение только посредством известного сравнения и сопоставления с каким-либо неподвижным телом. Так, люди, находящиеся в середине моря на плывущем корабле, если они не знают, что вода течёт, и не видят берегов, не заметят движения корабля. Ввиду этого можно сомневаться относительно покоя и неподвижности Земли. Я могу считать, что если бы я находился на Солнце, Луне или на других звёздах, то мне всегда казалось бы, что я нахожусь в центре неподвижного мира, вокруг которого вращается всё окружающее, вокруг которого вращается этот окружающий меня мир, в центре которого я нахожусь.
Суть относительности движения: в зависимости от выбора системы и тела отсчета, одно и то же движение может иметь разный характер и описываться по-разному.
Геоцентрическая и гелиоцентрическая системы отсчета за тело отсчета принимают соответственно землю и солнце.
Вот пример относительности механического движения. Представим, что автобус движется по дороге. По отношению к пешеходу, который стоит на остановке, его скорость равна, скажем, 60 км/ч. А относительно водителя, который едет по встречной полосе со скоростью 100 км/ч, автобус движется иначе. Говоря точнее, автобус приближается к водителю встречной машины со скоростью 160 км/ч.
При этом действует принцип относительности Галилея:
Если в двух замкнутых лабораториях, одна из которых равномерно прямолинейно (и поступательно) движется относительно другой, провести одинаковый механический эксперимент, результат будет одинаковым.
Принцип относительности по Галилею является частным случаем принципа относительности Эйнштейна.
В нашем справочнике вы более полную теорию по теме «Относительность движения». Но не будем углубляться в теорию, ведь наша сегодняшняя цель – это разбор практических задач.
Кстати! Для всех наших читателей действует скидка 10% на любой вид работы.
Задачи на относительность движения
Задача 1
Летящий звездолет посылает вперед радиосигналы длительностью t1. Внезапно он начинает принимать сигналы отраженные от находящегося впереди препятствия, длительность которых t2. С какой скоростью приближается звездолет к препятствию, если скорость распространения радиосигналов равна c?
Решение
Скорость распространения радиосигналов относительно звездолета до отражения:
Скорость распространения радиосигналов относительно звездолета после отражения:
До того, как достигнуть препятствия, сигнал пролетел путь:
путь после отражения:
Приравняем s1 и s2 и получим:
Ответ: v = c(t1 – t2)/(t1 + t2).
Задача 2
Катер проходит расстояние между двумя пунктами на реке по течению за время t1=3 часа, а против течения за t2=6 часов. Средняя скорость катера при движении туда и сразу обратно равна 10 км/ч. Найти собственную скорость катера и скорость течения реки.
Решение
По определению, средняя скорость v при равномерном прямолинейном движении равна отношению всего пройденного пути ко всему затраченному времени.
Из этого найдем расстояние между двумя пунктами:
Это же расстояние можно рассчитать по формулам:
Здесь v – скорость катера, u – скорость течения. Приравняем выражения:
Полученное выражение для скорости катера подставим в формулу для пути:
Отсюда:
Осталось подставить данные задачи и вычислить скорость течения:
Тогда скорость катера:
Ответ: 3,75 км/ч, 11,25 км/ч.
Задача 3
По дороге едет колонна автомобилей со скоростью 20 км/ч. Из середины колонны одновременно отправляются два мотоциклиста: один в голову колонны, другой в хвост. Первый мотоциклист приехал к месту на 6 минут раньше второго Какова длина колонны, если скорость мотоциклистов одинакова и равна 30 км/ч?
Решение
Расстояние, которое изначально нужно пройти мотоциклистам:
Скорость, с которой первый мотоциклист приближается к голове колоны:
Скорость с которой второй мотоциклист приближается к хвосту колоны
По условию:
или
Отсюда находим время движения:
Тогда длина колонны:
Ответ: 2,5 км.
Нужна помощь в решении задач? Профессиональный студенческий сервис всегда к вашим услугам.
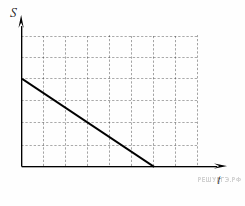
Задание 1 № 101. Может ли график зависимости пути от времени иметь следующий вид?
1) да
2) нет
3) может, если траектория прямолинейная
4) может, если тело возвращается в исходную точку
Решение.
Путь — это физическая величина, показывающая пройденное телом расстояние. Иначе говоря, это длина пройденного участка траектории. По определению, путь есть величина положительная, которая может только возрастать со временем, так что представленный график не может изображать зависимость пути от времени.
Правильный ответ: 2.
Задание 1 № 125. Вертолет поднимается вертикально вверх. Какова траектория движения точки на конце лопасти винта вертолета в системе отсчета, связанной с винтом?
1) точка
2) прямая
3) окружность
4) винтовая линия
Решение.
В системе отсчета, связанной с винтом, точка на конце лопасти не двигается. Следовательно, ее траектория в данной системе отсчета представляет собой точку.
Правильный ответ: 1.
Задание 1 № 126. Два автомобиля движутся по прямому шоссе: первый — со скоростью ν, второй — со скоростью -3 ν. Какова скорость второго автомобиля относительно первого?
|
1) |
2) |
3) |
4) |
Решение.
Скорость второго автомобиля относительно первого равна ν2 — ν 1=-3 ν- ν= -4ν
Правильный ответ: 2.
Задание 1 № 131. Лодка должна попасть на противоположный берег реки по кратчайшему пути в системе отсчета, связанной с берегом. Скорость течения реки u, а скорость лодки относительно воды ν . Чему должен быть равен модуль скорости лодки относительно берега?
1)
2)
3)
4)
Решение.
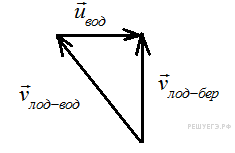
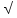
2 способ:
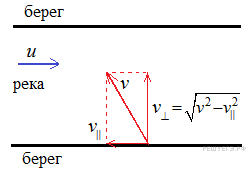
Правильный ответ: 4.
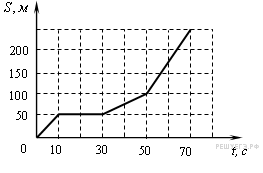
Задание 1 № 133. На рисунке представлен график зависимости пути S велосипедиста от времени t.
Определите интервал времени после начала отсчета времени, когда велосипедист двигался со скоростью 5 м/с.
1) от 50 с до 70 с
2) от 30 с до 50 с
3) от 10 с до 30 с
4) от 0 до 10 с
Решение.
Для того чтобы по графику зависимости пути от времени найти скорость движения тела в некоторый момент, необходимо вычислить тангенс угла наклона графика в соответствующей точке. Из графика видно, что в интервале от 0 до 10 с скорость велосипедиста была постоянна и равнялась
.
На других интервалах скорость была иная.
Правильный ответ: 4.
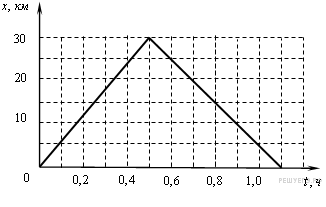
Задание 1 № 134. На рисунке представлен график движения автобуса из пункта A в пункт Б и обратно.
Пункт A находится в точке х=0, а пункт Б — в точке х=30 км. Чему равна максимальная скорость автобуса на всем пути следования туда и обратно? (Ответ дайте в километрах в час.)
Решение.
Для того чтобы по графику зависимости координаты от времени найти скорость движения тела в некоторый момент, необходимо вычислить тангенс угла наклона графика в соответствующей точке. Максимальной скорости соответствует максимальный угол наклона. Из приведенного графика видно, что с максимальной скоростью автобус движется из пункта A в пункт Б, скорость его при этом равна: 30-0/0,5=60 км/ч.
Задание 1 № 138. На рисунке приведен график зависимости проекции скорости тела от времени.
Чему равно ускорение тела в интервале времени от 30 до 40 с? (Ответ дайте в метрах в секунду в квадрате.)
Решение.
Из графика видно, что в интервале времени от 30 до 40 с проекция скорости тела не изменялась, а значит, проекция ускорения была равна нулю.
Задание 1 № 317. Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с. (Ответ дайте в метрах в секунду.)
Решение.
Вектор скорости пловца относительно берега есть сумма векторов скорости пловца относительно воды и скорости течения реки:. Поскольку пловец плывет по течению реки, получаем, что для величин скоростей выполняется соотношение: 0,4 + 0,3 =0,7 м/с.
Задание 1 № 3354. Четыре тела двигались по оси Ох. В таблице представлена зависимость их координат от времени.
|
t, с |
0 |
1 |
2 |
3 |
4 |
5 |
|
x1, м. |
0 |
2 |
4 |
6 |
8 |
10 |
|
x2, м |
0 |
0 |
0 |
0 |
0 |
0 |
|
x3, м |
0 |
1 |
4 |
9 |
16 |
25 |
|
x4, м |
0 |
2 |
0 |
-2 |
0 |
2 |
У какого из тел скорость могла быть постоянна и отлична от нуля?
Решение.
Таблица содержит информацию о положениях тел только в отдельные моменты времени. В промежутках между указанными временами тела могли двигаться абсолютно произвольно. Определим тело, скорость которого могла бы быть постоянной и отличной от нуля. При движении с постоянной скоростью координата тела за равные промежутки времени изменяется одинаково. Из таблицы видно, что этому свойству удовлетворяет только первое тело. Значит, скорость первого тела могла быть постоянной и не равной нулю.
Задание 1 № 3357. Вертолет равномерно поднимается вертикально вверх. Какова траектория крайней точки лопасти вертолета в системе отсчета, связанной с корпусом вертолета?
1) прямая линия
2) винтовая линия
3) окружность
4) эллипс
Решение.
Крайняя точка лопасти вертолета двигается по окружности вокруг оси вращения винта. Поскольку ось вращения жестко связана с корпусом вертолета, такую же траекторию описывает эта точка и относительно любой точки корпуса. Правильный ответ 3.
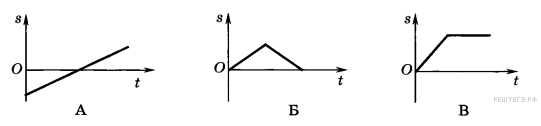
Задание 1 № 3539. На каком из графиков изображена возможная зависимость пройденного пути от времени?
1) А
2) Б
3) В
4) Такой график отсутствует
Решение.
Путь — это физическая величина, показывающая пройденное телом расстояние. Иначе говоря, это длина пройденного участка траектории. По определению, путь есть величина положительная, которая может только возрастать со временем. Этому требованию удовлетворяет только график В.
Правильный ответ: 3.
Задание 1 № 3540. Велосипедист, двигаясь под уклон, проехал расстояние между двумя пунктами со скоростью, равной 15 км/ч. Обратно он ехал вдвое медленнее. Какова средняя путевая скорость на всем пути? (Ответ дайте в километрах в час.)
Решение.
Необходимо различать два понятия: среднюю путевую скорость и среднюю скорость по перемещению. Средняя путевая скорость определяется как скорость прохождения пути: . То есть, буквально, надо весь пройденный телом путь разделить на все время, затраченное им на этот путь. Средняя путевая скорость представляет собой число, скаляр.
Разберемся теперь со второй средней скоростью. Средняя скорость по перемещению — это вектор, равный отношению перемещения ко времени, за которое оно совершено: . В нашей конкретной задаче, поскольку велосипедист вернулся в исходную точку, его перемещение равно нулю, а значит, его средняя скорость по перемещению тоже равна нулю.
Вычислим теперь среднюю путевую скорость. Обозначим расстояние между двумя пунктами через ? тогда весь путь пройденный велосипедистом равен . На первую половину пути велосипедист затратил время . На обратную дорогу — время . Все время пути составило . Окончательно, находим, что средняя путевая скорость велосипедиста равна
.
Задание 1 № 3541. Тело движется прямолинейно вдоль оси x. На графике представлена зависимость координаты тела от времени. В какой момент времени модуль перемещения относительно исходной точки имел максимальное значение? (Ответ дайте в секундах.)
Решение.
Из графика видно, что начальная координата тела равна . Модуль перемещения тела относительно исходной точки в любой момент определяется выражением: . Построим график этой функции и определим ее максимум. Из построенного графика ясно, что модуль перемещения относительно исходной точки максимален при и равен 20 м.
Ответ: 6 с
Задание 1 № 3544. Движение двух велосипедистов заданы уравнениями x1 =2 t и x2 =100- 8 t . Найдите координату x места встречи велосипедистов. Велосипедисты двигаются вдоль одной прямой. (Ответ дайте в метрах.)
Решение.
Встреча двух велосипедистов означает, что у них в некоторый момент времени совпадут координаты. Определим, когда именно произойдет встреча, для этого решим уравнение . Теперь не составляет труда определить координату места встречи:
Задание 1 № 3545.
На рисунке приведен график движения x(t) электрокара. Определите по этому графику путь, проделанный электрокаром за интервал времени от t1 = 1 c до t2 = 4 c. (Ответ дайте в метрах.)
Решение.
Путь — это физическая величина, показывающая пройденное телом расстояние. Иначе говоря, это длина пройденного участка траектории. Из графика видно, что в интервале времени от до электрокар двигался в положительном направлении оси . При этом его координата изменилась на . Последнюю, четвертую, секунду электрокар двигался в обратном направлении, изменение его координаты на этом участке равно . Таким образом, путь, пройденный машинкой за интервал времени от до равен .
Задание 1 № 3548. Пешеход идет по прямолинейному участку дороги со скоростью v. Навстречу ему движется автобус со скоростью 10v. С какой скоростью должен двигаться навстречу пешеходу велосипедист, чтобы модуль его скорости относительно пешехода и автобуса был одинаков?
1)
2)
3)
4)
Решение.
Обозначим искомую скорость велосипедиста через . Тогда, как видно из рисунка, велосипедист приближается к пешеходу со скоростью , а к автобусу — со скоростью .
Приравняв эти две скорости, находим требуемую скорость велосипедиста:
Правильный ответ: 1.
Задание 1 № 3549. Пароход движется по реке против течения со скоростью 5 м/с относительно берега. Определите скорость течения реки, если скорость парохода относительно берега при движении в обратном направлении равна 8 м/с. (Ответ дайте в метрах в секунду.)
Решение.
Обозначим искомую скорость течения реки через , а скорость парохода в стоячей воде — через . Тогда можно составить следующие уравнения. Скорость парохода вниз по течению равна . Скорость парохода вверх по течению: . Решая систему из двух этих уравнений, для скорости течения воды имеем .
Задание 1 № 3734.
Материальная точка движется вдоль оси OX. На рисунке представлен график зависимости проекции скорости этой материальной точки на ось OX от времени. Какой из приведенных ниже графиков может соответствовать зависимости координаты материальной точки от времени?
1) 1
2) 2
3) 3
4) 4
Решение.
Из графика видно, что проекция скорости материальной точки на ось OX положительна и постоянна, а значит, точка движется равномерно и в положительном направлении оси OX. Единственный график, удовлетворяющий обоим этим требованиям, — это график под номером 1.
Правильный ответ: 1.
Задание 1 № 3783. На рисунке представлены графики зависимости пройденного пути от времени для двух тел. На какую величину Δv скорость второго тела v2 больше скорости первого тела v1? (Ответ дайте в метрах в секунду.)
Решение.
Из графика видно, что для обоих тел пройденный путь линейно зависит от времени, а значит, оба тела двигались с постоянными по величине скоростями. Модуль скорости первого тела равен . Скорость же второго тела: . Следовательно, скорость второго тела больше скорости первого тела на величину
Задание 1 № 3867.
Тела 1 и 2 двигаются вдоль оси x. На рисунке изображены графики зависимости координат движущихся тел 1 и 2 от времени t. Чему равен модуль скорости 1 относительно тела 2? (Ответ дайте в метрах в секунду.)
Решение.
Используя график, определим проекции скоростей обоих тел. Для тела 1 имеем
Для тела 2:
Таким образом модуль скорости одного тела относительно другого равен
Задание 1 № 4077. Автобус везёт пассажиров по прямой дороге со скоростью 10 м/с. Пассажир равномерно идёт по салону автобуса со скоростью 1 м/с относительно автобуса, двигаясь от задней двери к кабине водителя. Чему равен модуль скорости пассажира относительно дороги? (Ответ дайте в метрах в секунду.)
Решение.
Согласно закону сложения скоростей, скорость тела относительно «неподвижной системы отсчёта» связана со скоростью этого тела относительно «подвижной системы отсчёта» и скоростью движения «подвижной с. о.» относительно «неподвижной» при помощи следующего соотношения: В данном случае, так как пассажир двигается вдоль автобуса по направлению его движения, для скорости пассажира относительно дороги имеем:
Ответ: 11 м/с
Задание 1 № 4186. Координата материальной точки изменяется с течением времени по закону x=3-2t. Какой из приведённых ниже графиков соответствует этой зависимости?
1) 1
2) 2
3) 3
4) 4
Решение.
Из зависимости видно, что координата убывает со временем, при этом в начальный момент времени координата равна а в начало координат материальная точка попадает в момент времени: Таким образом, зависимости соответствует график под номером 4.
Правильный ответ: 4.
Задание 1 № 4221. Координата материальной точки изменяется с течением времени по закону . x=3+ 2t. Какой из приведённых ниже графиков соответствует этой зависимости?
1)
2)
3)
4)
Решение.
Из зависимости видно, что координата возрастает со временем, при этом в начальный момент времени координата равна , а в момент времени координата равна . Таким образом, зависимости соответствует график под номером 3.
Правильный ответ: 3.
Задание 1 № 4409. По плоскости движутся четыре точечных тела —А, Б, В, Г. x=1+t., y=2 t, и , траектории которых изображены на рисунке. Зависимости координат одного из этих тел от времени имеют вид и . Это тело обозначено буквой
1) А
2) Б
3) В
4) Г
Решение.
На зависимость координат от времени и можно смотреть как на параметрическое задание прямой на плоскости .
Выразим время из первого уравнения и подставим во второе: . Из рисунка видно, что уравнению соответствует прямая .
Правильный ответ: 3
Задание 1 № 4444. По плоскости движутся четыре точечных тела — А,Б В, и Г, траектории которых изображены на рисунке. Зависимости координат одного из этих тел от времени имеют вид x=2t.и . y=1+ t. Это тело обозначено буквой
1) А
2) Б
3) В
4) Г
Решение.
На зависимость координат от времени и можно смотреть как на параметрическое задание прямой на плоскости .
Выразим время из первого уравнения и подставим во второе: . Из рисунка видно, что уравнению соответствует прямая A.
Правильный ответ: 1
Задание 1 № 4934. Два автомобиля движутся по прямому шоссе: первый со скоростью , второй со скоростью относительно шоссе. Скорость первого автомобиля относительно второго равна
1)
2)
3)
4)
Решение.
Скорость первого автомобиля относительно второго равна
.
Правильный ответ: 2.