Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
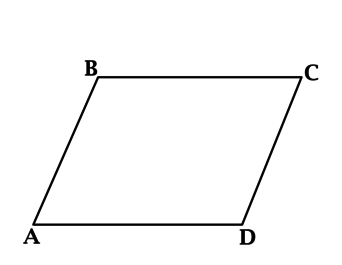
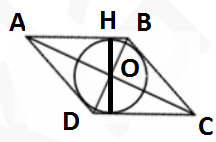
В параллелограмме ABCD AB = 3, AD = 21,
Найдите большую высоту параллелограмма.
2
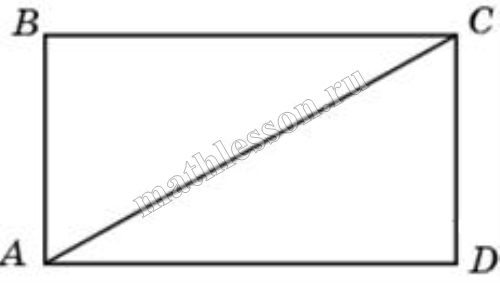
Найдите площадь квадрата, если его диагональ равна 1.
3
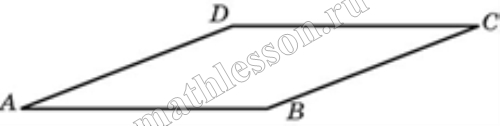
Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны.
4
Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2.
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.2 Параллелограмм, прямоугольник, ромб, квадрат, 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
5
Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника.
Пройти тестирование по этим заданиям
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Параллелограмм и его свойства
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства параллелограмма:
(blacktriangleright) Противоположные стороны попарно равны;
(blacktriangleright) Диагонали точкой пересечения делятся пополам;
(blacktriangleright) Противоположные углы попарно равны, а сумма соседних равна (180^circ).
Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:
(blacktriangleright) если противоположные стороны попарно равны;
(blacktriangleright) если две стороны равны и параллельны;
(blacktriangleright) если диагонали точкой пересечения делятся пополам;
(blacktriangleright) если противоположные углы попарно равны.
Площадь параллелограмма
Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.
Задание
1
#1783
Уровень задания: Легче ЕГЭ
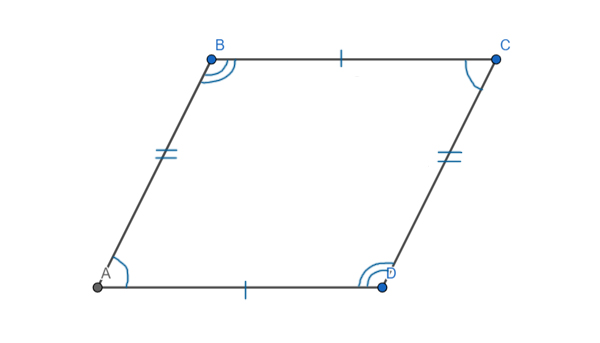
Периметр параллелограмма равен (100), его большая сторона равна (32). Найдите меньшую сторону параллелограмма.
Так как у параллелограмма противоположные стороны равны, то его периметр равен удвоенной сумме его непараллельных сторон, тогда сумма большей и меньшей сторон равна (100 : 2 = 50), значит, меньшая сторона параллелограмма равна (50 — 32 = 18).
Ответ: 18
Задание
2
#1784
Уровень задания: Равен ЕГЭ
Периметр параллелограмма равен (15). При этом одна сторона этого параллелограмма на (5) больше другой. Найдите меньшую сторону параллелограмма.
У параллелограмма противоположные стороны равны. Пусть (BC = AB +
5), тогда периметр параллелограмма (ABCD) равен (AB + BC + CD + AD =
AB + AB + 5 + AB + AB + 5 = 4cdot AB + 10 = 15), откуда находим (AB
= 1,25). Тогда меньшая сторона параллелограмма равна (1,25).
Ответ: 1,25
Задание
3
#273
Уровень задания: Равен ЕГЭ
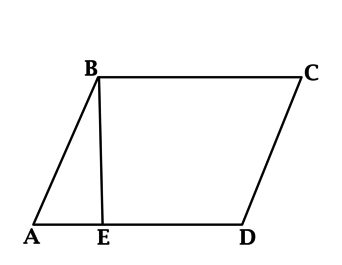
В параллелограмме (ABCD): (BE) – высота, (BE = ED = 5). Площадь параллелограмма (ABCD) равна 35. Найдите длину (AE).
Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию, тогда (35 = BE cdot AD = 5cdot(5 + AE)), откуда находим (AE = 2).
Ответ: 2
Задание
4
#1785
Уровень задания: Равен ЕГЭ
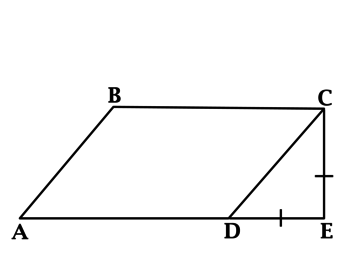
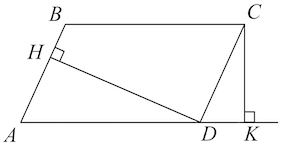
Из точки (C) параллелограмма (ABCD) опустили перпендикуляр на продолжение стороны (AD) за точку (D). Этот перпендикуляр пересёк прямую (AD) в точке (E), причём (CE = DE). Найдите (angle B) параллелограмма (ABCD). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle EDC = angle DCE). Так как (angle DEC = 90^{circ}), а сумма углов треугольника равна (180^{circ}), то (angle EDC =
45^{circ}), тогда (angle ADC = 180^{circ} — 45^{circ} =
135^{circ}). Так как в параллелограмме противоположные углы равны, то (angle B = angle ADC = 135^{circ}).
Ответ: 135
Задание
5
#1686
Уровень задания: Равен ЕГЭ
Диагональ (BD) параллелограмма (ABCD) перпендикулярна стороне (DC) и равна (4). Найдите площадь параллелограмма (ABCD), если (AD=5).
По теореме Пифагора находим: (AB^2=AD^2 — BD^2 = 25 — 16 = 9) (Rightarrow) (AB = 3). (S_{ABCD} = 4cdot3 = 12).
Ответ: 12
Задание
6
#1685
Уровень задания: Равен ЕГЭ
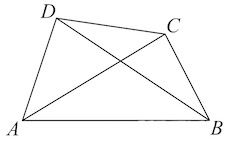
В параллелограмме (ABCD): (P_{triangle AOB} = 
(P_{triangle AOB} = AO + OB + AB), (P_{triangle AOD} = AO + OD + AD), (BO = OD) (Rightarrow) (P_{triangle AOD} — P_{triangle AOB} = AD — AB = 1), но (AD + AB = 7) (Rightarrow) (AD = 4), (AB = 3) (Rightarrow) (ADcdot AB = 12).
Ответ: 12
Задание
7
#3617
Уровень задания: Равен ЕГЭ
Стороны параллелограмма равны (9) и (15). Высота, опущенная на первую сторону, равна (10). Найдите высоту, опущенную на вторую сторону параллелограмма.
Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена. Следовательно, с одной стороны, площадь (S=9cdot 10), с другой стороны, (S=15cdot h), где (h) – высота, которую нужно найти.
Следовательно, [9cdot 10=15cdot hquadLeftrightarrowquad h=6]
Ответ: 6
Задачи из раздела «Геометрия на плоскости» являются обязательной частью аттестационного экзамена у выпускников средней школы. Теме «Параллелограмм и его свойства» в ЕГЭ традиционно отводится сразу несколько заданий. Они могут требовать от школьника как краткого, так и развернутого ответа с построением чертежа. Поэтому если одним из ваших слабых мест являются именно задачи на вычисление площадей параллелограмма или его сторон и углов, то вам непременно стоит повторить или вновь разобраться в материале.
Сделать это легко и эффективно вам поможет образовательный портал «Школково». Наши опытные специалисты подготовили необходимый теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко решить задачи ЕГЭ на вычисление площадей, сторон, углов или свойства биссектрисы параллелограмма. Найти базовую информацию вы можете в разделе «Теоретическая справка».
Чтобы успешно решить задачи ЕГЭ по теме «Параллелограмм и его свойства», предлагаем попрактиковаться в выполнении соответствующих упражнений. Большая подборка заданий представлена в блоке «Каталог». Специалисты портала «Школково» регулярно дополняют и обновляют данный раздел.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
24
Июл 2013
Категория: 01 Геометрия
01. Параллелограмм
2013-07-24
2022-09-11
Задача 1. Сумма двух углов параллелограмма равна . Найдите один из оставшихся углов. Ответ дайте в градусах.
Решение: + показать
Задача 2. Один угол параллелограмма больше другого на . Найдите больший угол. Ответ дайте в градусах.
Решение: + показать
Задача 3. Найдите больший угол параллелограмма, если два его угла относятся как Ответ дайте в градусах.
Решение: + показать
Задача 4. Диагональ параллелограмма образует с двумя его сторонами углы и
Найдите больший угол параллелограмма. Ответ дайте в градусах.
Решение: + показать
Задача 5. Периметр параллелограмма равен Меньшая сторона равна
Найдите большую сторону параллелограмма.
Решение: + показать
Задача 6. Две стороны параллелограмма относятся как а периметр его равен
Найдите большую сторону параллелограмма.
Решение: + показать
Задача 7. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна Найдите его большую сторону.
Решение: + показать
Задача 8. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.

Задача 9. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен
Решение: + показать
Задача 10. В параллелограмме высота, опущенная на сторону
из точки
равна
. Найдите синус угла
.
Решение: + показать
Задача 11. В параллелограмме
Найдите высоту, опущенную на сторону
Решение: + показать
Задача 12. В параллелограмме
Найдите большую высоту параллелограмма.
Решение: + показать
Задача 13. Площадь параллелограмма равна две его стороны равны
и
Найдите большую высоту этого параллелограмма.
Решение: + показать
Задача 14. В параллелограмме
. Найдите
.
Решение: + показать
Задача 15. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
Решение: + показать
Задача 16. Площадь параллелограмма равна
Точка
— середина стороны
. Найдите площадь трапеции
.
Решение: + показать
Задача 17. Площадь параллелограмма равна
Найдите площадь параллелограмма
вершинами которого являются середины сторон данного параллелограмма.
Решение: + показать
Задача 18. Найдите диагональ параллелограмма
, если стороны квадратных клеток равны 1.
Решение: + показать
Задача 19. Диагонали четырехугольника равны и
Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Решение: + показать
Вы можете пройти тест по теме «Параллелограмм. Вычисление углов и длин».
Автор: egeMax |
комментария 2
Привет! Сегодня повторим геометрическую фигуру параллелограмм и порешаем задачи на эту тему.
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.
Свойства параллелограмма:
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
3. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его четырёх сторон.
Признаки параллелограмма:
1. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник — параллелограмм.
2. Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник — параллелограмм.
3. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм
Площадь параллелограмма
Площадь параллелограмма равна произведению его основания на высоту.
S = h∙a
C другой стороны, каждая диагональ параллелограмма делит его на два равных треугольника. Применив формулу для площади треугольника через синус угла, получим, что площадь параллелограмма можно вычислить следующим образом:
S = a∙b∙sinα
a и b — стороны, α — величина угола между ними
Так же, разделив двумя диагоналями параллелограмм на 4 треугольника, и использовав вышеуказанную формулу для площади треугольника через синус угла, получается, площадь параллелограмма через диагонали можно представить в виде формулы:
S = ½∙d1∙d2∙sinφ
d1 и d2 — диагонали, φ — величина угла между ними
Эта формула справедлива для любого выпуклого четырёхугольника.
Задачи на параллелограмм.
Задача (Накрест лежащие углы)
Биссектриса тупого угла ∠ABC параллелограмма ABCD делит противоположную сторону AD в соотношении 1:3, считая от вершины острого угла. Бо́льшая сторона AD равна 12. Найдите периметр параллелограмма.
Решение:
Найдём отрезок AE. Всего отрезок AD содержит 4 части (1+3), а AE — это одна часть. Тогда получается AE = AD/4 = 12/4 = 3.
Углы ∠EBC и ∠BEA равны, т.к. эти углы накрест лежащие при параллельных прямых AD и BC и секущей BE.
Т.к. ∠EBC=∠BEA=∠ABE (Ведь BE — биссектриса), следовательно, треугольник ABE — равнобедренный (два угла равны ∠BEA = ∠ABE). Значит, боковые стороны равны AB=AE=3.
Теперь можно найти и периметр. По 1 свойству параллелограмма AB=DC=3, а так же AD=BC=12.
P=(12+3)*2 = 30
Ответ: 30
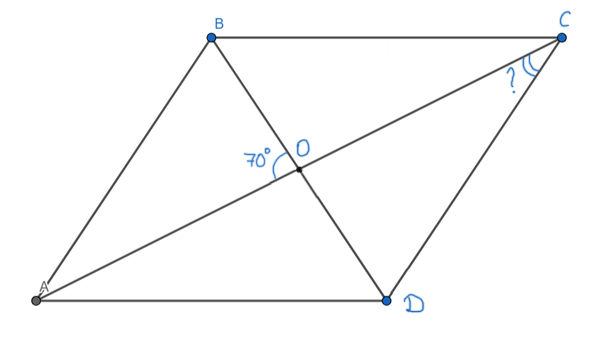
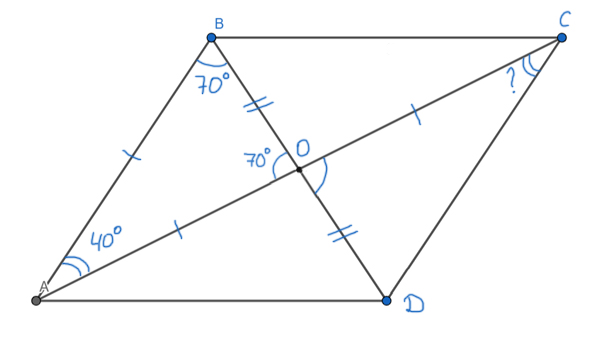
Задача (Свойство диагоналей)
В параллелограмме ABCD диагональ AC вдвое больше, чем сторона AB. Диагонали пересекаются в точке O. Угол ∠AOB=70°. Найдите угол ∠ACD. Ответ запишите в градусах.
Решение:
Воспользуемся свойством параллелограмма. Оно говорит, что диагонали параллелограмма в точке пересечения делятся пополам. Получается AO=OC=AB, т.к. AB — так же половина диагонали AC.
Получается треугольник ABO — равнобедренный. Тогда углы при основании раны ∠AOB= ∠ABO=70°. Т.к сумма углов в треугольнике ABO равна 180°, то ∠BAO = 180° — 70° — 70° = 40°.
Угол ∠BAO = ∠ОСВ (эти углы накрест лежащие при параллельных прямых AB и DC и секущей AC).
Значит, ∠BAO = ∠ОСВ = 40°.
Ответ: 40
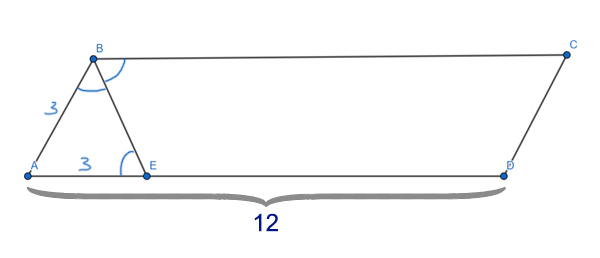
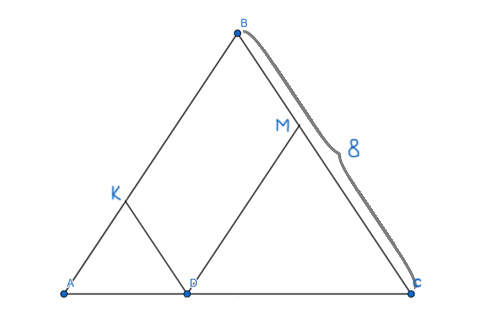
Задача (Используем параллельные прямые)
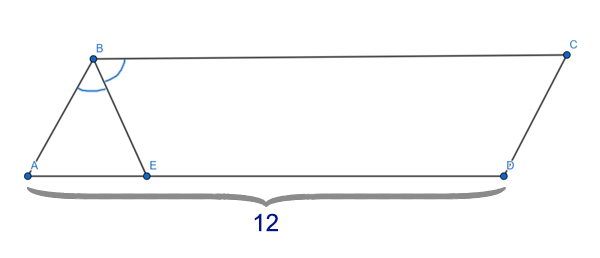
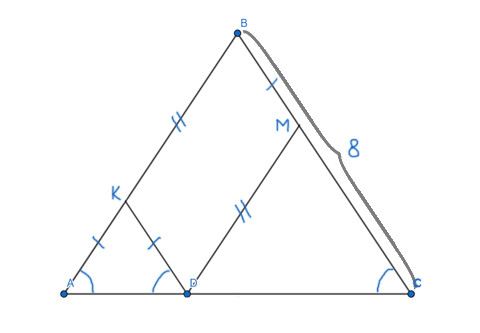
Боковая сторона равнобедренного треугольника равна 8. Из произвольной точки, на основании треугольника, проведены две прямы, параллельные боковым сторонам. Найдите периметр образовавшегося параллелограмма.
Решение:
Углы ∠KDA и ∠BCA являются соответственными при параллельных прямых KD и BC и секущей AC. Значит, они равны ∠KDA=∠BCA.
Получается, что треугольник AKD — равнобедренный. Ведь, ∠BAC=∠BCA (Т.к. это углы при основании в равнобедренном треугольнике ABC) ⇒ ∠BAC = ∠KDA, а если в треугольнике два угла равны, то такой треугольник — равнобедренный.
Чтобы найти периметр параллелограмма, достаточно найти сумму двух его пересекающихся сторон, и затем эту сумму нужно умножить на 2. Сумма двух пересекающихся сторон параллелограмма DKBM как раз равна боковой стороне треугольника ABC. Т.е. KD + KB = AB (АК=КD т.к. треугольник AKD равнобедренный).
PDKBM = 2*(KD + KB) = 2 * AB = 2 * 8 = 16
Ответ: 16
Задача (Два параллелограмма)
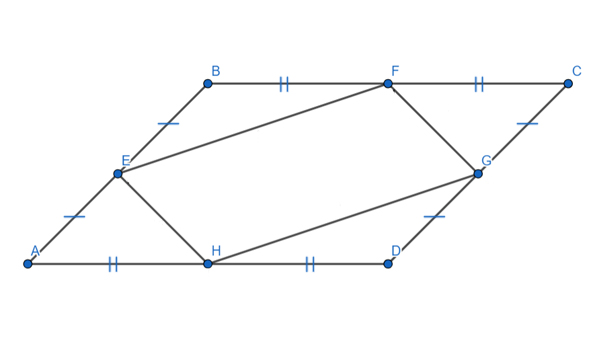
Площадь параллелограмма ABCD равна 77. Найдите площадь параллелограмма EFGH, вершинами которого являются середины сторон данного параллелограмма.
Решение:
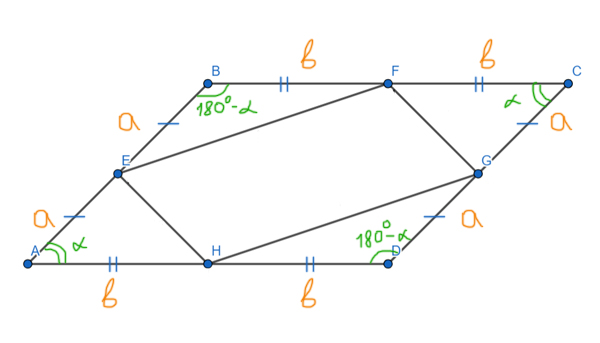
Обозначим AE=EB=CG=GD=a, BF=FC=AH=HD=b, ∠BAD=∠BCD=α, ∠ABC=∠ADC=180°-α.
Рассмотрим площади четырёх треугольников, которые получились внутри параллелограмма ABCD равны. Используем формулу для площади треугольника через синус угла.
SAEH = ½∙a∙b∙sinα
SEBF = ½∙a∙b∙sin(180°-α)
SFCG = ½∙a∙b∙sinα
SHGD = ½∙a∙b∙sin(180°-α)
Т.к. по формуле приведения sinα = sin(180°-α), то площади всех четырёх треугольников равны.
Площадь параллелограмма ABCD через синус угла α можно представить:
SABCD = AB∙AD∙sinα = 2a∙2b∙sinα = 4∙a∙b∙sinα
Тогда
SABCD — SAEH — SEBF — SFCG — SHGD =
4∙a∙b∙sinα — 4 ∙ (½∙a∙b∙sinα) = 2∙a∙b∙sinα
Получается, что если из площади параллелограмма ABCD вычесть площади четырех получившихся треугольников, то останется ровно половина от изначальной площади. Это и есть площадь параллелограмма EFGH.
SEFGH = ½ ∙ SABCD = ½ ∙ 77 = 38,5
Ответ: 38,5
Задача (Диагонали параллелограмма)
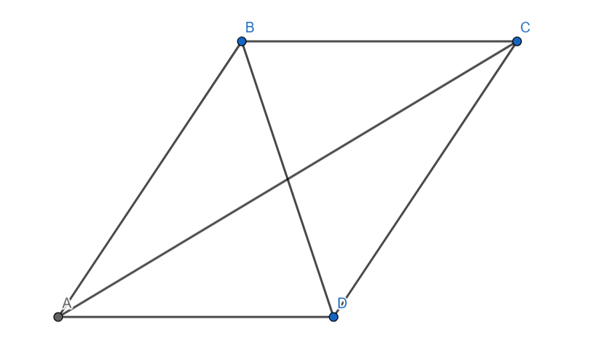
Диагонали параллелограмма равны 12 и 14. Найдите стороны параллелограмма, если их разность равна 4. В ответе запишите сумму двух его разных сторон.
Решение:
Здесь удобно воспользоваться 3 свойством, которое было описано в начале статьи.
Пусть AB=x, а BC=y.
Тогда по 3 свойству:
122 + 142 = x2 + x2 + y2 + y2
А с другой стороны, по условию
x — y = 4
x = 4 + y
Подставляем x в первое уравнение.
340 = 2∙(4+y)2 + 2∙y2
340 = 2∙(16 + 8∙y + y2) + 2∙y2
170 = 16 + 8∙y + y2 + y2
2∙y2 + 8∙y — 154 = 0
Получили квадратное уравнение.
y2 + 4∙y — 77 = 0
D = 16 + 4∙77 = 324
√D = 18
y1 = (-4 + 18)/2 = 7
y2 = (-4 — 18)/2 = -11
Отрицательное число не подходит.
x = 7 + 4 = 11.
Ответ: 18
Слайд 1
Четырехугольники 8 класс геометрия Параллелограмм . Решение задач 1 www.konspekturoka.ru Закрепить знания о свойствах и признаках параллелограмма в процессе решения задач
Слайд 2
www.konspekturoka.ru 2 Дано: Найти: 1 А В С D АВС D – параллелограмм, ∠ CAD = 16° , ∠ DCA= 37° , 16° 37° ∠ A — ? , ∠ B — ?, ∠ C — ?, ∠ D — ? Задача Решение Рассмотрим треугольник ∆ ACD : ∠ CAD +∠ DCA + ∠С D А = 180 ° ∠ 16° + ∠ 37 ° + ∠С D А = 180 ° ∠С D А = 180 ° — ( ∠ 16° + ∠ 37 ° ) ∠ B = ∠ D = 180 ° — 53° = 127° 127° 127° По свойству параллелограмма: ∠ A + ∠ B = 180 °, ∠ A + ∠127 ° = 180 ° ∠ A = 180 ° — ∠127 ° = 53°, ∠ A = 53°, ∠ A = ∠ C = 53°. Ответ: ∠ A = 53° , ∠ B = 127° , ∠ C = 53° , ∠ D = 127°.
Слайд 3
www.konspekturoka.ru 3 Дано: Найти: 2 А В С D Р АВС D = 48 см, AD на 3см больше АВ ; A B — ?, В C — ?, CD — ? AD -? Задача Ответ: Решение х х х + 3 х + 3 Если АВ = х (см), то AD = x + 3 (см). Р АВС D = 2(AD + AB) Р АВС D = 2(x + (x + 3)) 48 = 2x + 2x + 6 4x = 48 — 6 4x = 42 x = 42 : 4 x = 10,5 Если АВ = 10,5 см, то AD = x + 3 = 10,5 + 3 = 13,5 (см). АВ = CD = 10,5 см, AD = BC = 13,5 (см). АВ = CD = 10,5 см, AD = BC = 13,5 (см).
Слайд 4
03.12.2012 www.konspekturoka.ru 4 Дано: Найти: 3 А В С D Р АВС D = 48 см, AD — AB = 7 ( см); A B — ?, В C — ?, CD — ? AD -? Задача Ответ: Решение х х х + 7 х + 7 Если АВ = х (см), то AD = x + 7 (см). Р АВС D = 2(AD + AB) Р АВС D = 2(x + (x + 7)) 48 = 2x + 2x + 14 4x = 48 — 14 4x = 34 x = 34 : 4 x = 8 ,5 Если АВ = 8 ,5 см, то AD = x + 7 = 8 ,5 + 7 = 1 5 ,5 (см). АВ = CD = 8 ,5 см, AD = BC = 1 5 ,5 (см). АВ = CD = 8 ,5 см, AD = BC = 1 5 ,5 (см).
Слайд 5
www.konspekturoka.ru 5 Дано: Доказать: 4 АВС D – четырехугольник, B А ∥ CD, ∠A = ∠C АВС D – параллелограмм. Доказательство А В С D Задача 1 2 3 4 B А ∥ CD – по условию, следовательно ∠1 = ∠ 2 (накрест лежащие) Рассмотрим треугольники ∆ А BD и ∆ BCD : Так как сумма углов треугольника 180 °, то ∠3 = ∠ 4 ∆ А BC = ∆ ACD – по стороне и двум прилежащим углам (В D – общая, ∠1 = ∠ 2 , ∠ 3 = ∠ 4) . Поэтому B А = CD Если B А ∥ CD и B А = CD , то по 1 признаку параллелограмма четырехугольник АВС D – параллелограмм, ч. т. д.
Слайд 6
www.konspekturoka.ru 6 Дано: Найти: 5 Задача АВС D – параллелограмм, Р АВС D = 50 см, ∠С = 30°, BH ⊥AD, BH = 6,5 см A B — ?, В C — ? Решение Н ∟ По свойству параллелограмма ∠С = ∠А = 30 °. ∆АВН – прямоугольный, ∠Н = 90° ∠А = 30 °, следовательно: т. е АВ = 2· ВН = 2 · 6,5 = 13 (см) Р АВС D = 2(AD + AB) 50 = 2(13 + AD) 25 = 13 + AD AD = 25 – 13 AD = 12 Ответ: A B = 13 см, В C = 12 см. AD = ВС = 12 см А В С D
Слайд 7
www.konspekturoka.ru 7 Задача 6 Дано: Найти: А В С D АВС D – параллелограмм, АК – биссектриса ∠А ВК = 15 см, КС = 9см. Р АВС D = ? 1 2 3 Решение АВС D – параллелограмм, то ВС ∥ AD и ∠2 = ∠3, (как накрест лежащие ) ∠1 = ∠2 – по свойству биссектрисы, то и ∠1 = ∠3. К ∆АВК – равнобедренный, следовательно АВ = ВК = 15 см 15 см 9см АВ = С D , то и С D = 15 см, ВС = ВК + 9 = 15 + 9 = 24 (см). 15 см ВС = AD = 24 (см). Р АВС D = 2(AD + AB) = 2(24 + 15) = 78 (c м). Ответ: 78 (c м).
Слайд 8
8 Ответить на вопросы: www.konspekturoka.ru Спасибо за внимание! Какая фигура называется параллелограммом? Докажите, что в параллелограмме противоположные стороны и углы равны. Докажите, что в параллелограмме диагонали точкой пересечения делятся пополам. Сформулируйте и докажите признаки параллелограмма.
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Параллелограмм»
Открытый банк заданий по теме параллелограмм. Задания B6 из ЕГЭ по математике (профильный уровень)
Производная и первообразная функции
Задание №1066
Тип задания: 6
Тема:
Параллелограмм
Условие
В параллелограмме ABCD AB = 6, AD = 9, sin A = frac23. Найдите большую высоту параллелограмма.
Показать решение
Решение
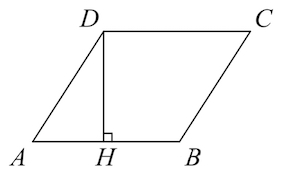
Площадь параллелограмма равна произведению стороны на высоту, проведённую к этой стороне, поэтому большая высота проведена к меньшей стороне. Проведём высоту DH к меньшей стороне и рассмотрим треугольник ADH.
sin A=frac{DH}{AD}. Получаем: DH=ADsin A= 9cdotfrac23= 6.
Ответ
6
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1062
Тип задания: 6
Тема:
Параллелограмм
Условие
Площадь параллелограмма равна 60, две его стороны равны 8 и 12. Найдите меньшую высоту этого параллелограмма.
Показать решение
Решение
Площадь параллелограмма равна произведению стороны на высоту, проведённую к этой стороне S = ah_a. Найдём высоты параллелограмма: h_1 = 60 : 8 = 7,5, h_2 = 60 : 12 = 5. Меньшая высота этого параллелограмма равна 5.
Ответ
5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №892
Тип задания: 6
Тема:
Параллелограмм
Условие
Площадь параллелограмма ABCD равна 324. Точка P — середина стороны BC. Найдите площадь трапеции APCD.
Показать решение
Решение
Точка P — середина стороны BC, поэтому PC=0,5BC. Обозначим h высоту параллелограмма, проведённую к стороне AD.
Тогда площадь параллелограмма S равна BCcdot h=324.
Площадь трапеции APCD равна frac{PC+AD}{2}cdot h= frac{0,5BC+BC}{2}cdot h= frac{1,5BC}{2}cdot h= 0,75S=243
Ответ
243
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №890
Тип задания: 6
Тема:
Параллелограмм
Условие
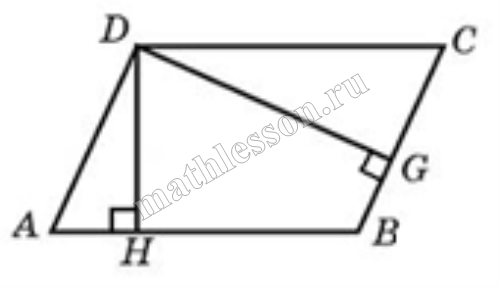
Стороны параллелограмма равны 8 и 16. Высота, опущенная на первую из этих сторон, равна 14. Найдите высоту, опущенную на вторую сторону параллелограмма.
Показать решение
Решение
Площадь параллелограмма равна произведению стороны на высоту, проведённую к этой стороне. Для параллелограмма ABCD выполняется S=ABcdot DH=CBcdot DE. Получаем 16DH=8cdot14, DH=7.
Ответ
7
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №295
Тип задания: 6
Тема:
Параллелограмм
Условие
Площадь параллелограмма ABCD равна 284. Точка E — середина CD. Найдите площадь треугольника ADE.
Показать решение
Решение
S_{ADE}=frac{DEcdot AM}{2}, AMperp DC
S_{ABCD}=ABcdot AM, AB=2DE.
ABcdot AM=284, 2DEcdot AM=284.
DEcdot AM=142, S_{ADE}=frac{142}{2}=71.
Ответ
71
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
ЕГЭ Профиль
Планиметрия: задачи, связанные с углами
Параллелограммы
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1001
|
В параллелограмме ABCD AB = 3, AD = 21, $$sin a = frac{6}{7} $$ . Найдите большую высоту параллелограмма. |
|
Ответ: 18
Задание 1003
|
Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны. |
|
Ответ: 6
Задание 1004
|
Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2. |
|
Ответ: 18
Задание 1011
Диагонали ромба равны $$2sqrt{5}$$ и $$4sqrt{5}$$ . Найдите радиус вписанной в ромб окружности.
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
|
Площадь ромба вычисляется как половина произведения диагоналей. То есть $$S = 0.5 *2sqrt{5}*4sqrt{5}=20$$ С другой стороны, площадь равна произведению основания на высоту, а высота равна двум радиусам вписанной окружности. То есть S = AB * 2 OH = AB * 2r Найдем AB по теореме Пифагора из треугольника ABO (его катеты равны половинам диагоналей): $$AB = sqrt{sqrt{5}^{2}+2sqrt{5}^{2}}=sqrt{5+20}=5$$ Приравняем площади: 20 = 5 * 2r, r = 2 |
|
Задание 1019
|
Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника. |
|
Ответ: 14
Задание 1020
|
Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника. |
|
Ответ: 48
Задание 1021
|
Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника. |
|
Ответ: 13
Задание 1022
| Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах. |  |
Ответ: 30
Задание 1023
|
Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма. |
|
Ответ: 6
Задание 1024
|
Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма |
 |
Ответ: 8
Задание 1025
|
Найдите площадь ромба, если его высота равна 2, а острый угол 30°. |
|
Ответ: 8
Задание 1027
|
Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ. |
|
Ответ: 3
Задание 1028
|
Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ. |
|
Ответ: 2
Задание 1029
|
Диагональ параллелограмма образует с двумя его сторонами углы 24 и 36. Найдите больший угол параллелограмма. Ответ дайте в градусах. |
|
Ответ: 120
Задание 1030
|
Периметр параллелограмма равен 46. Одна сторона параллелограмма на 3 больше другой. Найдите меньшую сторону параллелограмма. |
|
Ответ: 10