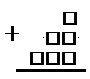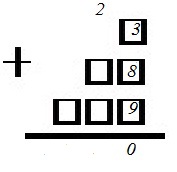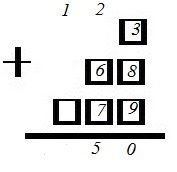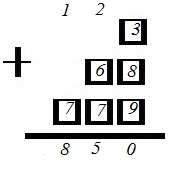Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Приведите пример трёхзначного числа, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9.
Источник: Демонстрационная версия ЕГЭ — 2015.
2
Найдите трёхзначное натуральное число, большее 400, которое при делении на 6 и на 5 даёт равные ненулевые остатки и первая слева цифра которого является средним арифметическим двух других цифр. В ответе укажите какое-нибудь одно такое число.
3
Найдите четырёхзначное число, кратное 22, произведение цифр которого равно 24. В ответе укажите какое-нибудь одно такое число.
4
Найдите трёхзначное число, кратное 25, все цифры которого различны, а сумма квадратов цифр делится на 3, но не делится на 9. В ответе укажите какое-нибудь одно такое число.
Номер в банке ФИПИ: FE8DFD
5
Приведите пример четырёхзначного натурального числа, кратного 4, сумма цифр которого равна их произведению. В ответе укажите ровно одно такое число.
Пройти тестирование по этим заданиям
19. Задачи на теорию чисел
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на теорию чисел
Задание
1
#1075
Уровень задания: Легче ЕГЭ
В ряд выписаны числа от (1) до (22). Можно ли между ними расставить знаки “(+)”( )и “(-)”( )так, чтобы в результате получился (0)?
Среди чисел (1, 2, 3, …, 22) всего (11) четных и (11) нечетных, то есть нечетных чисел нечетное количество, поэтому как бы мы ни поставили знаки в результате всегда получится нечетное число. А так как (0) – четное число, то так расставить знаки нельзя.
Ответ:
Нет
Задание
2
#1076
Уровень задания: Легче ЕГЭ
В ряд выписаны числа от (1) до (98). Можно ли между ними расставить знаки “(+)”( )и “(-)”( )так, чтобы в результате получилось (2)?
Среди чисел (1,2,3, …, 98) всего (49) четных и (49) нечетных, то есть нечетных чисел нечетное количество, поэтому как бы мы ни поставили знаки в результате всегда получится нечетное число. А так как (2) – четное число, то так расставить знаки нельзя.
Ответ:
Нет
Задание
3
#1077
Уровень задания: Легче ЕГЭ
Можно ли разменять (1000) рублей купюрами по (5, 25, 125) рублей так, чтобы всего оказалось (101) купюра? (купюры в (5, 25, 125) рублей бывают)
Так как у нас купюры только нечетного номинала, и их должно быть нечетное количество, то мы сможем ими разменять только нечетную сумму рублей, поэтому не сможем разменять (1000) рублей.
Ответ:
Нет
Задание
4
#1078
Уровень задания: Легче ЕГЭ
Можно ли разменять (600) рублей купюрами по (7, 49, 73) рубля так, чтобы всего оказалось (17) купюр? (купюры в (7, 49, 73) рубля бывают)
Так как у нас купюры только нечетного номинала, и их должно быть нечетное количество, то мы сможем ими разменять только нечетную сумму рублей, поэтому не сможем разменять (600) рублей.
Ответ:
Нет
Задание
5
#1079
Уровень задания: Легче ЕГЭ
Сумму двух целых чисел умножили на их произведение. Могло ли в результате получиться число (123456789)?
Предположим, что такое может быть. Пусть (a) и (b) – целые числа из нашей задачи, тогда ((a+b)cdot acdot b=123456789). Так как число (123456789) – нечетное, то (a), (b) – нечетные, но тогда число ((a+b)) – четное, но тогда число ((a+b)cdot acdot b) – четное, но (123456789) – нечетное, следовательно получили противоречие, а значит такого быть не могло.
Ответ:
Нет
Задание
6
#1080
Уровень задания: Легче ЕГЭ
Разность двух целых чисел умножили на их произведение. Могло ли в результате получиться число (10011001)?
Предположим, что такое может быть. Пусть (a) и (b) – целые числа из нашей задачи, тогда ((a-b)cdot acdot b=10011001). Так как число (10011001) – нечетное, то (a), (b) – нечетные, но тогда число ((a-b)) – четное, но тогда число ((a-b)cdot acdot b) – четное, но (10011001) – нечетное, следовательно получили противоречие, а значит такого быть не могло.
Ответ:
Нет
Задание
7
#1081
Уровень задания: Легче ЕГЭ
Можно ли представить (1) в виде суммы четырех дробей (dfrac{1}{a}+dfrac{1}{b}+dfrac{1}{c}+dfrac{1}{d}), где (a, b, c,
d) – нечетные натуральные числа?
Предположим, что можно. Тогда [dfrac{1}{a}+dfrac{1}{b}+dfrac{1}{c}+dfrac{1}{d}=1,] приведем в левой части все к общему знаменателю:
[dfrac{bcd+acd+abd+bcd}{abcd}=1qquadRightarrowqquad bcd+acd+abd+bcd=abcd.] Но так как (a, b, c, d) – нечетные натуральные числа, то получаем, что четное число равно нечетному – противоречие, значит так представить (1) нельзя.
Ответ:
Нет

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Задание 18 ЕГЭ 2022 математика 11 класс профильный уровень 30 задач с ответами, тема числовые наборы на карточках и числах, практические задачи для тренировки с ответами для подготовки к ЕГЭ 2022. Решаем!
Скачать задачи ЕГЭ 2022 с ответами
1)Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и их все возможные суммы (по 2, по 3 и т.д.) выписывают на доску в порядке неубывания. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляется одно такое число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11. а) Приведите пример задуманных чисел, для которых на доске будет записан набор 2, 4, 6, 8, 10. б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 1, 3, 4, 5, 6, 8, 10, 11, 12, 13, 15, 17, 18, 19, 20, 22? в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 7, 8, 10, 15, 16, 17, 18, 23, 24, 25, 26, 31, 33, 34, 41.
Ответ: а) 2, 2, 2, 2, 2; б) нет; в) 7, 8, 8, 8, 10 или 7, 8, 10, 16.
2)На доске написано число 2015 и еще несколько (не менее двух) натуральных чисел, не превосходящих 5000. Все написанные на доске числа различны. Сумма любых двух из написанных чисел делится на какое-нибудь из остальных. а) Может ли на доске быть написано ровно 1009 чисел? б) Может ли на доске быть написано ровно пять чисел? в) Какое наименьшее количество чисел может быть написано на доске?
Ответ: а) Может. Например, числа 1,2,3,5,7,…,2015; б) Может. Например, числа 1, 2, 3, 5, 2015; в) 4, например, 1, 2, 3, 2015.
3)На доске было написано 20 натуральных чисел (не обязательно различных), каждое из которых не превосходит 40. Вместо некоторых из чисел (возможно, одного) на доске написали числа, меньшие первоначальных на единицу. Числа, которые после этого оказались равными 0, с доски стѐрли. а) Могло ли оказаться так, что среднее арифметическое чисел на доске увеличилось? б) Среднее арифметическое первоначально написанных чисел равнялось 27. Могло ли среднее арифметическое оставшихся на доске чисел оказаться равным 34? в) Среднее арифметическое первоначально написанных чисел равнялось 27. Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.
Ответ: а) да; б) нет; в) 38 1/7
4)Задумано несколько целых чисел. Набор этих чисел и все их возможные суммы (по 2, по 3 и т. д.) выписывают на доску в порядке неубывания. Например, если задуманы числа 2, 3, 5, то на доске будет выписан набор 2, 3, 5, 5, 7, 8, 10. а) На доске выписан набор −11, −7, −5, −4, −1, 2, 6. Какие числа были задуманы? б) Для некоторых различных задуманных чисел в наборе, выписанном на доске, число 0 встречается ровно 4 раза. Какое наименьшее количество чисел могло быть задумано? в) Для некоторых задуманных чисел на доске выписан набор. Всегда ли по этому набору можно однозначно определить задуманные числа?
Ответ: а) −7, −4, 6; б) 5; в) нет.
5)На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно −3, среднее арифметическое всех положительных из них равно 4, среднее арифметическое всех отрицательных из них равно −8. а) Сколько чисел написано на доске? б) Каких чисел написано больше: положительных или отрицательных? в) Какое наибольшее количество положительных чисел может быть среди них?
Ответ: а) 44; б) отрицательных; в) 17.
6)На доске написано число 7. Раз в минуту Вася дописывает на доску одно число: либо вдвое большее какого-то из чисел на доске, либо равное сумме какихто двух чисел, написанных на доске (таким образом, через одну минуту на доске появится второе число, через две ― третье и т.д.). а) Может ли в какой-то момент на доске оказаться число 2012? б) Может ли в какой-то момент сумма всех чисел на доске равняться 63? в) Через какое наименьшее время на доске может появиться число 784?
Ответ: а) нет; б) да; в) 8 минут.
7)Каждое из чисел 1, −2, −3, 4, −5, 7, −8, 9 по одному записывают на 8 карточках. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, −2, −3, 4, −5, 7, −8, 9. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают. а) Может ли в результате получиться 0? б) Может ли в результате получиться 1? в) Какое наименьшее целое неотрицательное число может в результате получиться?
Ответ: а) нет; б) нет; в) 4.
8)Натуральные числа от 1 до 12 разбивают на четыре группы, в каждой из которых есть по крайней мере два числа. Для каждой группы находят сумму чисел этой группы. Для каждой пары групп находят модуль разности найденных сумм и полученные 6 чисел складывают. а) Может ли в результате получиться 0? б) Может ли в результате получиться 1? в) Каково наименьшее возможное значение полученного результата?
Ответ: а) нет; б) нет; в) 4.
9)На доске написано более 27, но менее 45 целых чисел. Среднее арифметическое этих чисел равно −5, среднее арифметическое всех положительных из них равно 9, а среднее арифметическое всех отрицательных из них равно −18. а) Сколько чисел написано на доске? б) Каких чисел написано больше: положительных или отрицательных? в) Какое наибольшее количество положительных чисел может быть среди них?
Ответ: а) 36; б) отрицательных; в) 16.
10)Из первых 22 натуральных чисел 1,2,…,22 выбрали 2 k различных чисел. Выбранные числа разбили на пары и посчитали суммы чисел в каждой паре. Оказалось, что все полученные суммы различны и не превосходят 27. а) Может ли получиться так, что сумма всех 2 k выбранных чисел равняется 170 и в каждой паре одно из чисел ровно в три раза больше другого? б) Может ли число k быть равным 11? в) Найдите наибольшее возможное значение числа k.
Ответ: а) нет; б) нет; в) 10.
11)На доске написано 10 неотрицательных чисел. За один ход стираются два числа, а вместо них записывается сумма, округлѐнная до целого числа (например, вместо 5,5 и 3 записывается 9, а вместо 3,3 и 5 записывается 8). а) Приведите пример 10 нецелых чисел и последовательности 9 ходов, после которых на доске будет записано число, равное сумме исходных чисел. б) Может ли после 9 ходов на доске быть написано число, отличающееся от суммы исходных чисел на 7? в) На какое наибольшее число могут отличаться числа, записанные на доске после 9 ходов, выполненных с одним и тем же набором исходных чисел в различном порядке?
Ответ: а) например, числа 0,99; 0,01; 0,99; 0,01; 0,99; 0,01; 0,99; 0,01; 0,99; 0,01 и любая последовательность ходов; б) нет; в) 5.
12)На проекте «Мисс Чистополь − 2019» выступление каждой участницы оценивают шесть судей. При этом каждый судья выставляет оценку — целое число баллов от 0 до 10 включительно. Известно, что за выступление Ангелины Курбановой все члены жюри выставили различные оценки. По старой системе оценивания итоговый балл за выступление определяется как среднее арифметическое всех оценок судей. По новой системе оценивания итоговый балл вычисляется следующим образом: отбрасываются наименьшая и наибольшая оценки, и считается среднее арифметическое четырех оставшихся оценок. а) Могут ли итоговые баллы, вычисленные по старой и новой системам оценивания, оказаться одинаковыми? б) Может ли разность итоговых баллов, вычисленных по старой и новой системам оценивания, оказаться равной 1 8 ? в) Найдите наибольшее возможное значение разности итоговых баллов, вычисленных по старой и новой системам оценивания.
Ответ: а) да; б) нет; в) 5/6
13)На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71). а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел. б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел? в) Найдите наибольшее возможное значение суммы получившихся чисел.
Ответ: а) 17 и 16; б) нет; в) 1650.
14)Набор состоит из 33 натуральных чисел, среди которых есть числа 3, 4 и 5. Среднее арифметическое любых 27 чисел этого набора меньше 2. а) Может ли такой набор содержать ровно 13 единиц? б) Может ли такой набор содержать менее 13 единиц? в) Докажите, что в любом таком наборе есть несколько чисел, сумма которых равна 28.
Ответ: а) да; б) нет.
15)Каждое из чисел 1, −2, −3, 4, −5, 7, −8, 9, 10, −11 по одному записывают на 10 карточках. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, −2, −3, 4, −5, 7, −8, 9, 10, −11. После этого числа на каждой карточке складывают, а полученные 10 сумм перемножают. а) Может ли в результате получиться 0? б) Может ли в результате получиться 1? в) Какое наименьшее целое неотрицательное число может в результате получиться?
Ответ: а) нет; б) нет; в) 4.
16)На доске написано несколько различных натуральных чисел, произведение любых двух из которых больше 40 и меньше 100. а) Может ли на доске быть 5 чисел? б) Может ли на доске быть 6 чисел? в) Какое наибольшее значение может принимать сумма чисел на доске, если их четыре?
Ответ: а) да; б) нет; в) 35.
17)На доске написано несколько (более одного) различных натуральных чисел, причем любые два из них отличаются не более чем в три раза. а) Может ли на доске быть 5 чисел, сумма которых равна 47? б) Может ли на доске быть 10 чисел, сумма которых равна 94? в) Сколько может быть чисел на доске, если их произведение равно 8000?
Ответ: а) да; б) нет; в) 2 или 3.
18)Задумано несколько натуральных чисел (не обязательно различных). Эти числа и все их возможные произведения (по 2 числа, по 3 числа и т. д.) выписывают на доску. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляют одно такое число n, а остальные числа, равные n, стирают. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 9, 12, 36. а) Приведите пример задуманных чисел, для которых на доске будет записан набор 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90. б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 3, 5, 7, 9, 15, 21, 35, 45, 105, 315, 945? в) Приведите все примеры шести задуманных чисел, для которых на доске будет записан набор, наибольшее число в котором равно 82.
Ответ: а) 2, 3, 3, 5; б) нет; в) 1, 1, 1, 1, 1, 82 или 1, 1, 1, 1, 2, 41.
19)Задумано несколько натуральных чисел (не обязательно различных). Эти числа и все их возможные произведения (по 2 числа, по 3 числа и т. д.) выписывают на доску. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляют одно такое число n, а остальные числа, равные n, стирают. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 9, 12, 36. а) Приведите пример задуманных чисел, для которых на доске будет записан набор 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150. б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 2, 5, 10, 11, 22, 25, 55, 110, 275, 550? в) Приведите все примеры пяти задуманных чисел, для которых на доске будет записан набор, наибольшее число в котором равно 91.
Ответ: а) 2, 3, 5, 5; б) нет; в) 1, 1, 1, 1, 91 или 1, 1, 1, 7, 13.
20)Саша берѐт пять различных натуральных чисел и проделывает с ними следующие операции: сначала вычисляет среднее арифметическое первых двух чисел, затем среднее арифметическое результата и третьего числа, потом среднее арифметическое полученного результата и четвѐртого числа, потом среднее арифметическое полученного результата и пятого числа — число A. а) Может ли число A равняться среднему арифметическому начальных пяти чисел? б) Может ли число A быть больше среднего арифметического начальных чисел в пять раз? в) В какое наибольшее целое число раз число A может быть больше среднего арифметического начальных пяти чисел?
Ответ: а) да, например: 1, 3, 8, 11, 2; б) нет; в) 2.
21)На доске написано 30 натуральных чисел. Какие-то из них красные, а какие-то зелѐные. Красные числа кратны 7, а зелѐные числа кратны 5. Все красные числа отличаются друг от друга, как и все зелѐные. Но между красными и зелѐными могут быть одинаковые. а) Может ли сумма зелѐных чисел быть меньше 2325, если на доске написаны только кратные 5 числа? б) Может ли сумма чисел быть 1467, если только одно число красное? в) Найдите наименьшее количество красных чисел, которое может быть при сумме 1467.
Ответ: а) Да; б) нет; в) 10.
22)На доске написано 30 натуральных чисел. Какие-то из них красные, а какие-то зелѐные. Красные числа кратны 8, а зелѐные числа кратны 3. Все красные числа отличаются друг от друга, как и все зелѐные. Но между красными и зелѐными могут быть одинаковые. а) Может ли сумма зелѐных чисел быть меньше 1395 = 3 + 6 +…+ 90, если на доске написаны только кратные 3 числа? б) Может ли сумма чисел быть 1066, если только одно число красное? в) Найдите наименьшее количество красных чисел, которое может быть при сумме 1066.
Ответ: а) Да; б) нет; в) 7.
23)На доске написано 100 различных натуральных чисел с суммой 5100. а) Может ли быть записано число 250? б) Можно ли обойтись без числа 11? в) Какое наименьшее количество чисел, кратных 11, может быть на доске?
Ответ: а) Нет; б) нет; в) 6.
24)На доске написано 100 различных натуральных чисел с суммой 5120. а) Может ли быть записано число 230? б) Можно ли обойтись без числа 14? в) Какое наименьшее количество чисел, кратных 14, может быть на доске?
Ответ: а) Нет; б) нет; в) 4.
25)На доске написано 30 различных натуральных чисел, каждое из которых либо четное, либо его десятичная запись заканчивается на цифру 7. Сумма написанных чисел равна 810. а) Может ли быть 24 четных числа? б) Может ли быть на доске ровно два числа, оканчивающихся на 7? в) Какое наименьшее количество чисел с последней цифрой 7 может быть на доске?
Ответ: а) да; б) нет; в) 4.
26)На доске написано 30 различных натуральных чисел, каждое или оканчивается на 9, или четное, а сумма чисел равна 877. а) Может ли быть на доске 27 четных чисел? б) Может ли быть на доске ровно два числа, оканчивающихся на 9? в) Какое наименьшее количество чисел с последней цифрой 9 может быть на доске?
Ответ: а) да; б) нет; в) 3.
27)В течение n дней каждый день на доску записывают натуральные числа, каждое из которых меньше 6. При этом каждый день (кроме первого) сумма чисел, записанных на доску в этот день, больше, а количество меньше, чем в предыдущий день. а) Может ли n быть больше 6? б) Может ли среднее арифметическое чисел, записанных в первый день, быть меньше 2, а среднее арифметическое всех чисел, записанных за все дни, быть больше 4? в) Известно, что сумма чисел, записанных в первый день, равна 5. Какое наибольшее значение может принимать сумма всех чисел, записанных за все дни?
Ответ: а) да, б) да, в) 34.
28)На доске написано n единиц, между некоторыми из которых поставили знаки + и посчитали сумму. Например, если изначально было написано n = 12 единиц, то могла получиться, например, такая сумма: 1 + 11 + 11 + 111 + 11 + 1 + 1 = 147. а) Могла ли сумма равняться 150, если n = 60? б) Могла ли сумма равняться 150, если n = 80? в) Чему могло равняться n, если полученная сумма чисел равна 150?
Ответ: а) да, б) нет, в) 150, 141, 132, 123, 114, 105, 96, 87, 78, 69, 60, 51, 42, 33, 24, 15.
29)На доске написано несколько различных натуральных чисел, которые делятся на 3 и оканчиваются на 4. а) Может ли сумма составлять 282? б) Может ли их сумма составлять 390? в) Какое наибольшее количество чисел могло быть на доске, если их сумма равна 2226?
Ответ: а) да, б) нет, в) 9.
30)На доске было написано несколько различных натуральных чисел. Эти числа разбили на три группы, в каждой из которых оказалось хотя бы одно число. К каждому числу из первой группы приписали справа цифру 6, к каждому числу из второй группы приписали справа цифру 9, а числа третьей группы оставили без изменений. а) Могла ли сумма всех этих чисел увеличиться в 9 раз? б) Могла ли сумма всех этих чисел увеличиться в 19 раз? в) В какое наибольшее число раз могла увеличиться сумма всех этих чисел?
Ответ: а) да, б) нет, в) в 11,6 раза.
31)На доске написаны три различных натуральных числа. Второе число равно сумме цифр первого, а третье равно сумме цифр второго. а) Может ли сумма этих чисел быть равна 420? б) Может ли сумма этих чисел быть равна 419? в) В тройке чисел первое число трѐхзначное, а третье равно 5. Сколько существует таких троек?
Ответ: а) да, б) нет, в) 85.
Смотрите также на нашем сайте:
Числа и их свойства 18 задание ЕГЭ 2022 профиль математика с ответами
Задание 15 ЕГЭ 2022 математика профиль задачи на вклады, кредиты, оптимизацию
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
14 марта 2020
В закладки
Обсудить
Жалоба
В данной работе рассмотрены примеры решения задачи №19 ЕГЭ по профильной математике.
chisla19.docx
Задание №19 может быть 4 типов:
1) Числа и их свойства.
2) Числовые наборы на карточках и досках.
3) Последовательности и прогрессии.
4) Сюжетные задачи: кино, театр, мотки верёвки и тому подобное.
Числа и их свойства
В зависимости от задачи можно использовать следующие методы:
1) Свойства делимости целых чисел (в частности, делимость на 2, 3, 4, 5, 7, 9, 11).
2) Работа с простыми и составными числами.
3) Работа с каноническим разложением натурального числа, количество делителей натурального числа.
4) Работа с НОД и НОК.
Автор: Бурмистрова Анна Владимировна, учитель математики.
Задание №19 ЕГЭ по математике базового уровня
Свойства чисел
Задание №19 ЕГЭ по математике весьма необычно. Для его решения необходимо применить знания в области теории чисел. Тем не менее, задание является весьма решаемым, однако для школьников с оценкой хорошо и ниже я рекомендовал бы оставить это задание на последнюю очередь. Перейдем к рассмотрению типового варианта.
Разбор типовых вариантов заданий №19 ЕГЭ по математике базового уровня
Вариант 19МБ1
Найдите трехзначное число, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9. В ответе укажите какое-нибудь оно такое число.
Алгоритм выполнения:
- Ввести условные обозначения.
- Записать условия с помощью условных обозначений.
- Преобразовать полученные выражения.
- Логически рассуждая перебрать все возможные варианты, проверить их соответствие условиям.
Решение:
Обозначим первую цифру числа x, а вторую – y. Тогда третье число с учетом суммы цифр равной 20 будет равно 20 – (x + y). (x + y) обязательно меньше 10, иначе сумма равная 20 не получится.
По условию сумма квадратов цифр делится на 3, но не делится на 9. Запишем сумму квадратов цифр:
x 2 + y2 + (20 – (x + y))2
Преобразуем полученное выражение. Преобразуем квадрат разности с учетом формулы приведения.
Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.
(20 – (x + y))2 = 400 -40(x + y) + (x + y)2
Подставим получившееся выражение в начальное, получим:
x 2 + y2 + (20 – (x + y))2 = x 2 + y2 + 400 — 40(x + y) + (x + y)2
Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.
(x + y)2= x2 + 2xy + y2
Подставим:
x 2 + y2 + (20 – (x + y))2 = x 2 + y2 + 400 — 40(x + y) + (x + y)2 = x 2 + y2 + 400 — 40(x + y) + x2 + 2xy + y2
Приведем подобные слагаемые(сложим x2 с x2 и y2 с y2), получим:
x 2 + y2 + 400 — 40(x + y) + x2 + 2xy + y2 = 2x 2 + 2y2 + 2 · 200 — 2 · 20(x + y) + 2xy
Вынесем множитель 2 за скобку:
2x 2 + 2y2 + 2 · 200 — 2 · 20(x + y) + 2xy = 2(x 2 + y2 + 200 — 20(x + y) + xy)
Для удобства объединим 200 и 20(x + y) и вынесем 20 за скобку, получим:
2(x 2 + y2 + 20(10 — (x + y)) + xy)
Множитель 2 – четный, поэтому он никак не влияет на делимость на 3 или 9. Можем его не брать в расчет и рассматривать выражение:
x 2 + y2 + 20(10 — (x + y)) + xy
Предположим, что и x, и y делятся на 3. Тогда x 2 + y2 + xy делится на 3, а 20(10 — (x + y)) – не делится. Следовательно, и вся сумма x 2 + y2 + 20(10 — (x + y)) + xy на 3 не делится.
Предположим, что на 3 делится только одна цифра. Тогда, учитывая, что (x + y) обязательно меньше 10, иначе сумма равная 20 не получится, подберем возможные пары.
(3;8), (6;5), (6;7), (6;8), (9;2), (9;4), (9;5), (9;7), (9;8).
Методом подстановки проверим, соответствуют эти пары условию.
x 2 + y2 + 20(10 — (x + y)) + xy = 3 2 + 82 + 20(10 — (3 + 8)) + 3 · 8 = 9 + 64 – 20 + 24 = 77
x 2 + y2 + 20(10 — (x + y)) + xy = 6 2 + 52 + 20(10 — (6 + 5)) + 6 · 5 = 36 + 25 – 20 + 30 = 71
x 2 + y2 + 20(10 — (x + y)) + xy = 6 2 + 72 + 20(10 — (6 + 7)) + 6 · 7 = 36 + 49 – 60 + 42 = 67
x 2 + y2 + 20(10 — (x + y)) + xy = 6 2 + 82 + 20(10 — (6 + 8)) + 6 · 8 = 36 + 64 – 80 + 48 = 68
x 2 + y2 + 20(10 — (x + y)) + xy = 9 2 + 22 + 20(10 — (9 + 2)) + 9 · 2 = 81 + 4 – 20 + 18 = 83
x 2 + y2 + 20(10 — (x + y)) + xy = 9 2 + 42 + 20(10 — (9 + 4)) + 9 · 4 = 81 + 16 – 60 + 36 = 73
Ни одна из полученных сумм не удовлетворяет условию «сумма квадратов цифр делится на 3, но не делится на 9».
Следующие пары можно не проверять, так как они дают уже имеющиеся тройки цифр. Предположим, что ни одна из цифр числа не делится на 3. Возможные пары:
(4;7), (5;7), (5;8), (7;8).
Проверим:
x 2 + y2 + 20(10 — (x + y)) + xy = 4 2 + 72 + 20(10 — (4 + 7)) + 4 · 7 = 16 + 49 – 20 + 28 = 73
x 2 + y2 + 20(10 — (x + y)) + xy = 5 2 + 72 + 20(10 — (5 + 7)) + 5 · 7 = 25 + 49 – 40 + 35 = 69
Сумма 69 удовлетворяет условию «сумма квадратов цифр делится на 3, но не делится на 9». Следовательно, подходят цифры 5,7,8 в любом порядке.
Ответ: 578
Вариант 19МБ2
На 6 карточках написаны цифры 1; 2; 3; 6; 9; 9 (по одной цифре на каждой карточке). В выражении □ + □□ + □□□ вместо каждого квадратика положили карточку из набора. Оказалось, что полученная сумма делится на 10. Найдите эту сумму. В ответе укажите какое-нибудь одно такое число.
Алгоритм выполнения:
- Вспомнить признак делимости на 10.
- Разместить последние цифры каждого слагаемого таким образом, чтобы в сумме получилось 10.
- Расположить оставшиеся карточки в произвольном порядке.
Решение:
1. Если сумма делится на 10 нацело, то последняя цифра должна быть 0, остальные цифры значения не имеют.
2. В первый квадрат поместим цифру 1, в следующем числе на последнем месте – цифру 3 (или 6), а в третьем – цифру 6 (или 3), получим (сумма 1+3+6=10):
3. Остальные цифры заполним произвольно, например, так:
и получится сумма
1+23+996 = 1020.
Ответ: 1020
Вариант 19МБ3
На 6 карточках написаны цифры 1; 2; 2; 3; 5; 7 (по одной цифре на каждой карточке). В выражении □ + □□ + □□□ вместо каждого квадратика положили карточку из набора. Оказалось, что полученная сумма делится на 20. Найдите эту сумму. В ответе укажите какое-нибудь одно такое число.
Алгоритм выполнения:
- Вспомнить признак делимости на 10 и сформулировать признак делимости на 20.
- Разместить последние цифры каждого слагаемого таким образом, чтобы в сумме получилось 10.
- Разместить предпоследние цифры каждого слагаемого таким образом, чтобы в сумме получилось четное число в результате с учетом суммы первых цифр.
- Расположить оставшиеся карточки в произвольном порядке.
Решение:
1. Чтобы сумма делилась на 20, она должна заканчиваться на 0 и вторая цифра с конца должна быть четной (делиться на 2). Чтобы в конце суммы получить 0, первые три карточки следует выбрать так:
2. Чтобы вторую цифру получить четной, можно взять карточки 2 и 7 (к ней будет добавляться еще 1 от первой суммы 10):
3. В последнее место помещаем оставшуюся цифру 1, в результате имеем:

2+23+175=200.
Ответ: 200
Вариант 19МБ4
Найдите четырехзначное число, кратное 15, произведение цифр которого больше 0, но меньше 25. В ответе укажите какое-нибудь одно такое число.
Алгоритм выполнения
- Если произведение >0, то, значит, оно не равно нулю. Следовательно, ни один из множителей не может быть равным 0.
- Если произведение кратно 15, следовательно, оно кратно 5 и кратно 3.
- Если произведение кратно 5, то результат его должен оканчиваться 0 или 5. В данном случае берем 5, т.к. 0 не может быть одним из множителей (см.п.1).
- Итак, последняя цифра числа равна 5. Тогда произведение первых трех равно 25:5=5. Это означает, что нужно подобать 3 цифры так, чтобы их произведение было менее 5.
- Из всех полученных наборов цифр выбираем такой, чтобы сумма этих цифр плюс 5 (последняя, 4-я цифра) была кратной 3.
Решение:
Поскольку по условию произведение всех цифр кратно 15, то оно кратно 5 и 3.
Кратность 5 означает, что последней цифрой числа может быть только 0 или 5. Но 0 в виде последней цифры означал бы, что произведение всех 4-х цифр стало бы равным 0; а это противоречит условию. Тогда последняя цифра искомого числа равна 5.
Тогда получим: x·y·z·5<25 → x·y·z<5, где x, y, z – соответственно, 1-я, 2-я и 3-я цифры искомого числа.
Меньше 5 произведение таких цифр: 1 1 1, 1 1 3, 1 1 2, 1 2 2.
Согласно признаку делимости на 3, выбираем из этих наборов такой, чтобы сумма его цифр плюс 5 делилась на 3:
1+1+1+5=8 – не подходит;
1+1+3+5=10 – не подходит;
1+2+2+5=10 – не подходит
1+1+2+5=9 – подходит.
Тогда условию задачи соответствуют числа: 1125, 1215, 2115.
Ответ: 1125, 1215, 2115
Вариант 19МБ5
Вычеркните в числе 85417627 три цифры так, чтобы получившееся число делилось на 18. В ответе укажите какое-нибудь одно получившееся число.
Алгоритм выполнения
- Число делится на 18, если оно кратно 2 и 9.
- Кратность 2 означает, что число должно быть четным. Поэтому сразу отбрасывают последнюю – нечетную – цифру 7.
- Кратность 9 означает, что сумма его цифр делится на 9. Значит, находим сумму оставшихся цифр. Далее определяем подходящее для полученной суммы число, кратное 9. Число должно быть таким, чтобы: а) оно было меньшим суммы цифр; б) разница между этой суммой и найденным числом позволяла выделить в числе 2 цифры, сумма которых была бы равной этой разнице. Вычеркиваем эти цифры.
Решение:
Т.к. по условию число кратно 18, то оно кратно 2 и кратно 9.
Поскольку число кратно 2, то оно должно оканчиваться четной цифрой. 7 – нечетная цифра, поэтому вычеркиваем ее. Осталось: 8541762.
Т.к. полученное число кратно 9, то сумма его цифр должна делиться на 9. Находим общую сумму его цифр: 8+5+4+1+7+6+2=33. Ближайшее число, которое делится на 9, – это 27.
33–27=6 – это сумма двух цифр, которые нужно вычеркнуть. Пары цифр, которые при этом в сумме дают 6, – это 5 и 1 или 4 и 2. Вычеркнув их, получаем соответственно: 84762 или 85176.
Кроме этого, на 9 делится 18. Тогда 33–18=15. В этом случае вычеркнуть придется 8 и 7. Получаем: 54162.
На 9 делится еще и 9, однако 33–9=24, а пары цифр, которые дали бы в сумме 24, естественно, не существует.
Ответ: 84762, 85176, 54162
Вариант 19МБ6
На шести карточках написаны цифры 3; 6; 7; 7; 8; 9 (по одной цифре на каждой карточке). В выражении
Вместо каждого квадратика положили карточку из данного набора. Оказалось, что полученная сумма делится на 10, но не делится на 20.
В ответе укажите какую-нибудь одну такую сумму.
Алгоритм выполнения
- Во 2-м предложении текста задачи фактически представлено условие, при котором сумма делится на 10, однако не делится на 2.
- Из п.1 следует, что результирующее число должно оканчиваться 0, а предпоследняя его цифра должна быть нечетной.
Решение:
Для удобства восприятия разместим карточки в столбик:
Если число делится на 10, но не делится на 20, значит, оно точно не делится на 2 без последнего нуля.
Поскольку число кратно 10, то оно должно оканчиваться нулем. Поэтому в последнем разряде (единиц) нужно расположить 3 карточки с такими цифрами, чтоб их сумма оканчивалась на 0. Подходят здесь карточки: 1) 6, 7, 7; 2) 3, 8, 9. Их суммы равны 20. Соответственно, 0 мы пишем под чертой, а 2 переносим на предыдущий разряд (десятков):
Чтобы число не делилось на 20, необходимо, чтобы перед нулем стояла нечетная цифра. Нечетная сумма здесь получится тогда, когда одно из слагаемых будет нечетным, а два других четными. Одно из этих (других) слагаемых – это перенесенная 2. Поэтому из оставшихся цифр следует взять: 1) 3 и 8; 2) 6 и 7. Получаем:
На место сотен ставим последнюю (оставшуюся) карточку с цифрой: 1) 9; 2) 7. Получаем, соответственно, числа 1030 и 850:
Ответ: 1030,850
Вариант 19МБ7
Найдите четное трехзначное натуральное число, сумма цифр которого на 1 меньше их произведения. В ответе укажите какое-нибудь одно такое число.
Алгоритм выполнения
- Вводим буквенные обозначения для цифр искомого числа. Исходя из условия задачи, составляем уравнение.
- Выражаем одну из цифр через 2 другие.
- Подбираем для этих 2-х (других) цифр значения так, чтобы 3-я (выраженная) представляло бы собой натуральное число. Вычисляем 3-ю цифру.
- Формируем искомое число так, чтобы оно было четным.
Решение:
Пусть цифры искомого числа – x, y, z. Тогда получаем:
xyz–(x+y+z)=1
xyz–x–y–z=1
zxy–z=x+y+1
z(xy–1)=x+y+1
z=(x+y+1)/(xy–1)
Знаменатель в этом выражении должен быть целым и положительным. Для простоты (а также для гарантии правильных расчетов) примем, что он должен быть равен 1. Тогда имеем: ху–1=1 → ху=2. Поскольку х и у это цифры, то их значения могут быть равными только 1 и 2 (т.к. только произведение этих однозначных натур.чисел дает в результате 2).
Отсюда z составляет: z=(1+2+1)/(1·2–1)=4/1=4.
Итак, имеем цифры: 1, 2, 4.
Т.к. по условию итоговое число должно быть четным, то оканчиваться оно может только 2 или 4. Тогда правильными вариантами чисел будут такие:
124, 142, 214, 412.
Ответ: 124, 142, 214, 412
Вариант 19МБ8
Найдите шестизначное число, которое записывается только цифрами 2 и 0 и делится на 24. В ответе укажите какое-нибудь одно такое число.
Алгоритм выполнения
- Если число делится на 24, значит, оно делится на 8 и на 3.
- Согласно признаку делимости на 8, 3 последних цифры его должны образовывать число, которое кратно 8.
- Чтобы число делилось на 3, необходимо, чтобы сумма его цифр делилась на 3. Учитывая уже сформированную 2-ю часть числа (см.п.2), дополняем его первыми тремя цифрами соответственно.
Решение:
Чтобы искомое число было кратно 24, требуется, чтобы оно делилось на 8 и в то же время на 3.
Число делится на 8, если последние его 3 цифры образуют число, кратное 8. С использованием только двоек и нулей такое трехзначное число можно образовать так: 000, 002, 020, 022, 200, 202, 220, 222. Из этих чисел на 8 делится только 000 и 200.
Теперь нужно дополнить искомое число первыми 3-мя цифрами так, чтобы оно делилось еще и на 3.
В 1-м случае это будет единственный вариант: 222000.
Во 2-м случае вариантов два: 220200, 202200.
Ответ: 222000, 220200, 202200
Вариант 19МБ9
Найдите четырехзначное число, кратное 15, произведение цифр которого больше 35, но меньше 45. В ответе укажите какое-нибудь одно такое число.
Алгоритм выполнения
- Если число кратно 15, значит, оно кратно 3 и 5.
- Применяем признак делимости на 5 и условие задачи, согласно которому произведение цифр числа ≠0. Так получаем, что последняя цифра искомого числа – только 5.
- Делим 35 на 5 и 45 на 5. Узнаем диапазон значений, которые может принимать произведение первых 3-х цифр числа. Узнаем, что оно может быть равно только 8.
- Определяем последовательности цифр, которые дают при перемножении 8.
- Проверяем полученные из найденных цифр числа на кратность трем.
Решение:
Кратность искомого числа 15 дает 2 условия: оно должно делиться на 5 и на 3.
Если число кратно 5, то оно должно оканчиваться цифрой 5 или 0. Однако 0 в данном случае использовать нельзя, поскольку при этом произведение цифр числа оказывается равным 0. По условию же это не так. Итак, последняя – 4-я – цифра числа равна 5.
По условию 35 < x·5 < 45, где х – произведение первых 3-х цифр числа. Тогда имеем: 7 < x < 9. Это неравенство верно только при х=8. Следовательно, для первых 3-х цифр должны выполняться равенства:
1·1·8=8, 1·2·4=8.
Отсюда получаем числа:
1185; 1245.
Проверяем их на кратность 3:
1+1+8+5=15;
1+2+4+5=12.
Вывод: оба найденные числа кратны 3. Плюс кратны их комбинации:
1815; 8115; 1425; 2145; 2415; 4125; 4215.
Ответ: 1815; 8115; 1425; 2145; 2415; 4125; 4215
Вариант 19МБ10
Найдите пятизначные число, кратное 25, любые две соседние цифры которого отличаются на 2. В ответе укажите какое-нибудь одно такое число.
Алгоритм выполнения
- Принимаем во внимание, что на 25 делятся числа, которые придется последовательно делить на 5 дважды. Определяем, какой парой цифр они должны оканчиваться.
- Учитывая, что 2-й частью условия является различие каждой соседней пары цифр исключительно на 2 единицы, выбираем подходящий вариант (или варианты) цифр.
- Способом подбора находим остальные цифры и, соответственно, числа. Одно из них запишем в ответе.
Решение:
Если число делится на 25, то оно должно оканчиваться на: 00, 25, 50, 75. Т.к. соседние цифры должны отличаться строго на 2, то использовать для 4-й и 5-й цифр можем только 75. Получаем: ***75.
Далее ищем 3-ю цифру:
- **975 или
- **575.
Дальше получаем по аналогии:
1) *7975 → 97975 или 57975;
2) *3575 → 13575 или 53575, *7575 → 57575 или 97575.
Ответ: 97975, 57975, 13575, 53575, 57575, 97575
Вариант 19МБ11
Найдите трехзначное натуральное число, большее 600, которое при делении на 3, на 4 и на 5 дает в остатке 1 и цифры которого расположены в порядке убывания слева направо. В ответе укажите какое-нибудь такое число.
Алгоритм выполнения
- Определяем диапазон значений для 1-й цифры числа (сотен).
- Определяем, какой может быть последняя цифра (единицы), приняв во внимание: 1) при делении на 5 дает в остатке 1; 2) на этом месте не может быть четная цифра, поскольку это одно из условий делимости на 4.
- Способом подбора определяем набор чисел, которые при делении на 3 дают в остатке 1.
- Из этого набора (см.п.3) отбрасываем числа, которые при делении на 4 дают остаток, отличный от 1.
Решение:
Т.к. искомое число >600 и при этом является трехзначным, то 1-й цифрой может быть только 6, 7, 8 или 9. Тогда получаем для искомого числа:
6***
7***
8***
9***
Если число при делении на 5 должно давать в остатке 1, значит, оно может оканчиваться только на 0+1=1 или на 5+1=6. Шестерку тут отбрасываем, поскольку в этом случае число четное и потенциально может делиться на 4. Поэтому имеем:
6**1
7**1
8**1
9**1
Если число при делении на 3 дает в остатке 1, значит, сумма его цифр должна быть кратной 3 плюс 1. Кроме того, учитываем, что цифры должны располагаться в числе в порядке убывания. Подбираем такие числа:
631
721
751
841
871
931
961
Из этой последовательности отбрасываем числа, для которых не выполняется условие о том, что число при делении на 4 должно давать в остатке 1.
Т.к. признак делимости на 4 заключается в том, что 2 последние цифры должны делиться на 4, то получаем:
для 631: 31=28+3, т.е. в остатке имеем 3; число не подходит
для 721: 21=20+1, т.е. в остатке – 1; число подходит
для 751: 51=48+3, т.е. в остатке – 3; число не подходит
для 841: 41=40+1, т.е. в остатке – 1; число подходит
для 871: 71=68+3, т.е. в остатке – 3; число не подходит
для 931: 31=28+3, т.е. в остатке – 3; число не подходит
для 961: 61=60+1, т.е. в остатке – 1; число подходит
Ответ: 721, 841, 961
Вариант 19МБ12
Найдите трехзначное натуральное число, большее 400, но меньшее 650, которое делится на каждую свою цифру и все цифры которого различны и не равны 0. В ответе укажите какое-нибудь одно такое число.
Алгоритм выполнения
- Из условия следует, что числа могут начинаться только на 4,5 или 6.
- При анализе чисел 4-й сотни отбрасываем числа: 1) 1-го десятка, т.к. в них содержится 0; 2) 4-го десятка, т.к. в этом случае первые две цифры совпадут; 3) числа 5-го десятка, т.к. они должны оканчиваться только на 5 или 0, что недопустимо. Кроме того, для всех четных десятков можно рассматривать только четные числа.
- Числа 5-й сотни отбрасываем полностью, т.к. чтобы делиться на каждую свою цифру, они должны оканчиваться 5 или 0.
- Для чисел 6-й сотни рассматривать можно только: 1) четные; 2) кратные 3; 3) не оканчивающиеся 0.
Решение:
Числа 40* и 4*0 отбрасываем, т.к. они содержат 0.
Числа 41* годятся только четные, т.к. это обязательное условия для кратности 4. Анализируем:
412 – подходит
414 – не подходит, т.к. в нем совпадают цифры
416 – не подходит, т.к. не делится на 6
418 – не подходит, т.к. не делится ни на 4, ни на 8
Из чисел 42* годятся только четные, поскольку должны делиться на 2:
422 и 424 – не подходят, т.к. в них совпадают цифры
426 – не подходит, т.к. не делится на 4
428 – не подходит, т.к. не делится на 8
Числа 43* годятся только четные и кратные 3. Поэтому тут подходит только 432.
Числа 44* не подходят полностью.
Числа 45* не подходят полностью, т.к. они должны оканчиваться только 5 (т.е. быть нечетными) или 0.
Числа 46*, 47*, 48*, 49* не подходят полностью, т.к. для каждого из них не выполняется 1 или несколько условий.
Числа 5-й сотни не годятся полностью. Они должны делиться на 5, а для этого оканчиваться либо 5, либо 0, что не допускается.
Числа 60* не годятся полностью.
Среди остальных можно рассматривать только четные, кратные 3, не оканчивающиеся 0. Опуская подробности перебора чисел, оговорим только, что из них годятся: 612, 624, 648. Для остальных не выполняется одно или несколько условий.
Ответ: 412, 432, 612, 624, 648
Вариант 19МБ13
Найдите четырехзначное число, кратное 45, все цифры которого различны и четны. В ответе укажите какое-нибудь одно такое число.
Алгоритм выполнения
- Если число кратно 45, значит, оно делится на 5 и на 9.
- Рассматривать следует только числа четных сотен.
- Оканчиваться числа могут только 0, т.к. 5 – нечетная цифра.
- Сумма цифр числа должна быть равна 18. Только в этом случае можно составить его из всех четных цифр.
Решение:
Т.к. по условию цифры должны быть четными, то рассматривать можно только числа 2-й, 4-й, 6-й и 8-й тысяч. Это значит, что начинаться оно может с 2, 4, 6 или 8.
Если число кратно 45, то оно кратно 5 и кратно 9.
Если число кратно 5, то оно должно оканчиваться 5 или 0. Но поскольку все цифры должны быть четными, то подходит здесь только 0.
Т.о., получаем шаблоны чисел: 2**0, 4**0, 6**0, 8**0. Отсюда следует, что для проверки кратности 9 требуется, чтобы сумма первых 3-х цифр была равной 9, или 18, или 27 и т.д. Но подходит тут только 18. Основания: 1) для получения в сумме 9 нужно, чтобы одно из слагаемых было нечетным, а это противоречит условию; 2) 27 не подходит потому, что даже если взять самую большую 1-ю цифру 8, то сумма 2-й и 3-й цифр будет равна 27–8=19, что превышает допустимый предел. Еще большие суммы цифр, кратные 9, не подходят тем более.
Рассматриваем числа по тысячам.
Числа 2**0. Сумма средних цифр равна: 18–2=16. Получить 16 из четных чисел можно только так: 8+8. Однако цифры не должны повторяться. Поэтому подходящих условию чисел здесь нет.
Числа 4**0. Сумма средних цифр: 18–4=14. 14=8+6. Поэтому получаем: 4680 или 4860.
Числа 6**0. Сумма средних цифр: 18–6=12. 12=6+6, что не подходит, т.к. цифры повторяются. 12=4+8. Получаем: 6480 или 6840.
Числа 8**0. Сумма средних цифр: 18–8=10. 10=2+8, что не подходит, т.к. при этом будет повторяться 8. 10=4+6. Получаем: 8460 или 8640.
Ответ: 4680, 4860, 6480, 6840, 8460, 8640
Свойства чисел
Задание №19 ЕГЭ по математике весьма необычно. Для его решения необходимо применить знания в области теории чисел. Тем не менее, задание является весьма решаемым, однако для школьников с оценкой хорошо и ниже я рекомендовал бы оставить это задание на последнюю очередь. Перейдем к рассмотрению типового варианта.
Разбор типовых вариантов заданий №19 ЕГЭ по математике базового уровня
Вариант 19МБ1
[su_note note_color=”#defae6″]
Найдите трехзначное число, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9. В ответе укажите какое-нибудь оно такое число.
[/su_note]
Алгоритм выполнения:
- Ввести условные обозначения.
- Записать условия с помощью условных обозначений.
- Преобразовать полученные выражения.
- Логически рассуждая перебрать все возможные варианты, проверить их соответствие условиям.
Решение:
Обозначим первую цифру числа x, а вторую – y. Тогда третье число с учетом суммы цифр равной 20 будет равно 20 – (x + y). (x + y) обязательно меньше 10, иначе сумма равная 20 не получится.
По условию сумма квадратов цифр делится на 3, но не делится на 9. Запишем сумму квадратов цифр:
x 2 + y2 + (20 – (x + y))2
Преобразуем полученное выражение. Преобразуем квадрат разности с учетом формулы приведения.
Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.
(20 – (x + y))2 = 400 -40(x + y) + (x + y)2
Подставим получившееся выражение в начальное, получим:
x 2 + y2 + (20 – (x + y))2 = x 2 + y2 + 400 – 40(x + y) + (x + y)2
Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.
(x + y)2= x2 + 2xy + y2
Подставим:
x 2 + y2 + (20 – (x + y))2 = x 2 + y2 + 400 – 40(x + y) + (x + y)2 = x 2 + y2 + 400 – 40(x + y) + x2 + 2xy + y2
Приведем подобные слагаемые(сложим x2 с x2 и y2 с y2), получим:
x 2 + y2 + 400 – 40(x + y) + x2 + 2xy + y2 = 2x 2 + 2y2 + 2 · 200 – 2 · 20(x + y) + 2xy
Вынесем множитель 2 за скобку:
2x 2 + 2y2 + 2 · 200 – 2 · 20(x + y) + 2xy = 2(x 2 + y2 + 200 – 20(x + y) + xy)
Для удобства объединим 200 и 20(x + y) и вынесем 20 за скобку, получим:
2(x 2 + y2 + 20(10 – (x + y)) + xy)
Множитель 2 – четный, поэтому он никак не влияет на делимость на 3 или 9. Можем его не брать в расчет и рассматривать выражение:
x 2 + y2 + 20(10 – (x + y)) + xy
Предположим, что и x, и y делятся на 3. Тогда x 2 + y2 + xy делится на 3, а 20(10 – (x + y)) – не делится. Следовательно, и вся сумма x 2 + y2 + 20(10 – (x + y)) + xy на 3 не делится.
Предположим, что на 3 делится только одна цифра. Тогда, учитывая, что (x + y) обязательно меньше 10, иначе сумма равная 20 не получится, подберем возможные пары.
(3;8), (6;5), (6;7), (6;8), (9;2), (9;4), (9;5), (9;7), (9;8).
Методом подстановки проверим, соответствуют эти пары условию.
x 2 + y2 + 20(10 – (x + y)) + xy = 3 2 + 82 + 20(10 – (3 + 8)) + 3 · 8 = 9 + 64 – 20 + 24 = 77
x 2 + y2 + 20(10 – (x + y)) + xy = 6 2 + 52 + 20(10 – (6 + 5)) + 6 · 5 = 36 + 25 – 20 + 30 = 71
x 2 + y2 + 20(10 – (x + y)) + xy = 6 2 + 72 + 20(10 – (6 + 7)) + 6 · 7 = 36 + 49 – 60 + 42 = 67
x 2 + y2 + 20(10 – (x + y)) + xy = 6 2 + 82 + 20(10 – (6 + 8)) + 6 · 8 = 36 + 64 – 80 + 48 = 68
x 2 + y2 + 20(10 – (x + y)) + xy = 9 2 + 22 + 20(10 – (9 + 2)) + 9 · 2 = 81 + 4 – 20 + 18 = 83
x 2 + y2 + 20(10 – (x + y)) + xy = 9 2 + 42 + 20(10 – (9 + 4)) + 9 · 4 = 81 + 16 – 60 + 36 = 73
Ни одна из полученных сумм не удовлетворяет условию «сумма квадратов цифр делится на 3, но не делится на 9».
Следующие пары можно не проверять, так как они дают уже имеющиеся тройки цифр.
Предположим, что ни одна из цифр числа не делится на 3.
Возможные пары:
(4;7), (5;7), (5;8), (7;8).
Проверим:
x 2 + y2 + 20(10 – (x + y)) + xy = 4 2 + 72 + 20(10 – (4 + 7)) + 4 · 7 = 16 + 49 – 20 + 28 = 73
x 2 + y2 + 20(10 – (x + y)) + xy = 5 2 + 72 + 20(10 – (5 + 7)) + 5 · 7 = 25 + 49 – 40 + 35 = 69
Сумма 69 удовлетворяет условию «сумма квадратов цифр делится на 3, но не делится на 9». Следовательно, подходят цифры 5,7,8 в любом порядке.
Ответ: 578
Вариант 19МБ2
[su_note note_color=”#defae6″]
На 6 карточках написаны цифры 1; 2; 3; 6; 9; 9 (по одной цифре на каждой карточке). В выражении □ + □□ + □□□ вместо каждого квадратика положили карточку из набора. Оказалось, что полученная сумма делится на 10. Найдите эту сумму. В ответе укажите какое-нибудь одно такое число.
[/su_note]
Алгоритм выполнения:
- Вспомнить признак делимости на 10.
- Разместить последние цифры каждого слагаемого таким образом, чтобы в сумме получилось 10.
- Расположить оставшиеся карточки в произвольном порядке.
Решение:
1. Если сумма делится на 10 нацело, то последняя цифра должна быть 0, остальные цифры значения не имеют.
2. В первый квадрат поместим цифру 1, в следующем числе на последнем месте – цифру 3 (или 6), а в третьем – цифру 6 (или 3), получим (сумма 1+3+6=10):
3. Остальные цифры заполним произвольно, например, так:
и получится сумма
1+23+996 = 1020.
Ответ: 1020
Вариант 19МБ3
[su_note note_color=”#defae6″]
На 6 карточках написаны цифры 1; 2; 2; 3; 5; 7 (по одной цифре на каждой карточке). В выражении □ + □□ + □□□ вместо каждого квадратика положили карточку из набора. Оказалось, что полученная сумма делится на 20. Найдите эту сумму. В ответе укажите какое-нибудь одно такое число.
[/su_note]
Алгоритм выполнения:
- Вспомнить признак делимости на 10 и сформулировать признак делимости на 20.
- Разместить последние цифры каждого слагаемого таким образом, чтобы в сумме получилось 10.
- Разместить предпоследние цифры каждого слагаемого таким образом, чтобы в сумме получилось четное число в результате с учетом суммы первых цифр.
- Расположить оставшиеся карточки в произвольном порядке.
Решение:
1. Чтобы сумма делилась на 20, она должна заканчиваться на 0 и вторая цифра с конца должна быть четной (делиться на 2). Чтобы в конце суммы получить 0, первые три карточки следует выбрать так:
2. Чтобы вторую цифру получить четной, можно взять карточки 2 и 7 (к ней будет добавляться еще 1 от первой суммы 10):
3. В последнее место помещаем оставшуюся цифру 1, в результате имеем:
и сумма равна:
2+23+175=200.
Ответ: 200
Вариант 19МБ4
[su_note note_color=”#defae6″]
Найдите четырехзначное число, кратное 15, произведение цифр которого больше 0, но меньше 25. В ответе укажите какое-нибудь одно такое число.
[/su_note]
Алгоритм выполнения
- Если произведение >0, то, значит, оно не равно нулю. Следовательно, ни один из множителей не может быть равным 0.
- Если произведение кратно 15, следовательно, оно кратно 5 и кратно 3.
- Если произведение кратно 5, то результат его должен оканчиваться 0 или 5. В данном случае берем 5, т.к. 0 не может быть одним из множителей (см.п.1).
- Итак, последняя цифра числа равна 5. Тогда произведение первых трех равно 25:5=5. Это означает, что нужно подобать 3 цифры так, чтобы их произведение было менее 5.
- Из всех полученных наборов цифр выбираем такой, чтобы сумма этих цифр плюс 5 (последняя, 4-я цифра) была кратной 3.
Решение:
Поскольку по условию произведение всех цифр кратно 15, то оно кратно 5 и 3.
Кратность 5 означает, что последней цифрой числа может быть только 0 или 5. Но 0 в виде последней цифры означал бы, что произведение всех 4-х цифр стало бы равным 0; а это противоречит условию. Тогда последняя цифра искомого числа равна 5.
Тогда получим: x·y·z·5<25 → x·y·z<5, где x, y, z – соответственно, 1-я, 2-я и 3-я цифры искомого числа.
Меньше 5 произведение таких цифр: 1 1 1, 1 1 3, 1 1 2, 1 2 2.
Согласно признаку делимости на 3, выбираем из этих наборов такой, чтобы сумма его цифр плюс 5 делилась на 3:
1+1+1+5=8 – не подходит;
1+1+3+5=10 – не подходит;
1+2+2+5=10 – не подходит
1+1+2+5=9 – подходит.
Тогда условию задачи соответствуют числа: 1125, 1215, 2115.
Ответ: 1125, 1215, 2115
Вариант 19МБ5
[su_note note_color=”#defae6″]
Вычеркните в числе 85417627 три цифры так, чтобы получившееся число делилось на 18. В ответе укажите какое-нибудь одно получившееся число.
[/su_note]
Алгоритм выполнения
- Число делится на 18, если оно кратно 2 и 9.
- Кратность 2 означает, что число должно быть четным. Поэтому сразу отбрасывают последнюю – нечетную – цифру 7.
- Кратность 9 означает, что сумма его цифр делится на 9. Значит, находим сумму оставшихся цифр. Далее определяем подходящее для полученной суммы число, кратное 9. Число должно быть таким, чтобы: а) оно было меньшим суммы цифр; б) разница между этой суммой и найденным числом позволяла выделить в числе 2 цифры, сумма которых была бы равной этой разнице. Вычеркиваем эти цифры.
Решение:
Т.к. по условию число кратно 18, то оно кратно 2 и кратно 9.
Поскольку число кратно 2, то оно должно оканчиваться четной цифрой. 7 – нечетная цифра, поэтому вычеркиваем ее. Осталось: 8541762.
Т.к. полученное число кратно 9, то сумма его цифр должна делиться на 9. Находим общую сумму его цифр: 8+5+4+1+7+6+2=33. Ближайшее число, которое делится на 9, – это 27.
33–27=6 – это сумма двух цифр, которые нужно вычеркнуть. Пары цифр, которые при этом в сумме дают 6, – это 5 и 1 или 4 и 2. Вычеркнув их, получаем соответственно: 84762 или 85176.
Кроме этого, на 9 делится 18. Тогда 33–18=15. В этом случае вычеркнуть придется 8 и 7. Получаем: 54162.
На 9 делится еще и 9, однако 33–9=24, а пары цифр, которые дали бы в сумме 24, естественно, не существует.
Ответ: 84762, 85176, 54162
Вариант 19МБ6
[su_note note_color=”#defae6″]
На шести карточках написаны цифры 3; 6; 7; 7; 8; 9 (по одной цифре на каждой карточке). В выражении
Вместо каждого квадратика положили карточку из данного набора. Оказалось, что полученная сумма делится на 10, но не делится на 20.
В ответе укажите какую-нибудь одну такую сумму.
[/su_note]
Алгоритм выполнения
- Во 2-м предложении текста задачи фактически представлено условие, при котором сумма делится на 10, однако не делится на 2.
- Из п.1 следует, что результирующее число должно оканчиваться 0, а предпоследняя его цифра должна быть нечетной.
Решение:
Для удобства восприятия разместим карточки в столбик:
Если число делится на 10, но не делится на 20, значит, оно точно не делится на 2 без последнего нуля.
Поскольку число кратно 10, то оно должно оканчиваться нулем. Поэтому в последнем разряде (единиц) нужно расположить 3 карточки с такими цифрами, чтоб их сумма оканчивалась на 0. Подходят здесь карточки: 1) 6, 7, 7; 2) 3, 8, 9. Их суммы равны 20. Соответственно, 0 мы пишем под чертой, а 2 переносим на предыдущий разряд (десятков):
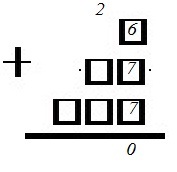
Чтобы число не делилось на 20, необходимо, чтобы перед нулем стояла нечетная цифра. Нечетная сумма здесь получится тогда, когда одно из слагаемых будет нечетным, а два других четными. Одно из этих (других) слагаемых – это перенесенная 2. Поэтому из оставшихся цифр следует взять: 1) 3 и 8; 2) 6 и 7. Получаем:
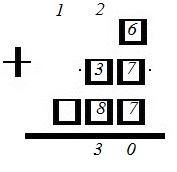
На место сотен ставим последнюю (оставшуюся) карточку с цифрой: 1) 9; 2) 7. Получаем, соответственно, числа 1030 и 850:
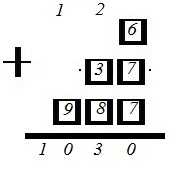
Ответ: 1030,850
Вариант 19МБ7
[su_note note_color=”#defae6″]
Найдите четное трехзначное натуральное число, сумма цифр которого на 1 меньше их произведения. В ответе укажите какое-нибудь одно такое число.
[/su_note]
Алгоритм выполнения
- Вводим буквенные обозначения для цифр искомого числа. Исходя из условия задачи, составляем уравнение.
- Выражаем одну из цифр через 2 другие.
- Подбираем для этих 2-х (других) цифр значения так, чтобы 3-я (выраженная) представляло бы собой натуральное число. Вычисляем 3-ю цифру.
- Формируем искомое число так, чтобы оно было четным.
Решение:
Пусть цифры искомого числа – x, y, z. Тогда получаем:
xyz–(x+y+z)=1
xyz–x–y–z=1
zxy–z=x+y+1
z(xy–1)=x+y+1
z=(x+y+1)/(xy–1)
Знаменатель в этом выражении должен быть целым и положительным. Для простоты (а также для гарантии правильных расчетов) примем, что он должен быть равен 1. Тогда имеем: ху–1=1 → ху=2. Поскольку х и у это цифры, то их значения могут быть равными только 1 и 2 (т.к. только произведение этих однозначных натур.чисел дает в результате 2).
Отсюда z составляет: z=(1+2+1)/(1·2–1)=4/1=4.
Итак, имеем цифры: 1, 2, 4.
Т.к. по условию итоговое число должно быть четным, то оканчиваться оно может только 2 или 4. Тогда правильными вариантами чисел будут такие:
124, 142, 214, 412.
Ответ: 124, 142, 214, 412
Вариант 19МБ8
[su_note note_color=”#defae6″]
Найдите шестизначное число, которое записывается только цифрами 2 и 0 и делится на 24. В ответе укажите какое-нибудь одно такое число.
[/su_note]
Алгоритм выполнения
- Если число делится на 24, значит, оно делится на 8 и на 3.
- Согласно признаку делимости на 8, 3 последних цифры его должны образовывать число, которое кратно 8.
- Чтобы число делилось на 3, необходимо, чтобы сумма его цифр делилась на 3. Учитывая уже сформированную 2-ю часть числа (см.п.2), дополняем его первыми тремя цифрами соответственно.
Решение:
Чтобы искомое число было кратно 24, требуется, чтобы оно делилось на 8 и в то же время на 3.
Число делится на 8, если последние его 3 цифры образуют число, кратное 8. С использованием только двоек и нулей такое трехзначное число можно образовать так: 000, 002, 020, 022, 200, 202, 220, 222. Из этих чисел на 8 делится только 000 и 200.
Теперь нужно дополнить искомое число первыми 3-мя цифрами так, чтобы оно делилось еще и на 3.
В 1-м случае это будет единственный вариант: 222000.
Во 2-м случае вариантов два: 220200, 202200.
Ответ: 222000, 220200, 202200
Вариант 19МБ9
[su_note note_color=”#defae6″]
Найдите четырехзначное число, кратное 15, произведение цифр которого больше 35, но меньше 45. В ответе укажите какое-нибудь одно такое число.
[/su_note]
Алгоритм выполнения
- Если число кратно 15, значит, оно кратно 3 и 5.
- Применяем признак делимости на 5 и условие задачи, согласно которому произведение цифр числа ≠0. Так получаем, что последняя цифра искомого числа – только 5.
- Делим 35 на 5 и 45 на 5. Узнаем диапазон значений, которые может принимать произведение первых 3-х цифр числа. Узнаем, что оно может быть равно только 8.
- Определяем последовательности цифр, которые дают при перемножении 8.
- Проверяем полученные из найденных цифр числа на кратность трем.
Решение:
Кратность искомого числа 15 дает 2 условия: оно должно делиться на 5 и на 3.
Если число кратно 5, то оно должно оканчиваться цифрой 5 или 0. Однако 0 в данном случае использовать нельзя, поскольку при этом произведение цифр числа оказывается равным 0. По условию же это не так. Итак, последняя – 4-я – цифра числа равна 5.
По условию 35 < x·5 < 45, где х – произведение первых 3-х цифр числа. Тогда имеем: 7 < x < 9. Это неравенство верно только при х=8. Следовательно, для первых 3-х цифр должны выполняться равенства:
1·1·8=8, 1·2·4=8.
Отсюда получаем числа:
1185; 1245.
Проверяем их на кратность 3:
1+1+8+5=15;
1+2+4+5=12.
Вывод: оба найденные числа кратны 3. Плюс кратны их комбинации:
1815; 8115; 1425; 2145; 2415; 4125; 4215.
Ответ: 1815; 8115; 1425; 2145; 2415; 4125; 4215
Вариант 19МБ10
[su_note note_color=”#defae6″]
Найдите пятизначные число, кратное 25, любые две соседние цифры которого отличаются на 2. В ответе укажите какое-нибудь одно такое число.
[/su_note]
Алгоритм выполнения
- Принимаем во внимание, что на 25 делятся числа, которые придется последовательно делить на 5 дважды. Определяем, какой парой цифр они должны оканчиваться.
- Учитывая, что 2-й частью условия является различие каждой соседней пары цифр исключительно на 2 единицы, выбираем подходящий вариант (или варианты) цифр.
- Способом подбора находим остальные цифры и, соответственно, числа. Одно из них запишем в ответе.
Решение:
Если число делится на 25, то оно должно оканчиваться на: 00, 25, 50, 75. Т.к. соседние цифры должны отличаться строго на 2, то использовать для 4-й и 5-й цифр можем только 75. Получаем: ***75.
Далее ищем 3-ю цифру:
- **975 или
- **575.
Дальше получаем по аналогии:
1) *7975 → 97975 или 57975;
2) *3575 → 13575 или 53575, *7575 → 57575 или 97575.
Ответ: 97975, 57975, 13575, 53575, 57575, 97575
Вариант 19МБ11
[su_note note_color=”#defae6″]
Найдите трехзначное натуральное число, большее 600, которое при делении на 3, на 4 и на 5 дает в остатке 1 и цифры которого расположены в порядке убывания слева направо. В ответе укажите какое-нибудь такое число.
[/su_note]
Алгоритм выполнения
- Определяем диапазон значений для 1-й цифры числа (сотен).
- Определяем, какой может быть последняя цифра (единицы), приняв во внимание: 1) при делении на 5 дает в остатке 1; 2) на этом месте не может быть четная цифра, поскольку это одно из условий делимости на 4.
- Способом подбора определяем набор чисел, которые при делении на 3 дают в остатке 1.
- Из этого набора (см.п.3) отбрасываем числа, которые при делении на 4 дают остаток, отличный от 1.
Решение:
Т.к. искомое число >600 и при этом является трехзначным, то 1-й цифрой может быть только 6, 7, 8 или 9. Тогда получаем для искомого числа:
6***
7***
8***
9***
Если число при делении на 5 должно давать в остатке 1, значит, оно может оканчиваться только на 0+1=1 или на 5+1=6. Шестерку тут отбрасываем, поскольку в этом случае число четное и потенциально может делиться на 4. Поэтому имеем:
6**1
7**1
8**1
9**1
Если число при делении на 3 дает в остатке 1, значит, сумма его цифр должна быть кратной 3 плюс 1. Кроме того, учитываем, что цифры должны располагаться в числе в порядке убывания. Подбираем такие числа:
631
721
751
841
871
931
961
Из этой последовательности отбрасываем числа, для которых не выполняется условие о том, что число при делении на 4 должно давать в остатке 1.
Т.к. признак делимости на 4 заключается в том, что 2 последние цифры должны делиться на 4, то получаем:
для 631: 31=28+3, т.е. в остатке имеем 3; число не подходит
для 721: 21=20+1, т.е. в остатке – 1; число подходит
для 751: 51=48+3, т.е. в остатке – 3; число не подходит
для 841: 41=40+1, т.е. в остатке – 1; число подходит
для 871: 71=68+3, т.е. в остатке – 3; число не подходит
для 931: 31=28+3, т.е. в остатке – 3; число не подходит
для 961: 61=60+1, т.е. в остатке – 1; число подходит
Ответ: 721, 841, 961
Вариант 19МБ12
[su_note note_color=”#defae6″]
Найдите трехзначное натуральное число, большее 400, но меньшее 650, которое делится на каждую свою цифру и все цифры которого различны и не равны 0. В ответе укажите какое-нибудь одно такое число.
[/su_note]
Алгоритм выполнения
- Из условия следует, что числа могут начинаться только на 4,5 или 6.
- При анализе чисел 4-й сотни отбрасываем числа: 1) 1-го десятка, т.к. в них содержится 0; 2) 4-го десятка, т.к. в этом случае первые две цифры совпадут; 3) числа 5-го десятка, т.к. они должны оканчиваться только на 5 или 0, что недопустимо. Кроме того, для всех четных десятков можно рассматривать только четные числа.
- Числа 5-й сотни отбрасываем полностью, т.к. чтобы делиться на каждую свою цифру, они должны оканчиваться 5 или 0.
- Для чисел 6-й сотни рассматривать можно только: 1) четные; 2) кратные 3; 3) не оканчивающиеся 0.
Решение:
Числа 40* и 4*0 отбрасываем, т.к. они содержат 0.
Числа 41* годятся только четные, т.к. это обязательное условия для кратности 4. Анализируем:
412 – подходит
414 – не подходит, т.к. в нем совпадают цифры
416 – не подходит, т.к. не делится на 6
418 – не подходит, т.к. не делится ни на 4, ни на 8
Из чисел 42* годятся только четные, поскольку должны делиться на 2:
422 и 424 – не подходят, т.к. в них совпадают цифры
426 – не подходит, т.к. не делится на 4
428 – не подходит, т.к. не делится на 8
Числа 43* годятся только четные и кратные 3. Поэтому тут подходит только 432.
Числа 44* не подходят полностью.
Числа 45* не подходят полностью, т.к. они должны оканчиваться только 5 (т.е. быть нечетными) или 0.
Числа 46*, 47*, 48*, 49* не подходят полностью, т.к. для каждого из них не выполняется 1 или несколько условий.
Числа 5-й сотни не годятся полностью. Они должны делиться на 5, а для этого оканчиваться либо 5, либо 0, что не допускается.
Числа 60* не годятся полностью.
Среди остальных можно рассматривать только четные, кратные 3, не оканчивающиеся 0. Опуская подробности перебора чисел, оговорим только, что из них годятся: 612, 624, 648. Для остальных не выполняется одно или несколько условий.
Ответ: 412, 432, 612, 624, 648
Вариант 19МБ13
[su_note note_color=”#defae6″]
Найдите четырехзначное число, кратное 45, все цифры которого различны и четны. В ответе укажите какое-нибудь одно такое число.
[/su_note]
Алгоритм выполнения
- Если число кратно 45, значит, оно делится на 5 и на 9.
- Рассматривать следует только числа четных сотен.
- Оканчиваться числа могут только 0, т.к. 5 – нечетная цифра.
- Сумма цифр числа должна быть равна 18. Только в этом случае можно составить его из всех четных цифр.
Решение:
Т.к. по условию цифры должны быть четными, то рассматривать можно только числа 2-й, 4-й, 6-й и 8-й тысяч. Это значит, что начинаться оно может с 2, 4, 6 или 8.
Если число кратно 45, то оно кратно 5 и кратно 9.
Если число кратно 5, то оно должно оканчиваться 5 или 0. Но поскольку все цифры должны быть четными, то подходит здесь только 0.
Т.о., получаем шаблоны чисел: 2**0, 4**0, 6**0, 8**0. Отсюда следует, что для проверки кратности 9 требуется, чтобы сумма первых 3-х цифр была равной 9, или 18, или 27 и т.д. Но подходит тут только 18. Основания: 1) для получения в сумме 9 нужно, чтобы одно из слагаемых было нечетным, а это противоречит условию; 2) 27 не подходит потому, что даже если взять самую большую 1-ю цифру 8, то сумма 2-й и 3-й цифр будет равна 27–8=19, что превышает допустимый предел. Еще большие суммы цифр, кратные 9, не подходят тем более.
Рассматриваем числа по тысячам.
Числа 2**0. Сумма средних цифр равна: 18–2=16. Получить 16 из четных чисел можно только так: 8+8. Однако цифры не должны повторяться. Поэтому подходящих условию чисел здесь нет.
Числа 4**0. Сумма средних цифр: 18–4=14. 14=8+6. Поэтому получаем: 4680 или 4860.
Числа 6**0. Сумма средних цифр: 18–6=12. 12=6+6, что не подходит, т.к. цифры повторяются. 12=4+8. Получаем: 6480 или 6840.
Числа 8**0. Сумма средних цифр: 18–8=10. 10=2+8, что не подходит, т.к. при этом будет повторяться 8. 10=4+6. Получаем: 8460 или 8640.
Ответ: 4680, 4860, 6480, 6840, 8460, 8640
Даниил Романович | Просмотров: 11.5k
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ПО
ТЕОРИИ ЧИСЕЛ
(ЗАДАНИЕ 19 ИЗ ЕГЭ ПО МАТЕМАТИКЕ, ПРОФИЛЬНЫЙ
УРОВЕНЬ)
Аннотация
Статья посвящена проблеме подготовки учащихся к решению задач по теории
чисел, которые входят в комплект заданий профильного уровня ЕГЭ по математике в
качестве задания под номером 19. Указанные задачи вызывают затруднение даже у
хорошо подготовленных участников, некоторые школьники даже не предпринимают
попыток решения этого задания. В статье перечислены необходимые методы и приемы
решения, а также даны рекомендации по подготовке учащихся к решению задания 19
ЕГЭ.
Ключевые
слова: математика, ЕГЭ, теория чисел.
Важной частью обучения математике сегодня является подготовка к Единому
государственному экзамену (ЕГЭ), особенно в старших классах. Желающие
продолжить обучение по техническим или математическим специальностям выбирают
профильный уровень ЕГЭ по математике, который отличается от базового более
высокой сложностью и разнообразием заданием.
Проведенный анализ результатов ЕГЭ по математике показывает, что у
обучающихся среди заданий по алгебре наибольшую сложность вызывают задачи 18 и
19, требующие развернутого ответа, т.е. уравнения и неравенства с параметром и
задача на исследование простейших математических моделей.
Мы считаем, что эти задачи необходимо рассматривать дополнительно,
обращая внимания на особенности решения. В частности, на некоторых сайтах
указывают, что задача 19 является олимпиадной [10; 11], а иногда даются
рекомендации не тратить время на ее решение [4]. Однако это задание включает в
себя элементы теории чисел и не выходит за пределы школьной программы [8, с.
161]. Как нам кажется, при определенных условиях можно повысить эффективность
подготовки учащихся с целью успешного решения последней задачи профильного
уровня ЕГЭ.
Элементы теории чисел представляют значимость именно для
математического образования, так как позволяют сформировать понятие числа как
основы числовых систем. Кроме того, изучение теории чисел положительно
воздействует на развитие логического мышления, формируют математическую
культуру учащихся, учит их работать с абстрактными понятиями [1, с. 99].
По мнению, И.Л. Мирошниченко и Е.Н. Селезневой необходимо регулярно
разбирать с учащимися задачи на теорию чисел, начиная с 5-6 класса. При этом
содержание задач должно соответствовать изучаемым темам. Например, авторы
приводят примеры задач, которые можно использовать в процессе изучения таких
тем, как «Признаки делимости», «Среднее арифметическое», «Арифметический
квадратный корень», «Квадратный трехчлен» и т.д. [3, с. 55].
Но не всегда один учитель ведет весь курс математики у одного класса,
часто происходят замены учителя, либо школьник меняет образовательное
учреждение. К тому же такой подход требует от учителя серьезных затрат времени
на поиск или составление задачи, подходящей по своему содержанию. Также не
следует исключать вероятности изменения структуры ЕГЭ, в результате чего задача
на теорию чисел будет исключена из комплекта заданий. Поэтому целенаправленную
подготовку учащихся начинают ближе к экзамену, обычно в старших классах.
В своей статье А.Е. Семенова указывает, что для решения задачи 19 ЕГЭ участники
экзамена должны знать признаки делимости, понятие наименьшего общего кратного,
а также свойства чисел [6, с. 994].
На наш взгляд, помимо указанных понятий, следует повторить и закрепить
с учащимися алгоритм нахождения наименьшего общего кратного и наибольшего
общего делителя, порядок вычисления арифметической и геометрической прогрессии.
При повторении следует основной упор сделать на решение задач, как заданных
явно («Последовательность n натуральных чисел представляет собой
арифметическую прогрессию. Может ли их сумма быть равна 10?»), так и в виде
сюжетной задаче: («12 одинаковых монет нужно разместить вдоль стенок квадратной
коробки так, чтобы возле каждой стенки находилось равное количество монет. Каким
образом можно выполнить?»).
В пособии А.Э. Сергеева и И.В. Соколовой выделены следующие группы
типовых задач, составленных по мотивам задания 19: прогрессии, уравнения в
целых числах, обыкновенные дроби, простые числа и свойства делителей [7].
Рассмотрим, какие знания, методы и приемы будут полезны при решении
задания 19 ЕГЭ:
– алгоритм Евклида для нахождения НОД;
– свойство делимости чисел: произведение чисел делится на простое
число, если один из множителей делится на это число;
– свойство делимости чисел: если число а не делится ни на одно простое
число меньше , то оно простое;
– метод математической индукции;
– методы решения линейного диофантова уравнения: поиск частного решения
и переход к общему; выразить одно неизвестное через другое; геометрический;
– перебор вариантов,
– метод
разложения числа на множители,
– метод остатков. [2; 5; 7].
Учитывая, что задание 19 можно отнести к нестандартным задачам, т.е. не
имеющим единого алгоритма решения, то мы считаем необходимым придерживаться
принципов регулярности, систематичности и последовательности при подготовке к
ее решению. Учащиеся должны хорошо ориентироваться в методах решения, знать
основные приемы, упрощающие решение, быть знакомы с типовыми задачами. Поэтому сначала
необходимо рассмотреть простые примеры, позволяющие отработать практическое
применение названых методов и приемов.
Например, изучение метода нахождения НОД с помощью алгоритма Евклида,
может включать в себя задачи различных уровней сложности:
1. Использование алгоритма на конкретном примере, т.е. нахождение НОД
любых двух натуральных чисел (числа могут называть сами учащиеся, либо учитель
выбирает трехзначные и четырехзначные числа).
2. Использование алгоритма для буквенных (нахождение НОД 2n+17 и n+7) или
числовых выражений (нахождение НОД 2100-1 и 2120-1).
3. Решение задач из сборника по подготовке к ЕГЭ (На какое число и при
каких натуральных значениях n сократима дробь ?).
Наиболее оптимальным вариантом подготовки учащихся, на наш взгляд,
является разработка элективного курса, направленного на знакомство учащихся с
теорией чисел. Курс может быть представлен также и в дистанционном формате,
например, на основе системы MOODLE, возможности использования которой в
обучении школьников математике описывается в работе одного из авторов данной статьи
[9]. Преимущество решения задач по теории чисел во внеурочной деятельности
состоит в том, чтобы научить решать тех школьников, которые стремятся получить
максимальный балл профильного уровня ЕГЭ.
Подводя итоги, можно сделать вывод, что сложность задания 19
профильного уровня ЕГЭ по математике вполне преодолима, если участник будет
заниматься дополнительной подготовкой, изучая элементы теории чисел.
Литература
1. Гапонова Ю.С. Роль и место элементарной теории чисел в математическом
образовании школьников // Концепция «общества знаний» в современной науке: сб.
ст. Межд. науч.-практ. конф. – Уфа: Аэтерна, 2018. – С. 98-103.
2. Иванова В.И. Линейное диофантово уравнение и 4 способы его решения
// Первое сентября. Открытый урок [Электронный ресурсы]. – Режим доступа: https://urok.1sept.ru/articles/501260.
3. Мирошниченко И.Л., Селезнева Е.Н. Элементы теории чисел в школьном
курсе математики // Вестник педагогического опыта. – 2019. – №44. – С. 51-55.
4. Ненко И. Как подготовиться к ЕГЭ по математике //
Нижний Новгород онлайн [Электронный
ресурсы]. – Режим доступа: https://www.nn.ru/news/articles/uchitelya_rasskazali_na_chem_v_ege_po_matematike_zavalivaetsya_kazhdyy_vtoroy/69093625/.
5. Свиридова А.В. Способы решений уравнений в целых числах
// Старт в науке [Электронный
ресурсы]. – Режим доступа: https://school-science.ru/4/7/828
6. Семенова А.Е. Элементы теории чисел в школьном курсе математики //
Аллея науки. – 2019. – Т. 3. – №5. – С. 993-995.
7. Сергеев А. Э., Соколова И. В. Теория чисел в задаче №19
профильного ЕГЭ по математике: учеб. пособие. – Краснодар : КубГАУ, 2019. – 108
с.
8. Соколова И.В., Сергеев А.Э. Методические рекомендации к
решению задачи № 19 профильного
ЕГЭ по математике // Современные проблемы науки и образования. – 2018. – № 6. –
С. 161.
9. Солощенко М.Ю., Петров И.Л. Использование системы MOODLE в
обучении школьников математике // Проектирование и реализация математического образования в школе и
вузе. Сборник научных трудов. – Стерлитамак, 2015. С. 63-66.
10. Структура ЕГЭ по математике 2019-2020 // Geniusmath [Электронный ресурсы]. – Режим доступа: http://courses.geniusmath.ru/blogs/read/struktura-iege-po-matiematikie-2019-2020/.
11. Шутова О. Профильный ЕГЭ по математике: что нужно
знать к 2021 году? // MaximumBlog [Электронный ресурсы]. – Режим доступа: https://blog.maximumtest.ru/post/profilnyj-ege-po-matematike-chto-nuzhno-znat.html.