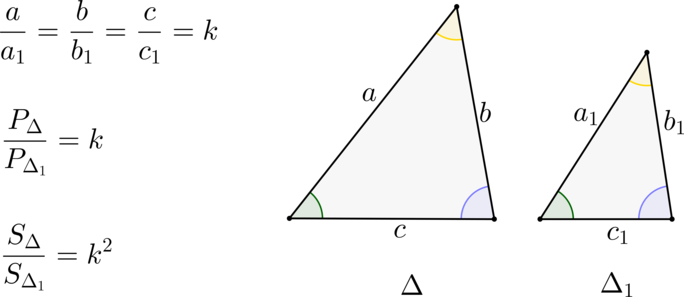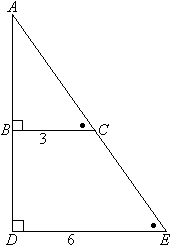23
Янв 2014
Категория: Планиметрия
Задачи на подобие треугольников
2014-01-23
2022-01-11
Рассмотрим задачи, при решении которых мы будем использовать подобие треугольников.
Уделим внимание как базовым задачам, так и задачам посложней.
В конце статье вы найдете задачи для самостоятельной работы
Задача 1. Через точки М и N, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая МN, параллельная стороне АС. Найдите длину СN, если ВС = 6, МN = 4 и АС = 9.
Решение: + показать
Задача 2. Прямая, параллельная основанию треугольника, делит его на треугольник и трапецию, площади которых относятся как 4:5. Периметр образовавшегося треугольника равен 20 см. Найдите периметр данного треугольника.
Решение: + показать
Задача 3. Через вершину прямого угла прямоугольного треугольника с катетами 6 и 8 см проведен перпендикуляр к гипотенузе. Вычислите площади образовавшихся треугольников.
Решение: + показать
Задача 4. Из одной точки проведены к кругу две касательные. Длина касательной равна 156, а расстояние между точками касания равно 120. Найдите радиус круга.
Решение: + показать
Задача 5. В трапеции меньшая диагональ
, равная 6, перпендикулярна основаниям
и
. Найдите сумму тупых углов
и
.
Решение:+ показать
Задача 6. Основания трапеции равны a и b. Определите длину отрезка, параллельного основаниям и делящего трапецию на равновеликие части.
Решение: + показать
Задачи для самостоятельной работы
1. Через точки E и F, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая EF, параллельная стороне АС. Найдите длину BС, если EF = 10, AC = 15 и FC = 9. (Ответ: 27).
2. В прямоугольном треугольнике проведена высота
к гипотенузе.
,
Найдите катет
. (Ответ: 20/3).
3. Прямая, параллельная основанию треугольника, отсекает от него треугольник, площадь которого в 8 раз меньше площади оставшейся части. Периметр большего треугольника равен 27. Найдите периметр меньшего треугольника. (Ответ: 9).
4. Основание треугольника 15 см, а боковые стороны 13 и 14 см. Высота разделена в отношении 2:3 (считая от вершины) и через точку деления проведена прямая, параллельная основанию. Найдите площадь образовавшейся при этом трапеции. (Ответ: 70,56 (возможно, вам потребуется формула Герона)).
5. В трапеции с основаниями
и
диагонали пересекаются в точке
. Площадь треугольника
равна 4, площадь треугольника
равна 9. Найдите площадь трапеции. (Ответ: 25).
6. Трапеция разделена диагоналями на четыре части. Определить ее площадь, если известны площади ее частей, прилежащих к основаниям и
. (Ответ:
).
Автор: egeMax |
комментариев 9
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 206 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
В остроугольном треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно.
а) Докажите, что прямые ЕН и АС параллельны;
б) Найдите отношение ЕН : АС, если угол АВС равен 30°.
Источник: Задания 16 (С4) ЕГЭ 2016, ЕГЭ — 2016 по математике. Основная волна 06.06.2016. Вариант 410. Запад
Объем первого куба в 8 раз больше объема второго куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Объем одного куба в 729 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Объем одного куба в 125 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Площадь трапеции ABCD равна 60, а одно из оснований трапеции втрое больше другого. Диагонали пересекаются в точке O; отрезки, соединяющие середину P основания AD с вершинами B и C, пересекаются с диагоналями трапеции в точках M и N соответственно. Найдите площадь четырёхугольника OMPN.
В трапеции ABCD BC||AD, Прямая, перпендикулярная
стороне CD, пересекает сторону АВ в точке М, а сторону CD — в точке N.
а) Докажите подобие треугольников АВN и DCM
б) Найдите расстояние от точки А до прямой ВN, если МС = 5, ВN = 3, а расстояние от точки D до прямой МС равно 6.
Источник: А. Ларин: Тренировочный вариант № 217.
На сторонах AB, BC и AC треугольника ABC отмечены точки C1, A1 и B1 соответственно, причём AC1 : C1B = 8 : 3, BA1 : A1C = 1 : 2, CB1 : B1A = 3 : 1. Отрезки BB1 и CC1 пересекаются в точке D.
а) Докажите, что ADA1B1 — параллелограмм.
б) Найдите CD, если отрезки AD и BC перпендикулярны, AC = 28, BC = 18.
Источник: ЕГЭ по математике 10.07.2020. Основная волна. Санкт-Петербург, Задания 16 ЕГЭ–2020
В треугольнике ABC известны стороны: AB = 7, BC = 8, AC = 9. Окружность, проходящая через точки A и C, пересекает прямые BA и BC соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL.
Источник: ЕГЭ по математике 07.06.2012 года, основная волна.
В треугольнике ABC известны стороны: AB = 5, BC = 6, AC = 7. Окружность, проходящая через точки A и C, пересекает прямые AB и BC соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL.
В треугольник ABC известны стороны: AB = 6, BC = 8, AC = 9. Окружность, проходящая через точки A и C, пересекает прямые BA и BC соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL.
В треугольник ABC известны стороны: AB = 14, BC = 18, AC = 20. Окружность, проходящая через точки A и C, пересекает прямые BA и BC соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL.
Площадь боковой поверхности пятиугольной пирамиды равна 13. Чему будет равна площадь боковой поверхности пирамиды, если все ее ребра уменьшить в 2 раза?
Источник: Добровольное тренировочное тестирование Санкт-Петербург 2013.
В трапеции ABCD с боковыми сторонами AB = 8 и CD = 5 биссектриса угла B пересекает биссектрисы углов A и C в точках M и N соответственно, а биссектриса угла D пересекает те же две биссектрисы в точках L и K, причем точка L лежит на основании BC.
а) Докажите, что прямая MK проходит через середину стороны AB.
б) Найти отношение KL : MN, если LM : KN = 4 : 7.
Источник: А. Ларин: Тренировочный вариант № 44.
Прямая, параллельная основаниям BC и AD трапеции ABCD, пересекает боковые стороны AB и CD в точках M и N. Диагонали AC и BD пересекаются в точке O. Прямая MN пересекает стороны OA и OD треугольника AOD в точках K и L соответственно.
а) Докажите, что MK = NL.
б) Найдите MN, если известно, что BC = 3, AD = 8 и MK : KL = 1 : 3.
Источник: А. Ларин: Тренировочный вариант № 46.
Продолжение медианы AE треугольника ABC пересекает описанную около треугольника окружность в точке D.
а) Докажите подобие треугольников ABC и AEC, если AC = CD.
б) Найдите длину отрезка BC, если длина каждой из хорд AC и DC равна 1.
Источник: А. Ларин: Тренировочный вариант № 69.
Четырехугольник ABCD вписан в окружность. Точка Х лежит на его стороне AD, причем ВХ || CD и CX || BA, и DX = 6.
а) Докажите, что треугольники АВХ и ВХС подобны.
б) Найдите ВС.
Источник: А. Ларин: Тренировочный вариант № 89.
Прямая p, параллельная основаниям BC и AD трапеции ABCD, пересекает прямые AB, AC, BD и CD в точках E, F, G и H соответственно, причём EF = FG.
а) Докажите, что точки пересечения прямой p с диагоналями AC и BD делят отрезок EН на три равных части;
б) Найдите EF, если BC = 3, AD = 4.
Источник: А. Ларин: Тренировочный вариант № 88.
В остроугольном треугольнике ABC проведены высоты AK и BP.
а) Докажите, что углы АКР и ABP равны.
б) Найдите длину отрезка PK, если известно, что AB = 5, BC = 6, CA = 4.
Источник: А. Ларин: Тренировочный вариант № 161.
Всего: 206 1–20 | 21–40 | 41–60 | 61–80 …
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Треугольник: задачи на подобие
(blacktriangleright) Треугольники подобны, если их углы равны, а сходственные стороны (лежащие напротив равных углов) относятся друг к другу с одним и тем же коэффициентом (k) (пропорциональны).
(blacktriangleright) Признаки подобия:
1. Два угла одного треугольника равны двум углам другого треугольника.
2. Три стороны одного треугольника пропорциональны трем сторонам другого треугольника.
3. Две стороны одного треугольника пропорциональны двум сторонам другого, а углы между этими сторонами равны.
(blacktriangleright) Площади подобных треугольников относятся как (k^2), а периметры – как (k).
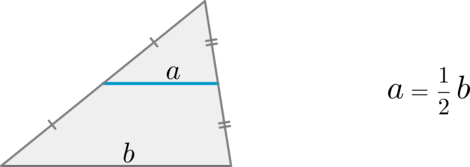
(blacktriangleright) Средняя линия треугольника – отрезок, соединяющий середины двух сторон. Она равна половине третьей стороны.
Задание
1
#3935
Уровень задания: Равен ЕГЭ
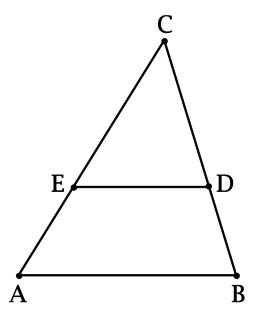
Точка (E) лежит на стороне (AC) треугольника (ABC), причём (dfrac{EC}{AE} = 2). Точка (D) лежит на (BC), причём (EDparallel AB). Найдите (AB), если (ED = dfrac{4}{3}).
Так как (EDparallel AB), то (angle CED = angle CAB), (angle CDE = angle CBA) (как соответственные при параллельных прямых и секущей), тогда треугольники (CED) и (CAB) подобны.
Так как (EC = 2cdot AE), то (AC = 3cdot AE), следовательно, [dfrac{AC}{EC} = dfrac{3cdot AE}{2cdot AE} = dfrac{3}{2}.]
Так как стороны (EC) и (AC) лежат против равных углов (в треугольниках (CED) и (CAB) соответственно), то [dfrac{AB}{ED} = dfrac{AC}{EC} = dfrac{3}{2},] откуда [AB = dfrac{3}{2}cdot ED = dfrac{3}{2}cdotdfrac{4}{3} = 2.]
Ответ:
2
Задание
2
#3937
Уровень задания: Равен ЕГЭ
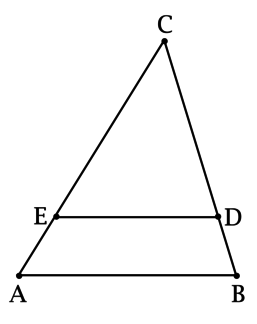
Точка (E) лежит на стороне (AC) треугольника (ABC), причём (dfrac{EC}{AE} = 3). Точка (D) лежит на (BC), причём (dfrac{CD}{CB} = 0,75). Найдите (angle CED — angle CAB). Ответ дайте в градусах.
Рассмотрим треугольники (CAB) и (CED):
(angle C) – общий,
[dfrac{CA}{CE} = dfrac{AE + CE}{CE} = dfrac{AE}{CE} + 1 = dfrac{1}{3} + 1 = dfrac{4}{3} = dfrac{CB}{CD},] тогда треугольники (CAB) и (CED) подобны по пропорциональности двух сторон и равенству углов между ними.
В подобных треугольниках против пропорциональных сторон лежат равные углы, тогда (angle CED = angle CAB), откуда (angle CED — angle CAB = 0^{circ}).
Ответ:
0
Задание
3
#3943
Уровень задания: Равен ЕГЭ
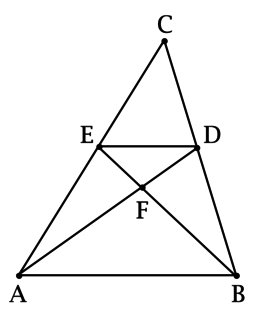
(F) – точка пересечения (AD) и (BE) – медиан треугольника (ABC). Известно, что (S_{ABF} = 1). Найдите (S_{DEF}).
(ED) – средняя линия треугольника (ABC), тогда (ED = 0,5cdot AB), (EDparallel AB).
Так как (EDparallel AB), то (angle DEF = angle ABF), (angle EDF = angle FAB) (как внутренние накрест лежащие при параллельных прямых и секущей), следовательно, треугольники (DEF) и (ABF) подобны (по двум углам). Так как (ED = 0,5cdot AB), причём стороны (ED) и (AB) лежат (в треугольниках (DEF) и (ABF) соответственно) против равных углов, то [dfrac{S_{DEF}}{S_{ABF}} = left(dfrac{ED}{AB}right)^2 = 0,5^2 = 0,25,] откуда с учётом того, что (S_{ABF} = 1) находим (S_{DEF} = 0,25).
Ответ:
0,25
Задание
4
#3936
Уровень задания: Сложнее ЕГЭ
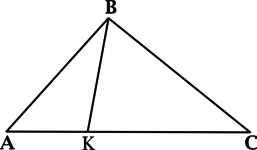
Отрезок (BK) соединяет вершину (B) треугольника (ABC) с точкой на противоположной стороне, причем (angle AKB = angle B). При этом известно, что (BK = 10), (AB = 12), (AC = 18). Найдите (BC).
Рассмотрим треугольники (ABK) и (ACB):
(angle AKB = angle B),
(angle A) – общий, тогда треугольники (ABK) и (ACB) подобны по двум углам.
В подобных треугольниках против равных углов лежат пропорциональные стороны, тогда [dfrac{BK}{BC} = dfrac{AB}{AC},] откуда (dfrac{10}{BC} = dfrac{12}{18}), следовательно (BC = 15).
Ответ:
15
Задание
5
#3938
Уровень задания: Сложнее ЕГЭ
Отрезок (BK) соединяет вершину (B) треугольника (ABC) с точкой на противоположной стороне. При этом известно, что (angle AKB = 105^{circ}), (AB = 12), (AC = 24), (AK = 6). Найдите (angle ABC). Ответ дайте в градусах.
Рассмотрим треугольники (ABK) и (ACB):
(angle A) – общий,
[dfrac{AB}{AC} = dfrac{AK}{AB},] тогда треугольники (ABK) и (ACB) подобны по пропорциональности двух сторон и равенству углов между ними.
В подобных треугольниках против пропорциональных сторон лежат равные углы, тогда (angle ABC = angle AKB = 105^{circ}).
Ответ:
105
Задание
6
#3939
Уровень задания: Сложнее ЕГЭ
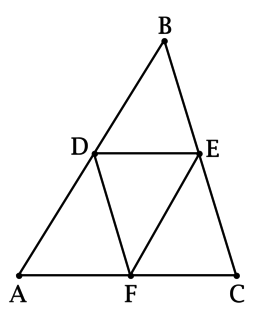
На сторонах (AB), (BC) и (AC) треугольника (ABC) лежат точки (D), (E) и (F) соответственно. Известно, что (dfrac{DF}{BC} = 0,5), (AC = 2cdot DE), (AB-EF=EF) (angle DEF = 61^{circ}), (angle EFD = 55^{circ}). Найдите (angle C). Ответ дайте в градусах.
Так как (angle DEF = 61^{circ}), (angle EFD = 55^{circ}), то (angle EDF = 180^{circ} — 61^{circ} — 55^{circ} = 64^{circ}).
Рассмотрим треугольники (ABC) и (EFD): по условию
[dfrac{DF}{BC} = 0,5 = dfrac{DE}{AC} = dfrac{EF}{AB},] тогда треугольники (ABC) и (EFD) подобны по пропорциональности трех сторон.
В подобных треугольниках против пропорциональных сторон лежат равные углы, тогда (angle C = angle EDF = 64^{circ}).
Ответ:
64
Задание
7
#3940
Уровень задания: Сложнее ЕГЭ
Отрезок (BK) соединяет вершину (B) треугольника (ABC) с точкой на противоположной стороне. При этом известно, что (AB = 12), (AC = 24), (AK = 6), (BK = 10), (BC = 20). Найдите (angle AKB — angle B). Ответ дайте в градусах.
Рассмотрим треугольники (ABK) и (ACB):
[dfrac{AB}{AC} = dfrac{AK}{AB} = dfrac{BK}{BC},] тогда треугольники (ABK) и (ACB) подобны по пропорциональности трех сторон.
В подобных треугольниках против пропорциональных сторон лежат равные углы, тогда (angle B = angle AKB), следовательно (angle AKB — angle B = 0^{circ}).
Ответ:
0
Как показывает статистика, планиметрические задачи вызывают наибольшие сложности у учащихся старших классов. Именно поэтому школьникам будет полезно освежить в памяти основные принципы решения задач с подобными треугольниками при подготовке к ЕГЭ. Причем еще раз повторить эту тему стоит всем ученикам, независимо от того, профильный или базовый уровень планирует сдавать выпускник.
Вместе с образовательным порталом «Школково» вы сможете качественно подготовиться к аттестационному испытанию. Чтобы решение задач ЕГЭ по теме «Подобные треугольники» давалось легко, рекомендуем вспомнить основную теорию. Найти ее вы можете в соответствующем разделе нашего сайта. Здесь представлены основные признаки подобных треугольников (для решения заданий ЕГЭ знать их необходимо), формула отношения их площадей и другая базовая информация. Ее специалисты образовательного портала «Школково» подготовили и изложили в максимально доступной форме.
Отточить навык решения задач ЕГЭ на нахождение сторон и углов подобных треугольников, а также, например, задачи по теореме Пифагора учащиеся также смогут на нашем сайте. В разделе «Каталог» представлен широкий перечень упражнений различной сложности, который постоянно обновляется.
В каждом задании прописано решение и дан правильный ответ. Выполнять задачи с применением признаков подобия площадей подобных треугольников можно в режиме онлайн.
Любое из представленных упражнений при необходимости можно сохранить в разделе «Избранное». Таким образом, к нему возможно будет вернуться в дальнейшем, к примеру, для обсуждения с преподавателем.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Описание презентации по отдельным слайдам:
-
1 слайд
Задачи на подобие треугольников в ЕГЭ.
-
2 слайд
Цель урока:
повторить признаки подобия треугольников;
детально рассмотреть задачу С4 ЕГЭ;
ввести понятие ортотреугольника -
3 слайд
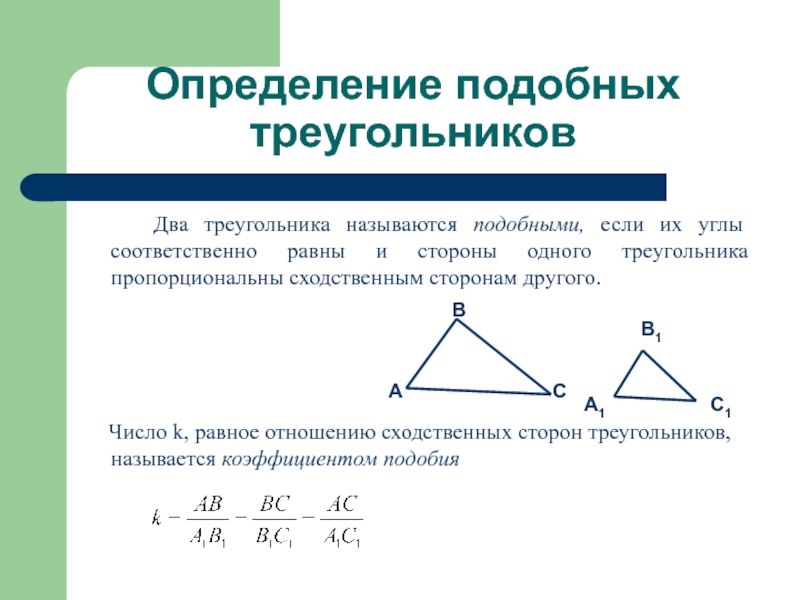
Определение подобных треугольников
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия
A
B
C
A1
B1
C1 -
4 слайд
Признаки подобия треугольников
I признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны
A
B
C
A1
B1
C1 -
5 слайд
Признаки подобия треугольников
II признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобныA
B
C
A1
B1
C1 -
6 слайд
Признаки подобия треугольников
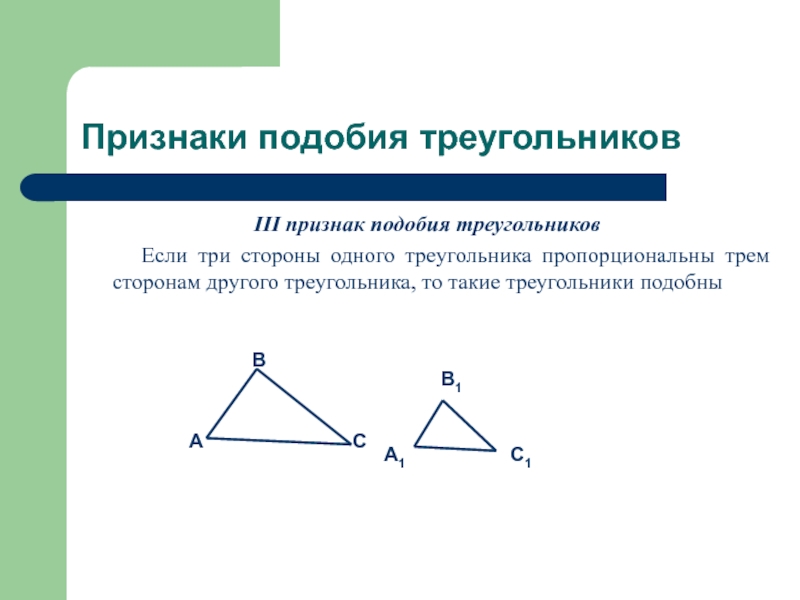
III признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобныA
B
C
A1
B1
C1 -
7 слайд
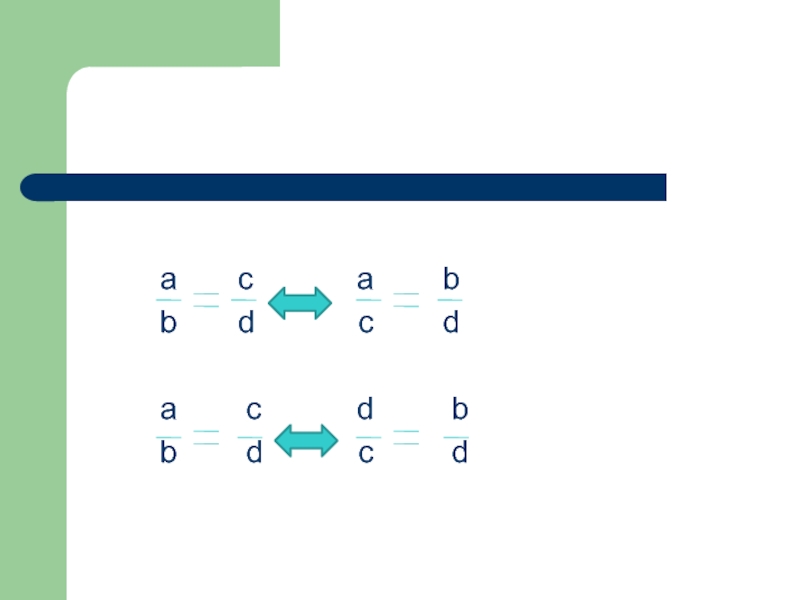
a c a b
b d c da c d b
b d c d -
8 слайд
Задача С4
Точки А1, В1, С1 – основания высот треугольника АВС. Углы треугольника А1В1С1 равны 90º, 60º и 30º. Найдите углы треугольника АВС. -
-
-
-
-
13 слайд
Определение ортотреугольника
А
С
В
А1
В1
С1 -
14 слайд
Свойства ортотреугольника
Ортотреугольник отсекает треугольники, подобные данному.
Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника.
3. Высоты треугольника являются биссектрисами ортотреугольника.
4. Ортотреугольник – это треугольник с наименьшим периметром, который можно вписать в этот треугольник .
5. Периметр ортотреугольника равен удвоенному произведению высоты треугольника на синус угла, из которого она исходит.
А
С
В
А1
В1
С1
О -
-
Подобные треугольники
Определение
Как правило, два треугольника считаются подобными если они имеют одинаковую форму, даже если они различаются размерами, повернуты или даже перевернуты.
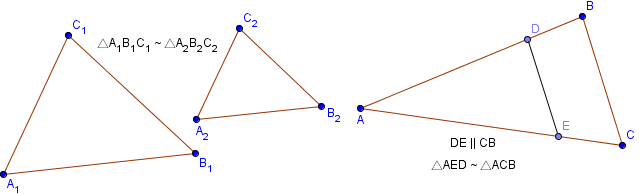
Математическое представление двух подобных треугольников A1B1C1 и A2B2C2 , показанных на рисунке, записывается следующим образом:
Два треугольника являются подобными если:
1. Каждый угол одного треугольника равен соответствующему углу другого треугольника:
∠A1 = ∠A2, ∠B1 = ∠B2 и∠C1 = ∠C2
2. Отношения сторон одного треугольника к соответствующим сторонам другого треугольника равны между собой:
$frac=frac=frac$
3. Отношения двух сторон одного треугольника к соответствующим сторонам другого треугольника равны между собой и при этом
углы между этими сторонами равны:
$frac=frac$ и $angle A_1 = angle A_2$
или
$frac=frac$ и $angle B_1 = angle B_2$
или
$frac=frac$ и $angle C_1 = angle C_2$
Не нужно путать подобные треугольники с равными треугольниками. У равных треугольников равны соответствующие длины сторон. Поэтому для равных треугольников:
Из этого следует что все равные треугольники являются подобными. Однако не все подобные треугольники являются равными.
Несмотря на то, что вышеприведенная запись показывает, что для выяснения, являются ли два треугольника подобными или нет, нам должны быть известны величины трех углов или длины трех сторон каждого треугольника, для решения задач с подобными треугольниками достаточно знать любые три величины из указанных выше для каждого треугольника. Эти величины могут составлять различные комбинации:
1) три угла каждого треугольника (длины сторон треугольников знать не нужно).
Или хотя бы 2 угла одного треугольника должны быть равны 2-м углам другого треугольника.
Так как если 2 угла равны, то третий угол также будет равным.(Величина третьего угла составляет 180 — угол1 — угол2)
2) длины сторон каждого треугольника (углы знать не нужно);
3) длины двух сторон и угол между ними.
Далее мы рассмотрим решение некоторых задач с подобными треугольниками. Сначала мы рассмотрим задачи, которые можно решить непосредственным использованием вышеуказанных правил, а затем обсудим некоторые практические задачи, которые решаются по методу подобных треугольников.
Практические задачи с подобными треугольниками
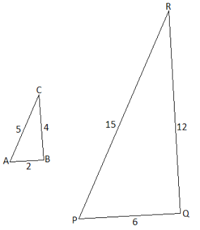
Пример №1: Покажите, что два треугольника на рисунке внизу являются подобными.
Решение:
Так как длины сторон обоих треугольников известны, то здесь можно применить второе правило:
Пример №2: Покажите, что два данных треугольника являются подобными и определите длины сторон PQ и PR.
Решение:
∠A = ∠P и ∠B = ∠Q, ∠C = ∠R(так как ∠C = 180 — ∠A — ∠B и ∠R = 180 — ∠P — ∠Q)
Из этого следует, что треугольники ΔABC и ΔPQR подобны. Следовательно:
$frac=frac=frac$
Пример №3: Определите длину AB в данном треугольнике.
Решение:
∠ABC = ∠ADE, ∠ACB = ∠AED и ∠A общий => треугольники ΔABC и ΔADE являются подобными.
$frac = frac<3> <6>= frac = frac = frac = frac<1> <2>Rightarrow 2times AB = AB + 4 Rightarrow AB = 4$
Пример №4:Определить длину AD (x) геометрической фигуры на рисунке.
Треугольники ΔABC и ΔCDE являются подобными так как AB || DE и у них общий верхний угол C.
Мы видим, что один треугольник является масштабированной версией другого. Однако нам нужно это доказать математически.
AB || DE, CD || AC и BC || EC
∠BAC = ∠EDC и ∠ABC = ∠DEC
Исходя из вышеизложенного и учитывая наличие общего угла C, мы можем утверждать, что треугольники ΔABC и ΔCDE подобны.
Следовательно:
$frac = frac<7> <11>= frac = frac<15> Rightarrow CA = frac<15 times 11> <7>= 23.57$
x = AC — DC = 23.57 — 15 = 8.57
Практические примеры
Пример №5: На фабрике используется наклонная конвеерная лента для транспортировки продукции с уровня 1 на уровень 2, который выше уровня 1 на 3 метра, как показано на рисунке. Наклонный конвеер обслуживается с одного конца до уровня 1 и с другого конца до рабочего места, расположенного на расстоянии 8 метров от рабочей точки уровня 1.
Фабрика хочет модернизировать конвеер для доступа к новому уровню, который находится на расстоянии 9 метров над уровнем 1, и при этом сохранить угол наклона конвеера.
Определите расстояние, на котором нужно установить новый рабочий пункт для обеспечения работы конвеера на его новом конце на уровне 2. Также вычислите дополнительное расстояние, которое пройдет продукция при перемещении на новый уровень.
Решение:
Для начала давайте обозначим каждую точку пересечения определенной буквой, как показано на рисунке.
Исходя из рассуждений, приведенных выше в предыдущих примерах, мы можем сделать вывод о том, что треугольники ΔABC и ΔADE являются подобными. Следовательно,
$frac = frac<3> <9>= frac = frac<8> Rightarrow AB = frac<8 times 9> <3>= 24 м$
x = AB — 8 = 24 — 8 = 16 м
Таким образом, новый пункт должен быть установлен на расстоянии 16 метров от уже существующего пункта.
А так как конструкция состоит из прямоугольных треугольников, мы можем вычислить расстояние перемещения продукции следующим образом:
Аналогично, $AC = sqrt = sqrt <24^2 + 9^2>= 25.63 м$
что является расстоянием, которое проходит продукция в данный момент при попадании на существующий уровень.
y = AC — AE = 25.63 — 8.54 = 17.09 м
это дополнительное расстояние, которое должна пройти продукция для достижения нового уровня.
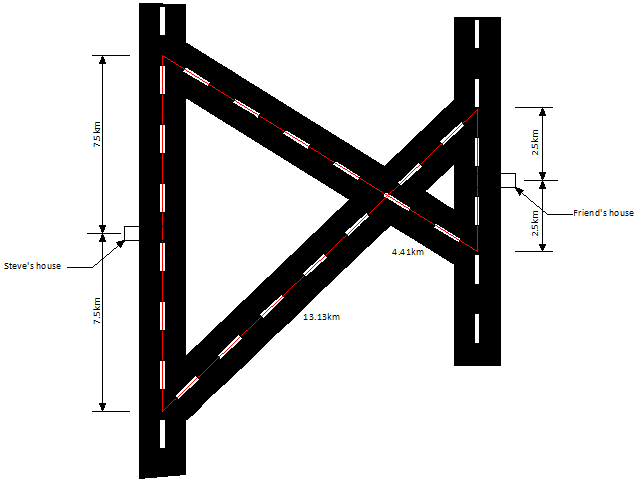
Пример №6: Стив хочет навестить своего приятеля, который недавно переехал в новый дом. Дорожная карта проезда к дому Стива и его приятеля вместе с известными Стиву расстояниями показана на рисунке. Помогите Стиву добраться к дому его приятеля наиболее коротким путем.
Решение:
Дорожную карту можно геометрически представить в следующем виде, как показано на рисунке.
Мы видим, что треугольники ΔABC и ΔCDE подобны, следовательно:
$frac = frac = frac$
В условии задачи сказано, что:
AB = 15 км, AC = 13.13 км, CD = 4.41 км и DE = 5 км
Используя эту информацию, мы можем вычислить следующие расстояния:
Стив может добраться к дому своего друга по следующим маршрутам:
A -> B -> C -> E -> G, суммарное расстояние равно 7.5+13.23+4.38+2.5=27.61 км
F -> B -> C -> D -> G, суммарное расстояние равно 7.5+13.23+4.41+2.5=27.64 км
F -> A -> C -> E -> G, суммарное расстояние равно 7.5+13.13+4.38+2.5=27.51 км
F -> A -> C -> D -> G, суммарное расстояние равно 7.5+13.13+4.41+2.5=27.54 км
Следовательно, маршрут №3 является наиболее коротким и может быть предложен Стиву.
Пример 7:
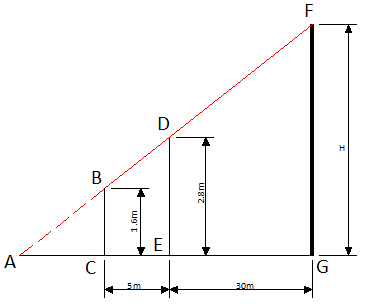
Триша хочет измерить высоту дома, но у нее нет нужных инструментов. Она заметила, что перед домом растет дерево и решила применить свою находчивость и знания геометрии, полученные в школе, для определения высоты здания. Она измерила расстояние от дерева до дома, результат составил 30 м. Затем она встала перед деревом и начала отходить назад, пока верхний край здания стал виден над верхушкой дерева. Триша отметила это место и измерила расстояние от него до дерева. Это расстояние составило 5 м.
Высота дерева равна 2.8 м, а высота уровня глаз Триши равна 1.6 м. Помогите Трише определить высоту здания.
Решение:
Геометрическое представление задачи показано на рисунке.
Сначала мы используем подобность треугольников ΔABC и ΔADE.
$frac = frac<1.6> <2.8>= frac = frac <5 + AC>Rightarrow 2.8 times AC = 1.6 times (5 + AC) = 8 + 1.6 times AC$
$(2.8 — 1.6) times AC = 8 Rightarrow AC = frac<8> <1.2>= 6.67$
Затем мы можем использовать подобность треугольников ΔACB и ΔAFG или ΔADE и ΔAFG. Давайте выберем первый вариант.
Егэ математика подобие треугольников
Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 36. Решение задач на применение признаков подобия треугольников. Вернуться к Списку уроков Тематического планирования.
Урок 36. Решение задач на применение
признаков подобия треугольников
Основные дидактические цели урока: сформировать у учащихся навыки применения признаков подобия треугольников при решении задач; совершенствовать навыки доказательств теорем.
Ход урока
I. Организационный момент.
Мотивация к учебной деятельности. (Учитель сообщает тему урока, формулирует цели урока.)
II. Актуализация знаний учащихся
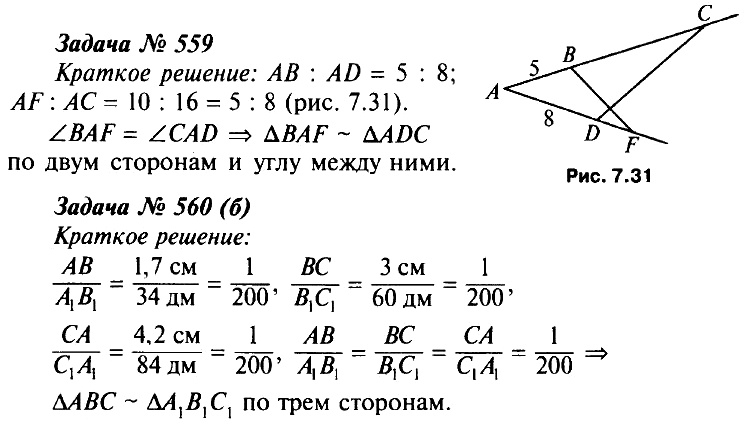
- Проверка домашнего задания. (Учитель проверяет решение задач № 559, 560 (б). Два ученика заранее готовят решение на доске.)
- Теоретический опрос. (Два ученика готовят доказательства теорем у доски.)
- Сформулируйте признаки подобия треугольников.
- Докажите теоремы, выражающие второй и третий признаки подобия треугольников.
- Работа по индивидуальным карточкам. (3—6 учеников работают по карточкам во время теоретического опроса.)
I уровень сложности
Подобны ли треугольники АВС и А1В1С1, если известно, что:
II уровень сложности
- Прямая, параллельная стороне MN треугольника MNK, пересекает стороны КМ и KN в точках Е и F соответственно, КЕ = 6 см, KN = 10 см, KF = 9 см, KN = 15 см. Найдите отношения. a) EF: MN, б) PKMN : РКЕF, в) SKEF : SKMN.
- Точка Е — середина стороны AD параллелограмма ABCD. В каком отношении прямая BE делит диагональ АС параллелограмма? Найдите отношение площади треугольника АВЕ и четырехугольника BCDE.
III уровень сложности
- Основания трапеции равны 9 и 6 см, а высота равна 10 см. Найдите разность расстояний от точки пересечения диагоналей трапеции до ее оснований.
- Докажите признак подобия прямоугольных треугольников по гипотенузе и катету.
- Решение задач по готовым чертежам.
- 1) Рис. 7.32. Найти: ∠C1, В1С1.
- 2) Рис. 7.33. Найти: ∠C, ∠C1
- 3) Рис. 7.34. Найти: ВМ.
- 4) Рис. 7.35. Найти: ВС.
- 5) Рис. 7.36. Найти: ∠DCA.
- 6) Рис. 7.37. Найти АВ, NC.
Ответы к задачам по готовым чертежам:
- 1) ∠C1 = 71°, В1С1 = 15 см.
- 2) ∠C = ∠C1 = 60°.
- 3) ВМ = 6 см.
- 4) BC = 20/3.
- 5)Обратите внимание! Ответ автора задания ∠DCA = 90°. Однако, этот ответ нельзя признать правильным в виду каких-то опечаток в рис.7.36. Единственный вывод из рисунка: треугольники ABC и АCD подобны (по трем сторонам), но в таком случае ответ должен быть 80°, а не 90°. Но самый противоречивый момент связан с тем, что треугольники с заявленными сторонами и углами не существуют. Если считать, что стороны на рисунке указаны правильно, то вместо 80° должно быть указано 92,73°, а вместо 55° должно быть 45,52°. Тогда правильный ответ будет ∠DCA = 92,73°.
- 6) АВ = 8, NC= 8.
(После окончания самостоятельного решения задач и самопроверки по готовым ответам выполняется самооценка.) Критерии оценивания:
- оценка «5» — правильно решены пять-шесть задачи;
- оценка «4» — правильно решены четыре задачи;
- оценка «3» — правильно решены две-три задачи;
- оценка «2» — не ставится.
(Учащиеся, справившиеся со всеми задачами, решают дополнительные задачи.)
Дополнительные задачи
- Диагональ АС трапеции ABCD (АВ||CD) делит ее на два подобных треугольника. Найдите площадь трапеции ABCD, если АВ = 25 см, ВС = 20 см, АС = 15 см.
Ответ : SABCD = 204 см 2 .
- Угол В треугольника AВС в два раза больше угла А. Биссектриса угла В делит сторону АС на части AD = 6 см и CD = 3 см. Найдите стороны треугольника АВС.
Ответ : АС = 9 см, АВ = 6√3 см, ВС = 3√3 см.
III. Самостоятельная работа
I уровень сложности
Вариант 1
- Рис. 7.38. Доказать: ΔАВС
ΔА1В1С1
Вариант 2
- Рис. 7.39. Доказать: ΔАВС
ΔА1B1С1.
II уровень сложности
Вариант 1.
- Рис. 7.40. Доказать: ΔАВС
ΔА1В1С1
Вариант 2
- Рис. 7.41. Доказать: ΔМВН
ΔСВA.
III уровень сложности
Вариант 1
- Дано: ∠1 = ∠2, AD = 4, АС = 9 (рис. 7.42). Найти: АВ, SABD : SABC.
- Диагонали четырехугольника ABCD пересекаются в точке О, АО • ВО = СО • DO. Докажите, что площади треугольников ACD и ABD равны.
Вариант 2
- Дано: ВС ⊥ АС, МН ⊥ ВС, 2МС = ВС, МН = 0,5АС (рис. 7.43). Доказать: АВ||СН. Найти. SАВС : SMCH.
- В трапеции ABCD AD и ВС — основания, О — точка пересечения диагоналей, АО : ОС = 3 : 2. Найдите отношение площадей треугольников АВС и ACD.
( Ответы на самостоятельную работу смотрите в уроке 37)
IV. Рефлексия учебной деятельности
- Сформулируйте признаки подобия треугольников.
- В каком случае подобны равносторонние, равнобедренные, прямоугольные треугольники?
Домашнее задание. Решить задачи № 562, 563, 604, 605.
Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 36. Решение задач на применение признаков подобия треугольников.
Задачи на подобие треугольников в ЕГЭ
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Задачи на подобие треугольников в ЕГЭ.
Цель урока: повторить признаки подобия треугольников; детально рассмотреть задачу С4 ЕГЭ; ввести понятие ортотреугольника
Определение подобных треугольников Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия
Признаки подобия треугольников I признак подобия треугольников Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны
Признаки подобия треугольников II признак подобия треугольников Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны
Признаки подобия треугольников III признак подобия треугольников Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны
a c a b b d c d a c d b b d c d
Задача С4 Точки А1, В1, С1 – основания высот треугольника АВС. Углы треугольника А1В1С1 равны 90º, 60º и 30º. Найдите углы треугольника АВС.
Свойства ортотреугольника Ортотреугольник отсекает треугольники, подобные данному. Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника. 3. Высоты треугольника являются биссектрисами ортотреугольника. 4. Ортотреугольник – это треугольник с наименьшим периметром, который можно вписать в этот треугольник . 5. Периметр ортотреугольника равен удвоенному произведению высоты треугольника на синус угла, из которого она исходит. О
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 988 человек из 78 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 310 человек из 68 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 673 человека из 75 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 538 770 материалов в базе
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 09.03.2018
- 353
- 0
- 09.03.2018
- 985
- 1
- 09.03.2018
- 51512
- 1335
- 09.03.2018
- 721
- 2
- 09.03.2018
- 4744
- 18
- 09.03.2018
- 2565
- 112
- 09.03.2018
- 438
- 4
- 09.03.2018
- 467
- 2
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 09.03.2018 1702
- PPTX 340 кбайт
- 15 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Ситдикова Ирина Масгутовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 2 месяца
- Подписчики: 0
- Всего просмотров: 17694
- Всего материалов: 10
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
В России классы будут переводить на дистант, если заболели 20% детей
Время чтения: 1 минута
В России планируют создадут сеть центров для подростков «группы риска»
Время чтения: 1 минута
В ЕГЭ обновили задания по математике
Время чтения: 2 минуты
В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид
Время чтения: 1 минута
В Калужской области школьники уйдут на каникулы с 7 по 20 февраля
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
источники:
http://uchitel.pro/%D1%83%D1%80%D0%BE%D0%BA-36-%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D0%B5-%D0%B7%D0%B0%D0%B4%D0%B0%D1%87-%D0%BD%D0%B0-%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5-%D0%BF%D1%80%D0%B8/
http://infourok.ru/zadachi-na-podobie-treugolnikov-v-ege-2719693.html
Слайд 1Задачи на подобие треугольников в ЕГЭ.

Слайд 2Цель урока:
повторить признаки подобия треугольников;
детально рассмотреть задачу С4 ЕГЭ;
ввести понятие ортотреугольника

Слайд 3Определение подобных треугольников
Два треугольника называются подобными, если их
углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия
Слайд 4Признаки подобия треугольников
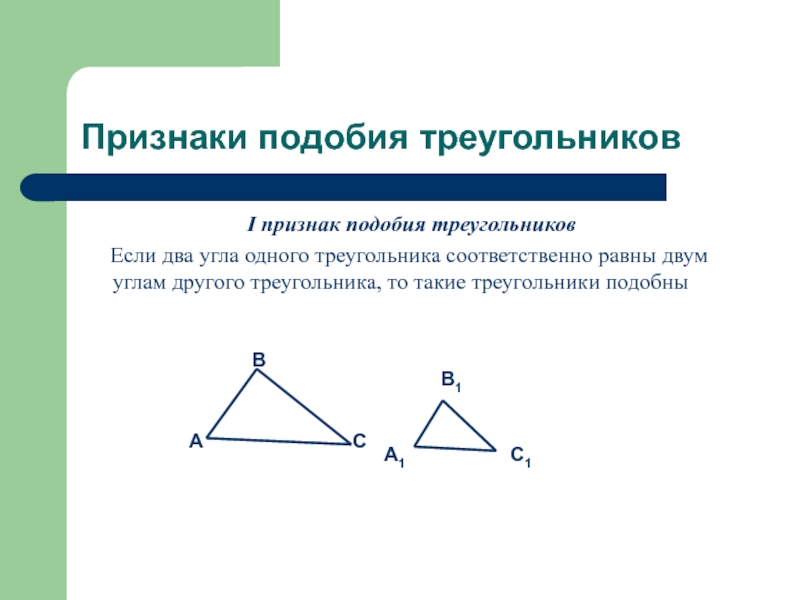
I признак подобия треугольников
Если два угла
одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны
Слайд 5Признаки подобия треугольников
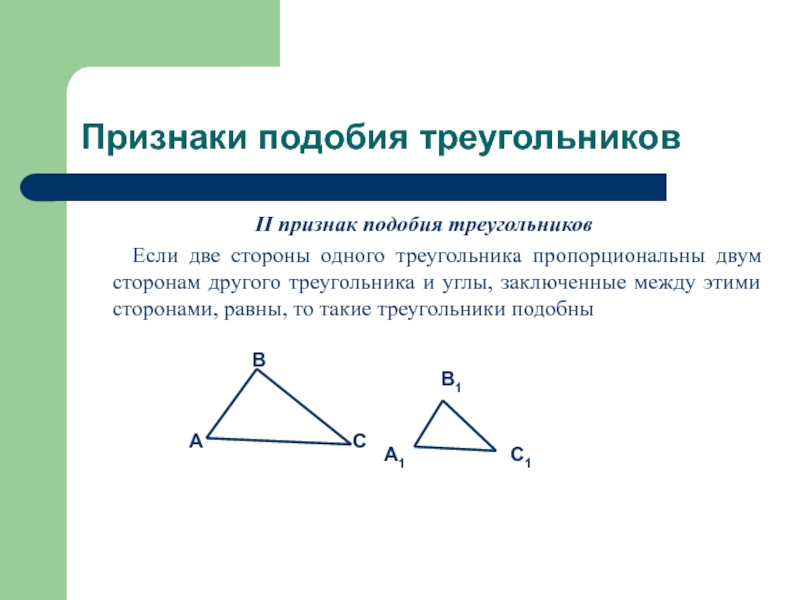
II признак подобия треугольников
Если две стороны
одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны
Слайд 6Признаки подобия треугольников
III признак подобия треугольников
Если три стороны
одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны
Слайд 7
a
c a b
b d c d
a c d b
b d c d
Слайд 8Задача С4
Точки А1, В1, С1 – основания высот треугольника АВС. Углы
треугольника А1В1С1 равны 90º, 60º и 30º. Найдите углы треугольника АВС.

Слайд 14Свойства ортотреугольника
Ортотреугольник отсекает треугольники, подобные данному.
Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника.
3. Высоты треугольника являются биссектрисами ортотреугольника.
4. Ортотреугольник – это треугольник с наименьшим периметром, который можно вписать в этот треугольник .
5. Периметр ортотреугольника равен удвоенному произведению высоты треугольника на синус угла, из которого она исходит.