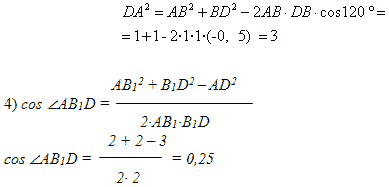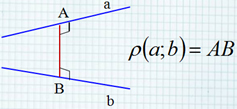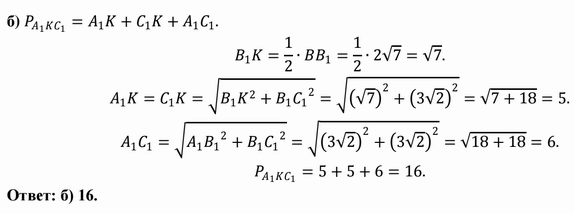Задачи на построение сечений егэ профиль - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

В основании правильной треугольной призмы ABCA₁B₁C₁ лежит треугольник со стороной 6. Высота призмы равна 4. Точка N  — середина ребра A₁C₁.

а)  Постройте сечение призмы плоскостью BAN.

б)  Найдите периметр этого сечения.

В правильной четырехугольной пирамиде PABCD, все ребра которой равны 4, точка K ― середина бокового ребра AP.

а)  Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC.

б)  Найдите площадь сечения.

Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 1.

На ребре AA₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ взята точка E так, что A₁E : EA = 5 : 3, на ребре BB₁  — точка F так, что B₁F : FB = 5 : 11, а точка T − середина ребра B₁C₁. Известно, что AD = 10, AA₁  =  16.

а)  Докажите, что плоскость EFT проходит через вершину D₁.

б)  Найдите площадь сечения параллелепипеда плоскостью EFT.

На ребре AA₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ взята точка E так, что A₁E  =  6EA. Точка T  — середина ребра B₁C₁. Известно, что AD  =  12, AA₁  =  14.

а)  Докажите, что плоскость ETD₁ делит ребро BB₁ в отношении 4 : 3.

б)  Найдите площадь сечения параллелепипеда плоскостью ETD₁.

Основанием прямой четырехугольной призмы ABCDA’B’C’D’ является квадрат ABCD со стороной высота призмы равна Точка K  — середина ребра BB’. Через точки K и С’ проведена плоскость α, параллельная прямой BD’.

а)  Докажите, что сечение призмы плоскостью α является равнобедренным треугольником.

б)  Найдите периметр треугольника, являющегося сечением призмы плоскостью α.

Источник: ЕГЭ по математике 2015. Досрочная волна, резервная волна (часть С)

Пройти тестирование по этим заданиям

Источник

14. Задачи по стереометрии

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи на построение сечений

Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.

Важные факты и теоремы, необходимые для построения сечений

(blacktriangleright) Определение: две прямые параллельны, если они лежат в одной плоскости и не пересекаются.
Если через две прямые нельзя провести одну плоскость, то такие прямые скрещиваются.

(blacktriangleright) Теорема о параллельности трех прямых: если (aparallel b, bparallel c), то и (aparallel c).

(blacktriangleright) Определение: прямая и плоскость параллельны, если они не имеют общих точек.

Признак параллельности прямой и плоскости: прямая, не лежащая в плоскости, параллельна этой плоскости, если она параллельна некоторой прямой из этой плоскости.

(blacktriangleright) Определение: две плоскости параллельны, если они не имеют общих точек.

Признак параллельности двух плоскостей: если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости параллельны.

(blacktriangleright) Если две плоскости пересекаются, то их линия пересечения — прямая.

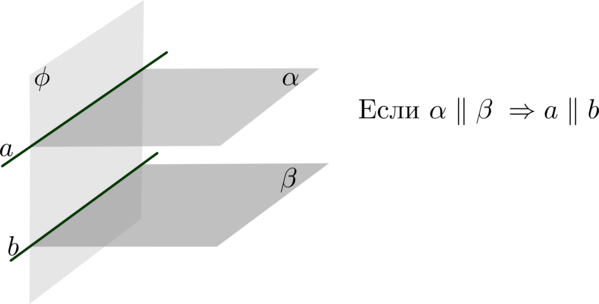
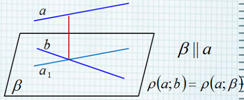
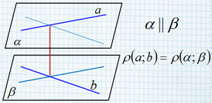
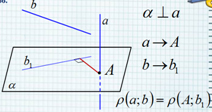
(blacktriangleright) Если две параллельные плоскости пересечены третьей, то их линии пересечения параллельны (см. рис.)

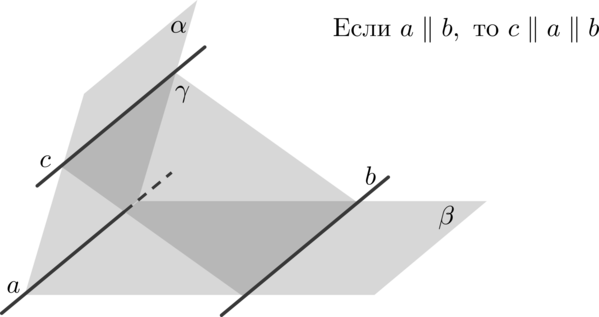
(blacktriangleright) Если плоскости (alpha) и (beta) пересекаются по прямой (a), а плоскости (beta) и (gamma) пересекаются по прямой (b), причем (aparallel b), то плоскости (alpha) и (gamma) пересекутся по прямой (cparallel aparallel b).

Задание
1

#999

Уровень задания: Легче ЕГЭ

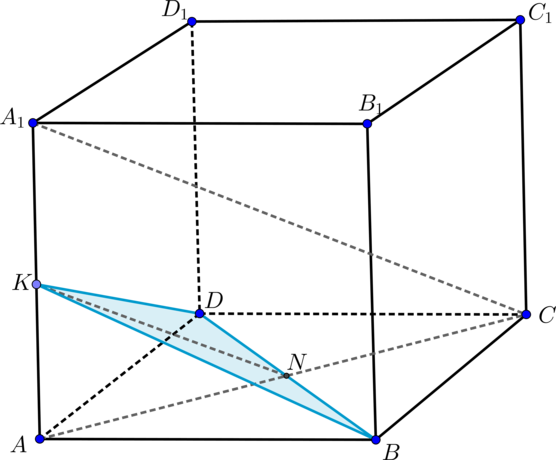
Дан куб (ABCDA_1B_1C_1D_1). Через точку (K), середину ребра (AA_1), и точку (B) проведите плоскость (alpha) параллельно диагонали (A_1C).

Т.к. (A_1Cparallel alpha Rightarrow A_1C) параллельна некоторой прямой, содержащейся в (alpha). Рассмотрим плоскость (AA_1C_1C), в которой находится (A_1C). Т.к. точка (Kin AA_1C_1C), то проведем в этой плоскости (KN parallel A_1C) (по теореме Фалеса (N) – середина (AC)).

Т.к. (ABCDA_1B_1C_1D_1) – куб, то (N) – точка пересечения диагоналей квадрата (ABCD), следовательно, (Nin BD). Таким образом, получили сечение (KBD) куба плоскостью (alpha).

Ответ:

Рисунок.

Задание
2

#3981

Уровень задания: Легче ЕГЭ

Дан куб (ABCDA_1B_1C_1D_1). На ребрах (AA_1) и (BC) отмечены точки (M) и (N) соответственно, причем (AM:MA_1=2:1), а (N) – середина (BC). Найдите сечение куба плоскостью (DMN).

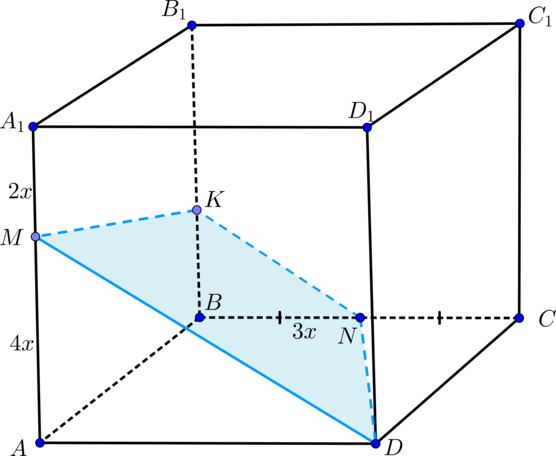
Т.к. грани (ADD_1A_1) и (BCC_1B_1) куба параллельны, то плоскость (DMN) пересечет их по параллельным прямым. Таким образом, проведем (NKparallel DM). Таким образом, (DNKM) – искомое сечение.

Необходимо найти точное расположение точки (K).

Обозначим ребро куба за (6x). Т.к. (bigtriangleup ADM sim
bigtriangleup BNK Rightarrow dfrac{BK}{AM}=dfrac{BN}{AD}
Rightarrow BK=2x). Таким образом, (BK:KB_1=1:2).

Ответ:

Рисунок.

Задание
3

#3804

Уровень задания: Равен ЕГЭ

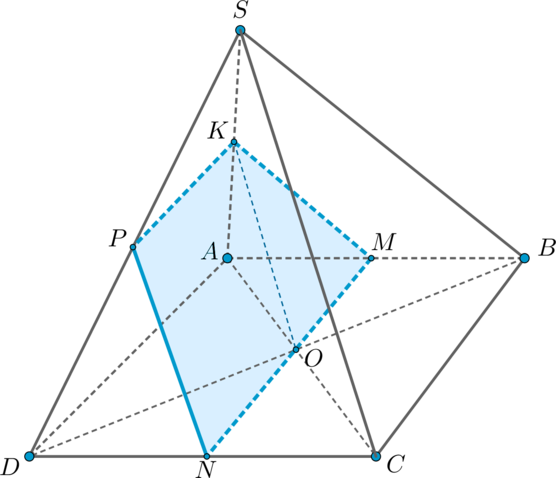
(SABCD) – четырехугольная пирамида, в основании которой лежит квадрат (ABCD), а две боковые грани (SAB) и (SAD) представляют собой прямоугольные треугольники с прямым углом (angle A).

1) Проведите плоскость (alpha) через точку пересечения диагоналей основания параллельно грани (SBC).

2) Найдите площадь сечения пирамиды плоскостью (alpha), если (SA=AB=a).

1) Пусть (ACcap BD=O). Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Заметим, что т.к. (angle SAB=angle SAD=90^circ Rightarrow
SAperp
(ABC)).

Проведем в плоскости (SAC) прямую (OKparallel SC). Т.к. (O) – середина (AC), то по теореме Фалеса (K) – середина (SA). Через точку (K) в плоскости (SAB) проведем (KMparallel SB) (следовательно, (M) – середина (AB)). Таким образом, плоскость, проходящая через прямые (OK) и (KM), и будет искомой плоскостью.

Необходимо найти сечение пирамиды этой плоскостью. Соединив точки (O) и (M), получим прямую (MN).

Т.к. (alphaparallel (SBC)),то (alpha) пересечет плоскость (SCD) по прямой (NPparallel SC) (если (NPcap SC ne varnothing), то (alphacap (SBC)ne varnothing), что невозможно ввиду их параллельности).

Таким образом, (KMNP) – искомое сечение, причем (KPparallel
ADparallel MN Rightarrow) это трапеция.

2) Т.к. все точки (K,M,N,P) – середины отрезков (SA, AB, CD, SD) соответственно, то:

а) (MN=AD=a)

б) (KP=dfrac{1}{2}AD=dfrac{a}{2})

в) (KM=dfrac{1}{2}SB=dfrac{asqrt2}{2})

Заметим, что по теореме о трех перпендикулярах (SBperp BC
Rightarrow KMperp MN). Таким образом, (KMNP) – прямоугольная трапеция.

(S_{KMNP}=dfrac{KP+MN}{2}cdot KM=dfrac{3sqrt2}{8}a^2)

Ответ:

1) Рисунок.

2) (dfrac{3sqrt2}{8}a^2)

Задание
4

#1003

Уровень задания: Равен ЕГЭ

Дана правильная треугольная пирамида (SABC) с вершиной (S). Проведите плоскость через середину ребра (AC) и точки пересечения медиан граней (ASB) и (CSB). Найдите площадь сечения пирамиды этой плоскостью, если (AB=21, AS=12sqrt2).

1) Пусть(K) – середина (AC), (SX, AL) – медианы грани (ASB), (CL,
SY) – медианы грани (CSB), (ALcap SX=M, CLcap SY=N). (SO) – высота пирамиды.

Найдем сечение пирамиды плоскостью (MNK).
Т.к. пирамида правильная, то (triangle SXY) – равнобедренный, (SM=SN=dfrac{2}{3}SX Rightarrow MNparallel XY Rightarrow
MNparallel (ABC)). Таким образом, плоскость (MNK) содержит прямую (MN), параллельную (ABC), следовательно, плоскость (MNK) пересечет плоскость (ABC) по прямой, параллельной (MN) (если это не так, то линия пересечения этих плоскостей (lcap MN=E Rightarrow Ein
(ABC)) и (Ein MN Rightarrow MN) не может быть параллельна ((ABC))).

Прямая, проходящая через точку (K) и параллельная (MN) (или (XY)) – это (AC). Следовательно, сечением является равнобедренный треугольник (ALC).

2) Пусть (LKcap SO=H). Тогда по теореме о трех перпендикулярах (HKperp AC) как наклонная ((HOperp (ABC), OKperp AC) как проекция). Следовательно, и (LKperp AC).

Тогда (S_{ALC}=dfrac{1}{2}ACcdot LK).

Рассмотрим (triangle SKB: BK=ABcdot
dfrac{sqrt3}{2}=dfrac{21sqrt3}{2} Rightarrow cos
B=dfrac{7sqrt3}{12sqrt2}).

Тогда по теореме косинусов для (triangle KLB):

(KL^2=dfrac{729}{4} Rightarrow KL=dfrac{27}{2})

Значит, (S_{ALC}=dfrac{567}{4}).

Ответ:

(dfrac{567}{4}).

Задание
5

#3792

Уровень задания: Сложнее ЕГЭ

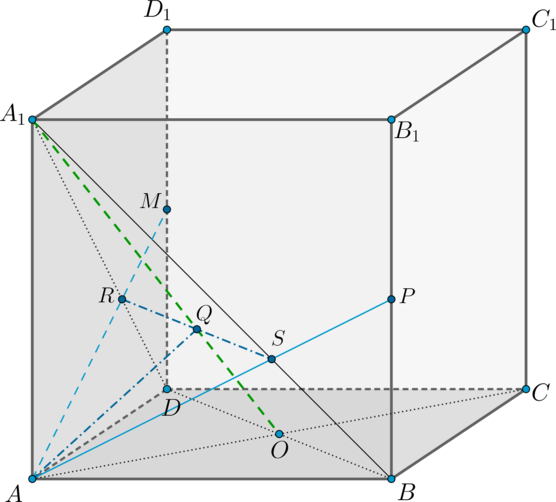
Дан куб (ABCDA_1B_1C_1D_1). Диагонали основания (AC) и (BD) пересекаются в точке (O). Найдите сечение куба плоскостью (alpha), проходящей через точку (A) перпендикулярно прямой (A_1O).

1) Если (A_1Operp alpha), то (A_1O) перпендикулярно двум пересекающимся прямым, лежащим в плоскости (alpha). Построим эти две прямые.

Рассмотрим плоскость (AA_1C_1C) ((A_1O) лежит в этой плоскости). Проведем в ней (AQperp A_1O). Теперь необходимо через их точку пересечения (точку (Q)) провести еще одну прямую перпендикулярно (A_1O).

Рассмотрим для этого плоскость (A_1BD) ((A_1O) лежит в этой плоскости). Проведем через точку (Q) прямую (RSperp A_1O). Т.к. по теореме о трех перпендикулярах (A_1Operp BD) как наклонная ((A_1Aperp (ABC), AOperp BD) – проекция), то (RSparallel BD).

2) Проведем прямые (AR) и (AS). Они могут пересечь либо сами ребра (DD_1) и (BB_1), либо их продолжения. Т.к. от этого зависит вид сечения, определим расположение точек (R) и (S).

Обозначим ребро куба за (a). Тогда (AO=dfrac{asqrt2}{2}=dfrac
a{sqrt2}). Рассмотрим прямоугольный (triangle AA_1O). Так как (AQperp A_1O), то по свойству прямоугольного треугольника (triangle AA_1Qsim triangle AA_1O). Следовательно, [dfrac{A_1Q}{AA_1}=dfrac{AA_1}{A_1O}] Так как по теореме Пифагора (A_1O=sqrt{a^2+frac{a^2}2}=dfrac{sqrt6 a}2), то [A_1Q=dfrac{AA_1^2}{A_1O}=dfrac{sqrt6}3a]

Так как (RSparallel BD), то (triangle A_1DOsim triangle A_1RQ), следовательно, [dfrac{A_1R}{A_1D}=dfrac{A_1Q}{A_1O}=dfrac{sqrt6}3:dfrac{sqrt6}2=
dfrac23] Аналогично (A_1S:A_1B=2:3).

Заметим, что (triangle AA_1Rsim triangle MDR) с коэффициентом подобия (2) ((A_1R:RD=2:1)), следовательно, (MD=frac12AA_1).
Аналогично (PB=frac12AA_1).

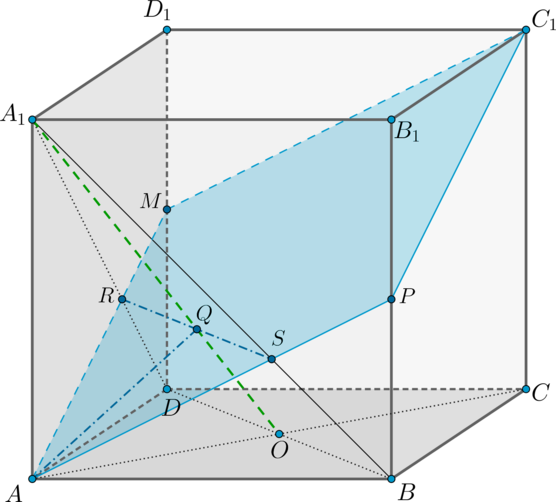
Таким образом, получили линии пересечения плоскостей (AA_1D_1) и (AA_1B_1) с плоскостью (alpha) – прямые (AM) и (AP).

3) Так как плоскости (AA_1B_1) и (DD_1C_1) параллельны, то плоскость (alpha) пересечет их по параллельным прямым. Следовательно, в плоскости (DD_1C_1) через точку (M) нужно провести прямую, параллельную (AP).
Так как (M) и (P) – середины (DD_1) и (BB_1), то (MC_1parallel
AP).

Таким образом, сечение куба плоскостью (alpha) – это четырехугольник (AMC_1P) (который, вообще говоря, является ромбом, так как (AM=AP=MC_1) и (MC_1parallel AP)).

Ответ:

Рисунок.

Задание
6

#2451

Уровень задания: Сложнее ЕГЭ

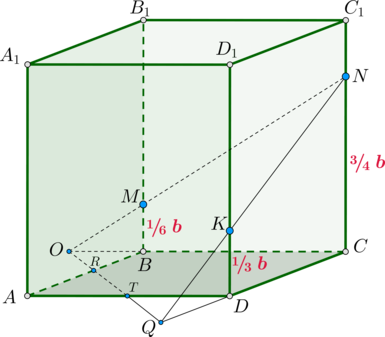
Дан прямоугольный параллелепипед (ABCDA_1B_1C_1D_1), в основании которого лежит квадрат (ABCD). На ребрах (BB_1), (CC_1), (DD_1) отмечены точки (M, N, K) соответственно так, что (BM:MB_1=1:5), (CN:NC_1=3:1), (DK:KD_1=1:2).
Найдите отношение отрезков, на которые делит плоскость (MNK) диагональ (AC).

Обозначим ребро основания за (a), а боковое ребро за (b). Тогда из условия задачи следует, что (BM=frac16b), (CN=frac34b), (DK=frac13b).

Найдем положение точек (R) и (T), в которых плоскость пересекает ребра (AB) и (AD) соответственно.

1) Продлим отрезки (NK) и (CD) до пересечения в точке (Q). Тогда (triangle QDKsim triangle QNC). Следовательно,

[dfrac{QD}{QC}=dfrac{KD}{NC} quad Rightarrow quad
dfrac{QD}{QD+a}=dfrac{frac13b}{frac34b}=dfrac49 quad
Rightarrow quad QD=dfrac45a.]

Аналогично из (triangle OMBsim triangle ONC) получаем, что [OB=dfrac27a.]

Соединив точки (Q) и (O), получим точки пересечения плоскости с ребрами (AB) и (AD).

2) Рассмотрим основание.

(triangle OBRsim triangle OCQ), следовательно,

[dfrac{OB}{OC}=dfrac{BR}{CQ} quad Rightarrow quad
dfrac{frac27a}{frac97a}=dfrac{BR}{frac95a} quad Rightarrow
quad BR=dfrac25a.]

(triangle OBRsim triangle TAR), следовательно,

[dfrac{OB}{AT}=dfrac{BR}{AR}quad Rightarrow quad
dfrac{frac27a}{AT}=dfrac{frac25a}{frac35a} quad Rightarrow
quad AT=dfrac37a.]

3) Для того, чтобы найти, в каком отношении (RT) поделит (AC), проведем прямую (RGparallel AD), (Gin AC).

Тогда (triangle ARG) – прямоугольный и (angle RAG=45^circ), то есть он равнобедренный и (RG=frac35a). Тогда по теореме Фалеса (AG:AC=AR:AB=3:5), следовательно, т.к. (AC=asqrt2), то (AG=frac{3sqrt2}5a).

(triangle ASTsim triangle RSG), следовательно,

[dfrac{AT}{RG}=dfrac{AS}{SG} quad Rightarrow quad
dfrac{frac37a}{frac35a}=dfrac{AS}{frac{3sqrt2}5a-AS} quad
Rightarrow quad AS=dfrac{sqrt2}4a.]

Тогда (SC=asqrt2-frac{sqrt2}4a=frac{3sqrt2}4a) и (AS:SC=1:3).

Ответ:

(1:3)

Теме «Построение сечения» в ЕГЭ по математике профильного уровня посвящается, как правило, несколько заданий. Они могут требовать от школьника как краткого ответа, так и полного развернутого решения. Если одним из ваших слабых мест являются именно задачи на сечения (в ЕГЭ при этом вы хотите получить конкурентные баллы), непременно стоит повторить или вновь разобраться в материале.

Сделать это наиболее эффективно вам поможет образовательный математический проект «Школково». Наши специалисты подготовили теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко справиться с решением задач на сечение.

Полезная информация

Для того чтобы выполнить построение сечений в ЕГЭ, нужно отметить точки пересечения пространственной фигуры с ребрами и произвести их соединение, начертив отрезки.

Необходимо запомнить

Производится соединение только двух точек, которые лежат в плоскости одной грани. Прежде чем приступить к решению задачи на построение сечений, полезно повторить материал о параллельных прямых. Сделать это вы можете, посетив раздел «Теоретическая справка».

Также необходимо запомнить, что пересечение секущей плоскости параллельных граней возможно только по параллельным отрезкам.

В том случае, когда в плоскости грани обозначена только одна точка, которая принадлежит плоскости сечения, следует отметить еще одну дополнительную. Для того чтобы это сделать, нужно определить точки пересечения прямых, которые уже построены, с теми, которые лежат в тех же гранях.

Выполнив построение сечений многогранников в задачах, которые представлены в нашем «Каталоге», вы сможете закрепить изученный материал и успешно справиться с подобным заданием на ЕГЭ в Москве.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

29
Ноя 2015

13 Задание (2022) (C2)СТЕРЕОМЕТРИЯ

Учимся строить сечения многогранников. Часть 2.

Эта статья для тех, кто хочет научиться строить сечения. Она содержит 11 заданий для построения сечений, подсказки и ответы к каждому заданию. Рекомендую сначала прочитать эту статью и посмотреть это видео.

Вспомним, что сечение многогранника плоскостью представляет собой плоский многоугольник, вершины которого принадлежат сторонам, а ребра — граням многогранника. Две соседние вершины принадлежат одной грани многогранника.

Чтобы найти точку, лежащую одновременно в двух плоскостях, нужно найти точку пересечения прямой, лежащей в первой плоскости, с прямой, лежащей во второй плоскости.

В подсказках и ответах изображение дополнительных прямых, используемых при построении сечения, сплошными линиями или пунктирными, не зависит от того, видимы эти прямые или нет.

Рядом с каждой дополнительной прямой указан ее порядковый номер при построении сечения. Все прямые проведены через две точки, принадлежащие определенной плоскости. Прямые пронумерованы в порядке их построения. Рекомендуется при использовании подсказки и воспроизведении построения сечения проговаривать, какой плоскости принадлежит данная прямая, каким плоскостям принадлежит точка их пересечения.

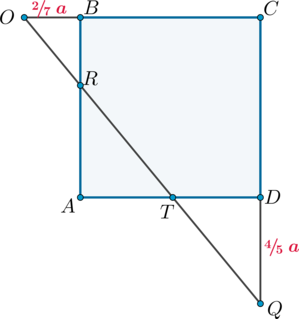
Постройте сечения, проходящие через точки .

Задание 1:

Подсказка. показать

Ответ. показать

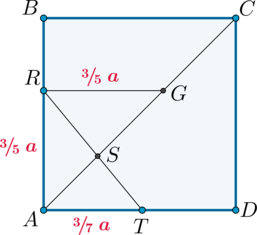
Задание 2:

Подсказка: показать

Ответ: показать

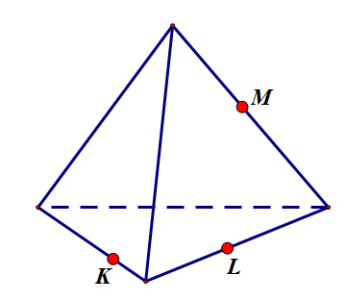
Задание 3:

Подсказка: показать

Ответ: показать

Задание 4:

Подсказка: показать

Ответ: показать

Задание 5:

Подсказка: показать

Ответ: показать

Задание 6:

Подсказка: показать

Ответ: показать

Задание 7:

Подсказка: показать

Ответ: показать

Задание 8:

Подсказка: показать

Ответ: показать

Задание 9:

Подсказка: показать

Ответ: показать

Задание 10:

Подсказка: показать

Ответ: показать

Задание 11:

Подсказка: показать

Ответ: показать

И. В. Фельдман, репетитор по математике.

Для вас другие записи этой рубрики:

Как найти расстояние от точки до прямой с помощью метода координат
Угол между плоскостями. Метод координат. Задание 14
Задание С2 из тренировочной работы 28 января 2014
Видеолекция 9. «Метод координат. Задание С2. Расстояния в пространстве»
Как построить чертеж в стереометрической задаче
Видеолекция «Метод координат. Задание 14. Углы в пространстве»

Источник

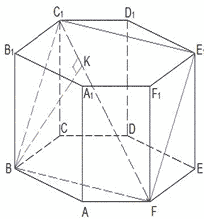
1.
На ребре АА₁
куба АBCDA₁B₁C₁D₁ отмечена
точка К так, что АК=4, КА₁=1.

Точка О – центр грани
АВСD
куба.

А) Постройте сечение
куба плоскостью D₁ОК

Б) Найдите объем
меньшей из частей куба, на которые он разбивается данной плоскостью.

2.
В основании прямой призмы АBCDA₁B₁C₁D₁ лежит
квадрат АВСD со стороной 2. Высота призмы равна . Точка Е лежит на диагонали ВD₁ ,
причем ВЕ=2. А) Постройте сечение призмы плоскостью А₁С₁Е

Б) Найдите угол наклона
этой плоскости к плоскости АВС.

3.
В кубе АBCDA₁B₁C₁D₁ все
ребра равны 7. На его ребре ВВ₁ отмечена точка К так, что КВ=4. Через
точки К и С₁
проведена плоскость α, параллельная прямой ВD₁.

А) Докажите, что А₁Р:РВ₁=1:3,
где Р – точка пересечения плоскости α с ребром А₁В₁

Б) Найдите объем большей
из частей куба, на которые он делится данной плоскостью.

4. На ребре AA₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ взята точка

E так, что A₁E : EA =1: 2 , на ребре BB1₁ — точка F так, что B₁F : FB =1:5 ,

а
точка T — середина ребра B₁C₁ . Известно, что AB = 4 , AD = 2, AA₁ = 6.

а)
Докажите, что плоскость EFT проходит через вершину D₁ .

б)
Найдите угол между плоскостью EFT и плоскостью BB₁C₁.

5
.
Все
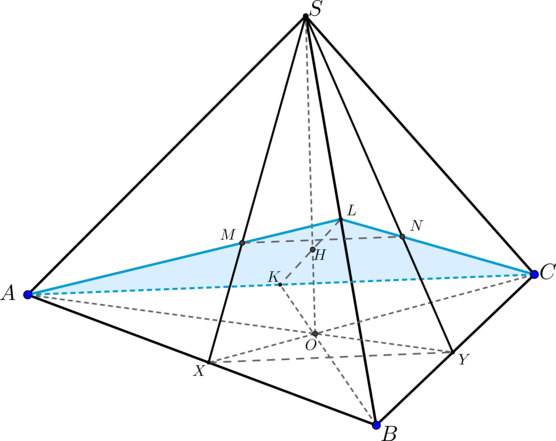
рёбра правильной треугольной пирамиды SBCD с вершиной S равны 18. Основание O высоты
SO этой пирамиды является серединой отрезка SS₁, M — середина ребра SB , точка L лежит на
ребре CD так, что

CL : LD = 7 : 2.

а)
Докажите, что сечение пирамиды SBCD плоскостью S₁LM — равнобокая трапеция.

б) Вычислите длину
средней линии этой трапеции.

6.
В правильной четырехугольной пирамиде МАВСD c вершиной
М стороны основания равны 3, а боковые ребра равны 8. Найдите площадь сечения
пирамиды плоскостью, проходящей через точку В и середину ребра МD,
параллельно прямой АС.

Источник

1. Повторение.

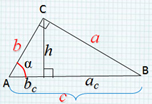
1.1.Соотношения между сторонами и углами
прямоугольного треугольника

Формулы: a² + b²= c²

1.2.Теорема косинусов

Квадрат стороны треугольника равен сумме
квадратов двух других сторон минус удвоенное
произведение этих сторон на косинус угла между
ними.

a² = b² + c²– 2bc·cosA

1.3. Угол между пересекающимися и
скрещивающимися прямыми.

За
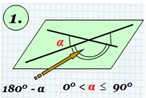
угол между пересекающимися прямыми принимают
острый угол, образованный этими прямыми.

Угол между скрещивающимися прямыми АВ и СD
определяется как угол между пересекающимися
прямыми А₁В₁ и С₁D₁, при
этом А₁В₁|| АВ и С₁D₁|| CD.

1.4. Угол между плоскостями (АСН) и (СНD) – это
двугранный угол АСНD, где СН ребро.

Точки
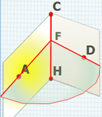
А и D лежат на гранях этого угла. AF CH, FD CH.

Угол AFD – линейный угол двугранного угла АCHD

2. Решение задач.

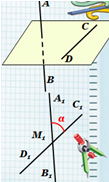
Задача №1.В правильной треугольной
призме ABCA₁B₁C₁, все рёбра которой
равны 1, найдите косинус угла между прямыми АВ₁
и ВС₁.

Решение:

1) Продлим плоскость ВСС₁, тогда (AB₁, ВС₁) = (AB₁, DВ₁) =
AВ₁D, т. к. C₁В || B₁D.

2) AB_{1 =}B₁D =из ABB_1.

3) из ABD по теореме
косинусов:

Ответ: 0,25.

Задача №2. В кубе ABCDA₁B₁C₁D₁
найдите угол между прямой AC₁ и плоскостью
ВСC₁.

Решение:

1) ВС₁ — проекция прямой АС₁ на
плоскость (ВCС₁), так как AB (ВCС₁), то AB ВС₁;

(AC₁, (ВCС₁))
= (AС₁,С₁В) = AC₁B, т.е. АВC₁ – прямоугольный.

2) Пусть АВ = а, тогда ВС₁ = а из C₁CB.

3) .

4) AC₁B = arctg .

Ответ: arctg .

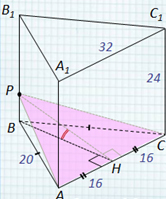
Задача №3. Основанием прямой
треугольной призмы ABCA₁B₁C₁,
является равнобедренный треугольник АВС, в
котором АВ = ВС = 20, АС = 32. Боковое ребро
призмы равно 24. Точка Р принадлежит ребру ВВ₁,
причем ВР : РВ₁= 1 : 3. Найдите тангенс
угла между плоскостями А₁В₁С₁
и АСР.

Решение:

1) Так как (АВС) || (А₁В₁С₁), то (( А₁В₁С₁) ,
(АСР)) = ((АВС),(АСР)).

2) Т.к. ВН АС (высота
р/б ),то по теореме о
трех перпендикулярах РН АС.

3) Тогда РНВ –
линейный угол двугранного РАСВ. Найдем его из прямоугольного РНВ.

4) РВ = 1/4 ВВ₁ = 1/4 · 24 = 6,

5) ВН² = АВ² – АН²(из AНВ)

ВН² = 20² – 16² = 144, ВН = 12;

6) tg РНВ = PB/HB = 6/12 = 0,5.

Ответ: 0,5.

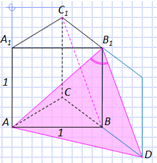
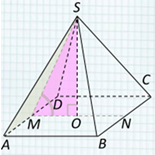
Задача №4. В правильной
четырехугольной пирамиде SABCD, все ребра которой
равны 1, найдите косинус угла между прямой AB и
плоскостью SAD.

Решение:

1) Так как ABCD – квадрат, то АВ AD. Поэтому проекция AB на плоскость (SAD)
будет AD. Значит,
искомый угол – двугранный угол при ребре
основания AD.

2) SM – высота грани SAD, SM =/2,
МО || АВ, МО = 0,5АВ = 0,5.

3) ?SMO – искомый угол, косинус которого найдем из
прямоугольного SMO.

сos ?SMO =
= =

Ответ :.

3. Повторение.

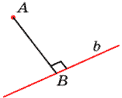
3.1. Расстояние от точки до прямой.

Определение. Расстоянием от
точки до прямой в пространстве называется длина
перпендикуляра, проведённого из данной точки к
данной прямой.

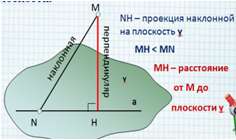
3.2. Расстояние от точки до плоскости.

Определение. Расстоянием от
точки до плоскости является длина
перпендикуляра, проведённого из данной точки к
данной плоскости.

3.3. Расстояние между скрещивающимися
прямыми.

Общим перпендикуляром двух скрещивающихся
прямых называют отрезок с концами на этих прямых,
являющийся перпендикуляром к каждой из них.

Определение. Расстоянием между
скрещивающимися прямыми называют длину их
общего перпендикуляра.

1 способ. Расстояние между скрещивающимися
прямыми равно расстоянию от любой точки одной из
этих прямых до плоскости, проходящей через
вторую прямую параллельно первой прямой.

2 способ. Расстояние между скрещивающимися
прямыми равно расстоянию между двумя
параллельными плоскостями, содержащими эти
прямые.

3 способ. Расстояние между скрещивающимися
прямыми равно расстоянию между их проекциями на
плоскость, перпендикулярную одной из них.

4. Решение задач.

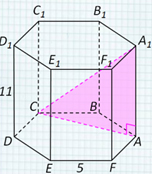
Задача №5. В правильной шестиугольной
призме ABCDEFA₁B₁C₁D₁E₁F₁,
стороны основания которой равны 5, а боковые
рёбра равны 11, найдите расстояние от точки С
до прямой A₁F₁.

Решение:

1) Так как ABCDEF – правильный шестиугольник, то
прямые AC и AF перпендикулярны.

CA AFпо доказанному,

CA A₁А по
определению правильной призмы

CA (АA₁F₁)
по признаку перпендикулярности прямой и
плоскости, т.е.

СА – перпендикуляр к плоскости, CA₁—
наклонная, A₁А – проекция наклонной,

A₁А A₁F₁;
A₁F₁– прямая в плоскости.

Тогда по теореме о трёх перпендикулярах CA₁ A₁F₁, значит,
длина отрезка CA₁ равна искомому расстоянию.

2) Из АВС (АВ=ВС=5, B = 120^o)

по теореме косинусов найдём СА: , ,

3) Из CAA_1,по теореме
Пифагора найдём CA₁:

CA₁²= 75 + 121 = 196

CA₁ = 14

Ответ: 14.

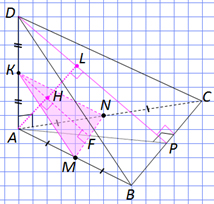
Задача №6.

Ребро AD пирамиды DABC перпендикулярно
плоскости основания АВС. Найдите расстояние
от А до плоскости, проходящей через середины
ребер АВ, АС и АD, если АD = 2, АВ = АС = 10, ВС
= 4.

Решение:

1) Построим плоскость КМN.

Т. к. КМ – средняя линия АDВ,
КМ?DВ,

MN — средняя линия АВC, МN
||| CВ, то (KMN) || (BCD) по признаку

параллельности плоскостей. АР – медиана и
высота р/б АВC.

KF – медиана и высота р/б KMN.

DP BC по теореме о трёх
перпендикулярах, KF || DP.

Искомое расстояние AH равно половине расстояния
от вершины А до плоскости BCD, т.к. (KMN) || (BCD) и KF –
средняя линия ADP.

2) LDA и ADP подобны по двум углам, тогда LA:AP=AD:DP,
тогда AL = (AP*AD):DP.

Найдём АР из АВР по
теореме Пифагора (АВ=10, ВР = 2 ):

AP² = AB² – BP² = 100 – 20 = 80, АР= 4

Найдём DР из АDР по
теореме Пифагора: DP² = AD² + AP² = 20 +
80 = 100, DP = 10.

Тогда AL =( 4 · 2):10=4. Итак, АН = 1/2 AL =
2.

Ответ: 2.

Задача №7.

В правильной шестиугольной призме АВCDEFA₁B₁C₁D₁E₁F₁ все
рёбра равны 1.

а) Постройте сечение призмы плоскостью,
проходящей через точки B, С₁ и F.

б) Найдите расстояние от точки В до прямой C₁F.

Решение.

а) Сечение – четырёхугольник BC₁E₁F с
диагональю C₁F.

Сторона ВC₁= — диагональ квадрата ВВ1С1С со
стороной 1.

Сторону BF найдём из ABF по
теореме косинусов:

BF²=AB²+AF²-2 * AB * AF * cosBAF;

BF²=AB²+AF²-2 * AB * AF * cos120⁰= 3.

Тогда

Так как CBF=90°, то по
теореме о трёх перпендикулярах, BF BC₁.

Значит,
сечение BC₁E₁F – прямоугольник.
Диагональ прямоугольника C₁F²=BF²+BC₁²;
C₁F²=3+2=5.

Отсюда

б) Сечение – прямоугольник BC₁E₁F.

ВК C₁F, ВК –
искомое расстояние от точки В до прямой C₁F.

Найдем ВК как высоту из FBС₁,

Используя 2 формулы площади треугольника.

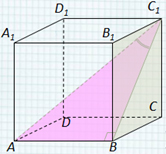
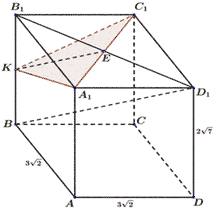
Задача №8.

Основанием прямой четырехугольной призмы
является квадрат ABCD со стороной , высота призмы равна . Точка K — середина ребра ВВ1.
Через точки K и С₁ проведена плоскость a,
параллельная прямой BD₁.

а) Докажите, что сечение призмы плоскостью a
является равнобедренным треугольником.

б) Найдите периметр треугольника, являющегося
сечением призмы плоскостью a.

Решение.

а) Для построения сечения призмы плоскостью a,
проведём КЕ || BD₁, E € B₁ D₁.

Плоскость a проходит через точки К, С₁и
Е.

Так как К – середина ВВ₁ и КЕ || BD₁, то
Е – середина диагонали А₁ С₁квадрата
А₁ В₁ С₁ Д₁. Значит,
плоскость a пересекает

грань А₁ В₁ С₁ Д₁по
диагонали А₁ С₁.

Соединив точки К, С₁ и А₁, получаем А₁ КС₁ — сечение
призмы плоскостью a.

А₁КВ₁ = С₁ КВ₁ по двум
сторонам и углу между ними (А₁ В₁ = С ₁В₁
, , В₁ К –
общая сторона).

Из равенства треугольников следует, что А₁К
= С₁К, значит А₁
КС₁ — равнобедренный.

5. Задачи для самостоятельного решения.

На ребре AA₁ прямоугольного
параллелепипеда ABCDA₁B₁C₁D₁
взята точка E так, что A₁E : EA = 2:5, на ребре BB₁
— точка F так, что B₁F : FB =1: 6, а точка Т —
середина ребра B₁ C₁. Известно, что AB = 5,
AD = 6 , AA₁ =14.

а) Докажите, что плоскость EFT проходит через
вершину D₁ .

б) Найдите угол между плоскостью EFT и плоскостью
AA₁B₁ .

Ответ. б) arctg .

2) Дана правильная треугольная призма ABCA₁B₁C₁,
все рёбра которой равны 4.

Через точки A, С₁ и середину T ребра
А₁В₁ проведена плоскость.

а) Докажите, что сечение призмы указанной
плоскостью является прямоугольным
треугольником.

б) Найдите угол между плоскостью сечения и
плоскостью ABC .

Ответ. б) arctg 2.

3) В правильной шестиугольной призме А…F₁
все рёбра равны 2.

а) Докажите, что плоскость ВВ₁F
перпендикулярна прямой В₁С_1.

б) Найдите расстояние от точки В до плоскости F В₁С_1.

Ответ. б) .

4) В пирамиде DАВС известны длины ребер
АВ=АС=DВ=DС=13, DА =6, ВС=24.

а) Постройте прямую, перпендикулярную прямым DА
и ВС.

б) Найдите расстояние между прямыми DА и ВС.

Ответ. б) 4.

5) Высота правильной треугольной пирамиды равна
20, а медиана её основания равна 6.

а) Постройте сечение пирамиды плоскостью,
проходящей через её вершину и перпендикулярной
ребру основания.

б) Найдите тангенс угла, который образует
боковое ребро с плоскостью основания.

Ответ. б) 5.

6) В правильной четырёхугольной пирамиде МАВСD с
вершиной М сторона основания равна 3, а боковое
ребро равно 6.

а) Постройте сечение пирамиды плоскостью,
проходящей через точку С и середину ребра МА
параллельно прямой ВD.

б) Найдите площадь этого сечения.

Ответ. б) 6.

Презентация.

Используемая литература.

1) И.В. Ященко, С.А. Шестаков, А.С. Трепалин
“Подготовка к ЕГЭ по математике 2016, профильный
уровень”, Москва, издательство МЦНМО, 2016.

2) Интернет-ресурсы:

http://www.fipi.ru/
http://mathege.ru/or/ege/Main
https://math-ege.sdamgia.ru/
http://alexlarin.net/
https://ege-ok.ru/

Источник