Всего: 21 1–20 | 21–21
Добавить в вариант
На рисунке представлено расположение двух неподвижных точечных электрических зарядов: 
и +2q. Как направлен (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор напряжённости суммарного электрического поля этих зарядов в точке А? Ответ запишите словом (словами).
Источник: ЕГЭ по физике 13.07.2020. Основная волна
На рисунке представлено расположение двух неподвижных отрицательных точечных электрических зарядов: –q и –q. Как направлен относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор напряжённости суммарного электрического поля этих зарядов в точке А? Ответ запишите словом (словами).
Источник: ЕГЭ по физике 2021. Досрочная волна. Вариант 1
На рисунке изображён вектор напряжённости 
электрического поля в точке С, которое создано двумя точечными зарядами: qA и qB.
Каков заряд qB, если заряд qA равен +2 нКл? Ответ укажите со знаком. Ответ дайте в нКл.
Аналоги к заданию № 1922: 20035 Все
Источник: Демонстрационная версия ЕГЭ—2021 по физике
Два точечных положительных заряда: q1 = 30 нКл и q2 = 10 нКл находятся в вакууме на расстоянии L = 0,5 м друг от друга. Определите величину напряжённости электрического поля этих зарядов в точке А, расположенной на прямой, соединяющей заряды, на расстоянии 2L от второго заряда (см. рис.). Ответ приведите в ньютонах на кулон.
Источник: ЕГЭ по физике 05.05.2014. Досрочная волна. Вариант 1.
Два точечных отрицательных заряда: q1 = −20 нКл и q2 = −40 нКл находятся в вакууме на расстоянии L = 1,5 м друг от друга. Определите величину напряжённости электрического поля этих зарядов в точке А, расположенной на прямой, соединяющей заряды, на одинаковом расстоянии от обоих зарядов. Ответ приведите в вольтах на метр.
Источник: ЕГЭ по физике 05.05.2014. Досрочная волна. Вариант 2., ЕГЭ по физике 05.05.2014. Досрочная волна. Вариант 3.
Два одинаковых по модулю точечных заряда находятся на оси OX. В точке с координатой x0 = 0 м расположен отрицательный заряд; а в точке с координатой x1 = a = 0,15 м — положительный заряд. В точке с координатой x2 = 3a проекция на ось OX вектора напряжённости электростатического поля, созданного этими зарядами, равна 200 В/м. Определите модуль каждого из этих зарядов. Ответ дайте в нанокулонах.
Аналоги к заданию № 24967: 25000 Все
Два точечных отрицательных заряда: q1 = −30 нКл и q2 = −10 нКл находятся в вакууме на расстоянии L = 0,5 м друг от друга. Определите величину напряжённости электрического поля этих зарядов в точке А, расположенной на прямой, соединяющей заряды, на расстоянии 2L от второго заряда (см. рис.). Ответ приведите в ньютонах на кулон.
Источник: ЕГЭ по физике 05.05.2014. Досрочная волна. Вариант 4.
Два маленьких заряженных металлических шарика одинакового радиуса расположены так, что расстояние между их центрами равно 2a (см. рис.).
Шарики приводят в соприкосновение и затем разводят на прежнее расстояние. Как изменятся при этом физические величины, указанные в таблице? Для каждой величины определите соответствующий характер изменения:
1) увеличится;
2) уменьшится;
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Модуль напряжённости электростатического поля в точке А | Потенциал точки А |
Два одинаковых маленьких шарика с электрическими зарядами q1 = 3 мкКл и q2 = −1 мкКл удерживаются на расстоянии a = 4 м друг от друга. Шарики соединяют на короткое время длинным тонким проводником. Как в результате этого изменятся следующие физические величины: электрический заряд первого шарика; модуль напряжённости электростатического поля, создаваемого обоими шариками в точке B.
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Электрический заряд первого
шарика |
Модуль напряжённости
электростатического поля, создаваемого обоими шариками в точке B |
Точки A, O и B расположены в вакууме на одной прямой. Расстояние ОВ = 3 · ОА (см. рисунок). В точку А поместили неподвижный точечный электрический заряд 3 нКл. Какой заряд нужно поместить в точку В, чтобы напряжённость электрического поля в точке О была равна нулю? Ответ запишите в нанокулонах.
Аналоги к заданию № 31886: 31931 Все
Точечный положительный заряд величиной 2 мкКл помещён между двумя протяжёнными пластинами, равномерно заряженными разноимёнными зарядами. Модуль напряжённости электрического поля, создаваемого положительно заряженной пластиной, равен 103 кВ/м, а поля, создаваемого отрицательно заряженной пластиной, в 2 раза больше. Определите модуль электрической силы, которая будет действовать на указанный точечный заряд. Ответ дайте в ньютонах.
Положительный электрический заряд равномерно распределён по очень длинной непроводящей нити BC. Точка A находится напротив одного из концов этой нити, так, что отрезки AB и BC перпендикулярны. Куда направлен вектор напряжённости электростатического поля, создаваемого в точке A заряженной нитью? В качестве ответа запишите номер стрелки (целое число от 1 до 6).
Отрицательный электрический заряд равномерно распределён по очень длинной непроводящей нити BC. Точка A находится напротив одного из концов этой нити, так, что отрезки AB и BC перпендикулярны. Куда направлен вектор напряжённости электростатического поля, создаваемого в точке A заряженной нитью? В качестве ответа запишите номер стрелки (целое число от 1 до 6).
Аналоги к заданию № 23300: 23332 Все
На горизонтальной плоскости в вершинах правильного пятиугольника закреплены 5 одинаковых положительных зарядов Q = 1 мкКл, расположенные на расстоянии R = 2 м от центра этого пятиугольника. На вертикальной прямой, проведённой из этого центра, на высоте 0,75R над плоскостью находится положительный заряд q = 4 мкКл. Найдите модуль и направление силы F , действующей на него со стороны остальных зарядов.
Два точечных заряда +q и –q расположены на одной прямой на расстоянии 3r друг от друга. На расстоянии 2r от положительного заряда и r от отрицательного заряда на этой же прямой располагают третий заряд +2q (см. рис.).
Определите, как изменятся модуль напряжённости электрического поля в точке А и потенциал точки А. Для каждой величины определите соответствующий характер изменения:
1) увеличится;
2) уменьшится;
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Модуль напряжённости
электрического поля в точке А |
Потенциал точки А |
Точка B находится в середине отрезка AC. Неподвижные точечные заряды –q и –2q (q = 2 нКл) расположены в точках A и C соответственно (см. рис.). Какой положительный заряд надо поместить в точку A взамен заряда –q, чтобы напряжённость электрического поля в точке B увеличилась в 4 раза? (Ответ дайте в нКл.)
Решение · ·
Во внешнем однородном электростатическом поле напряжённостью 400 В/м находится точечный положительный заряд q = 3 нКл. Точки A и B расположены на расстоянии 30 см от заряда q (см. рис.).
Установите соответствие между отношениями физических величин и численными значениями этих отношений. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ОТНОШЕНИЕ ФИЗИЧЕСКИХ ВЕЛИЧИН
А) отношение модуля напряжённости результирующего электростатического поля в точке A к модулю напряжённости внешнего электростатического поля
Б) отношение модуля напряжённости электростатического поля заряда q в точке B к модулю напряжённости результирующего электростатического поля в точке B
ЧИСЛЕННОЕ ЗНАЧЕНИЕ ОТНОШЕНИЯ
1) 0,25
2) 0,6
3) 1,25
4) 3
Заряды 10 и 16 нКл расположены на расстоянии 7 мм друг от друга. Какая сила будет действовать на заряд 2 нКл, помещенный в точку, удаленную на 3 мм от меньшего заряда и на 4 мм от большего? Ответ запишите в мН.
Всего: 21 1–20 | 21–21
Электрическое поле. ЗАДАЧИ с решениями
Формулы, используемые на уроках по теме «Электрическое поле. ЗАДАЧИ» в 10-11 классах при подготовке к ЕГЭ.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Электрон движется без начальной скорости вдоль силовой линии однородного электрического поля напряженностью Е = 2 • 104 Н/Кл. Какой путь S он пролетит прежде, чем его скорость станет v = 100 км/с ? Среда — воздух. Модуль заряда электрона е = 1,6 • 10–19 Кл, его масса me = 9,1 • 10–31 кг.
Задача № 2.
Пылинка с зарядом q = 1 нКл неподвижно висит в однородном электрическом поле напряженностью Е = 2 • 104 Н/Кл, вектор напряженности которого направлен вверх (рис. 2-9). Найти массу пылинки т. Сколько избыточных электронов N содержит пылинка? 
Смотреть решение и ответ
Задача № 3.
Заряженный шар диаметром D находится в равновесии в жидком диэлектрике плотностью р1 с диэлектрической проницаемостью ε (рис. 2-10). Найти поверхностную плотность зарядов на шаре σ, если плотность вещества шара р2. Напряженность электрического поля в диэлектрике Е, вектор напряженности направлен вверх. 
Смотреть решение и ответ
Задача № 4.
На каком расстоянии г2 от точечного заряда напряженность электрического поля этого заряда в жидком диэлектрике с диэлектрической проницаемостью ε2 = 81 (вода) такая же, как на расстоянии r1 = 9 см от этого заряда в воздухе?
Смотреть решение и ответ
Задача № 5.
Электрон влетает в однородное электрическое поле со скоростью v0, направленной перпендикулярно вектору напряженности Е (рис. 2-11). Под каким углом φ к линиям вектора напряженности будет направлен вектор его скорости через время t полета в поле? Чему будет равна работа сил поля А за это время? Чему будет равна кинетическая энергия электрона Wк через время t ? Напряженность поля Е. Масса электрона те и его заряд е известны. 
Задача № 6.
Тонкая металлическая пластинка массой m падает вертикально вниз равноускоренно так, что ее плоскость остается горизонтальной. Падению пластинки противодействует сила сопротивления среды Fсоnp. Найти напряженность электрического поля Е, возникающего внутри пластинки вследствие инерции свободных электронов. Масса электрона me, его заряд е.
Задача № 7.
К бесконечной, вертикальной, равномерно заряженной плоскости прикреплена одним кондом невесомая нить, на другом конце которой находится одноименно с нитью заряженный шарик радиусом R = 0,5 см, несущий заряд q = 1 • 10–10 Кл. Плотность вещества шарика р = 2 • 103 кг/м3. Натяжение нити Fн = 4,9 • 10–2 Н. Какой угол а образует с плоскостью нить, на которой висит шарик (рис. 2-12)? Среда – воздух. Чему равна поверхностная плотность σ зарядов на плоскости? 
Задача № 8.
Сфера радиусом R = 1 см равномерно заряжена. Поверхностная плотность зарядов на сфере σ = 10 нКл/см2. Найти напряженность Е1 электрического поля на расстоянии r1 = 10 см от центра сферы (рис. 2-13). Построить график зависимости напряженности Е от расстояния r в пределах от r0 = 0 до r1 = 10 см. Среда — воздух. 
Задача № 9.
Заряды q1 = 20 нКл и q2 = 10 нКл расположены на расстоянии r = 10 см друг от друга. Найти напряженность электрического поля Е1, созданного этими зарядами в точке 1, расположенной на расстоянии r1 = 4 см от заряда q1 и напряженность Е2 в точке 2, расположенной на расстоянии г2 = 2 см от заряда q2 (рис. 2-15). Среда — вакуум. 
Задача № 10.
Два одноименных точечных заряда q и 4q расположены на расстоянии r друг от друга. На каком расстоянии r1 от заряда q находится точка М, в которой напряженность поля этих зарядов Е = 0? На каком расстоянии r2 от заряда q находится такая точка, если эти заряды разноименные?
Задача № 11.
На расстоянии г = 3 см от поверхности шара радиусом R = 2 см находится точечный отрицательный заряд q = –2 нКл. Шар заряжен положительно с поверхностной плотностью зарядов σ = 2 нКл/м2. Найти напряженность поля Е, созданного заряженным шаром и точечным зарядом, в точке, расположенной на расстоянии r1 = 4 см от центра шара, и г2 = 3 см от заряда q. Среда — воздух.
Задача № 12.
В вершинах равностороннего треугольника со стороной а находятся заряды q, –q и q. Найти напряженность поля Е, созданного этими зарядами в центре треугольника. Среда — воздух.
(с) В учебных целях использованы цитаты из учебного пособия «Новый репетитор по физике для подготовки к ЕГЭ : задачи и методы их решения / И.Л. Касаткина; под ред. Т.В. Шкиль. — Ростов н /Д : Феникс».
Это конспект по теме «Электрическое поле. ЗАДАЧИ с решениями». Выберите дальнейшие действия:
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей»
- Подробности
- Обновлено 13.08.2018 18:42
- Просмотров: 1289
«Физика — 10 класс»
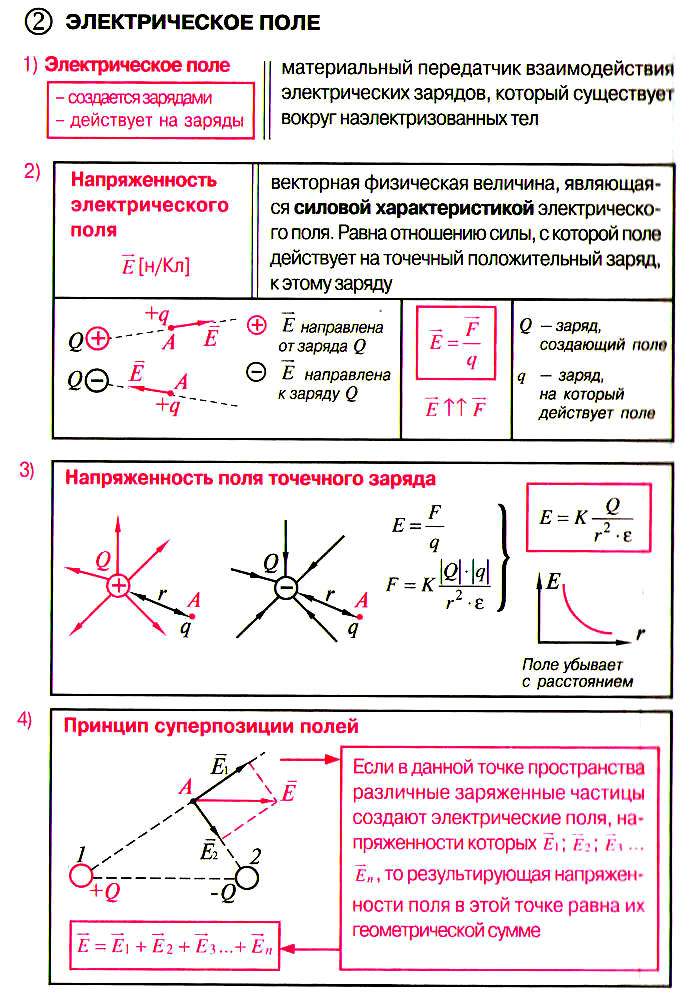
При решении задач с использованием понятия напряжённости электрического поля нужно прежде всего знать формулы (14.8) и (14.9), определяющие силу, действующую на заряд со стороны электрического поля, и напряжённость поля точечного заряда. Если поле создаётся несколькими зарядами, то для расчёта напряжённости в данной точке надо сделать рисунок и затем определить напряжённость как геометрическую сумму напряжённостей полей.
Задача 1.
Два одинаковых положительных точечных заряда расположены на расстоянии r друг от друга в вакууме. Определите напряжённость электрического поля в точке, расположенной на одинаковом расстоянии r от этих зарядов.
Р е ш е н и е.
Согласно принципу суперпозиции полей искомая напряжённость 
равна геометрической сумме напряжённостей полей, созданных каждым из зарядов (рис. 14.17): = 1 + 2.
Модули напряжённостей полей зарядов равны:
Диагональ параллелограмма, построенного на векторах 1 и 2, есть напряжённость результирующего поля, модуль которой равен:
Задача 2.
Проводящая сфера радиусом R = 0,2 м, несущая заряд q = 1,8 • 10-4 Кл, находится в вакууме. Определите: 1) модуль напряжённости электрического поля на её поверхности; 2) модуль напряжённости 1 электрического поля в точке, отстоящей на расстоянии r1 = 10 м от центра сферы; 3) модуль напряжённости 0 в центре сферы.
Р е ш е н и е.
Электрическое поле заряженной сферы вне её совпадает с полем точечного заряда. Поэтому 
Следовательно,
3) напряжённость поля в любой точке внутри проводящей сферы равна
нулю: Е0 = 0.
Задача 3.
В однородное электрическое поле напряжённостью Е0 = 3 кН/Кл внесли точечный заряд q = 4 • 10-10 Кл. Определите напряжённость электрического поля в точке А, находящейся на расстоянии r = 3 см от точечного заряда. Отрезок, соединяющий заряд и точку А, перпендикулярен силовым линиям однородного электрического поля.
Р е ш е н и е.
Согласно принципу суперпозиции напряжённость электрического поля в точке А равна векторной сумме напряжённостей однородного поля 0 и поля 1, созданного в этой точке внесённым электрическим зарядом. На рисунке 14.18 показаны эти два вектора и их сумма. По условию задачи векторы 0 и 1 взаимно перпендикулярны. Напряжённость поля точечного заряда 
Тогда напряжённость электрического поля в точке А равна:
Задача 4.
В вершинах равностороннего треугольника со стороной а = 3 см находятся три точечных заряда q1 = q2 = 10-9 Кл, q3 = -2 • 10-9 Кл. Определите напряжённость электрического поля в центре треугольника в точке О.
Р е ш е н и е.
Согласно принципу суперпозиции полей напряжённость поля в точке О равна векторной сумме напряжённостей полей, созданных каждым зарядом в отдельности: 0 = 1 + 2 + 3, причём 
где
На рисунке 14.19 показаны векторы напряжённостей 1, 2, 3. Сначала сложим векторы 1 и 2. Как видно из рисунка, угол между этими векторами равен 120°. Следовательно, модуль суммарного вектора равен модулю l1l и направлен в ту же сторону, что и вектор 3.
Окончательно запишем:
Задача 5.
Расстояние между двумя неподвижными зарядами q1 = -2 X 10-9 Кл и q2 = 10-9 Кл равно 1 м. В какой точке напряжённость электрического поля равна нулю?
Р е ш е н и е.
Очевидно, что на отрезке между зарядами напряжённость не может быть равна нулю, так как напряжённости полей 1 и 2, созданных этими зарядами, направлены в одну сторону (рис. 14.20).
Следовательно, напряжённость поля может быть равна нулю или справа, или слева от зарядов на линии, проходящей через эти заряды.
Так как модуль первого заряда больше, чем модуль второго, то эта точка должна находиться ближе ко второму заряду, т. е. в нашем случае справа от зарядов. Расстояние от второго заряда до точки А обозначим через х. Тогда из условия, что |‘1| = ‘2, можно записать: 
Решая это уравнение, получаем 
Окончательно 
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Электростатика — Физика, учебник для 10 класса — Класс!ная физика
Что такое электродинамика —
Электрический заряд и элементарные частицы. Закон сохранения заряд —
Закон Кулона. Единица электрического заряда —
Примеры решения задач по теме «Закон Кулона» —
Близкодействие и действие на расстоянии —
Электрическое поле —
Напряжённость электрического поля. Силовые линии —
Поле точечного заряда и заряженного шара. Принцип суперпозиции полей —
Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» —
Проводники в электростатическом поле —
Диэлектрики в электростатическом поле —
Потенциальная энергия заряженного тела в однородном электростатическом поле —
Потенциал электростатического поля и разность потенциалов —
Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности —
Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» —
Электроёмкость. Единицы электроёмкости. Конденсатор —
Энергия заряженного конденсатора. Применение конденсаторов —
Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»
Цель урока: Применять принцип суперпозиции для определения напряженности электрического поля
Цель урока: Применять принцип суперпозиции для определения напряженности электрического поля
Принцип суперпозиции полей
Закон Кулона Сила взаимодействия неподвижных точечных зарядов в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними
Закон Кулона
Сила взаимодействия неподвижных точечных зарядов в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
Электростатическое поле Вид материи, осуществляющий взаимодействие между электрически заряженными частицами
Электростатическое поле
Вид материи, осуществляющий взаимодействие между электрически заряженными частицами.
Напряженность поля- силовая характеристика электрического поля
Напряженность поля- силовая характеристика электрического поля
Отношение силы,с которой поле действует на точечный заряд, к этому заряду
Напряженность – векторная величина
Напряженность – векторная величина
Направление вектора напряженности совпадает с направлением силы, действующей на положительный заряд, и противоположно направлению силы, действующей на отрицательный заряд.
Модуль напряженности поля точечного заряда зависит прямо пропорционально от модуля заряда и обратно пропорционально от квадрата расстояния до него
Модуль напряженности поля точечного заряда
зависит прямо пропорционально от модуля заряда и обратно пропорционально от квадрата расстояния до него.
Решение задач
Решение задач
Ступень сложности 1 Между двумя точечными зарядами 4 • 10 -9
Ступень сложности 1
Между двумя точечными зарядами
4 • 10 -9 Кл и -5 • 10 -9 Кл
расстояние равно 0,6 м.
Найти напряженность поля в средней точке между зарядами
Дано: Решение:
Ступень сложности 2 В двух вершинах
Ступень сложности 2
В двух вершинах А и С квадрата со стороной 3м расположены разноименные заряды q1 и q2 модули которых одинаковы и равны 2 •10 -6 Кл.
Найти напряженность поля в двух других вершинах квадрата.
Дано: Решение:
Принцип суперпозиции, решение задач
Ступень сложности 3 В трех вершинах квадрата со стороной 0,4 м находятся одинаковые положительные заряды по 5 • 10 -9
Ступень сложности 3
В трех вершинах квадрата со стороной 0,4 м находятся одинаковые положительные заряды по 5 • 10 -9 Кл каждый.
Найти напряженность поля в четвертой вершине.
Дано: Решение:
Принцип суперпозиции, решение задач
Ступень сложности 4 Два одноименных заряда величиной по 10 –7
Ступень сложности 4
Два одноименных заряда величиной
по 10 –7 Кл расположены на расстоянии 12 см друг от друга.
Какова напряженность поля в точке, расположенной на перпендикуляре, восстановленном из середины прямой, соединяющей заряды, и удаленной от этой прямой на 16 см?
Дано: Решение:
Принцип суперпозиции, решение задач
Ступень сложности 5 Два точечных заряда 5 • 10 -9
Ступень сложности 5
Два точечных заряда
5 • 10 -9 Кл и -2,7 • 10 -9 Кл расположены
на расстоянии 40 см друг от друга.
Найти напряженность поля в точке А, находящейся на расстоянии 20 см от первого заряда и 30 см от второго заряда.
Дано: Решение:
Принцип суперпозиции, решение задач
Принцип суперпозиции, решение задач
Принцип суперпозиции, решение задач
Принцип суперпозиции полей Если в данной точке пространства различные заряженные частицы создают электрические поля, напряженности которых и т
Принцип суперпозиции полей
Если в данной точке пространства различные заряженные частицы создают электрические поля, напряженности которых
и т.д. , то результирующая напряженность поля равна их векторной сумме
Теория
| 1. | Как решать задание ЕГЭ |
Задания
| 1. |
Задание на понимание закона Кулона
Сложность: |
1 |
| 2. |
Задание на понимание принципа суперпозиции электростатических полей (1)
Сложность: |
2 |
| 3. |
Задание на понимание принципа суперпозиции электростатических полей (2)
Сложность: |
2 |
Экзаменационные задания (подписка)
| 1. |
Как на ЕГЭ (1). Электрическое поле. Законы постоянного тока. Расчёт физической величины
Сложность: |
1 |
| 2. |
Как на ЕГЭ (2). Электрическое поле. Законы постоянного тока. Расчёт физической величины
Сложность: |
1 |
| 3. |
Как на ЕГЭ (3). Электрическое поле. Законы постоянного тока. Расчёт физической величины
Сложность: |
1 |
| 4. |
Как на ЕГЭ (4). Электрическое поле. Законы постоянного тока. Расчёт физической величины
Сложность: |
1 |
Тесты
| 1. |
Тренировка по теме Электрическое поле. Законы постоянного тока. Расчёт физической величины
Сложность: лёгкое |
5 |
Материалы для учителей
| 1. | Методическое описание |
Задание 17667
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 17967
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18002
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18054
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18089
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18229
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18299
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18328
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18357
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18384
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18843
Введите ответ в поле ввода
Решение
→
Задание 18905
Введите ответ в поле ввода
Решение
→
Задание 18998
Введите ответ в поле ввода
Решение
→
1.5 Принцип суперпозиции. Решение задач.
Принцип
суперпозиции — принцип наложения или сложения. В нашем случае – сложения полей.
Если в данной точке пространства поле создано, не одним, двумя зарядами, то
общая напряженность поля равна векторной сумме напряженностей каждого
поля в отдельности.
Разберем
принцип суперпозиции электрических полей на примере решения задач.
Даны два заряда. Нужно найти напряженность
поля в точке,
№ 1 — лежащей на прямой, соединяющей
заряды
№ 2 — не лежащей на прямой,
соединяющей заряды
Вначале поймем, что значит точка, лежащая
на прямой соединяющей заряды, и не лежащая на этой прямой.
Пусть даны два заряда:
Проводим прямую, соединяющую эти заряды:
Отметим точки, лежащие на этой прямой и не
лежащие на это прямой:
Точки А,В,С лежат на прямой, точка D
– не лежит. Значит, суть задач данного типа в следующем: определить
напряженность поля в какой-либо указанной точке. Или дана напряженность, а
нужно найти точку, в которой эта напряженность имеет данное значение.
Ну вот, теперь перейдем к задачам.
Разберем
решение задач типа №1.
Дано: q1
= 2 нКл (= 2·10-9 Кл); q2
= — 2 нКл (= — 2·10-9 Кл); r
= 2 см (= 2·10-2 м).
Определить напряженность в точке, лежащей
на расстоянии 1 см от второго заряда.
Смотрим на рисунок: расстояние 1 см от
точки А до заряда q2
обозначила буквой х (икс). Можно было обозначить любой другой буквой a,
b,
z и т.п. – как вам нравится. Мне сегодня нравится икс х, значит, пусть
будет икс х.
Познакомимся с алгоритмом решения задач
на принцип суперпозиций на примере решения самих задач.
1)
Представим, что второго заряда нет. Мысленно закроем его, и увидим такую
картинку:
В точке А заряд q1
создает поле с напряженностью Е1. Так как заряд положительный, то
напряженность направлена от заряда и лежит на прямой, соединяющей заряд и точку
А (см. рис 1):
Расстояние от заряда до точки равно (r
+ х). Значит, формула для напряженности поля, созданного зарядом q1,
будет выглядеть вот так: 
Поскольку все величины, входящие в формулу
известны, вычислим:
Итак, напряженность поля, созданного
зарядом q1
в точке А равна Е1 = 20 кН/Кл.
2) Теперь представим, что первого
заряда q1
нет:
Теперь в точке А
поле создается только зарядом q2.
Так как заряд отрицательный, напряженность Е2
из точки А направлена к заряду. Еще один нюанс. Оба заряда q1
и q2
равны по величине, но заряд q2
находится к точке А ближе, значит его напряженность будет больше – длина
вектора Е2 больше, чем длина вектора Е1 (взгляните на
рисунок 1).
Расстояние от заряда до точки равно х.
Значит, формула для напряженности поля, созданного зарядом q1,
будет выглядеть вот так: 
(помним, в формулу
подставляем модули величин зарядов)
Поскольку все величины, входящие в формулу
известны, вычислим:
Итак, напряженность поля, созданного
зарядом q2
в точке А равна Е2 = 180 кН/Кл.
3) Объединяем рисунки 1 и 2:
W
Обращаю внимание. Стрелочка Е1 смотрит вправо и по длине меньше,
чем стрелочка Е2!
По принципу
суперпозиции (наложения) полей, общая напряженность равна векторной сумме
напряженностей каждого заряда:
(*)
Мы знаем, что
нужно «избавиться от векторов»: перейти к проекциям этих векторов.
Учитывая Е2 > Е1
проекция формулы (*) будет выглядеть так:
Е = Е2 – Е1.
Осталось посчитать: Е = Е2 – Е1
= 180 кН/Кл — 20 кН/Кл = 160 кН/Кл .
Ответ: напряженность Е = 160 кН/Кл,
направлена влево.
Самостоятельная работа №1 .
Решите
эту же задачу для условия
1.1
точка А находится на расстоянии 1 см слева
от заряда q2.
(Ответ : 360 кН/Кл)
1.2
Точка А находится в центре между зарядами,
и оба заряда положительны и равны 2нКл (0 кН/Кл)
Разберем
решение задач типа № 2.
Исходное условие тоже:
Дано: q1
= 2 нКл (= 2·10-9 Кл); q2
= — 2 нКл (= — 2·10-9 Кл); r
= 2 см (= 2·10-2 м).
Определить напряженность в точке, лежащей
на расстоянии 3 см от зарядаq1
и 4 см от заряда q2.
(Числа 3 и 4 придумала сама только что, так что ответы могут быть корявые. В
таком случае, будем округлять) .
Итак, делаем рисунок по условию задачи:
Понимаем, что расстояния в 3 см и 4 см
нужно как-то обозначить. Пусть будет: а = 3 см = 3·10-2 м, b
= 2 см = 2·10-2 м. Можно дописать в «Дано».
Начинаем рассуждать как в задаче №1:
Предполагаем, что заряда q2
– нет. Закрываем его (мысленно). Тогда в точке С напряженность создается только
зарядом q1
. Обозначим ее Е1.
Теперь пишем формулу для Е1 :
Аналогичные действия проводим для заряда q2:
E1
= 20 кН/Кл, Е2 = 45 кН/Кл. Е1 < Е2 —
Объясните, почему?
Объединяем два последних рисунка:
Нам нужно найти суммарное значение
напряженности в точке С. По принципу суперпозиции:
(*)
Как сложить два вектора, не лежащие на
одной прямой? Правило параллелограмма. Достраиваем на векторах Е1 и
Е2 параллелограмм и проводим диагональ из той же точки. Это и будет
искомый вектор 
:
Таким образом, задача свелась в геометрии.
Чтобы найти диагональ в параллелограмме, нужно знать стороны параллелограмма
(мы их знаем – 20 и 45) и угол α – острый угол в параллелограмме.
По теореме косинусов
. (**)
Угол можно узнать из треугольника со
сторонами 2см, 3 см и 2 см.
Рассмотрите рисунок. Самостоятельно
докажите, что угол при вершине Е1 в параллелограмме равен углу при
вершине С треугольника.
Запишем теорему косинусов для
треугольника Сq1q2:
r2 =
a2
+ b2
– 2abcosα
Подставляем значения в сантиметрах:
22 = 32 + 22 — 2·3·2·cos
α
4 = 9 + 4 – 12 cos α
4 = 13 — 12 cos α
12 cos α
= 13-4 = 9
cos α
= 9/12 = 3/4.
Итак, косинус вычислили и получили ¾ или
0,75.
Возвращаемся к формуле (**). Подставляем
теперь уже все известные величины и вычисляем ответ кН/Кл:
Е2 = 202 + 452
— 2·20·45·0,75 = 1075;
33,8 кН/Кл
Ответ: 33,8 кН/Кл.
Самостоятельная работа №2 .
Решить
задачи:
2.1
*Заряды по 0,1 мкКл расположены на
расстоянии 6 см друг от друга. Найти напряженность поля в точке, удаленной на
расстояние 5 см от каждого из зарядов. Решить эту задачу для случаев а) оба
заряда положительные; б) один заряд положительный, а другой отрицательный.
(Ответ: а) 576 кН/Кл; б) 432 кН/Кл) :
2.2
**В вершинах равностороннего треугольника
со стороной а находятся заряды +q,
+q
и – q.
Найти напряженность поля Е в центре треугольника. (Ответ 
)