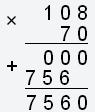Задачи на проценты егэ теория

Оглавление

Введение…………….…………………………………………
.…….3

Необходимые
математические понятия…………………………………4

1. Примеры

Задания
базового уровня сложности………….………………………6

Задания повышенного уровня сложности…………………………15

2. Задачи для
самостоятельного решения

Задания
базового уровня сложности………….…………………….19

Задания повышенного уровня сложности………………………….27

Список использованной
литературы……………………………..…..29

Введение

          
В школьном курсе математики тема «Проценты» изучается на первом этапе основной
школы, когда обучающиеся в силу возрастных особенностей ещё не могут получить
полноценные представления о процентах, об их роли в повседневной жизни. Задачи
на проценты включены в материалы итоговой аттестации за курс основной школы, в
задания ОГЭ и ЕГЭ. 

Данное пособие используется на
консультациях и на уроках при решении задач на проценты. и надеемся, что оно
поможет нам при сдаче экзаменов. 

Тип задания по кодификатору
требований. Задание  на использование приобретенных
знаний и умений в практической деятельности и повседневной жизни, проверяющее
умение решать прикладные задачи, в том числе социально-экономического и
физического характера, на наибольшие и наименьшие значения.

Характеристика задания: Несложная
текстовая задача, моделирующая реальную или близкую к реальной ситуацию.

Комментарий: Для
решения задачи обычно достаточно понимания того, что процент это просто одна
сотая часть некоторой величины.

Необходимые математические понятия

Процент – это сотая часть величины или числа.

Перевод
дроби в проценты: Чтобы
перевести обыкновенную дробь в проценты, нужно сначала перевести её в
десятичную дробь, а потом умножить на 100 и добавить знак %.

Представление
процентов десятичными дробями: Чтобы проценты перевести в число, нужно убрать знак % и разделить число
на 100.

%	Дробь	%	Дробь
100	1	12,5	0,125
50	0,5	10	0,1
25	0,25	5	0,05
20	0.2	1	0,01

Чтобы высчитать какой-либо процент от числа,
следует само число разделить на 100, а полученный результат умножить на
количество процентов. (чтобы найти a% от b, надо b*0,01a)

Чтобы найти число по его указанному проценту, нужно
заданное число разделить на указанную величину процента, а результат умножить
на 100.

(если известно, что a% 
числа х равно b, то х=b:
0,01а)

Чтобы найти процентное отношение
чисел, надо отношение этих чисел умножить на 100%.

Отношение двух
чисел – это частное от деления одного из них на другое.

Пропорция – это
верное равенство двух отношений.

В пропорции a:b
=c:dчисла
a
и d
называют крайними, а числа b
и c
– средними членами пропорции.

Основное свойство пропорции:
произведение крайних членов пропорции равно произведению её средних членов.

Концентрация
= * 100%

Заданиях базового уровня сложности

1.                 
Средний вес мальчиков того же возраста,
что и Коля, равен 69кг. Вес Коли составляет 150% среднего веса. Сколько
килограммов весит Коля?

Решение:

1 способ с помощью пропорции

69 кг – 100%

x кг – 150%                  

=

x=

x===103,5

Ответ: вес Коли составляет 103,5кг.

2 способ по определения процента

1)69*100=0,69(кг) – составляет 1%.

2)0,69*150=103,5(кг) – вес Коли.

Ответ: 103,5 кг.

2.                 
После уценки холодильника его новая цена
составила 0,5 старой цены. На сколько процентов уменьшилась цена холодильника в
результате уценки?

Решение:

Пусть цена холодильника до уценки
составляет 100%=1.

1)1*0,5=0,5=50(%) – новая цена холодильника.

2)100-50=50(%) – уменьшилась цена
холодильника в результате уценки.

Ответ: на 50%.

3.                 
В начале года число абонентов телефонной
компании «Сибирь» составляло 800 тысяч человек, а в конце года их стало 880
тысяч человек. На сколько процентов увеличилось за год число абонентов этой
компании?

Решение:

 
800 тыс. человек – 100%

  880 тыс. человек – x%

=

=110

110% — составило число абонентов т/к
«Сибирь» в конце года.

2)110-100=10(%) – увеличилось за год число
абонентов компании.

Ответ: на 10%.

4.                 
Поступивший в продажу в марте мобильный
телефон стоил 2800рублей. В октябре он стал стоить 2520 рублей. На сколько
процентов снизилась цена на мобильный телефон в период с марта по октябрь?

Решение:

1)2800:100=28(руб.) – составляет 1%.

2)2520:28=90(%) – составила цена в
октябре.

3)100-90=10(%) – снизилась цена на
мобильный телефон с марта по октябрь.

Ответ: 10%.

5.                 
Плата за телефон составляет 350 рублей в
месяц. В следующем году она увеличится на 12%. Сколько рублей придется платить
ежемесячно за телефон в следующем году?

Решение:

350 руб. – 100%

X руб. – 112%

=

 

х=56*7=392

Ответ: 392 руб. придется платить
ежемесячно за телефон в следующем году.

6.                 
В начале учебного года в  школе было 700
учащихся, а к концу учебного года их стало 903. На сколько процентов
увеличилось за учебный год число учащихся?

Решение:

700 уч-ся – 100%

903 уч-ся – х%

=

х==129

2)129-100=29(%) – увеличилось за учебный
год число обучающихся.

Ответ: 29%.

7.                 
Сберегательный банк начисляет на срочный
вклад 17% годовых. Вкладчик  положил на счёт 1100 рублей. Сколько рублей будет
на этом счёте через год, если никаких операций, кроме начисления процентов, со
счётом производиться не будет?

Решение:

1)1100:100=11(руб.) –  составляет 1%.

2)11*17=187(руб.) – составляет 17%.

3)1100+187=1287(руб.) – будет на счету
через год.

Ответ:1287 рублей.

Можно через пропорцию:

1100 – 100%

х – 17%

=

х==187

1100+187=1287(руб.) – будет на счету через
год.

8.                 
Стоимость проезда в электричке составляет
231 рубль. Студентам предоставляется скидка 50%. Сколько рублей будет стоить
проезд для 4 взрослых и 12 студентов?

Решение:                                          
                                                                  

1)231:2=115,5(р) – билет для студента.

2)115,5*12+231*4+2310(руб.) – стоит проезд
для 4 взрослых и 12 студентов.

Ответ: 2310 рублей.

9.                 
Для приготовления фарша взяли говядину и
свинину в отношении 22: 3. Сколько процентов фарша составляет говядина?

Решение:

1)22+3=25(ч) – составляет фарш.

25ч.=100%

2)100:25=4(%) – 1 часть.

3)22*4=88(%) – составляет говядина.

Ответ: 88%.

10.             
Спортивный магазин проводит акцию. Любая
футболка стоит 400 рублей. При покупке двух футболок – скидка на вторую
футболку 40%. Сколько рублей придётся заплатить за покупку двух футболок в
период действия акции?

Решение:

1)400:100=4(р) – составляет 1%.

2)40*4=160(р) – скидка на 2 футболку.

3)400-160=240(р) – стоит 2 футболка.

4)400+240=640(руб.) – стоят две футболки в период
действия акции.

Ответ: 640 рублей.

Можно через пропорцию:

400 – 100%

х – 40%

=

х==160 скидка на 2
футболку.

400-160=240(р) – стоит 2 футболка.

400+240=640(руб.) – стоят две футболки в период
действия акции.

11. На счет
в банке, доход по ко­то­ро­му со­став­ля­ет 15% годовых, внес­ли 24 тыс. р.
Сколь­ко тысяч руб­лей будет на этом счете через год, если ни­ка­ких опе­ра­ций
со сче­том про­во­дить­ся не будет?

Решение: Найдем, сколь­ко про­цен­тов будет через год:

1) 100%+15%=115% 2)
115%:100%=1,15 3) 24  тыс рублей

Ответ: 27,6 тыс. руб

Можно через пропорцию:

24 – 100%

х – 15%

=

х==3,6

24+3,6=27,6 тыс. руб – будет на счету
через год.

Ответ: 27,6 тыс рублей

12. Городской бюд­жет со­став­ля­ет
45 млн. р., а рас­хо­ды на одну из его ста­тей со­ста­ви­ли 12,5%. Сколь­ко руб­лей
по­тра­че­но на эту ста­тью бюджета?

Решение:

45000000 – 100%

х – 12,5%

=

х==5625000

Ответ: 5625000 рублей

13. Государству при­над­ле­жит 60% акций предприятия,
осталь­ные акции при­над­ле­жат част­ным лицам. Общая при­быль пред­при­я­тия
после упла­ты на­ло­гов за год со­ста­ви­ла 40 млн. р. Какая сумма в рублях из
этой при­бы­ли долж­на пойти на вы­пла­ту част­ным акционерам?

Решение: Если 60%
акций принадлежит государству, то 100%-60%=40% принадлежит частным лицам.

40000000 – 100%

х – 40%

=

х==16000000

Ответ: 16000000 рублей

14. Товар на рас­про­да­же
уце­ни­ли на 20%, при этом он стал сто­ить 680 р. Сколь­ко стоил товар до
распродажи?

Решение:

Если уценили на 20%, то новая цена составит 80%.

 680 – 80%

х – 100%

=

х==850

Ответ: 850 рублей

15. Виноград стоит 160 руб­лей за килограмм, а ма­ли­на
— 200 руб­лей за килограмм. На сколь­ко про­цен­тов ви­но­град де­шев­ле
малины?

Решение:

1) Виноград дешевле
малины 200-160=40 рублей.

2) Разделим 40 : 200=0,2

3) Переводим десятичную
дробь на процент 0,2

Ответ: 20%

16. Чашка, ко­то­рая сто­и­ла 90 рублей, продаётся с
10%-й скидкой. При по­куп­ке 10 таких чашек по­ку­па­тель отдал кас­си­ру
1000 рублей. Сколь­ко руб­лей сдачи он дол­жен получить?

Решение:

1) 90 – 100%

    х – 10%

    х==9

2) 90-9=81 рубль стоимость одной чашки

3) 81*10=810 стоимость 10 чашек

4) 1000-810=190 рублей сдача

Ответ: 190 рублей

17. Ту­ри­сти­че­ская фирма ор­га­ни­зу­ет трех­днев­ные
ав­то­бус­ные экс­кур­сии. Сто­и­мость экс­кур­сии для од­но­го че­ло­ве­ка со­став­ля­ет
3500 р. Груп­пам предо­став­ля­ют­ся скид­ки: груп­пе от 3 до 10 че­ло­век —
5%, груп­пе более 10 че­ло­век — 10%. Сколь­ко за­пла­тит за экс­кур­сию груп­па
из 8 че­ло­век?

Решение:

1) 3500·8=28000р.
Стоимость экс­кур­сии для 8 че­ло­век без учёта скид­ки

2) 28000 – 100%

    х – 5%

    х== 1400 предоставляется скидка

3) 28000-1400=26600 р. стоимость экскурсии
с учетом скидки

Ответ: 26600 р.

18. Ма­га­зин де­ла­ет
пен­си­о­не­рам скид­ку на опре­делённое ко­ли­че­ство про­цен­тов от сто­и­мо­сти
по­куп­ки. Батон хлеба стоит в ма­га­зи­не 20 руб­лей, а пен­си­о­нер за­пла­тил
за него 19 руб­лей 40 ко­пе­ек. Сколь­ко про­цен­тов со­став­ля­ет скид­ка для
пен­си­о­не­ра?

Решение:

 20 – 100%

 19,40
– х%

 =

 
х==97

2)
100%-97%=3%  скидку получает пенсионер

Ответ:
3 %

19. Магазин дет­ских
то­ва­ров за­ку­па­ет по­гре­муш­ку по опто­вой цене 190 руб­лей за одну штуку
и продаёт с 20-процентной наценкой. Сколь­ко будут сто­ить 3 такие погремушки,
куп­лен­ные в этом магазине?

Решение:

100% + 20% = 120%

190 – 100%

х – 120%

=

х==228

228·3=684 руб стоимость трех погремушек

Ответ: 684 рублей

20. В го­ро­де
190 000 жи­те­лей, при­чем 29% – это пен­си­о­не­ры. Сколь­ко при­мер­но
че­ло­век со­став­ля­ет эта ка­те­го­рия жи­те­лей? Ответ округ­ли­те до тысяч.

Решение.

190000 – 100%

     х       –  29%

=

х==55100 ≈ 55 000
человек.

Ответ: 55000 человек

21. Какая сумма (в рублях) будет про­став­ле­на
в кас­со­вом чеке, если сто­и­мость то­ва­ра 520 р., и по­ку­па­тель опла­чи­ва­ет
его по дис­конт­ной карте с 5%-ной скидкой?

Решение.

520 – 100%

  х   –   5%

=

х==26 руб — скидка, ко­то­рую
по­лу­ча­ет по­ку­па­тель опла­чи­вая товар по дис­конт­ной карте с 5%-ной
скидкой.

520 — 26 = 494 руб

Ответ: 494 руб ито­го­вая
цена со скид­кой

22. Рас­хо­ды на одну из ста­тей го­род­ско­го
бюд­же­та со­став­ля­ют 12,5%. Вы­ра­зи­те эту часть бюд­же­та де­ся­тич­ной
дро­бью.

Решение.

12,5 : 100% = 0,125

Ответ: 0,125

23. Флакон шампуня стоит 160 рублей. Какое
наибольшее число флаконов можно купить на 1000 рублей во время распродажи,
когда скидка составляет 25% ?

Решение.

160 – 100%

  х   –   25%

=

х==40 руб составляет скидка

160 — 40 = 120 руб стоит флакон после
скидки

1000 : 120 = 8,3

Значит, можно будет купить 8 флаконов
шампуня.

Ответ: 8

Задания
повышенного уровня сложности

1. Имеются два сосуда, содержащие
10 кг и 16 кг раствора кислоты различной концентрации. Если их слить
вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные
массы этих растворов, то полученный раствор будет содержать 61% кислоты.
Сколько килограммов кислоты содержится в первом растворе?

Решение.

Пусть концентрация первого раствора
— х, концентрация второго раствора — y. Составим
систему уравнений согласно условию задачи:

Таким образом, в первом растворе
содержится  килограмма
кислоты.

Ответ: 8,7.

2. Имеются два сосуда, содержащие
4 кг и 16 кг раствора кислоты различной концентрации. Если их слить
вместе, то получится раствор, содержащий 57% кислоты. Если же слить равные
массы этих растворов, то полученный раствор будет содержать 60% кислоты.
Сколько килограммов кислоты содержится в первом растворе?

Решение.

Пусть концентрация первого раствора — х,
концентрация второго раствора — y. Составим систему уравнений согласно условию
задачи:

 Таким образом, в первом растворе
содержится  килограмма
кислоты

Ответ: 2,6

3. Све­жие фрук­ты со­дер­жат 80% воды, а
вы­су­шен­ные — 28%. Сколь­ко сухих фрук­тов по­лу­чит­ся из 288 кг све­жих
фрук­тов?

Решение.

Свежие фрук­ты со­дер­жат 20% пи­та­тель­но­го
вещества, а вы­су­шен­ные — 72%. В 288 кг све­жих фрук­тов со­дер­жит­ся
0,2 · 288 = 57,6 кг пи­та­тель­но­го вещества. Такое
ко­ли­че­ство пи­та­тель­но­го ве­ще­ства будет со­дер­жать­ся в  кг вы­су­шен­ных
фруктов.

Ответ: 80.

4. Свежие фрук­ты со­дер­жат 86 % воды, а
вы­су­шен­ные — 23 %. Сколь­ко тре­бу­ет­ся све­жих фрук­тов для при­го­тов­ле­ния
72 кг вы­су­шен­ных фруктов?

Решение.

Заметим, что сухая часть све­жих фрук­тов
со­став­ля­ет 14%, а вы­су­шен­ных — 77%. Значит, для при­го­тов­ле­ния 72 кг
вы­су­шен­ных фрук­тов тре­бу­ет­ся  кг
свежих.

Ответ: 396 кг.

5. Первый сплав содержит 5% меди, второй
– 11% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух
сплавов получили  третий сплав, содержащий 10% меди. Найдите массу третьего
сплава. Ответ дайте в килограммах.

Решение:

По условию задачи из двух сплавов получили третий
сплав, составим уравнение.

	Масса сплава (кг)	Концентрация(%)	Масса меди (кг)
1 сплав	х	5	0,05х
2 сплав	х=4	11	0,11(х+4)
3 сплав	2х+4	10	0,1(2х+4)

По
условию задачи из двух сплавов получили третий сплав, составим уравнение.

0,05х+0,11(х+4)=0,1(2х+4)

0,05х+0,11х+0,44=0,2х+0,4

0,05х+0,11х-0,2х=0,4-0,44

-0,04х=-0,04

х=1

1кг-масса 1 сплава.

2)2*1+4=6(кг) – масса третьего сплава.

Ответ: 6 кг.

6. Смешав 70% и 60% растворы кислоты и добавив 2кг
чистой воды, получили 50% раствор кислоты. Если бы вместо 2кг воды добавили 2кг
90% раствора той же кислоты, то получили бы 70% раствор кислоты. Сколько
килограммов 70% раствора использовали для получения смеси?

Решение:

	Масса веществ (кг)	Концентрация(%)	Масса кислоты (кг)
1 раствор	х	70	0,7х
2 раствор	у	60	0,6у
3 раствор	х+у+2	50	0,7х+0,6у=0,5(х+у+2)
4 раствор	х+у+2	70	0,7х+0,6у+0,5*2=0,7(х+у+2)

Составим
выражения для вычисления массы кислоты в 3 и 4 растворах, составим систему
уравнений:

0,7х+0,6у=0,5(х+у+2)

0,7х+0,6у+1,8=0,7(х+у+2)

0,7х+0,6у=0,5х+0,5у+1

0,7х+0,6у+1,8=0,7х+0,7х+1,4

0,7х+0,6у-0,5х-0,5у=1

0,7х+0,6у-0,7х-0,7у=1,4-1,8

0,2х+0,1у=1

-0,1у=-0,4

0,2х=0,6

х=0,6:0,2

х=6:2

х=3

3кг. 70% раствора использовали для получения смеси.

Ответ: 3кг.

Задачи для самостоятельного решения

Задания базового уровня сложности

1.1 Средний вес мальчиков
того же возраста, что и Вова,
равен 54 кг. Вес Вовы
составляет 135% среднего веса.
Сколько килограммов весит Вова?

1.2 Средний вес мальчиков
того же возраста, что и Толя, равен 68 кг.
Вес Толи составляет 125%
среднего веса. Сколько килограммов весит Толя?

1.3 Средний вес мальчиков того же возраста, что и Саша,
равен 55 кг. Вес Саши
составляет 110% среднего веса.
Сколько килограммов весит Саша?

2.1 После уцен­ки
те­ле­ви­зо­ра его новая цена со­ста­ви­ла 0,52 ста­рой. На сколь­ко про­цен­тов
умень­ши­лась цена те­ле­ви­зо­ра в ре­зуль­та­те уцен­ки?

2.2 После уцен­ки телевизора его новая цена со­ста­ви­ла 0,98
старой. На сколь­ко процентов умень­ши­лась цена те­ле­ви­зо­ра в ре­зуль­та­те
уценки?

2.3  После уцен­ки
телевизора его новая цена со­ста­ви­ла 0,55 старой. На сколь­ко процентов умень­ши­лась
цена те­ле­ви­зо­ра в ре­зуль­та­те уценки?

3.1 В начале года число
абонентов телефонной компании «Восток» составляло 500 тыс. чел., а в
конце года их стало 575 тыс. чел. На сколько процентов увеличилось за
год число абонентов этой компании?

3.2 В начале года число
абонентов телефонной компании «Запад» составляло 400 тыс. чел., а в
конце года их стало 420 тыс. чел. На сколько процентов увеличилось за
год число абонентов этой компании?

3.3 В начале года число
абонентов телефонной компании «Север» составляло 600 тыс. чел., а в
конце года их стало 660 тыс. чел. На сколько процентов увеличилось за
год число абонентов этой компании?

4.1 Поступивший в про­да­жу
в ян­ва­ре мо­биль­ный те­ле­фон стоил 3000 рублей. В марте он стал сто­ить
2790 рублей. На сколь­ко про­цен­тов сни­зи­лась цена на мо­биль­ный те­ле­фон
в пе­ри­од с ян­ва­ря по март?

4.2 По­сту­пив­ший в про­да­жу
в ян­ва­ре мо­биль­ный те­ле­фон стоил 2400 руб­лей. В но­яб­ре он стал сто­ить
1200 руб­лей. На сколь­ко про­цен­тов сни­зи­лась цена на мо­биль­ный те­ле­фон
в пе­ри­од с ян­ва­ря по но­ябрь?

4.3 Поступивший в про­да­жу
в фев­ра­ле мобильный те­ле­фон стоил 1800 рублей. В июне он стал сто­ить 1530
рублей. На сколь­ко процентов сни­зи­лась цена на мо­биль­ный телефон в пе­ри­од
с фев­ра­ля по июнь?

5.1 Плата за те­ле­фон
составляет 220 руб­лей в месяц. В сле­ду­ю­щем году она уве­ли­чит­ся на 10%.
Сколь­ко придётся пла­тить ежемесячно за те­ле­фон в сле­ду­ю­щем году?

5.2 Плата за те­ле­фон
составляет 360 руб­лей в месяц. В сле­ду­ю­щем году она уве­ли­чит­ся на 4%.
Сколь­ко придётся пла­тить ежемесячно за те­ле­фон в сле­ду­ю­щем году?

5.3 Плата за те­ле­фон
составляет 210 руб­лей в месяц. В сле­ду­ю­щем году она уве­ли­чит­ся на 15%.
Сколь­ко придётся пла­тить ежемесячно за те­ле­фон в сле­ду­ю­щем году?

6.1 В на­ча­ле учеб­но­го
года в школе было 840 уча­щих­ся, а к концу года их стало 966. На сколь­ко про­цен­тов
уве­ли­чи­лось за год число уча­щих­ся?

6.2  В на­ча­ле учебного
года в школе было 1100 учащихся, а к концу года их стало 869. На сколь­ко
процентов умень­ши­лось за год число учащихся?

6.3 В на­ча­ле учебного
года в школе было 500 учащихся, а к концу года их стало 455. На сколь­ко
процентов умень­ши­лось за год число учащихся?

7.1 Сберегательный банк начисляет на срочный вклад 15% годовых. Вкладчик
положил на счет 900 р. Какая сумма будет на этом счете через год, если
никаких операций со счетом проводиться не будет?

7.2 Сберегательный банк начисляет на срочный вклад 12% годовых.
Вкладчик положил на счет 600 р. Какая сумма будет на этом счете через год,
если никаких операций со счетом проводиться не будет?

7.3 Сберегательный банк начисляет на срочный вклад 20% годовых. Вкладчик
положил на счет 900 р. Какая сумма будет на этом счете через год, если
никаких операций со счетом проводиться не будет?

8.1 Стоимость
про­ез­да в при­го­род­ном элек­тро­по­ез­де со­став­ля­ет 140 рублей. Школь­ни­кам
предо­став­ля­ет­ся скидка 50%. Сколь­ко руб­лей будет стоить про­езд для
5 взрос­лых и 3 школьников?

8.2 Стоимость
про­ез­да в при­го­род­ном элек­тро­по­ез­де со­став­ля­ет 140 рублей. Школь­ни­кам
предо­став­ля­ет­ся скидка 50%. Сколь­ко руб­лей будет стоить про­езд для
5 взрос­лых и 3 школьников?

8.3 Стоимость
про­ез­да в при­го­род­ном элек­тро­по­ез­де со­став­ля­ет 140 рублей. Школь­ни­кам
предо­став­ля­ет­ся скидка 50%. Сколь­ко руб­лей будет стоить про­езд для
5 взрос­лых и 3 школьников?

9.1
Для
приготовления фарша взяли говядину и свинину в отношении 9:31. Сколько процентов
фарша составляет говядина?

9.2 Для приготовления фарша взяли говядину
и свинину в отношении 11:39. Сколько процентов фарша составляет говядина?

9.3
Для
приготовления фарша взяли говядину и свинину в отношении 1:24. Сколько
процентов фарша составляет говядина?

10.1 Спор­тив­ный ма­га­зин про­во­дит акцию: «Любая фут­бол­ка по цене 200
руб­лей. При по­куп­ке двух фут­бо­лок — скид­ка на вто­рую 75%». Сколь­ко руб­лей
придётся за­пла­тить за по­куп­ку двух фут­бо­лок?

10.2 Спор­тив­ный
ма­га­зин про­во­дит акцию: «Любая фут­бол­ка по цене 300 руб­лей. При по­куп­ке
двух фут­бо­лок — скид­ка на вто­рую 70%». Сколь­ко руб­лей придётся за­пла­тить
за по­куп­ку двух фут­бо­лок?

10.3 Спор­тив­ный
ма­га­зин про­во­дит акцию: «Любой сви­тер по цене 600 руб­лей. При по­куп­ке
двух сви­те­ров — скид­ка на вто­рой 80%». Сколь­ко руб­лей придётся за­пла­тить
за по­куп­ку двух сви­те­ров?

11.1 На счет
в банке, доход по которому составляет 20% годовых, внесли 16 тыс. р. Сколько
тысяч рублей будет на этом счете через год, если никаких операций со счетом
проводиться не будет?

11.2 На счет
в банке, доход по которому составляет 18% годовых, внесли 15 тыс. р. Сколько
тысяч рублей будет на этом счете через год, если никаких операций со счетом
проводиться не будет?

11.3 На счет
в банке, доход по которому составляет 15% годовых, внесли 24 тыс. р. Сколько
тысяч рублей будет на этом счете через год, если никаких операций со счетом
проводиться не будет?

12.1
Городской бюджет составляет 50 млн. р., а расходы на одну из его статей
составили 35%. Сколько рублей потрачено на эту статью бюджета?

12.2
Городской бюджет составляет 42 млн. р., а расходы на одну из его статей
составили 7,5%. Сколько рублей потрачено на эту статью бюджета?

12.3 Городской бюджет составляет 68 млн. р., а расходы на одну из его
статей составили 22,5%. Сколько рублей потрачено на эту статью бюджета?

13.1 Государству принадлежит 20% акций предприятия,
остальные акции принадлежат частным лицам. Общая прибыль предприятия после
уплаты налогов за год составила 80 млн. р. Какая сумма из этой
прибыли должна пойти на выплату частным акционерам?

13.2
Государству принадлежит 80% акций предприятия, остальные акции принадлежат
частным лицам. Общая прибыль предприятия после уплаты налогов за год составила
50 млн. р. Какая сумма из этой прибыли должна пойти на выплату
частным акционерам?

13.3
Государству принадлежит 60% акций предприятия, остальные акции принадлежат
частным лицам. Общая прибыль предприятия после уплаты налогов за год составила
60 млн. р. Какая сумма из этой прибыли должна пойти на выплату
частным акционерам?

14.1 Товар
на распродаже уценили на 5%, при этом он стал стоить 570 р. Сколько стоил
товар до распродажи?

14.2 Товар на распродаже уценили на 30%, при этом он
стал стоить 770 р. Сколько стоил товар до распродажи?

14.3 Товар на распродаже уценили на 40%, при этом он стал
стоить 960 р. Сколько стоил товар до распродажи?

15.1
Клубника стоит 180 руб­лей за килограмм, а клюк­ва — 250 руб­лей за килограмм.
На сколь­ко про­цен­тов клуб­ни­ка де­шев­ле клюквы?

15.2
Черешня стоит 150 руб­лей за килограмм, а ви­но­град — 160 руб­лей за
килограмм. На сколь­ко про­цен­тов че­реш­ня де­шев­ле винограда?

15.3
Гелевая ручка стоит 50 руб­лей, а шариковая — 30 руб­лей. На сколь­ко про­цен­тов
шариковая  де­шев­ле гелевой?

16.1
Кисть, ко­то­рая сто­и­ла 240 руб­лей, продаётся с 25%-й скид­кой. При по­куп­ке
двух таких ки­стей по­ку­па­тель отдал кас­си­ру 500 руб­лей. Сколь­ко руб­лей
сдачи он дол­жен по­лу­чить?

16.2 Набор
полотенец, ко­то­рый стоил 200 рублей, продаётся с 3%-й скидкой. При по­куп­ке
этого на­бо­ра по­ку­па­тель отдал кас­си­ру 500 рублей. Сколь­ко руб­лей сдачи
он дол­жен получить?

16.3 Набор
фло­ма­сте­ров, ко­то­рый стоил 160 руб­лей, продаётся с 25%-й скид­кой. При по­куп­ке
трёх таких на­бо­ров по­ку­па­тель отдал кас­си­ру 500 руб­лей. Сколь­ко руб­лей
сдачи он дол­жен по­лу­чить?

17.1
Туристическая фирма ор­га­ни­зу­ет трехдневные ав­то­бус­ные экскурсии. Сто­и­мость
экскурсии для од­но­го человека со­став­ля­ет 2500 р. Груп­пам предоставляются
скидки: груп­пе от 3 до 10 человек  — 5%, груп­пе более 10 человек  — 10%. Сколь­ко заплатит за экс­кур­сию группа из 12
человек?

17.2
Туристическая фирма ор­га­ни­зу­ет трехдневные ав­то­бус­ные экскурсии. Сто­и­мость
экскурсии для од­но­го человека со­став­ля­ет 3500 р. Груп­пам предоставляются
скидки: груп­пе от 3 до 10 человек  — 5%, груп­пе более 10 человек  — 10%. Сколь­ко заплатит за экс­кур­сию группа из 14
человек?

17.3
Туристическая фирма ор­га­ни­зу­ет трехдневные ав­то­бус­ные экскурсии. Сто­и­мость
экскурсии для од­но­го человека со­став­ля­ет 2500 р. Груп­пам предоставляются
скидки: груп­пе от 3 до 10 человек  — 5%, груп­пе более 10 че­ло­век —  10%. Сколь­ко заплатит за экс­кур­сию группа из
6 человек?

18.1 Ма­га­зин де­ла­ет пен­си­о­не­рам
скид­ку на опре­делённое ко­ли­че­ство про­цен­тов от сто­и­мо­сти по­куп­ки.
Батон хлеба стоит в ма­га­зи­не 15 руб­лей, а пен­си­о­нер за­пла­тил за него
14 руб­лей 55 ко­пе­ек. Сколь­ко про­цен­тов со­став­ля­ет скид­ка для пен­си­о­не­ра?

18.2 Магазин де­ла­ет пенсионерам скид­ку
на определённое ко­ли­че­ство процентов от сто­и­мо­сти покупки. Пакет сока
стоит в ма­га­зи­не 75 рублей, а пен­си­о­нер заплатил за него 61 рубль 50
копеек. Сколь­ко процентов со­став­ля­ет скидка для пенсионера?

18.3 Магазин де­ла­ет пенсионерам скид­ку
на определённое ко­ли­че­ство процентов от сто­и­мо­сти покупки. Батон хлеба
стоит в ма­га­зи­не 30 рублей, а пен­си­о­нер заплатил за него 26 руб­лей 40
копеек. Сколь­ко процентов со­став­ля­ет скидка для пенсионера?

19.1 Магазин дет­ских товаров за­ку­па­ет
погремушку по опто­вой цене 100 руб­лей за одну штуку и продаёт с 35-процентной
наценкой. Сколь­ко будут сто­ить 2 такие погремушки, куп­лен­ные в этом
магазине?

19.2 Магазин дет­ских товаров за­ку­па­ет погремушку
по опто­вой цене 60 руб­лей за одну штуку и продаёт с 15-процентной наценкой.
Сколь­ко будут сто­ить 2 такие погремушки, куп­лен­ные в этом магазине?

19.3 Магазин дет­ских товаров за­ку­па­ет
погремушку по опто­вой цене 100 руб­лей за одну штуку и продаёт с 5-процентной
наценкой. Сколь­ко будут сто­ить 4 такие погремушки, куп­лен­ные в этом
магазине?

20.1 В го­ро­де 240000 жителей, при­чем
37% – это пенсионеры. Сколь­ко примерно че­ло­век составляет эта ка­те­го­рия
жителей? Ответ округлите до тысяч.

20.2 В го­ро­де 210000 жителей, при­чем
16% – это дети до 14 лет. Сколь­ко примерно че­ло­век составляет эта ка­те­го­рия
жителей? Ответ округлите до тысяч.

20.3 В го­ро­де 70000 жителей, при­чем 39%
– это пенсионеры. Сколь­ко примерно че­ло­век составляет эта ка­те­го­рия
жителей? Ответ округлите до тысяч.

21.1 Какая сумма (в рублях) будет
проставлена в кассовом чеке, если стоимость товара 710 р., и покупатель
оплачивает его по дисконтной карте с 10%-ной скидкой?

21.2 Какая сумма (в рублях) будет проставлена
в кассовом чеке, если стоимость товара 700 р., и покупатель оплачивает его по
дисконтной карте с 7%-ной скидкой?

21.3 Какая сумма (в рублях) будет
проставлена в кассовом чеке, если стоимость товара 600 р., и покупатель
оплачивает его по дисконтной карте с 9%-ной скидкой?

22.1 Расходы на одну из ста­тей городского
бюд­же­та составляют 17,5%. Вы­ра­зи­те эту часть бюд­же­та десятичной
дробью. 

22.2 Расходы на одну из ста­тей городского
бюд­же­та составляют 22,5%. Вы­ра­зи­те эту часть бюд­же­та десятичной дробью.

22.3 Расходы на одну из ста­тей городского
бюд­же­та составляют 22%. Вы­ра­зи­те эту часть бюд­же­та десятичной дробью.

23.1 Шариковая
ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на
900 рублей после повышения цены на 10%?

23.2  Тетрадь стоит 40 рублей. Какое
наибольшее число таких тетрадей можно будет купить на 750 рублей после
понижения цены на 10%?

Задания
повышенного уровня сложности

1.1 Имеются два сосуда, содержащие 40 кг и 30 кг раствора кислоты
различной концентрации. Если их слить вместе, то получим раствор, содержащий
73% кислоты. Если же слить равные массы этих растворов, то полученный раствор
будет содержать 72% кислоты. Сколько килограммов кислоты содержится во втором
растворе?

1.2
Имеются два сосуда, содержащие 12 кг и 8 кг раствора кислоты
различной концентрации. Если их слить вместе, то получим раствор, содержащий
65% кислоты. Если же слить равные массы этих растворов, то полученный раствор
будет содержать 60% кислоты. Сколько килограммов кислоты содержится во втором
растворе?

1.3
Имеются два сосуда, содержащие 30 кг и 20 кг раствора кислоты
различной концентрации. Если их слить вместе, то получим раствор, содержащий
81% кислоты. Если же слить равные массы этих растворов, то полученный раствор
будет содержать 83% кислоты. Сколько килограммов кислоты содержится во втором
растворе?

2.1 Имеются два сосуда, содержащие 40 кг и
20 кг раствора кислоты различной концентрации. Если их слить вместе, то
получится раствор, содержащий 33% кислоты. Если же слить равные массы этих
растворов, то полученный раствор будет содержать 47% кислоты. Сколько
килограммов кислоты содержится в первом растворе?

2.2 Имеются два сосуда, содержащие 24 кг и
26 кг раствора кислоты различной концентрации. Если их слить вместе, то
получится раствор, содержащий 39% кислоты. Если же слить равные массы этих
растворов, то полученный раствор будет содержать 40% кислоты. Сколько
килограммов кислоты содержится в первом растворе?

2.3 Имеются два сосуда, содержащие 22 кг и
18 кг раствора кислоты различной концентрации. Если их слить вместе, то
получится раствор, содержащий 32% кислоты. Если же слить равные массы этих
растворов, то полученный раствор будет содержать 30% кислоты. Сколько
килограммов кислоты содержится в первом растворе?

3.1 Свежие фрукты содержат 86% воды, а высушенные — 23%. Сколько сухих
фруктов получится из 341 кг свежих фруктов?

3.2 Свежие фрукты содержат 78% воды, а
высушенные  22%. Сколько сухих фруктов получится из 78 кг свежих
фруктов?

3.3 Свежие фрукты содержат 75% воды, а
высушенные — 25%. Сколько сухих фруктов получится из 135 кг свежих фруктов?

4.1 Свежие фрук­ты со­дер­жат
80% воды, а вы­су­шен­ные — 28%. Сколь­ко тре­бу­ет­ся све­жих фрук­тов
для при­го­тов­ле­ния 80 кг вы­су­шен­ных фруктов?

4.2 Свежие фрук­ты со­дер­жат 88% воды, а
вы­су­шен­ные — 30%. Сколь­ко тре­бу­ет­ся све­жих фрук­тов для при­го­тов­ле­ния
72 кг вы­су­шен­ных фруктов?

4.3 Свежие фрук­ты со­дер­жат 88% воды, а вы­су­шен­ные — 30%. Сколь­ко
тре­бу­ет­ся све­жих фрук­тов для при­го­тов­ле­ния 72 кг вы­су­шен­ных
фруктов?

5.1 Первый сплав со­дер­жит 5% меди, вто­рой — 13% меди. Масса вто­ро­го
спла­ва боль­ше массы пер­во­го на 4 кг. Из этих двух спла­вов по­лу­чи­ли тре­тий
сплав, со­дер­жа­щий 10% меди. Най­ди­те массу тре­тье­го сплава.

6.1 Смешав 60%−ый и 30%−ый рас­тво­ры кис­ло­ты
и до­ба­вив 5 кг чи­стой воды, по­лу­чи­ли 20%−ый рас­твор кислоты. Если бы вме­сто
5 кг воды до­ба­ви­ли 5 кг 90%−го рас­тво­ра той же кислоты, то по­лу­чи­ли бы
70%−ый рас­твор кислоты. Сколь­ко ки­ло­грам­мов 60%−го рас­тво­ра ис­поль­зо­ва­ли
для по­лу­че­ния смеси?

Список использованной литературы

1.ЕГЭ 2017. Математика. 50 вариантов типовых тестовых
заданий [Текст]/ под редакцией И.В. Ященко. – М.: Издательство «Экзамен»,
2017.- 247с.

2.ОГЭ 2017. Математика. 3 модуля. Основной
государственный экзамен. 50 вариантов типовых тестовых заданий [Текст]/ под
редакцией И.В. Ященко. – М.: Издательство «Экзамен», 2017.- 279 с.

3. «Федеральный институт педагогических измерений».
Открытый банк заданий ОГЭ и ЕГЭ по математике.  

4. ОГЭ 3000 задач с ответами по математике. Все
задания части 1/И.В.Ященко. — М.: Издательство «Экзамен», издательство МЦНМО,
2017. — 463 с. 

Основные определения

Когда мы описываем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.

Чтобы называть сотые доли, придумали процент (1/100): с латинского языка — «за сто».

Процент — это одна сотая часть от любого числа. Обозначается вот так: %.

Как перевести проценты в десятичную дробь? Нужно убрать знак % и разделить число на 100. Например, 18% — это 18 : 100 = 0,18.

А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:

• 0,18 = 0,18 · 100% = 18%.

А вот, как перевести проценты в десятичную дробь — обратным действием:

• 18% : 100% = 0,18.

Выразить дробь в процентах просто. Для перевода сначала превратим ее в десятичную дробь, а потом используем предыдущее правило и переведем десятичную дробь в проценты:

Типы задач на проценты

В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.

Тип 1. Нахождение процента от числа

Чтобы найти процент от числа, нужно число умножить на процент.

Задача. Блогер записал 500 видео для тиктока, но его продюсер сказал, что 20% из них — отстой. Сколько роликов придется перезаписать блогеру?

Как решаем: нужно найти 20% от общего количества снятых роликов (500).

20% = 0,2

500 * 0,2 = 100

Ответ: из общего количества снятых роликов продюсер забраковал 100 штук.

Тип 2. Нахождение числа по его проценту

Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.

Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.

Задача. Школьник решил 40 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?

Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 40 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.

40 : 0,16 = 40 · 100 : 16 = 250

Ответ: 250 задач собрано в этом учебнике.

Тип 3. Нахождение процентного отношения двух чисел

Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.

Задача. В секретном чатике 25 человек. 10 из них — девочки. Сколько процентов девочек в чате?

Как решаем: поделим 10 на 25, полученную дробь переведем в проценты.

10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 40%

Ответ: в чатике 40% девочек.

Тип 4. Увеличение числа на процент

Чтобы увеличить число на некоторое количество процентов, можно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.

А можно воспользоваться формулой:

a = b · (1 + с : 100),

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом месяце стикерпак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикер-пак?

Как решаем: можно найти 12% от 110:

0,12 · 110 = 13,2.

Прибавить к исходному числу:

110 + 13,2 = 123,2 рубля.

Или можно воспользоваться формулой, тогда:

110 · (1 + 12 : 100) = 110 · 1,12 = 123,2.

Ответ: стоимость стикерпака в этом месяце — 123 рубля 20 копеек.

Тип 5. Уменьшение числа на процент

Чтобы уменьшить число на несколько процентов, можно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.

А можно воспользоваться формулой:

a = b · (1 − с : 100),

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом году школу закончили 100 ребят. А в этом году выпускников на 25% меньше. Сколько выпускников в этом году?

Как решаем: можно найти 25% от 100:

0,25 · 100 = 25.

Вычесть из исходного числа 100 − 25 = 75 человек.

Или можно воспользоваться формулой, тогда:

100 · (1 − 25 : 100) = 75/p>

Ответ: 75 выпускников в этом году.

Тип 6. Задачи на простые проценты

Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.

Формула расчета выглядит так:

S = а · (1 + у · х : 100),

где a — исходная сумма,

S — сумма, которая наращивается,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Марии срочно понадобились деньги и она взяла на один год в долг 70 000 рублей под 8% ежемесячно. Сколько денег она вернет через год?

Как решаем: подставим в формулу данные из условий задачи.

70 000 · (1 + 12 · 8 : 100) = 137 200

Ответ: 137 200 рублей вернет Мария через год.

Тип 7. Задачи на сложные проценты

Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.

Формула расчета выглядит так:

S = а · (1 + х : 100)^y,

где S — наращиваемая сумма,

a — исходная,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Антон хочет оформить вклад 10 000 рублей на 5 лет в банке, который дает 10% годовых. Какую сумму снимет Антон через 5 лет хранения денег в этом банке?

Как решаем: просто подставим в формулу данные из условий задачи:

10000 · (1 + 10 : 100)3 = 13 310

Ответ: 13 310 рублей снимет Антон через год.

Курсы по математике для учеников с 1 по 11 классы. Вводный урок — бесплатно!

Способы нахождения процента

Деление числа на 100

При делении на 100 получается 1% от этого числа. Это правило можно использовать по-разному. Например, чтобы узнать процент от суммы, нужно умножить их на размер 1%. А чтобы перевести известное значение, следует разделить его на размер 1%. Этот метод отлично помогает в вопросе, как перевести целое число в проценты.

Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?

Как решаем:

1. Переведем 15% в рубли:

   250 : 100 = 2,5 — это 1% от стоимости шоколада,

   значит 2,5 * 15 = 37,5 — это 15%.

2. 250 — 37,5 = 212,5.

3. 212,5 < 225.

Ответ: выгоднее воспользоваться скидкой 15%.

Составление пропорции

Пропорция — определенное соотношение частей между собой.

С помощью метода пропорции можно рассчитать любые %. Выглядит это так:

• a : b = c : d.

Читается: а относится к b так, как с относится к d. Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение.

Рассмотрим пример. На сколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?

Как решаем:

1. Узнаем сколько стоит футболка сейчас в % соотношении:

   100 — 14 = 86,

   значит 1390 рублей это 86%.

2. Составим пропорцию:

   1390 : 100 = х : 86,

   х = 86 * (1390 : 100),

   х = 1195,4.

3. 1390 — 1195,4 = 194,6.

Ответ: купить спортивную футболку выгоднее на 194,6 рубля.

Соотношения чисел

Есть случаи, когда найти процент от числа проще, если представить проценты в виде простых дробей. В таком случае будем искать часть числа.

• 10% — десятая часть целого. Чтобы найти десять %, понадобится известное разделить на 10.

• 20% — пятая часть целого. Чтобы вычислить двадцать % от известного, его нужно разделить на 5.

• 25% — четверть целого. Чтобы вычислить двадцать пять %, понадобится известное разделить на 4.

• 50% — половина целого. Чтобы вычислить половину, нужно известное разделить на 2.

• 75% — три четверти целого. Чтобы вычислить семьдесят пять %, нужно известное значение разделить на 4 и умножить на 3.

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Как решаем:

1. 100 — 25 = 75,

   значит нужно заплатить 75% от первоначальной цены.

2. Используем правило соотношения чисел:

   8500 : 4 * 3 = 6375.

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Задачи на проценты с решением

Как мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ.

Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?

Как решаем:

76 · 0,7 = 53,2 кг

Ответ: масса воды 53,2 кг

Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?

Как решаем:

Обозначим первоначальную цену товара через х. После первого понижения цена станет равной.

х — 0,4х = 0,6x

Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим:

0,6х — 0,25 * 0,6x = 0,45x

После двух понижений изменение цены составит:

х — 0,45x = 0,55х

Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%.

Ответ: 55%.

Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто?

Как решаем:

По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто

100 — 8 = 92

Получается, что стоимость одной пары брюк — это 23% стоимости пальто.

92 : 4 = 23

Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто.

23 * 5 = 115

Ответ: пять пар брюк на 15% дороже, чем одно пальто.

Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены.

Как решаем:

По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода.

Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход.

Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%.

А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27.

Ответ: заработок жены составляет 27%.

Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?

Как решаем:

Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%.

Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества.

Значит, 19 килограммов питательного вещества в абрикосах — это 10% веса свежих абрикосов. Найдем число по проценту.

19 : 0,1 = 190

Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги.

---

Задачи на проценты

---

[su_box title=”Описание задания” style=”soft” box_color=”#c1e8cc” title_color=”#0c0a0a”]

В задании №3 ЕГЭ по математике нам предстоит решить простую задачу на проценты или часть от целого. Данные задачи в большинстве случаев интуитивно понятны, так как взяты из реальных жизненных ситуаций, тем не менее необходимо быть внимательным при их выполнении.

Тематика заданий: часть от целого, доли, проценты

Бал: 1 из 20

Сложность задания: ♦♦◊

Примерное время выполнения: 3 мин.

[/su_box]

---

Разбор типовых вариантов заданий №3 ЕГЭ по математике базового уровня

---

Вариант 3МБ1

[su_note note_color=”#defae6″]

Банк начисляет на срочный вклад 8% годовых. Вкладчик положил на счёт 7000 рублей. Сколько рублей будет на этом счёте через год, если никаких операций, кроме начисления процентов, со счётом проводиться не будет?

[/su_note]

Алгоритм выполнения:

• Вариант 1.

1. Сложить 100% и процент годовых.
2. Найти 1% от суммы, для этого сумму разделить на 100.
3. Умножить стоимость 1% на искомое количество процентов.

• Вариант 2.

1. Сложить 100% и процент годовых.
2. Полученные проценты перевести в десятичную дробь (разделить на сто).
3. Найти процент от числа (число умножить на полученную десятичную дробь).

Решение:

• Вариант 1.

Вклад 8 % годовых означает, что начальная сумма 7000 рублей через год увеличится на 8%, то есть составит 100+8=108% от исходной суммы.

Способ нахождения процента от числа №1. Для того, чтобы найти процент от числа нужно данное число разделить на 100(узнать сколько составляет 1 %), а затем умножить на искомое количество процентов.

Вычислим 108% от 7000, получим:

1. 7000 : 100 = 70(рублей) – составит 1 %.
2. 70 · 108 = 7560(рублей) – составит вклад через год.

• Вариант 2.

Вклад 8 % годовых означает, что начальная сумма 7000 рублей через год увеличится на 8%, то есть составит 100+8=108% от исходной суммы.

Способ нахождения процента от числа №2. Для того, чтобы найти процент от числа, нужно перевести искомый процент в десятичную дробь(разделить на сто), затем умножит число на полученную десятичную дробь.

108% = 108 : 100 = 1,08

7000 · 1,08 или

.

Выполнив умножение столбиком, имеем:

Ответ: 7560.

---

Вариант 3МБ2

[su_note note_color=”#defae6″]

Банк начисляет на срочный вклад 7 % годовых. Вкладчик положил на счёт 3000 рублей. Сколько рублей будет на этом счёте через год, если никаких операций, кроме начисления процентов, со счётом проводиться не будет?

[/su_note]

Алгоритм выполнения:

• Вариант 1.

1. Сложить 100% и процент годовых.
2. Найти 1% от суммы, для этого сумму разделить на 100.
3. Умножить стоимость 1% на искомое количество процентов.

• Вариант 2.

1. Сложить 100% и процент годовых.
2. Полученные проценты перевести в десятичную дробь (разделить на сто).
3. Найти процент от числа (число умножить на полученную десятичную дробь).

Решение:

• Вариант 1.

Вклад 7 % годовых означает, что начальная сумма 3000 рублей через год увеличится на 7%, то есть составит 100+7=107% от исходной суммы.

Способ нахождения процента от числа №1. Для того, чтобы найти процент от числа нужно данное число разделить на 100(узнать сколько составляет 1 %), а затем умножить на искомое количество процентов.

Вычислим 107% от 3000, получим:

1. 3000 : 100 = 30(рублей) – составит 1 %.
2. 30 · 107 = 3210(рублей) – составит вклад через год.

• Вариант 2.

Вклад 7 % годовых означает, что начальная сумма 3000 рублей через год увеличится на 7%, то есть составит 100+7=107% от исходной суммы.

Способ нахождения процента от числа №2. Для того, чтобы найти процент от числа, нужно перевести искомый процент в десятичную дробь (разделить на сто), затем умножит число на полученную десятичную дробь.

107% = 107 : 100 = 1,07

3000 · 1,07 или

Ответ: 3210.

---

Вариант 3МБ3

[su_note note_color=”#defae6″]

В сентябре 1 кг слив стоил 40 рублей, в октябре сливы подорожали на 40%, а в ноябре ещё на 15%. Сколько рублей стоил 1 кг слив после подорожания в ноябре?

[/su_note]

Алгоритм выполнения:

1. Найти сколько составляет один процент от начальной стоимости.
2. Сложить 100% и на сколько процентов произошло подорожание впервые.
3. Умножить стоимость одного процента на полученное количество процентов.
4. Найти стоимость 1% от новой стоимости.
5. Сложить 100 % и количество процентов, на которое подорожал товар во второй раз.
6. Умножить стоимость одного процента на полученное количество процентов.

Решение с пояснениями:

Найдем сколько составляет один процент от начальной стоимости:

40 : 100 = 0,4 (рублей) – составляет 1 % от начальной стоимости.

Сложим 100% и на сколько процентов произошло подорожание впервые.

100 + 40 = 140 (%) – составила стоимость от начальной цены после первого подорожания.

Умножим стоимость одного процента на полученное количество процентов.

140 · 0,4 = 56 (рублей) – стали стоить сливы в октябре.

Найдем стоимость 1% от новой стоимости.

56 : 100 = 0,56 (рубля) – 1% от новой стоимости.

Сложим 100 % и количество процентов, на которое подорожал товар во второй раз.

100 + 15 = 115 (%) – составила стоимость в ноябре от цены в октябре.

Умножим стоимость одного процента на полученное количество процентов.

115 · 0,56 = 64,4 (рубля) – конечная стоимость.

Решение в общем виде:

Подорожание на 40% означает увеличение стоимости на 140%, то есть, 40 рублей становятся равными

 рублей.

Затем, в ноябре стоимость слив увеличилась еще на 15%, что составило

 рублей.

Замечание: обратите внимание, что в данной задаче нельзя просто складывать проценты 40+15=55% и вычислять 155% от 40 рублей! Это будет приводить к неверным решениям.

Ответ: 64,4.

---

Вариант 3МБ4

[su_note note_color=”#defae6″]

В сентябре 1 кг винограда стоил 90 рублей, в октябре виноград подорожал на 20 %, а в ноябре ещё на 25 %. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?

[/su_note]

Алгоритм выполнения:

1. Найти сколько составляет один процент от начальной стоимости.
2. Сложить 100% и на сколько процентов произошло подорожание впервые.
3. Умножить стоимость одного процента на полученное количество процентов.
4. Найти стоимость 1% от новой стоимости.
5. Сложить 100 % и количество процентов, на которое подорожал товар во второй раз.
6. Умножить стоимость одного процента на полученное количество процентов.

Подробный разбор:

Найдем сколько составляет один процент от начальной стоимости:

90 : 100 = 0,9 (рублей) – составляет 1 % от начальной стоимости.

Сложим 100% и на сколько процентов произошло подорожание впервые.

100 + 20 = 120 (%) – составила стоимость от начальной цены после первого подорожания.

Умножим стоимость одного процента на полученное количество процентов.

120 · 0,9 = 108 (рублей) – стали стоить сливы в октябре.

Найдем стоимость 1% от новой стоимости.

108 : 100 = 1,08 (рубля) – 1% от новой стоимости.

Сложим 100 % и количество процентов, на которое подорожал товар во второй раз.

100 + 25 = 125 (%) – составила стоимость в ноябре от цены в октябре.

Умножим стоимость одного процента на полученное количество процентов.

125 · 1,08 = 135 (рублей) – конечная стоимость.

Решение в общем виде:

Подорожание на 20% означает увеличение стоимости на 120%, то есть, для 90 рублей имеем:

 рублей.

Затем, в ноябре стоимость слив увеличилась еще на 25%, что составило

 рублей.

Замечание: обратите внимание, что в данной задаче нельзя просто складывать проценты 20+25=45% и вычислять 145% от 90 рублей! Это будет приводить к неверным решениям.

Ответ: 135.

---

Вариант 3МБ5

[su_note note_color=”#defae6″]

Ивану Кузьмичу начислена заработная плата 20000 рублей. Из этой суммы вычитается налог на доход физических лиц в размере 13 %. Сколько рублей он получит после уплаты подоходного налога?

[/su_note]

Алгоритм выполнения:

• Вариант 1.

1. Вычесть из 100% налог в процентах.
2. Найти 1% от начальной суммы, для этого сумму разделить на 100.
3. Умножить стоимость 1% на искомое количество процентов.

• Вариант 2.

1. Вычесть из 100% налог в процентах.
2. Полученные проценты перевести в десятичную дробь (разделить на сто).
3. Найти процент от числа (число умножить на полученную десятичную дробь).

Решение:

• Вариант 1.

Вычтем из 100% налог в процентах.

100 – 13 = 87 (%) – получит Иван Кузьмич после вычета налога.

Найдем 1 % от начальной суммы.

20000 : 100 = 200 (рублей) – составит 1%.

Найдем 87% от 20000.

87 · 200 = 17400 (рублей) – получит Иван Кузьмич.

• Вариант 2.

Вычтем из 100% налог в процентах. 100 – 13 = 87 (%)

Полученные проценты переведем в десятичную дробь (разделить на сто). 87 : 100 = 0,87

Найдем процент от числа (число умножить на полученную десятичную дробь).

20000 · 0,87 = 17400 (рублей)

Ответ: 17400 рублей получит Иван Кузьмич.

---

Вариант 3МБ6

[su_note note_color=”#defae6″]

ЕГЭ по физике сдавали 25 выпускников школы, что составляет треть от общего числа выпускников. Сколько выпускников этой школы не сдавали экзамен по физике?

[/su_note]

Решение:

Нам известно, что количество учеников, сдававших ЕГЭ по физике равно 25, и это составляет 1/3 от общего числа выпускников. Значит 25 – это 1/3, тогда общее число учеников:

25 • 3 = 75

Количество учеников, не сдававших ЕГЭ по физике, равно:

75 – 25 = 50

Ответ: 50

---

Вариант 3МБ7

[su_note note_color=”#defae6″]

Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена стоимость футболки?

[/su_note]

Алгоритм выполнения

1. От 800 отнимаем 680. Узнаем, сколько рублей составило снижение.
2. Делим результат вычитания на 800. Это даст нам долю, которую составляет скидка от первоначальной стоимости.
3. Полученное число умножаем на 100. Получаем снижение в процентах.

Решение:

800 – 680 = 120 (руб.) – составляет снижение

120 : 800 = 0,15 – доля скидки

0,15 ·100 = 15 %

Ответ: 15

---

Вариант 3МБ8

[su_note note_color=”#defae6″]

В магазине вся мебель продается в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 5% от стоимости купленной мебели. Шкаф стоит 3500 рублей (наверное, это было очень давно – прим. ред. 🙂 ) Во сколько рублей обойдется покупка этого шкафа вместе со сборкой?

[/su_note]

Алгоритм выполнения

1. Определяем, сколько составляет 5% от стоимости мебели. Для этого 3500 делит на 100 и умножаем на 5.
2. К 3500 прибавляем полученное число.

Решение:

3500 : 100 · 5 = 175 (руб.) – стоимость сборки мебели

3500 + 175 = 3675 (руб.) стоит мебель со сборкой

Ответ: 3675

---

Вариант 3МБ9

[su_note note_color=”#defae6″]

Товар на распродаже уценили на 40%, при этом он стал стоить 840 рублей. Сколько рублей стоит товар до распродажи?

[/su_note]

Алгоритм выполнения

1. От 100 % вычитаем 40%, чтобы найти, сколько процентов составляет уцененная стоимость. Получим 60 %.
2. Воспользуемся правилом нахождения целого по его части. Для этого 840 разделим на 60 и умножим на 100.

Решение:

100 – 40 = 60 % – составляет цена товара после его уценки.

840 : 60 · 100 = 1400 (руб.)

1400

---

Вариант 3МБ10

[su_note note_color=”#defae6″]

Магазин делает пенсионерам скидку. Батон хлеба стоит в магазине 15 рублей, а пенсионер заплатил за него 14 рублей 40 копеек (грандиозная скидка – прим. ред. 😉 ) Сколько процентов составила скидка для пенсионера?

[/su_note]

Алгоритм выполнения

1. От 15 руб. отнимаем 14 руб.40 коп. Так найдем сумму скидки. Выразим эту сумму в рублях.
2. Полученное число разделим на 15 и умножим на 100 %.

Решение:

15 руб. – 14 руб.40 коп. = 60 коп. = 0,6 руб.

0,6 : 15 ·100 % = 4 %.

Ответ: 4

---

Вариант 3МБ11

[su_note note_color=”#defae6″]

Число хвойных деревьев в парке относится к числу лиственных как 93:7. Других деревьев в парке нет. Сколько процентов деревьев в парке составляют лиственные?

[/su_note]

Алгоритм выполнения

1. Суммируем 93 и 7, чтобы найти общее кол-во деревьев в парке.
2. Кол-во лиственных деревьев (7) делим на общее кол-во деревьев и умножаем на 100 %.

Решение:

93 + 7 = 100 (шт.) – деревьев всего в парке.

7 : 100 ·100 = 7 %

Ответ: 7

---

Вариант 3МБ12

[su_note note_color=”#defae6″]

Городской бюджет составляет 48 млн. рублей, а расходы на одну из его статей составили 40%. Сколько миллионов рублей потрачены на эту статью бюджета?

[/su_note]

Алгоритм выполнения

Нужно применить правило нахождения части от целого по ее проценту. Для этого целое делится на 100 и умножается на кол-во процентов.

Решение:

48 : 100 · 40 = 19,2 (млн.руб.)

Ответ: 19,2

---

Вариант 3МБ13

[su_note note_color=”#defae6″]

Поступивший в продажу в феврале мобильный телефон стоил 1800 рублей. В июне он стал стоить 1530 рублей. На сколько процентов снизилась цена мобильного телефона в период с февраля по июнь?

[/su_note]

Алгоритм выполнения

1. Из 1800 вычитаем 1530. Определяем, сколько рублей составила скидка.
2. Полученное число делим на первоначальную цену и умножаем на 100 %.

Решение:

1800 – 1530 = 270 (руб.) – скидка

270 : 1800 · 100 = 15 %

Ответ: 15

---

Вариант 3МБ14

[su_note note_color=”#defae6″]

В период распродажи магазин снижал цены дважды: в первый раз на 10%, во второй – на 25%. Сколько рублей стал стоить чайник после второго снижения цен, если до начала распродажи он стоил 1600 рублей?

[/su_note]

Алгоритм выполнения

1. Определяем, сколько (в руб.) составляет 10 % от стоимости чайника. Для этого 1600 делим на 100 и умножаем на 10.
2. От первоначальной стоимости отнимаем сумму скидки, составляющей 10 %.
3. Полученную цену со скидкой делим на 100 и умножаем на 25. Так найдем величину скидки (в руб.) после второго снижения цены.
4. От числа, полученного в п.2 отнимаем число, полученное в п.3.

Решение:

1600 : 100 · 10 = 160 (руб.) – составляет скидка в 10 %

1600 – 160 = 1440 (руб.) – стал стоить чайник после понижения цены на 10 %

1440 : 100 · 25 = 360 (руб.) составляет скидка в 25 %

1440 – 360 = 1080 (руб.)

Ответ: 1080

---

Вариант 3МБ15

[su_note note_color=”#defae6″]

Магазин детских товаров закупает погремушки по оптовой цене 110 рублей за одну штуку и продает с наценкой 30%. Сколько рублей будут стоить 4 такие погремушки, купленные в этом магазине?

[/su_note]

Алгоритм выполнения

1. Определяем, сколько рублей составляет наценка в 30 %. Для этого закупочную стоимость делим на 100 и умножаем на 30.
2. К закупочной стоимости прибавляет сумму наценки.
3. Полученное число умножаем на 4.

Решение:

110 : 100 · 30 = 33 (руб.) – равна наценка

110 + 33 = 143 (руб.) – стоит погремушка в магазине

143 · 4 = 572 (руб.) – стоят 4 погремушки

Ответ: 572

---

Вариант 3МБ16

[su_note note_color=”#defae6″]

Число больных гриппом в школе уменьшилось за месяц в два раза. На сколько процентов уменьшилось число больных гриппом?

[/su_note]

Алгоритм выполнения

1. Обозначим число больных через х. Тогда кол-во больных через месяц станет равным х/2.
2. х/2 делим на х и умножаем на 100 %. Так найдем кол-во процентов, которое составит число больных через месяц по отношению к первоначальному их кол-ву. В процессе вычисления х сократится.

Решение:

х / 2 : х · 100 % = х / 2· 1 / х· 100 % =1 / 2 · 100 % = 0,5 · 100 % = 50 %

Ответ: 50

Даниил Романович | Просмотров: 14.5k

Типы задач на проценты и способы их решения в заданиях ОГЭ и ЕГЭ

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

В настоящее время людям часто приходится встречаться с понятием «процент». Современный человек должен уметь вычислять скидку на интересующий его товар; решать задачи на смеси, сплавы, растворы, в которых без процентов не обойтись. Например, нужно знать, как правильно приготовить маринад для консервирования, как смешать клей для обоев, как приготовить раствор для заливки фундамента дома, как разбавить уксусную кислоту для употребления в пищу. На этикетках продуктов питания часто указывается массовая доля вещества, например, жира, выраженная в процентах. Задачи на проценты встречаются на ОГЭ и ЕГЭ базового и профильного уровней. Это, как правило, практико-ориентированные задания. Поскольку мне тоже предстоит сдавать экзамен по математике, я решил рассмотреть задачи на проценты и способы их решения в задачах ОГЭ и ЕГЭ. Так как будущую профессию я хочу связать с экономической специальностью, руководствуясь примером моей мамы, которая работает в банке, я быстро определился с практической частью моего проекта. Я провел интервью с сотрудником банка, которому задал интересующие меня вопросы.

Цель проекта: исследовать типы задач на проценты и способы их решения в заданиях ОГЭ и ЕГЭ.

Задачи проекта:

Изучить историю возникновения процентов.

Проанализировать информационные источники по теме: «Типы задач на проценты и способы их решения в заданиях ОГЭ и ЕГЭ».

Разобрать решение задач на проценты из ОГЭ и ЕГЭ.

Провести интервьюирование сотрудника и клиентов банка ПАО КБ «УБРиР» города Асбеста с целью понять, как начисляются проценты на кредиты и вклады.

Разработать анкету и провести анкетирование среди обучающихся основной школы №12, обработать результаты.

Объект исследования: задачи на проценты.

Предмет исследования: типы задач на проценты и способы их решения.

Гипотеза: опираясь на знания по математике, полученные в 5-6 классах по теме «Проценты», можно решить любую задачу на проценты из банка задач ОГЭ и ЕГЭ.

Методы исследования:

Изучить литературу по данной теме.

Решение задач на проценты из ОГЭ и ЕГЭ.

Интервьюирование сотрудника и клиентов банка ПАО КБ «УБРиР» города Асбеста.

Анкетирование и обработка его результатов.

Теоретическая часть

1. Истрия возникновения процентов

Слово «процент» происходит от латинского «pro centum», что буквально означает «за сотню» или «со ста». Процентами очень удобно пользоваться на практике, так как они выражают части целых чисел в одних и тех же сотых долях. Это даёт возможность упрощать расчёты и легко сравнивать части между собой и целыми. Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась ещё в древности у вавилонян, которые пользовались шестидесятеричными дробями. Уже в клинописных табличках вавилонян содержатся задачи на расчет процентов. До нас дошли составленные ими таблицы, которые позволили быстро определять сумму процентных денег. Были известны проценты и в Индии. Индийские математики вычисляли проценты, применяя так называемое тройное правило, т.е. пользуясь пропорцией. Они умели производить более сложные вычисления с применением процентов[19, 3].

Денежные расчёты с процентами были особенно распространены в Древнем Риме. Они называли процентами деньги, которые платил должник заимодавцу за каждую сотню. Римский сенат даже должен был установить максимально допустимый процент, взимаемый с должника, так как некоторые заимодавцы усердствовали в получении процентных денег. От римлян проценты перешли к другим народам.

В средние века в Европе в связи с широким развитием торговли особенно много внимания обращали на умение вычислять проценты. В то время приходилось рассчитывать не только проценты, но и проценты с процентов, т.е. сложные проценты, как называют их в наше время. Отдельные конторы и предприятия для облегчения труда при вычислении процентов разрабатывали свои особые таблицы, которые составляли коммерческий секрет фирмы[5].

Впервые опубликовал таблицы для расчёта процентов в 1584 г. Симон Стевин — инженер из города Брюгге (Нидерланды). Стевин известен замечательным разнообразием научных открытий, в том числе — особой записи десятичных дробей.

Долгое время под процентами понимались исключительно прибыль или убыток на каждые сто рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчётах, статистике, науке и технике. Ныне процент — это частный вид десятичных дробей, сотая доля целого, принимаемого за единицу [8].

Знак «%» происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчётах часто писалось сокращённо cto. Отсюда путём дальнейшего упрощения в скорописи буквы t в наклонную черту произошёл современный символ для обозначения процента. Существует и другая версия возникновения этого знака. Предполагается, что этот знак произошёл в результате нелепой опечатки, совершенной наборщиком. В 1685 году в Париже была опубликована книга — руководство по коммерческой арифметике, где по ошибке наборщик вместо cto напечатал %. После этой ошибки многие математики также стали употреблять знак % для обозначения процентов, и постепенно он получил всеобщее признание.

Иногда применяют и более мелкие доли целого — тысячные, т.е. десятые части процента. Их называют «промилле» (от латинского pro mille — «с тысячи»), обозначаемые ‰ по аналогии со знаком %. Изобретение математических знаков и символов значительно облегчило изучение математики и способствовало ее дальнейшему развитию.

Таким образом, появились проценты далеко в прошлом и в настоящее время понятие «процент» очень активно используется в банковской системе, в торговле (скидка на товар, различные акции в магазинах и пр.), экономике (налогообложении и пр.), статистике и др. Также понятие процент встречается на ОГЭ по математике.

2. Типы задач на проценты и способы их решения

В настоящие время задачи на проценты в заданиях ОГЭ встречаются под номерами 1-5 и 22, причём в одной задаче сочетаются сразу несколько типов задач на проценты. Также задачи на проценты встречаются в заданиях ЕГЭ базового и профильного уровней. Рассмотрим некоторые из них.

Тип 1: Находим процент (дробь) от числа.

Способ решения: что бы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь.

Задача. За месяц на предприятии изготовили 500 приборов. 20% изготовленных приборов не смогли пройти контроль качества. Сколько приборов не прошло контроль качества?

Решение. Нужно найти 20% от общего количества изготовленных приборов. 20% = 0,2. 500 * 0,2 = 100. 100 из общего количества изготовленных приборов контроль не прошло.

Тип 2: Находим число по его проценту (дроби).

Способ решения: Что бы найти число от данного числа процентов, нужно количество процентов записать десятичной дробью, а затем умножить число равное количеству процентов на проценты, записанные десятичной дробью.

Задача. Готовясь к экзамену, школьник решил 38 задач из пособия для самоподготовки. Что составляет 23% числа всех задач в пособии. Сколько всего задач собрано в этом пособии для самоподготовки?

Решение. Мы не знаем, сколько всего задача в пособии. Но зато нам известно, что 38 задач составляют 23% от общего их количества. Запишем 23% в виде дроби: 0,23. Далее нам следует известную нам часть целого разделить на ту долю, которую она составляет от всего целого: 38/0,25 = 38 * 100/25 = 152. Именно 152 задачи включили в этот сборник.

Тип 3: Находим процентное отношение двух чисел (часть от целого числа).

Способ решения: Число процент, которого нужно узнать, надо сначала разделить на второе число, затем умножить на сто.

Задача. В классе 30 учеников. 14 из них – девочки. Сколько процентов девочек в классе?

Решение. Чтобы узнать, какой процент составляет одно число от другого, нужно то число, процент которого требуется найти, разделить на общее количество и умножить на 100%. Значит, 14/30*100% = 7/15*100% = 7*100%/15 = 47%.

Тип 4: Увеличиваем число на процент.

Способ решения: нужно к данному числу прибавить это же число делённое на сто и умноженное на количество процентов, на которое должно увеличиться число.

Задача. На прошлогоднем экзамене по математике 140 старшеклассников получили пятерки. В этом году число отличников выросло на 15%. Сколько человек получили пятерки за экзамен по математике в этом году?

Решение. Если некое число а увеличено на х%, то оно увеличилось в (1 + х /100) раз. Откуда а * (1 + х /100). Подставим в эту формулу данные нам по условию задачи цифры и получим ответ: 140 * (1 + 15/100) = 161.

Тип 5: Уменьшаем число на процент.

Способ решения: нужно из данного числа вычесть это же число, делённое на сто и умноженное на количество процентов, на которое должно уменьшиться число.

Задача. Год назад школу закончили 100 ребят. А в этом году выпускников на 25% меньше. Сколько выпускников в этом году?

Решение. Если число а уменьшено на х% и при этом 0 ≤ х ≤ 100, то число уменьшено в (1 – х/100) раз. И нужное нам число находим по формуле а * (1 – х/100). Подставляем цифры из условия задачи и получаем ответ: 100 * (1 – 25/100) = 75.

Тип 6: Задачи на простые проценты.

Способ решения: формула для расчета простых процентов:

A=P*(1+IT), где

T-количество периодов;

                         I-процентная ставка;

                         P-вкладываемая сумма;

                         A-получаемая сумма.

Задача. Родители взяли в банке кредит 5000 рублей сроком на год под 15% ежемесячно. Сколько денег они заплатят банку через год?

Решение. Простые проценты называются так, потому что они начисляются многократно, но всякий раз к исходной сумме. Если обозначить исходную сумму как а, сумму, которая наращивается, как S, процентную ставку как х% и количество периодов начисления процента как у, то формулу можно записать так: S = а * (1 + у * х/100). Теперь подставим сюда цифры из условия задачи и узнаем, сколько денег родители заплатят банку: 

S = 5000 · (1 + 12 · 0,15) = 14000.

Тип 7: Задачи на сложные проценты.

Способ решения: формула для начисления сложного процента:

S=A*(1+R)^T

A- СУММАВКЛАДА;

R- СТАВКА ПРОЦЕНТА;

T- КОЛИЧЕСТВО ПЕРИОДОВ;

S- ПОЛУЧАЕМАЯ СУММА.

Задача. На этот раз сумма кредита 25000 рублей, взятых под те же 15% сроком на 3 месяца. Снова надо узнать, сколько денег придется заплатить банку по истечении срока кредита.

Решение. Сложные проценты отличаются от простых тем, что процент много раз начисляется не к исходной сумме, а к сумме с уже начисленными раньше процентами. Пускай снова S – наращиваемая сумма, а – исходная, х% — процентная ставка, у – количество периодов начисления процента. В этом случае формула принимает вид: S = а * (1 + х/100)^у. Подставляем цифры из условия: S = 25000 * (1 + 15/100)³ = 38021,875 – искомая сумма.

Кстати, простые задачи на проценты можно очень легко решать с помощью пропорции. Этот метод наглядный и дает такой же результат, так что выбирать можно каждому тот способ решения, который кажется проще.

Таким образом, мною выделено семь типов задач на проценты, подробно описан способ их решения и также приведены конкретные примеры.

Практическая часть.

3. Решение задач на проценты из ОГЭ и ЕГЭ.

Мною в теоретической части проекта было выделено семь типов задач на проценты, теперь подробнее рассмотрим решение задач из ОГЭ и ЕГЭ базового и профильного уровней.

Тип 1: Находим процент (дробь) от числа.

Задача из ЕГЭ по математике базового уровня.

Задание 3 № 26631

В городе N живет 200 000 жителей. Среди них 15% детей и подростков. Среди взрослых жителей 45% не работает (пенсионеры, студенты, домохозяйки и т. п.). Сколько взрослых жителей работает?

Решение: Численность детей в городе N составляет 200 000   0,15 – это  30 000. Численность взрослого населения 200 000 − 30 000 = 170 000 человек. Из них не работает 170 000*0,45 = 76 500 человек. Значит, работает 170 000 − 76 500 = 93 500 человек.

Ответ: 93 500.

Тип 2: Находим число по его проценту.

Задача из ЕГЭ по математике базового уровня.

Задание 3 № 77340

В школе 124 ученика изучают французский язык, что составляет 25% от числа всех учеников. Сколько учеников учится в школе?

Решение: Разделим 124 на 0,25:

Значит, в школе учится 496 учеников.

Ответ: 496.

Тип 3: Находим процентное отношение двух чисел (часть от целого числа).

Задача из ОГЭ по математике.

Вариант №11

Задача№3 На сколько процентов сократилась посевная площадь после того, как земледелец устроил терассы. Ответ округлите до десятых.

Решение:

По теореме Пифагора найдём сторону AB

AB²=AC²+BC²=12²+35²=144+1225=1369

AB = 37

2. Найдём посевную площадь

S=40*37=1480 м²

3. Найдём посевную площадь после устройства терасс

S=35*40=1400

4. Составим пропорцию

1480-100%

1400-x%

X=(1400*100)/1480=94.6

5.100-94.6=5.4

Ответ: 5.4

Тип 4: Увеличиваем число на процент.

Задача из ЕГЭ по математике базового уровня.

Задание 3 № 26619

Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?

Решение: После повышения цены ручка станет стоить 40 + 0,1·40 = 44 рубля. Разделим 900 на 44:

Значит, можно будет купить 20 ручек.

Ответ: 20.

Тип 5: Уменьшаем число на процент.

Задание из ОГЭ по математике.

Вариант №6. Задача №4. Доставка печи из магазина до участка стоит 500 рублей. При покупке печи ценой свыше 20000 рублей магазин делают 3% скидку на товар и 35% процентов скидку на доставку. Сколько будет стоить доставка печи «кентавр» вместе с доставкой на этих условиях?

Решение:

1. Найдём сколько составляет 3% от 25000.

25000*0,03=750 рубля

2. Вычисляем стоимость печи со скидкой 3%

25000-750=24250 рубля

3. Найдём сколько составляет 35% от 500.

500*0,35=175 рубля

4.Вычисляем стоимость доставки со скидкой 35%.

500-175=325 рубля

5. 24250+375=24575 рубля

Ответ: 24575

Тип 6: Задачи на простые проценты.

Задание из ОГЭ по математике.

Задание 5 № 367104

В таблице даны условия банковского вклада в трех различных банках. Предполагается, что клиент кладет на счет 10 000 рублей на срок 1 год. В каком банке к концу года вклад окажется наибольшим? В ответе укажите сумму этого вклада в рублях.

Банк	Обслуживание счета *	Процентная ставка (% годовых) **
Банк А	40 руб. в год	2
Банк Б	8 руб. в месяц	3,5
Банк В	Бесплатно	1,5

* В начале года или месяца со счета снимается указанная сумма в уплату за ведение счета
** В конце года вклад увеличивается на указанное количество процентов.

Решение.

Рассмотрим все варианты.

В банке A после снятия суммы в уплату за ведение счета на счету останется 10 000 − 40 = 9 960 руб. К концу года на счету окажется 9 960 + 0,02 · 9 960 = 10 159,2 руб.

В банке Б в качестве платы за ведение счета за год снимается со счета 12 · 8 = 96 руб. Таким образом, проценты начисляются на сумму 10 000 − 96 = 9 904 руб. К концу года на счету окажется 9 904 + 0,035 · 9 904 = 10 250,64 руб.

В банке В плата за ведение счета не взимается, таким образом, проценты будут начисляться на первоначальную сумму. К концу года на счету окажется 10 000 + 0,015 · 10 000 = 10 150 руб.

Ответ: 10 250,64.

Тип 7: Задачи на сложные проценты.

Задача из сборника: Математика. Профильный уровень 50 вариантов, под ред. И.В.Ященко, М.:Экзамен, 2018

31 декабря 2016 года Василий взял в банке 5460000 рублей в кредит под 20% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Василий переводит в банк х рублей. Какой должна быть сумма х, чтобы Василий выплатил долг тремя равными платежами (то есть за три года)?

Решение:Sо=So*a=So(1+a)=5460000(1+0,2)=5460000*1,2, где So-сумма кредита, a-процентная ставка, x-определенная сумма ежегодного платежа.

Составляем уравнение

(((5460000*1,2-х)*1,2-х)*1,2-х)=0

((5460000*1,2²-2,2х)*1,2-х)=0

5460000*1,2³-3,64х=0

3,64х=5460000*1,2³

Х==2592000 рублей.

Ответ: 2592000 рублей-сумма ежегодного платежа.

Таким образом, мною было выделено семь типов задач на проценты, рассмотрены задачи с сайтов решу ОГЭ и решу ЕГЭ, сборников под ред. И.В.Ященко Математика: ОГЭ, ЕГЭ базовый и профильный уровень.

Опрос клиентов и сотрудника банка ПАО КБ «УБРиР»

города Асбеста

Для того, что бы узнать, как проценты влияют на банковские операции, мною проведено интервьюирование сотрудника банка ПАО КБ «УБРиР». Также, чтобы узнать владеют ли клиенты банка информацией об операциях с процентами, мною был проведён опрос среди клиентов данного банка. Для этого я разработал сценарий интервью, который представлен в Приложении 1.

В ходе интервью мы выяснили, что в банке предоставляются два вида

платежей по кредитам:

1. Аннуитетный платеж – представляет собой равные ежемесячные транши (платежи), растянутые на весь срок кредитования. В сумму транша включены: часть ссудной задолженности и начисленный процент. При этом, в первые месяцы (или годы) кредита большую часть транша составляют проценты, а меньшую – погашаемая часть основного долга. Ближе к концу кредитования пропорция меняется: большая часть транша идет на погашение «тела» кредита, меньшая – на проценты. При этом общий размер транша всегда остается одинаковым[6, 7].

2. Дифференцированный платеж – представляет собой неравные ежемесячные транши, пропорционально уменьшающиеся в течение срока кредитования. Наибольшие платежи – в первой четверти срока, наименьшие – в четвертой четверти. «Срединные» платежи обычно сравнимы с аннуитетом. Ежемесячно тело кредита уменьшается на равную долю, процент же насчитывается на остаток задолженности. Поэтому сумма транша меняется от выплаты к выплате. Если в задаче присутствуют слова «равными платежами» или «долг уменьшается на одну и ту же величину», то речь идет о дифференцированном платеже.

В ходе интервью сотрудник банка ПАО КБ «УБРиР» представил мне график погашения кредита дифференцированными платежами, который представлен ниже.

Параметры сделки:
Сумма кредита — 1 200 000 руб.
Срок кредита — 12 месяцев
Процентная ставка — 13 %
График погашения кредита дифференцированными платежами
Месяц	Ежемесячный платеж (руб.)	Погашение процентов (руб.)	Погашение основного долга (руб.)	Остаток основного долга (руб.)
1	113 000,00	13000	100 000	1 200 000
2	111 916,67	11917	100 000	1 100 000
3	110 833,33	10833	100 000	1 000 000
4	109 750,00	9750	100 000	900 000
5	108 666,67	8667	100 000	800 000
6	107 583,33	7583	100 000	700 000
7	106 500,00	6500	100 000	600 000
8	105 416,67	5417	100 000	500 000
9	104 333,33	4333	100 000	400 000
10	103 250,00	3250	100 000	300 000
11	102 166,67	2167	100 000	200 000
12	101 083,33	1083	100 000	100 000
ИТОГО:	1 284 500,00	84500,00	1 200 000

Для расчёта доли процентов в дифференцированных платежах использовалась следующая формула:

In – сумма, которая идёт на погашение процентов по кредиту в данный расчётный период;

Sn – остаток задолженности по кредиту;

p – годовая процентная ставка.

Действительно, рассчитаем долю процентов в дифференцированных платежах за первый платёж: .

Расчёт остатка ссудной задолженности:

Sn = 1 200 000 – 100 000 = 1 100 000 руб. 

Расчёт начисленных процентов:

I n = 1 100 000 * 13 % / 12 = 11 917 руб.

В процессе интервью сотрудник банка ПАО КБ «УБРиР» также предоставил информацию, как вычисляется доходность по вкладу. На сайте банка представлены виды вкладов (Приложение 2).

Используя полученные данные, получены следующие расчёты:

Параметры вклада следующие:

Сумма вклада – 200 000 руб.

Срок – 210 дней

Процентная ставка – 6 % годовых.

Для расчета размера дохода по вкладу используем формулу простых процентов.

Первоначальную сумму вклада нужно умножить на годовую процентную ставку и разделить на число дней в текущем году.

Таким образом я узнал, сколько процентов будет начисляться в день.

Затем полученную сумму необходимо умножить на срок вклада.

Например, вы размещаете на вклад 200 000 руб.

Находим, сколько процентов будет начислено в день:

200 000 * 6% / 365 = 32 ,88 руб.

Полученную сумму умножаем на срок вклада – 210 дней.

32,88 * 210 = 6905 руб.

Чтобы узнать, какую сумму выдаст банк при снятии вкладанеобходимо прибавить к ним первоначальную сумму вклада.

В нашем случае – 200 000 руб.

200 000 + 6905 = 206 905 руб.

Таким образом, в ходе интервью с сотрудниками и клиентами банка ПАО КБ «УБРиР» я получил подробную информацию о том, как вычисляются доходность по вкладу и задолженность по кредиту.

5. Анкетирование

Мною была разработана анкета для обучающихся шестых, седьмых и девятых классов:

1.Умеешь ли ты решать задачи на процент?

_____________________________________________________________

2.Решал ли ты задачи на процент на сайте Решу ОГЭ?

_____________________________________________________________

3.Где по-твоему могут встретиться проценты в жизни?

_____________________________________________________________

4.Планируешь ли ты в будущем взять кредит или оформить вклад?

_____________________________________________________________

5.Сможешь ли ты рассчитать переплату по кредиту или доходность по вкладу?

Проанализировав результаты анкетирования, получил следующую информацию:

Опрошены обучающиеся шестого, седьмого, девятого классов основной школы № 12. Всего участвовало в анкетировании 72 человека. Результаты представлены ниже:

6 класс	Да	Нет
1 вопрос	86%	14%
2 вопрос	28%	72%
3 вопрос	магазин 72% банк-18% незнаю-10%
4 вопрос	21%	79%
5 вопрос	22%	78%

7 класс	Да	Нет
1 вопрос	85%	15%
2 вопрос	50%	50%
3 вопрос	магазин 57% банк-43%
4 вопрос	21%	79%
5 вопрос	50%	50%

9 класс	Да	Нет
1 вопрос	85%	15%
2 вопрос	98%	2%
3 вопрос	магазин 62% банк-38%
4 вопрос	76%	24%
5 вопрос	86%	14%

Для наглядности результатов изобразим результаты в виде диаграмм.

1. Умеешь ли ты решать задачи на проценты?

2. Решал ли ты задачи на проценты на сайте «Решу ОГЭ»?

4. Планируешь ли ты в будущем взять кредит или оформить вклад?

5. Сможешь ли ты рассчитать переплату по кредиту или доходность по вкладу

Таким образом, можно сделать вывод, что большинство школьников умеют решать задачи на процент и смогут рассчитать переплату по кредиту или доходность по вкладу. Задачи на процент лучше умеют решать ученики из 9 класса, так как скоро им предстоит сдавать ОГЭ, половина учеников седьмого класса начинает готовиться к ОГЭ, а в шестом классе задачи данного типа интересуют меньшие количество обучающихся.

Заключение

В современной жизни очень важно уметь правильно выполнять операции с процентами. Для того чтобы понять, как решаются задачи на проценты, а так же как рассчитать доходность по вкладу или переплату по кредиту, я решил исследовать эту тему.

Работая над проектом, я научился находить информацию, обрабатывать ее и выделять в ней главное. Выяснил, что появились проценты давно, и в настоящее время понятие «процент» очень активно используется в банковской системе, в торговле (скидка на товар, различные акции в магазинах и пр.), экономике (налогообложении и пр.), статистике и др. Также задачи на проценты встречается на ОГЭ и ЕГЭ базового и профильного уровней по математике.

Сегодня трудно найти экономически развитую страну, где отсутствуют кредитные продукты и вклады. В настоящее время существует различные виды кредитов и вкладов. В своей работе я подробно рассмотрел кредит с дифференцированным платежом, а также изучил расчет доходности по вкладу, используя метод простых процентов. В ходе работы выделил наиболее выгодный способ для погашения кредита – с помощью дифференцированного платежа.

Проведя анкетирование среди обучающихся шестых, седьмых, девятых классов основной школы № 12, я выяснил, что не все школьники умеют решать задачи на проценты и смогут рассчитать переплату по кредиту или доходность по вкладу. Задачи на проценты лучше умеют решать только ученики из 9 класса, так как скоро им предстоит сдавать ОГЭ, половина учеников седьмого класса начинает готовиться к ОГЭ, а в шестом классе задачи данного типа интересуют меньшее количество людей.

Я рассмотрел 7 прототипов задач из ЕГЭ базового и профильного уровня. Все задачи подробно разобраны и дается полное объяснение их решения. При разборе заданий я использовал знания по математике 5 и 6 класса. Но для меня пока сложными являются задания № 17 ЕГЭ по «Финансовой математике». Я уверен, что работа над проектом, полученные знания и умения пригодятся мне на ОГЭ и ЕГЭ по математике. Также я считаю, что эти знания и умения обязательно пригодятся мне в повседневной жизни. Думаю, что без труда смогу научить своих одноклассников решать задачи на проценты. Материал моего проекта будет полезен для обучающихся выпускных классов как пособие для подготовки к ОГЭ и ЕГЭ, к олимпиадам по экономике и математике.

Таким образом, можно сделать вывод, что поставленные задачи

решены и цель достигнута, гипотеза подтвердилась.

Свою будущую профессию я хочу связать с экономической специальностью. Работа над проектом для меня была интересной и увлекательной. И это еще раз подтвердило, что направление моей будущей профессиональной деятельности выбрано правильно.

Список литературы

1. Абчук В. «Занимательная экономика и бизнес», С-П: Тригон,1998.

2. Банковское дело. Справочное пособие. Под ред. Ю. А. Бабичевой- М.:

«Экономика», 1994.

3. Буслаев А.“Сложные проценты”. Газета “Математика” №30. 2002. стр.29

4. Вигман С.Л. Финансы,  кредит, деньги в вопросах и ответах: учеб. пособие.-

М: ТК Велби, Изд-во Проспект, 2010

5.Вигдорчик Е., Нежданова Т. Элементарная математика в экономике и

бизнесе.- М., 1997.

6. Демин Ю. Все о кредитах. Понятно и просто. – СПб.: Питер, 2007

7. Ершов Ю.С. «Финансовая математика в вопросах и ответах», Новосибирск:

Сибирское соглашение, 1999.

8. Кац М. “Проценты”. Газета “Математика” №20. 2004. стр.22; №22. 2004.

стр.29; №23. 2004. стр.28

9. Колягин Ю. М., Ткачёва М. В. и др. Алгебра 7 класс: учебник для общеобразовательных организаций- М.: Просвещение, 2018

10. Лаврушин О.И. Деньги, кредит, банки: Учебник. — М.: Финансы и

статистика, 2000

11. Липцис И.В. «Экономика без тайн», Москва, изд. «Вита» 2004г.

12. Математика. ЕГЭ Профильный уровень 50 вариантов, под ред. И.В.Ященко,

М.:Экзамен, 2020

13. Математика. ЕГЭ Базовый уровень 50 вариантов, под ред. И.В.Ященко,

М.:Экзамен, 2020

14. Математика. ОГЭ по математике 50 вариантов, под ред. И.В.Ященко,

М.:Экзамен, 2020

15. Процентные вычисления. 10-11кл.:Учеб.метод.пособие/Г.В.Дорофеев,

Е.А.Седова. — М.: Дрофа, 2003

16. Петрова И.Н.. Проценты на все случаи жизни. М.: «Просвещение», 2006.

17. Савицкая Е.В., Серегина С.Ф. Уроки экономики в школе. – М.: Вита-Пресс,1999.

18. Седова Е.А. Проценты в X классе общеобразовательного направления. //

журнал «Математика в школе».-1994-№4. 

19. Энциклопедия для детей. Т. 11. Математика/Глав. Ред. М.Д. Аксенова. М.: Аванта+, 2001.

20. Сайт решу ОГЭ математика [https://math-oge.sdamgia.ru/]

21. Сайт решу ЕГЭ математика базовый уровень[https://mathb-ege.sdamgia.ru/]

22. Сайт решу ЕГЭ математика профельный уровень[https://math-ege.sdamgia.ru/]

23. Сайт ПАО КБ «УБРиР» [https://www.ubrr.ru/]

Приложение 1

Сценарий интервьюирования сотрудника и

клиентов банка ПАО КБ «УБРиР».

Я на крыльце банка.

Очень часто люди обращаются в банк по разным причинам. В большинстве случаев, для оформления кредита или вклада. В основе данных банковских продуктов лежит начисление процентов. Правильно рассчитать стоимость кредита и доходность по вкладу помогут мне сотрудники Асбестовского офиса Уральского банка реконструкции и развития.

В юридическом отделе спрашиваю у клиента:

— Добрый день. Подскажите, пожалуйста, с какой целью вы посетили банк?

Клиент банка отвечает.

Я:

— На что вы обращаете внимание при выборе того или иного кредита?

Клиент банка отвечает.

В юридическом отделе спрашиваю старшего специалиста по кредитованию юридических лиц:

— Здравствуйте. Пожалуйста, объясните, что такое кредит?

Кредитный специалист отвечает.

Я:

— Клиенты при выборе кредитного продукта, особое внимание обращают на размер процентной ставки и способ начисления процентов. Расскажите, как начисляются проценты в вашем банке при кредитовании?

Кредитный специалист отвечает.

Я:

— Подскажите, возможно ли рассмотреть пример начисления процентов?

Кредитный специалист отвечает.

Я:

— На сайте вашего банка очень большой выбор кредитных продуктов. На мой взгляд, наиболее выгодные условия кредитования предлагаются по кредиту «Бизнес-привилегия». Давайте рассмотрим дифференцированные платежи по данному кредиту.

Специалист банка отвечает.

Я:

— Спасибо большое! Теперь я понял, как начисляются проценты на кредит. А этот график я приложу к своему проекту.

Я спрашиваю у клиента:

— Добрый день. Подскажите, пожалуйста, для чего вы посетили банк?

Клиент банка отвечает.

Я:

— Чем Вы будете руководствоваться, выбирая вклад?

Клиент банка отвечает.

Я подхожу к специалисту банка и спрашиваю:

— Здравствуйте, на сайте банка я познакомился с различными видами вкладов для физических лиц. Меня привлек вклад «Мобильный Он-Лайн». Не могли бы Вы рассказать, как начисляются проценты по этому вкладу? Например, я бы хотел оформить вклад на 200 000 рублей на срок 210 дней.

Специалист отвечает.

Я:

— Действительно, очень легко. Теперь я понял принцип начисления процентов по вкладам. А как узнать какую сумму выдаст банк при снятии вклада?

Специалист отвечает.

Я:

— Спасибо! Теперь я знаю, что такое доходность вклада.

Приложение 2

Просмотров работы: 2671

«Хороший учитель обязан понимать, что никакую задачу нельзя исчерпать до конца. Этот взгляд он должен прививать и своим ученикам».
Д. Пойа.

Введение.

Особое внимание я уделяю текстовым задачам на проценты, которые часто встречаются в практике вступительных экзаменов в экономические вузы, но недостаточно полно рассматриваются в школе. Умение выполнять процентные вычисления, − безусловно, одна из самых необходимых математических компетенций. Однако не только те, кто уже давно окончили школу, робеют при виде процентов. Даже на ЕГЭ решаемость задач на проценты не превышает 20 % . Это говорит о том, что такого типа задачи следует решать не только в младших классах, где изучается эта тема, но и на протяжении всех лет обучения в школе.

1. При решении задач на проценты используются основные формулы:

1% числа а равен а.

р% от числа а равно  а.

Если известно, что некоторое число а составляет р% от х, то х можно найти из пропорции

а   − р%

х   − 100%,

откуда х= а.

Пусть имеются числа a, b, причем а<b. Тогда

Число b больше числа а на100%.

Число а меньше числаbна100%.

2. Формула сложных процентов.

Если на вклад положена сумма а денежных единиц, банк начисляет р% годовых, то через n лет сумма на вкладе составит

aден.ед.

3. Задачи на проценты.

Задача 1.

Умных людей на 45 % меньше, чем красивых, 36% умных обладают красивой внешностью. Каков процент умных людей среди красивых?

Решение: пусть х − количество красивых людей, тогда количество умных людей:

х − 0,45х = 0,55х.

Среди умных 36% составляют красивые люди, следовательно, количество умных и одновременно красивых людей:

0,36 ·0,55х= 0,198х.

Составим пропорцию:

х −  100%

0,198х −  а%.

Отсюда получим:

а = 19,8%.

Ответ: 19,8%

Учащиеся с интересом решают текстовые задачи на проценты, которые ближе к реальной жизни. Особый «прикол» представляет собой подача задач не из задачника, а прямо с газетной полосы. Тут уж не возникает мыслей о ненужности математики. А «процентная журналистика» в связи с разразившимся экономическим кризисом на страницах газет буквально процветает.

Задача 2.

Цены на путевки уже подросли: например, туры во Францию − на 20%. Можно ли сказать, на сколько процентов раньше тур во Францию был дешевле?

Решение: пусть х − старая цена, а n − новая цена.

1) Составим первую пропорцию:

х −  100%

n − 120%,

Получим n=1,2х.

2) Составим вторую пропорцию:

1,2х − 100%

х − (100-а%)

(100-а) 1,2х = 100х

Решив уравнение, получим: а ≈17%.

Ответ:17%.

4. Использование формулы сложных процентов.

Задача 3.

На банковский счет было положено 10 тыс. руб. После того, как деньги пролежали один год, со счета сняли 1 тыс. руб. Еще через год на счету стало 11 тыс. руб. Определите, какой процент годовых начисляет банк.

Решение: пусть банк начисляет р% годовых.

1) Сумма в 10000 рублей, положенная на банковский под р% годовых, через год возрастет до величины

10000+

2) Когда со счета снимут 1000 руб., там останется 9000+100р руб.

3) Еще через год последняя величина за счет начисления процентов возрастет до величины

9000+100р+

По условию эта величина равна 11000:

Решив это уравнение получим: =10, =−200 − отрицательный корень не подходит.

Ответ:10%

Задача 4. (ЕГЭ-2015)

Банк под определенный процент принял некоторую сумму. Через год четверть накопленной суммы была снята со счета. Но банк увеличил процент годовых на 40%. К концу следующего года накоплена сумма в 1,44 раза превысила первоначальный вклад. Каков процент новых годовых?

Решение: от суммы вклада ситуация не изменится. Положим в банк 4 рубля (делится на 4). Через год сумма на счету увеличится ровно в p раз и станет равной (4p) рублей.

Поделим её на 4 части, унесём домой (p) рублей, оставим в банке (3p) рублей.

Известно, что к концу следующего года в банке оказалось 4·1,44 = 5,76 рублей. Итак, число (3p) превратилось в число (5,76). Во сколько раз оно увеличилось?

 

Таким образом, найден второй повышающий коэффициент k банка.

Интересно, что произведение обоих коэффициентов равно 1,92:

 

Из условия следует, что второй коэффициент на 0,4 больше первого.

 

 

Избавившись от запятых, сделаем замену t = 10р:

 

Из такого уравнения получить 12 совсем просто.

Итак, p = 1,2, k = 1,6.

В 1,2 раза увеличилась сумма вклада первый раз, в 1,6 раз — во второй раз.

Было 100%, стало 160%. Новый процент годовых равен 160%-100% = 60%.

Ответ: 60%.

Задача 5. (ЕГЭ-2015)

В банк помещена сумма 3900 тысяч рублей под 50% годовых. В конце каждого из первых четырех лет хранения после вычисления процентов вкладчик дополнительно вносил на счет одну и ту же фиксированную сумму. К концу пятого года после начисления процентов оказалось, что 

размер вклада увеличился по сравнению с первоначальным на 725%. 

Какую сумму вкладчик ежегодно добавлял к вкладу?

Решение: пусть х рублей – вкладчик ежегодно добавлял ко вкладу.

50% годовых означает, что каждый год сумма на счету вкладчика увеличивается в 1,5 раза. Если вкладчик ничего бы не добавлял к первоначальной сумме, то через год на его счету было бы 3900·1,5, через два года — 3900·1,52 и так далее.

 Посчитаем, какой доход принесли все четыре добавки.

х∙1,5⁴ + х∙1,5³ + х∙1,5² +х∙1,5

Для этого вынесем х за скобку и вычислим сумму геометрической прогрессии, в которой b = 1,5 и q = 1,5.

Известно, что размер вклада увеличился по сравнению с первоначальным на 725%. 

Это значит, что он стал составлять 825% от начального, т.е. увеличился в 8,25 раз.

Сумма всех слагаемых последнего столбика в 8,25 раз больше, чем 3900 тыс.руб.

Ответ: 210 тысяч рублей.

5. Литература.

1. С.Я. Криволапов. Пособие по математике для абитуриентов. М., 2004.
2. Математика в школе. №6, 2009.
3. Типовые варианты ЕГЭ-2015.

• Решение

•   Видеорешение