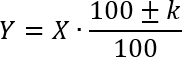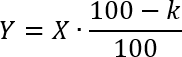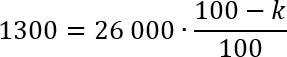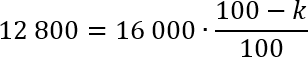Задачи на проценты формулы егэ

«Хороший учитель обязан понимать, что никакую задачу нельзя исчерпать до конца. Этот взгляд он должен прививать и своим ученикам».
Д. Пойа.

Введение.

Особое внимание я уделяю текстовым задачам на проценты, которые часто встречаются в практике вступительных экзаменов в экономические вузы, но недостаточно полно рассматриваются в школе. Умение выполнять процентные вычисления, − безусловно, одна из самых необходимых математических компетенций. Однако не только те, кто уже давно окончили школу, робеют при виде процентов. Даже на ЕГЭ решаемость задач на проценты не превышает 20 % . Это говорит о том, что такого типа задачи следует решать не только в младших классах, где изучается эта тема, но и на протяжении всех лет обучения в школе.

1. При решении задач на проценты используются основные формулы:

1% числа а равен а.

р% от числа а равно  а.

Если известно, что некоторое число а составляет р% от х, то х можно найти из пропорции

а   − р%

х   − 100%,

откуда х= а.

Пусть имеются числа a, b, причем а<b. Тогда

Число b больше числа а на100%.

Число а меньше числаbна100%.

2. Формула сложных процентов.

Если на вклад положена сумма а денежных единиц, банк начисляет р% годовых, то через n лет сумма на вкладе составит

aден.ед.

3. Задачи на проценты.

Задача 1.

Умных людей на 45 % меньше, чем красивых, 36% умных обладают красивой внешностью. Каков процент умных людей среди красивых?

Решение: пусть х − количество красивых людей, тогда количество умных людей:

х − 0,45х = 0,55х.

Среди умных 36% составляют красивые люди, следовательно, количество умных и одновременно красивых людей:

0,36 ·0,55х= 0,198х.

Составим пропорцию:

х −  100%

0,198х −  а%.

Отсюда получим:

а = 19,8%.

Ответ: 19,8%

Учащиеся с интересом решают текстовые задачи на проценты, которые ближе к реальной жизни. Особый «прикол» представляет собой подача задач не из задачника, а прямо с газетной полосы. Тут уж не возникает мыслей о ненужности математики. А «процентная журналистика» в связи с разразившимся экономическим кризисом на страницах газет буквально процветает.

Задача 2.

Цены на путевки уже подросли: например, туры во Францию − на 20%. Можно ли сказать, на сколько процентов раньше тур во Францию был дешевле?

Решение: пусть х − старая цена, а n − новая цена.

1) Составим первую пропорцию:

х −  100%

n − 120%,

Получим n=1,2х.

2) Составим вторую пропорцию:

1,2х − 100%

х − (100-а%)

(100-а) 1,2х = 100х

Решив уравнение, получим: а ≈17%.

Ответ:17%.

4. Использование формулы сложных процентов.

Задача 3.

На банковский счет было положено 10 тыс. руб. После того, как деньги пролежали один год, со счета сняли 1 тыс. руб. Еще через год на счету стало 11 тыс. руб. Определите, какой процент годовых начисляет банк.

Решение: пусть банк начисляет р% годовых.

1) Сумма в 10000 рублей, положенная на банковский под р% годовых, через год возрастет до величины

10000+

2) Когда со счета снимут 1000 руб., там останется 9000+100р руб.

3) Еще через год последняя величина за счет начисления процентов возрастет до величины

9000+100р+

По условию эта величина равна 11000:

Решив это уравнение получим: =10, =−200 − отрицательный корень не подходит.

Ответ:10%

Задача 4. (ЕГЭ-2015)

Банк под определенный процент принял некоторую сумму. Через год четверть накопленной суммы была снята со счета. Но банк увеличил процент годовых на 40%. К концу следующего года накоплена сумма в 1,44 раза превысила первоначальный вклад. Каков процент новых годовых?

Решение: от суммы вклада ситуация не изменится. Положим в банк 4 рубля (делится на 4). Через год сумма на счету увеличится ровно в p раз и станет равной (4p) рублей.

Поделим её на 4 части, унесём домой (p) рублей, оставим в банке (3p) рублей.

Известно, что к концу следующего года в банке оказалось 4·1,44 = 5,76 рублей. Итак, число (3p) превратилось в число (5,76). Во сколько раз оно увеличилось?

 

Таким образом, найден второй повышающий коэффициент k банка.

Интересно, что произведение обоих коэффициентов равно 1,92:

 

Из условия следует, что второй коэффициент на 0,4 больше первого.

 

 

Избавившись от запятых, сделаем замену t = 10р:

 

Из такого уравнения получить 12 совсем просто.

Итак, p = 1,2, k = 1,6.

В 1,2 раза увеличилась сумма вклада первый раз, в 1,6 раз — во второй раз.

Было 100%, стало 160%. Новый процент годовых равен 160%-100% = 60%.

Ответ: 60%.

Задача 5. (ЕГЭ-2015)

В банк помещена сумма 3900 тысяч рублей под 50% годовых. В конце каждого из первых четырех лет хранения после вычисления процентов вкладчик дополнительно вносил на счет одну и ту же фиксированную сумму. К концу пятого года после начисления процентов оказалось, что 

размер вклада увеличился по сравнению с первоначальным на 725%. 

Какую сумму вкладчик ежегодно добавлял к вкладу?

Решение: пусть х рублей – вкладчик ежегодно добавлял ко вкладу.

50% годовых означает, что каждый год сумма на счету вкладчика увеличивается в 1,5 раза. Если вкладчик ничего бы не добавлял к первоначальной сумме, то через год на его счету было бы 3900·1,5, через два года — 3900·1,52 и так далее.

 Посчитаем, какой доход принесли все четыре добавки.

х∙1,5⁴ + х∙1,5³ + х∙1,5² +х∙1,5

Для этого вынесем х за скобку и вычислим сумму геометрической прогрессии, в которой b = 1,5 и q = 1,5.

Известно, что размер вклада увеличился по сравнению с первоначальным на 725%. 

Это значит, что он стал составлять 825% от начального, т.е. увеличился в 8,25 раз.

Сумма всех слагаемых последнего столбика в 8,25 раз больше, чем 3900 тыс.руб.

Ответ: 210 тысяч рублей.

5. Литература.

1. С.Я. Криволапов. Пособие по математике для абитуриентов. М., 2004.
2. Математика в школе. №6, 2009.
3. Типовые варианты ЕГЭ-2015.

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Задачи на проценты считаем проценты с помощью формулы

13 ноября 2013

Сегодня мы продолжим штурмовать задачи на проценты из ЕГЭ по математике. Но делать это мы будем с помощью специальной формулы, которая так и называется — формула простого процента.

Предлагаю оформить ее в виде теоремы:

Теорема о простом проценте. Пусть нам дана некоторая исходная величина x, дано ее изменение в процентах k, а нужно найти новую величину y, равную результату этих изменений. Тогда новая величина выражается по формуле:

где плюс или минус ставится в зависимости от того, увеличивается величина по условию задачи или уменьшается.

Давайте посмотрим, как эта формула работает на практике.

Задача. Среди 26 000 семей города 1300 семей — многодетные. Какой процент многодетные семьи составляют от всех семей города?

Решаем эту задачу. Согласно нашей формуле, у нас должно быть три числа: x, k и y. Причем x — это исходная величина, т.е. общее количество семей, которых по условию задачи 26 000 штук. Получим:

x = 26 000

Кроме того, известно количество многодетных семей. Всего их 1300, т.е. y = 1300. Осталось разобраться с числом k. В данной задаче оно означает, насколько процентов надо уменьшить исходное количество семей, чтобы получить только многодетные семьи. Что ж, давайте посмотрим. Записываем формулу простого процента:

Как видим, при коэффициенте k стоит знак минус, поскольку для получения многодетных семей мы должны убрать из 26 000 семей тех, которые не является многодетными. Вот сейчас и уберем. Подставляем числа в формулу:

Сразу сокращаем по два нуля у множителя 26 000 и знаменателя 100. Таким образом, дробь лишается знаменателя. Разделим полученное уравнение еще на 10. Другими словами, зачеркнем слева и справа по одному нулю. Получим:

130 = 26 · (100 − k)

Что ж, разделим обе стороны еще на 26. Получим:

100 − k = 5;
k = 100 − 5 = 95.

Итак, мы получили: для того, чтобы из 26 000 семей осталось только 1300 многодетных семей, надо вычесть 95% тех, кто не является многодетными. Следовательно, на многодетные семьи остается лишь 5% от общего числа. Это и есть ответ — то, что нам требовалось найти по условию задачи.

Задача B2 на проценты №2

Переходим ко второй задаче.

Задача. Мобильный телефон стоил 16 000 рублей. Через некоторое время цены на эту модель снизили до 12 800 рублей. На сколько процентов была снижена цена?

Эта задача уже гораздо больше подходит для решения по формуле простого процента. Давайте посмотрим: у нас опять фигурируют 3 величины: исходная стоимость x, проценты k и итоговая стоимость y.

Сначала телефон стоил 16 000 рублей. Очевидно, что это начальная цена:

x = 16 000

Затем, после снижения цены телефон стал стоить 12 800 рублей. Это итоговая цена:

y = 12 800

Как видим, от нас снова требуют найти проценты. Что ж, подставляем в формулу и считаем. При этом сама формула простых процентов будет той же самой:

При коэффициенте k будет стоять минус, потому что по условию задачи стоимость телефона снижается. Итак, подставляем наши числа в формулу и записываем уравнение:

По традиции, сразу сокращаем нули в знаменателе дроби и в числе, стоящем перед дробью. При этом знаменатель дроби исчезнет (поскольку окажется равен единице), а в числителе останется просто 160. Далее разделим обе стороны уравнения на 10, сократив таким образом еще под одному нулю слева и справа. Перепишем полученное уравнение:

1280 = 16 · (100 − k)

Разделим обе стороны уравнения еще на 16 и получим:

100 − k = 1280 : 16

Можно, конечно разделить 1280 : 16 столбиком. Но давайте не будем усложнять себе жизнь, а просто вспомним, что 16 · 16 = 256. Тогда для того, чтобы получить 128, достаточно записать 16 · 8 = 128. Следовательно, имеем:

16 · 16 = 256;
16 · 8 = 128;
16 · 8 · 10 = 1280.

В этом случае наше деление сводится к следующей конструкции:

1280 : 16 = 16 · 8 · 10 : 16 = 8 · 10 = 80

Как видите, все легко сокращается. Переписываем наше уравнение:

100 − k = 80;
k = 100 − 80 = 20.

Итого мобильный телефон подешевел на 20%. Вот и все решение задачи.

Как видите, формула простого процента во многих случаях упрощает решение задачи или, как минимум, делает его более наглядным. Обязательно возьмите эту формулу на вооружение!

Смотрите также:

1. Формула простого процента: неизвестно конечное значение
2. Формула простого процента: как найти исходное значение
3. Сложные выражения с дробями. Порядок действий
4. Специфика работы с логарифмами в задаче B15
5. Задача B5: площадь фигуры без клеток
6. Углы и отрезки в стереометрии — 2