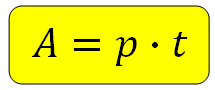Задачи на производительность 11 класс егэ - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей за час изготавливает второй рабочий, если известно, что первый за час изготавливает на 1 деталь больше?

Заказ на 156 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей за час изготавливает первый рабочий, если известно, что он за час изготавливает на 1 деталь больше второго?

На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?

Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 1., Пробный экзамен по математике Санкт-Петербург 2015. Вариант 1., ЕГЭ по математике 07.06.2021. Основная волна. Подмосковье

На изготовление 99 деталей первый рабочий тратит на 2 часа меньше, чем второй рабочий на изготовление 110 таких же деталей. Известно, что первый рабочий за час делает на 1 деталь больше, чем второй. Сколько деталей в час делает второй рабочий?

Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй  — за три дня?

Пройти тестирование по этим заданиям

Источник

25
Окт 2013

Категория: 09 Текстовые задачиТекстовые задачи

09. Задачи на работу

2013-10-25
2022-09-11

Возможно, при решении задач вы столкнетесь с громоздким дискриминантом… Что делать в таком случае смотрите здесь и здесь

Задача 1. Заказ на деталей первый рабочий выполняет на часа быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на детали больше?

Решение: + показать

Задача 2. Первая труба пропускает на литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом литров она заполняет на минуты дольше, чем вторая труба?

Решение: + показать

Задача 3. Первая труба пропускает на литр воды в минуту меньше, чем вторая труба. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом литров она заполняет на минуты дольше, чем вторая труба заполняет резервуар объемом литра?

Решение: + показать

Задача 4. Двое рабочих, работая вместе, могут выполнить работу за дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за дней выполняет такую же часть работы, какую второй — за дня?

Решение: + показать

Задача 5. Каждый из двух рабочих одинаковой квалификации может выполнить заказ за часов. Через часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?

Решение: + показать

Задача 6. Один мастер может выполнить заказ за часов, а другой — за часов. За сколько часов выполнят заказ оба мастера, работая вместе?

Решение: + показать

Задача 7. Игорь и Паша красят забор за часов. Паша и Володя красят этот же забор за час, а Володя и Игорь — за часов. За сколько часов мальчики покрасят забор, работая втроем?

Решение: + показать

Задача 8. Две трубы наполняют бассейн за часов минут, а одна первая труба наполняет бассейн за часов. За сколько часов наполняет бассейн одна вторая труба?

Решение: + показать

Задача 9. Петя и Митя выполняют одинаковый тест. Петя отвечает за час на вопросов текста, а Митя — на Они одновременно начали отвечать на вопросы теста, и Петя закончил свой тест позже Мити на минут. Сколько вопросов содержит тест?

Решение: + показать

Задача 10. Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было рабочих, а во второй — рабочих. Через дней после начала работы в первую бригаду перешли рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Найдите, сколько дней потребовалось на выполнение заказов.

Решение: + показать

Вы можете пройти тест по задачам на работу

Автор: egeMax |

комментария 3

Печать страницы

Источник

Примем объем работы за единицу. Пусть x — количество дней, за которое необходимо выполнить всю работу Виктору; за y дней работу выполнит Алексей, Андрей выполнит всю работу за z дней; тогда frac{1}{x} — производительность Виктора, frac{1}{y} — производительность Алексея, frac{1}{z} — производительность Андрея.

По первому условию Виктор и Алексей сделают всю работу за 8 дней, значит, их общая производительность frac18. Составим уравнение frac{1}{x}+frac{1}{y}=frac18.

По второму условию Виктор и Андрей сделают всю работу за 8 дней. Значит, их общая производительность frac18. Составим уравнение frac{1}{x}+frac{1}{z}=frac18.

По третьему условию Андрей и Алексей выполнят всю работу за 12 дней. Значит, их общая производительность frac{1}{12}. Составим уравнение frac{1}{y}+frac{1}{z}=frac{1}{12}.

Получим систему уравнений:

begin{cases} frac{1}{x}+frac{1}{y}=frac18,\ frac{1}{x}+frac{1}{z}=frac18,\ frac{1}{y}+frac{1}{z}=frac{1}{12}; end{cases}

2left( frac{1}{x}+frac{1}{y}+frac{1}{z} right )=frac18+frac18+frac{1}{12},

2left( frac{1}{x}+frac{1}{y}+frac{1}{z} right )=frac13,

frac{1}{x}+frac{1}{y}+frac{1}{z}=frac16,

1:frac16=6 (дней).

Итак, всю работу Виктор, Алексей и Андрей сделают за 6 дней.

Источник

Скачать материал

Выберите документ из архива для просмотра:

Задачи на совместную работу.docx

Задачи на совместную работу.pptx

Выбранный для просмотра документ Задачи на совместную работу.docx

Скачать материал

Сейчас обучается 1079 человек из 83 регионов

Сейчас обучается 28 человек из 12 регионов

Сейчас обучается 140 человек из 45 регионов

Выбранный для просмотра документ Задачи на совместную работу.pptx

Скачать материал

Описание презентации по отдельным слайдам:

1 слайд

Задачи на совместную работу
Обобщение знаний. Решение задач.
Учитель: Коряковцева Н.В.
2 слайд

Задача 1
Два каменщика, работая вместе, могут выполнить задание за 12 часов. Производительность труда первого и второго каменщика относятся как 1:3. Каменщики договорились работать поочерёдно. Сколько времени должен работать первый каменщик, чтобы задание было выполнено за 20 часов?
3 слайд

Решение 1
1)Условно принимаем всю работу за 1.
Пусть х – производительность первого, тогда 3х – производительность второго.
1 4х =12, х = 1 48 , 3х = 1 16
2)Пусть у ч. – время I, тогда (20 – у) ч. – время II.
1 48 у + 1 16 (20-у)=1, у=6.
Ответ: 6 часов должен проработать первый каменщик.
4 слайд

Задача 2.
Отец с сыном должны вскопать огород. Производительность труда у отца в 2 раза больше, чем у сына. Работая вместе, они могут вскопать огород за 4 часа. Однако, вместе они проработали только 1 час, потом некоторое время работал один сын, а заканчивал работу один отец. Сколько часов в общей сложности проработал в огороде отец, если вся работа была выполнена за 7 часов?
5 слайд

Решение 2
За 4 часа сын может вскопать 1 3 огорода, отец — 2 3 .
За 1 час сын вскопает 1 12 часть, отец — 1 6 , а вместе за час 1 4 , то есть через 1 час совместной работы останется 3 4 огорода и 6 часов работы.
Пусть у часов – время работы отца, (6-у) часов – время сына.
1 12 (6-у)+ 1 6 у= 3 4 , у = 3 ч.
1+3 = 4 ч.
Ответ: 4 часа работал отец.
6 слайд

Задача 3
Два плотника, работая вместе, могут выполнить задание за 36 часов. Производительность труда первого и второго плотников относятся как 3:4. Плотники договорились работать поочерёдно. Какую часть этого задания должен выполнить второй плотник, чтобы всё задание было выполнено за 69,3 часа?
7 слайд

Решение 3
За 36 часов первый работник выполнит 3 7 задания, а второй — 4 7 .
За 1 час первый выполнит 1 84 , а второй — 1 63 задания.
Пусть у часов – время работы II, (69,3-у) часов – время I.
1 63 (69,3-у)+ 1 84 у=1, у = 25,2 ч. – время II
25,2∙ 1 84 =0,3
Ответ: 0,3 задания должен выполнить второй плотник.
8 слайд

Задача 4
Два фермера, работая вместе, могут вспахать поле за 25 часов. Производительность труда первого и второго фермеров относятся как 2:5. Фермеры планируют работать поочерёдно. Сколько времени должен проработать второй фермер, чтобы поле было вспахано за 45,5 часов?
9 слайд

Решение 4
За 25 часов I фермер может вспахать 2 7 поля, а II — 5 7 .
За 1 час I фермер может вспахать 2 175 часть, а II — 1 35 .
Пусть у часов – время работы II, (45,5-у) часов – время I.
1 35 (45,5-у)+ 2 175 у=1,
у = 17,5 ч.
Ответ: 17,5 часов должен проработать второй фермер.
10 слайд

Задача 5
Набор химических реактивов состоит из трёх веществ. Массы первого, второго и третьего веществ в этом наборе относятся, как 3:7:10. Массу первого вещества увеличили на 8%, а второго – на 4%. На сколько процентов надо уменьшить массу третьего вещества, чтобы масса всего набора не изменилась?
11 слайд

Решение 5
Условно примем массу всех веществ за 1.
Тогда масса первого вещества будет 3 20 , второго — 7 20 , а третьего 1 2
При изменении массы:
I — 3 20 ∙1,08
II — 7 20 ∙1,04
III — 1 2 х
3 20 ∙1,08+ 7 20 ∙1,04+ 1 2 х=1,
3∙1,08+7∙1,04+10х=20,
3,24+7,28+10х=20,
10х=9,48,
х=0,948.
1-0,948=0,052 – 5,2%
Ответ: на 5,2% необходимо уменьшить массу третьего вещества.
12 слайд

Задача 6
Подарочный набор состоит из трёх сортов конфет. Массы конфет первого, второго и третьего сорта в этом наборе относятся как 1:2:8. Массу конфет первого сорта увеличили на 20%, а второго – на 6%. На сколько процентов надо уменьшить массу конфет третьего сорта, чтобы масса всего набора не изменилась?
13 слайд

Решение 6
Условно примем массу всего набора за 1.
Тогда масса конфет первого сорта будет 1 11 , второго — 2 11 , а третьего 8 11
При изменении массы:
I — 1 11 ∙1,2
II — 2 11 ∙1,06
III — 8 11 х
1 11 ∙1,2+ 2 11 ∙1,06+ 8 11 х=1,
1∙1,08+2∙1,04+8х=11,
1,08+2,08+8х=11,
8х=7,84,
х=0,98.
1-0,98=0,02 – 2%
Ответ: на 2% необходимо уменьшить массу третьего сорта.
14 слайд

Задача 7
Объём ежегодной добычи нефти первой, второй и третьей скважины относится как 7:6:5. Планируется уменьшить годовую добычу нефти из первой скважины на 4%, а из второй – на 2%. На сколько процентов нужно увеличить годовую добычу нефти из третьей скважины, чтобы суммарный объём добываемой за год нефти не изменился?
15 слайд

Решение 7
Условно примем объём добываемой нефти за 1.
Тогда добыча нефти из первой скважины будет 7 18 , второй — 1 3 , а третьей 5 18
При изменении добычи:
I — 7 18 ∙0,96
II — 1 3 ∙0,98
III — 5 18 х
7 18 ∙0,96+ 1 3 ∙0,98+ 5 18 х=1,
7∙0,96+6∙0,98+5х=18,
6,72+5,88+5х=11,
5х= — 1,6,
х= — 0,32.
1- (- 0,32)=1,32 – 132%
Ответ: на 32% необходимо увеличить объём добываемой нефти из третьей скважины.
16 слайд

Задача 8
Три насоса, работая вместе, заполняют цистерну нефтью за 5 часов. Производительность насосов относится как 4:3:1. Сколько процентов объёма цистерны будет заполнено за 8 часов совместной работы второго и третьего насосов?
17 слайд

Решение 8
За 5 часов первый насос наполнит 1 2 цистерны, второй — 3 8 и третий 1 8 .
За 1 час второй наполнит 3 40 , а третий — 1 40 объёма.
Совместно они заполнят за 1 час 1 10 объёма,
а за 8 часов 8 10 , что составит 80%.
Ответ: 80%.
18 слайд

Задача 9
Три насоса, работая вместе, заполняют бак с керосином за 2 часа 30 минут. Производительность насосов относится как 3:5:8. Сколько процентов объёма будет заполнено за 1 час 18 минут совместной работы второго и третьего насосов?
19 слайд

Решение 9
За 2,5 часа первый насос наполнит 3 16 бака, второй — 5 16 и третий 1 2 .
За 1 час второй наполнит 1 8 , а третий — 1 5 объёма.
Совместно они заполнят за 1 час: 1 8 + 1 5 = 13 40 объёма,
а за 1 3 10 часа: 13 40 ∙ 13 40 = 169 400 = 0,4225, что составит 42,25%.
Ответ: 42,25%.
20 слайд

Задача 10
Две трубы вместе наполняют бассейн за 3 часа. Одна первая труба может наполнить бассейн на 2,5 часа быстрее, чем вторая труба. За сколько часов может наполнить бассейн одна первая труба?
21 слайд

Решение 10
Условно обозначим объём бассейна за 1.
Пусть х часов время наполнения бассейна первой трубой, тогда (х+2,5) ч. – время наполнения второй трубой.
1 х — производительность I,
1 х+2,5 — производительность II
1 х + 1 х+2,5 = 1 3 ,
1 х + 1 х+2,5 − 1 3 =0,
3х+7,5+3х− х 2 −2,5х 3х(х+2,5) =0,
х 2 -3,5х+7,5=0,
х=5.
Ответ: за 5 часов.

Краткое описание документа:

Текстовые задачи вызывают у выпускников из-за отсутствия достаточного опыта. Данный материал можно использовать для самостоятельной и совместной работы при подготовке к экзаменам в 11 классе. Он поможет учителю организовать практическую работу по этому разделу, содержит рекомендации по подходам к решению задач на совместную работу, примеры решений с пояснениями.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 153 784 материала в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

Другие материалы

Вам будут интересны эти курсы:

Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
Курс повышения квалификации «Экономика: инструменты контроллинга»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Страхование и актуарные расчеты»
Курс повышения квалификации «Финансы предприятия: актуальные аспекты в оценке стоимости бизнеса»
Курс повышения квалификации «Организация маркетинга в туризме»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Управление сервисами информационных технологий»
Курс профессиональной переподготовки «Корпоративная культура как фактор эффективности современной организации»
Курс профессиональной переподготовки «Методика организации, руководства и координации музейной деятельности»
Курс профессиональной переподготовки «Стандартизация и метрология»

Источник

11. Сюжетные текстовые задачи

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи на производительность труда

(blacktriangleright) Задачи из данной подтемы в определенном смысле схожи с задачами на прямолинейное движение: роль скорости здесь играет производительность труда (p) , роль расстояния — объем работы (A). Формула: [{large{A=pcdot t}}]

(blacktriangleright) Значит, например, если два рабочих работают одновременно, то производительность их общей работы (p) равна сумме производительностей каждого: (p=p_1+p_2).

Задание
1

#2823

Уровень задания: Легче ЕГЭ

Четыре одинаковых кота съедают четыре пачки корма “Корм 1” за четыре дня. Пять таких же котов съедают пять пачек корма “Корм 2” за пять дней. Во сколько раз больше период, на который одному такому коту хватит одной пачки корма “Корм 2”, чем период, на который одному такому коту хватит одной пачки корма “Корм 1”?

По условию четыре кота съедают четыре пачки корма “Корм 1” за четыре дня, тогда каждый кот ест свою пачку корма “Корм 1” четыре дня. Аналогично каждый кот ест свою пачку корма “Корм 2” пять дней, следовательно, искомая величина равна (5 : 4 = 1,25).

Ответ: 1,25

Задание
2

#855

Уровень задания: Равен ЕГЭ

Один маляр может покрасить забор за 2 часа, а второй маляр тот же забор – за 3 часа. За сколько часов маляры покрасят такой же забор, работая вместе?

За час первый маляр красит (dfrac{1}{2}) забора, а второй (dfrac{1}{3}) забора.

Вместе за час они красят (dfrac{1}{2} + dfrac{1}{3} = dfrac{5}{6}) забора.

Таким образом, малярам понадобится (1 : dfrac{5}{6} = 1,2) часа.

Ответ: 1,2

Задание
3

#2139

Уровень задания: Равен ЕГЭ

Один гигантский комар может выпить литр крови за полчаса, а второй гигантский комар – за четверть часа. За сколько минут гигантские комары выпьют литр крови на двоих?

За час первый комар выпивает (2) литра, а второй (4) литра.

Вместе за час они выпьют (2 + 4 = 6) литров.

Таким образом, комарам на распитие литра крови понадобится (dfrac{1}{6}) часа, то есть (10) минут.

Ответ: 10

Задание
4

#851

Уровень задания: Равен ЕГЭ

Таня может перемыть гору посуды за 20 минут, а Настя за 60 минут. За сколько минут девочки перемоют две горы посуды, работая вместе?

За минуту Таня моет (dfrac{1}{20}) часть одной горы посуды, а Настя (dfrac{1}{60}) часть горы посуды.

Вместе за минуту они моют (dfrac{1}{20} + dfrac{1}{60} = dfrac{1}{15}) горы посуды.

Таким образом, на две горы посуды девочкам понадобится (2 : dfrac{1}{15} = 30) минут.

Ответ: 30

Задание
5

#850

Уровень задания: Равен ЕГЭ

Боря может поклеить обои в комнате общежития за 10 часов, а его сосед Савва – за 6 часов. За сколько часов ребята поклеят обои в комнате, работая вместе?

За час Боря клеит (dfrac{1}{10}) часть комнаты, а Савва (dfrac{1}{6}) часть комнаты.

Вместе за час они клеят (dfrac{1}{10} + dfrac{1}{6} = dfrac{8}{30}) комнаты.

Таким образом, ребятам понадобится (1 : dfrac{8}{30} = 3,75) часа.

Ответ: 3,75

Задание
6

#849

Уровень задания: Равен ЕГЭ

Отличник Илья решает все 300 уравнений из учебника за 2 часа, а двоечница Уля решает все 300 уравнений из учебника за 30 часов. Уля решала уравнения из учебника 10 часов, после чего на помощь пришёл Илья. Сколько времени в итоге Уля потратила на получение всех решений всех уравнений (в том числе с помощью Ильи)? Ответ дайте в часах.

За час Уля решает (dfrac{1}{30}) всех уравнений, а Илья (dfrac{1}{2}) всех уравнений.

За первые 10 часов Уля решила (10cdotdfrac{1}{30} = dfrac{1}{3}) всех уравнений, после чего ей оставалось ещё (1 — dfrac{1}{3} = dfrac{2}{3}) всех уравнений.

За час совместной работы Уля и Илья решали (dfrac{1}{30} + dfrac{1}{2} = dfrac{8}{15}) от всех уравнений, тогда (dfrac{2}{3}) от всех уравнений они решили за (dfrac{2}{3} : dfrac{8}{15} = 1,25) часа.

В итоге Уля потратила (10 + 1,25 = 11,25) часа.

Ответ: 11,25

Задание
7

#848

Уровень задания: Равен ЕГЭ

Лев съедает антилопу за 20 минут, а львица съедает такую же антилопу за 30 минут. Спустя 10 минут после того, как лев приступил к поеданию антилопы, к нему присоединилась львица, и они доели антилопу вместе. Сколько минут в такой ситуации потребовалось на поедание антилопы льву и львице?

В минуту лев съедает (dfrac{1}{20}) антилопы, а львица (dfrac{1}{30}) антилопы.

За 10 минут лев съел (dfrac{1}{20} cdot 10 = dfrac{1}{2}) антилопы, после чего осталось (1 — dfrac{1}{2} = 0,5) антилопы.

Поедая вместе, лев и львица в минуту съедают (dfrac{1}{20} + dfrac{1}{30} = dfrac{1}{12}) антилопы, тогда

с начала совместного поедания до конца прошло (0,5 : dfrac{1}{12} = 6) минут.

Всего на антилопу льву и львице потребовалось (10 + 6 = 16) минут.

Ответ: 16

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Sorry, your request has been denied.

1. Решение текстовых задач «на работу»

Подготовка к ЕГЭ по математике
Решение текстовых
задач «на работу»
0011 0010 1010 1101 0001 0100 1011
1
2
4

2. Результаты решения текстовых задач на ЕГЭ по математике.

Результаты решения текстовых
задач
на1011ЕГЭ по математике.
0011 0010 1010 1101
0001 0100
Общее количество
учащихся
ирешивших верно
Результаты ЕГЭ в Рабочеостровской
школе
1
40
30
2
4
Ряд1
Ряд2
20
10
0
2003 г. 2004 г. 2005 г. 2006 г. 2007 г.
Год

3. Особенности решения задач «на работу».

0011 0010 1010 1101 0001 0100 1011
А=Р*t, где А-работа
Р- производительность труда
t- время
Р=А/t
t=А/Р
Если в условии не дана вся работа, то её можно
принять за 1
• Общая производительность равна сумме
производительностей.
1
2
4

4. Пример 1

Для наполнения плавательного бассейна
водой имеются три насоса. Первому насосу для
наполнения бассейна требуется времени в три
раза меньше, чем второму, и на 2 ч больше,
чем третьему. Три насоса, работая вместе,
наполнили бы бассейн за 3ч, но по условиям
эксплуатации одновременно должны работать
только два насоса. Определите минимальную
стоимость наполнения бассейна, если 1ч работы
любого из насосов стоит 140 рублей.
Решение: Эту задачу удобно решать с
помощью таблицы.
0011 0010 1010 1101 0001 0100 1011
1
2
4

5.

Работа
Время, час
Производительность
0011 0010 1010 1101 0001 0100 1011
1 насос
1
2 насос
1
3 насос
1
X
ВМЕСТЕ
1
3
х+2
3(х + 2)
1/х+2
1
1/3(х+2)
2
4
1/X
1/3

6. Алгоритм решения задачи

0011 0010 1010 1101 0001 0100 1011
1. Внесем в таблицу известные величины (
работу примем за 1)
2. Одну из неизвестных величин обозначим за
х.
3. Остальные неизвестные величины выразим
через х, используя условие задачи или
формулы.
. 4Составим уравнение.
5. Решим уравнение и ответим на главный
вопрос задачи.
1
2
4

7. Уравнение

0011 0010 1010 1101 0001 0100 1011
1/х+2 + 1/3(х+2) + 1/х = 1/3
Решив уравнение, мы найдем х=6
6ч- время наполнения бассейна третьим насосом.
Тогда время первого насоса 8ч, второго 24ч.
Значит минимальное время работы двух насосов – это
время работы 1 и3 насосов ,т.е. 14ч
• Определим минимальную стоимость наполнения
бассейна двумя насосами.
• 140*14=1960(руб.)
Ответ: 1960 руб.
1
2
4

8. Реши сам!

0011 0010 1010 1101 0001 0100 1011
• Два маляра, работая вместе, могут за 1ч
покрасить стену площадью 40 кв.м.
Первый маляр, работая отдельно, может
покрасить 50 кв. м стены на 4ч быстрее,
чем второй покрасит 90 кв.м такой же
стены. За сколько часов первый маляр
сможет покрасит 100 кв. м стены?
• Ответ: 4ч
1
2
4

9. Пример 2

0011 0010 1010 1101 0001 0100 1011
1
2
4

10. Пример 3

0011 0010 1010 1101 0001 0100 1011
• Бак заполняют керосином за 2часа 30
минут с помощью трех насосов,
работающих вместе.
Производительности насосов относятся
как 3:5:8. Сколько процентов объёма
будет заполнено за 1час 18 минут
совместной работы второго и третьего
насосов?
1
2
4

0011 0010 1010 1101 0001 0100 1011
Так как объём бака не указан, то примем объём бака за 1. Пусть
коэффициент пропорциональности равен х, тогда производительности
насосов соответственно равны 3х, 5х, 8х. И время наполнения бака при
совместной работе всех трех насосов равно 1/3х+5х+8х = 1/ 16х или, по
условию задачи, 2ч 30 мин.
Решим уравнение 1/16х = 2,5
Х =1/ 40
Производительность второго насоса равна 1/ 40 * 5 = 1/ 8
Производительность третьего насоса равна 1/ 40 * 8 = 1/ 5.
Совместная производительность второго и третьего насосов равна 1/ 8 +
1/ 5 =13/40
За 1ч 30мин второй и третий насосы наполнят 13/ 40 * 78/ 60 = 13/ 40 *
1,3 = 16,9/ 40 = 0,4225 объёма бака.
Итак, при совместной работе 2 и 3 насосов за 1ч 18 мин будет
заполнено 0,4225 *100% =42,25% объёма бака.
1
2
4

12. Реши сам !

0011 0010 1010 1101 0001 0100 1011
Два фермера, работая вместе могут вспахать
поле за 25 ч. Производительности труда
первого и второго фермеров относятся как 2:5.
Фермеры планируют работать поочередно.
Сколько времени должен проработать второй
фермер, чтобы это поле было вспахано за 45,5
ч?
• Ответ: 28 ч.
1
2
4

Задачи на работу решаются просто. В этой статье мы с вами рассмотрим типовые задания условия которых связаны с рабочими изготавливающими детали. Алгоритм решения задач идентичен алгоритму решения задач на движение. Перед дальнейшим изучением материала обязательно посмотрите статью, где мы решали задания на движение. Итак, формула:

Здесь A — работа, t — время, а величина p, которая по смыслу является скоростью работы, носит специальное название — производительность. Она показывает, сколько работы сделано в единицу времени. Например, Вася красит забор. Количество метров, которые он красит за час — это и есть его производительность. То есть это скорость работы.

Правила решения задач на работу:

1. А = р∙t, из этой формулы легко найти t или p.

2. Если объем работы не важен в задаче и нет никаких данных, позволяющих его найти — работа принимается за единицу. Построен дом (один), покрашен забор (один), наполнен резервуар. А вот если речь идет о количестве кирпичей, количестве деталей, литрах воды — работа как раз и равна этому количеству.

3. Если трудятся двое рабочих (два экскаватора, два мастера, Даша и Маша…) или трое (не важно) — их производительности суммируются. Очень логичное правило.

4. В качестве переменной «х» удобно взять (в абсолютном большинстве задач) именно производительность. Так же, как в задах на движение мы за «х» принимаем скорость.

Вы убедитесь, что задачи на работу и движение очень схожи.

Рассмотрим задачи:

Заказ на 240 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?

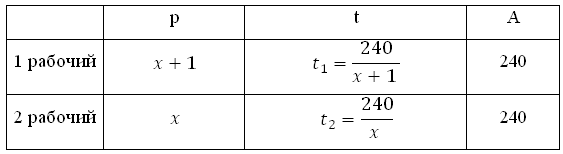
Как и в задачах на движение, заполним таблицу.

В колонке «работа» и для первого, и для второго рабочего запишем: 240. В задаче спрашивается, сколько деталей в час делает второй рабочий, то есть какова его производительность. Примем её за х. Тогда производительность первого рабочего равна х + 1 (он делает на одну деталь в час больше).

Поскольку t = A/p, время работы первого рабочего равно t₂ = 240/(х + 1), время работы второго равно t₂ = 240/х.

Первый рабочий выполнил заказ на час быстрее. Следовательно, времени он затрачивает на 1 час меньше, чем второй, то есть t₁ на 1 меньше, чем t₂, значит

Мы уже решали такие уравнения. Оно легко сводится к квадратному:

Очевидно, производительность рабочего не может быть отрицательной величиной. Значит, отрицательный корень не подходит.

Ответ: 15

Решить самостоятельно:

Посмотреть решение

26593. Заказ на 156 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 1 деталь больше?

В колонке «работа» и для первого, и для второго рабочего запишем 156.

В задаче спрашивается, сколько деталей в час делает первый рабочий, то есть какова его производительность. Примем её за х (деталей в час). Тогда производительность второго рабочего будет равна х–1 (он делает на одну деталь в час меньше).

Поскольку t=A/p, то время работы первого рабочего будет равно:Время работы второго равно:Занесём данные в таблицу:

Первый рабочий выполнил заказ на час быстрее. Следовательно, времени он затрачивает на 1 час меньше, чем второй. ЗначитМожем записать:Уравнение сводится к квадратному:

Очевидно, что производительность рабочего не может быть отрицательной величиной. Таким образом производительность первого рабочего равна 13 деталей в час.

Ответ: 13

На изготовление 40 деталей первый рабочий затрачивает на 6 часов меньше, чем второй рабочий на изготовление 70 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает второй рабочий?

Данная задача практически не отличается от предыдущей, разница лишь в объёме работы. Примем производительность второго рабочего за х.

Тогда производительность первого рабочего равна х + 3 (он делает в час на три детали больше). Заполним графу «время» в таблице:

Сравнение будем проводить по времени. Сказано, что первый затрачивает на 6 часов меньше, чем второй. Значит

Таким образом, второй рабочий в час делает 7 деталей.

Ответ: 7

26594. На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?

Для удобства занесём данные в таблицу.

В колонке «работа» для первого запишем 475, для второго рабочего запишем 550. В задаче спрашивается, сколько деталей в час делает первый рабочий, то есть какова его производительность. Примем её за х (деталей в час).

Тогда производительность второго рабочего будет равна х–3 (он делает на три детали в час меньше).

Поскольку t=A/p, то время работы первого рабочего будет равно

Время работы второго равноЗанесём данные в таблицу:

Сказано, что первый рабочий тратит на свой заказ на 6 часов меньше. Можем записать:

Уравнение сводится к квадратному:

Очевидно, что производительность рабочего не может быть величиной. Первый рабочий делает 25 деталей в час.

Ответ: 25

Решить самостоятельно:

Посмотреть решение

На этом всё. В будущем мы рассмотрим задачи на работу, которые несколько отличаются от представленных выше. Но вы увидите, что и в них нет ничего особо сложного, не пропустите! Успехов вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

РЕШЕНИЕ ПРОТОТИПОВ ЗАДАЧ НА СОВМЕСТНУЮ РАБОТУ.

1.1. Петя и Ваня выполняют одинаковый тест. Петя отвечает за час на 8 вопросов текста, а Ваня — на 9. Они одновременно начали отвечать на вопросы теста, и Петя закончил свой тест позже Вани на 20 минут. Сколько вопросов содержит тест?

Решение.

Пусть х – число вопросов, тогда

Время Пети =

Время Вани =

20 минут = часа

Уравнение:

— = , 9x- 8x = 24, х = 24. Ответ. 24

2.1.В помощь садовому насосу, перекачивающему 5 литров воды за 2 минуты, подключили второй насос, перекачивающий тот же объем воды за 3 минуты. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 25 литров воды?

Решение.

1-ый насос: 5 литров за 2 минуты, производительность — за 1 мин

2-ой насос: 5 литров за 3 минуты, производительность — за 1 мин

Общая производительность + =

• t = 25, t=6.

3.1. Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?

Решение.

2-я труба за х часов, тогда 1-ая за (х+6) часов

Производительности 1/х и 1/(х+6).

(+) •4 = 1.

4(х+6) +4х = х2 +6х

х2 – 2х – 24 = 0

х =6, х = -4

Ответ.6

4.1. Две трубы наполняют бассейн за 1 час 55 минут, а одна первая труба наполняет бассейн за 46 часов. За сколько часов наполняет бассейн одна вторая труба?

Решение. Примем работу за 1.

1ч55мин = ч. – время работы двух труб.

Х- время второй трубы, – производительность. Производительность первой —

( + = 1

+ =

= —

х = 2. Ответ.2.

5.1. Игорь и Паша красят забор за 9 часов. Паша и Володя красят этот же забор за 12 часов, а Володя и Игорь — за 18 часов. За сколько часов мальчики покрасят забор, работая втроем?

Решение. Работа = 1.

Производительности.

И+П=1/9=4/36

П+В=1/12=3/36

В+И=1/18=2/36

Сложим уравнения:

2(И+П+И)= (4+3+2)/36,

2(И+П+И)=9/36,

2(И+П+И)=1/4,

И+П+В=1/8 общая производительность. t =1: 1/8=8часов.

Ответ.8.

6.1. Даша и Маша пропалывают грядку за 12 минут, а одна Маша — за 20 минут. За сколько минут пропалывает грядку одна Даша?

Решение. х – время Даши. Работа = 1. Производительность

Д+М=1/12, М=1/20,

Д=1/12-1/20=1/30, за 30 минут.

Ответ.30.

7.1. Первый насос наполняет бак за 20 минут, второй — за 30 минут, а третий — за 1 час. За сколько минут наполнят бак три насоса, работая одновременно?

Решение.

Производительность : 1-ый- , 2-ой- , 3-ий-

Общая производительность + + = .

t = 1, t = 10. за 10 минут.

Ответ. 10.

8.1. Один мастер может выполнить заказ за 12 часов, а другой — за 6 часов. За сколько часов выполнят заказ оба мастера, работая вместе?

Решение.

– производительность первого, – второго.

+ = , •t = 1, t = 4.

Ответ.4.

9.1. Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 15 часов. Через 3 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?

Решение.

1-ый выполнит весь заказ за 15 часов – в 1 час он выполнит 1/15 работы, а за 3 часа 1/5 работы.

Осталось выполнить 4/5 работы.

Определим время совместной работы:

: ( • = 6

Поэтому на выполнение всего заказа потребуется 6 + 3 = 9 часов.

Ответ: 9.

Другое решение.

Один рабочий работал 3 часа. Остальные 12 часов они работали вместе, т.е. в два раза быстрее. Поэтому вдвоем они работали только 6 часов. Значит, все время работы 9 часов.

Ответ. 9.

10.1. Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй — за три дня?

Решение.

х производительность первого, у – второго. По условию задачи составим систему уравнений

х •12 = 1, 20х = 1, х = , t = 20.

Ответ.20.

Получим систему уравнений:

begin{cases} frac{1}{x}+frac{1}{y}=frac18, frac{1}{x}+frac{1}{z}=frac18, frac{1}{y}+frac{1}{z}=frac{1}{12}; end{cases}

2left( frac{1}{x}+frac{1}{y}+frac{1}{z} right )=frac18+frac18+frac{1}{12},

2left( frac{1}{x}+frac{1}{y}+frac{1}{z} right )=frac13,

frac{1}{x}+frac{1}{y}+frac{1}{z}=frac16,

1:frac16=6 (дней).

Итак, всю работу Виктор, Алексей и Андрей сделают за 6 дней.

Источник

2-й способ решения – без таблицы

Как обойтись без составления таблицы?

Сразу составить уравнение.

Для этого определим, какая величина нам не нужна в уравнении, чтобы затем приравнять.

Производительность? Ее и надо найти. Работа? Она нам дана по условию, поэтому глупо от нее избавляться. Остается время: оно нам и неизвестно, и не нужно.

Слева от знака равно будем писать формулу времени для первого рабочего, а справа – для второго.

Напомню, что первый работал на ( displaystyle 2) часа дольше, поэтому к времени второго надо будет прибавить ( displaystyle 2):

( displaystyle frac{112}{x}=frac{112}{x+1}+2)

То же самое уравнение, что и в первом способе, только без таблицы и системы уравнений.

А теперь вспомним, что я говорил в сааамом начале: задачи на работу и на движение – это то же самое. Спорное заявление, да? Ну, давай проверим, есть ли аналогия.

Во-первых, сравним формулы:

Движение	Работа
( displaystyle v=frac{S}{t})	( displaystyle P=frac{A}{t})
Скорость движения	Скорость выполнения работы, т.е. производительность
Пройденный путь	Выполненная работа
Потраченное на движение время	Потраченное на работу время

Теперь рассмотрим задачу:

Пример №1

Расстояние ( displaystyle 112) км первый велосипедист проезжает на ( displaystyle 2) часа дольше, чем второй.

Сколько км в час проезжает первый велосипедист, если известно, что второй за час проезжает на один километр больше, чем первый?

Ничего не напоминает? Да я же просто заменил слова: «Заказ» на «расстояние», «деталь» на «километр», «рабочий» на «велосипедист», «выполняет» на «проезжает». Суть осталась той же. Даже решение будет точно таким же (разберу здесь только II способ – без таблицы).

Пусть скорость первого ( displaystyle x), тогда второго ( displaystyle x+1). Сколько времени едет первый? ( displaystyle frac{112}{x}). Сколько времени едет второй? ( displaystyle frac{112}{x+1}). На сколько время первого больше, чем второго? На ( displaystyle 2) часа:

( displaystyle frac{112}{x}=frac{112}{x+1}+2).

То же самое уравнение! Вот и получается, что работа и движение – одно и то же.

Как решать задачи на совместную работу

Задачи на совместную работу отличаются от обычных, представленных выше, тем, что в них работа выполняется одновременно (совместно) несколькими рабочими (трубами и т.д.).

Пример №2

Первая труба заполняет бассейн за ( displaystyle 6) часов, а вторая – за ( displaystyle 4).

За какое время они заполнят бассейн, работая вместе?

Решение

Во-первых, давай придумаем аналогию с движением.

Придумал?

Бассейн – это путь. Допустим, из ( displaystyle A) в ( displaystyle B). Итак, первый автомобиль проезжает путь ( displaystyle AB) за ( displaystyle 6) часов, второй – за ( displaystyle 4).

А теперь как сформулировать вопрос? За какое время они проедут весь путь, двигаясь вместе? Бред.

Если двигаться параллельно, то каждый проходит весь путь самостоятельно. А в какой ситуации нам важно, какой путь автомобили проходят в сумме? Все гениальное просто: если они движутся навстречу друг другу!

Тогда что нас просят найти? Время, через которое они встретятся.

Поразмысли немного над этой аналогией. Все понял? Тогда идем дальше.

Какова «скорость» (а по-настоящему, производительность) первого? Путь (работа) деленный на время: ( displaystyle {{P}_{1}}=frac{A}{{{t}_{1}}}=frac{A}{6}). А второго? ( displaystyle {{P}_{2}}=frac{A}{{{t}_{2}}}=frac{A}{4}).

С какой производительностью работают две трубы вместе (не забывай, это задачи на совместную работу)? Берем количество литров, которое налила в бассейн первая труба за один час, прибавляем количество литров, которое налила в бассейн вторая труба за один час, – именно столько наливают в бассейн обе трубы за один час. То есть производительности складываются:

( displaystyle P={{P}_{1}}+{{P}_{2}})

То же самое, что и относительная скорость: с какой скоростью второй автомобиль приближается к первому? Со скоростью, равной сумме скоростей: ( displaystyle v={{v}_{1}}+{{v}_{2}}).

Итак,

( displaystyle P={{P}_{1}}+{{P}_{2}}=frac{A}{6}+frac{A}{4}=frac{5A}{12}).

Тогда время, за которое с такой производительностью будет выполнена работа ( A):

( displaystyle t=frac{A}{P}=frac{A}{frac{5A}{12}}=frac{12}{5}=2,4) (ч)

Итак, правило:

При совместной работе производительности складываются

А теперь давай рассмотрим самый сложный пример, научившись решать который, ты сможешь с легкостью справится с любой задачей на ЕГЭ.

Пример 8

На изготовление ( displaystyle 600) деталей первый рабочий тратит на ( displaystyle 10) часов меньше, чем второй рабочий на изготовление ( displaystyle 500) таких же деталей. За какое время, работая совместно, они изготовят партию в ( displaystyle 1000) деталей, если известно, что за час первый рабочий делает на ( displaystyle 5) деталей больше?

Решение:

Давай определимся, что нам нужно найти? Нам нужно найти время, за которое рабочие изготовят ( displaystyle 1000) деталей, то есть: ( displaystyle frac{1000}{{{P}_{1}}+{{P}_{2}}}).

Значит, нужно найти ( displaystyle {{P}_{1}}) и ( displaystyle {{P}_{2}}).

Первый рабочий за час делает на ( displaystyle 5) деталей больше. Обозначим производительность первого рабочего за х, тогда производительность второго – ( displaystyle x-5).

( displaystyle 600) деталей первый рабочий делает за ( displaystyle {{t}_{1}}) часов, а ( displaystyle 500) таких же деталей второй рабочий делает за ( displaystyle {{t}_{2}}={{t}_{1}}+10) часов.

То есть: ( displaystyle {{t}_{1}}=frac{600}{x}, a {{t}_{2}}={{t}_{1}}+10=frac{500}{x-5}).

Приравняв ( displaystyle {{t}_{1}}), получаем уравнение:

Источник