Задачи на производительность егэ профильная математика

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Еще один тип текстовых задач в вариантах ЕГЭ по математике — это задачи на работу.

Задачи на работу также решаются с помощью одной-единственной формулы: . Здесь — работа, — время, а величина , которая по смыслу является скоростью работы, носит специальное название — производительность. Она показывает, сколько работы сделано в единицу времени. Например, продавец в супермаркете надувает воздушные шарики. Количество шариков, которые он надует за час — это и есть его производительность.

Правила решения задач на работу очень просты.

1. , то есть работа производительность время. Из этой формулы легко найти или .
2. Если объем работы не важен в задаче и нет никаких данных, позволяющих его найти — работа принимается за единицу. Построен дом (один). Написана книга (одна). А вот если речь идет о количестве кирпичей, страниц или построенных домов — работа как раз и равна этому количеству.
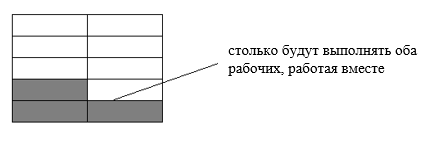
3. Если трудятся двое рабочих (два экскаватора, два завода…) — их производительности складываются. Очень логичное правило.
4. В качестве переменной удобно взять именно производительность.

Покажем, как все это применяется на практике.

---

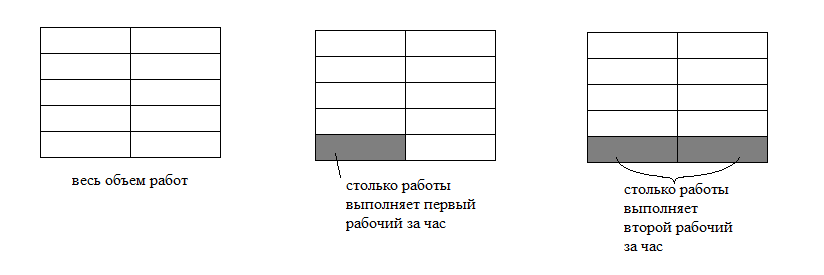
1. Заказ на деталей первый рабочий выполняет на час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на деталь больше?

Так же, как и в задачах на движение, заполним таблицу.

В колонке «работа» и для первого, и для второго рабочего запишем: . В задаче спрашивается, сколько деталей в час делает второй рабочий, то есть какова его производительность. Примем ее за . Тогда производительность первого рабочего равна (он делает на одну деталь в час больше). , время работы первого рабочего равно , время работы второго равно .

первый рабочий
второй рабочий

Первый рабочий выполнил заказ на час быстрее. Следовательно, на меньше, чем , то есть

Мы уже решали такие уравнения. Оно легко сводится к квадратному:

Дискриминант равен . Корни уравнения: , . Очевидно, производительность рабочего не может быть отрицательной — ведь он производит детали, а не уничтожает их Значит, отрицательный корень не подходит.

Ответ: .

---

2. Двое рабочих, работая вместе, могут выполнить работу за дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй — за три дня?

В этой задаче (в отличие от предыдущей) ничего не сказано о том, какая это работа, чему равен ее объем. Значит, работу можем принять за единицу.

А что же обозначить за переменные? Мы уже говорили, что за переменную удобно обозначить производительность. Пусть — производительность первого рабочего. Но тогда производительность второго нам тоже понадобится, и ее мы обозначим за .

По условию, первый рабочий за два дня делает такую же часть работы, какую второй — за три дня. Значит, . Отсюда .

Работая вместе, эти двое сделали всю работу за дней. При совместной работе производительности складываются, значит,

.

Итак, первый рабочий за день выполняет всей работы. Значит, на всю работу ему понадобится дней.

Ответ: .

---

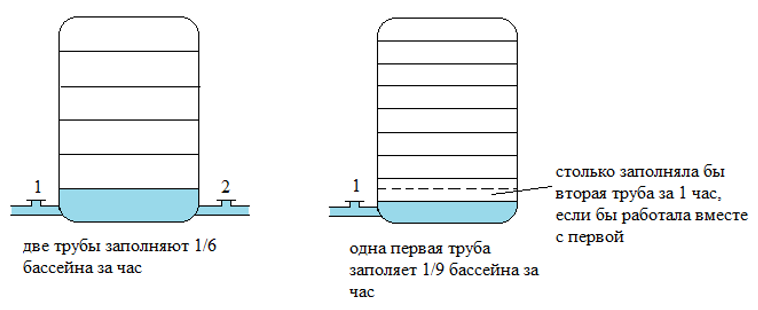
3. Первая труба пропускает на литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом литров она заполняет на минуты дольше, чем вторая труба заполняет резервуар объемом литров?

Всевозможные задачи про две трубы, которые наполняют какой-либо резервуар для воды — это тоже задачи на работу. В них также фигурируют известные вам величины — производительность, время и работа.

Примем производительность первой трубы за . Именно эту величину и требуется найти в задаче. Тогда производительность второй трубы равна , поскольку она пропускает на один литр в минуту больше, чем первая. Заполним таблицу

первая труба
вторая труба

Первая труба заполняет резервуар на две минуты дольше, чем вторая. Значит, . Составим уравнение:

и решим его.

Ответ: .

. Андрей и Паша красят забор за часов. Паша и Володя красят этот же забор за часов, а Володя и Андрей — за часов. За сколько часов мальчики покрасят забор, работая втроем?

Мы уже решали задачи на движение. Правила те же. Отличие лишь в том, что здесь работают трое, и переменных будет тоже три. Пусть — производительность Андрея, — производительность Паши, а — производительность Володи. Забор, то есть величину работы, примем за — ведь мы ничего не можем сказать о его размере.

	производительность	работа
Андрей
Паша
Володя
Вместе

Андрей и Паша покрасили забор за часов. Мы помним, что при совместной работе производительности складываются. Запишем уравнение:

Аналогично,


Тогда


.
Можно искать , и по отдельности, но лучше просто сложить все три уравнения. Получим, что

Значит, работая втроем, Андрей, Паша и Володя красят за час одну восьмую часть забора. Весь забор они покрасят за часов.
Ответ: .

---

Читаем дальше: Задачи на проценты

Примем объем работы за единицу. Пусть x — количество дней, за которое необходимо выполнить всю работу Виктору; за y дней работу выполнит Алексей, Андрей выполнит всю работу за z дней; тогда frac{1}{x} — производительность Виктора, frac{1}{y} — производительность Алексея, frac{1}{z} — производительность Андрея.

По первому условию Виктор и Алексей сделают всю работу за 8 дней, значит, их общая производительность frac18. Составим уравнение frac{1}{x}+frac{1}{y}=frac18.

По второму условию Виктор и Андрей сделают всю работу за 8 дней. Значит, их общая производительность frac18. Составим уравнение frac{1}{x}+frac{1}{z}=frac18.

По третьему условию Андрей и Алексей выполнят всю работу за 12 дней. Значит, их общая производительность frac{1}{12}. Составим уравнение frac{1}{y}+frac{1}{z}=frac{1}{12}.

Получим систему уравнений:

begin{cases} frac{1}{x}+frac{1}{y}=frac18,\ frac{1}{x}+frac{1}{z}=frac18,\ frac{1}{y}+frac{1}{z}=frac{1}{12}; end{cases}

2left( frac{1}{x}+frac{1}{y}+frac{1}{z} right )=frac18+frac18+frac{1}{12},

2left( frac{1}{x}+frac{1}{y}+frac{1}{z} right )=frac13,

frac{1}{x}+frac{1}{y}+frac{1}{z}=frac16,

1:frac16=6 (дней).

Итак, всю работу Виктор, Алексей и Андрей сделают за 6 дней.

ЕГЭ Профиль №9. Задачи на работуadmin2022-10-25T19:28:59+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №9. Задачи на работу

Задача 1. Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше? Пусть x дет/ч делает второй рабочий, тогда (x + 1) дет/ч делает первый рабочий. v (дет/ч) t (ч) А (дет) Первый рабочий (x + 1) (frac{{110}}{{x + 1}}) 110 Второй рабочий (x) (frac{{110}}{x}) 110 Первый рабочий на изготовление 110 деталей тратит на 1 час меньше. Следовательно: (frac{{110}}{x} — frac{{110}}{{x + 1}} = 1,,,, Leftrightarrow ,,,,frac{{110left( {x + 1} right) — 110x}}{{xleft( {x + 1} right)}} = 1,,,, Leftrightarrow ,,,,frac{{110}}{{xleft( {x + 1} right)}} = 1,,,, Leftrightarrow ,,,,,xleft( {x + 1} right) = 110,,,, Leftrightarrow ) ( Leftrightarrow ,,,,{x^2} + x — 110 = 0,;,,,,,,,,,D = 1 + 4 cdot 110 = 441;)  ({x_1} = frac{{ — 1 + 21}}{2} = 10;,,,,{x_2} = frac{{ — 1 — 21}}{2} =  — 11.) Так как (x > 0), то второй рабочий делает 10 деталей в час. Ответ: 10.

Задача 2. На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий? Пусть x дет/ч делает первый рабочий, тогда (x — 3) дет/ч делает второй рабочий. v (дет/ч) t (ч) А (дет) Первый рабочий (x) (frac{{475}}{x}) 475 Второй рабочий (x — 3) (frac{{550}}{{x — 3}}) 550 Первый рабочий тратит на 6 часов меньше. Следовательно: (frac{{550}}{{x — 3}} — frac{{475}}{x} = 6,,,, Leftrightarrow ,,,,frac{{550x — 475left( {x — 3} right)}}{{xleft( {x — 3} right)}} = 6,,,, Leftrightarrow ,,,,frac{{550x — 475x + 475 cdot 3}}{{xleft( {x — 3} right)}} = 6,,,, Leftrightarrow ,,,,) (6xleft( {x — 3} right) = 75x + 475 cdot 3,,left| {,:,} right.3,,,, Leftrightarrow ,,,,2{x^2} — 6x = 25x + 475,,,, Leftrightarrow ,,,,2{x^2} — 31x — 475 = 0;) (D = 961 + 8 cdot 475 = 4761;,,,,,,,,sqrt D  = 69;)     ({x_1} = frac{{31 + 69}}{4} = 25;,,,,{x_2} = frac{{31 — 69}}{4} =  — frac{{19}}{2}.) Так как (x > 3), то первый рабочий делает 25 деталей за час. Ответ: 25.

Задача 3. Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй — за три дня? Пусть первый рабочий, работая отдельно, выполнил работу за х дней. Так как второй рабочий за 3 дня выполняет такую часть работы, которую первый за 2 дня, то он выполнит всю работу за (frac{3}{2}x) дней. Пусть объём равен А: v (ед/день) t (дней) А (ед) Первый рабочий (frac{A}{x}) (x) A Второй рабочий (frac{{2A}}{{3x}}) (frac{3}{2}x) A Работая вместе, то есть с общей производительностью (frac{A}{x} + frac{{2A}}{{3x}}), рабочие выполняют всю работу (А) за 12 дней. Следовательно: (left( {frac{A}{x} + frac{{2A}}{{3x}}} right) cdot 12 = A,,,, Leftrightarrow ,,,,frac{{3A + 2A}}{{3x}} cdot 12 = A,,,, Leftrightarrow ,,,,frac{{5A cdot 4}}{x} = A,,,left| {:A} right.,,,,,, Leftrightarrow ,,,,,,,frac{{20}}{x} = 1,,,, Leftrightarrow ,,,,x = 20.) Таким образом, первый рабочий, работая отдельно, выполнит работу за 20 дней. Ответ: 20.

Задача 4. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 1 минуту дольше, чем вторая труба? Пусть первая труба пропускает x литров в минуту, тогда вторая пропускает (x + 1) литр в минуту. v (л/мин) t (мин) А (л) Первая труба (x) (frac{{110}}{x}) 110 Вторая труба (x + 1) (frac{{110}}{{x + 1}}) 110 Первая труба тратит на 1 мин больше чем вторая. Следовательно: (frac{{110}}{x} — frac{{110}}{{x + 1}} = 1,,,, Leftrightarrow ,,,,frac{{110left( {x + 1} right) — 110x}}{{xleft( {x + 1} right)}} = 1,,,, Leftrightarrow ,,,,frac{{110}}{{xleft( {x + 1} right)}} = 1,,,, Leftrightarrow ,,,,,xleft( {x + 1} right) = 110,,,, Leftrightarrow ) ( Leftrightarrow ,,,,{x^2} + x — 110 = 0,,,,,,,,,,D = 1 + 4 cdot 110 = 441;)   ({x_1} = frac{{ — 1 + 21}}{2} = 10;,,,,{x_2} = frac{{ — 1 — 21}}{2} =  — 11.) Так как (x > 0), то первая труба пропускает 10 литров в минуту. Ответ: 10.

Задача 5. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 2 минуты дольше, чем вторая труба заполняет резервуар объемом 99 литров? Пусть первая труба пропускает x литров в минуту, тогда вторая пропускает (x + 1) литр в минуту. v (л/мин) t (мин) А (л) Первая труба (x) (frac{{110}}{x}) 110 Вторая труба (x + 1) (frac{{99}}{{x + 1}}) 99 Первая труба тратит на 2 минуты больше чем вторая. Следовательно: (frac{{110}}{x} — frac{{99}}{{x + 1}} = 2,,,, Leftrightarrow ,,,,frac{{110left( {x + 1} right) — 99x}}{{xleft( {x + 1} right)}} = 2,,,, Leftrightarrow ,,,,frac{{110x + 110 — 99x}}{{xleft( {x + 1} right)}} = 2,,,, Leftrightarrow ,,,,,) ( Leftrightarrow ,,,,2xleft( {x + 1} right) = 11x + 110,,,, Leftrightarrow ,,,,2{x^2} + 2x = 11x + 110,,,,, Leftrightarrow ,,,,2{x^2} — 9x — 110 = 0) (D = 81 + 8 cdot 110 = 961;,,,,,,,{x_1} = frac{{9 + 31}}{4}, = 10;,,,,,{x_2} = frac{{9 — 31}}{4} =  — frac{{11}}{2}.) Так как (x > 0), то первая труба пропускает 10 литров в минуту. Ответ: 10.

Задача 6. Первая труба пропускает на 5 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 375 литров она заполняет на 10 минут быстрее, чем первая труба заполняет резервуар объемом 500 литров? Пусть вторая труба пропускает x литров в минуту, тогда первая пропускает (x — 5) литров в минуту. v (л/мин) t (мин) А (л) Первая труба (x — 5) (frac{{500}}{{x — 5}}) 550 Вторая труба (x) (frac{{375}}{x}) 375 Первая труба тратит на 10 минут больше чем вторая. Следовательно: (frac{{500}}{{x — 5}} — frac{{375}}{x} = 10,,,, Leftrightarrow ,,,,frac{{500x — 375left( {x — 5} right)}}{{xleft( {x — 5} right)}} = 10,,,, Leftrightarrow ,,,,frac{{500x — 375x + 375 cdot 5}}{{xleft( {x — 5} right)}} = 10,,,, Leftrightarrow ) ( Leftrightarrow ,,,,,10xleft( {x — 5} right) = 125x + 375 cdot 5,,left| {,:} right.,5,,,, Leftrightarrow ,,,,2{x^2} — 10x = 25x + 375,,,, Leftrightarrow ,,,,2{x^2} — 35x — 375 = 0;) (D = {35^2} + 8 cdot 375 = {5^2} cdot {7^2} + 8 cdot {5^2} cdot 15 = {5^2}left( {49 + 120} right) = {5^2} cdot 169;,,,,,,,,,,sqrt D  = 5 cdot 13 = 65;) ({x_1} = frac{{35 + 65}}{4}, = 25;,,,,,{x_2} = frac{{35 — 65}}{4} =  — frac{{15}}{2}.) Так как (x > 0), то вторая труба пропускает 25 литров в минуту. Ответ: 25.

Задача 7. Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 15 часов. Через 3 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа? После 3 часов работы первому на выполнение заказа осталось работать ещё 12 часов, но так как к нему присоединился второй рабочий, и они стали работать вместе, то им на завершение заказа потребуется 6 часов. Следовательно, заказ будет выполнен за 3 + 6 = 9 часов. Ответ: 9.

Задача 8. Один мастер может выполнить заказ за 12 часов, а другой — за 6 часов. За сколько часов выполнят заказ оба мастера, работая вместе? Первый мастер за 1 час выполняет (frac{1}{{12}}) часть работы, а второй (frac{1}{6}). Следовательно, работая вместе, два мастера выполняют (frac{1}{{12}} + frac{1}{6} = frac{1}{4}) часть работы. Поэтому всю работу мастера выполнят за 4 часа. Ответ: 4. Замечание: Выведем формулу для совместной работы двух рабочих. Пусть первый рабочий может выполнить работу А за время ({t_1}), а второй за время ({t_2}). Тогда производительность первого рабочего ({W_1} = frac{A}{{{t_1}}}), второго ({W_2} = frac{A}{{{t_2}}}). Следовательно, при совместной работе их общая производительность будет равна: (frac{A}{{{t_1}}} + frac{A}{{{t_2}}}). Пусть ({t_{совм}}) — время за которое будет выполнена работа А при совместной работе. Тогда (frac{A}{{{t_{совм}}}}) будет общая производительность двух рабочих, которая равна (frac{A}{{{t_1}}} + frac{A}{{{t_2}}}), то есть: (frac{A}{{{t_1}}} + frac{A}{{{t_2}}} = frac{A}{{{t_{совм}}}}). Сократив на А, получим: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}). Если работа выполняется тремя субъектами за время ({t_1}), ({t_2}) и ({t_3}) соответственно, то время совместного выполнения того же объёма работы равно: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{{t_{совм}}}}). Так как первый рабочий выполняет заказ за 12 часов, а второй за 6 часов, то ({t_1} = 12), ({t_2} = 6). Тогда: (frac{1}{{12}} + frac{1}{6} = frac{1}{{{t_{совм}}}},,,,,, Leftrightarrow ,,,,,frac{1}{4} = frac{1}{{{t_{совм}}}},,,,,, Leftrightarrow ,,,,,,{t_{совм}} = 4).

Задача 9. Первый насос наполняет бак за 20 минут, второй — за 30 минут, а третий — за 1 час. За сколько минут наполнят бак три насоса, работая одновременно? Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). В данном случае ({t_1} = 20) минут, ({t_2} = 30) минут, ({t_3} = 1) час = 60 минут: (frac{1}{{20}} + frac{1}{{30}} + frac{1}{{60}} = frac{1}{{{t_{совм}}}},,,,, Leftrightarrow ,,,,,frac{{3 + 2 + 1}}{{60}} = frac{1}{{{t_{совм}}}},,,,,, Leftrightarrow ,,,,,frac{6}{{60}} = frac{1}{{{t_{совм}}}},,,,, Leftrightarrow ,,,,,,{t_{совм}} = 10). Ответ: 10.

Задача 10. Игорь и Паша красят забор за 9 часов. Паша и Володя красят этот же забор за 12 часов, а Володя и Игорь — за 18 часов. За сколько часов мальчики покрасят забор, работая втроем? Пусть Игорь, Паша и Володя каждый покрасят забор за время ({t_1}), ({t_2}) и ({t_3})соответственно. Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Тогда получим систему уравнений: (left{ {begin{array}{*{20}{c}}  {frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{9};} \   {frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{12}};} \   {frac{1}{{{t_1}}} + frac{1}{{{t_3}}} = frac{1}{{18.}}} end{array}} right.) Прибавим к первому уравнению второе и третье: (frac{2}{{{t_1}}} + frac{2}{{{t_2}}} + frac{2}{{{t_3}}} = frac{1}{9} + frac{1}{{12}} + frac{1}{{18}},,,,, Leftrightarrow ,,,,,frac{2}{{{t_1}}} + frac{2}{{{t_2}}} + frac{2}{{{t_3}}} = frac{1}{4},left| {,:2,,,,, Leftrightarrow } right.,,,,,frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{8}.) Так как спрашивают, за сколько часов мальчики покрасят забор, работая втроем, то: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{{t_{совм}}}}). Следовательно: (frac{1}{{{t_{совм}}}} = frac{1}{8},,,,, Leftrightarrow ,,,,,,{t_{совм}} = 8.) Ответ: 8.

Задача 11. Даша и Маша пропалывают грядку за 12 минут, а одна Маша — за 20 минут. За сколько минут пропалывает грядку одна Даша? Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Пусть ({t_1} = 20) минут время, за которое Маша пропалывает грядку, а ({t_2}) – время за которое Даша. При этом ({t_{совм}} = 12) минут. (frac{1}{{20}} + frac{1}{{{t_2}}} = frac{1}{{12}},,,,, Leftrightarrow ,,,,,frac{1}{{{t_2}}} = frac{1}{{12}} — frac{1}{{20}},,,,, Leftrightarrow ,,,,frac{1}{{{t_2}}} = frac{1}{{30}},,,,,, Leftrightarrow ,,,,,{t_2} = 30) минут. Ответ: 30.

Задача 12. Две трубы наполняют бассейн за 3 часа 36 минут, а одна первая труба наполняет бассейн за 6 часов. За сколько часов наполняет бассейн одна вторая труба? Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Пусть ({t_1} = 6) часов время, за которое первая труба наполняет бассейн, а ({t_2}) – время второй трубы. При этом ({t_{совм}} = 3) часа 36 минут = (3frac{{36}}{{60}}) часа = (frac{{18}}{5}) часа. (frac{1}{6} + frac{1}{{{t_2}}} = frac{5}{{18}},,,, Leftrightarrow ,,,,frac{1}{{{t_2}}} = frac{5}{{18}} — frac{1}{6},,,,, Leftrightarrow ,,,,frac{1}{{{t_2}}} = frac{1}{9},,,,, Leftrightarrow ,,,,{t_2} = 9) часов. Ответ: 9.

Задача 13. Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба? Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Пусть x – минут время, за которое вторая труба наполняет резервуар, а x + 6 минут время первой трубы. При этом ({t_{совм}} = 4) минуты: (frac{1}{{x + 6}} + frac{1}{x} = frac{1}{4},,,,, Leftrightarrow ,,,,,,frac{{x + x + 6}}{{xleft( {x + 6} right)}} = frac{1}{4},,,,, Leftrightarrow ,,,,{x^2} + 6x = 4left( {2x + 6} right),,,, Leftrightarrow ,,,,,{x^2} — 2x — 24 = 0;) (D = 4 + 4 cdot 24 = 100;,,,,,,{x_1} = frac{{2 + 10}}{2} = 6;,,,,,{x_2} = frac{{2 — 10}}{2} =  — 4.) Так как (x > 0), то вторая труба наполнит резервуар за 6 минут. Ответ: 6.

Задача 14. В помощь садовому насосу, перекачивающему 5 литров воды за 2 минуты, подключили второй насос, перекачивающий тот же объем воды за 3 минуты. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 25 литров воды? Первый нанос перекачивает (frac{5}{2}) л/мин, а второй (frac{5}{3}) л/мин. Тогда вместе они перекачивают (frac{5}{2} + frac{5}{3} = frac{{25}}{6}) л/мин. Следовательно, 25 литров они перекачают за (25:frac{{25}}{6} = 6) минут. Ответ: 6.

Задача 15. Петя и Ваня выполняют одинаковый тест. Петя отвечает за час на 8 вопросов текста, а Ваня — на 9. Они одновременно начали отвечать на вопросы теста, и Петя закончил свой тест позже Вани на 20 минут. Сколько вопросов содержит тест? Пусть тест содержит х вопросов. v (в/ч) t (ч) А (в) Петя 8 (frac{x}{8}) х Ваня 9 (frac{x}{9}) х Так как Петя закончил свой тест на 20 минут ((frac{1}{3}) часа) позже Вани, то: (frac{x}{8} — frac{x}{9} = frac{1}{3},,,, Leftrightarrow ,,,,frac{x}{{72}} = frac{1}{3},,,,, Leftrightarrow ,,,,x = 24.) Следовательно, тест содержит 24 вопроса. Ответ: 24.

Задача 16. Плиточник должен уложить 175 м2 плитки. Если он будет укладывать на 10 м2 в день больше, чем запланировал, то закончит работу на 2 дня раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник? Пусть плиточник планирует укладывать х м2 плитки в день. v (м2/дн) t (дн) А (м2) План х (frac{{175}}{x}) 175 Сверх плана (x + 10) (frac{{175}}{{x + 10}}) 175 Следовательно: (frac{{175}}{x} — frac{{175}}{{x + 10}} = 2,,,, Leftrightarrow ,,,,frac{{175left( {x + 10} right) — 175x}}{{xleft( {x + 10} right)}} = 2,,,, Leftrightarrow ,,,,frac{{175 cdot 10}}{{xleft( {x + 10} right)}} = 2,,,, Leftrightarrow ) ( Leftrightarrow ,,,,2xleft( {x + 10} right) = 175 cdot 10,,left| {,:} right.2,,,, Leftrightarrow ,,,,{x^2} + 10x — 875 = 0) (D = 100 + 4 cdot 875 = 3600;,,,,,{x_1} = frac{{ — 10 + 60}}{2} = 25;,,,,,{x_2} = frac{{ — 10 — 60}}{2} =  — 35.) Так как (x > 0), то плиточник планировал укладывать 25 м2 плитки в день. Ответ: 25.

Задача 17. Первый и второй насосы наполняют бассейн за 9 минут, второй и третий — за 14 минут, а первый и третий — за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе? Пусть первый, второй и третий насосы заполняют бассейн за время ({t_1}), ({t_2}) и ({t_3}) соответственно. Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Тогда получим систему уравнений: ()(left{ {begin{array}{*{20}{c}}   {frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{9};} \   {frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{14}};} \   {frac{1}{{{t_1}}} + frac{1}{{{t_3}}} = frac{1}{{18.}}} end{array}} right.) Прибавим к первому уравнению второе и третье: (frac{2}{{{t_1}}} + frac{2}{{{t_2}}} + frac{2}{{{t_3}}} = frac{1}{9} + frac{1}{{14}} + frac{1}{{18}},,,,, Leftrightarrow ,,,,,frac{2}{{{t_1}}} + frac{2}{{{t_2}}} + frac{2}{{{t_3}}} = frac{5}{{21}},left| {,:2,,,,, Leftrightarrow } right.,,,,,,frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{5}{{42}}.) Так как спрашивается, за сколько минут три насоса заполнят бассейн, работая вместе, то: (frac{1}{{{t_{совм}}}} = frac{5}{{42}},,,,, Leftrightarrow ,,,,,,{t_{совм}} = 8,4) минуты. Ответ: 8,4.

Задача 18. Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали строить два одинаковых дома. В первой бригаде было 16 рабочих, а во второй — 25 рабочих. Через 7 дней после начала работы в первую бригаду перешли 8 рабочих из второй бригады, в результате чего оба дома были построены одновременно. Сколько дней потребовалось бригадам, чтобы закончить работу в новом составе? Количество рабочих будем считать производительностью. Пусть в новом составе рабочие доделывали дома t дней. В сумме до и после перехода рабочих каждая из бригад выполнила всю работу. Тогда: (16 cdot 7 + 24 cdot t = 25 cdot 7 + 17t,,,, Leftrightarrow ,,,,7t = 25 cdot 7 — 16 cdot 7,,,, Leftrightarrow ,,,,t = 9.) Следовательно, рабочим понадобилось 9 дней, чтобы закончить работу в новом составе. Ответ: 9.

Печать страницы

Суть задач на производительность следующая: некоторую работу выполняют несколько человек или механизмов, работающих с постоянной для каждого из них производительностью. Они могут выполнять эту работу либо по отдельности, либо совместно друг с другом. Алгоритм решения здесь такой же, как и алгоритм решения задач на движение:

1. Анализ данных.
2. Составление таблицы.
3. Составление уравнения.
4. Решение уравнения.

Основные особенности решения задач на производительность:

• Задачи на производительность схожи с задачами на движение. Основная формула при решении: V = v·t. Сравните её с формулой для решения задач на движение S = v·t. Роль скорости v здесь играет производительность труда, а роль расстояния S — объем работы V.
• Объем работы может быть не дан по условию и его не нужно находить при решении задачи (нам просто напросто не важно, какой объем работы выполняется). В таком случае его можно обозначить какой-нибудь буквой, например, V или A. В процессе решения эта переменная, которой мы обозначили объем, сократится и её значение не придется находить.
• Также, если объем работы не дан по условию, удобно принять его просто за 1; тогда время t, требующееся для выполнения всей работы, иv – производительность труда, связаны формулой:

$ t=frac{1}{upsilon}. $

• В отличие от задач на движение, в задачах на производительность скорости выполнения работы не могут вычитаться, а могут только складываться друг с другом. Если два человека или механизма по отдельности работают с производительностями v₁ и v₂, то вместе они будут работать быстрее (никак не медленнее), с суммарной производительностью v₁ + v₂, а время совместной работы будет равно:

$ t=frac{1}{upsilon_{1}+upsilon_{2}} $

Пример:

Первый рабочий за час делает на 5 деталей больше, чем второй, и выполняет заказ, состоящий из 200 деталей, на 2 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?

Решение:

В задаче требуется найти производительность второго рабочего. Примем его скорость за x. Заполним таблицу.

	v, дет/ч	t, ч	V, дет
Первый рабочий	x + 5	$ frac{200}{x+5} $	200
Второй рабочий	x	$ frac{200}{x} $	200

В условии задачи сказано, что первый рабочий выполняет заказ на 2 часа быстрее, чем второй. На основании этого составим уравнение:

$ {frac{200}{x+5}+2=frac{200}{x} frac{200+2x+10}{x+5}=frac{200}{x}.} $

2x² + 210x = 200x + 1000;

x² + 5x – 500 = 0.

Получаем два корня, x₁= 20 и x₂= –25. Второй корень не подходит, так как производительность не может быть отрицательной.

Ответ: 20 дет/ч.

Виды задач на производительность:

1. Задачи на совместную работу:

Задачи на совместную работу — это тип задач, в которых объектами, выполняющими работу, являются люди или группы людей: рабочие, ученики, операторы, бригады рабочих и т п. Объекты могут выполнять работу по отдельности, а могут — вместе.

Разберем простой пример. Двум рабочим требуется выполнить работу. Допустим, первый рабочий выполняет всю работу за 10 часов, а второй — за 5. Давайте найдем, за сколько часов рабочие справятся с работой, выполняя её вместе.

Получается, что если принять весь объем работ за 1, то первый рабочий выполняет $ frac{1}{10} $ всей работы за час, а второй $ frac{1}{10} $ то есть $ frac{1}{10} $ всей работы за час. На рисунке весь объем работ — это 10 «кирпичиков», первый выполняет 1 «кирпичик» за час, а второй — 2. Тогда вместе они будут выполнять $ frac{1}{10}+ frac{1}{5}= frac{3}{10} $  всей работы за час, или 3 «кирпичика»:

Чтобы найти совместную производительность рабочих, мы сложили друг с другом их собственные производительности. Теперь, чтобы найти время, за которое оба рабочих справятся с работой, выполняя её вместе, разделим полный объем работ на совместную производительность:

$ 1/frac{3}{10}=frac{10}{3}=3frac{1}{3} $

То есть вместе рабочие справятся с работой за 3 $ frac{1}{3} $ часа, или за 3 часа 20 минут.

2. Задачи на бассейны и трубы:

Отдельно можно выделить группу задач на производительность — задачи на заполнение бассейна несколькими трубами. В таких задачах рабочим будут соответствовать насосы (или трубы) разной производительности, а объему работы — объем бассейна или иного резервуара.

Рассмотрим пример. Две трубы наполняют бассейн за 6 часов, а одна первая труба наполняет бассейн за 9 часов. За сколько часов наполняет бассейн одна вторая труба?

Получается, что за 1 час две трубы наполняют $ frac{1}{6} $ часть бассейна, а одна первая труба наполняет $ frac{1}{9} $ часть бассейна: Так как вместе трубы наполняют бассейн водой со скоростью, равной сумме скоростей отдельно каждой из труб, то вторая труба наполняет бассейн со скоростью $ frac{1}{6}- frac{1}{9}= frac{1}{18} $.

Таким образом, вторая труба заполнит бассейн за $ 1/frac{1}{18}=18 $ часов.

Производительность труда в задаче 17

2 октября 2015

Задачи этого типа появились в ЕГЭ относительно недавно, но застали врасплох как учеников, так и многих учителей. А всё потому что решаются они с помощью производной — инструмента, совершенно непривычного для второй части экзамена.

Задача 17. Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно ${{t}^{2}}$часов в неделю, то за эту неделю они производят $3t$единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно ${{t}^{2}}$часов в неделю, то за эту неделю они производят $4t$единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей.

В приведённом условии есть важный момент, после осознания которого у вас вообще не будет проблем с решением подобных задач. Дело в том, что величина $t$, указанная для первого завода и для второго — это не одно и то же число! Другими словами, суммарное время рабочих на первом и другом заводе будет разным.

Для решения введём новые переменные: ${{a}^{2}}$ — суммарное время рабочих на первом заводе, ${{b}^{2}}$ — суммарное время на втором. С учётом производительности получим:

$begin{align}& {{a}^{2}}to 3a \& {{b}^{2}}to 4b \end{align}$

Таким образом, затратив суммарно ${{a}^{2}}+{{b}^{2}}$ часов времени, мы получим $3a+4b$ единиц продукции в неделю. Всё остальное — элементарная математика, подробно описанная в видеоуроке:

В прошлый раз мы рассматривали довольно «противные» задачи, связанные с вычислением времени в задачах про кредиты. Но это было очень просто по сравнению с тем, что мы будем рассматривать сегодня, а именно экономическую задачу 17 про производительность труда, в которой требуется применять производную. Эти задачи появились в ЕГЭ по математике относительно недавно, и те, кто уже с ними столкнулся, оценили, что, во-первых, условие таких задач довольно длинное, а, во-вторых, в каждой из таких задач есть неприятная зацепка, на которой «прогорели» очень многие ученики.

Думаю, вы уже догадались, что речь идет о той самой задачи 17, когда у Григория есть два завода, и еще указана производительность труда, и требуется оценить, какое наибольшее количество продукции можно произвести на этих двух заводах, если распределить нагрузку оптимально. Но на самом деле, в этих задачах 17 нет ничего сложного, даже чуть проще, чем многие задачи на кредиты. Поэтому сейчас мы рассмотрим одно из таких заданий, внимательно пробежимся по каждому пункту и посмотрим, как именно должно выглядеть идеальное ее решение.

Задача № 1

Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно ${{t}^{2}}$ часов в неделю, то за эту неделю они производят $3t$ единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно ${{t}^{2}}$ часов в неделю, то за эту неделю они производят $4t$. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей.

Григорий готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?

Шаг первый: вводим переменные

Прежде всего, перед тем как переходить к непосредственному решению задачи 17 из ЕГЭ по математике, попытаться что-то посчитать, составить какие-то формулы, поймите одну простую вещь: величина ${{t}^{2}}$, данная и в первом, и во втором предложении, никак не связаны друг с другом. Коэффициент $t$ нам дан исключительно для того, чтобы сравнить производительность на разных заводах при одинаковом расходе времени. Думаю, это сравнение абсолютно очевидно: на первом производительность составляет $3t$, а на втором — $4t$, т.е. чуть побольше. На практике это означает следующее: давайте распишем, что происходит на каждом из них.

На первом заводе у нас расходуется ${{a}^{2}}$ времени (после замены) и производится $3a$ единиц продукции. На втором — ${{b}^{2}}$ времени и $4b$ продукции.

А теперь давайте сложим расходы времени и суммарный выпуск продукта.

Получим, что суммарный расход времени составляет ${{a}^{2}}+{{b}^{2}}$, а суммарный расход продукции — $3a+4b$. При этом еще раз обращаю ваше внимание: никто не говорил, что ${{a}^{2}}$ и ${{b}^{2}}$ должны быть равны. Ключевое слово здесь «если» и в первом, и во втором случае. Именно поэтому мы так смело меняем коэффициенты $t$ на $a$ в первом случае и на $b$ во втором случае.

Шаг второй: составляем и решаем уравнение

Давайте посмотрим, что у нас получилось. ${{a}^{2}}+{{b}^{2}}$ — это суммарный расход времени. Поскольку Григорий платит рабочему 500 рублей за каждый час работы, то всего он сможет заплатить такую сумму:

[500cdot left( {{a}^{2}}+{{b}^{2}} right)=5000000]

Вот и первое уравнение.

На самом деле, основная сложность этой задачи 17 про производительность труда — вовсе не составление уравнения. Она состоит в том, что нужно понять, что на первом и на втором заводе время разное. Именно поэтому для первого мы везде заменили $t$ на $a$, а для второго — $t$ на $b$. В итоге как вы сейчас увидите, мы получим одно уравнение с двумя неизвестными, которое легко упрощается — одна неизвестная легко выражается через другую. И поэтому вся функция, выражающая количество произведенного товара, на самом деле зависит от одной-единственной переменной, в нашем случае это будет переменная $a$.

Далее, я думаю, все понятно: у нас есть функция, отрезок, на котором эта функция рассматривается, а все, что нам требуется найти — это наибольшее значение этой функции на данном отрезке. Вообщем, классическая задача для применения производных, в нашем случае новая задача 17 из ЕГЭ по математике.

Суммарный выпуск продукции ($S$) равен:

[S=3a+4bto max ]

Вот теперь задача и проявилась: имея ограничение на $a$ и $b$, нам нужно добиться того, чтобы $S$ принимала свое максимальное значение. Для начала давайте немножко поработаем с уравнением: $$

[500cdot left( {{a}^{2}}+{{b}^{2}} right)=5000000left| :500 right.]

[{{a}^{2}}+{{b}^{2}}=10000]

Отсюда выразим $b$:

[{{b}^{2}}=10000-{{a}^{2}}]

[b=sqrt{10000-{{a}^{2}}}]

Конечно, тут следовало бы перед выражением поставить $pm $, однако у нас речь идет о времени, а оно не может быть отрицательным, поэтому мы берем положительное значение. Итого суммарный объем выпускаемого товара может быть выписан как функция от одной-единственной переменной $a$:

[S=3a+4sqrt{10000-{{a}^{2}}}]

Шаг третий: находим максимальное значение функции

Теперь нам нужно найти максимальное значение этой функции на всей области определения, а совершенно очевидно, что величину $a$, т.е. количество товара, выпущенного на первом заводе, увеличивать до бесконечности нельзя, просто потому что корень имеет конкретную область определения — величина, стоящая под корнем, не должна быть отрицательной. Давайте запишем это:

[10000-{{a}^{2}}ge 0]

[{{a}^{2}}le 10000]

[left| a right|le 100]

[ain left[ 0;100 right]]

Итого мы получили классическую задачу из первой части ЕГЭ по математике: у нас есть функция, есть интервал, соответственно, нужно найти максимальное значение этой функции на заданном интервале. Давайте считать производную:

[{S}’=3+4cdot frac{1cdot left( 10000-{{a}^{2}} right)}{2sqrt{10000-{{a}^{2}}}}=3+frac{4cdot left( -2a right)}{2sqrt{10000-{{a}^{2}}}}=]

[=3-frac{4a}{sqrt{10000-{{a}^{2}}}}]

[3-frac{4a}{sqrt{10000-{{a}^{2}}}}=0]

Решаем полученное уравнение:

[3=frac{4a}{sqrt{sqrt{10000-{{a}^{2}}}}}]

[3sqrt{10000-{{a}^{2}}}=4a]

[9left( 10000-{{a}^{2}} right)=16{{a}^{2}}]

[90000-9{{a}^{2}}=16{{a}^{2}}]

[25{{a}^{2}}=90000]

[5a=3cdot 100]

[a=frac{3cdot 100}{5}=60]

Теперь, зная, чему равно $a$, легко найти $b$:

[b=sqrt{10000-3600}=sqrt{6400}=80]

Однако для полного и обоснованного решения необходимо понять знак производной. Давайте начертим числовую прямую и отметим на ней $a=60$ и посмотрим, что происходит при $a gt 60$:

Например, если взять $a=99$ мы получим следующее:

[10000-{{99}^{2}}={{100}^{2}}-{{99}^{2}}=left( 100-99 right)left( 100+99 right)=199]

Если посмотрим на исходное выражение, то очевидно, что $sqrt{199} lt 99$, но посчитав его, получаем в ответе отрицательное число.

Отсюда следует, что$a=60$является точкой максимума, т.е. именно той, которую мы и хотели найти. Именно в ней наша исходная функция принимает исходное значение. Осталось подставить в $S$ полученное значение $a$ и $b$:

[S=3cdot 60+4cdot 80=180+320=500]

Окончательный ответ: 500 единиц товара.

Нюансы решения

Как видите, все оказалось не так уж и сложно. Единственно, что нам нужно запомнить — это то, что величина ${{t}^{2}}$, когда речь идет о первом заводе дает нам информацию о производительности труда именно на нем, т.е. связывает время, затраченное на производство и количество продукции в рамках только него.

Величина ${{t}^{2}}$, относящаяся ко второму заводу, говорит нам именно о нем и никак не связана с первым.

Более того, считать, что количество времени, затраченного рабочими на первом и на втором заводах, абсолютно одинаково — это вообще глупость, потому что в этом случае полученное уравнение оказалось бы намного проще и решалось бы как элементарное линейное: нам бы не потребовалось никаких производных, никаких доказательств, что мы получили точку максимума — мы просто бы разделили зарплату между рабочими первого и второго производств пополам.

Поэтому запомните: время, потраченное на первом и на втором заводах, разное, поэтому пусть на первом потрачено ${{a}^{2}}$ времени, а на втором — ${{b}^{2}}$. В этом случае задача действительно становится сложнее, при этом интересней и вполне достойной называться задачей 17 из ЕГЭ по математике.

Задача № 2

А в качестве десерта предлагаю решить еще одну такую же задачу 17 из ЕГЭ по математике, однако выкладки в этот раз будут минимальными, по возможности такими, какие и нужно делать на экзамене по математике.

Сергей владеет двумя промышленными заводами, выпускающими одинаковую продукцию. На втором заводе установлено современное оборудование, поэтому на нем может быть выпущено больше единиц продукции. Известно, что если рабочие первого завода суммарно трудятся ${{t}^{2}}$ часов в неделю, то выпускают $t$ единиц продукции. А если рабочие второго завода суммарно трудятся ${{t}^{2}}$ часов в неделю, то выпускают $2t$ единиц продукции. Ставка заработной платы рабочего составляет 500 рублей в час.

Сергей готов платить рабочим 30 250 000 рублей в неделю. На какое максимальное количество единиц продукции он может рассчитывать?

Шаг первый: вводим переменные

Если рабочие на первом заводе трудятся ${{x}^{2}}$, то это дает нам $x$ единиц товара. На втором ${{y}^{2}}$ времени дает нам $y$ товаров. Вновь складываем расходы времени — ${{x}^{2}}+{{y}^{2}}$ и отдельно складываем объем продукции — $x+2y$. Величина ${{x}^{2}}+{{y}^{2}}$ — это суммарный расход времени за неделю.

Шаг второй: составляем и решаем уравнение

Поскольку за каждый час работы платится 500 рублей, то суммарный расход денег за неделю составит:

[500cdot left( {{x}^{2}}+{{y}^{2}} right)=30250000]

[{{x}^{2}}+{{y}^{2}}=60500]

Таким способом, ограничения на ${{x}^{2}}$ и ${{y}^{2}}$ найдены.

Теперь необходимо записать сумму:

[S=x+2yto max ]

Опять же будем считать производную, но для этого сначала необходимо выразить $y$ через $x$:

[{{y}^{2}}=60500-{{x}^{2}}]

[y=sqrt{60500-{{x}^{2}}}]

Подставляем найденное значение $y$ в нашу формулу и получаем:

[S=x+2cdot sqrt{60500-{{x}^{2}}}]

Находим производную этой конструкции:

[{S}’=1+2frac{1left( -2x right)}{2sqrt{60500-{{x}^{2}}}}=1-frac{2x}{sqrt{60500-{{x}^{2}}}}]

Вновь приравниваем полученное выражение к нулю:

[1-frac{2x}{sqrt{60500-{{x}^{2}}}}=0]

[frac{1}{1}=frac{2x}{sqrt{60500-{{x}^{2}}}}]

[sqrt{60500-{{x}^{2}}}=2x]

[60500-{{x}^{2}}=4{{x}^{2}}]

[60500=5{{x}^{2}}]

[{{x}^{2}}=frac{60500}{5}=121cdot 100]

[x=11cdot 10=110]

Шаг третий: находим максимальное значение функции

Мы получили критическую точку функции $S$. Теперь необходимо доказать, что это точка максимума. Для этого начертим вновь прямую, отметим на ней полученную точку 110 и возьмем любое число, больше чем 110. Однако для упрощения дальнейших выкладок предлагаю взять не рандомное число как в прошлый раз, а посчитать его с помощью следующего метода. Для начала давайте найдем $y$. Запишем такое выражение:

[y=2x=220]

Очевидно, что 220 больше 110, и если мы поставим его в нашу функцию, то получим число на отмеченном интервале:

Давайте подставим:

${S}’left( 220 right)=1-frac{2cdot 220}{sqrt{60500-{{220}^{2}}}}=1-frac{440}{sqrt{60500-48400}}=$

$=1-frac{440}{sqrt{12100}}=1-frac{440}{110}=1-4=-3$

Следовательно, справа от числа 110 мы получаем отрицательную производную, а слева, естественно, будет положительная.

Итого 110 — точка максимума. Это является строгим обоснованием.

Теперь подставляем в выражение $x$ и $y$, которые мы нашли:

[S=110+2cdot 220=110+440=550]

Ответ: 550 единиц товара.

Ключевые моменты решения задач17 на производительность труда из ЕГЭ по математике

Все, что нам нужно знать — это:

1. Правило вычисления производных сложных функций.
2. Правила решения несложных уравнений.

Кроме того, хотел бы отметить, что не надо бояться работать с большими числами. Такие выражения, когда у нас появляются пятизначные и более числа, абсолютно типичны для последних задач 17 из ЕГЭ по математике, потому что они реально трудные. Но на самом деле, в этих задачах из ЕГЭ нет ничего трудного. Вам только нужно знать следующее:

• ${{a}^{2}}to a$ и ${{b}^{2}}to 2b$ — как связано затраченное время с объемом выпущенного товара;
• $S=a+2bto max $ — суммарный объем товара находится по несложной формуле.

Кроме того, необходимо понимать, как связано время, затраченное на первом производстве и на втором, т.е. каковы максимальны ограничения на это время.

А дальше дело техники: считаем производную, решаем уравнение, подставляем в исходное ограничение и получаем окончательный ответ.

Надеюсь, это видео поможет вам построить собственный завод, где вы будете платить рабочим по 30 млн. рублей в неделю, если такой суммы вам окажется недостаточно, заходите на наш сайт, подписывайтесь на паблик ВКонтакте и на канал в YouTube. До новых встреч!

Смотрите также:

1. Задачи на кредит с плавающим платежом
2. Задачи с экономическим содержанием — основные формулы
3. Тест к уроку «Что такое логарифм» (средний)
4. Решение задач B12: №440—447
5. Как решать задачу 18: графический подход
6. Нестандартные задачи B2: кредит в банке