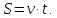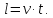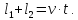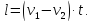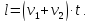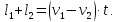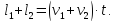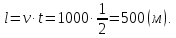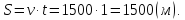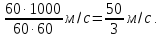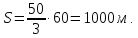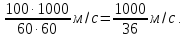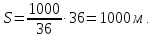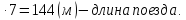«Решение
задач на движение протяженных тел».
Текстовые задачи являются традиционным заданием ЕГЭ и относятся к
категории заданий, которые вызывают у учащихся трудности при решении. Причиной
тому служат неумение читать условие задачи, непонимание логики задачи,
неумение составлять уравнение. Поэтому есть необходимость уделить особое
внимание этому виду заданий, тем более некоторые типы задач не изучаются в
школьном курсе математики.
Выделяют следующие основные группы:
1)
Задачи «на движение»;
2)
Задачи «на работу»;
3)
Задачи «на проценты,
концентрацию, части, доли».
Разумеется, тематический список текстовых задач не исчерпан
этими группами, но умение решать такие задачи является ключевым при подготовке
к решению задач по теме «Задачи на составление уравнений», задачи 11
профильного уровня ЕГЭ. [6]
В свою очередь каждую группу задач можно разбить на подгруппы.
Основными типами задач «на движение» являются следующие:
1) Движение на встречу друг с другом;
2) Движение в одном направлении;
3) Движение с изменениями в режиме движения:
а) Движение с задержкой в пути;
б) Другие изменения в режиме
движения.
4) Движение по воде;
5) Движение по окружности;
6) Задачи на среднюю скорость;
7) Движение протяженных объектов. [5]
По способу решения выделим задачи, приводящие к уравнениям и
задачи, приводящие к системе двух уравнений, хотя на экзамене предлагаются и
задачи, в которых для нахождения неизвестных, можно пользоваться условиями, не
записывающимися в форме уравнения.
Рассмотрим более подробно один из типов этих задач, а именно
задачи «на движение протяженных объектов», т.к. это один из типов задач «на
движение», которому не уделяется внимание в школьном курсе математики.
Задачи на
движение обычно содержат следующие величины:
t– время,
v–
скорость,
S–
расстояние
и формулы,
выражающие закон равномерного движения:
S= v∙t.
Применять эти
формулы можно, если величины S, t и v выражены в одинаковых единицах измерения.
Например, S (м), t (с) и v (м/с).
Протяженными
будем считать тела, длина которых соизмерима с расстоянием, которое они
проезжают.
В задачах
на движение протяженных тел требуется, как правило, определить длину одного из
них. Наиболее типичная ситуация:
-определение
длины поезда, проезжающего мимо столба; лесополосы определенной длины; другого
двигающегося поезда
-длина
протяженной платформы. [6]
В первом
случае поезд проходит мимо столба расстояние, равное длине поезда, во
втором случае — расстояние, равное сумме длин поезда и платформы.
Рассмотрим
примеры решения таких задач арифметическим способом или с помощью уравнения,
(систем уравнений).
Задача 1. Поезд, двигаясь
равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 30
секунд. Найти длину поезда в метрах. [4]
Решение: Зная скорость движения v = 60 км/ч = 1000 м/мин и время, за
которое он проезжает мимо столба t = 30 сек. = 1212мин, можно найти длину поезда как пройденное расстояние S = v⋅t, S=1000⋅12=500 (м).
Ответ: 500м.
Задача 2. Поезд, двигаясь
равномерно со скоростью 90 км/ч, проезжает мимо лесополосы, длина которого 800
метрам, за 1 минуту. Найти длину поезда в метрах. [5]
Решение: Зная скорость движения v = 90 км/ч = 1500 м/мин и время, за
которое он проезжает мимо лесополосы длиной 800 метров за t = 1мин, можно найти длину
поезда как пройденное расстояние S=v⋅t,
S=1500⋅1=1500,
1500-800=700 (м). (Минус длина лесополосы 800 метров и
получим длину поезда равную 700 метров).
Ответ: 700 м.
Задача
3. Поезд, двигаясь равномерно со скоростью 60 км/ч,
проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите
длину поезда в метрах.
Решение:
Решим задачу с помощью уравнения.
Пусть
х (м) – длина поезда,
Тогда
S=(х+400) м, t=1/60 ч., v=60 км/ч=60 000 м/ч.
S=
v⋅t ,
(х+400)=60
000∙ 1/60,
х+400=
1000,
х=600.
Ответ:
600м.
При решении задач на движение двух тел часто очень удобно считать
одно тело неподвижным, а другое — приближающимся к нему со скоростью, равной
сумме скоростей этих тел (при движении навстречу) или разности скоростей (при
движении вдогонку).
Задача
4: По морю параллельными курсами в одном направлении
следуют два сухогруза: первый длиной 120 метров, второй — длиной 80
метров. Сначала второй сухогруз отстает от первого, и в некоторый момент
времени расстояние от кормы первого сухогруза до носа второго составляет 400
метров. Через 12 минут после этого уже первый сухогруз отстает от второго так,
что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На
сколько километров в час скорость первого сухогруза меньше скорости второго?
[5]
Решение:
Будем считать, что первый сухогруз неподвижен, а
второй приближается к нему со скоростью v (м/мин) , равной разности скоростей
второго и первого сухогрузов. Тогда за 12 минут второй сухогруз проходит
расстояние 400м+ 120м +600м +80м =1200м.
v
= S
/ t,
v
= 1200:12 = 100(м/мин) = 6000 (м/ч) = 6 (км/ч).
Ответ:
6 км/ч.
Задача
5: По двум параллельным железнодорожным путям в одном
направлении следуют пассажирский и товарный поезда, скорости которых равны
соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам.
Найдите длину пассажирского поезда, если время, за которое он прошел мимо
товарного поезда, равно 1 минуте. Ответ дайте в метрах. [2]
Решение:
Решим задачу с помощью уравнения.
Пусть
х (м) – длина пассажирского поезда,
Тогда
S =(х+600) м, t =1мин., v =1000 м/мин.,
S=
v⋅t
х +600 =1000 ⋅ 1,
х +600 =1000,
х =400.
Ответ: 400м.
Задача 6: По двум параллельным
железнодорожным путям друг навстречу другу следуют скорый и пассажирский
поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина
пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если
время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ
дайте в метрах. [5]
Решение:
65
+35 =100 (км/ч) =100 000 (м/ч)
Скорость
навстречу друг другу (сумма скоростей при движении навстречу друг другу). Решим
задачу с помощью уравнения.
Пусть
х (м) – длина товарного поезда,
Тогда
S =(х+700) м, t = 36 с.= 36/60 мин.=36/ 3600 ч.=0,01ч.
v
=100 000 м/ч.,
S=
v⋅t
х +700 =100 000 ⋅ 0,01,
х +700 =1000,
х =300.
Ответ: 300м.
Задача
7. Мальчик сбежал вниз по движущемуся эскалатору
и насчитал 30 ступенек. Затем он пробежал вверх по тому же эскалатору с той же
скоростью относительно эскалатору и насчитал 70 ступенек. Сколько ступенек он
насчитал бы, спустившись по неподвижному эскалатору? [2]
Решение:
Пусть N — число
ступенек эскалатора, y— скорость
эскалатора, x— мальчика.
N/(x+y)
-время движения вниз, равное
30/х,
N/(x—y) — время
движения вверх, равное 70/х.
Отсюда
N/(x+y)
= 30/х,
N/(x—y) = 70/х.
Делим
первое на второе, получаем (x—y) /(x+y)
= 3/7. Отсюда,
как было у получаем
y=0,4x.
Тогда подставляем в
первое уравнение и получаем N=42.
Следовательно, он
пробежит 42 ступеньки по неподвижному эскалатору.
Ответ: 42.
Для закрепления материала предлагаются задачи для самостоятельного
решения:
1.
Поезд, двигаясь равномерно со скоростью 55 км/ч, проезжает мимо
идущего в том же направлении параллельно путям со скоростью 5 км/ч пешехода за
30 секунд. Найдите длину поезда. [5]
2.
Поезд, двигаясь равномерно со скоростью 54 км/ч, проезжает мимо
идущего в том же направлении параллельно путям со скоростью 6 км/ч пешехода за
30 секунд. Найдите длину поезда. Ответ дайте в метрах. [5]
3.
Поезд проходит мимо неподвижного наблюдателя за 7 секунд, а мимо
платформы длиной 378 метров – за 25 секунд. Найдите длину поезда в метрах. [1]
4. По
двум параллельным железнодорожным путям друг навстречу другу следуют
пассажирский и товарный поезда, скорости которых равны соответственно 70 км/ч и
30 км/ч. Длина товарного поезда равна 1400 метрам. Найдите длину пассажирского
поезда, если время, за которое он прошел мимо товарного поезда, равно 3
минутам.
Ответ дайте в метрах. [5]
5. По
двум параллельным железнодорожным путям друг навстречу другу следуют скорый и
пассажирский поезда, скорости которых равны соответственно 70 км/ч и 50 км/ч.
Длина пассажирского поезда равна 600 метрам. Найдите длину скорого поезда, если
время, за которое он прошел мимо пассажирского поезда, равно 30 секундам. Ответ
дайте в метрах. [6]
6. Пассажирский поезд едет со скоростью 60 км/ч, навстречу ему по
параллельной колее едет товарный состав. Человек в купе пассажирского поезда
засек время, за которое товарный состав прошел мимо него. Найдите длину
товарного состава, если это время равно 20 секунд, а скорость товарного
состава равна 30 км/ч. Ответ дайте в метрах. [6]
7. По
морю параллельными курсами в одном направлении следуют две баржи: первая
длиной 60 метров, вторая — длиной 40 метров. Сначала вторая баржа
отстает от первой, и в некоторый момент времени расстояние от кормы первой
баржи до носа второй составляет 200 метров. Через 18 минут после этого уже
первая баржа отстает от второй так, что расстояние от кормы второй баржи до
носа первой равно 300 метрам. На сколько километров в час скорость первой баржи
меньше скорости второй? [6]
8. По
морю параллельными курсами в одном направлении следуют две баржи: первая
длиной 70 метров, вторая — длиной 30 метров. Сначала вторая баржа
отстает от первой, и в некоторый момент времени расстояние от кормы первой
баржи до носа второй составляет 250 метров. Через 14 минут после этого уже
первая баржа отстает от второй так, что расстояние от кормы второй баржи до
носа первой равно 350 метрам. На сколько километров в час скорость первой баржи
меньше скорости второй? [6]
9. По
морю параллельными курсами в одном направлении следуют два сухогруза: первый
длиной 110 метров, второй — длиной 70 метров. Сначала второй сухогруз
отстает от первого, и в некоторый момент времени расстояние от кормы первого
сухогруза до носа второго составляет 200 метров. Через 8 минут после этого уже
первый сухогруз отстает от второго так, что расстояние от кормы второго
сухогруза до носа первого равно 500 метрам. На сколько километров в час
скорость первого сухогруза меньше скорости второго? [6]
10. Мальчик сбежал вниз по движущемуся эскалатору и насчитал 30
ступенек. Затем он пробежал вверх по тому же эскалатору с той же скоростью
относительно эскалатора и насчитал 150 ступенек. Сколько ступенек он насчитал
бы, спустившись по неподвижному эскалатору? [1]
11. Два человека одновременно стали спускаться, считая ступеньки по
движущемуся вниз эскалатору метро, причем один шаг вдвое быстрее другого. Один
из них отсчитал по окончании движения 60 ступенек, а второй — 40. Сколько
ступенек пришлось бы отсчитать при движении по неподвижному эскалатору? [2]
12. Лида спустилась вниз по движущемуся вниз эскалатору за 24 секунды.
По неподвижному эскалатору с той же скоростью относительно него она спустилась
за 42 секунды. За сколько секунд она спустится, стоя на ступеньках движущегося
эскалатора? [6]
13. Таня спустилась вниз по движущемуся вниз эскалатору за 28 секунд.
По неподвижному эскалатору с той же скоростью относительно него она спустилась
за 44 секунды. За сколько секунд она спустится, стоя на ступеньках движущегося
эскалатора? [6]
14. Ваня сбежал вниз по движущемуся эскалатору и насчитал 40 ступенек.
Затем он пробежал вверх по тому же эскалатору с той же скоростью относительно
эскалатора и насчитал 60 ступенек. Сколько ступенек он насчитал бы, спустившись
по неподвижному эскалатору? [6]
Ответы
к задачам для самостоятельного решения:
1. 500м,
2. 400м , 3. 147 м, 4. 600м, 5. 400м, 6.
500м, 7. 2км/ч, 8. 3км/ч,
9.
6,6 км/ч , 10. 50 , 11. 120 , 12. 56 , 13. 77,
14. 48 .
Всего: 101 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Два человека отправляются из одного дома на прогулку до опушки леса, находящейся в 4,4 км от дома. Один идёт со скоростью 2,5 км/ч, а другой — со скоростью 3 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от дома произойдёт их встреча? Ответ дайте в километрах.
Иван и Алексей договорились встретиться в Н-ске. Они едут к Н-ску разными дорогами. Иван звонит Алексею и узнаёт, что тот находится в 168 км от Н-ска и едет с постоянной скоростью 72 км/ч. Иван в момент звонка находится в 165 км от Н-ска и ещё должен по дороге сделать 30-минутную остановку. С какой скоростью должен ехать Иван, чтобы прибыть в Н-ск одновременно с Алексеем?
Из городов A и B навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 3 часа раньше, чем велосипедист приехал в A, а встретились они через 48 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
Из городов A и B навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 4 часа раньше, чем велосипедист приехал в A, а встретились они через 50 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
Из городов A и B навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 2 часа раньше, чем велосипедист приехал в A, а встретились они через 1 час 20 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
Источник: Пробный ЕГЭ по математике, Санкт-Петербург, 04.03.2018. Вариант 1.
Из городов A и B навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 12 часов раньше, чем велосипедист приехал в A, а встретились они через 2 часа 30 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
Источник: Пробный ЕГЭ по математике, Санкт-Петербург, 04.03.2018. Вариант 2.
Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 8 км. Путь из А в В занял у туриста 2 часа 45 минут, из которых 1 час 15 минут ушёл на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 2 км/ч. Ответ дайте в км/ч.
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути — со скоростью 78 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 48 км/ч. Ответ дайте в км/ч.
Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч?
Расстояние между городами A и B равно 150 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в Найдите расстояние от A до
Ответ дайте в километрах.
Из двух городов, расстояние между которыми равно 480 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 75 км/ч и 85 км/ч?
Из двух городов, расстояние между которыми равно 320 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 75 км/ч и 85 км/ч?
Автомобиль выехал с постоянной скоростью 75 км/ч из города А в город В, расстояние между которыми равно 275 км. Одновременно с ним из города С в город В, расстояние между которыми равно 255 км, с постоянной скоростью выехал мотоциклист. По дороге он сделал остановку на 50 минут. В результате автомобиль и мотоцикл прибыли в город В одновременно. Найдите скорость мотоциклиста. Ответ дайте в км/ч.
Расстояние между городами A и B равно 403 км. Из города A в город B выехал автомобиль, а через 1 час следом за ним со скоростью 90 км/ч выехал мотоцикл, догнал автомобиль в городе C и повернул обратно. Когда мотоцикл вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
Расстояние между городами A и B равно 798 км. Из города A в город B выехал автомобиль, а через 3 часа следом за ним со скоростью 120 км/ч выехал мотоцикл, догнал автомобиль в городе C и повернул обратно. Когда мотоцикл вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
Автомобиль выехал с постоянной скоростью 90 км/ч из города А в город В, расстояние между которыми равно 270 км. Одновременно с ним из города С в город В, расстояние между которыми равно 162 км, с постоянной скоростью выехал мотоциклист. По дороге он сделал остановку на 45 минут. В результате автомобиль и мотоцикл прибыли в город В одновременно. Найдите скорость мотоциклиста. Ответ дайте в км/ч.
Автомобиль выехал с постоянной скоростью 72 км/ч из города А в город В, расстояние между которыми равно 360 км. Одновременно с ним из города С в город В, расстояние между которыми равно 270 км, с постоянной скоростью выехал мотоциклист. По дороге он сделал остановку на 30 минут. В результате автомобиль и мотоцикл прибыли в город В одновременно. Найдите скорость мотоциклиста. Ответ дайте в км/ч.
Из двух городов, расстояние между которыми равно 250 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 50 км/ч и 75 км/ч?
Из двух городов, расстояние между которыми равно 390 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 50 км/ч и 80 км/ч?
Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени — со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Всего: 101 1–20 | 21–40 | 41–60 | 61–80 …
Задачи на движение протяженных тел
Протяженными будем считать тела, длина которых соизмерима с расстоянием, которое они проезжают.
В задачах на движение протяженных тел обычно требуется определить длину одного из них. Наиболее типичные ситуации, предлагаемые в таких задачах, — определить длину поезда проезжающего мимо:
-
придорожного столба;
-
идущего параллельно путям пешехода;
-
лесополосы определенной длины;
-
другого двигающегося поезда.
Помним, что во всех задачах на движение используется только одна формула: это формула пути
Если поезд движется мимо столба, то он проходит расстояние равное его длине. Обозначим:
l – длина поезда,
v – скорость поезда,
Если поезд движется мимо протяженной лесополосы (платформы), то он проходит расстояние равное сумме длины самого поезда и лесополосы. Обозначим:
l1 – длина поезда,
l2 – длина лесополосы (платформы),
v – скорость поезда,
Если поезд движется мимо движущегося человека, то учитываем направление движения человека. Если он движется навстречу, то скорости складываются, если в одну сторону, то находим разность скоростей. Обозначим:
l – длина поезда,
v1 – скорость поезда,
v2 – скорость человека,
В одну сторону:
В разные стороны:
Если поезд движется мимо движущегося поезда, то учитываем направление движения второго поезда. Если он движется навстречу, то скорости складываются, если в одну сторону, то находим разность скоростей. Обозначим:
l1 – длина первого поезда,
l2 – длина второго поезда,
v1 – скорость первого поезда,
v2 – скорость второго поезда,
В одну сторону:
В разные стороны:
Рассмотрим несколько задач.
Задача 1. Поезд, двигаясь равномерно со скоростью 60км/ч, проезжает мимо придорожного столба за 30 секунд. Найти длину поезда в метрах.
Решение:
v = 60 км/ч = 1000 м/мин, t = 30 сек. = 1/2 мин. Длину поезда находим как пройденное расстояние:
Ответ: 500 метров.
Задача 2. Поезд, двигаясь равномерно со скоростью 90 км/ч, проезжает мимо лесополосы, длина которой равна 800 метрам, за 1 минуту. Найти длину поезда в метрах.
Решение:
v = 90 км/ч = 1500 м/мин, t = 1 мин. Тогда пройденное поездом расстояние:
Это собственная длина поезда плюс длина лесополосы. Длина поезда равна: 1500 – 800 = 700 (м).
Ответ: 700 метров.
Задача 3. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.
Решение: Так как поезда двигаются в одном направлении, их относительная скорость равна:
v = 90 – 30 = 60 км/ч =
За 60 секунд один поезд проходит мимо другого, то есть преодолевает расстояние:
Это длина пассажирского и товарного поездов. Тогда длина пассажирского поезда равна:
1000 – 600 = 400 (м).
Ответ: 400 метров.
Задача 4. По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошёл мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
Решение: Так как поезда двигаются в противоположных направлениях, их относительная скорость равна:
v = 65 + 35 = 100 км/ч =
За 36 секунд один поезд проходит мимо другого, то есть преодолевает расстояние:
Это расстояние, равное сумме длин обоих поездов. Значит, длина скорого поезда равна:
1000 – 700 = 300 (м).
Ответ: 300 метров.
Задача 5. Поезд проходит мимо неподвижного наблюдателя за 7 секунд, а мимо платформы длиной 378 метров – за 25 секунд. Найдите длину поезда.
Решение: Из первого условия следует, что за 7 секунд поезд проедет расстояние, равное собственной длине поезда. За 25 же секунд ему надо проехать собственно саму длину платформы, т.е. 378 метров и ещё надо «вытащить» головной вагон вперед на расстояние, равное длине поезда.
1) 25 – 7 = 18 (с) – время, за которое поезд проехал 378 м
2) 378 : 18 = 21 (м/с) – скорость поезда
3) 21
Ответ: 144 м.
Задача 6. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и скорый поезда. Скорый поезд, двигаясь со скоростью 120 км/ч, догнал пассажирский поезд и прошёл мимо него за 100 секунд. Найдите скорость пассажирского поезда, если его длина составляет 800 метров, а длина скорого поезда – 700 метров. Ответ дайте в км/ч.
Решение: Считаем, что пассажирский поезд неподвижен, а скорый приближается к нему со скоростью, равной разности скоростей поездов.
1) 700 + 800 = 1500 (м) – прошёл скорый поезд за 100 секунд
2) 1500 : 100 = 15 (м/с) – разность скоростей (скорость вдогонку)
15 м/с =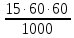
3) 120 – 54 = 66 (км/ч) – скорость пассажирского поезда.
Ответ: 66 км/ч.
Задача 7. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 110 метров, второй — длиной 90 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 1000 метров. Через 16 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 400 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Решение: Пока сухогрузы перейдут из первого положения во второе, второй сухогруз переместился относительно первого на
1000 + 110 + 90 + 400 = 1600 (м).
Пусть v — разность скоростей сухогрузов, тогда
v = 1600 : 16 = 100 м/мин = 6 км/ч.
Ответ: на 6 км/ч.
10 сентября 2021
В закладки
Обсудить
Жалоба
Задачи на движение протяжённых объектов
Текстовая задача ЕГЭ по математике (№8). По материалам открытого банка ФИПИ.
1. Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах.
2. Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.
3. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
4. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.
5. По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошёл мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
Ответы
1. 800
2. 600
3. 6
4. 400
5. 300
На чтение 9 мин Просмотров 18.1к. Опубликовано 16 ноября, 2020
Задачи на движение начинают проходить в 5 классе и решают все оставшиеся учебные годы вплоть до 11 класса. В ЕГЭ по математике вы найдете задачи на движение в задании 11, в котором собраны все текстовые задачи. Рассмотрим как надо решать задачи на движение из ЕГЭ. Но сначала немного теории.
Содержание
- Как решать задачи на движение
- Примеры решения
- Виды задач на движение
- Движение навстречу друг другу, движение в противоположных направлениях
- Движение друг за другом (вдогонку)
- Задачи на движение по кругу
- Задачи на движение мимо объекта
- Задачи на движение по течению и против течения
- Задачи на движение из ЕГЭ по математике (профильный уровень)
- Задача 1.
- Задача 2.
- Задача 3
- Задача 4
- Задача 5
Как решать задачи на движение
Решение задач на движение подчиняется четкому алгоритму, который состоит из нескольких этапов:
- Анализ данных.
- Составление таблицы.
- Составление уравнения.
- Решение уравнения.
Остановимся подробно на каждом пункте:
1. Первое, с чего нужно начать — медленно и вдумчиво прочитать условие задачи, то есть проанализировать данные.
Чтобы наглядно представить задачу, необходимо сделать рисунок и отобразить на нем все известные по условию задачи величины.
2. Второй шаг — составить таблицу по условию задачи, внести в таблицу известные величины и ввести неизвестные.
Таблица состоит из трех столбцов S, v и t (путь, скорость и время) и нескольких строк. При заполнении каждой строки сначала выбираем и заполняем тот столбец, информация о котором дана в задаче. Еще один столбец записываем в роли неизвестного (чаще всего, это то, что требуется найти в задаче). В третью, оставшуюся колонку вписываем связь характеристик из двух уже заполненных столбцов по формуле:
S = v · t.
В таблице получается столько строчек, сколько каждый из объектов задачи действовал (то есть, перемещался) или мог бы действовать.
3. Следующий шаг — при помощи сделанного рисунка и заполненной таблицы составить уравнение или систему уравнений.
По окончании заполнения таблицы оказывается, что есть часть информации, которая не вошла в таблицу. Эта информация характеризует те значения величин в колонках, которые вычисляются в третью очередь, то есть по формуле. На основании этой информации и данных из третьей колонки составляем уравнение.
4. Решить полученное уравнение и прийти к ответу.
Когда уравнение составлено, последний шаг — это решить его, и, в конце концов, получить ответ.
Будьте внимательны, если за неизвестное вы приняли не то, что требуется найти в задаче. В этом случае следует выразить то, что нужно найти через полученное решение уравнения.
Если, решив уравнение, вы получили несколько ответов, то следует отобрать только имеющие смысл решения. Помните, что путь, скорость и время не могут быть отрицательными.
Примеры решения
Пример:
Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
Решение:
В задаче требуется найти скорость второго, более медленного, велосипедиста. Примем его скорость за x. Заполним таблицу:
| v, км/ч | t, ч | S, км | |
| Первый велосипедист | x + 10 | 60 | |
| Второй велосипедист | x | 60 |
В условии задачи сказано, что первый велосипедист прибыл к финишу на 3 часа раньше второго. На основании этого составим уравнение:
3x2 + 90x = 600 + 60x;
x2 + 10x – 200 = 0.
Получаем два корня, x1 = 10 и x2 = –20. Второй корень не подходит, так как скорость не может быть отрицательной.
Ответ: 10 км/ч.
Виды задач на движение
Движение навстречу друг другу, движение в противоположных направлениях
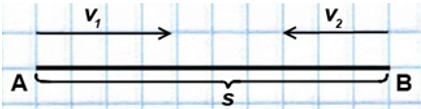
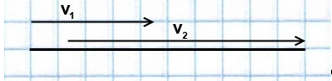
Если два объекта движутся навстречу друг другу, то они сближаются:
При движении в противоположном направлении объекты удаляются:
В обоих случаях объекты как бы «помогают» друг другу преодолеть общее для них расстояние, «действуют сообща». Поэтому чтобы найти их совместную скорость (это и будет скорость сближения или удаления), нужно складывать скорости объектов:
v = v1 + v2.
Движение друг за другом (вдогонку)
При движении в одном направлении объекты также могут как сближаться, так и удаляться. В этом случае они как бы «соревнуются» в преодолении общего расстояния, «действуют друг против друга». Поэтому их совместная скорость будет равна разности скоростей.
Если скорость идущего впереди объекта меньше скорости объекта, следующего за ним, то они сближаются. Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:
Если объект, идущий впереди, движется с большей скоростью, чем идущий следом за ним, то они удаляются. Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:
Таким образом:
При движении навстречу друг другу и движении в противоположных направлениях скорости складываем.
При движении в одном направлении скорости вычитаем.
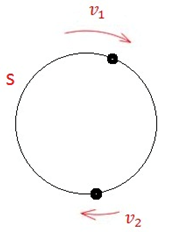
Задачи на движение по кругу
При движении по кругу объекты могут:
При этом пройденные расстояния измеряются длиной круговой трассы, равной S.
- Если два объекта начинают движение по кругу из одной и той же точки, то в момент первой встречи более быстрый объект пройдет расстояние на один круг больше.
- Если два объекта начинают движение по кругу из разных точек, расстояние между которыми равно S0, то в момент первой встречи догоняющий объект пройдет на S0 км большее расстояние, чем догоняемый.
- Если через определенное время t первый объект опережает второй на m кругов, то разница пройденных объектами расстояний будет равна m · S: S1 – S2 = m · S.
Задачи на движение мимо объекта
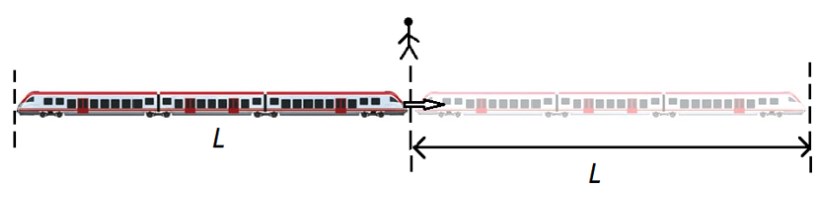
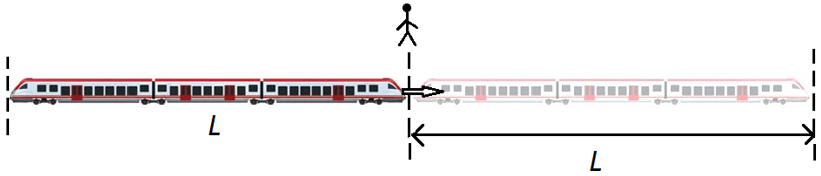
В задачах на движение мимо объекта обязательно присутствуют протяженные тела — поезда, туннели, корабли и т. п. Зачастую движущимся объектом является поезд.
Если поезд длиной L движется мимо точечного объекта (столба, светофора, человека), то он проходит расстояние, равное его длине L:
S = L = v0 · t.
При этом, если точечный объект (пешеход, велосипедист) тоже движется, то совместная скорость равна сумме скоростей, если поезд и объект двигаются в разных направлениях (как в пункте 1), и равна разности скоростей, если они двигаются в одном направлении (как в пункте 2).
Если поезд длиной L1 движется мимо протяженного объекта (туннеля, лесополосы) длиной L2, то он проходит расстояние, равное сумме длин самого поезда и протяженного объекта:
S = L1 + L2 = v0 · t.
При этом, если протяженный объект (например, другой поезд) тоже движется, то совместная скорость равна сумме скоростей, если оба объекта двигаются в разных направлениях, и равна разности скоростей (из большей вычитается меньшая), если они двигаются в одном направлении.
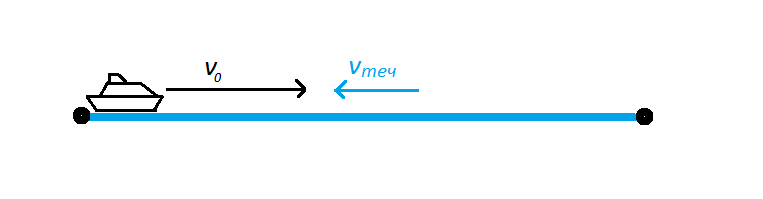
Задачи на движение по течению и против течения
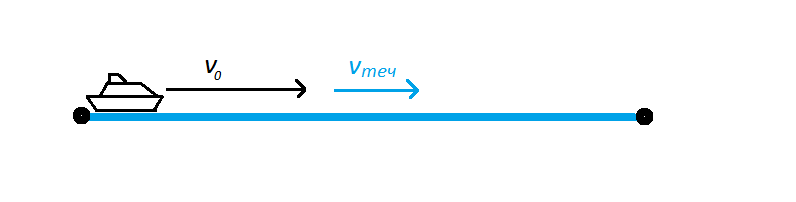
В задачах на движение помимо собственной скорости плывущего тела нужно учитывать скорость течения.
При движении по течению скорость течения прибавляется к скорости плывущего тела: v = v0 + vтеч.
При движении против течения скорость течения отнимается от скорости плывущего тела: v = v0 – vтеч.
Задачи на движение из ЕГЭ по математике (профильный уровень)
Задача 1.
Из одной точки круговой трассы, длина которой равна 44 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 112 км/ч, и через 48 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение: Пусть скорость второго автомобиля равна v км/ч. За 4/5 часа первый автомобиль прошел на 44 км больше, чем второй, отсюда имеем:
112 ∙ = v ∙
= v ∙
+ 44 ⇔ 4 ∙ v = 112 ∙ 4 – 44 ∙ 5 ⇔ v = 57.
Следовательно, скорость второго автомобиля была равна 57 км/ч.
Ответ: 57 км/ч.
Задача 2.
Из пункта A круговой трассы выехал велосипедист, а через 10 минут следом за ним отправился мотоциклист. Через 2 минуты после отправления он догнал велосипедиста в первый раз, а еще через 3 минуты после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 5 км. Ответ дайте в км/ч.
Решение:
До первой встречи велосипедист провел на трассе 1/5 часа, а мотоциклист 1/30 часа. Пусть скорость мотоциклиста равна v км/ч, тогда скорость велосипедиста равна
Тогда если скорость велосипедиста – это 1 единица отношения, то скорость мотоциклиста – это 6 единиц отношения.
Так как они едут в одном направлении, их общая скорость 5 единиц отношения.
∙5 ед.отн. = 5
1 ед.отн. = 20
6 ед.отн. = 120
Таким образом, скорость мотоциклиста была равна 120 км/ч.
Ответ: 120 км/ч.
Задача 3
Часы со стрелками показывают 3 часа ровно. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?
Решение: Скорость движения минутной стрелки 12 делений/час (под одним делением здесь подразумевается расстояние между соседними цифрами на циферблате часов), а часовой ― 1 деление/час. До девятой встречи минутной и часовой стрелок минутная должна сначала 8 раз «обогнать» часовую, то есть пройти 8 кругов по 12 делений. Пусть после этого до четвертой встречи часовая стрелка пройдет L делений. Тогда общий путь минутной стрелки складывается из найденных 96 делений, ещё 3 изначально разделяющих их делений (поскольку часы показывают 3 часа) и последних L делений. Приравняем время движения для часовой и минутной стрелок:
, отсюда
, отсюда
и
.
Ответ: через 9 минут.
Задача 4
Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение:
Данную задачу можно интерпретировать (представить её, как задачу на линейное движение): Два автомобиля одновременно начинают движение в одном направлении. Скорость первого равна 80 км/ч. Через 40 минут он опережает второго на 14 км (т. к. сказано, что на один круг). Найти скорость второго. Очень важно в заданиях на движение представить сам процесс этого движения.
Сравнение так же производим по расстоянию.
За x принимаем искомую величину ― скорость второго. Время движения 40 минут (2/3 часа) для обоих. Заполним графу «расстояние»:
| v | t | S | |
| 1 | 80 | 2/3 | |
| 2 | x | 2/3 |
Расстояние, пройденное первым, больше расстояния, который прошёл второй на 14 км.
80 ∙ больше, чем x ∙
больше, чем x ∙
на 14.
80 ∙ = x ∙
= x ∙
+ 14;
–
–
= x ∙
;
160 – 42 = х ∙ 2;
х = 59.
Скорость второго автомобиля 59 (км/ч).
Ответ: 59 км/ч.
Задача 5
Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 6 часов позже автомобилиста. Ответ дайте в км/ч.
Решение:
Пусть v км/ч – скорость велосипедиста, тогда скорость автомобилиста равна v + 40 км/ч. Велосипедист был в пути на 6 часов больше, отсюда имеем:
Таким образом, скорость велосипедиста была равна 10 км/ч.
Ответ: 10 км/ч.
В задачах на движение по прямой часто надо отыскать среднюю скорость транспортного средства.
Средняя скорость – это величина, равная отношению пути, пройденного телом, ко времени, за которое пройден этот путь.
$v_{ср}={S_{общий}}/{t_{общее}}$
Пример:
Первые $140$ км автомобиль ехал со скоростью $70$ км/ч, следующие $220$ км — со скоростью $80$ км/ч, а затем $30$ км — со скоростью $120$ км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение:
Для простоты решения задачи сделаем таблицу.
| $S_1=140км$ | $S_2=220км$ | $S_3=30км$ |
| $v_1=70$км/ч | $v_2=80$км/ч | $v_3=120$км/ч |
| $t_1-?$ | $t_2-?$ | $t_3-?$ |
Получилось три участка пути, про каждый участок мы знаем его путь и скорость, но для расчета средней скорости необходимо знать путь и время каждого участка. Найдем время каждого участка пути, для этого разделим путь на скорость.
$t_1={S_1}/{v_1}={140}/{70}=2$ часа
$t_2={S_2}/{v_2}={220}/{80}=2.75$ часа
$t_3={S_3}/{v_3}={30}/{120}=0.25$ часа
$v_{ср}={S_1+S_2+S_3}/{t_1+t_2+t_3}={140+220+30}/{2+2.75+0.25}={390}/{5}=78$ км/ч
Ответ: $78$ км/ч
Иногда встречаются такие задачи на движение, в которых учитываются размеры транспортного средства. Чаще всего в таких задачах необходимо рассчитать длину поезда, например.
Поезд, двигаясь равномерно со скоростью $60$ км/ч, проезжает мимо платформы, длина которой равна $200$ метрам, за $3$ минуты. Найдите длину поезда в метрах.
Решение:
Считается, что поезд проедет полностью мимо платформы, если он проедет длину платформы и еще свою длину.
Найдем расстояние, которое поезд проедет за три минуты. Время переведем в секунды и умножим на скорость поезда, которую переведем из км/ч в м/с.
$3$ минуты $=3·60=180$ секунд
$60$ км/ч$={60}/{3.6}={600}/{36}={50}/{3}$ м/с
$S=v·t={50·180}/{3}=3000$ метров
Чтобы найти длину поезда из всего пройденного пути за $3$ минуты вычтем длину платформы:
$l=3000-200=2800$ метров.
Ответ: $2800$
Пример:
Два велосипедиста одновременно отправились в пробег протяжённостью $84$ километра. Первый ехал со скоростью, на $5$ км/ч большей скорости второго, и прибыл к финишу на $5$ часов раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
Решение:
Пусть $х$ км/ч –скорость второго велосипедиста, тогда $(х+5)$ км/ч – скорость первого велосипедиста.
Создаем стандартную таблицу и столбец $«v»$ заполняем данными с неизвестными.
| $S$(км) | $v$(км) | $t$(ч) | |
| Первый велосипедист | $(x+5)$ | ||
| Второй велосипедист | $x$ |
Так как расстояние, которое проехали велосипедисты одинаково и равно $84$ км, заполняем столбец $«S»$.
| $S$(км) | $v$(км) | $t$(ч) | |
| Первый велосипедист | $84$ | $(x+5)$ | |
| Второй велосипедист | $84$ | $x$ |
Третий столбец заполняем по формуле $t={S}/{v}$.
| $S$(км) | $v$(км) | $t$(ч) | |
| Первый велосипедист | $84$ | $(x+5)$ | ${84}/{(x+5)}$ |
| Второй велосипедист | $84$ | $x$ | ${84}/{x}$ |
Именно содержимое третьего столбца будем использовать для составления уравнения к задаче. По условию задачи разница между временами движения велосипедистов равна $5$ часов. Дольше в пути находился второй велосипедист, следовательно, из большего времени отнимаем меньшее время и все это равно разнице времен.
${84}/{х}-{84}/{(х+5)}=5$
Перенесем все слагаемые в левую сторону уравнения
${84}/{х}-{84}/{(х+5)}-5=0$
Приведем все слагаемые к общему знаменателю $х(х+5)$, тогда к первой дроби дополнительный множитель равен $(х+5)$, ко второй $х$, а к третьему слагаемому $(х^2+5х)$.Получаем:
${84х+420-84х-5х^2-25х}/{х(х+5)}=0$
Далее проговариваем: дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.
$84х+420-84х-5х^2-25х=0; х(х+5)≠0$
Найдем сначала корни знаменателя (ОДЗ дроби)
$х(х+5)≠0$
$х≠0$ или $х+5≠0$
$х≠0$ или $х≠-5$
Найдем корни числителя.
$84х+420-84х-5х^2-25х=0;$
Приведем подобные слагаемые и расставим поставим их в порядке убывания степеней
$-5х^2-25х+420=0$
Разделим уравнение на $(-5)$
$х^2+5х-84=0$
По теореме Виета
$х_1=-12, х_2=7$
$х_1=-12$ нам не подходит, так как отрицательная величина.
$х_2=7$ км/ч – скорость велосипедиста.
Ответ: $7$
Некоторые нюансы в задачах с круговым движением:
- В задачах на движение по окружности желательно делать рисунок, чтобы расставить величины и увидеть взаимосвязь между транспортными средствами.
- Если транспортные средства начали двигаться из одной точки в диаметрально противоположных направлениях, то между ними расстояние равное половине длины окружности.
- Если в задаче сказано, что транспортные средства двигаются в одном направлении, то необходимо узнать их скорость опережения: для этого из большей скорости вычитается меньшая.
- Любую задачу на круговое движение можно представить как задачу на прямолинейном отрезке, мысленно развернув круговую трассу в прямую.
Пример:
Из одной точки круговой трассы, длина которой равна $18$ км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна $92$ км/ч, и через $45$ минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение:
Сделаем рисунок к задаче, для этого мысленно развернем круговую трассу в прямую.
$S=18$ км
$t=45$мин$={3}/{4}$часа
Пусть $х$ км/ч — скорость второго автомобиля.
Скорость опережения равна разности скоростей.
Тогда скорость опережения равна $v_{опережения}=(92-х)$. Так как первый автомобиль обгонит второй на один круг за $45$ минут, то скорость опережения можно выразить еще одним способом: для этого длину круга надо разделить на время опережения.
Не забываем перевести время из минут в часы $45$минут$={45}/{60}={3}/{4}$часа
$v_{опережения}={S}/{t}={18}/{{3}/{4}}={18·4}/{3}=24$
Так как мы разными записями выразили скорость опережения, то для составления уравнения приравняем обе записи друг к другу.
$92-х=24$
$-х=24-92$
$х=68$ км/ч – скорость второго автомобиля.
Ответ: $68$
Скорость по течению реки равна сумме собственной скорости транспортного средства и скорости течения реки
$v=v_{собственная}+v_{течения реки}$
Чтобы найти скорость против течения, нужно отнять от собственной скорости транспортного средства скорость течения реки
$v=v_{собственная}-v_{течения реки}$
Пример:
Катер прошел против течения реки $120$ км и вернулся обратно, затратив на обратный путь на $4$ часа меньше времени. Найдите скорость катера в стоячей воде, если скорость течения реки $4$ км/ч. Ответ дайте в км/ч.
Решение:
Для начала необходимо за «х» взять неизвестную. В нашем случае(и чаще всего) за «х» берется скорость.
Пусть $х$ км/ч – собственная скорость катера, тогда $(х+4)$ км/ч – скорость катера по течению; $(х-4)$ км/ч – скорость катера против течения.
Создаем стандартную таблицу и столбец $«v»$ заполняем данными с неизвестными.
| $S$(км) | $v$(км/ч) | $t$(ч) | |
| По течению | $(x+4)$ | ||
| Против течения | $(x-4)$ |
Так как расстояние, которое катер проплыл по течению и против течения одинаково и равно $120$ км, заполняем столбец $«S»$
| $S$(км) | $v$(км/ч) | $t$(ч) | |
| По течению | $120$ | $(x+4)$ | |
| Против течения | $120$ | $(x-4)$ |
Третий столбец заполняем по формуле $t={S}/{v}$
| $S$(км) | $v$(км/ч) | $t$(ч) | |
| По течению | $120$ | $(x+4)$ | ${120}/{(х+4)}$ |
| Против течения | $120$ | $(x-4)$ | ${120}/{(х-4)}$ |
Именно содержимое третьего столбца будем использовать для составления уравнения к задаче. По условию задачи разница между временами движения против течения и по течению равна $4$ часа, следовательно, из большего времени отнимаем меньшее время и все это равно разнице времен.
${120}/{(х-4)}-{120}/{(х+4)}=4$
Решим полученное дробно рациональное уравнение, для этого перенесем все слагаемые в левую часть.
${120}/{(х-4)}-{120}/{(х+4)}-4=0$
Приведем дроби к общему знаменателю $(х-4)(х+4)$, тогда к первой дроби дополнительный множитель равен $(х+4)$, ко второй $(х-4)$, а к третьему слагаемому $(х+4)(х-4)$. Получаем:
${120(х+4)-120(х-4)-4(х-4)(х+4)}/{(х-4)(х+4)}=0$
Далее проговариваем: дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.
$120(х+4)-120(х-4)-4(х-4)(х+4)=0; (х-4)(х+4)≠0$
Найдем сначала корни знаменателя (ОДЗ дроби)
$(х-4)(х+4)≠0$
$х-4≠0$ или $х+4≠0$
$х≠4$ или $х≠-4$
Найдем корни числителя.
$120(х+4)-120(х-4)-4(х-4)(х+4)=0$
Для этого раскроем скобки и приведем подобные слагаемые.
$120х+480-120х+480-4х^2+64=0$
$-4х^2+1024=0$
$-4х^2=-1024$
Разделим обе части уравнения на $(-4)$
$х^2=256$
$х_{1,2}=±16$
Так как за «х» мы брали собственную скорость катера, а она отрицательной быть не может, следовательно, нам подходит только корень $х=16$ км/ч
Ответ: $16$
Пример:
От пристани $А$ к пристани $В$, расстояние между которыми равно $70$ км, отправился с постоянной скоростью первый теплоход, а через $1$ час после этого следом за ним, со скоростью, на $8$ км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт $В$ оба теплохода прибыли одновременно.
Решение:
Пусть $х$ км/ч- это скорость первого теплохода, тогда $(х+8)$ км/ч –это скорость второго теплохода.
Составим таблицу, в которой заполним столбцы путь $«S»$ и скорость $«v»$ по условию задачи, а третий столбец время $«t»$ заполним по формуле $t={S}/{v}$
| $S$(км) | $v$(км/ч) | $t$(ч) | |
| Первый теплоход | $70$ | $x$ | ${70}/{х}$ |
| Второй теплоход | $70$ | $(x+8)$ | ${70}/{(х+8)}$ |
Так как второй теплоход выехал на час позже, то время его в пути на час меньше относительно времени первого теплохода. Составим и решим уравнение: из большего времени отнимаем меньшее время и все это равно разнице времен
${70}/{х}-{70}/{(х+8)}=1$
${70}/{х}-{70}/{(х+8)}-1=0$
Приводим дроби к общему знаменателю
${70(х+8)-70х-х(х+8)}/{х(х+8)}=0$
${70х+560-70х-х^2-8х}/{х(х+8)}=0$
Найдем сначала корни знаменателя(ОДЗ дроби)
$х(х+8)≠0$
$х≠0$ или $х+8≠0; х≠-8$
Найдем корни числителя
$70х+560-70х-х^2-8х=0$
$-х^2-8х+560=0$
$х^2+8х-560=0$
По т.Виета $х_1+х_2=-8$
$х_1∙х_2=-560$
$х_1=-28; х_2=20$, первый корень нам не подходит, так как он отрицательный, следовательно скорость первого теплохода равна $20$ км/ч.
Ответ: $20$
Решение текстовых задач на движение подчиняется четкому алгоритму, который состоит из нескольких этапов:
- Анализ данных.
- Составление таблицы.
- Составление уравнения.
- Решение уравнения.
Остановимся подробно на каждом пункте:
1. Первое, с чего нужно начать — медленно и вдумчиво прочитать условие задачи, то есть проанализировать данные.
Чтобы наглядно представить задачу, необходимо сделать рисунок и отобразить на нем все известные по условию задачи величины.
2. Второй шаг — составить таблицу по условию задачи, внести в таблицу известные величины и ввести неизвестные.
Таблица состоит из трех столбцов S, v и t (путь, скорость и время) и нескольких строк. При заполнении каждой строки сначала выбираем и заполняем тот столбец, информация о котором дана в задаче. Еще один столбец записываем в роли неизвестного (чаще всего, это то, что требуется найти в задаче). В третью, оставшуюся колонку вписываем связь характеристик из двух уже заполненных столбцов по формуле:
S = v · t.
В таблице получается столько строчек, сколько каждый из объектов задачи действовал (то есть, перемещался) или мог бы действовать.
3. Следующий шаг — при помощи сделанного рисунка и заполненной таблицы составить уравнение или систему уравнений.
По окончании заполнения таблицы оказывается, что есть часть информации, которая не вошла в таблицу. Эта информация характеризует те значения величин в колонках, которые вычисляются в третью очередь, то есть по формуле. На основании этой информации и данных из третьей колонки составляем уравнение.
4. Решить полученное уравнение и прийти к ответу.
Когда уравнение составлено, последний шаг — это решить его, и, в конце концов, получить ответ.
- Будьте внимательны, если за неизвестное вы приняли не то, что требуется найти в задаче. В этом случае следует выразить то, что нужно найти через полученное решение уравнения.
- Если, решив уравнение, вы получили несколько ответов, то следует отобрать только имеющие смысл решения. Помните, что путь, скорость и время не могут быть отрицательными.
Пример:
Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
Решение:
В задаче требуется найти скорость второго, более медленного, велосипедиста. Примем его скорость за x. Заполним таблицу:
| v, км/ч | t, ч | S, км | |
|---|---|---|---|
|
Первый велосипедист |
x + 10 |
$ frac{60}{x+10} $ |
60 |
|
Второй велосипедист |
x |
$ frac{60}{x} $ |
60 |
В условии задачи сказано, что первый велосипедист прибыл к финишу на 3 часа раньше второго. На основании этого составим уравнение:
$ frac{60}{x+10}+3=frac{60}{x} $
$ frac{60+3x+30}{x+10}=frac{60}{x} $
3x2 + 90x = 600 + 60x;
x2 + 10x – 200 = 0.
Получаем два корня, x1 = 10 и x2 = –20. Второй корень не подходит, так как скорость не может быть отрицательной.
Ответ: 10 км/ч.
Виды задач на движение:
1. Движение навстречу друг другу, движениев противоположных направлениях:
Если два объекта движутся навстречу друг другу, то они сближаются:
При объекты удаляются:
В обоих случаях объекты как бы «помогают» друг другу преодолеть общее для них расстояние, «действуют сообща». Поэтому чтобы найти их совместную скорость (это и будет скорость сближения или удаления), нужно складывать скорости объектов:
v = v1 + v2.
2. Движение друг за другом (вдогонку):
При движении в одном направлении объекты также могут как сближаться, так и удаляться. В этом случае они как бы «соревнуются» в преодолении общего расстояния, «действуют друг против друга». Поэтому их совместная скорость будет равна разности скоростей.
Если скорость идущего впереди объекта меньше скорости объекта, следующего за ним, то они сближаются. Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:
$ {upsilon_{c}=upsilon_{1}-upsilon_{2};\ upsilon_{1}>upsilon_{2}.} $
Если объект, идущий впереди, движется с большей скоростью, чем идущий следом за ним, то они удаляются. Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:
$ {upsilon_{y}=upsilon_{2}-upsilon_{1};\ upsilon_{2}>upsilon_{1}.} $
Таким образом:
- При движении навстречу друг другу и движении в противоположных направлениях скорости складываем.
- При движении в одном направлении скорости вычитаем.
3. Движение по кругу:
При движении по кругу объекты могут:
- сближаться, если скорость догоняющего больше скорости догоняемого. Скорость сближения будет равна $ upsilon_{c}=upsilon_{1}-upsilon_{2}; $
- отдаляться, если скорость догоняющего меньше скорости догоняемого. Скорость удаления будет равна $ upsilon_{y}=upsilon_{2}-upsilon_{1}. $
При этом пройденные расстояния измеряются длиной круговой трассы, равной S.
- Если два объекта начинают движение по кругу из одной и той же точки, то в момент первой встречи более быстрый объект пройдет расстояние на один круг больше.
- Если два объекта начинают движение по кругу из разных точек, расстояние между которыми равно S0, то в момент первой встречи догоняющий объект пройдет на S0км большее расстояние, чем догоняемый.
- Если через определенное время t первый объект опережает второй на m кругов, то разница пройденных объектами расстояний будет равна m · S:
S1 – S2 = m · S.
4. Движение мимо объекта:
В задачах на движение мимо объекта обязательно присутствуют протяженные тела — поезда, туннели, корабли и т. п. Зачастую движущимся объектом является поезд.
- Если поезд длиной L движется мимо точечного объекта (столба, светофора, человека), то он проходит расстояние, равное его длине L:
S = L = v0 · t.
При этом, если точечный объект (пешеход, велосипедист) тоже движется, то совместная скорость равна сумме скоростей, если поезд и объект двигаются в разных направлениях (как в пункте 1), и равна разности скоростей, если они двигаются в одном направлении (как в пункте 2).
- Если поезд длиной L1 движется мимо протяженного объекта (туннеля, лесополосы) длиной L2, то он проходит расстояние, равное сумме длин самого поезда и протяженного объекта:
S = L1 + L2 = v0 · t.
При этом, если протяженный объект (например, другой поезд) тоже движется, то совместная скорость равна сумме скоростей, если оба объекта двигаются в разных направлениях, и равна разности скоростей (из большей вычитается меньшая), если они двигаются в одном направлении.
5. Движение по воде:
В задачах на движение помимо собственной скорости плывущего тела нужно учитывать скорость течения.
- При движении по течению скорость течения прибавляется к скорости плывущего тела: v = v0 + vтеч.
- При движении против течения скорость течения отнимается от скорости плывущего тела: v = v0 – vтеч.
- Скорость плота считается равной скорости течения.