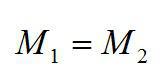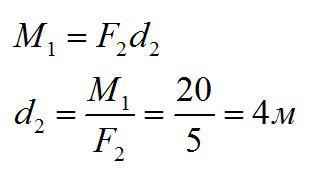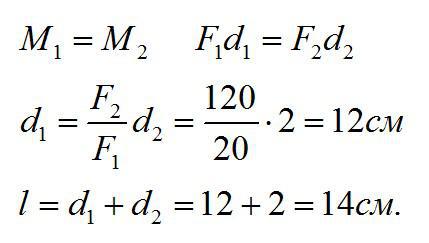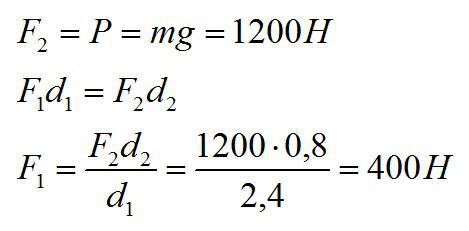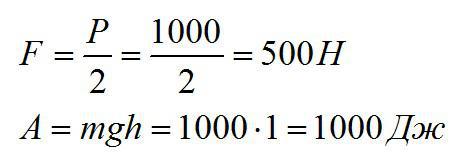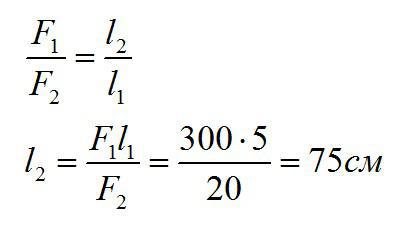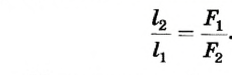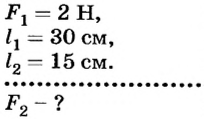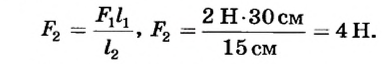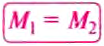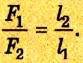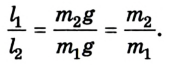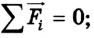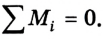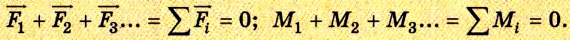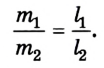Всего: 37 1–20 | 21–37
Добавить в вариант
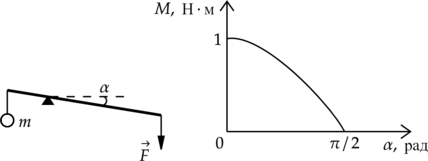
Из лёгкого жёсткого стержня сделан горизонтальный рычаг с длинами плеч 40 см и 200 см. К короткому концу рычага на нити подвешен груз массой m, а к длинному концу рычага для уравновешивания приложена некоторая сила. Человек начинает медленно опускать длинный конец рычага, прикладывая к нему вертикально вниз силу (см. рис.). На графике показана зависимость момента M силы тяжести груза m (относительно точки опоры рычага) от угла α между рычагом и горизонтом.
Из приведённого ниже списка выберите все правильные утверждения на основании анализа графика.
1) При повороте рычага плечо действующей на груз силы тяжести не изменяется.
2) Когда уравновешенный рычаг горизонтален, модуль приложенной к его длинному концу силы равен 0,5 Н.
3) Масса груза m равна 250 г.
4) При увеличении угла α момент силы относительно точки опоры рычага уменьшается.
5) Момент силы относительно точки опоры рычага всё время больше 1 Н·м.
Из лёгкого жёсткого стержня сделан горизонтальный рычаг с длинами плеч 50 см и 200 см. К короткому концу рычага на нити подвешен груз массой m, а к длинному концу рычага для уравновешивания приложена некоторая сила. Человек начинает медленно опускать длинный конец рычага, прикладывая к нему вертикально вниз силу (см. рис.). На графике показана зависимость момента M силы тяжести груза m (относительно точки опоры рычага) от угла α между рычагом и горизонтом.
Из приведённого ниже списка выберите все правильные утверждения на основании анализа графика.
1) При повороте рычага плечо действующей на груз силы тяжести не изменяется.
2) Когда уравновешенный рычаг горизонтален, модуль приложенной к его длинному концу силы равен 0,5 Н.
3) Масса груза m равна 250 г.
4) При увеличении угла α сила давления рычага на опору уменьшается.
5) Момент силы относительно точки опоры рычага всё время не превышает 1 Н·м.
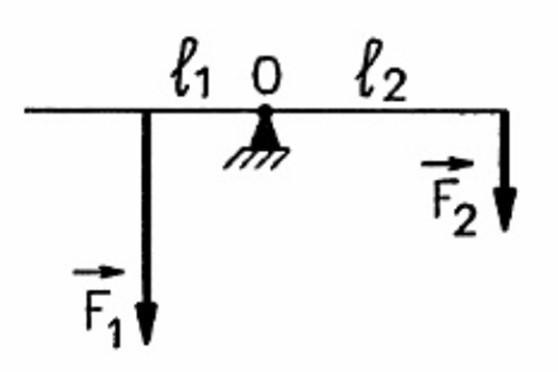
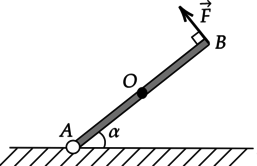
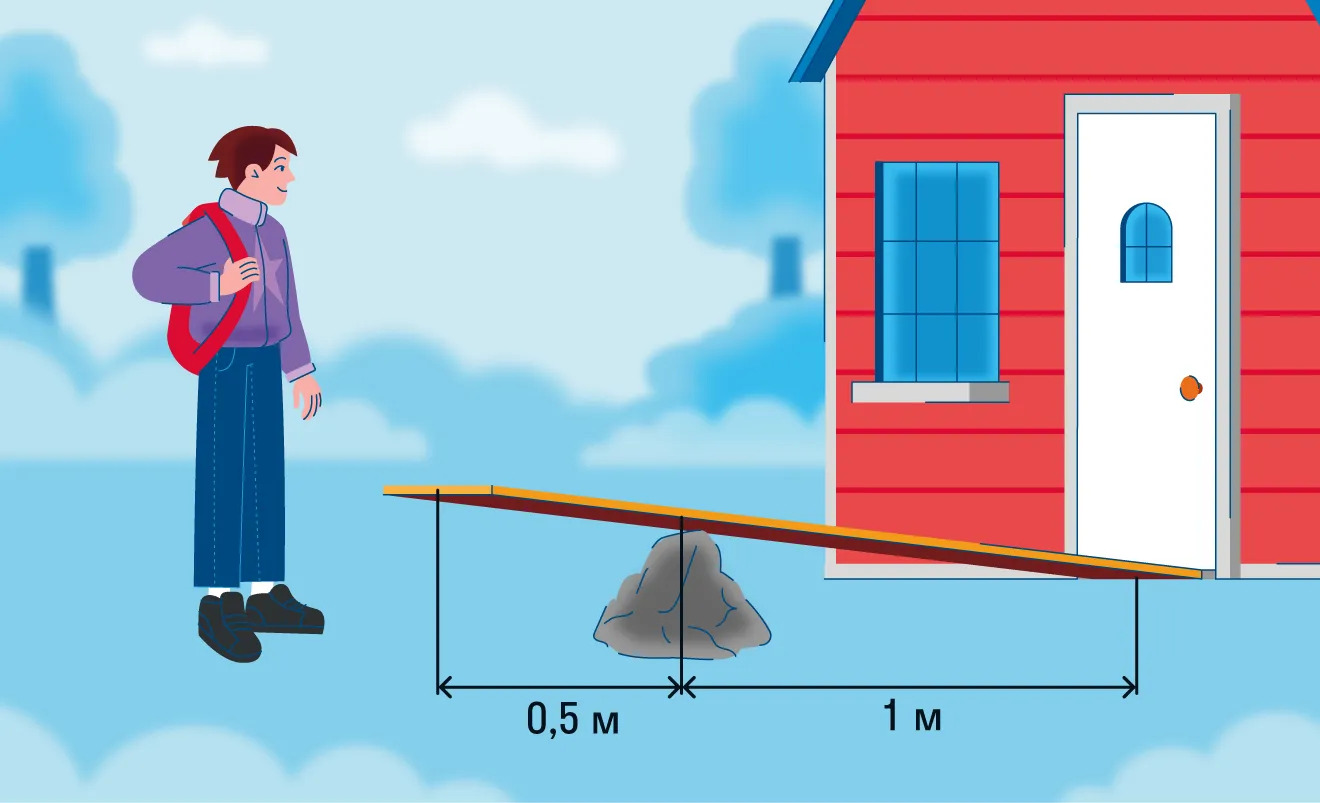
Под действием веса груза mg и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз? (Ответ дайте в ньютонах)
Под действием веса груза mg и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, а груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы F равен 240 Н, то каков модуль силы тяжести, действующей на груз? (Ответ дайте в ньютонах.)
Под действием веса груза, равного mg, и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы тяжести, действующей на груз, равен 1500 Н, то каков модуль силы F? (Ответ дайте в ньютонах.)
Под действием веса груза, равного mg, и силы F рычаг, представленный на рисунке, находится в равновесии. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы mg равен 30 Н, а груз на плоскость не давит, то каков модуль силы F, действующей на рычаг? (Ответ дайте в ньютонах.)
Источник: Демонстрационная версия ЕГЭ—2022 по физике
Под действием веса груза, равного mg, и силы F рычаг, представленный на рисунке, находится в равновесии. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы тяжести, действующей на груз, равен 1 500 Н, а груз на плоскость не давит, то каков модуль силы F? (Ответ дайте в ньютонах.)
Под действием веса груза, равного mg, и силы F рычаг, представленный на рисунке, находится в равновесии. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы F равен 300 Н, а груз на плоскость не давит, то каков модуль силы тяжести, действующей на груз? (Ответ дайте в ньютонах.)
Под действием веса груза, равного mg, и силы F рычаг, представленный на рисунке, находится в равновесии. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы F равен 150 Н, а груз на плоскость не давит, то каков модуль силы тяжести, действующей на груз? (Ответ дайте в ньютонах.)
Под действием веса груза, равного mg, и силы F рычаг, представленный на рисунке, находится в равновесии а груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы тяжести равен 30 Н, то каков модуль силы F? (Ответ дайте в ньютонах.)
Под действием веса груза, равного mg, и силы F рычаг, представленный на рисунке, находится в равновесии. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы F равен 120 Н, а груз на плоскость не давит, то модуль силы тяжести, действующей на груз? (Ответ дайте в ньютонах.)
Под действием веса груза, равного mg, и силы F рычаг, представленный на рисунке, находится в равновесии. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы F равен 600 Н, а груз на плоскость не давит, то каков модуль силы тяжести, действующей на груз? (Ответ дайте в ньютонах.)
К легкому рычагу сложной формы с точкой вращения в точке O (см. рис.) подвешен груз массой 2 кг и прикреплена пружина, второй конец которой прикреплен к неподвижной стене. Рычаг находится в равновесии, а сила натяжения пружины равна 15 Н. На каком расстоянии x от оси вращения подвешен груз, если расстояние от оси до точки крепления пружины равно 10 см? (Ответ дайте в сантиметрах.)
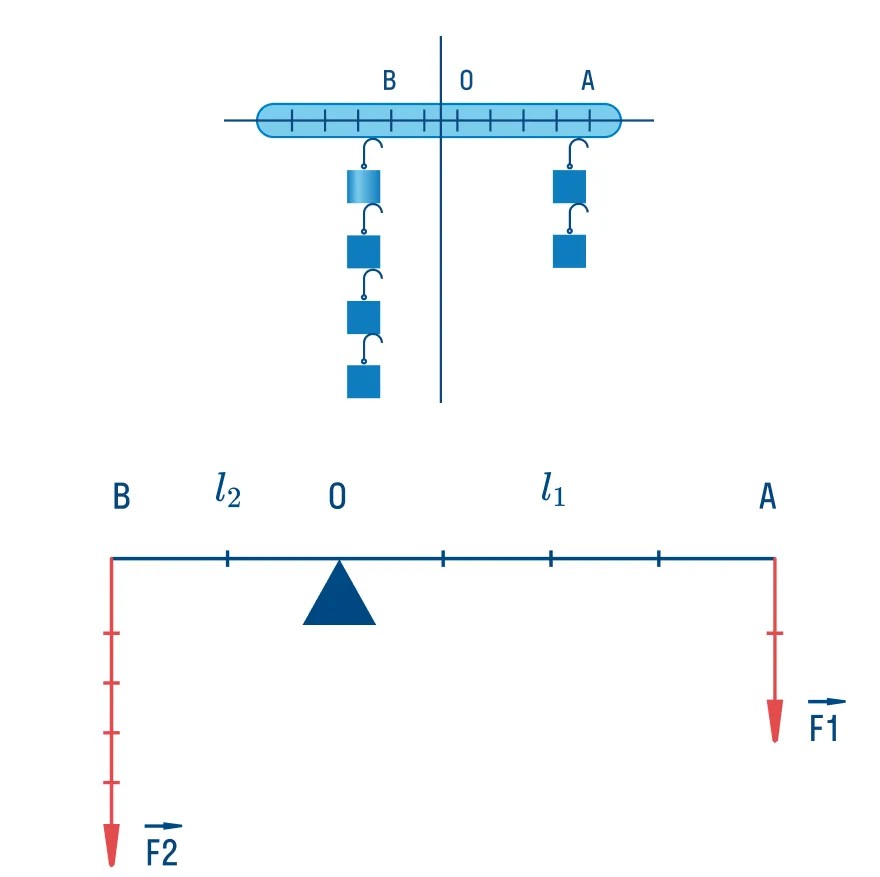
Тело массой 0,3 кг подвешено к правому плечу невесомого рычага (см. рис.). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия? Ответ приведите в килограммах.
На рычаг действуют две силы. Момент первой силы относительно оси вращения рычага равен 50 Н · м. Какова величина второй силы, если её плечо относительно этой же оси равно 0,5 м и рычаг при этом находится в равновесии?
Ответ дайте в Ньютонах.
Источник: Демонстрационная версия ЕГЭ—2022 по физике
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рис.). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?
Источник: Демонстрационная версия ЕГЭ—2018 по физике
На рисунке изображена система, состоящая из невесомого рычага и идеального блока. Масса груза 100 г. Какова величина силы F, если система находится в равновесии? (Ответ дайте в ньютонах.) Ускорение свободного падения принять равным 10 м/с2.
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рис.).
Чему равна масса груза, который надо подвесить ко второму делению левого плеча рычага для достижения равновесия? (Ответ дайте в килограммах.)
Задания Д28 C1 № 3804
Груз удерживают на месте с помощью рычага, приложив вертикальную силу 400 Н (см. рис.). Рычаг состоит из шарнира и однородного стержня массой 20 кг и длиной 4 м. Расстояние от оси шарнира до точки подвеса груза равно 1 м. Чему равна масса груза? Ответ приведите в килограммах.
Источник: Демонстрационная версия ЕГЭ—2013 по физике.
Всего: 37 1–20 | 21–37
ЗАДАЧИ НА РЫЧАГИ
1. На концах рычага действуют силы 2Н и 18 Н.
Длина рычага 1 м. Где находиться точка опоры, если рычаг в равновесии.
2. Пользуясь системой подвижных и неподвижных
блоков, необходимо поднять груз массой 60 кг. Из скольких подвижных и неподвижных
блоков должна состоять система, чтобы этот груз мог поднять один человек,
прикладывая силу в 65Н?
3. На концах невесомого рычага действуют силы 100Н и 140Н.
Расстояние от точки опоры до меньшей силы равно 7 см. Определите расстояние от
точки опоры до большой силы. Определите длину рычага.(Ответ:5см; 12см)
4.

действием силы тяжести груза
и силы F рычаг, представленный на рисунке, находится в
равновесии. Вектор силы F перпендикулярен рычагу. Расстояния
между точками приложения сил и точкой опоры, а также проекции этих расстояний
на вертикальную и горизонтальную оси указаны на рисунке. Если модуль силы F равен
120 Н, то каков модуль силы тяжести, действующей на груз? (Ответ дайте в
ньютонах.)
5. Под
действием силы тяжести mg груза и силы F рычаг,
представленный на рисунке, находится в равновесии.

силы F перпендикулярен рычагу. Расстояния между точками
приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную
и горизонтальную оси указаны на рисунке. Если модуль силы F равен
240 Н, то каков модуль силы тяжести, действующей на груз? (Ответ дайте в
ньютонах.)
6.

действием силы тяжести mg груза и силы F рычаг,
представленный на рисунке, находится в равновесии. Расстояния между точками
приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную
и горизонтальную оси указаны на рисунке. Если модуль силы тяжести, действующей
на груз, равен 1 500 Н, то каков модуль силы F? (Ответ
дайте в ньютонах.
7.
7
представленный на рисунке, находится в равновесии. Расстояния между точками
приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную
и горизонтальную оси указаны на рисунке. Если модуль силы mg равен
30 Н, то каков модуль силы F, действующей на груз? (Ответ
дайте в ньютонах.)
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода? (Ответ дайте в ньютонах.) Трение в осях блоков мало. Блоки и нити считайте невесомыми.
Источник: Яндекс: Тренировочная работа ЕГЭ по физике. Вариант 1.
2
К левому концу невесомого стержня прикреплен груз массой 3 кг (см. рис.).
Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии? (Ответ дайте в килограммах.)
3
На рычаг действуют две силы. Момент первой силы относительно оси вращения рычага равен 50 Н · м. Какова величина второй силы, если её плечо относительно этой же оси равно 0,5 м и рычаг при этом находится в равновесии?
Ответ дайте в Ньютонах.
Источник: Демонстрационная версия ЕГЭ—2022 по физике
4
Под действием веса груза mg и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, а груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы F равен 240 Н, то каков модуль силы тяжести, действующей на груз? (Ответ дайте в ньютонах.)
5
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рис.).
Чему равна масса груза, который надо подвесить ко второму делению левого плеча рычага для достижения равновесия? (Ответ дайте в килограммах.)
Пройти тестирование по этим заданиям
Задачи на простые механизмы с решениями
Формулы, используемые на уроках «Задачи на простые механизмы,
условия равновесия рычага, блоки, золотое правило механики».
Название величины |
Обозначение |
Единица измерения |
Формула |
Сила |
F |
Н |
F1l1 = F2l2 |
Плечо силы |
l |
м |
|
Момент силы |
M |
Нм |
M = Fl |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
С помощью рычага рабочий поднимает плиту массой 120 кг. Какую силу он прикладывает к большему плечу рычага, равному 2,4 м, если меньшее плечо 0,8 м?
Задача № 2.
На концах рычага действуют силы 20 Н и 120 Н. Расстояние от точки опоры до большей силы равно 2 см. Определите длину рычага, если рычаг находится в равновесии.
Задача № 3.
На рисунке изображен рычаг, имеющий ось вращения в точке О. Груз какой массы надо подвесить в точке В для того, чтобы рычаг был в равновесии?
Задача № 4.
На меньшее плечо рычага действует сила 300 Н, на большее — 20 Н. Длина меньшего плеча 5 см. Определите длину большего плеча.
Задача № 5.
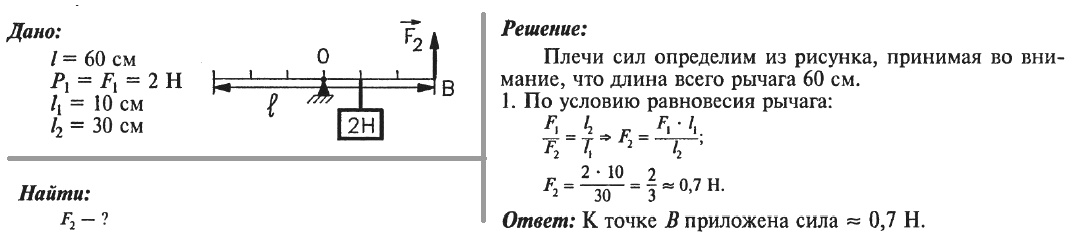
Рычаг длиной 60 см находится в равновесии. Какая сила приложена в точке В?
Задача № 6.
Момент силы действующей на рычаг, равен 20 Н*м. Найти плечо силы 5 Н, если рычаг находится в равновесии.
Задача № 7.
Какое усилие необходимо приложить, чтобы поднять груз 1000 Н с помощью подвижного блока? Какая совершится работа при подъеме груза на 1 м? (Вес блока и трение не учитывать).
Задача № 8.
Система блоков находится в равновесии. Определите вес правого груза. (Вес блоков и силу трения не учитывать).
Задача № 9.
При помощи подвижного блока поднимают груз, прилагая силу 105 Н. Определите силу трения, если вес блока равен 20 Н, а вес груза 180 Н.
Задача № 10.
ОГЭ
Стержень цилиндрической формы длиной l = 40 см состоит на половину своей длины из свинца и наполовину — из железа. Найти расстояние от центра тяжести до центра симметрии стержня. Плотность свинца p1 = 11,4 г/см3, плотность железа p2 = 7,8 г/см3.
Решение. Центр тяжести тела (центр масс) — точка приложения силы притяжения его к земле — веса тела P. У тел, имеющих какую-либо симметрию, он совпадает с центром симметрии. Например, у однородного цилиндра центр тяжести расположен на его оси в центре цилиндра. Тело, закреплённое на оси, проходящей через его центр тяжести, находится в состоянии безразличного равновесия. Мысленно закрепим стержень AB на оси, перпендикулярной стержню и проходящей через его центр тяжести C, отстоящий от его геометрического центра O на расстояние x в сторону более тяжёлой половины стержня. Центры инерций половинок размещены на расстояниях l/4 от середины стержня.
х = (11,4–7,8)/(11,4+7,8) • 0,4/4 = 0,01875 ≈ 0,019 (м)
Ответ: 1,9 см.
Задача № 11.
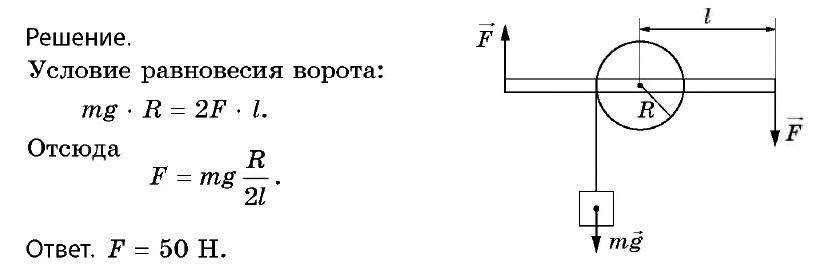
ЕГЭ
Масса якоря корабля m = 50 кг. Радиус барабана, на который наматывают якорную цепь, R = 0,2 м, длина каждой из двух ручек ворота l = 1 м. Какую силу нужно приложить к каждой из них, чтобы поднять якорь?
Краткая теория для решения задачи на простые механизмы.
Конспект урока «Задачи на простые механизмы с решениями».
Следующая тема: «Задачи на КПД простых механизмов».
Простые механизмы.
-
Рычаг.
-
Неподвижный блок.
-
Подвижный блок.
-
Наклонная плоскость.
-
Золотое правило механики.
-
КПД механизма.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: простые механизмы, КПД механизма.
Механизм — это приспособление для преобразования силы (её увеличения или уменьшения).
Простые механизмы — это рычаг и наклонная плоскость.
Рычаг.
Рычаг — это твёрдое тело, которое может вращаться вокруг неподвижной оси. На рис. 1) изображён рычаг с осью вращения . К концам рычага (точкам
и
) приложены силы
и
. Плечи этих сил равны соответственно
и
.
Условие равновесия рычага даётся правилом моментов: , откуда
.
 |
| Рис. 1. Рычаг |
Из этого соотношения следует, что рычаг даёт выигрыш в силе или в расстоянии (смотря по тому, с какой целью он используется) во столько раз, во сколько большее плечо длиннее меньшего.
Например, чтобы усилием 100 Н поднять груз весом 700 Н, нужно взять рычаг с отношением плеч 7 : 1 и положить груз на короткое плечо. Мы выиграем в силе в 7 раз, но во столько же раз проиграем в расстоянии: конец длинного плеча опишет в 7 раз большую дугу, чем конец короткого плеча (то есть груз).
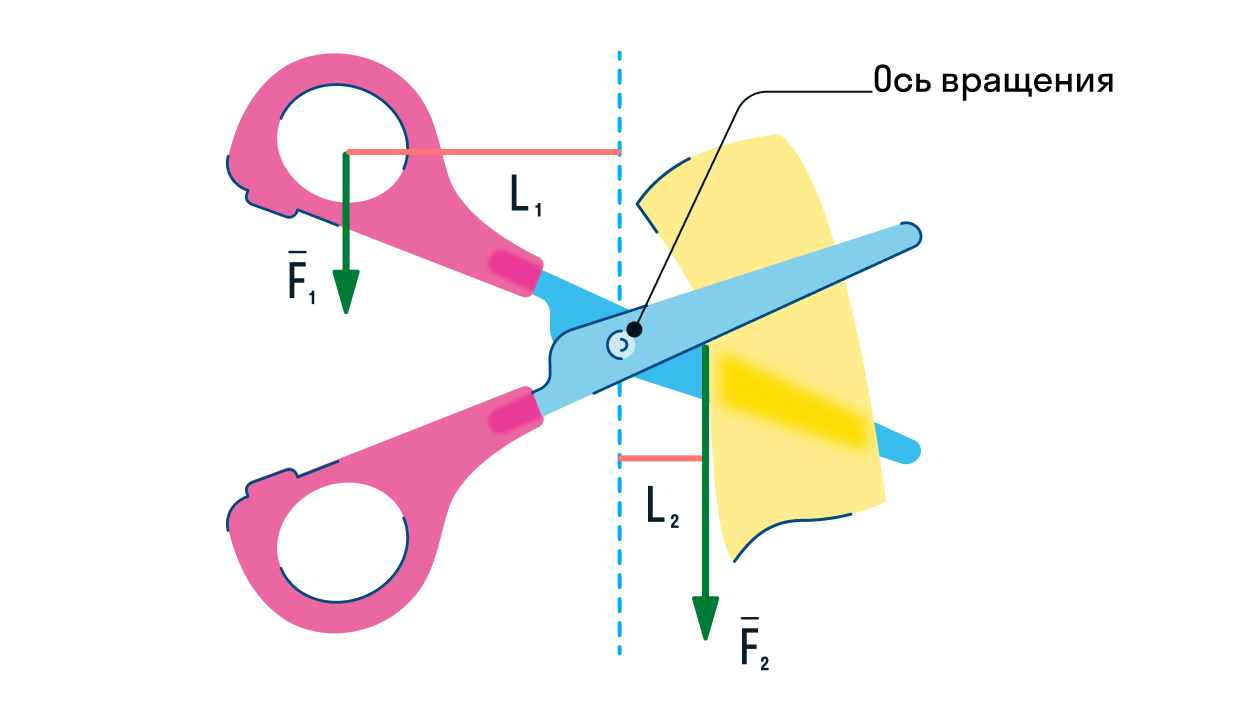
Примерами рычага, дающего выигрыш в силе, являются лопата, ножницы, плоскогубцы. Весло гребца — это рычаг, дающий выигрыш в расстоянии. А обычные рычажные весы являются равноплечим рычагом, не дающим выигрыша ни в расстоянии, ни в силе (в противном случае их можно использовать для обвешивания покупателей).
к оглавлению ▴
Неподвижный блок.
Важной разновидностью рычага является блок — укреплённое в обойме колесо с жёлобом, по которому пропущена верёвка. В большинстве задач верёвка считается невесомой нерастяжимой нитью.
На рис. 2 изображён неподвижный блок, т. е. блок с неподвижной осью вращения (проходящей перпендикулярно плоскости рисунка через точку ).
 |
На правом конце нити в точке закреплён груз весом
. Напомним, что вес тела — это сила, с которой тело давит на опору или растягивает подвес. В данном случае вес
прило жен к точке
, в которой груз крепится к нити.
К левому концу нити в точке приложена сила
.
Плечо силы равно
, где
— радиус блока. Плечо веса
равно
. Значит, неподвижный блок является равноплечим рычагом и потому не даёт выигрыша ни в силе, ни в расстоянии: во-первых, имеем равенство
, а во-вторых, в процессе движении груза и нити перемещение точки
равно перемещению груза.
Зачем же тогда вообще нужен неподвижный блок? Он полезен тем, что позволяет изменить направление усилия. Обычно неподвижный блок используется как часть более сложных механизмов.
к оглавлению ▴
Подвижный блок.
На рис. 3 изображён подвижный блок, ось которого перемещается вместе с грузом. Мы тянем за нить с силой , которая приложена в точке
и направлена вверх. Блок вращается и при этом также движется вверх, поднимая груз, подвешенный на нити
.
 |
В данный момент времени неподвижной точкой является точка , и именно вокруг неё поворачивается блок (он бы «перекатывается» через точку
). Говорят ещё, что через точку
проходит мгновенная ось вращения блока (эта ось направлена перпендикулярно плоскости рисунка).
Вес груза приложен в точке
крепления груза к нити. Плечо силы
равно
.
А вот плечо силы , с которой мы тянем за нить, оказывается в два раза больше: оно равно
. Соответственно, условием равновесия груза является равенство
(что мы и видим на рис. 3: вектор
в два раза короче вектора
).
Следовательно, подвижный блок даёт выигрыш в силе в два раза. При этом, однако, мы в те же два раза проигрываем в расстоянии: чтобы поднять груз на один метр, точку придётся переместить на два метра (то есть вытянуть два метра нити).
У блока на рис. 3 есть один недостаток: тянуть нить вверх (за точку ) — не самая лучшая идея. Согласитесь, что гораздо удобнее тянуть за нить вниз! Вот тут-то нас и выручает неподвижный блок.
 |
На рис. 4 изображён подъёмный механизм, который представляет собой комбинацию подвижного блока с неподвижным. К подвижному блоку подвешен груз, а трос дополнительно перекинут через неподвижный блок, что даёт возможность тянуть за трос вниз для подъёма груза вверх. Внешнее усилие на тросе снова обозначено вектором .
Принципиально данное устройство ничем не отличается от подвижного блока: с его помощью мы также получаем двукратный выигрыш в силе.
к оглавлению ▴
Наклонная плоскость.
Как мы знаем, тяжёлую бочку проще вкатить по наклонным мосткам, чем поднимать вертикально. Мостки, таким образом, являются механизмом, который даёт выигрыш в силе.
В механике подобный механизм называется наклонной плоскостью. Наклонная плоскость — это ровная плоская поверхность, расположенная под некоторым углом к горизонту. В таком случае коротко говорят: «наклонная плоскость с углом
«.
Найдём силу, которую надо приложить к грузу массы , чтобы равномерно поднять его по гладкой наклонной плоскости с углом
. Эта сила
, разумеется, направлена вдоль наклонной плоскости (рис. 5).
 |
Выберем ось так, как показано на рисунке. Поскольку груз движется без ускорения, действующие на него силы уравновешены:
.
Проектируем на ось :
,
откуда
.
Именно такую силу нужно приложить, что двигать груз вверх по наклонной плоскости.
Чтобы равномерно поднимать тот же груз по вертикали, к нему нужно приложить силу, равную . Видно, что
, поскольку
. Наклонная плоскость действительно даёт выигрыш в силе, и тем больший, чем меньше угол
.
Широко применяемыми разновидностями наклонной плоскости являются клин и винт.
к оглавлению ▴
Золотое правило механики.
Простой механизм может дать выигрыш в силе или в расстоянии, но не может дать выигрыша в работе.
Например, рычаг с отношением плеч 2 : 1 даёт выигрыш в силе в два раза. Чтобы на меньшем плече поднять груз весом , нужно к большему плечу приложить силу
. Но для поднятия груза на высоту
большее плечо придётся опустить на
, и совершённая работа будет равна:
т. е. той же величине, что и без использования рычага.
В случае наклонной плоскости мы выигрываем в силе, так как прикладываем к грузу силу , меньшую силы тяжести. Однако, чтобы поднять груз на высоту
над начальным положением, нам нужно пройти путь
вдоль наклонной плоскости. При этом мы совершаем работу
т. е. ту же самую, что и при вертикальном поднятии груза.
Данные факты служат проявлениями так называемого золотого правила механики.
Золотое правило механики. Ни один из простых механизмов не даёт выигрыша в работе. Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, и наоборот.
Золотое правило механики есть не что иное, как простой вариант закона сохранения энергии.
к оглавлению ▴
КПД механизма.
На практике приходится различать полезную работу A полезн, которую нужно совершить при помощи механизма в идеальных условиях отсутствия каких-либо потерь, и полную работу Aполн,
которая совершается для тех же целей в реальной ситуации.
Полная работа равна сумме:
-полезной работы;
-работы, совершённой против сил трения в различных частях механизма;
-работы, совершённой по перемещению составных элементов механизма.
Так, при подъёме груза рычагом приходится вдобавок совершать работу по преодолению силы трения в оси рычага и по перемещению самого рычага, имеющего некоторый вес.
Полная работа всегда больше полезной. Отношение полезной работы к полной называется коэффициентом полезного действия (КПД) механизма:
=Aполезн/Аполн.
КПД принято выражать в процентах. КПД реальных механизмов всегда меньше 100%.
Вычислим КПД наклонной плоскости с углом при наличии трения. Коэффициент трения между поверхностью наклонной плоскости и грузом равен
.
Пусть груз массы равномерно поднимается вдоль наклонной плоскости под действием силы
из точки
в точку
на высоту
(рис. 6). В направлении, противоположном перемещению, на груз действует сила трения скольжения
.
 |
Ускорения нет, поэтому силы, действующие на груз, уравновешены:
.
Проектируем на ось X:
. (1)
Проектируем на ось Y:
. (2)
Кроме того,
, (3)
Из (2) имеем:
.
Тогда из (3):
.
Подставляя это в (1), получаем:
.
Полная работа равна произведению силы F на путь, пройденный телом вдоль поверхности наклонной плоскости:
Aполн=.
Полезная работа, очевидно, равна:
Аполезн=.
Для искомого КПД получаем:
Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Простые механизмы.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Как известно, вся классическая механика делится на кинематику, динамику и статику. Про кинематику и динамику мы уже писали, а сегодня расскажем про статику и займемся решением задач.
Не забывайте подписаться на наш телеграм-канал и получать полезную рассылку каждый день.
Задачи на статику и равновесие тел
Мы не будем решать страшные задачи по теормеху, сопротивлению материалов или предмету Тут Моя Могила Теория Машин и Механизмов (ТММ). Разберем несколько примеров, связанных с равновесием и простейшими механизмами.
Именно на базе статики строится знаменитый сопромат, столь нелюбимый технарями.
Задача №1. Момент силы
Условие
На рычаг в состоянии равновесия действуют две силы. Момент первой равен 20 Н*м. Модуль второй силы равен 5 Н. Найдите плечо второй силы.
Решение
Запишем условие равновесия рычага:
Отсюда:
Ответ: 4м.
Задача №2. Статика
Условие
На концах рычага действуют силы с модулями 20 и 120 Н соответственно. Рычаг находится в равновесии. Найдите длину рычага, если расстояние от точки опоры до большей силы равно 2 см.
Решение
Запишем равенство моментов:
Ответ: 14 см.
В этой задаче мы не переводили размерности в систему СИ.
Задача №3. Расчет силы
Условие
Рабочий на стройке поднимает плиту с помощью рычага. Большее плечо равно 2,4м, меньшее — 0,8м. Какую силу прикладывает рабочий к большему плечу рычага, если масса плиты равна 120 кг?
Решение
Обозначим большее плечо через d1. К нему рабочий прикладывает искомую силу F1. Вторая сила, приложенная к меньшему плечу, равна весу плиты.
Ответ: 400 Н.
Задача№4. Подвижный блок
Условие
Какую силу нужно приложить, чтобы поднять груз весом 1000 Н с помощью подвижного блока? Какую работу совершит эта сила при подъеме груза на 1 метр?
Подвижный блок позволяет выиграть в усилии в два раза.
Решение
Найдем силу и работу:
Ответ: 500 Н, 1000 Дж.
Задача №5. Нахождение плеча рычага
Условие
На плечи рычага действуют силы 300 Н и 20 Н. Меньшее плечо равно 5см. Найдите большее плечо рычага.
Решение
Условие равновесия рычага можно записать так:
Ответ: 75 см.
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Вопросы и ответы по статике
Вопрос 1. Что нужно, чтобы тело находилось в равновесии, каково условие равновесия тел?
Ответ. Из законов Ньютона известно, что тело движется равномерно или покоится, если равнодействующая всех сил, приложенных к нему, равна нулю. Это и есть условие равновесия.
Это условие справедливо только для тела, которое может двигаться поступательно, но не может вращаться вокруг некоторой оси.
Вопрос 2. Каково условие равновесия для вращающихся тел?
Ответ. Если тело имеет неподвижную ось вращения, то оно находится в равновесии, если алгебраическая сумма моментов всех сил, приложенных к телу относительно этой оси, равна нулю.
Вопрос 3. Что такое момент силы?
Ответ. Момент силы — скалярная физическая величина, равная произведению модуля силы F на плечо силы d.
Вопрос 4. Что такое плечо силы?
Ответ. Плечо силы — это длина перпендикуляра, проведенного от оси вращения к линии действия силы.
Вопрос 5. Материальные тела в статике считаются упругими, или абсолютно твердыми?
Ответ. Абсолютно твердыми. Деформации и изменение размеров тела под действием сил не принимаются во внимание при решении задач, если иное не оговорено в условии.
Вопрос 6. Что такое рычаг в механике?
Ответ. Рычаг — простейший механизм. Рычагом может быть любое тело, которое может вращаться вокруг неподвижной опоры или подвеса. Используется для создания большего усилия на меньшем плече за счет меньшего усилия на длинном плече.
Статика: определение
Статика — раздел теоретической механики, изучающий основы равновесия тел.
Нужна помощь в решении более сложных заданий? Не знаете, как решать задачи по теоретической механике? Обращайтесь в профессиональный студенческий сервис.
5. Механика (объяснение явлений)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Статика
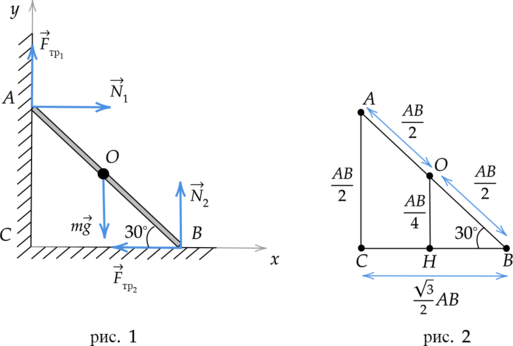
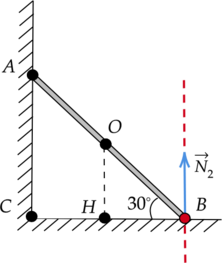
Прут массой 5 кг опирается на две точки горизонтальной и вертикальной поверхностей, образуя с первой угол (30^circ) (см. рисунок). Длина прута (AB = 2sqrt{3}) м. Из приведенного ниже списка выберите два верных утверждения, описывающих эту ситуацию.
1) Модуль силы реакции опоры, действующей на прут со стороны вертикальной поверхности, в два раза больше модуля силы трения, действующей на него со стороны горизонтальной поверхности.
2) Момент силы тяжести относительно оси, проходящей через точку (B) перпендикулярно плоскости рисунка, равен 75 Н(cdot)м.
3) Длина плеча силы трения, действующей на прут со стороны вертикальной поверхности, относительно оси, проходящей через точку (O) перпендикулярно плоскости рисунка, составляет 1 м.
4) Момент силы реакции опоры, действующей на прут со стороны горизонтальной поверхности, относитльно оси, проходящей через точку (B) перпендикулярно плоскости рисунка, равен нулю.
5) Длина прута на 20(%) больше длины плеча действующей на него со стороны горизонтальной поверхности силы реакции опоры относительно точки (C).
1) (color{red}{smalltext{Неверно }})
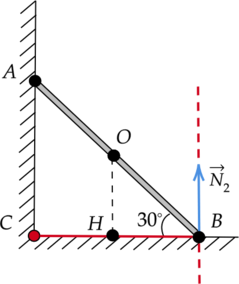
Укажем все силы, действующие на прут (рис. 1):
(F_text{тр1}), (N_1) — сила трения и сила реакции опоры, действующие на прут со стороны вертикальной поверхности;
(mg) — сила тяжести;
(F_text{тр2}) и (N_2) — сила трения и сила реакции опоры, действующие на прут со стороны горизонтальной поверхности.
Запишем второй закон Ньютона с учетом того, что прут покоится: [vec{F}_text{тр1} + vec{N}_1 + mvec{g} + vec{F}_text{тр2} + vec{N}_2 = 0] Введем оси (Ox) и (Oy) (рис. 1) и спроецируем на них все силы: [begin{cases}
Ox: N_1 — F_text{тр2} = 0
Oy: F_text{тр1} — mg + N_2 = 0
end{cases}
Rightarrow hspace{3mm}
begin{cases}
N_1 = F_text{тр2}
F_text{тр1} — mg + N_2 = 0
end{cases}] Таким образом, сила реакции опоры (N_1), действующая на прут со стороны вертикальной поверхности, равна силе трения (F_text{тр2}), действующей на него со стороны горизонтальной поверхности.
2) (color{green}{smalltext{Верно }})
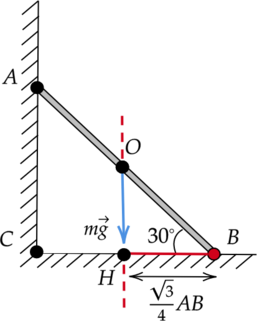
Момент силы тяжести относитльно оси, проходящей через точку (B) перпендикулярно плоскости рисунка, равен: [M = mgcdot l,] где (l) — плечо силы. Упростим модель (рис. 1) до двух подобных треугольников (Delta ABC) и (Delta OBH) (рис. 2) и, обратившись к геометрии, выразим длины всех отрезков через сторону (AB).
По рисунку видно, что плечом силы тяжести (l) является отрезок (HB), равный (dfrac{sqrt{3}}{4}AB). Таким образом, момент силы тяжести равен: [M = 5text{ кг}cdot 10text{ }dfrac{text{м}}{text{с}^2}cdotdfrac{sqrt{3}}{4}cdot 2sqrt{3}text{ м} = 75 text{ Н}cdottext{м}]
3) (color{red}{smalltext{Неверно }})
Плечо – это кратчайшее расстояние между осью вращения и линией действия силы.
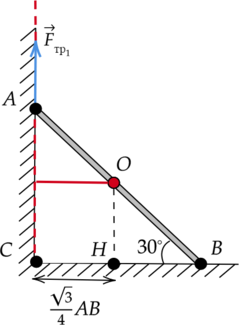
По рисунку видно, что плечом силы трения, действующей на прут со стороны вертикальной поверхности, относительно оси, проходящей через точку (O) перпендикулярно плоскости рисунка, является отрезок, равный по длине отрезку (CH).
Исходя из рис. 2: [CH = dfrac{sqrt{3}}{4}AB] [CH = dfrac{sqrt{3}}{4}cdot 2sqrt{3}text{ м} = 1,5text{ м}]
4) (color{green}{smalltext{Верно }})
Момент силы трения (M) равен произведению модуля силы реакции опоры (N_2) на ее плечо (l): [M=N_2cdot l] По рисунку видно, что длина плеча силы трения (l) относительно точки (B) равна нулю (так как ось вращения, проходящая через точку (B), перпендикулярна линии действия силы реакции опоры).
Следовательно, и момент силы реакции (M) так же равен нулю: [M = N_2cdot 0text{ м} = 0text{ H}cdottext{м}]
5) (color{red}{smalltext{Неверно }})
По рисунку видно, что плечом силы реакции опоры (N_2), действующей на прут со стороны горизонтальной поверхности, является отрезок (CB).
Исходя из рис. 2: [CB = dfrac{sqrt{3}}{2} AB hspace{2 mm} Rightarrow hspace{2 mm} AB = dfrac{2}{sqrt{3}}] [AB approx 1,15 hspace{1 mm} CB] Следовательно, длина прута (AB) приблизительно на 15(%) больше длины плеча действующей на него со стороны горизонтальной поверхности силы реакции опоры относительно точки (C).
Ответ: 24
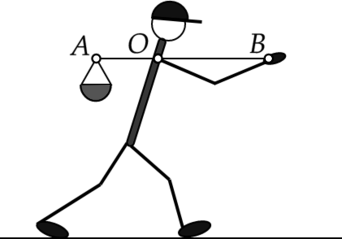
Трудолюбивый Вася собрал в лесу 5 кг ягод. Вася хорошо знал физику, поэтому он нашел палку длиной 1,2 м и решил понести корзину с ягодами так, как показано на рисунке. К концу (B) палки в начале пути Вася прикладывал постоянную вертикальную силу, равную 25 Н. Из приведенного ниже списка выберите два верных утверждения, описывающих эту ситуацию. Массой палки пренебречь.
1) Длина короткого конца палки (относительно точки (O)) составляет 40 см.
2) Момент силы, действующей на конец палки (A), относительно точки (O) равен 25 Н(cdot)м.
3) Плечо вертикальной силы, прикладываемой Васей к концу (B) палки, в два раза больше плеча силы, действующей на конец (A).
4) Момент вертикальной силы, действующей на конец (B) палки относительно точки (O) равен 2 Н(cdot)м.
5) Если Вася устанет и будет прикладывать к концу (B) палки силу на 10 Н меньшую, чем прикладывал в начале пути, то ему нужно будет съесть 3 кг собранных ягод, чтобы палка осталась в равновесии (при неизменных прочих условиях).
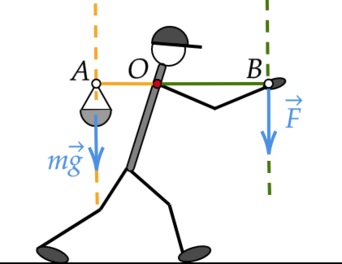
1) (color{green}{smalltext{Верно }})
Чтобы рычаг (палка) достиг равновесия, моменты сил, действующих на него справа и слева, должны быть равны: (M_1=M_2). В то же время моменты сил (M_1) и (M_2) по определению равны произведению силы на ее плечо: [M_1 = F_1l_1] [M_2 = F_2l_2] На конец (A) палки действует единственная сила — сила тяжести (Rightarrow) (F_1 = mg).
На конец (B) действует вертикальная сила, которую прикладывает Вася (Rightarrow) (F_2 = F).
По рисунку видно, что плечом силы тяжести относительно точки (O) является отрезок (AO), а плечом силы (F) относительно той же точки — отрезок (OB), причем (OB = AB — AO).
Таким образом: [M_1 = mgcdot AO] [M_2 = Fcdot OB] Приравнивая, получаем: [mgcdot AO = Fcdot OB] [mgcdot AO = Fcdot (AB — AO)] [AO = dfrac{Fcdot AB}{F + mg}] [AO = dfrac{25text{ Н}cdot 1,2text{ м}}{25text{ Н}+5text{ кг}cdot 10text{ }dfrac{text{м}}{text{с}^2}} = 0,4text{ м}] Тогда конец (OB) равен: [OB = AB — AO] [OB = 1,2text{ м} — 0,4text{ м} = 0,8text{ м}] Таким образом, длина короткого конца палки действительно составляет 0,4 м = 40 см.
2) (color{red}{smalltext{Неверно }})
Момент силы, действующей на конец палки (A), относительно точки (O) равен: [M = mgcdot AO] [M = 5text{ кг}cdot10text{ }dfrac{text{м}}{text{с}^2}cdot 0,4text{ м} = 20text{ Н}cdottext{м}]
3) (color{green}{smalltext{Верно }})
Найдем отношение плеч: [dfrac{OB}{AO} = dfrac{AB — AO}{AO} = dfrac{1,2text{ м} — 0,4text{ м}}{0,4text{ м}} = 2]
4) (color{red}{smalltext{Неверно }})
Момент вертикальной силы, действующей на конец (B) палки относительно точки (O) равен: [M = Fcdot OB] [M = 25text{ Н}cdot 0,8text{ м} = 20text{ Н}cdottext{м}]
5) (color{red}{smalltext{Неверно }})
Запишем условие равновесия рычага (палки) для двух случаев — до того, как Вася устал, и после: [Fcdot OB = mgcdot AO] [F’cdot OB = m’gcdot AO] Поделим первое выражение на второе и выразим массу (m’) с учетом того, что (F’ = F — 10text{ H}): [dfrac{Fcdot OB}{F’cdot OB} = dfrac{mgcdot AO}{m’gcdot AO}] [m’ = dfrac{mF’}{F} = dfrac{m(F -10text{ Н})}{F}] [m’ = dfrac{5text{ кг}cdot(25text{ Н}-10text{ Н})}{25text{ Н}} = 3text{ кг}] Таким образом, Васе нужно съесть (Delta m = m-m’ = 5text{ кг} — 3text{ кг} = 2text{ кг}) ягод.
Ответ: 13
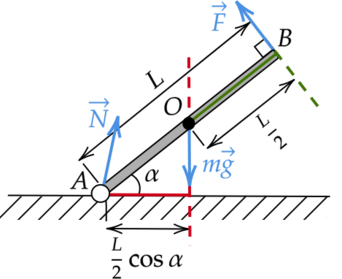
Доску массой 2 кг удерживают с силой, направленной перпендикулярно ее поверхности. Доска образует с горизонтом угол (alpha = 60^circ) (см. рисунок). Длина доски составляет 160 см.
Из приведенного ниже списка выберите два верных утверждения, описывающих эту ситуацию.
1) Длина плеча силы тяжести относительно оси, проходящей через точку (A) перпендикулярно плоскости рисунка, составляет 40 см.
2) На доску действуют с силой (F), равной 50 Н.
3) Длина плеча силы (F) относительно точки (O) в три раза меньше длины доски.
4) Момент силы (F) относительно оси, проходящей через точку (O) перпендикулярно плоскости рисунка, равен 400 мН(cdot)м.
5) Момент силы тяжести относительно оси, проходящей через точку (A) перпендикулярно плоскости рисунка, равен 8 Н(cdot)м.
1) (color{green}{smalltext{Верно }})
По рисунку видно, что длина плеча силы тяжести (mg) относительно оси, проходящей через точку (A) перпендикулярно плоскости рисунка, равна: [l = dfrac{L}{2}cosalpha] [l = dfrac{1,6text{ м}}{2}cos{60}^circ = 0,4text{ м} = 40text{ см}]
2) (color{red}{smalltext{Неверно }})
Чтобы доска находилась в равновесии, алгебраическая сумма моментов сил, действующих на нее, должна равняться нулю.
Мы ничего не знаем о силе реакции опоры (N), поэтому правило моментов удобнее записать относительно точки (A). В этом случае плечо силы реакции опоры (N) равно нулю. Следовательно, и момент этой силы “зануляется”. [FL — mgdfrac{L}{2}cos{alpha} = 0] [FL = mgdfrac{L}{2}cos{alpha}] [F = dfrac{mg}{2}cos{alpha}] [F = dfrac{2text{ кг}cdot10text{ м/с}^2}{2}cos{60}^circ = 5text{ Н}]
3) (color{red}{smalltext{Неверно }})
По рисунку видно, что длина плеча (OB) силы (F) относительно точки (O) в два раза меньше длины доски (AB).
4) (color{red}{smalltext{Неверно }})
Момент силы (F) относительно оси, проходящей через точку (O) перпендикулярно плоскости рисунка, равен: [M = Fcdotdfrac{L}{2}] [M = 5text{ Н}cdotdfrac{1,6text{ м}}{2} = 4text{ Н}cdottext{м} = 4000text{ мН}cdottext{м}]
5) (color{green}{smalltext{Верно }})
Момент силы тяжести относительно оси, проходящей через точку (A) перпендикулярно плоскости рисунка, равен: [M = mgcdotdfrac{L}{2}cos{alpha}] [M = 2text{ кг}cdot10text{ }dfrac{text{м}}{text{с}^2}cdotdfrac{1,6text{ м}}{2}cos{60}^circ = 8text{ Н}cdottext{м}]
Ответ: 15
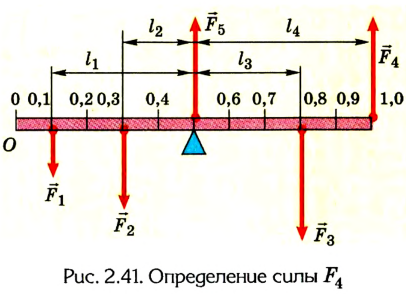
Очень лёгкая рейка закреплена на горизонтальной оси (O), перпендикулярной плоскости рисунка, и может вращаться вокруг неё без трения. К рейке приложены четыре силы, изображенные на рисунке.
Из приведенного ниже списка выберите два правильных утверждения
1) Относительно оси (O) максимальное плечо имеет сила (F_4)
2) Относительно оси (O) минимальное плечо имеет сила (F_1)
3) Относительно оси (O) минимальным будет момент, создаваемы силой (F_2)
4) Относительно оси (O) максимальным будет момент, создаваемый силой (F_4)
5) Под действием всех изображенных на рисунке рейка будет вращаться
1) Плечо это — кратчайшее расстояние между линией действия силы и связанной с ней точкой (полюсом или осью вращения). В данном случае макисмальное расстояние будет до силы (F_4)
2) Из пункта 1 минимальное плечо будет до силы (F_2)
3) Момент вычисляет по формуле: [M=Flsin alpha,] где (F) – сила, (l) – плечо силы, (alpha) – угол между силой и плечом.
Найдем моменты для каждой из сил, проецируя силы на ось, перпендикулярную оси вращения [M_1=F_1l_1=20text{ см}cdot 1 text{ Н}=20text{ Н $cdot $ см}] [M_2=F_2l_2=10text{ см}cdot 1 text{ Н}=10text{ Н $cdot $ см}] [M_3=F_3l_3=30text{ см}cdot 3 text{ Н}=90text{ Н $cdot $ см}] [M_4=F_4l_4=40text{ см}cdot 2 text{ Н}=80text{ Н $cdot $ см}] Минимальным будет момент (M_2)
4) Из пункта 3) максимальным будет момент (F_3)
5) У нас силы (F_2) и (F_3) будут вращать рейку по часовой стрелке, а силы (F_1) и (F_4) против часовой стрелки, следовательно, чтобы рейка находилась в равновесии должно выполняться условие [M_2+M_3=M_1+M_4 Rightarrow 10text{ Н $cdot $ см}+90text{ Н $cdot $ см}=20text{ Н $cdot $ см}+ 80text{ Н $cdot $ см}] Как мы видим условие равновесия соблюдено, а значит, рейка вращаться не будет.
Ответ: 13
Из лёгкого жёсткого стержня сделан горизонтальный рычаг с длинами плеч 40 см и 100 см. К короткому концу рычага на нити подвешен груз массой (m), а к длинному концу рычага для уравновешивания приложена некоторая сила. Человек начинает медленно опускать длинный конец рычага, прикладывая к нему вертикально вниз силу (см. рисунок). На графике показана зависимость момента (M) силы тяжести груза (m) (относительно точки опоры рычага) от угла (alpha) между рычагом и горизонтом.
Из приведённого ниже списка выберите два правильных утверждения на основании анализа графика.
1) При повороте рычага плечо действующей на груз силы тяжести не изменяется.
2) Когда уравновешенный рычаг горизонтален, модуль приложенной к его длинному концу силы равен 1 Н.
3) Масса груза (m) равна 500 г.
4) При увеличении угла (alpha) момент силы относительно точки опоры рычага уменьшается.
5) Момент силы (F) относительно точки опоры рычага всё время больше 1 Н(cdot)м.
1) При повороте рычага плечо силы тяжести уменьшается.
2) По графику видно, что при уравновешенном в горизонтальном положении рычага, момент силы равен (M=1) Н(cdot) м, откуда сила [F=dfrac{M}{l_2}=dfrac{1text{ Н$cdot$ м}}{1text{ м}}=1text{ Н}] 3) По правилу моментов [M_1=M_2] или [mgl_1=Fl_2] Откуда масса груза [m=dfrac{Fl_2}{gl_1}=dfrac{1text{ Н$cdot$ м}}{10text{ Н/кг}cdot 0,4text{ м}}=250text{ г}] 4) При увеличении угла (alpha) момент силы (F) относительно точки опоры рычага, равный моменту силы тяжести, уменьшается.
5) По графику момент силы (F) все время не превосходит 1 Н(cdot) м
Ответ: 24

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Содержание:
Рычаг:
Взаимодействие может происходить через промежуточные тела.
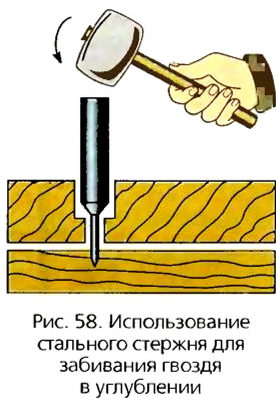
Взаимодействие может происходить не только при непосредственном контакте, но и при наличии промежуточных тел. Таких примеров можно привести большое количество. Так, если мастер забивает гвоздь в углублении, он ставит на головку гвоздя металлический стержень и по нему ударяет молотком (рис. 58). Молоток действует на стержень, который, в свою очередь, уже действует на гвоздь.
Можно ли изменять значения силы
Если взаимодействие между телами происходит через промежуточные тела, то можно изменять силы взаимодействия между ними. Оно может изменить как направление силы, так и ее значение. Одним из примеров такого использования промежуточных тел для взаимодействия между телами является рычаг. В быту и на производстве можно наблюдать много таких примеров.
Часто можно видеть, как тяжелый предмет поднимают или перемещают с помощью металлического стержня (рис. 59). В этом случае стержень называют рычагом.
Что такое рычаг
Рычагом называют жесткий стержень, имеющий ось вращения.
Ось вращения рычага может проходить через один из его концов или посередине рычага — между точками приложения сил.
Под действием нескольких сил рычаг может вращаться или быть неподвижным. В последнем случае говорят, что рычаг уравновешен.
Как уравновесить рычаг
Выясним, при каких условиях рычаг, на который действует несколько сил, будет уравновешен.
Для этого возьмем деревянную планку с отверстием посередине и поместим ее на оси, закрепленной в штативе (рис. 60). Это и будет рычаг. Слева от оси вращения повесим в точке А на расстоянии 10 см гирьку массой 102 г. В этом случае говорят, что точка А является точкой действия силы 1 Н. Под действием этой силы рычаг начнет вращаться против часовой стрелки. Для того чтобы он не вращался и оставался в горизонтальном положении, на другом конце рычага найдем такую точку В, при закреплении в которой гирьки массой 102 г рычаг перестанет вращаться. Измерив расстояние ОВ, увидим, что оно также равно 10 см. Таким образом, OA = ОВ, если Fl = F2. Если направление действия силы перпендикулярно к направлению оси вращения рычага, то расстояние от его оси вращения к направлению действия силы называют плечом силы.
Если силы, действующие на рычаг, находящийся в равновесии, равны, то равны и плечи этих сил.
Если левую гирьку оставить прикрепленной в точке А, а в точке В подвесить две такие гирьки массой по 102 г каждая, то равновесие рычага нарушится и он начнет вращаться. Достигнуть равновесия в этом случае можно, изменяя положение точки подвеса двух гирек. Так можно установить новое положение точки подвеса С. Измерив оба плеча, увидим, что правое плечо ОС в два раза меньше левого плеча OA.
В случае равновесия рычага плечо большей силы меньше, и наоборот, плечо меньшей силы больше.
Используя свойства пропорции, получаем
В уравновешенном рычаге плечи сил обратно пропорциональны силам.
Что такое момент силы
Физическую величину, равную произведению силы на плечо, называют моментом силы. Единицей измерения момента силы является ньютон-метр (Н-м).
Сформулируем условие равновесия рычага в общем виде.
Рычаг пребывает в равновесии, если момент силы, вращающий рычаг по часовой стрелке, равен моменту силы, вращающему рычаг против часовой стрелки.
Конструктивно рычаг может быть таким, что силы будут действовать по одну сторону от оси вращения. Условие равновесия для него будет такое же, как и для рычага, рассмотренного выше.
Используя условие равновесия рычага, можно рассчитывать силы, действующие на него, или плечи этих сил.
Пример:
На одно из плеч рычага длиной 30 см действует сила 2 Н. Какая сила должна подействовать на другое плечо этого рычага длиной 15 см, чтобы он оставался неподвижным.
Дано:
Решение
При условии равновесия рычага 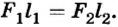
Ответ. На второе плечо рычага должна подействовать сила 4 Н.
Где используют рычаги
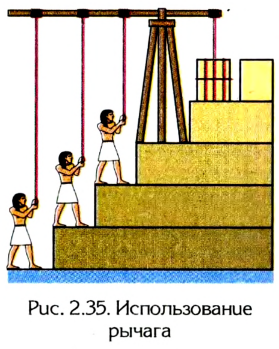
Рычаг известен человеку с того времени, когда человек взял палку, чтобы сбить плод с дерева. И вся следующая история человечества связана с использованием рычагов. Так, исследования историков показывают, что при строительстве пирамид древние египтяне использовали рычаги для поднятия тяжелых блоков на значительную высоту (рис. 61). Историкам науки известно, что древние римляне использовали рычаги для создания различных строительных и военных машин (рис. 62). Значительный вклад в теорию рычагов внес древнегреческий ученый и изобретатель Архимед. Сконструированные им машины помогали оборонять греческие города от захватчиков, подавать воду для орошения полей (рис. 63), перемещать значительные грузы на стройках, выполнять большое количество других подобных работ.
Рычаги широко используются и в современной технике, в самых разнообразных машинах.
Рычагом является стрела подъемного крана, используемого в строительстве. Она дает возможность получить выигрыш в силе или расстоянии. Момент силы, действующей на конце стрелы при подъеме груза, уравновешивается моментом противовеса, находящегося на противоположном конце стрелы.
Принцип рычага используется во многих устройствах и инструментах, которыми мы пользуемся ежедневно. На рисунке 64 изображены некоторые из них. На них легко найти части, исполняющие роль рычагов.
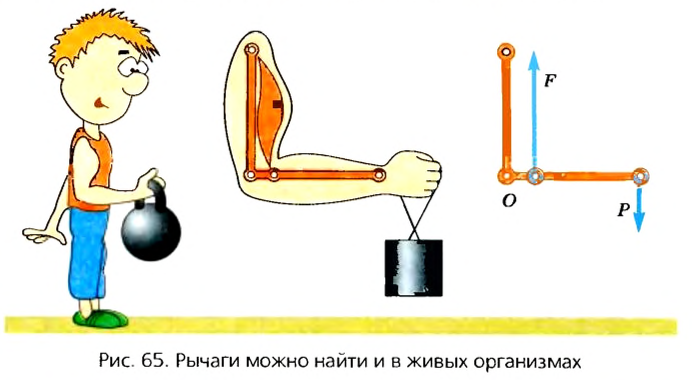
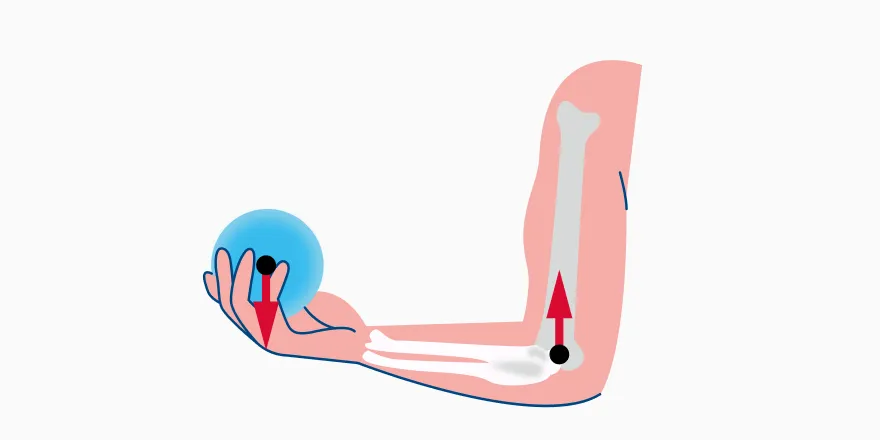
Рычаги можно найти и в живых организмах. По принципу рычага работают руки человека (рис. 65), ноги, голова.

Условие равновесия рычага и момент силы
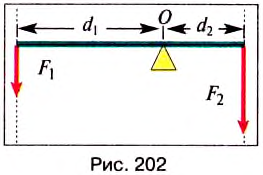
Как уже отмечалось, рычаг — твёрдое тело, которое может вращаться около неподвижной опоры. Его применяют для изменения направления и значения силы, например для уравновешивания большой силы малой. Рычаг имеет следующие характеристики
(рис. 202).
Точка приложения силы — это точка, в которой на рычаг действует другое тело.
Ось вращения — прямая, проходящая через неподвижную точку опоры рычага О, и вокруг которой он может свободно вращаться. Рассмотрим случай, когда ось вращения расположена между точками приложения сил 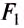
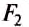
Линия действия силы — это прямая, вдоль которой направлена сила.
Плечо силы — кратчайшее расстояние от оси вращения тела О до линии действия силы. Плечо силы обозначается буквой d. Единицей плеча силы в СИ является один метр (1 м).
Опыт. Возьмём рычаг, подобный изображённому на рис. 203. На расстоянии 10 см от оси вращения подвесим к нему 6 грузиков, каждый массой по 100 г. Чтобы уравновесить рычаг двумя такими же грузиками, нам придётся их подвесить с другой стороны рычага, но на расстоянии 30 см.
Следовательно, для того чтобы рычаг находился в равновесии, нужно к длинному плечу приложить силу, во столько раз меньшую, во сколько раз его длина больше длины короткого плеча. Такое правило рычага описывают формулой обратно пропорциональной зависимости: 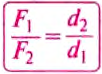
где 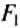
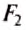
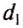
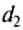
Рычаг находится в равновесии тогда, когда значения сил, действующих на него, обратно пропорциональны плечам этих сил.
С тех пор, когда Архимед установил правило рычага, оно просуществовало в первозданном виде почти 1900 лет. И лишь в 1687 г. французский учёный П. Вариньон придал ему более общую форму, используя понятие момента силы.
Момент силы М— это физическая величина, значение которой опре-Г деляется произведением модуля силы F, вращающей тело, и ее плеча d : 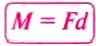
Единицей момента силы в СИ является один ньютон-метр (1 Н • м), равный моменту силы 1 Н, приложенной к плечу 1 м.
Докажем, что рычаг находится в равновесии под действием двух сил, если значение момента М1 силы, вращающей рычаг против часовой стрелки, равно значению момента М2 силы, вращающей его по часовой стрелке, т.е.:
Из правша рычага 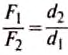
равенство: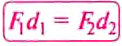
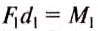
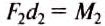
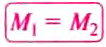
что и требовалось доказать. Итак, правило (условие) равновесия рычага можно ещё сформулировать так.
Рычаг находится в равновесии под действием двух сил, если значение момента силы, вращающей рычаг против часовой стрелки, равно значению момента силы, вращающей его по часовой стрелке.
Момент силы — важная физическая величина, она характеризует действие силы, показывает, что оно зависит и от модуля силы, и от её плеча. Например, мы знаем, что действие силы на дверь зависит и от модуля силы, и оттого, где приложена сила: дверь тем легче повернуть, чем дальше от оси вращения приложена сила, действующая на неё; гайку легче открутить длинным гаечным ключом, чем коротким; ведро тем легче вытянуть из колодца, чем длиннее ручка ворота.
Основы статики и равновесие рычага
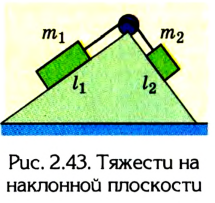
Еще в давние времена люди использовали обычную палку в качестве рычага, выигрывая этим в силе. На рисунке 2.35 показано, как с помощью рычага можно поднять по ступенькам большие каменные глыбы, например для строительства пирамид.
В древних книгах по механике, написанных учеными Греции и Египта, главным образом рассматривались вопросы статики. Важнейшие открытия в этой области принадлежали великому греческому философу Аристотелю, который и дал название «механика» науке, изучающей простейшие движения материальных тел, находящихся в природе или создающихся людьми в процессе их деятельности.
Ученые уже тогда понимали значение статики как одной из основных составляющих фундамента механики. Дальнейшее развитие науки и, особенно, техники подтвердило правильность их вывода: действие огромного количества £ механизмов и машин базируется на законах о равновесии сил.
Аристотель (384-322 до н. э.) — один из известнейших ученых Древней Греции. Изучал вопросы ста-тики, разработал классификацию механических движений, сформулировал закон прямолинейного распространения света, объяснил природу атмосферных явлений и др.
Основы науки о равновесии были заложены еще Архимедом. Именно он ввел в физику такое понятие, как центр тяжести и момент силы относительно точки и оси, определил положение центра тяжести для многих тел и фигур, математически обосновал законы рычага, сформулировал правила приложения параллельных сил.
- Заказать решение задач по физике
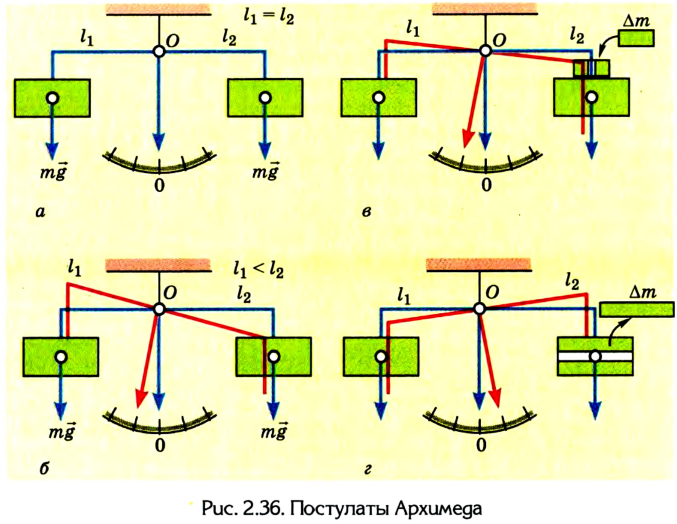
В своей работе «О равновесии плоских фигур» Архимед опирался на положения, которые считал само собой разумеющимися:
Архимед (287-212 до н. э.) — древнегреческий физик, математик, исследователь, инженер. Изучал условия равновесия тел, простые механизмы, плавание тел и др. Установил, что соотношение длины любой окружности к ее диаметру (число 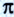
- одинаковые грузы, приложенные к одинаковым плечам рычага, уравновешиваются (рис. 2.36, а);
- одинаковые грузы, приложенные к неодинаковым плечам рычага, не находятся в равновесии; груз, приложенный к более длинному рычагу, падает (рис. 2.36, б);
- если грузы, подвешенные к неодинаковым плечам рычага, уравновешиваются и к одному из них что-либо прибавить, то равновесие нарушится и этот груз будет падать (рис. 2.36, в);
- если при тех же условиях, что в предыдущем случае, один груз уменьшить, то равновесие нарушится, и тогда другой груз будет падать (рис. 2.36, г).
Рычаг находится в равновесии, если плечи сил обратно пропорциональны значениям сил, действующих на него
Из этих положений Архимед сделал вывод: грузы пребывают в равновесии, когда плечи рычага обратно пропорциональны грузам:
Условия равновесия тел. Устойчивое и неустойчивое равновесие
Равновесие — состояние тела, при котором в рассматриваемой системе отсчета отсутствуют перемещения каких-либо его точек под действием приложенных к нему сил.
Вспомним, что момент силы относительно какой-либо оси равен произведению модуля силы на ее плечо: М = Fl. Плечом силы l называется кратчайшее расстояние от оси вращения до линии действия данной силы. Момент силы считается положительным, если сила стремится повернуть тело по часовой стрелке, и отрицательным, если такое действие противоположно. Для равновесия тел необходимы два условия: 1) геометрическая сумма приложенных к телу сил равна нулю:
2) алгебраическая сумма моментов сил относительно любой неподвижной оси равна нулю:
Момент силы: М = Fl.
Условия равновесия тел:
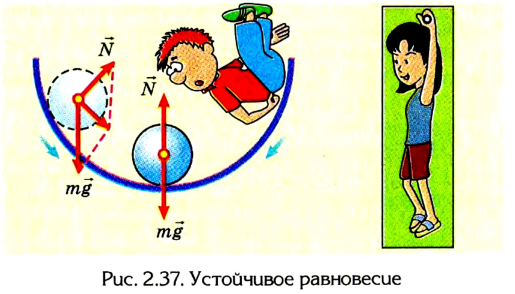
Равновесие устойчивое, если при незначительном смещении тело вновь возвращается в положение равновесия (рис. 2.37).
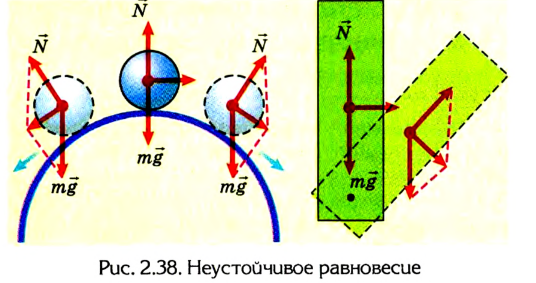
При неустойчивом равновесии незначительное смещение тела вызывает в дальнейшем значительное удаление его от исходного положения (рис. 2.38).
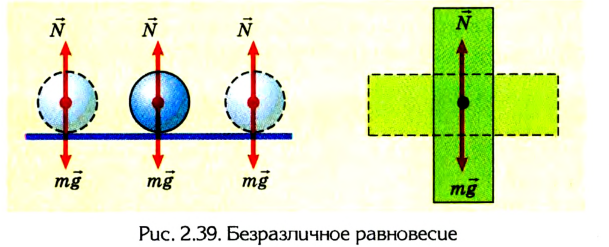
Равновесие тела может быть устойчивым, неустойчивым и безразличным.
Если любые смещения тела не нарушают его состояния равновесия, то можно говорить о безразличном равновесии (рис. 2.39).
Примеры решения задач на равновесие рычага
Рассмотрим примеры решения задач статики.
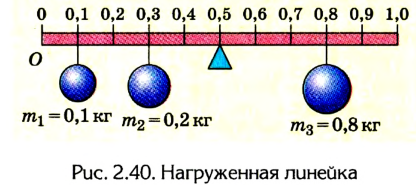
Пример №1
Метровая линейка, весом которой можно пренебречь, положена средним делением на подставку и нагружена гирями (рис. 2.40). Какого направления и значения сила должна быть приложена на делении 1 м для того, чтобы линейка находилась в равновесии? Какой будет сила реакции опоры, если приложить эту силу?
Решение:
Выполняем рисунок в соответствии с условием задачи (рис. 2.41), указав силы и их плечи. Линейка под действием моментов сил может вращаться вокруг неподвижной оси О, которая проходит через точку О. Будем считать положительными все моменты, вращающие систему по часовой стрелке. В задаче это момент силы 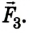
Для упрощения вычислений значение ускорения свободного падения будем считать равным 10
Предположим, что для равновесия системы на конце линейки 1 м должна быть приложена сила 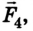
Ответ: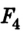
Пример №2
Метровая линейка, весом которой можно пренебречь, положена крайними точками на две опоры и нагружена гирями, как в предыдущей задаче. Нужно определить силы реакции опор 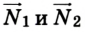
Решение:
Чтобы определить силу реакции опоры 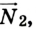
Чтобы определить силу реакции опоры 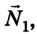
Чтобы найти силы реакции опор, можно воспользоваться правилом сложения параллельных сил. Им же можно пользоваться и для контроля найденных значений.
Ответ: 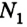
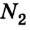
Оригинальный метод решения задач статики был предложен Симоном Сте-вином (1548-1620). Для случаев равновесия тел на наклонной плоскости он доказал, что массы тел соотносятся как длины плоскостей, которые их образуют (рис. 2.43):
Он же установил принцип сложения статических сил (треугольник сил): три силы, действующие на одну точку, находятся в равновесии тогда, когда они бывают параллельны и пропорциональны трем сторонам плоского треугольника (рис. 2.44). Приведем пример решения одной из задач статики с применением треугольника сил.
Пример №3
На кронштейне висит лампа весом 4 Н. Найти значение сил упругости в деталях ОА и ОВ.
Дано:
Р = 4 Н
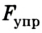
Решение:
Выбираем масштаб построения треугольника. Пусть 1 см на рисунке соответствует значению силы 1 Н. Теперь строим сторону треугольника
А’В’, длина которой известна: 4 см = 4 Н. Эта сторона параллельна направлению силы тяжести, действующей на лампу. Из точки А’ проводим линию, параллельную направлению действия силы в подвесе ОА, а потом из точки В’ — параллельную направлению действия силы в упоре ОВ. На пересечении линий находится точка О’. Таким образом мы получили замкнутый треугольник сил. Зная масштаб, при помощи линейки измеряем значения силы упругости в подвесе ОА (О’А’) и силы реакции в упоре ОВ (О’В’).
- Блоки в физике
- Движение тела под действием нескольких сил
- Наклонная плоскость в физике
- Давление газов и жидкостей
- Равнодействующая сила и движение тела под действием нескольких сил
- Сила давления в физике и единицы давления
- Механическое давление в физике
- Столкновения в физике
Момент силы. Задачи на рычаги.
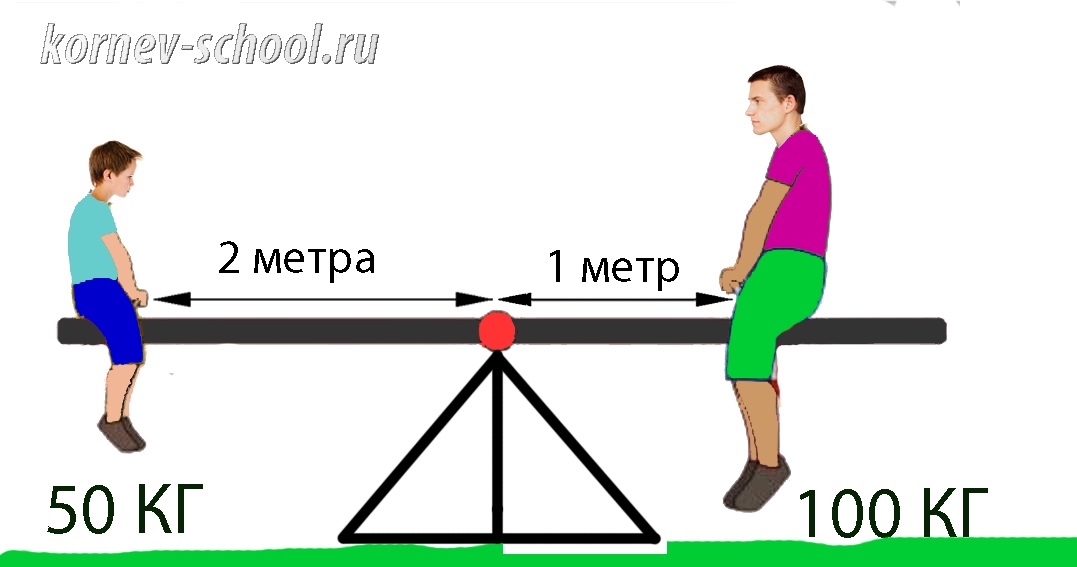
Почему легкий мальчик и взрослый тяжелый мужчина уравновешивают друг друга?
Условие равновесия рычага:
(F_1l_1=F_2l_2)
Для решения простейших задач на рычаги достаточно того, что написано выше
Ниже будет приведено подробное объяснение.
Репетитор по физике
8 916 478 10 32
Плечом силы называют кратчайшее расстояние между линией действия силы и точкой опоры.
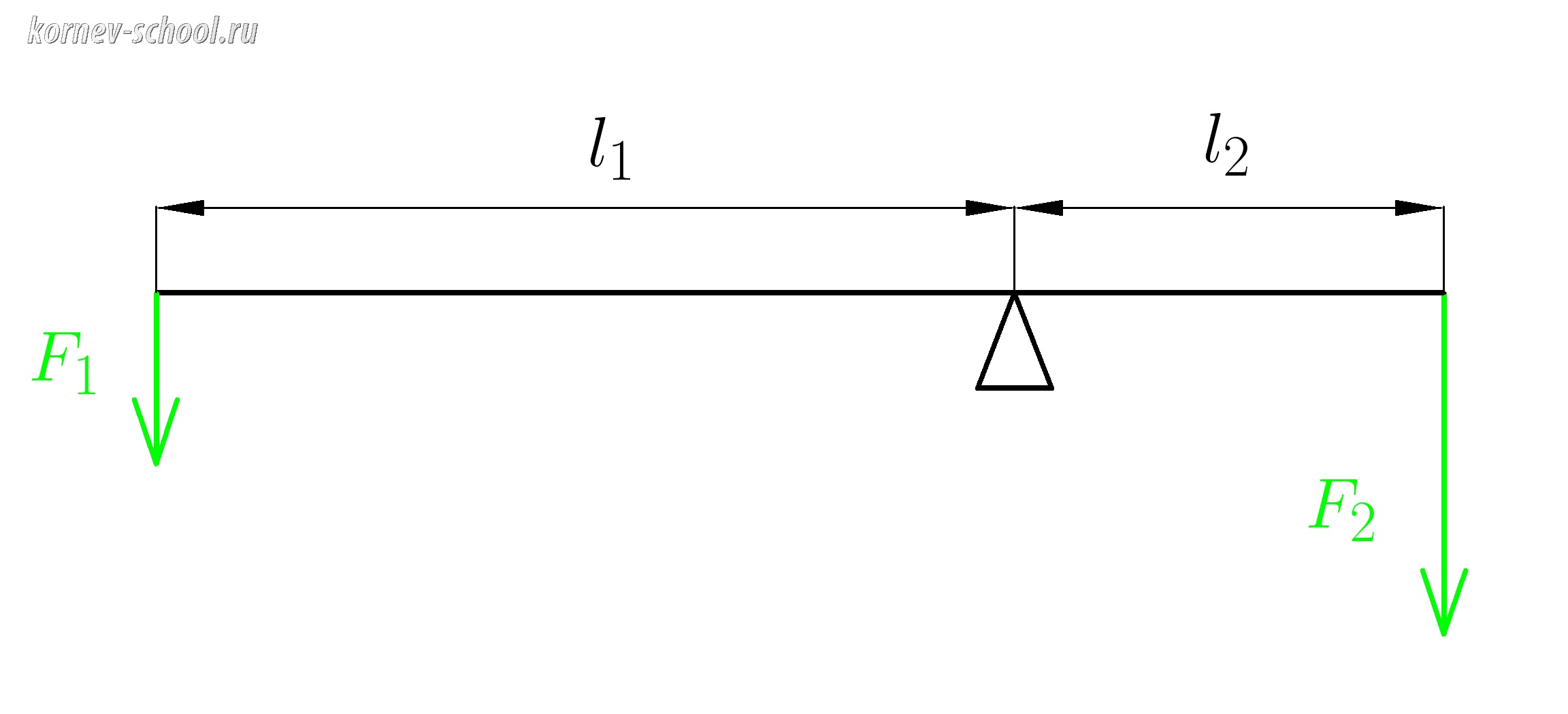
( l_1 ) — плечо силы (F_1 ;;;;; ) ( ;;; l_2 ) — плечо силы (F_2 )
Моментом силы называют произведение (умножение) силы на ее плечо:
(M=Fl) .
Момент силы ( F_1 ) пытается закрутить рычаг против часовой стрелки
Момент силы ( F_2 ) пытается закрутить рычаг по часовой стрелке
Условие равновесия:
Рычаг будет находиться в равновесии если сумма моментов, закручивающих его по часовой стрелке будет равна
сумме моментов, закручивающих его против часовой стрелки.
На нашем рисунке один момент закручивает рычаг по часовой,а другой против часовой стрелки, по этому
условие равновесия для нашего случая выглядит вот так:
(M_1=M_2 )
(F_1l_1=F_2l_2)
Задача 1.
Рычаг изображенный на рисунке находится в равновесии.
Сила (F_2=100Н ) , плечо этой силы (l_2=2м).
Найти силу (F_1) , если ее плечо (l_1=4м).

Показать ответ
Показать решение
Видеорешение
Задача 2.
Рычаг изображенный на рисунке находится в равновесии.
Сила (F_2=6Н ) , плечо этой силы (l_2=0,8м).
Найти силу (F_1) , если ее плечо (l_1=1,6м).

Показать ответ
Показать решение
Видеорешение
Задача 3.
Рычаг изображенный на рисунке находится в равновесии.
Сила (F_1=70Н ) , плечо этой силы (l_1=6м).
Найти силу (F_2) , если ее плечо (l_2=1,5м).
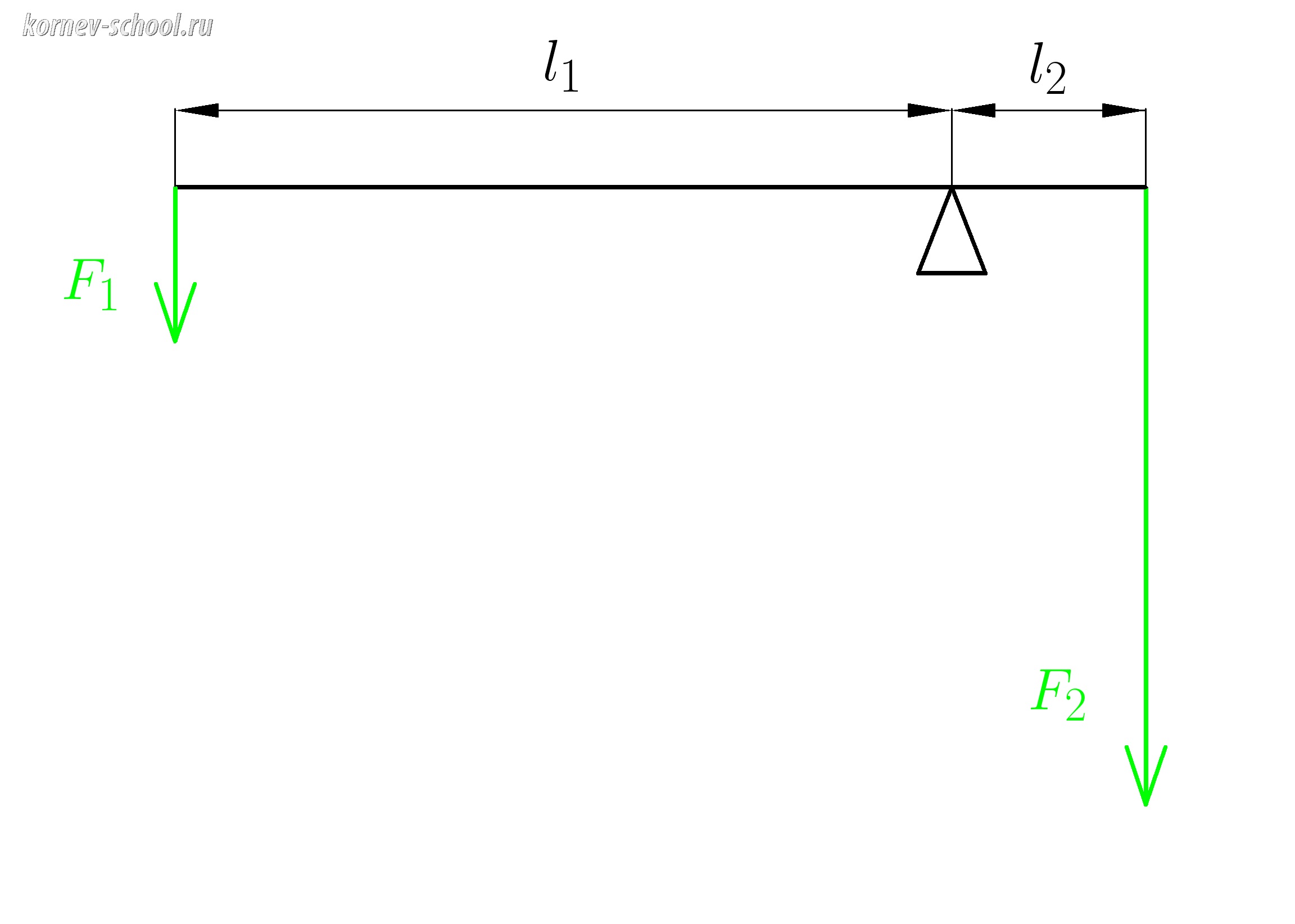
Показать ответ
Показать решение
Видеорешение
Задача 5.
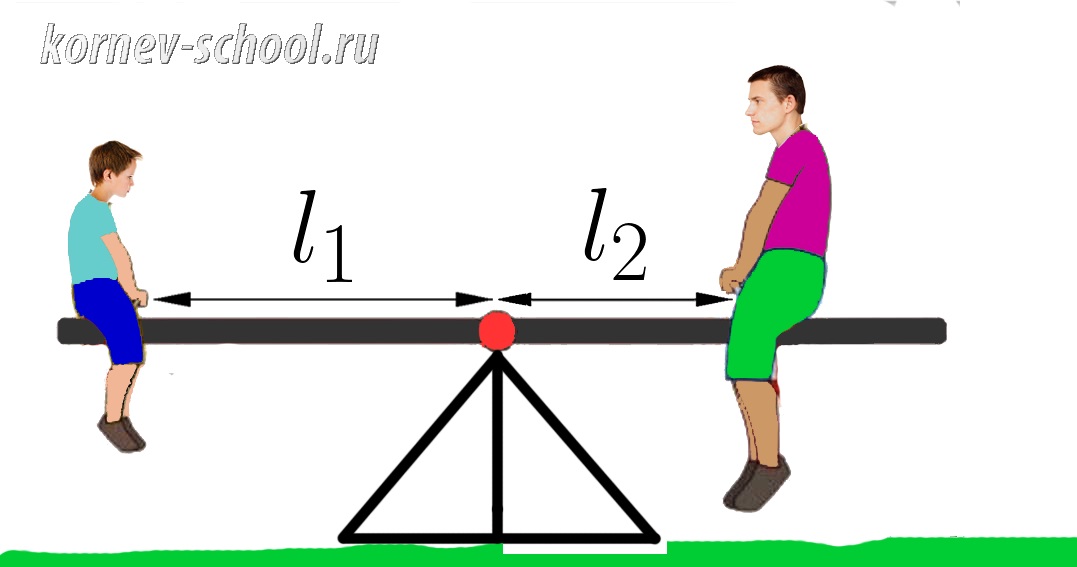
Отец и сын сидят на качелях, при этом они оба не касаются земли и качели находятся в равновесии.
Масса отца составляет 80 килограмм, при этом он сидит на расстоянии (l_2=0,9 м ) от точки опоры качелей.
Найти массу сына, если он сидит на расстоянии (l_1=1,8 м ) от точки опоры качелей.
Показать ответ
Показать решение
Видеорешение
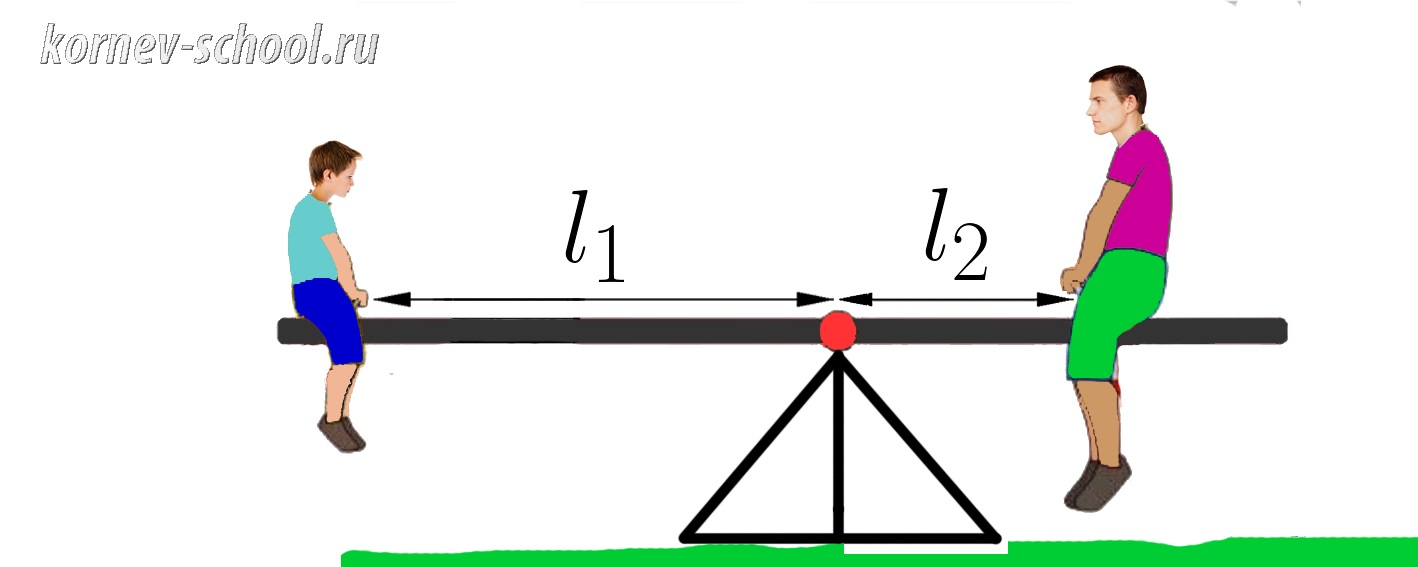
Задача 6.
Отец и сын сидят на качелях, при этом они оба не касаются земли и качели находятся в равновесии.
Масса отца составляет 90 килограмм, при этом он сидит на расстоянии (l_2=0,7 м ) от точки опоры качелей.
На каком расстоянии от точки опоры сидит ребенок, если его масса составляет 30 килограмм ?
Показать ответ
Показать решение
Видеорешение
5. Механика (объяснение явлений)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Статика
Прут массой 5 кг опирается на две точки горизонтальной и вертикальной поверхностей, образуя с первой угол (30^circ) (см. рисунок). Длина прута (AB = 2sqrt{3}) м. Из приведенного ниже списка выберите два верных утверждения, описывающих эту ситуацию.
1) Модуль силы реакции опоры, действующей на прут со стороны вертикальной поверхности, в два раза больше модуля силы трения, действующей на него со стороны горизонтальной поверхности.
2) Момент силы тяжести относительно оси, проходящей через точку (B) перпендикулярно плоскости рисунка, равен 75 Н(cdot)м.
3) Длина плеча силы трения, действующей на прут со стороны вертикальной поверхности, относительно оси, проходящей через точку (O) перпендикулярно плоскости рисунка, составляет 1 м.
4) Момент силы реакции опоры, действующей на прут со стороны горизонтальной поверхности, относитльно оси, проходящей через точку (B) перпендикулярно плоскости рисунка, равен нулю.
5) Длина прута на 20(%) больше длины плеча действующей на него со стороны горизонтальной поверхности силы реакции опоры относительно точки (C).
1) (color{red}{smalltext{Неверно }})
Укажем все силы, действующие на прут (рис. 1):
(F_text{тр1}), (N_1) — сила трения и сила реакции опоры, действующие на прут со стороны вертикальной поверхности;
(mg) — сила тяжести;
(F_text{тр2}) и (N_2) — сила трения и сила реакции опоры, действующие на прут со стороны горизонтальной поверхности.
Запишем второй закон Ньютона с учетом того, что прут покоится: [vec{F}_text{тр1} + vec{N}_1 + mvec{g} + vec{F}_text{тр2} + vec{N}_2 = 0] Введем оси (Ox) и (Oy) (рис. 1) и спроецируем на них все силы: [begin{cases}
Ox: N_1 — F_text{тр2} = 0\
Oy: F_text{тр1} — mg + N_2 = 0
end{cases}
Rightarrow hspace{3mm}
begin{cases}
N_1 = F_text{тр2}\
F_text{тр1} — mg + N_2 = 0
end{cases}] Таким образом, сила реакции опоры (N_1), действующая на прут со стороны вертикальной поверхности, равна силе трения (F_text{тр2}), действующей на него со стороны горизонтальной поверхности.
2) (color{green}{smalltext{Верно }})
Момент силы тяжести относитльно оси, проходящей через точку (B) перпендикулярно плоскости рисунка, равен: [M = mgcdot l,] где (l) — плечо силы. Упростим модель (рис. 1) до двух подобных треугольников (Delta ABC) и (Delta OBH) (рис. 2) и, обратившись к геометрии, выразим длины всех отрезков через сторону (AB).
По рисунку видно, что плечом силы тяжести (l) является отрезок (HB), равный (dfrac{sqrt{3}}{4}AB). Таким образом, момент силы тяжести равен: [M = 5text{ кг}cdot 10text{ }dfrac{text{м}}{text{с}^2}cdotdfrac{sqrt{3}}{4}cdot 2sqrt{3}text{ м} = 75 text{ Н}cdottext{м}]
3) (color{red}{smalltext{Неверно }})
Плечо – это кратчайшее расстояние между осью вращения и линией действия силы.
По рисунку видно, что плечом силы трения, действующей на прут со стороны вертикальной поверхности, относительно оси, проходящей через точку (O) перпендикулярно плоскости рисунка, является отрезок, равный по длине отрезку (CH).
Исходя из рис. 2: [CH = dfrac{sqrt{3}}{4}AB] [CH = dfrac{sqrt{3}}{4}cdot 2sqrt{3}text{ м} = 1,5text{ м}]
4) (color{green}{smalltext{Верно }})
Момент силы трения (M) равен произведению модуля силы реакции опоры (N_2) на ее плечо (l): [M=N_2cdot l] По рисунку видно, что длина плеча силы трения (l) относительно точки (B) равна нулю (так как ось вращения, проходящая через точку (B), перпендикулярна линии действия силы реакции опоры).
Следовательно, и момент силы реакции (M) так же равен нулю: [M = N_2cdot 0text{ м} = 0text{ H}cdottext{м}]
5) (color{red}{smalltext{Неверно }})
По рисунку видно, что плечом силы реакции опоры (N_2), действующей на прут со стороны горизонтальной поверхности, является отрезок (CB).
Исходя из рис. 2: [CB = dfrac{sqrt{3}}{2} AB hspace{2 mm} Rightarrow hspace{2 mm} AB = dfrac{2}{sqrt{3}}] [AB approx 1,15 hspace{1 mm} CB] Следовательно, длина прута (AB) приблизительно на 15(%) больше длины плеча действующей на него со стороны горизонтальной поверхности силы реакции опоры относительно точки (C).
Ответ: 24
Трудолюбивый Вася собрал в лесу 5 кг ягод. Вася хорошо знал физику, поэтому он нашел палку длиной 1,2 м и решил понести корзину с ягодами так, как показано на рисунке. К концу (B) палки в начале пути Вася прикладывал постоянную вертикальную силу, равную 25 Н. Из приведенного ниже списка выберите два верных утверждения, описывающих эту ситуацию. Массой палки пренебречь.
1) Длина короткого конца палки (относительно точки (O)) составляет 40 см.
2) Момент силы, действующей на конец палки (A), относительно точки (O) равен 25 Н(cdot)м.
3) Плечо вертикальной силы, прикладываемой Васей к концу (B) палки, в два раза больше плеча силы, действующей на конец (A).
4) Момент вертикальной силы, действующей на конец (B) палки относительно точки (O) равен 2 Н(cdot)м.
5) Если Вася устанет и будет прикладывать к концу (B) палки силу на 10 Н меньшую, чем прикладывал в начале пути, то ему нужно будет съесть 3 кг собранных ягод, чтобы палка осталась в равновесии (при неизменных прочих условиях).
1) (color{green}{smalltext{Верно }})
Чтобы рычаг (палка) достиг равновесия, моменты сил, действующих на него справа и слева, должны быть равны: (M_1=M_2). В то же время моменты сил (M_1) и (M_2) по определению равны произведению силы на ее плечо: [M_1 = F_1l_1] [M_2 = F_2l_2] На конец (A) палки действует единственная сила — сила тяжести (Rightarrow) (F_1 = mg).
На конец (B) действует вертикальная сила, которую прикладывает Вася (Rightarrow) (F_2 = F).
По рисунку видно, что плечом силы тяжести относительно точки (O) является отрезок (AO), а плечом силы (F) относительно той же точки — отрезок (OB), причем (OB = AB — AO).
Таким образом: [M_1 = mgcdot AO] [M_2 = Fcdot OB] Приравнивая, получаем: [mgcdot AO = Fcdot OB] [mgcdot AO = Fcdot (AB — AO)] [AO = dfrac{Fcdot AB}{F + mg}] [AO = dfrac{25text{ Н}cdot 1,2text{ м}}{25text{ Н}+5text{ кг}cdot 10text{ }dfrac{text{м}}{text{с}^2}} = 0,4text{ м}] Тогда конец (OB) равен: [OB = AB — AO] [OB = 1,2text{ м} — 0,4text{ м} = 0,8text{ м}] Таким образом, длина короткого конца палки действительно составляет 0,4 м = 40 см.
2) (color{red}{smalltext{Неверно }})
Момент силы, действующей на конец палки (A), относительно точки (O) равен: [M = mgcdot AO] [M = 5text{ кг}cdot10text{ }dfrac{text{м}}{text{с}^2}cdot 0,4text{ м} = 20text{ Н}cdottext{м}]
3) (color{green}{smalltext{Верно }})
Найдем отношение плеч: [dfrac{OB}{AO} = dfrac{AB — AO}{AO} = dfrac{1,2text{ м} — 0,4text{ м}}{0,4text{ м}} = 2]
4) (color{red}{smalltext{Неверно }})
Момент вертикальной силы, действующей на конец (B) палки относительно точки (O) равен: [M = Fcdot OB] [M = 25text{ Н}cdot 0,8text{ м} = 20text{ Н}cdottext{м}]
5) (color{red}{smalltext{Неверно }})
Запишем условие равновесия рычага (палки) для двух случаев — до того, как Вася устал, и после: [Fcdot OB = mgcdot AO] [F’cdot OB = m’gcdot AO] Поделим первое выражение на второе и выразим массу (m’) с учетом того, что (F’ = F — 10text{ H}): [dfrac{Fcdot OB}{F’cdot OB} = dfrac{mgcdot AO}{m’gcdot AO}] [m’ = dfrac{mF’}{F} = dfrac{m(F -10text{ Н})}{F}] [m’ = dfrac{5text{ кг}cdot(25text{ Н}-10text{ Н})}{25text{ Н}} = 3text{ кг}] Таким образом, Васе нужно съесть (Delta m = m-m’ = 5text{ кг} — 3text{ кг} = 2text{ кг}) ягод.
Ответ: 13
Доску массой 2 кг удерживают с силой, направленной перпендикулярно ее поверхности. Доска образует с горизонтом угол (alpha = 60^circ) (см. рисунок). Длина доски составляет 160 см.
Из приведенного ниже списка выберите два верных утверждения, описывающих эту ситуацию.
1) Длина плеча силы тяжести относительно оси, проходящей через точку (A) перпендикулярно плоскости рисунка, составляет 40 см.
2) На доску действуют с силой (F), равной 50 Н.
3) Длина плеча силы (F) относительно точки (O) в три раза меньше длины доски.
4) Момент силы (F) относительно оси, проходящей через точку (O) перпендикулярно плоскости рисунка, равен 400 мН(cdot)м.
5) Момент силы тяжести относительно оси, проходящей через точку (A) перпендикулярно плоскости рисунка, равен 8 Н(cdot)м.
1) (color{green}{smalltext{Верно }})
По рисунку видно, что длина плеча силы тяжести (mg) относительно оси, проходящей через точку (A) перпендикулярно плоскости рисунка, равна: [l = dfrac{L}{2}cosalpha] [l = dfrac{1,6text{ м}}{2}cos{60}^circ = 0,4text{ м} = 40text{ см}]
2) (color{red}{smalltext{Неверно }})
Чтобы доска находилась в равновесии, алгебраическая сумма моментов сил, действующих на нее, должна равняться нулю.
Мы ничего не знаем о силе реакции опоры (N), поэтому правило моментов удобнее записать относительно точки (A). В этом случае плечо силы реакции опоры (N) равно нулю. Следовательно, и момент этой силы “зануляется”. [FL — mgdfrac{L}{2}cos{alpha} = 0] [FL = mgdfrac{L}{2}cos{alpha}] [F = dfrac{mg}{2}cos{alpha}] [F = dfrac{2text{ кг}cdot10text{ м/с}^2}{2}cos{60}^circ = 5text{ Н}]
3) (color{red}{smalltext{Неверно }})
По рисунку видно, что длина плеча (OB) силы (F) относительно точки (O) в два раза меньше длины доски (AB).
4) (color{red}{smalltext{Неверно }})
Момент силы (F) относительно оси, проходящей через точку (O) перпендикулярно плоскости рисунка, равен: [M = Fcdotdfrac{L}{2}] [M = 5text{ Н}cdotdfrac{1,6text{ м}}{2} = 4text{ Н}cdottext{м} = 4000text{ мН}cdottext{м}]
5) (color{green}{smalltext{Верно }})
Момент силы тяжести относительно оси, проходящей через точку (A) перпендикулярно плоскости рисунка, равен: [M = mgcdotdfrac{L}{2}cos{alpha}] [M = 2text{ кг}cdot10text{ }dfrac{text{м}}{text{с}^2}cdotdfrac{1,6text{ м}}{2}cos{60}^circ = 8text{ Н}cdottext{м}]
Ответ: 15
Очень лёгкая рейка закреплена на горизонтальной оси (O), перпендикулярной плоскости рисунка, и может вращаться вокруг неё без трения. К рейке приложены четыре силы, изображенные на рисунке.
Из приведенного ниже списка выберите два правильных утверждения
1) Относительно оси (O) максимальное плечо имеет сила (F_4)
2) Относительно оси (O) минимальное плечо имеет сила (F_1)
3) Относительно оси (O) минимальным будет момент, создаваемы силой (F_2)
4) Относительно оси (O) максимальным будет момент, создаваемый силой (F_4)
5) Под действием всех изображенных на рисунке рейка будет вращаться
1) Плечо это — кратчайшее расстояние между линией действия силы и связанной с ней точкой (полюсом или осью вращения). В данном случае макисмальное расстояние будет до силы (F_4)
2) Из пункта 1 минимальное плечо будет до силы (F_2)
3) Момент вычисляет по формуле: [M=Flsin alpha,] где (F) – сила, (l) – плечо силы, (alpha) – угол между силой и плечом.
Найдем моменты для каждой из сил, проецируя силы на ось, перпендикулярную оси вращения [M_1=F_1l_1=20text{ см}cdot 1 text{ Н}=20text{ Н $cdot $ см}] [M_2=F_2l_2=10text{ см}cdot 1 text{ Н}=10text{ Н $cdot $ см}] [M_3=F_3l_3=30text{ см}cdot 3 text{ Н}=90text{ Н $cdot $ см}] [M_4=F_4l_4=40text{ см}cdot 2 text{ Н}=80text{ Н $cdot $ см}] Минимальным будет момент (M_2)
4) Из пункта 3) максимальным будет момент (F_3)
5) У нас силы (F_2) и (F_3) будут вращать рейку по часовой стрелке, а силы (F_1) и (F_4) против часовой стрелки, следовательно, чтобы рейка находилась в равновесии должно выполняться условие [M_2+M_3=M_1+M_4 Rightarrow 10text{ Н $cdot $ см}+90text{ Н $cdot $ см}=20text{ Н $cdot $ см}+ 80text{ Н $cdot $ см}] Как мы видим условие равновесия соблюдено, а значит, рейка вращаться не будет.
Ответ: 13
Из лёгкого жёсткого стержня сделан горизонтальный рычаг с длинами плеч 40 см и 100 см. К короткому концу рычага на нити подвешен груз массой (m), а к длинному концу рычага для уравновешивания приложена некоторая сила. Человек начинает медленно опускать длинный конец рычага, прикладывая к нему вертикально вниз силу (см. рисунок). На графике показана зависимость момента (M) силы тяжести груза (m) (относительно точки опоры рычага) от угла (alpha) между рычагом и горизонтом.
Из приведённого ниже списка выберите два правильных утверждения на основании анализа графика.
1) При повороте рычага плечо действующей на груз силы тяжести не изменяется.
2) Когда уравновешенный рычаг горизонтален, модуль приложенной к его длинному концу силы равен 1 Н.
3) Масса груза (m) равна 500 г.
4) При увеличении угла (alpha) момент силы относительно точки опоры рычага уменьшается.
5) Момент силы (F) относительно точки опоры рычага всё время больше 1 Н(cdot)м.
1) При повороте рычага плечо силы тяжести уменьшается.
2) По графику видно, что при уравновешенном в горизонтальном положении рычага, момент силы равен (M=1) Н(cdot) м, откуда сила [F=dfrac{M}{l_2}=dfrac{1text{ Н$cdot$ м}}{1text{ м}}=1text{ Н}] 3) По правилу моментов [M_1=M_2] или [mgl_1=Fl_2] Откуда масса груза [m=dfrac{Fl_2}{gl_1}=dfrac{1text{ Н$cdot$ м}}{10text{ Н/кг}cdot 0,4text{ м}}=250text{ г}] 4) При увеличении угла (alpha) момент силы (F) относительно точки опоры рычага, равный моменту силы тяжести, уменьшается.
5) По графику момент силы (F) все время не превосходит 1 Н(cdot) м
Ответ: 24

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Представили эту картину? Впечатляюще, правда? Как вы думаете, механизм, о котором идет речь, действительно волшебный или же его действие основано на физических законах?
Сегодня мы разгадаем эту загадку, а еще узнаем:
-
какие механизмы использовали древние строители;
-
что такое рычаг и где он применяется;
-
что такое плечо рычага и момент силы;
-
закон равновесия рычага и золотое правило механики.
Будет интересно, мы обещаем!
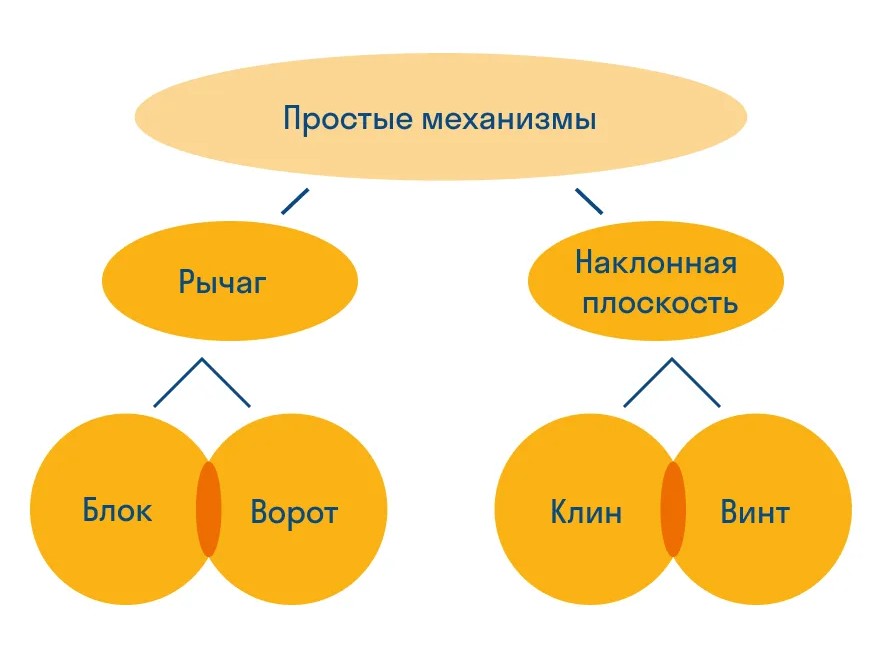
Простые механизмы
Строительство домов, памятников, дворцов и фонтанов — дело не из простых, поэтому еще в древние времена люди изобрели механизмы, которые позволяли упростить процесс.
Простые механизмы — это устройства, которые позволяют изменить величину или направление приложенных к ним сил.
В общем случае простой механизм позволяет затратить меньше усилий для выполнения работы, приложить меньшую силу, получив при этом значительный результат.
К простым механизмам относятся рычаги (на основе которых были созданы блоки и ворот), а также наклонная плоскость, принцип действия которой был заложен в работу клина и винтов.
Обычно простые механизмы — это элементы более сложных устройств, которые используются в быту и промышленности. Без них выполнять такую работу, как поднятие тяжелых предметов на высоту, было бы невозможно.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Рычаг в физике
Рычаг — это твердое тело, которое может вращаться вокруг неподвижной опоры.
Самый простой пример рычага вы могли видеть в мультфильмах или фильмах: герой подставляет большую доску под камень, опирает ее на бочку или ведро, прикладывает силу к краю доски и… поднимает камень! С помощью такой конструкции можно приподнять любой предмет, весь секрет только в расположении опоры (оси вращения) и правильном распределении усилия.
На рисунке представлен демонстрационный рычаг.
— точка опоры, слева и справа от которой подвешены грузы. Заметим, что количество грузов неравное, но рычаг остается в положении равновесия.
Но главное назначение рычага — не быть в равновесии, а давать выигрыш в силе. Каким образом? Все дело в том, что на рычаг могут действовать разные по величине силы, и точки приложения этих сил располагаются на разном расстоянии от точки опоры. Правильно распределив силы и подобрав расстояние до опоры, можно поднять груз, вес которого намного больше, чем сила, приложенная для его подъёма.
Плечо силы рычага
Плечо силы рычага — это кратчайшее расстояние от точки опоры до точки приложения силы.
На рисунке, который мы рассмотрели, отрезки
и
являются плечом сил
и
соответственно.
Чтобы найти плечо, необходимо из точки опоры опустить перпендикуляр на линию действия силы, длина этого перпендикуляра является плечом данной силы.
Условие равновесия рычага
В каком случае рычаг находится в равновесии? Как необходимо расположить точки приложения сил, чтобы достигнуть этого состояния? Это условие было сформулировано еще много столетий назад.
Рычаг будет находится в равновесии, если силы, действующие на него, обратно пропорциональны плечам этих сил:
, где
и
— приложенные к рычагу силы,
и
— плечи сил
и
соответственно.
Давайте еще раз рассмотрим рисунок:
Предположим, вес одного груза —
, а единичный отрезок равен 1 м. Тогда
м,
м:
Момент силы и рычаги
Правило равновесия рычагов можно переписать, используя понятие «момент силы». Но что это такое?
Момент силы — это произведение величины силы на ее плечо.
В теме 7 класса «Рычаги в физике» вы также можете встретить и другое определение.
Момент силы — физическая величина, характеризующая действие силы на объект, которое вызывает его вращательное движение.
Простыми словами, момент силы — это величина, которая дает характеристику вращательному усилию. Представьте, что вам необходимо закрутить гайку с помощью гаечного ключа. Вы берете ключ, причем автоматически перемещаете руки на его крайнюю часть — так выполнять действие намного проще. Говоря физическим языком, вы увеличиваете плечо силы, чтобы не прикладывать много усилий для закручивания гайки. А еще таким образом вы увеличиваете величину момента вращения.
В физике момент силы обозначается буквой
а измеряется в
Формула момента силы:
Преобразуем условие равновесия рычагов, умножив накрест по основному свойству пропорции:
а так как
то
А значит, сформулировать условие равновесия рычага можно так: рычаг будет находиться в равновесии, когда моменты сил, приложенных к его разным концам, равны.
Задачи
Закрепим пройденный материал, решив парочку задач.
Задача 1
Длина меньшего плеча рычага — 0,05 м, большего — 0,8 м. На меньшее плечо действует 16 H. Какую силу нужно приложить к большему плечу, чтобы уравновесить рычаг (весом рычага можно пренебречь)?
Ответ: 0,012 м.
Золотое правило механики
Как мы видим, рычаги могут дать значительный выигрыш в силе. Этим свойством пользовались древние строители, когда возводили монументальные сооружения. Но помимо выгоды, есть и достаточно плохая новость: чем больший выигрыш в силе нам нужно получить, тем значительнее должны отличаться плечи сил.
Представьте, что вам необходимо поднять камень в тонну при вашей массе 50 кг. Силы отличаются в 200 раз! А значит, и плечи сил должны отличаться во столько же. Если между камнем и точкой опоры будет 0,5 метра, то расстояние от вас до точки опоры должно быть не менее 100 метров. Придется очень потрудиться, чтобы найти доску такой длины.
Золотое правило механики гласит: во сколько раз мы выигрываем в силе, во столько же раз проигрываем в расстоянии.
Применение рычагов
Рычаги встречаются нам ежедневно в обычной жизни, просто до изучения этой темы вы могли их не замечать. Так, ножницы, щипцы для раскалывания орехов, пинцет, механические весы и весло в лодке являются типичными рычагами: у них есть явная точка опоры и плечи сил.
В теле человека тоже есть система рычагов. К ним можно отнести кости рук, ног, пальцев и даже челюсть и череп. Мышцы руки, такие как бицепс и трицепс, тоже можно назвать рычагами: они участвуют во многих движениях, поочередно растягиваясь и сжимаясь.
Виды рычагов
Рычаги делятся на три вида по своему строению. Рассмотрим каждый из них.
В рычаге первого типа точки приложения сил лежат по разные стороны от точки опоры, силы направлены в одну сторону. Одна из сил стремится повернуть рычаг по часовой стрелке, другая — против часовой стрелки.
Примеры: лом, пила, ножницы, плоскогубцы, детские качели.
В рычаге второго рода обе точки приложения сил лежат по одну сторону от точки опоры, причем одна из сил имеет меньшее плечо. Примером такого рычага является обычная садовая тачка: чтобы поднять груз, находящийся в ней, необходимо направить нашу силу вверх, чуть приподнимая тачку.
Еще к рычагам второго типа можно отнести щипцы для колки орехов, ключ для открывания бутылок.
В рычаге третьего типа обе точки приложения сил лежат по одну сторону от точки опоры, но тело, которое необходимо поднять, имеет большее плечо силы. Чтобы поднять такое тело, нам необходимо приложить силу, во много раз превышающую вес груза. К таким рычагам можно отнести ложку, метлу, заднюю дверь багажника и капот легковых автомобилей.
Великий греческий ученый Архимед как-то сказал: «Дайте мне точку опоры, и я сдвину (переверну) Землю!». Имел ли он в виду, что может действительно создать такой масштабный рычаг, сейчас никто не подтвердит. Но мы точно знаем: уверенность в своих силах и знаниях позволит вам справиться с любым сложным делом. Именно такую уверенность дают онлайн-курсы физики в школе Skysmart. Записывайтесь на уроки, и тогда все вам будет нипочем: и школьные уроки физики, и лабораторные работы, и даже олимпиады. И тогда вы, как и Архимед, сможете сказать про себя: я могу сдвинуть даже Землю!💪
Как известно, вся классическая механика делится на кинематику, динамику и статику. Про кинематику и динамику мы уже писали, а сегодня расскажем про статику и займемся решением задач.
Не забывайте подписаться на наш телеграм-канал и получать полезную рассылку каждый день.
Задачи на статику и равновесие тел
Мы не будем решать страшные задачи по теормеху, сопротивлению материалов или предмету Тут Моя Могила Теория Машин и Механизмов (ТММ). Разберем несколько примеров, связанных с равновесием и простейшими механизмами.
Именно на базе статики строится знаменитый сопромат, столь нелюбимый технарями.
Задача №1. Момент силы
Условие
На рычаг в состоянии равновесия действуют две силы. Момент первой равен 20 Н*м. Модуль второй силы равен 5 Н. Найдите плечо второй силы.
Решение
Запишем условие равновесия рычага:
Отсюда:
Ответ: 4м.
Задача №2. Статика
Условие
На концах рычага действуют силы с модулями 20 и 120 Н соответственно. Рычаг находится в равновесии. Найдите длину рычага, если расстояние от точки опоры до большей силы равно 2 см.
Решение
Запишем равенство моментов:
Ответ: 14 см.
В этой задаче мы не переводили размерности в систему СИ.
Задача №3. Расчет силы
Условие
Рабочий на стройке поднимает плиту с помощью рычага. Большее плечо равно 2,4м, меньшее — 0,8м. Какую силу прикладывает рабочий к большему плечу рычага, если масса плиты равна 120 кг?
Решение
Обозначим большее плечо через d1. К нему рабочий прикладывает искомую силу F1. Вторая сила, приложенная к меньшему плечу, равна весу плиты.
Ответ: 400 Н.
Задача№4. Подвижный блок
Условие
Какую силу нужно приложить, чтобы поднять груз весом 1000 Н с помощью подвижного блока? Какую работу совершит эта сила при подъеме груза на 1 метр?
Подвижный блок позволяет выиграть в усилии в два раза.
Решение
Найдем силу и работу:
Ответ: 500 Н, 1000 Дж.
Задача №5. Нахождение плеча рычага
Условие
На плечи рычага действуют силы 300 Н и 20 Н. Меньшее плечо равно 5см. Найдите большее плечо рычага.
Решение
Условие равновесия рычага можно записать так:
Ответ: 75 см.
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Вопросы и ответы по статике
Вопрос 1. Что нужно, чтобы тело находилось в равновесии, каково условие равновесия тел?
Ответ. Из законов Ньютона известно, что тело движется равномерно или покоится, если равнодействующая всех сил, приложенных к нему, равна нулю. Это и есть условие равновесия.
Это условие справедливо только для тела, которое может двигаться поступательно, но не может вращаться вокруг некоторой оси.
Вопрос 2. Каково условие равновесия для вращающихся тел?
Ответ. Если тело имеет неподвижную ось вращения, то оно находится в равновесии, если алгебраическая сумма моментов всех сил, приложенных к телу относительно этой оси, равна нулю.
Вопрос 3. Что такое момент силы?
Ответ. Момент силы — скалярная физическая величина, равная произведению модуля силы F на плечо силы d.
Вопрос 4. Что такое плечо силы?
Ответ. Плечо силы — это длина перпендикуляра, проведенного от оси вращения к линии действия силы.
Вопрос 5. Материальные тела в статике считаются упругими, или абсолютно твердыми?
Ответ. Абсолютно твердыми. Деформации и изменение размеров тела под действием сил не принимаются во внимание при решении задач, если иное не оговорено в условии.
Вопрос 6. Что такое рычаг в механике?
Ответ. Рычаг — простейший механизм. Рычагом может быть любое тело, которое может вращаться вокруг неподвижной опоры или подвеса. Используется для создания большего усилия на меньшем плече за счет меньшего усилия на длинном плече.
Статика: определение
Статика — раздел теоретической механики, изучающий основы равновесия тел.
Нужна помощь в решении более сложных заданий? Не знаете, как решать задачи по теоретической механике? Обращайтесь в профессиональный студенческий сервис.