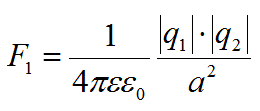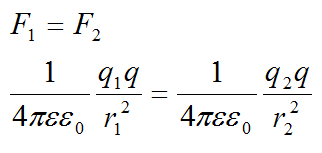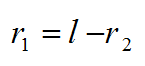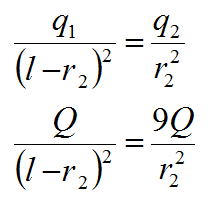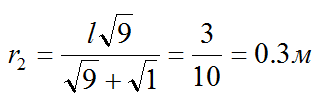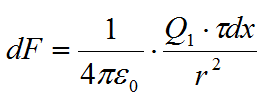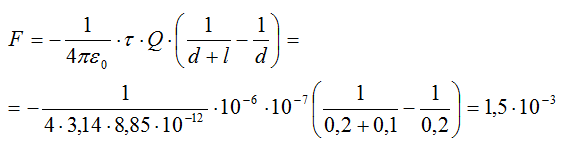Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Между двумя точечными заряженными телами сила электрического взаимодействия равна 12 мН. Если заряд одного тела увеличить в 3 раза, а заряд другого тела уменьшить в 4 раза и расстояние между телами уменьшить в 2 раза, то какова будет сила взаимодействия между телами? (Ответ дайте в мН.)
2
Между двумя точечными заряженными телами сила электрического взаимодействия равна 24 мН. Если заряд одного тела увеличить в 2 раза, а заряд другого тела уменьшить в 3 раза и расстояние между телами увеличить в 2 раза, то какова будет сила взаимодействия между телами? (Ответ дайте в мН.)
3
Между двумя точечными заряженными телами сила электрического взаимодействия равна 20 мН. Если заряд одного тела увеличить в 4 раза, а заряд другого тела уменьшить в 5 раз и расстояние между телами уменьшить в 2 раза, то какова будет сила взаимодействия между телами? (Ответ дайте в мН.)
4
Между двумя точечными заряженными телами сила электрического взаимодействия равна 12 мН. Если заряд одного тела увеличить в 2 раза, а заряд другого тела уменьшить в 3 раза и расстояние между телами уменьшить в 2 раза, то какова будет сила взаимодействия между телами? (Ответ дайте в мН.)
5
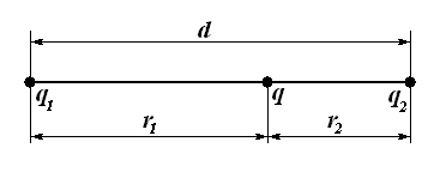
Два точечных заряда — отрицательный, равный по модулю 3 мкКл, и положительный, равный по модулю 4 мкКл, расположены на расстоянии 1 м друг от друга. На расстоянии 1 метр от каждого из этих зарядов помещают положительный заряд Q, модуль которого равен 2 мкКл. Определите модуль силы, действующей на заряд Q со стороны двух других зарядов. Ответ выразите в мН и округлите до целого числа.
Пройти тестирование по этим заданиям
ЕГЭ Закон Кулона. ЗАДАЧИ с решениями
Формулы, используемые на уроках «Задачи на взаимодействие зарядов и закон Кулона».
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Два шарика, расположенных на расстоянии г = 20 см друг от друга, имеют одинаковые по модулю заряды и взаимодействуют в воздухе с силой F = 0,3 мН. Найти число нескомпенсированных электронов N на каждом шарике.

Задача № 2.
С какой силой взаимодействовали бы в воздухе две капли воды массами по m = 1 г, расположенные на расстоянии г = 50 см друг от друга, если бы одной из них передали 10% всех электронов, содержащихся в другой капле?
Задача № 3.
Два одинаковых шарика зарядили так, что заряд одного из них оказался по модулю в п раз больше другого. Шарики привели в соприкосновение и развели на вдвое большее, чем прежде, расстояние. Во сколько раз изменилась сила их кулоновского взаимодействия, если их заряды до соприкосновения были разноименными?
Задача № 4.
Два маленьких заряженных шарика взаимодействуют в вакууме с некоторой силой, находясь на расстоянии r1 друг от друга. На каком расстоянии r2 друг от друга они будут взаимодействовать в среде с диэлектрической проницаемостью ε2, если сила их взаимодействия останется прежней?
Задача № 5.
Маленьким шариком с зарядом q коснулись внутренней поверхности очень большого незаряженного металлического шара, в результате чего на большом шаре поверхностная плотность зарядов стала равна σ. Найти объем V большого шара. Среда — воздух.
Смотреть решение и ответ

Задача № 6.
Два металлических шарика имеют массу m = 10 г каждый. Какое число электронов N надо удалить с каждого шарика, чтобы сила их кулоновского отталкивания стала равна силе их гравитационного тяготения друг к другу?
Смотреть решение и ответ

Задача № 7.
Между двумя одноименными точечными зарядами q1 = 1 • 10–8 Кл и q2 = 4 • 10–8 Кл, расстояние между которыми r = 9 см, помещают третий заряд q0 так, что все три заряда оказываются в равновесии. Чему равен этот третий заряд q0 и каков его знак? На каком расстоянии r1 от заряда q1 он располагается?
Задача № 8.
Заряды q1 = 20 нКл и q2 = –30 нКл расположены на некотором расстоянии друг от друга (рис. 1-10). Заряд q0 помещают сначала в точку 1, расположенную слева от заряда q1 на расстоянии r/2 от него, а затем в точку 2, расположенную между зарядами q1 и q2. Найти отношение силы F1, с которой заряды q1 и q2 действуют на заряд q0 в точке 1, к силе F2, с которой они действуют на него в точке 2.
Задача № 9.
В вершинах равностороннего треугольника находятся одинаковые заряды q = 2 нКл (рис. 1-11). Какой заряд q0 надо поместить в центр треугольника С, чтобы система всех этих зарядов оказалась в равновесии? Будет ли равновесие устойчивым?
Задача № 10.
В вершинах квадрата расположены заряды q (рис. 1-12). Какой заряд q0 и где надо поместить, чтобы вся система зарядов оказалась в равновесии? Будет ли равновесие устойчивым?
Задача № 11.
В трех соседних вершинах правильного шестиугольника со стороной а расположены положительные заряды q, а в трех других — равные им по модулю, но отрицательные заряды. С какой силой F эти шесть зарядов будут действовать на заряд q0, помещенный в центр шестиугольника (рис. 1-13)?
Задача № 12.
Два одинаковых маленьких шарика массами по m = 10 г каждый заряжены одинаково и подвешены на непроводящих и невесомых нитях так, как показано на рис. 1-14. Какой заряд q должен быть на каждом шарике, чтобы нити испытывали одинаковое натяжение? Среда — воздух, длина каждой нити l = 30 см.
Задача № 13.
На изолирующей нити подвешен маленький шарик массой m = 1 г, имеющий заряд q1 = 1 нКл. К нему снизу подносят на расстояние г = 2 см другой заряженный маленький шарик, и при этом сила натяжения нити уменьшается вдвое. Чему равен заряд q2 другого шарика? Среда — воздух.
Задача № 14.
Два одинаковых маленьких шарика подвешены на невесомых нитях длиной I каждая в одной точке. Когда им сообщили одинаковые заряды q, шарики разошлись на угол а (рис 1-16). Найти силу натяжения Fн каждой нити. Среда — воздух.
Задача № 15.
Два одинаково заряженных шарика, подвешенных на нитях равной длины, разошлись на некоторый угол (рис. 1-17, а). Чему равна плотность материала шариков р, если после погружения их в керосин угол между нитями не изменился (рис. 1-17, б)? Относительная диэлектрическая проницаемость воздуха ε1 = 1, относительная диэлектрическая проницаемость керосина ε2 = 2. Плотность керосина р0 = 800 кг/м3.
(с) В учебных целях использованы цитаты из учебного пособия «Новый репетитор по физике для подготовки к ЕГЭ : задачи и методы их решения / И.Л. Касаткина; под ред. Т.В. Шкиль. — Ростов н /Д : Феникс».
Это конспект по теме «ЕГЭ Закон Кулона. ЗАДАЧИ с решениями». Выберите дальнейшие действия:
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Закон Кулона .
Заряды одного знака отталкиваются, а заряды разных знаков притягиваются
Положительный заряд ( q_1=5 нКл ) и отрицательный заряд (q_2=-2 мкКл ) будут притягиваться
В формуле заряды ( q_1 и q_2 ) заключены в модули
(F=kdfrac{left | q_1 right | left | q_2 right | }{R^2} )
Если заряды одного знака, то формулу можно записать без модулей:
(F=kdfrac{q_1q_2}{R^2} )
(k ) — коэффициент пропорциональности
( k=9 cdot 10^{9} ;; dfrac {Нcdot м^2}{Кл^2} )
(q_1 ) — первый заряд
(q_2 ) — второй заряд
(R ) — расстояние между зарядами
Задача 1.
Найти силу с которой отталкиваются друг от друга два точечных заряда ( q_1=10^{-6} Кл ; и ; q_2=10^{-7} Кл ,)
если расстояние между зарядами (R=1м .)
( k=9 cdot 10^{9} ;; dfrac {Нcdot м^2}{Кл^2} )
Показать ответ
Показать решение
Видеорешение
Задача 2.
Найти силу с которой отталкиваются друг от друга два точечных заряда ( q_1=1 нКл ; и ; q_2=5 нКл ,)
если расстояние между зарядами (R=1 см .)
( k=9 cdot 10^{9} ;; dfrac {Нcdot м^2}{Кл^2} )
Показать ответ
Показать решение
Видеорешение
Задача 3.
Два точечных заряда отталкиваются друг от друга с силой (F=7,2 cdot 10^{-5} Н ) и находятся на расстоянии (R=10 см ) друг от друга
Первый заряд (q_1= 8 нКл . )
Найти заряд (q_2 . )
( k=9 cdot 10^{9} ;; dfrac {Нcdot м^2}{Кл^2} )
Дать ответ в нанокулонах.
Показать ответ
Показать решение
Видеорешение
Задача 4.
На каком расстоянии находятся друг от друга точечные заряды (q_1=5 мкКл ; и ; q_2=2 мкКл , ) если
они взаимодействуюм друг с другом с силой (F=0,09 Н )
( k=9 cdot 10^{9} ;; dfrac {Нcdot м^2}{Кл^2} )
Показать ответ
Показать решение
Видеорешение
Задача 7.
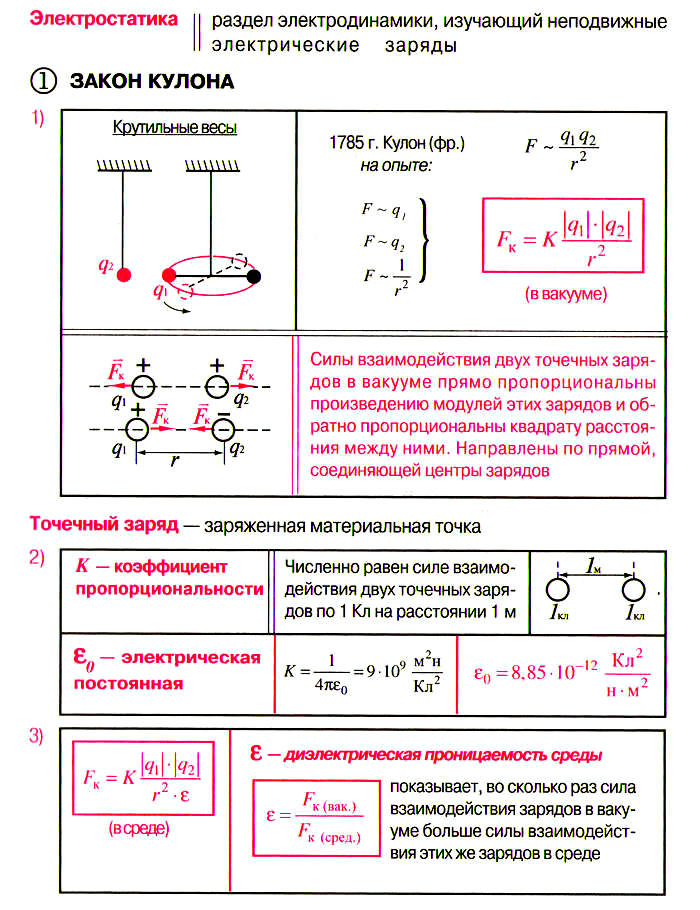
Заряды (q_1=5 мкКл,q_2=2 мкКл ;и;q_3=40 нКл ) расположены как показано на рисунке.
(R_1= 60см, R_2=40см. )
Какая сила будет действовать на третий заряд со стороны первого и второго зарядов?
( k=9 cdot 10^{9} ;; dfrac {Нcdot м^2}{Кл^2} )
Показать ответ
Показать решение
Видеорешение
Задача 8.
Заряды (q_1=50 мкКл,q_2=225 мкКл ;и;q_3=125 мкКл ) расположены как показано на рисунке.
(R_1= 150см, R_2=100см. )
Какая сила будет действовать на первый заряд со стороны второго и третьего зарядов?
( k=9 cdot 10^{9} ;; dfrac {Нcdot м^2}{Кл^2} )
Показать ответ
Показать решение
Видеорешение
Задача 9.
Заряды (q_1=1 мкКл,q_2=3 мкКл ;и;q_3=8,1 мкКл ) расположены как показано на рисунке.
(R_1= 100см, R_2=90см. )
Какая сила будет действовать на второй заряд со стороны первого и третьего зарядов?
Куда направлена эта сила?
( k=9 cdot 10^{9} ;; dfrac {Нcdot м^2}{Кл^2} )
Показать ответ
Показать решение
Видеорешение
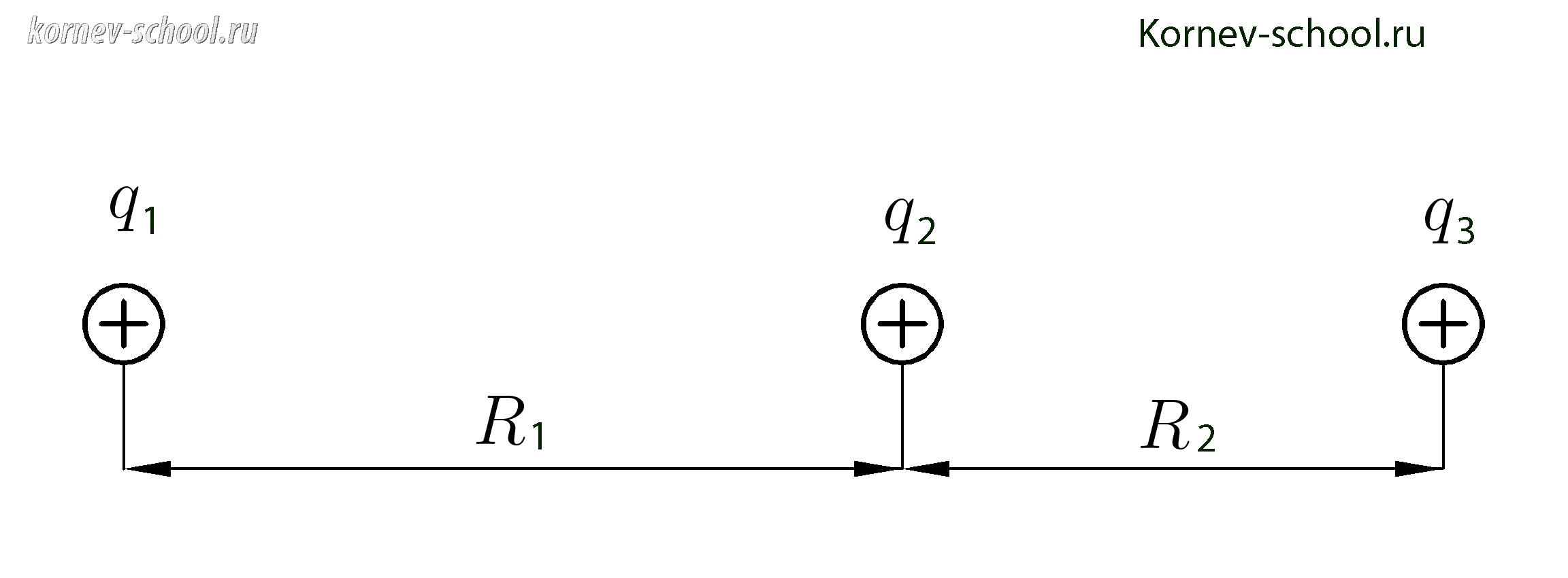
Задача 10.
Заряды (q_1=1 мкКл,q_2=3 мкКл ;и;q_3=-8,1 мкКл ) расположены как показано на рисунке.
(R_1= 100см, R_2=90см. )
Какая сила будет действовать на третий заряд со стороны первого и второго зарядов?
Куда направлена эта сила?
( k=9 cdot 10^{9} ;; dfrac {Нcdot м^2}{Кл^2} )
Показать ответ
Показать решение
Видеорешение
Закон Кулона: сложные задачи
В этой статье собраны задачи довольно сложные, требующие знания и геометрии так же, как и физики. Здесь мы вспомним законы Ньютона, и еще раз повторим как разложить силы на проекции по осям.
Задача 1.
Три точечных заряда мкКл,
и
расположены на окружности радиусом
см так, как показано на рисунке. Найти модуль и направление (угол с горизонтом) силы, действующей на заряд
со стороны двух других.
Задача 1
Модуль силы взаимодействия зарядов и
равен (заряды отталкиваются):
Модуль силы взаимодействия зарядов и
равен (заряды притягиваются):
Расстояние , или сразу
, определим из теоремы Пифагора:
Треугольник равнобедренный, острые углы равны
, поэтому угол
— прямой, и смежный с ним угол (угол между векторами сил
и
) также прямой. Поэтому равнодействующую можно определить по теореме Пифагора:
Определим угол наклона равнодействующей к горизонту. Проще всего определить тангенс угла :
Однако — не искомый угол. Искомый угол – это угол
. Он равен
. Угол
дополняет угол
до
, поэтому
Искомый угол:
Ответ: 18 Н, .
Задача 2.
На гладкую замкнутую непроводящую нить длиной см нанизаны три бусинки с зарядами
мкКл,
и
. Система находится в равновесии. Найти силу натяжения нити
.
Задача 2
Задача довольно-таки непростая, так как сразу понятно, что, имея одноименные заряды, шарики будут отталкиваться друг от друга и в результате расположатся в вершинах треугольника, только вот длины сторон этого треугольника и его углы непонятно, какие.
Обозначим стороны через , а углы через
. Тогда можно записать теорему синусов для данного треугольника:
Модули сил взаимодействия между зарядами будут равны:
Из рисунка понятно, что, поскольку шарики все нанизаны на одну и ту же нить, и сила ее натяжения не может быть разной на отдельных участках, а везде одинакова, то
Отсюда имеем:
Или
Тогда
Известно, что , подставим:
Найдем :
Найдем :
И, наконец, :
Тогда
Ответ: 10 Н
Задача 3.
Три шарика соединены между собой одинаковыми резиновыми шнурами так, что получился правильный треугольник. Система лежит на гладком горизонтальном столе. Какие одинаковые заряды надо сообщить шарикам, чтобы площадь треугольника увеличилась в 4 раза? Коэффициент жесткости каждого шнура , начальная длина
.
Площадь изменяется пропорционально квадрату коэффициента подобия, поэтому, если площадь выросла вчетверо, то, следовательно, длина шнура увеличилась вдвое: .
Тогда модуль силы взаимодействия между соседними зарядами равен:
Причем удлинение шнура равно: .
Откуда величина заряда равна:
Ответ:
Задача 4.
По кольцу, расположенному горизонтально, могут свободно перемещаться три шарика. Заряд первого шарика , второго и третьего —
каждый. Чему равно отношение зарядов
, если при равновесии дуга между зарядами
составляет
?
Задача 4
Шарики будут находиться в равновесии, если будет соблюдаться условие
По теореме синусов можем записать, что
Здесь — модули сил. Например,
Определим , по теореме косинусов для треугольника
:
Или
Тогда сила равна:
Сила взаимодействия между зарядами равна:
Определим из ранее записанной теоремы синусов соотношение сил:
С другой стороны,
Приравняем правые части:
Откуда
В знаменателе имеем , заменим его выражением
:
Ответ:
Задача 5.
В центре равностороннего треугольника находится заряд мкКл. Какие одинаковые заряды следует поместить в вершинах треугольника, чтобы вся система находилась в равновесии?
Рассмотрим рисунок:
Задача 5
Необходимо, чтобы заряды в вершинах отталкивались, поэтому они должны быть отрицательными.
Из рисунка понятно, что условие равновесия
Откуда
— радиус описанной окружности данного треугольника, поэтому
.
Ответ: 1 мкКл.
Задача 6.
В непроводящей сфере радиусом см находятся 4 маленьких шарика массой
г каждый. Какие по величине одноименные заряды нужно сообщить шарикам, чтобы в положении равновесия они расположились в углах квадрата со стороной
?
Задача 6
Шарики упали бы вниз, на донышко, да не тут-то было. Сила Кулона не дает им приблизиться друг к другу, и поэтому они разошлись на то максимальное расстояние, которое позволила им сила тяжести. Шарики опираются о стенку сферы и на них действует, кроме упомянутых силы тяжести и кулоновой силы, еще и сила реакции опоры.
Нарисуем вид сверху: из рисунка понятно, что расстояние между шариками, находящимися по диагонали квадрата, не равно , то есть шарики расположились не на диаметре сферы, а ниже. Определим, насколько: в прямоугольном треугольнике
определим длину катета
. Нам известна длина гипотенузы, она равна радиусу сферы, ведь
— ее центр. Расстояние
— радиус окружности сечения той плоскостью, в которой расположились шарики. Его можно найти из треугольника
:
Тогда
Тогда получается, что треугольник равнобедренный, и оба острых угла у него по
.
Запишем уравнение по второму закону Ньютона:
Распишем по осям:
Определим кулонову силу. Каждый шарик взаимодействует с тем, что напротив него (по диагонали), и с обоими смежными шариками. Тогда:
Задача 6
Найдем силу реакции опоры:
Подставим силу реакции и кулонову силу:
Ответ: 2,7 мкКл
Никакой воды. Только типовые задачи с подробным разъяснением и ответом.
Полезная и ежедневная рассылка для студентов всех специальностей – на нашем телеграм-канале.
Задача 1
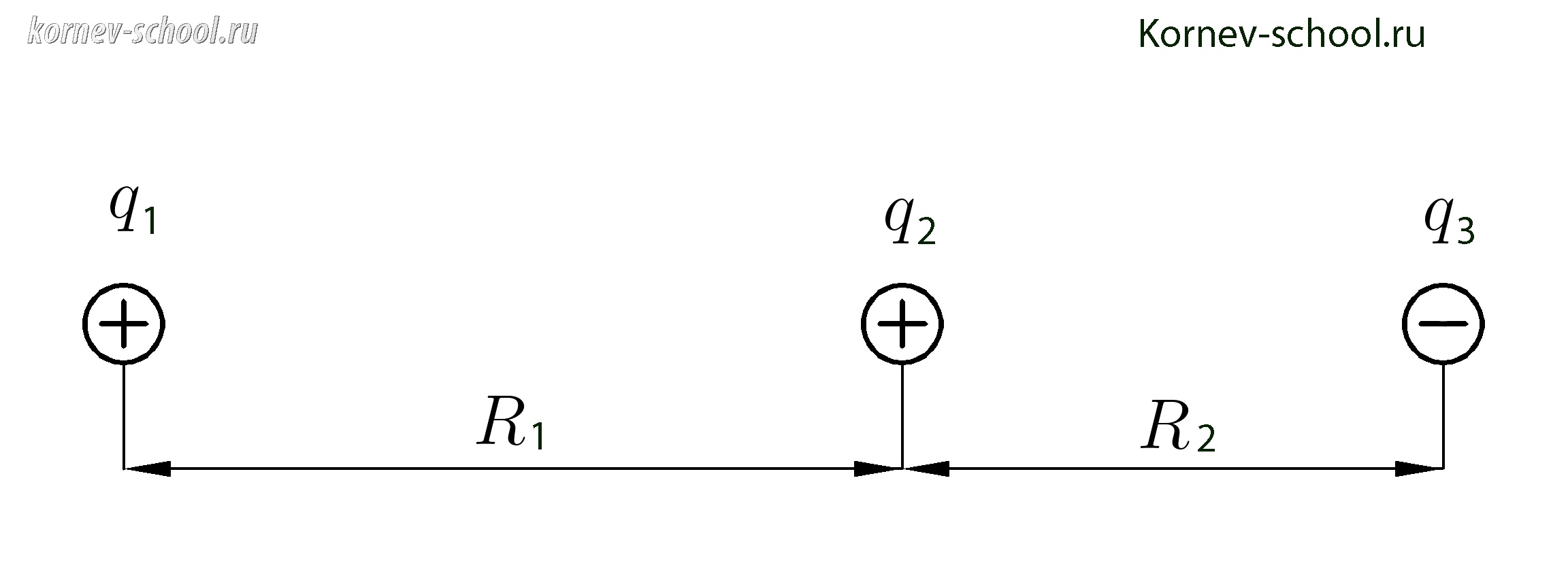
Три одинаковых точечных заряда q1=q2=q3=2 нКл находятся в вершинах равностороннего треугольника со стороной a=10 см. Определить модуль и направление силы F, действующей на один из зарядов со стороны двух других.
Решение
Очевидно, задача требует рисунка. Выполним его:
В данной задаче при решении применяется закон Кулона:
Сила взаимодействия двух точечных зарядов в вакууме направлена вдоль прямой, соединяющей эти заряды, пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними. Она является силой притяжения, если знаки зарядов разные, и силой отталкивания, если эти знаки одинаковы.
Сила, с которой взаимодействуют заряды 1 и 2 равна:
Так заряды равны, то
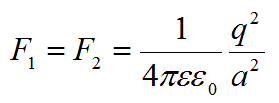
Треугольник равносторонний, все его углы равны 60 градусов. Искомая сила направлена по биссектрисе угла и находится по формуле:

Осталось подставить значения из условия и вычислить:
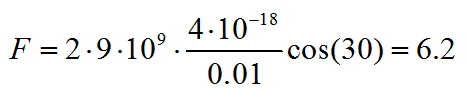
Ответ: 6,2 мкН.
Задача 2
Два положительных точечных заряда Q и 9Q закреплены на расстоянии d=100 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещение зарядов возможны только вдоль прямой, проходящей через закрепленные заряды.
Решение
Снова выполним рисунок:
Для равновесия зарядов необходимо, чтобы они действовали друг на друга с одинаковыми силами:
Из условия можно вычислить:
Сократим и перепишем равенство сил:
Отсюда находим:
При вычислении не забываем переводить все величины в систему СИ
Для устойчивого равновесия заряд q должен быть положительным. Если он сместится из положения равновесия ближе к заряду q2, то сила отталкивания со стороны этого заряда возрастет, а со стороны заряда q1 – уменьшится, и заряд q возвратится в положение равновесия.
Ответ: r1=0.7м, r2=0.3м, заряд положительный.
А теперь задача посложнее, с интегралами. Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Задача 3
Тонкий стержень длиной l=10 см равномерно заряжен с линейной плотностью заряда τ=1 мкКл/м. На продолжении оси стержня на расстоянии d=20см от ближайшего его конца находится точечный заряд Q1 =100нКл. Определить силу взаимодействия заряженного стержня и точечного заряда.
Решение
Вот как выглядит рисунок к этой задаче:
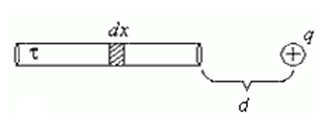
Закон Кулона позволяет вычислить силу взаимодействия точечных зарядов. По условию задачи, один из зарядов не является точечным, а представляет собой заряд, равномерно распределенный по длине стержня. Если выделить на стержне дифференциально малый участок длиной dx, то находящийся на нем заряд dQ=τ·dx можно рассматривать как точечный, и тогда по закону Кулона сила взаимодействия между зарядами Q1 и dQ.
r — расстояние от выделенного элемента до заряда Q1. В условии задачи не указана среда это значит, что заряды находятся в вакууме (ε=1). Чтобы найти силу, проинтегрируем выражение:
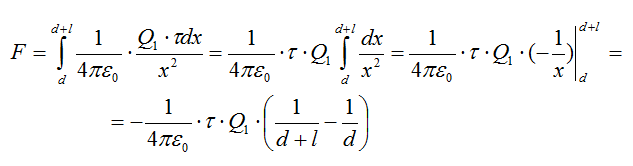
Подставляем значения и получаем:
Ответ: 1,5∙10-3Н
За скорой помощью в решении задач разной сложности обращайтесь к специалистам студенческого сервиса.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Тема 12.
Электрическое поле. Законы постоянного тока
12
.
01
Электростатика. Закон Кулона
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
электрическое поле. законы постоянного тока
12.01Электростатика. Закон Кулона
12.02Электростатика. Напряженность и потенциал электрического поля
12.03Конденсаторы
12.04Электрический ток. Закон Ома
12.05Работа тока. Закон Джоуля – Ленца
Решаем задачи
Два одинаковых проводящих шарика, обладающих зарядами 80 нКл и 20 нКл, находятся на некотором
расстоянии друг от друга. Их приводят в соприкосновение и разводят на прежнее расстояние. На
сколько процентов увеличится в результате сила взаимодействия?
Показать ответ и решение
Сила взаимодействия зарядов — сила Кулона, которая равна:
где — диэлектрическая проницаемость диэлектрика,
— электрическая постоянная,
и
— заряды первого и второго
шарика, — расстояние между шариками.
По закону сохранения заряда:
Из формулы (1) видно, что сила Кулона прямо пропорциональна произведению модулей зарядов.
Поэтому отношение модуля силы Кулона до приведения шариков в соприкосновение к модулю силы Кулона после равно
отношению произведению модулей зарядов шариков до взаимодействия к произведению модулей зарядов шариков после
соприкосновения.
Найдем произведение модулей зарядов до их взаимодействия:
С учетом (2) найдем произведение модулей зарядов после их взаимодействия:
Найдем, на сколько процентов увеличится в результате сила взаимодействия:
Следовательно, сила взаимодействия увеличится на 56,25%
Показать ответ и решение
Пусть первоначальный заряд первого шарика равен , а
. Тогда
— заряд второго шарика.
По закону Кулона для начального положения:
После соприкосновения шариков их общий заряд распределится поровну и станет равным у каждого шарика:
По закону Кулона для конечного положения:
Выразим :
Подставим значения:
Т.к. должен быть больше
, то их отношение
должно быть больше 1. Значит,
.
Показать ответ и решение
Пусть — заряд второго шарика до соприкосновения, значит заряд первого шарика до соприкосновения будет равен
. После соприкосновения шариков их заряды распределились поровну и стали равны каждый
.
По закону Кулона для начального и конечного положений шариков:
Во сколько раз уменьшится модуль сил взаимодействия двух небольших металлических шариков одинакового диаметра, имеющих
заряды нКл и
нКл, если шарики привести в соприкосновение и раздвинуть на прежнее расстояние?
Демоверсия 2023
Показать ответ и решение
Сила Кулона в первом случае равна:
где — коэффициент пропорциональности,
и
— заряды,
— расстояние между зарядами.
При соприкосновении заряд распределится между шарами и станет равным:
Тогда для второго случая сила Кулона равна:
То есть сила уменьшится:
Два одинаковых точечных заряда, модуль которых Кл, расположены в вакууме на расстоянии 3 м друг от друга.
Определите модуль силы (в мкН), с которой первый заряд действует на второй.
Демоверсия, 2022
Показать ответ и решение
Сила Кулона равна:
где — коэффициент пропорциональности,
и
— заряды,
— расстояние между зарядами.
По условию:
Во сколько раз увеличится модуль сил взаимодействия двух небольших металлических шариков одинакового диаметра, имеющих
заряды нКл и
нКл, если шарики привести в соприкосновение, а затем раздвинуть их на прежнее
расстояние?
Показать ответ и решение
Сила Кулона в первом случае равна:
где — коэффициент пропорциональности,
и
— заряды,
— расстояние между зарядами.
При соприкосновении заряд распределится между шарами и станет равным:
Тогда для второго случая сила Кулона равна:
Тогда
Увеличение силы:
Два одинаковых металлических шарика заряжены положительными зарядами и
. Центры шариков находятся на некотором
расстоянии друг от друга. Шарики привели в соприкосновение. Во сколько раз необходимо увеличить расстояние между их
центрами, чтобы сила взаимодействия осталась прежней?
Показать ответ и решение
Сила Кулона в первом случае равна:
где — коэффициент пропорциональности,
и
— заряды,
— расстояние между зарядами.
При соприкосновении заряд распределится между шарами и станет равным:
Тогда для второго случая сила Кулона равна:
где – искомая величина.
Так как , то
То есть расстояние надо увеличить в 1,25 раз.
Чему равна энергия взаимодействия точечных зарядов 2 мкКл и 3 мкКл, находящихся на расстоянии 30 см друг от друга? (Ответ
дайте в мДж)
Показать ответ и решение
Энергия взаимодействия равна:
где — коэффициент пропорциональности,
и
— заряды,
— расстояние между зарядами.
Расстояние между двумя точечными электрическими зарядами уменьшили в 2 раза, и один из зарядов
увеличили в 3 раза. Во сколько раз увеличится сила взаимодействия между зарядами?
Показать ответ и решение
Сила Кулона для первого случая равна:
где — коэффициент пропорциональности,
и
— заряды,
— расстояние между зарядами.
Тогда для второго случая сила Кулона равна:
Следовательно, сила увеличится в 12 раз.
Расстояние между двумя точечными электрическими зарядами увеличили в 2 раза, и один
из зарядов уменьшили в 4 раза. Во сколько раз уменьшится сил взаимодействия между
зарядами?
Показать ответ и решение
Сила Кулона для первого случая:
где — коэффициент пропорциональности,
и
— заряды,
— расстояние между зарядами.
Тогда для второго случая сила Кулона:
Следовательно, сила уменьшится в 16 раз.
Модуль силы взаимодействия между двумя неподвижными точечными зарядами равен . Чему станет равен модуль этой силы,
если увеличить заряд одного тела в 4 раза, а второго — в 2 раза? Ответ дайте как .
Показать ответ и решение
Сила Кулона для первого случая:
где — коэффициент пропорциональности,
и
— заряды,
— расстояние между зарядами.
Тогда для второго случая сила Кулона равна:
Следовательно, сила увеличится в 8 раз.
Расстояние между двумя точечными электрическими зарядами уменьшили в 4 раза, а один
из зарядов увеличили в 3 раза. Во сколько раз увеличатся силы взаимодействия между
зарядами?
Показать ответ и решение
Сила Кулона в первом случае равна:
где — коэффициент пропорциональности,
и
— заряды первого и второго тел,
— расстояние между
зарядами.
Тогда для второго случая:
Следовательно, сила увеличится в 48 раз.
Расстояние между двумя точечными электрическими зарядами уменьшили в 3 раза, каждый из зарядов
увеличили в 3 раза. Во сколько раз увеличился модуль сил электростатического взаимодействия между
ними?
Демоверсия 2019
Показать ответ и решение
Сила Кулона:
при увеличении каждого заряда сила возрастет в 9 раз, а при уменьшении расстояния в 3 раза, сила еще раз возрастет в 9 раз,
следовательно, сила возрастет в 81 раз.
Расстояние между двумя точечными электрическими зарядами уменьшили в 4 раза, каждый из зарядов
увеличили в 4 раза. Во сколько раз увеличился модуль сил электростатического взаимодействия между
ними?
Показать ответ и решение
Согласно закону Кулона, сила взаимодействия электрических зарядов прямо пропорциональна произведению величин зарядов и
обратно пропорциональна квадрату расстояния между ними: . При увеличении каждого заряда в 4 раза, сила
увеличится в 16 раз. При уменьшении расстояния между зарядами в 4 раза, сила увеличивается в 16 раз, значит в итоге сила
увеличится в раз.
С какой электрической силой взаимодействуют в вакууме два неподвижных положительно заряженных шарика,
находящихся на расстоянии 7 см друг от друга? Заряд каждого шарика нКл. Ответ выразите в мкН и округлите до
целых.
Показать ответ и решение
Введем обозначения величин: — сила электрического взаимодействия шариков;
и
— первый и второй заряды
соответственно; — расстояние между зарядами.
По закону Кулона:
Между двумя точечными заряженными телами сила электрического взаимодействия равна = 48 мН. Если заряд одного тела
увеличить в 2 раза, а заряд другого тела уменьшить в 3 раза и расстояние между телами увеличить в 2 раза, то какова будет сила
взаимодействия между телами? (Ответ дайте в мН.)
Показать ответ и решение
Сила Кулона для первого случая:
где — коэффициент пропорциональности,
и
— заряды первого и второго тел,
— расстояние между
зарядами.
Тогда для второго случая сила Кулона находится по формуле:
Следовательно, сила уменьшилась в 6 раз:
Во сколько раз уменьшится модуль сил кулоновского взаимодействия двух точечных зарядов, если
расстояние между ними увеличить в 1,5 раза?
Показать ответ и решение
Сила Кулона в первом случае равна:
где — коэффициент пропорциональности,
и
— заряды,
— расстояние между зарядами.
Тогда для второго случая сила Кулона равна:
Следовательно, сила уменьшится в 2,25 раза.
Силы электростатического взаимодействия между двумя точечными заряженными телами равны по модулю . Во сколько раз
уменьшится модуль сил электростатического взаимодействия между этими телами, если расстояние между ними увеличить в 3
раза?
Показать ответ и решение
Сила Кулона в первом случае:
где — коэффициент пропорциональности,
и
— заряды первого и второго тел,
— расстояние между
зарядами.
Тогда для второго случая сила Кулона равна:
Следовательно, сила уменьшится в 9 раза.
Два точечных заряда взаимодействуют в вакууме на расстоянии 10 см с такой же силой, как в
диэлектрике на расстоянии 5 см. Определите диэлектрическую проницаемость диэлектрика.
Показать ответ и решение
Сила Кулона для первого случая равна:
Во втором случае расстояние между точечными зарядами стало равным 5 см, то есть уменьшилось в два раза.
Сила Кулона для второго случая равна:
где — диэлектрическая проницаемость диэлектрика,
— диэлектрическая постоянная,
и
— заряды,
— расстояние
между зарядами.
По условию (1) равно (2). Выразим диэлектрическую проницаемость диэлектрика:
Два точечных заряда находятся в вакууме на расстоянии 0,03 м друг от друга. Если их поместить в
жидкий диэлектрик и увеличить расстояние между ними на 3 см, то сила взаимодействия зарядов
уменьшится в 8 раз. Найдите диэлектрическую проницаемость диэлектрика.
Показать ответ и решение
Сила Кулона для первого случая равна:
Во втором случае расстояние между точечными зарядами увеличилось на 3 см и стало равным 6 см, то есть увеличилось в два
раза.
Сила Кулона для второго случая равна:
где — диэлектрическая проницаемость диэлектрика,
— диэлектрическая постоянная,
и
— заряды,
— расстояние
между зарядами.
Подставим (2) в (1) и выразим диэлектрическую проницаемость диэлектрика:
Электрическое поле
1 В задачах этого параграфа, если нет специальных оговорок, считать заряды точечными и находящимися в вакууме (воздухе).
Задача 7.1
С какой силой взаимодействуют два заряда по 10 нКл, находящиеся на расстоянии 3 см друг от друга?

Задача 7.2
На каком расстоянии друг от друга заряды 1 мкКл и 10 нКл взаимодействуют с силой 9 мН?

Задача 7.3
Во сколько раз надо изменить расстояние между зарядами при увеличении одного из них в 4 раза, чтобы сила взаимодействия осталась прежней?

Задача 7.4
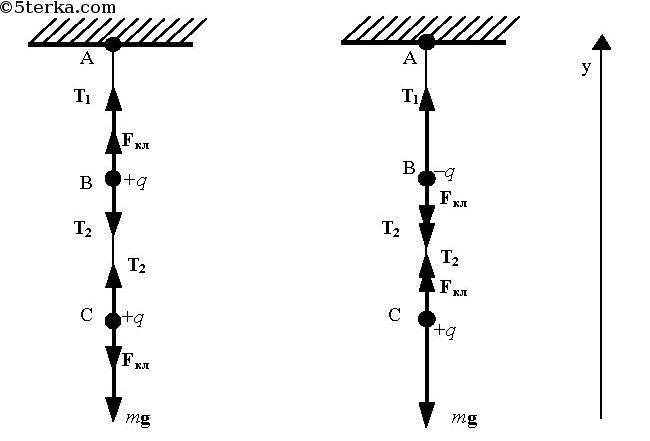
Одинаковые шарики массой по 0,2 г подвешены на нити так, как показано на рисунке. Расстояние между шариками ВС = 3 см. Найти силу натяжения нити на участках АВ и ВС, если шарикам сообщили одинаковые по модулю заряды по 10 нКл. Рассмотреть случаи: а) заряды одноименные; б) заряды разноименные.

Задача 7.5
Два шарика, расположенные на расстоянии 10 см друг от друга, имеют одинаковые отрицательные заряды и взаимодействуют с силой 0,23 мН. Найти число избыточных электронов на каждом шарике.

Задача 7.6
Заряды 10 и 16 нКл расположены на расстоянии 7 мм друг от друга. Какая сила будет действовать на заряд 2 нКл, помещенный в точку, удаленную на 3 мм от меньшего заряда и на 4 мм от большего?

Задача 7.7
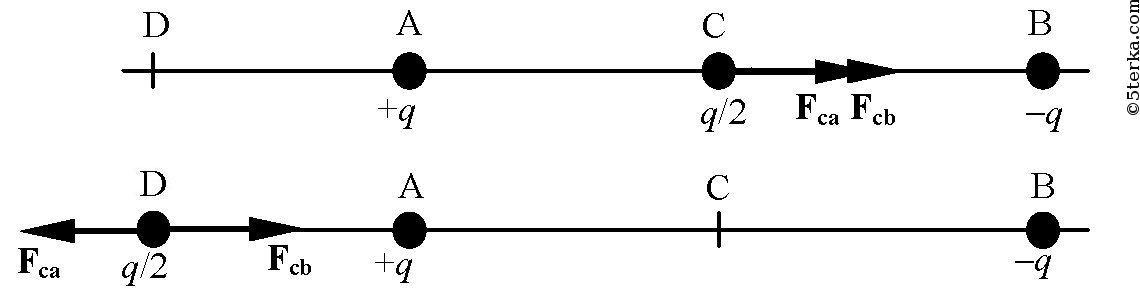
Заряды +q и -q расположены так, как показано на рисунке 73. Заряд q/2 помещают сначала в точку С, а затем в точку D. Сравнить силы (по модулю), действующие на этот заряд, если DA = АС = СВ.
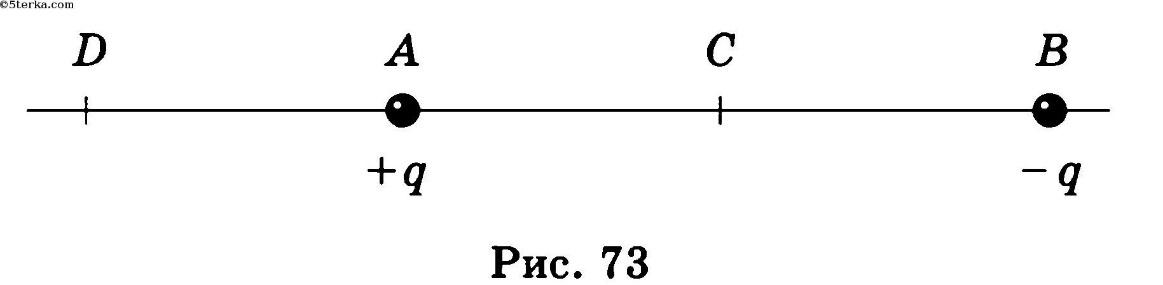

Задача 7.8
Два заряда по 25 нКл каждый, расположенные на расстоянии 24 см друг от друга, образуют электростатическое поле. С какой силой это поле действует на заряд 2 нКл, помещенный в точку, удаленную на 15 см от каждого из зарядов, если заряды, образующие поле, одноименные? разноименные?
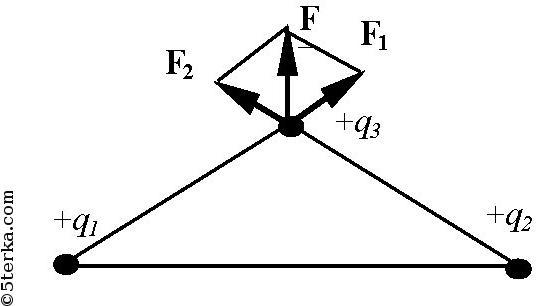
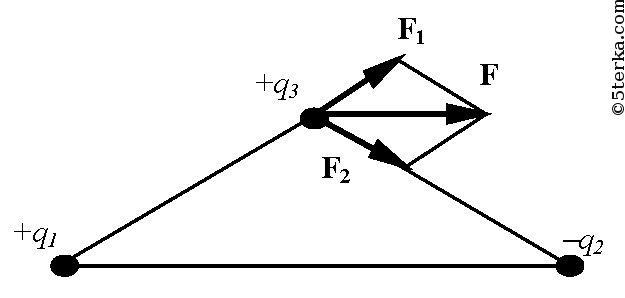

Задача 7.9
Какая сила действует на заряд 12 нКл, помещенный в точку, в которой напряженность электрического поля равна 2 кВ/м?

Задача 7.10
С каким ускорением движется электрон в поле напряженностью 10 кВ/м?

Задача 7.11
Найти напряженность поля заряда 36 нКл в точках, удаленных от заряда на 9 и 18 см.

Задача 7.12
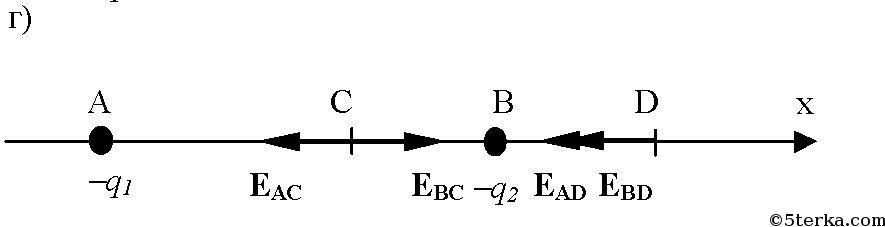
В точке А расположен заряд q1, в точке В — заряд q2. Найти проекцию на ось X вектора напряженности результирующего поля в точках С и D, если АС = 6 см, СВ = BD = 3 см. Решить задачу для следующих значений зарядов: a) q1 = 40 нКл, q2 = 10 нКл; б) q1 = 40 нКл, q2 = -10 нКл; в) q1 = -40 нКл, q2 = 10 нКл; г) q1 = -40 нКл, q2 = -10 нКл.
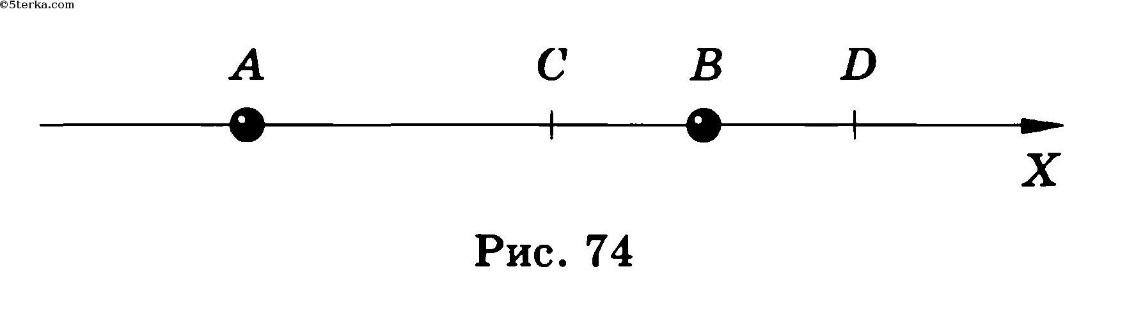
- q1 = 40 нКл, q2 = 10 нКл;

б) q1 = 40 нКл, q2 = -10 нКл;
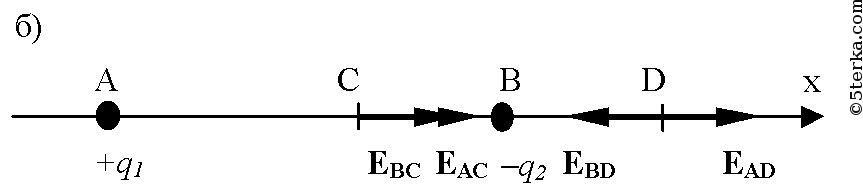
в) q1 = -40 нКл, q2 = 10 нКл;
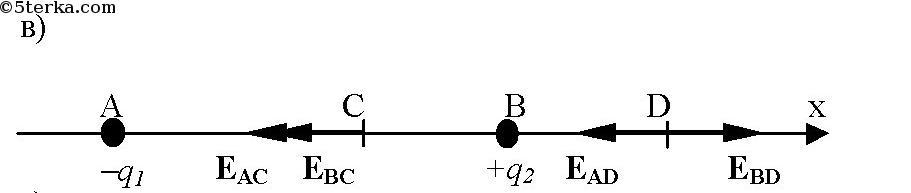
г) q1 = -40 нКл, q2 = -10 нКл.

7