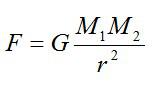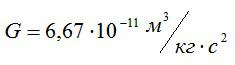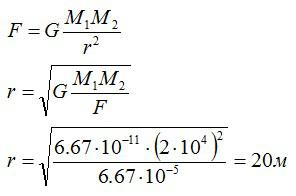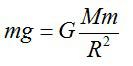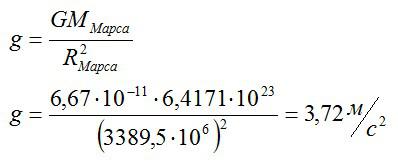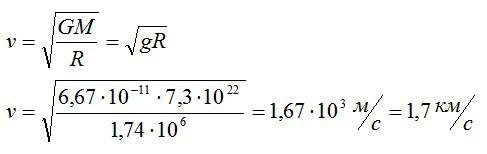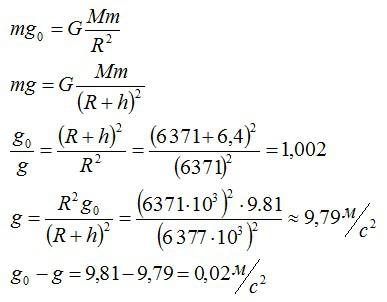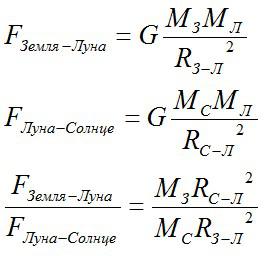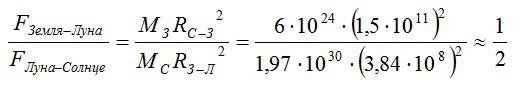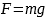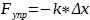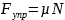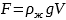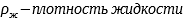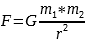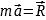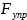Задачи на силу притяжения егэ

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Закон всемирного тяготения – фундаментальный закон природы, согласно которому все предметы притягиваются между собой. Это проявление гравитационного взаимодействия. Если хотите узнать о гравитации больше – читайте наш отдельный материал.

На своем телеграм-канале мы ежедневно отбираем полезную и интересную информацию. Подписывайтесь!

Закон всемирного тяготения: формулировка, примеры

Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорционально квадрату расстояния между ними.

Примеры действия закона всемирного тяготения: 

• яблоко, летящее на голову Ньютона; 
• движение небесных тел; 
• свет, поглощаемый черной дырой.

Закон всемирного тяготения был сформулирован Ньютоном в 1682 году. Размышляя над законами движения планет, которые ранее были открыты Кеплером, Ньютон хотел узнать, какие силы действуют на небесные тела и заставляют их двигаться определенным образом.

Вопросы на закон всемирного тяготения

Вопрос 1. Если все предметы притягиваются, то почему Луна не падает на Землю, Земля не падает на Солнце и т.д.?

Ответ. Все дело в скорости движения небесных тел. Луна движется вокруг Земли со скоростью равной примерно 1 км/с. Этой скорости недостаточно, чтобы покинуть орбиту, и достаточно, чтобы Луна не упала на Землю. Можно сказать, что Луна падает на Землю, но это падение никогда не заканчивается.

Вопрос 2. Что из этих величин является фундаментальной физической константой: гравитационная постоянная G или ускорение свободного падения g?

Ответ. Гравитационная постоянная G является одинаковой для всех тел в природе и в любой точке Вселенной. Ее значение:

Ускорение свободного падения g в пределах Земли варьируется в зависимости от координат и высоты подъема тела над поверхностью. На других планетах значение g будет совершенно иным, так как оно зависит от массы и размеров небесного тела. 

Вопрос 3. Как развивалась теория тяготения после Ньютона и до наших дней?

Ответ. Классическая теория тяготения Ньютона господствовала в физике на протяжении более чем двух веков. В 1915 году Эйнштейн показал, что она является частным случаем общей теории относительности.

Вопрос 4. Что такое первая и вторая космические скорости?

Ответ. Первая космическая скорость – скорость, с которой спутник должен двигаться вокруг Земли или другого космического объекта, чтобы оставаться на орбите и не падать. Для Земли значение первой космической скорости равно 7,91 км/с.
Вторая космическая скорость – скорость, необходимая для того, чтобы покинуть орбиту небесного тела. Значение: 11,2 км/с.

Вопрос 5. С гравитационной постоянной разобрались. Ну а что такое гравитационная неустойчивость?

Ответ. Гравитационная неустойчивость – флуктуации (возмущения, небольшие отклонения) плотности и скорости вещества в пространстве под действием сил тяготения. Гравитационная неустойчивость является причиной возникновения галактик, звезд и звездных скоплений.

Кстати! Для наших читателей действует скидка 10% на любой вид работы.

Задачи на закон всемирного тяготения с решениями

Хотите узнать, как решать задачи на закон всемирного тяготения? Вот памятка по решению любых задач и отдельная статья про задачи на движение тел под действием силы тяжести. 

Задача №1. Применение закона всемирного тяготения

Условие 

Два одинаковых шара притягиваются друг к другу с силой 6,67*10^-5 Ньютона. Масса каждого шара равна 20 тонн. Найдите расстояние между шарами. 

Решение

По закону всемирного тяготения

Ответ: 20 метров.

Задача №2. Расчет ускорения свободного падения на Марсе

Условие

Каково ускорение свободного падения на Марсе?

Решение

Сначала по справочнику найдем значения массы и радиуса Марса:

По закону всемирного тяготения для тела массы m на Марсе:

Сократим m и получим формулу для ускорения свободного падения:

Ответ: 3,72 метра на секунду в квадрате.

Задача №3. Нахождение первой космической скорости на поверхности Луны

Условие

Какова первая космическая скорость на поверхности Луны?

Решение

Первая космическая скорость у поверхности планеты находится по формуле:

Также из этой задачи можно найти ускорение свободного падения на Луне. Оно равно 1,61 м/с2.

Ответ: 1,7 км/с.

Задача №4. Изменение ускорения свободного падения с четом высоты

Условие

Воздушный шар поднимается на высоту 6 километров. Как изменится ускорение свободного падения на этой высоте?

Решение

Запишем закон всемирного тяготения сначала для поверхности Земли, а потом для высоты h. Обозначим ускорение свободного падения на уровне моря как g нулевое.

Ответ: Ускорение свободного падения уменьшится на 0,02 м/с2.

Задача №5. Применение закона всемирного тяготения

Условие

Определите, какая из сил притяжения больше: сила между Землей и Луной или сила между Луной и Солнцем

Решение

Чтобы понять, какая сила больше, нужно их сравнить.

Учитывая, что расстояние между Землей и Луной гораздо меньше, чем расстояние межу Землей и Солнцем, вместо расстояния между Луной и Солнцем можно взять расстояние Земля-Солнце.

Ответ: сила притяжения между Луной и Солнцем примерно в два раза больше.

Нужна помощь в решении задач и других заданий? Обращайтесь в профессиональный студенческий сервис.

ЕГЭ-11 Физика  Задание №2
 Закон всемирного тяготения.

№1 Две планеты с одинаковыми массами обращаются по круговым
орбитам вокруг звезды. Для первой из них сила притяжения к звезде в 4 раза
больше, чем для второй. Каково отношение радиусов орбит первой и второй планет?

№2 У
поверхности Земли на космонавта действует сила тяготения 720 Н. Какая сила
тяготения действует со стороны Земли на того же космонавта в космическом
корабле, движущемся по круговой орбите вокруг Земли на расстоянии трёх земных радиусов
от её центра? 

№3 Космонавт
на Земле притягивается к ней с силой 700 Н. С какой приблизительно силой
он будет притягиваться к Марсу, находясь на его поверхности, если радиус Марса
в 2 раза меньше, а масса — в 10 раз меньше, чем у Земли?

№4 Сила
притяжения Земли к Солнцу в 22,5 раза больше, чем сила притяжения Марса к
Солнцу. Во сколько раз расстояние между Марсом и Солнцем больше расстояния
между Землёй и Солнцем, если масса Земли в 10 раз больше массы Марса?

№5 Модуль
силы гравитационного взаимодействия двух точечных тел, расположенных на
расстоянии четырёх метров друг от друга, равен 5 Н. Каков будет модуль силы
гравитационного взаимодействия этих тел, если расстояние между ними увеличить
на 1 м?

№6 Две
звезды одинаковой массы притягиваются друг к другу с силами, равными по
модулю F. Во сколько раз уменьшился бы модуль сил притяжения между
звёздами, если бы расстояние между их центрами увеличилось в 1,5 раза, а масса
каждой звезды уменьшилась в 2 раза?

№7 Чему
равен модуль силы тяжести, действующей на тело массой 9 кг, на высоте, равной
половине радиуса Земли?

№8 Модуль
ускорения свободного падения вблизи поверхности астероида равен 0,2 м/с².
Чему будет равен модуль ускорения свободного падения вблизи поверхности другого
астероида, объём которого в 8 раз меньше? Оба астероида однородные, сферические
и состоят из железа. Ответ выразите в м/с².

№9 Сила
гравитационного взаимодействия небольших тел массами m и M,
находящихся на расстоянии R₁ = 100 км друг от
друга, равна по модулю F. Сила гравитационного взаимодействия
небольших тел массами 2m и M, находящихся на
расстоянии R₂ друг от друга, равна по модулю F/50.
На какую величину отличаются расстояния R₁ и R₂?

№10

№11

№12

№13 К
вертикально расположенной пружине динамометра, корпус которого прикреплён к
потолку, подвешен груз массой 8 кг. Каково будет показание динамометра, если
человек, стоящий под грузом, будет пробовать опустить этот груз, действуя на
него направленной вниз силой 50 Н?

Ответы
:

№	1	2	3	4	5	6	7	8	9	10	11	12	13
ответ	0,5	80	280	1,5	3,2	9	40	0,1	1000	0,25	0,5	1	130

Сила тяготения. Задачи второго уровня.

Всем доброго времени суток! Сегодня на повестке дня задачи на отыскание силы тяготения, скоростей, ускорений и весов тел на различных высотах и на разных планетах: словом, все, что связано с законом всемирного тяготения!

Поскольку задач много, а времени – мало (как обычно), то хочется разобрать не самые простые задачи. Надеюсь, данная подборка задач будет вам интересна, потому что решений этих задач я не нашла в Интернете – и по этой же причине не хочу рассматривать совсем простые задачи, решения которых  в сети легко отыскать.

Начнем, пожалуй.

Задача 1. Два одинаковых  однородных шара, соприкасаясь, притягивают друг друга с силой . Как изменится сила, если увеличить массу каждого шара в раз?  Плотность шаров не изменяется.

Сила тяготения равна — поэтому неплохо бы узнать радиус шариков. Вспомним формулу объема шара: , откуда , то есть

Масса и объем связаны плотностью вещества:

Тогда

То есть сила тяготения равна

Если масса шаров изменится в раз при той же плотности, то это означает, что изменятся их радиусы, так как зависимость объема от радиуса шара – прямая:

Сила тоже изменится:

Найдем теперь отношение сил:

Ответ:

Задача 2. Две точечные массы и расположены на расстоянии друг от друга. Где следует расположить точечную массу , чтобы сила гравитационного воздействия на нее со стороны масс и равнялась ?

Так как силы в данном случае направлены от первого тела к телу (вправо) и от второго тела к телу (влево), то есть такое положение массы , что эти силы станут равны и  друг друга скомпенсируют. Тогда можем записать:

Так как , то

Раскрыв скобки, можем записать ,

Или

Ответ:

Задача 3. Два шарика массами , соединенные стержнем пренебрежимо малой массы, образуют гантель. Расстояние между центрами шариков . Найти силу, действующую на гантель в поле тяжести точечной массы , находящейся на расстоянии от середины гантели. . Исследовать полученные выражения для силы при , , при каком она максимальна и чему будет равна.

Запишем расстояние от каждого из шариков до точечной массы :

Тогда силы взаимного притяжения каждого из шариков и массы М такие:

Эти силы можно разложить каждую на два составляющих вектора – на вектора, направленные от одного шарика к другому, вдоль гантели (вследствие равенства по длине и противоположного направления они компенсируют друг друга), и перпендикулярные к гантели. Эти две составляющие сонаправлены, поэтому именно их сумма определяет силу взаимодействия.

Определим эти составляющие сил:

Так как эти силы равны, и направлены в одну сторону, сложим их:

При условии пренебрежем величиной в знаменателе, тогда

При условии пренебрежем величиной в знаменателе, тогда

Ответ: ,  ,  

Задача 4. Три материальные точки массами кг, кг, кг находятся в точках с радиус-векторами ,  , . Найти гравитационную силу, действующую на частицу, имеющую массу , со стороны частиц с массами и .

Рассмотрим рисунок. Из него видно, что сила, которую мы ищем – это равнодействующая сил и (изображена красным вектором). Найти ее можно как векторную сумму сил и .

Для определения сил тяготения между массами нам понадобится знать расстояния между ними. Определим их, зная радиус-векторы точечных масс, так же, как определяют длину отрезка по координатам его концов. Тогда

Модуль силы равен:

Модуль силы равен:

Равнодействующая:

Сила направлена вдоль оси — так как тела и лежат на одной вертикали:

Силу возможно разложить на две составляющие, направленные по осям. Разложим силу :

Равнодействующая тогда будет равна:

Определим и : так как , следовательно,

, а .

Тогда:

Подставляем числа:

Ответ:

Задача 5. С какой силой притягивается к центру земли тело массой , находящееся в глубокой шахте, если расстояние от него до центра земли равно ? Плотность земли считать постоянной и равной .

Здесь надо понимать, что тело будет притягиваться только той частью массы планеты, которая находится «под» ним. Силы, с которыми тело будет притягивать  та часть планеты, что «выше» тела, будут компенсированы силами, с которыми тело будет притягивать та часть планеты, которая «выше» тела, но в противоположном полушарии (на рисунке зеленым и красным цветами показаны силы, которые компенсируют друг друга).

Здесь — «внутренняя часть» планеты, та, что «под» телом.

Ответ:

Задача 6. Определить максимальную скорость камня, брошенного без начальной скорости в прямой тоннель, прорытый через центр Земли с одной стороны на другую. Вращение Земли не учитывать.

Камень будет лететь равноускоренно, по крайней мере, до центра. Но, так как полет будет все время сокращать расстояние между камнем и центром планеты, то ускорение свободного падения будет все время уменьшаться, пока не станет равным нулю в середине тоннеля. Поэтому для расчета возьмем среднее ускорение: .

Тогда расстояние, которое камень пролетит до центра, равно радиусу Земли – 6400 км.

Отсюда :

Скорость при равноускоренном движении без начальной скорости:

Таким образом, скорость, которую приобретет камень, будет равна первой космической скорости, или 8000 м/c.

Задача 7. Две звезды вращаются вокруг общего центра масс с периодом  и постоянными по модулю скоростями и . Найти массы звезд и расстояние между ними.

Так как звезды вращаются вокруг одного центра, не обгоняя друг друга, следовательно, у них одна и та же угловая скорость вращения: , и, очевидно, один и тот же период обращения: . Период – время прохождения одного круга. Первая звезда проходит круг длиной , а вторая — , то есть скорость первой — , скорость второй — . Ну а расстояния звезд от центра вращения — ,  . Сумма расстояний – это как раз расстояние между звездами:

Чтобы найти массы звезд, используем силу тяготения между ними. Раз система в равновесии, значит, сила тяготения равна центробежной силе. Сила тяготения между звездами:

Центростремительное ускорение для первой звезды:

Центробежная сила:

Приравниваем силу тяготения и центробежную:

Сокращаем и «вытаскиваем» массу :

Вместо подставим , вместо .

Тогда:

Аналогично, приравнивая центробежную силу для звезды массой и силу тяготения, получим:

Сокращаем и «вытаскиваем» массу :

Вместо подставим , вместо .

Тогда:

Ответ: , , .

Задача 8. Определить силу натяжения троса, связывающего два спутника массой каждый, которые обращаются вокруг Земли на расстояниях и так, что трос всегда направлен радиально. Масса Земли .

Силой тяготения между спутниками пренебрежем. Следовательно, на каждый из них действует сила тяготения земли, сила натяжения троса и центробежная сила. Так как канат всегда направлен радиально (по радиусу), то у спутников одна и та же угловая скорость: .

Центростремительное ускорение первого спутника: , второго спутника .

Центробежная сила, действующая на первый спутник: , на второй спутник: .

Уравнение по второму закону Ньютона для первого спутника:

Уравнение по второму закону Ньютона для второго спутника:

Здесь и — силы тяготения между спутниками и Землей:

Сложим уравнения, составленные по второму закону Ньютона. Получим:

Или:

Так как угловая скорость спутников одна и та же , то можно записать, что , а

Подставим:

«Вытащим» :

Определим теперь силу натяжения каната:

Подставляем в это выражение квадрат скорости, полученный выше:

Или, наконец,

Ответ:

В настоящее время ЕГЭ по физике проходит в виде решения задач. Задание, содержащиеся в КИМах определяются согласно кодификатору элементов содержания и требований к подготовке выпускников к проведению ЕГЭ.
Для успешной подготовки к ЕГЭ, в этой статье рассмотрена физика, а именно раздел динамики, включая формулы для подготовки к ЕГЭ, статья охватывает следующие темы:
– Первый закон И. Ньютона;
– Второй закон И. Ньютона;
– Третий закон И. Ньютона;
– Закон всемирного тяготения;
– Сила упругости. Закон Гука.
Приступим к изучению тем и примеров решения задач.
В динамике выделяют три закона открытых И. Ньютоном, они позволяют определить движение для любой системы.
Первый закон Ньютона

Первый закон открыт в конце 17 века. Закон звучит следующим образом: существуют инерциальные системы отсчёта, в которых тела движутся равномерно и прямо по линии, если на них не оказывают влияние другие силы.
Закон инерции: в случае, когда на тело не оказывают влияния внешние воздействий, то у данного тела сохраняется состояние покоя. Это значит, что все тела могут оставаться в первоначальном состоянии, то есть если тело находится в движении, то оно будет в таком же состоянии. Если оно неподвижно, то продолжает стоять без изменений, пока не появится сила, заставляющая его двигаться.
Инерциальной системой отсчёта называют систему, находящуюся в состоянии движении или покое.
Неинерциальной системой называют движущуюся с ускорением систему.
Инерциальными считаются системы, находящиеся в состоянии покоя или движения, при этом, движение должно быть равномерным и прямолинейным.
Неинерциальными считаются системы, имеющие ускорение.
Существует также гелиоцентрическая модель отсчёта, в ней начало координат совмещено с солнцем.
Первый закон Ньютона не содержит формул, поэтому рассмотрим примеры:
– Наиболее популярным объяснением является резкое торможение. Тело движется в направлении автомобиля, поэтому при резком торможении автомобиль сильно дёргается. Если же автомобиль плавно затормозит, соответственно, его движение будет нерезким;
– Движение наверх и вниз. Американские горки поднимаются наверх за счёт накопленной потенциальной энергии при крутом спуске.
Второй закон Ньютона

Второй закон открыт около 1666 года, он гласит: В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, является пропорциональным вызывающим его силам. Силы для ускорения предмета зависят от его массы.
Ньютон нашёл общее между ускорением и силой, F– сила, действующая на тело, масса – m, ускорение –a.
Важно помнить о том, что:
– Этот закон называют основополагающим в разделе динамики;
– Тело подразумевает точку, её движение находят в инерциальной системе отсчёта.
Формула второго закона: ma = F, F = ma.
Пример. При попытке пнуть мяч, мы выбираем направление, в котором он должен полететь. Чем больше силы мы вкладываем в пинок, тем дальше он будет лететь.
Рассмотрим ещё один пример – толкать автомобиль. Таким образом, если толкать автомобиль в два раза сильнее, то он даст в два раза больше ускорения.
Рассмотрим примеры решения задач:
1. Тело движется по прямолинейному направлению с силой, которая равна 10H. Зависимость тела от времени представляет собой: х = 3 – 2t + t^2.
Найти: массу (M).
Решение: Сначала следует найти ускорение, далее – найти массу. Применяем следующие формулы:
х = 3 – 2t + t^2
v = dx / dt
a = dv / dt
v = -2 + 2t
a = 2м / с^2
Теперь нужно подставить значения, используя формулу второго закона.
M = 10 / 2 = 5 кг.
Ответ: 5 килограмм.
2. Велосипедист спускается с горки с ускорением 0,6 м / с^2. Общая масса составляет 50 кг.
Найти: F
Решение:
а = 0,6 м/с^2
m = 50 кг.
Помним формулу второго закона: F = mа. Далее подставляет известные значения.
F = 50 кг * 0,6 = 30 H.
Ответ: F = 30 H.
Третий закон Ньютона

Третий закон открыли в 1725 году: действию F всегда есть противодействие, то есть взаимодействия двух дел равны и направлены по прямой в противоположные стороны. Формула: F12 = -F21.
Пример. Для строительства моста нужно высчитать нагрузку. Данную нагрузку можно узнать с помощью третьего закона. При этом, на мост давят держащие опоры, поэтому строительство ведётся по определённой схеме, которая рассчитывает большую выносливость.
Рассмотрим пример решения задачи: на стуле стоит портфель. На него действуют силы равные 500 H. Согласно третьему закону сверху на него действует та же сила, равная 500 H.
Следует, что F1 = F2. То есть, чем больше масса тела, тем меньше его ускорение.
Следует помнить о том, что третий закон применяется исключительно в инерциальных системах отсчёта.
Закон всемирного тяготения
В школьной программе изучение закона всемирного тяготения при подготовке к ЕГЭ является важной темой. Издавна люди смотрели на звёзды и понимали, что ими что-то движет. Но люди не догадывались, что притяжением управляет один закон. В 1687 году И. Ньютон открыл закон всемирного тяготения.
Согласно известной всем версии, Ньютон увидел падающее с дерева яблоко. Он стал размышлять о том, что на все тела действует некая определённая сила, которая позволяет им притягиваться к Земле.
Формула данного закона выглядит таким образом: F=G*(m1*m2)/r2. При этом, G – постоянная гравитации, равная 6,67408(31)•10−11. Это величина, которая воздействует на любой объект нашей планеты.
Позднее закон всемирного тяготения стали применять в астрономии и механике, так как с его помощью объясняется процесс движения различных тел. Любой объект будет находиться в невесомости, объясняется это тем, что объект находится в космосе и сила притяжения на него не действует.
Примером закона всемирного тяготения является запуск в космос спутника (это произошло в 1957 году). При этом, спутник постоянно находился в равном расстоянии над Землёй, это обусловлено тем, что наша планета притягивает одинаково в различных направлениях.
Рассмотрим несколько задач с применением данного закона:
1. На какой высоте над нашей планетой сила тяготения будет меньше в два раза, чем на Земле?
Решение: На поверхности планеты Fт = G(mM/R2), следует, что на высоте Fт = G(mM/(R+h)2). Согласно условию, Fт1/ Fт = 0,5. Далее, К2/(R+h) 2 = 0,5. Выходит, корень из двух, значит, 1,4.
Ответ: h = 0,4 R.
2. Найти силу притяжения двух книг массой по 600 гр., при условии, что находятся на расстоянии одного метра.
m1 = m2 = 600 гр.
R = 1.
G = 6,67 * 10^-11 H * m2 / кг2.
Найти: F
Решение: Используем формулу F = G (m1m2 / r2)
F = (6,67 * 10^-11 * 0,6 * 0,6) / 1^2 = 2,4 H
Ответ: 2,4 H.
Сила упругости. Закон Гука

Закон Гука является основным в теории упругости. Немаловажное значение в процессе подготовки к сдаче ЕГЭ по физике имеет тема о силе упругости, открытая Робертом Гуком – английский учёный, данный закон открыл в 1660 году в возрасте двадцати пяти лет.
Закон гласит: сила упругости, которая возникает при растяжении или сжатии тела является пропорциональной значению по изменению длины тела.
Сила упругости – это сила, которая возникает при деформации тела, данная сила возвращает тело в его первоначальное состояние.
При деформации тело пытается вернуться в первоначальное состояние, это объясняется электромагнитным воздействием на молекулярном уровне.
Формула закона: пусть х – упругость тела, тогда Fx = -kx, k – жёсткость тела.
Жёсткость зависит от материала и размера тела, она составляет ньютон на метр (1Н / м). Чем больше жёсткость, тем меньше оно подвержено деформации под воздействием сил. Стоит помнить о том, что закон Гука достоверно применяют при упругой деформации, т.е. деформация должна быть малой. При большой деформации тела длина перестаёт быть прямо пропорциональной силе, а при сильной деформации тело разрушается.
Рассмотрим пример задачи: проволоку разрезали ровно пополам, её жёсткость составляет 90 H/m. Нужно найти жёсткость обеих проволок.
Решение: k = F/x.
Согласно условию задачи, жёсткость пропорциональна длине проволоки.
k1 = 2k = 180 H/m.
Ответ: 180 H/m.
Таким образом, мы рассмотрели одни из важных тем раздела динамики: три закона Исаака Ньютона, закон всемирного тяготения и силу упругости, закон Роберта Гука. Изучив данные материалы по теме и просмотрев примеры решения задач, вы сможете решить схожие задание на ЕГЭ по физике. 

Из последних КИМов ЕГЭ по физике следует, что задание 2 относится к разделу «Динамика» и может содержать расчетные задачи по следующим темам: «Законы Ньютона, закон всемирного тяготения, закон Гука, сила трения».

Основные формулы, которые необходимо знать для успешного решения задания 2.

Сила тяжести		m — масса тела g=10 м/с2 – ускорение свободного падения
Сила упругости		Δx – удлинение пружины k – коэффициент жесткости пружины
Сила трения		µ — коэффициент трения N – сила реакции опоры
Сила Архимеда (выталкивающая сила)		V – объём погруженной части тела g=10 м/с2 – ускорение свободного падения
Сила притяжения между телами (закон Всемирного тяготения)		G = 6,67*10-11 Н*м2/кг2 – гравитационная постоянная m1 и m2 — массы взаимодействующих тел r – расстояние между телами
Второй закон Ньютона		m – масса тела R – равнодействующая всех сил, действующих на тело a – ускорение, с которым движется тело под действием этих сил

Алгоритм решения

При решении задач из раздела «Динамика» желательно придерживаться следующего алгоритма решения:

1. Сделать рисунок, на котором указать вектора всех сил, действующих на тело.

2. Если тело двигается с ускорением, указать направление этого ускорения. Если тело покоится или двигается равномерно, его ускорение a=0.

3. Составить уравнение движения (второй закон Ньютона) для рассматриваемого тела в его векторном виде.

3. Выбрать систему координат и спроецировать полученное уравнение на выбранные оси координат.

4. Расшифровать неизвестные величины, вошедшие в уравнение движения.

5. Решить полученную систему уравнений.

Задание 2
– это расчётные задачи базового уровня сложности, и для решения некоторых из них этот алгоритм будет чересчур подробным и перегруженным, так как их можно решить и без вспомогательного рисунка или даже без записи второго закона Ньютона. Это касается, например, заданий, в которых на тело действует только одна сила. Но привычка решать задания по приведенному выше алгоритму поможет ученикам успешно справиться с расчетными задачами по разделу «Динамика» повышенного и высокого уровней сложности – такие задания могут стоять в ЕГЭ под номерами 25 и 29.

Ответом на задание 2 является число, именно его нужно вписать в бланк ответов 1, не указывая единицы измерения.

Примеры решения с разбором

Пример решения 2 задания по физике (ЕГЭ-2019)

Пружина жёсткостью 2*10⁴
Н/м одним концом закреплена в штативе. На какую величину она растянется под действием силы 400 Н?

Ответ: ___________________________ см.

Решение:

Сделаем чертёж

Пружина под действием силы F
привели в растянутое состояние. Кроме растягивающей силы F
и силы упругости
, стремящейся вернуть пружину в нерастянутое состояние, больше никакие силы на нее не действуют.

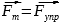
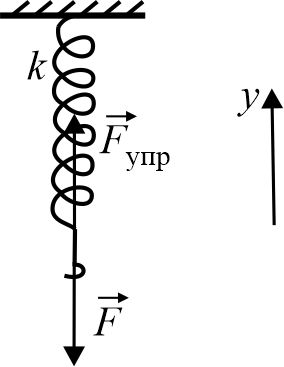
Запишем проекции сил на вертикальную ось Oy

F=F_упр

По закону Гука, сила упругости F_упр = k
*Δx, следовательно,

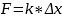
k
— коэффициент жёсткости пружины, Δx
– её удлинение.

Выразим величину растяжения пружины

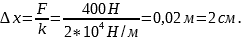
Ответ: 2

Пример решения 2 задания по физике (ЕГЭ – 2020. Вариант 1 досрочного ЕГЭ)

Тело движется по горизонтальной плоскости. Нормальная составляющая силы воздействия тела на плоскость равна 40 Н, сила трения равна 10 Н. Определите коэффициент трения скольжения.

Ответ: _______ .

Решение:

Силу трения можно найти по формуле

F_тр= µN,

где N – сила реакции опоры, или по-другому нормальная составляющая силы воздействия тела на плоскость.

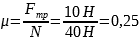
Ответ: 0,25.

Пример решения 2 задания по физике (ЕГЭ – 2020. Демонстрационный вариант)

Два одинаковых маленьких шарика массой m каждый, расстояние между центрами которых равно r, притягиваются друг к другу с силами, равными по модулю 0,2 пН. Каков модуль сил гравитационного притяжения двух других шариков, если масса каждого из них равна 2m, а расстояние между их центрами равно 2r?

Ответ: _______ пН.

Решение:

По закону Всемирного тяготения шары массами m₁и m₂, находящиеся друг от друга на расстоянии r,
притягиваются друг к другу с силой

.

В первом случае

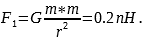
Во втором случае

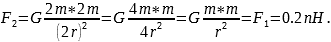
Ответ: 0,2

Пример решения 2 задания по физике (ЕГЭ – 2019. Демонстрационный вариант)

По горизонтальному полу по прямой равномерно тянут ящик, приложив к нему горизонтальную силу 35 Н. Коэффициент трения скольжения между полом и ящиком равен 0,25. Чему равна масса ящика?

Ответ _______ кг.

Решение:

Сделаем чертёж, на котором обозначим все силы, действующие на тело.

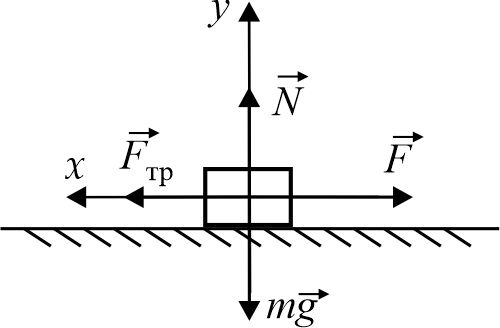
По второму закону Ньютона, равнодействующая всех сил, действующих на тело, будет равна нулю, так как по условию задачи тело движется равномерно, то есть ускорение тела a=0.

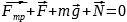
Запишем это в проекциях на оси Ox и Oy

Ox: F_тр
– F = 0,

Oy: N — m g=0.

Откуда N = mg, следовательно,

F_тр = µ N = µ mg.

Масса тела

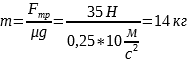
Ответ: 14

Пример решения 2 задания по физике (ЕГЭ – 2018)

К пружине подвесили груз массой 150 г, вследствие чего пружина удлинилась на 1 см. Чему будет равно удлинение этой пружины, если к ней подвесить груз 450 г?

Ответ: __________ см.

Решение:

Переведём единицы измерения физических величин в систему СИ

m₁ = 150 г = 0,15 кг, m₂ = 450 г = 0,45 кг, Δx=1 см = 0,01 м.

Сделаем чертёж, на котором обозначим все силы, действующие на тело.

На тело действует сила тяжести (F_т
= mg), направленная вертикально вниз, и сила упругости со стороны пружины (F_упр
= k Δx), направленная вертикально вверх.

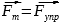
В проекции на вертикальную ось Oy.

F_т
=F_упр

mg = kΔx (1)

k
— коэффициент жёсткости пружины, Δx
– её удлинение.

Найдём, чему равен коэффициент жёсткости пружины

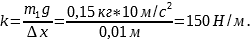
Выразим из выражения (1) удлинение пружины во втором случае

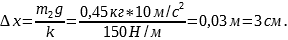
Ответ: 3