Задачи на системы счисления егэ информатика - Помощь в подготовке к экзаменам и поступлению

Всего: 570 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Запись числа N в системе счисления с основанием 6 содержит две цифры, запись этого числа в системе счисления с основанием 5 содержит три цифры, а запись в системе счисления с основанием 11 заканчивается на 1.

Чему равно N?

Запись числа N в системе счисления с основанием 7 содержит две цифры, запись этого числа в системе счисления с основанием 6 содержит три цифры, а запись в системе счисления с основанием 11 заканчивается на 2.

Чему равно N?

В системе счисления с основанием N запись числа 41₁₀ оканчивается на 2, а запись числа 131₁₀  — на 1. Чему равно число N?

В системе счисления с основанием N запись числа 79₁₀ оканчивается на 2, а запись числа 111₁₀  — на 1. Чему равно число N?

Запись числа 69₁₀ в системе счисления с основанием N оканчивается на 1 и содержит 4 цифры. Чему равно основание этой системы счисления N?

Запись числа 68₁₀ в системе счисления с основанием N оканчивается на 2 и содержит 4 цифры. Чему равно основание этой системы счисления N?

К записи натурального числа в восьмеричной системе счисления справа приписали два нуля. Во сколько раз увеличилось число? Ответ запишите в десятичной системе счисления.

Десятичное число 57 в некоторой системе счисления записывается как 212.

Определите основание системы счисления.

Запись числа 338 в системе счисления с основанием N содержит 3 цифры и оканчивается на 2. Чему равно максимально возможное основание системы счисления?

Запишите число 83 в троичной системе счисления. В ответе укажите только цифры, основание системы счисления писать не нужно.

Источник: ЕГЭ по информатике 05.05.2014. Досрочная волна. Вариант 1.

Запишите число 128 в пятеричной системе счисления. В ответе укажите только цифры, основание системы счисления писать не нужно.

Источник: ЕГЭ по информатике 05.05.2014. Досрочная волна. Вариант 2.

Решите уравнение: 121_x + 1₁₀ = 101₈

Ответ запишите в троичной системе (основание системы счисления в ответе писать не нужно).

Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11?

Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 26, запись которых в троичной системе счисления оканчивается на 22?

Сколько значащих цифр в записи десятичного числа 357 в системе счисления с основанием 7?

В системе счисления с некоторым основанием десятичное число 144 записывается в виде 264. Укажите это основание.

Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в троичной системе счисления оканчивается на 21.

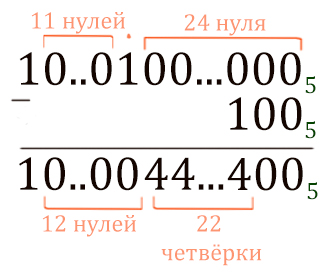
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 100, запись которых в системе счисления с основанием 5 оканчивается на 11?

Запись числа 65_8 в некоторой системе счисления выглядит так: 311_q. Найдите основание системы счисления q.

Запись числа 23₁₀ в некоторой системе счисления выглядит так: 212_q. Найдите основание системы счисления q.

Всего: 570 1–20 | 21–40 | 41–60 | 61–80 …

Источник

На уроке рассматривается 14 задание, решение и объяснение ЕГЭ по информатике

Содержание:

Объяснение заданий 14 ЕГЭ по информатике
- Перевод числа из любой системы счисления в десятичную
- Особенности при переводах в разные системы счисления
Решение заданий 14 ЕГЭ по информатике
- Определите наибольшее/наименьшее значение x, y
- Сколько цифр или сумма цифр
- Найти основание системы счисления и уравнения

14-е задание: «Операции в системах счисления»

Уровень сложности

— повышенный,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 5 минут.

Проверяемые элементы содержания: Знание позиционных систем счисления

До ЕГЭ 2021 года — это было задание № 16 ЕГЭ

Типичные ошибки и рекомендации по их предотвращению:

«Основные ошибки связаны с невнимательностью при выполнении арифметических действий
в недесятичных системах счисления. Например, вычитания единицы в ситуации типа: 1010000₂ – 1»

ФГБНУ «Федеральный институт педагогических измерений»

С основами темы можно ознакомиться в теории к заданию 1.

Перевод числа из любой системы счисления в десятичную

Чтобы перевести, например, 10045_N, из системы счисления с основанием N в десятичную систему, нужно умножить значение каждой цифры на N в степени, равной разряду этой цифры:

Особенности при переводах в разные системы счисления

Некоторые правила, которые нужно знать, при работе с системами счисления:

последняя цифра (крайняя справа) в записи числа в системе счисления с основанием N – представляет собой остаток от деления этого числа на N:

7₁₀ = 111₂
7/2 = остаток 1

две крайние справа цифры числа в системе счисления с основанием N – это остаток от деления этого числа на N², и так далее:

7₁₀ = 111₂
11₂=3₁₀
7/2² = остаток 3₁₀ (11₂)

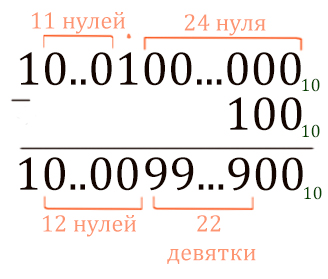
десятичное число 10^N записывается как единица и N нулей:

1_1

тогда как десятичное число 2^N в двоичной системе записывается как единица и N нулей:

а десятичное число 3^N записывается в троичной системе в виде единицы и N нулей:

можно сделать аналогичные выводы для любой системы счисления с основанием a; общее правило:

десятичное 10^N-1 записывается как N девяток:

1_11

тогда как десятичное число 2^N-1 в двоичной системе записывается как N единиц:

а десятичное число 3^N-1 записывается в троичной системе как N двоек:

значит есть общее правило: число a^N-1 в системе счисления с основанием a записывается как N старших цифр этой системы, то есть, цифр (a-1)

1_1

десятичное число 10^N-10^M = 10^M * (10^N-M – 1) записывается как N-M девяток, за которыми стоят M нулей:

тогда как десятичное число 2^N – 2^K при K < N в двоичной системе записывается как N – K единиц и K нулей:

то есть, существует общее правило:

1_11

Также следует знать, что верны равенства:

Решение заданий 14 ЕГЭ по информатике

Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ

Определите наибольшее/наименьшее значение x, y

14_14:

Операнды арифметического выражения записаны в системе счисления с основанием 15.

82x19₁₅ – 6x073₁₅

В записи чисел переменной x обозначена неизвестная цифра из алфавита 15-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 11. Для найденного значения x вычислите частное от деления значения арифметического выражения на 11 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.net:

uses school;
begin
  foreach var x in '0123456789abcde' do
  begin
    var a := dec('82'+ x +'19', 15);
    var b :=dec('6' + x +'073', 15);
    var sum := a - b;
    if sum mod 11 = 0 then
    begin
      print(sum / 11);
      break;
    end
  end;
end.

Python:

С++:

Ответ: 7806

Сколько цифр или сумма цифр

14_12:

Значение арифметического выражения

43∙7¹⁰³ – 21∙7⁵⁷ + 98

записали в системе счисления с основанием 7.
Найдите сумму цифр получившегося числа и запишите её в ответе в десятичной системе счисления.

✍Решение:

✎ Решение с использованием программирования:

PascalABC.net, Решение 1:

begin
  var x,s: Biginteger;
  x := 43*Biginteger.Pow(7, 103) - 21*Biginteger.Pow(7, 57) + 98;
  // в получившемся числе рассматриваем каждую цифру в 7-й системе сч.
  s:=0;
  while x > 0 do
  begin
    s:=s+ x mod 7; // добавляем цифру правого разряда
    x := x div 7; // убираем разряд числа в 7-й системе сч.
  end;
  println(s);
end.

PascalABC.net, Решение 2:

uses school;
 
begin
  var n: bigInteger;
  n := 43 * Biginteger.Pow(7, 103) - 21 * Biginteger.Pow(7, 57) + 98;
  print(n.ToString.ToBase(7).CountOf('1') +
    n.ToString.ToBase(7).CountOf('2') * 2 + 
    n.ToString.ToBase(7).CountOf('3') * 3 +
    n.ToString.ToBase(7).CountOf('4') * 4 +
    n.ToString.ToBase(7).CountOf('5') * 5 +
    n.ToString.ToBase(7).CountOf('6') * 6);
end.

Python:

x = 43*7**103 - 21*7**57 + 98
s = 0
# в получившемся числе рассматриваем каждую цифру в 7-й системе сч.
while x: 
    s+= x % 7 # добавляем цифру к сумматору
    x //= 7 # убираем разряд числа в 7-й системе сч.
print( s )

С++:

Результат: 276

14_1:

Значение арифметического выражения:
2¹⁰²⁴ + 4⁶⁴ — 64
записали в системе счисления с основанием 2.

Сколько цифр «1» содержится в этой записи?

Типовые задания для тренировки

✍Решение:

✎ Решение с использованием программирования:

PascalABC.net, Решение 1:

begin
  var k := 0;
  var x: Biginteger;
  x := Biginteger.Pow(2, 1024) + Biginteger.Pow(4, 64) - 64;
  // в получившемся числе рассматриваем каждую цифру в 2-й системе сч.
  while x > 0 do
  begin
    if x mod 2 = 1 then k += 1; // если цифра = 1, то считаем ее
    x := x div 2; // убираем разряд числа в 2-й системе сч.
  end;
  println(k);
end.

PascalABC.net, Решение 2:

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(2, 1024) + Biginteger.Pow(4, 64) - 64;
  print(x.ToString.ToBase(2).CountOf('1'));
end.

Python:

x = 2**1024 + 4**64 - 64
k = 0
# в получившемся числе рассматриваем каждую цифру в 2-й системе сч.
while x: 
    if x % 2 == 1: # если цифра = 1, то считаем ее
        k += 1
    x //= 2 # убираем разряд числа в 2-й системе сч.
print( k )

С++:

✎ Решение теоретическое:

Существует правило:

2^N = 10..0₂(1 единица и N нулей)

Чтобы воспользоваться этим правилом, преобразуем общее выражение к степеням двойки:

2¹⁰²⁴ + (2²)⁶⁴ - 2⁶ = 2¹⁰²⁴ + 2¹²⁸ - 2⁶

При переводе в двоичную систему получим:

10...0 (1024 нуля) + 10...0 (128 нулей) - 10...0 (6 нулей)

Обратим внимание, что разница между числами большая. Т.е. при выполнении сложения в столбик, единицы в одном и том же разряде быть не могут. Так:

 10....00000  - 1024 нуля
+
       10..0  - 128 нулей
_________________________
 10....10..0

Из первого слагаемого 10…0 (1024 нуля) запомним одну единицу в старшем бите, остальные нули нас не интересуют, так как далее мы воспользуемся другим правилом — для разницы:

 10....00000  - 1024 нуля
+
       10..0  - 128 нулей
_________________________
 10....10..0  - запомним единицу

Существует также правило:

2^N — 2^K = 1…1 (N - K единиц)0…0(K нулей)

По формуле выполним вычитание 2¹²⁸ — 2⁶: получим 1..1 (122 единицы) 0..0(6 нулей):

 10..0000000  - 128 нулей
-
     1000000  
_________________________
 11..1000000  - 122 единицы и 6 нулей

Прибавим к 122 получившимся единицам еще одну из первого слагаемого (10…0 (1024 нуля)) и получим:

122 + 1 = 123 единицы

Результат: 123

Также можно посмотреть видео решения 14 задания ЕГЭ по информатике (аналитическое решение):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

14_3: 14 задание. Демоверсия ЕГЭ 2018 информатика:

Значение арифметического выражения:
49¹⁰ + 7³⁰ – 49
записали в системе счисления с основанием 7.

Сколько цифр «6» содержится в этой записи?

Типовые задания для тренировки

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.net, решение 1:

begin
  var x: Biginteger;
  x := Biginteger.Pow(49, 10) + Biginteger.Pow(7, 30) - 49;
  // в получившемся числе рассматриваем каждую цифру в 7-й системе сч.
  var k:=0;
  while x > 0 do
  begin
    if x mod 7 = 6 then k+=1; // если цифра = 6, то считаем ее
    x := x div 7; // убираем разряд числа в 7-й системе сч.
  end;
  println(k);
end.

PascalABC.net, решение 2:

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(49, 10) + Biginteger.Pow(7, 30) - 49;
  print(x.ToString.ToBase(7).CountOf('6'));
end.

Python:

x = 49**10 + 7**30 - 49
k = 0
# в получившемся числе рассматриваем каждую цифру в 7-й системе сч.
while x: 
    if x % 7 == 6: # если цифра = 6, то считаем ее
        k += 1
    x //= 7 # убираем разряд числа в 7-й системе сч.
print( k )

С++:

✎ Решение теоретическое:

Приведем все числа к степеням 7:

7²⁰ + 7³⁰ - 7²

Расставим операнды выражения в порядке убывания степеней:

7³⁰ + 7²⁰ - 7²

Вспомним две формулы для работы со системами счисления:

1.
aⁿ = 10..0_a
       ⁿ
2.
aⁿ - a^m = (a-1)..(a-1)0..0_a
              ^n-m       ^m

Переведем первое число согласно формуле 1:

7³⁰ = 10..0
        ³⁰

В данном числе нет цифры 6, как и в остальных числах.
Цифра 6 появляется при выполнении вычитания.
Подсчитаем все «6», используя формулу 2:

0 + (20 - 2) = 18

Получаем шестерок: 18

Результат: 18

Подробное решение 14 задания демоверсии ЕГЭ смотрите на видео (аналитическое решение):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

14_2:

Значение арифметического выражения:
4⁵⁰⁰ + 3*4²⁵⁰⁰ + 16⁵⁰⁰ — 1024
записали в системе счисления с основанием 4.

Сколько цифр «3» содержится в этой записи?

Типовые задания для тренировки

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.net:

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(4,500) + 3*Biginteger.Pow(4,2500) + Biginteger.Pow(16,500) - 1024;
  print(x.ToString.ToBase(4).CountOf('3'));
end.

Python:

x = 4**500 + 3*4**2500 + 16**500 - 1024
k = 0
# в получившемся числе рассматриваем каждую цифру в 4-й системе сч.
while x: 
    if x % 4 == 3: # если цифра = 3, то считаем ее
        k += 1
    x //= 4 # убираем разряд числа в 4-й системе сч.
print( k )

С++:

Результат: 496

Подробное решение данного 14 задания ЕГЭ по информатике можно посмотреть на видео (аналитическое решение):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

14_5:

Значение арифметического выражения: 8¹⁰²⁴ + 8³² – 65 – записали в системе счисления с основанием 8. Сколько цифр «7» содержится в этой записи?

Типовые задания для тренировки

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.net:

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(8,1024) + Biginteger.Pow(8,32) - 65;
  print(x.ToString.ToBase(8).CountOf('7'));
end.

Python:

x = 8**1024 + 8**32 - 65
k = 0
# в получившемся числе рассматриваем каждую цифру в 8-й системе сч.
while x: 
    if x % 8 == 7: # если цифра = 7, то считаем ее
        k += 1
    x //= 8 # убираем разряд числа в 8-й системе сч.
print( k )

С++:

✎ Решение теоретическое:

Приведем все числа к степеням восьмерки:

65 = 64 + 1 = 8² + 8⁰;

Получаем:

8¹⁰²⁴ + 8³² - (8² + 8⁰);
8¹⁰²⁴ + 8³² - 8² - 8⁰

Вспомним две формулы для работы с системами счисления:

1.
aⁿ = 10..0_a
       ⁿ
2.
aⁿ - a^m = (a-1)..(a-1)0..0_a
              ^n-m       ^m

Переведем первое число согласно формуле 1:

8¹⁰²⁴ = 10..0
        ¹⁰²⁴

В данном числе нет цифры 7, как и в остальных числах.
Цифра 7 появляется при выполнении вычитания. У нас два таких действия, идущих подряд. Это неудобно. Необходимо, чтобы действия чередовались (a + b — c + d — e…)
Вспомним еще одну формулу:

-2ⁿ = -2ⁿ⁺¹ + 2ⁿ

! Формула предназначена для чисел в двоичной системе счисления, но для подсчета цифр "7" в 8-й (или "6" в 7-й и т.п.) ее можно использовать (для поиска единиц или нулей она не подходит!!!)

В нашем случае заменим часть выражения:

-8² = -8³ + 8²
! обратите внимание, что тождество неверно, но
при поиске количества "7" этой формулой можно воспользоваться
(для поиска единиц или нулей она не подходит!)


Получаем:

8¹⁰²⁴ + 8³² - 8³ + 8²- 8⁰

Получили чередование операций «+» и «-«.
Теперь посчитаем все «7», используя формулу 2:

0 + (32 - 3) + (2 - 0) = 31

Получаем семерок: 31

Результат: 31

14_13:

Сколько значащих нулей в двоичной записи числа 4³⁵⁰ + 8³⁴⁰ – 2³²⁰ – 12?

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.net, решение 1:

begin
  var b2 := biginteger(2);
  var numb := (2 * b2) ** 350 + (4 * b2) ** 340 - (1 * b2) ** 320 - 12;
  var digit: biginteger;
  var n := 0;
  while numb > 0 do
  begin
    digit := numb mod 2;
    if digit = 0 then n += 1;
    numb := numb div 2
  end;
  print(n)
 end.

PascalABC.net, решение 2:

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(4,350) + Biginteger.Pow(8,340) - Biginteger.Pow(2,320) - 12;
  print(x.ToString.ToBase(2).CountOf('0'));
end.

Python:

x = 4**350 + 8**340 - 2**320 - 12
print(x)
k = 0
while x:
  if x % 2 == 0: k += 1
  x //= 2
     print( k )

С++:

✎ Решение теоретическое:

4³⁵⁰ + 8³⁴⁰ – 2³²⁰ – 12

По возможности приведем каждое слагаемое к степеням 2. Получим:

(2²)³⁵⁰ + (2³)³⁴⁰ - 2³²⁰ - 3*2² =
(2²)³⁵⁰ + (2³)³⁴⁰ - 2³²⁰ - 12 =
2⁷⁰⁰ + 2¹⁰²⁰ - 2³²⁰ - (2³ + 2²)

Далее рассуждаем так: количество нулей можно найти, если из общего количества цифр в результирующем числе вычесть количество не нулей (любых других цифр).
Расположим операнды по убыванию:

2¹⁰²⁰ + 2⁷⁰⁰ - 2³²⁰ - 2³ - 2²

Наибольшее число 2¹⁰²⁰, в нем 1021 разряд в двоичной с.с. (одна единица и 1020 нулей). То есть всего 1021 знаков.
Для того, чтобы избежать два подряд идущих минуса, воспользуемся правилом -2ⁿ = -2ⁿ⁺¹+2ⁿ и преобразуем выражение:

2¹⁰²⁰ + 2⁷⁰⁰ - 2³²¹+ 2³²⁰- 2⁴ + 2³ - 2²

Посчитаем количество не нулей в каждом операнде:

2¹⁰²⁰ -> один не ноль
2⁷⁰⁰ - 2³²¹ -> 379 не нулей
2³²⁰- 2⁴ -> 316 не нулей 
2³ - 2² -> один не ноль
Итого: 1+ 379+316 +1 = 697

Получаем нулей:

1021 - 697 = 324

Результат: 324

Найти основание системы счисления и уравнения

14_7:

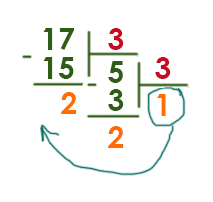
Укажите, сколько всего раз встречается цифра 2 в записи чисел 13, 14, 15, …, 23 в системе счисления с основанием 3.

Типовые задания для тренировки

✍ Решение:

Для начала достаточно перевести первое и последнее число предложенного интервала в троичную систему счисления. Сделаем это:

1.
 13 | 3 
 12   4 | 3 
  1   3   1   
      1
131₀ = 111₃

2.
23 | 3 
21   7 | 3 
2    6   2
     1
23₁₀ = 212₃

Теперь добавим промежуточные числа в троичной системе счисления (прибавляя единицу к каждому очередному полученному числу), не забывая, что в троичной системе всего три цифры (0, 1 и 2):

111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212

На всякий случай стоит посчитать количество полученных чисел и сравнить их с количеством чисел в исходной последовательности.
Теперь осталось посчитать количество цифр 2 в полученной последовательности. Их 13:

111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212

Ответ: 13

✍ Решение:

Разделим уравнение на три части и вычислим каждую часть отдельно (выделим части разным цветом):

204_N+1 = 204_N + 26₁₆
 1       2     3

Используем формулу разложения числа по степеням основания:

1. 
₂₁₀
204_N+1

По формуле получаем:
2*(N+1)² + 0*(N+1)¹ + 4*(N+1)⁰ =
= 2*(N² + 2N + 1) + 0 + 4 = 2N² + 4N + 6

Выполним то же самое для остальных двух частей:

2.
₂₁₀
204_N

По формуле получаем:
2*N² + 0*N¹ + 4*N⁰ =
= 2N2 + 4

3.
26₁₆ = 38₁₀

Подставим результаты всех частей в уравнение:

2N² + 4N + 6 = 2N² + 4 + 38;
4N = 36;
N = 9

Результат: 9

✍ Решение:

Вместо обозначения искомой системы счисления введем неизвестное x:

144_x + 24_x = 201_x

Запишем формулу перевода в десятичную систему счисления каждого из слагаемых и сумму исходного равенства:

144 + 24 = 201
1*x² + 4*x¹ + 4*x⁰ + 2*x¹ + 4*x⁰ = 2*x² + 0*x¹ + 1*x⁰

Упростим полученное уравнение:

x² - 6x - 7 = 0

Решим уравнение:

D = b² - 4ac = 36 - 4*1*(-7) = 64
x = (-b ± √D)/2a
x1 = (6 + 8)/2 = 7
x2 = (6 - 8)/2 - не подходит
x = 7

Ответ: 7

14_9:

В некоторой системе счисления записи десятичных чисел 68 и 94 заканчиваются на 3. Определите основание системы счисления.

Типовые задания для тренировки

✍ Решение:

Вспомним правило:

Последняя цифра записи числа в системе счисления с основанием X — это остаток от деления этого числа на X

Примем искомую систему счисления за x. Тогда, исходя из приведенного правила имеем:

94 / x = некоторое число и остаток 3
и
68 / x = некоторое число и остаток 3

Поскольку x должно быть целым числом, то следующее деление должно выполняться без остатка:

91/x 
65/x

Иными словами x — наибольший общий делитель чисел 91 и 65.
Найдем НОД, например, по алгоритму Евклида:

91 - 65 = 26
65 - 26 = 39
39 - 26 = 13
26 - 13 = 13

Получаем результат 13.

Ответ: 13

14_10:

Некоторое число X из десятичной системы счисления перевели в системы счисления с основаниями 16, 8. Часть символов при записи утеряна. Позиции утерянных символов обозначены *:

X = *5₁₆ = *0*₈

Сколько чисел соответствуют условию задачи?

Типовые задания для тренировки

✍ Решение:

Данные числа с утерянными символами переведем из 16-й и из 8-й системы счисления в двоичную. Перевод будем делать триадами и тетрадами, неизвестные позиции оставим пустыми:

1. *5₁₆
    *   |    5  ₁₆

* * * * | 0 1 0 1 ₂

2. *0*₈
  *  |  0  |  *  ₈
* * *|0 0 0|* * * ₂

Сопоставим известные и неизвестные биты в обеих получившихся масках:

* * 0 0 0 1 0 1

Неизвестными остались 7-й и 8-й бит. Они не могут быть одновременно нулями, так как для *0*₈ тогда исчезнет старший разряд. Поэтому оставшиеся варианты будут такими:

1. 01000101
2. 10000101
3. 11000101

Итого 3 варианта.

Ответ: 3

Предлагаем посмотреть видео решения данного 14 задания ЕГЭ (аналитическое решение):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

14_4:

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 75 оканчивается на 13.

Типовые задания для тренировки

✍ Решение:

Так как 75 должно оканчиваться на 13, то имеем два общих случая:

1. 75₁₀ = 13_N 
2. 75₁₀ = ...13_N (число оканчивается на 13)

Рассмотрим подробно каждый случай.

1 случай:

Остаток должен быть равен 3 (последнее число в неизвестной системе), а частное должно равняться 1 (предпоследнее число в неизвестной системе):

 75|N 
  N|1  отсюда имеем => 75 - N = 3; т.е. N = 72
  3

Таким образом, мы получили одно из искомых оснований (72).

2 случай:

Искомое оканчивается на цифру 3, значит:

 75|N 
 72|y  отсюда имеем => 75 = Ny + 3, где N - целое, неотриц.
  3

и далее, частное от деления — 1 (предпоследнее число):

 75|N  
 72|  y |N   => y = Nz + 1, где z - целое, неотриц.
  3  y-1|z
       1

Получаем два равенства (систему уравнений):

75 = Ny + 3
y = Nz + 1

Подставим y из второго равенства в первое:

75 = N (Nz + 1) + 3;
75 = N²z + N + 3;
75 = N²z + N

Выразим z:

z = (72 - N)/N²

Учитывая то, что z — целое неотрицательное число, то 72 — N должно быть кратно N², т.е. в числителе не может быть простого числа.
Простое число 67 получается путем вычитания из 72 числа 5. Соответственно, 5 нам не подходит: N ≠ 5:

72 - 5 / 5² = 67 / 25  не делится, - не подходит!

Еще одно простое число — 71 получится при вычитании 72 — 1. Единица не подходит, так как при переводе в конце числа никак не останется 13: N ≠ 1.
Раз в знаменателе N², то отбросим все числа, квадрат которых больше 72: 9, 10, … и т.д. до бесконечности: N < 9
Раз в итоговом числе есть число 13, значит основание системы счисления больше 3 (т.е. цифра три присутствует в системах, начиная с 4-й): N >= 4
Проверим оставшиеся варианты — 4, 6, 7, 8:

 75 | 4 
 72 | 18| 4 
  3   16| 2
       2  => не подходит! должна быть единица

 75 | 6 
 72 | 12| 6 
  3   12| 1
       0  => не подходит! должна быть единица

 75 | 7 
 70 
  5 => не подходит! должна быть 3

 75 | 8 
 72 | 9| 8 
  3   8| 1
       1  => подходит!

Результат: 8,72

Видеоразбор решения (аналитический способ):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

14_11:

Выражение 2⁵*3²⁵ записано в троичной системе счисления. Определите, сколько в этой записи цифр 0, 1 и 2.

✍ Решение:

Первый сомножитель:

2⁵ = 32

Переведем в троичную систему счисления (делением на 3, переписываем остатки).
Результат:
32₁₀= 1012₃

Для рассмотрения второго сомножителя будем использовать правило:

Получим:

3²⁵ = 10..0{25 нулей}₃

Выполним произведение, но для простоты счета, представим, что нулей не 25, а только 3:

В исходном числе было 3 нуля, стало 4. Значит если было 25 нулей, то станет 25 + 1 = 26.
Единиц = 2, двоек = 1.

Ответ: «0»=26, «1»=2, «2»=1

Смотрите видео разбора на нашем канале (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Источник

ЕГЭ – 1. Системы счисления и двоичное представление информации

в памяти компьютера (базовый уровень, примерное время

решения – 1 минута). Теория по теме – здесь.

Рассмотрим различные задачи, которые встречаются в данном задании, и способы их решения. Начнем с самых простых задач, которые вряд ли будут на ЕГЭ, но решение которых позволит нам быстро и просто решать самые сложные, и придем к самым сложным.

Задача 1. Как представлено число 75₁₀ в двоичной системе счисления?

a) 1001011₂b) 111101₂ c) 101011₂ d) 1001001₂

Решение. Для быстрого и точного решения задачи достаточно разложить исходное число на сумму степеней двойки, а затем записать «1» на место существующей степени и «0» — на место пропущенной степени двойки.

Тогда 73₁₀= 2⁶ + 2³ + 2⁰ = 1001001₂

(шестая степень есть – 1, пятой нет – 0, четвертой нет – 0, третья есть – 1, второй нет – 0, первой нет – 0, нулевая есть – 1).

Возможные ловушки:

если исходное число четное, то нужно не забыть о нулевой степени числа.
вариант ответа b). Нужно помнить правильность перевода числа из десятичной системы счисления в двоичную, что десятичная система не «дружит» ни с какой другой в окружении систем с основанием, меньшим 100 (а на другие задачи мы не решаем), и пользоваться таблицей «дружбы» для перевода в двоичную систему счисления нельзя.

Проверка решения: По закономерности 4 из теоретической части: N^L-1≤ Ch ^L.

Тогда 64 ≤ 73 ⁶ ≤ 73 ⁷

Длина результата равна 7, как и в полученном ответе.

Эта проверка действует на оба варианта из возможных совершенных ошибок.

На ЕГЭ более вариантов ответов не предусматривается.

Ответ: 1001001

Задача 2. Сколько единиц в двоичной записи числа 187 ?

Решение. Для быстрого и точного решения задачи достаточно разложить исходное число на сумму степеней двойки, а затем посчитать количество присутствующих степеней.

Тогда 187 = 128 + 32 + 16 + 8 + 2 + 1 , то есть будет всего шесть степеней двойки.

Заметим, что более никаких действий для получения ответа здесь выполнять не нужно!

Для проверки правильности решения достаточно сложить полученные числа и сравнить их с исходным числом.

Ответ: 6

Задача 3. Сколько нулей в двоичной записи числа 204 ?

Тогда 205 = 128 + 64 + 8 + 4 , то есть будет всего 4 степени двойки. А длина числа при переводе в двоичную систему счисления будет равна 8 (2⁷ ≤ 205 ⁸). Тогда количество нулей в числе будет рано разнице между ними: 8 — 4 = 4.

Заметим, что более никаких действий для получения ответа здесь выполнять не нужно!

Ответ: 4

Задача 4. Как записывается число A95₁₆ в восьмеричной системе счисления?

Решение. Шестнадцатеричная и восьмеричная системы счисления являются «дружественными» («родственными») системами, поэтому для решения задания достаточно использовать таблицу «дружбы» и принцип перевода чисел с ее помощью (см. теорию по теме).

Тогда A95₁₆= 1010 1001 0101₂ = 101 010 010 101₂ = 5225₈.

Ответ: 5225

Задача 5. Дано: а = 9C₁₆, b = 236₈. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?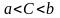

a) 10011010₂ b) 10011110₂ c) 10011101₂ d) 11011110₂

Решение. Заметим главное: исходные числа даны здесь в различных системах счисления. Для решения задачи нужно сначала привести их в одну – любую, удобную Вам для вычислений, а затем выполнять дальнейшие действия.

Здесь числа даны в дружественных восьмеричной, шестнадцатеричной и двоичной системах, поэтому удобнее всего перевести первое число и ответы в восьмеричную систему и найти подходящий вариант решения.

Тогда 9C₁₆= 1001 1100₂= 10 011 100₂ = 234₈;

a) 10011010₂ = 10 011 010₂ = 232₈;

b) 10011110₂= 10 011 110₂ = 236₈;

c) 10011101₂= 10 011 101₂ = 235₈;

d) 11011110₂= 11 011 110₂ = 336₈.

Правильный ответ – с), но рекомендуется не останавливаться, а проверить все варианты ответов, чтобы быть уверенным в правильном решении.

Ответ: с

Задача 6. Даны 4 целых числа, записанные в двоичной системе:

10111010, 10110100, 10101111, 10101100.
Сколько среди них чисел, меньших, чем 9C₁₆ + 37₈?

Тогда 9C₁₆ = 1001 1100₂ = 10 011 100₂ =234₈;

234₈ + 37₈ = 273₈;

10111010₂ = 272₈ (подходит);

10110100₂ = 264₈ (подходит);

10111111₂ = 277₈ (не подходит);

10101100₂ = 259₈ (подходит).

Ответ: 3

Задача 7. Укажите наибольшее четырёхзначное шестнадцатеричное число, двоичная запись которого содержит ровно 5 значащих нулей. В ответе запишите только само шестнадцатеричное число, основание системы счисления указывать не нужно.

Решение. Наибольшее четырехзначное шестнадцатеричное число равно FFFF. Чтобы число с пятью значащими нулями оставалось наибольшим, нули должны стоять в конце числа, тогда переводим две последние цифры в двоичную систему счисления, заменяем там последние пять цифр на нули и переводим обратно в шестнадцатеричную систему, получаем:

FF₁₆ = 11111111₂ = 11100000₂ = E0₁₆

Ответ: FFE0

Задача 8. (А.Н. Носкин) Задан отрезок [a, b]. Число a – наименьшее число, восьмеричная запись которого содержит ровно 3 символа, один из которых – 3. Число b – наименьшее число, шестнадцатеричная запись которого содержит ровно 3 символа, один из которых – F. Определите количество натуральных чисел на этом отрезке (включая его концы).

Решение.

a = 103₈; b = 10F₁₆ = 1 0000 1111₂ = 417₈

417₈ – 103₈ + 1 = 315₈ = 205 (плюс 1, потому что в разность входит только один конец отрезка, добавляем второй).

Ответ: 205

Задача 9. (Е.В. Куцырь) Определите количество натуральных чисел, кратных основанию четверичной системы счисления и удовлетворяющих неравенству: 734₈  x ₁₆

Решение.

1E4₁₆= 1 1110 0100₂ = 744₈

744₈ – 734₈ = 10₈= 8 – всего в интервале, включая исходное число. Тогда чисел, кратных 4, в интервале ровно 2.

Ответ: 2

Источник

Мы подошли к 14 заданию из ЕГЭ по информатике 2022. Оно связано с различными системами счисления. Что такое различные системы счисления, мы рассматривали в этой статье. Так же будет полезно посмотреть эту статью.

Переходим к первому тренировочному 14-ому заданию из ЕГЭ по информатике. Раньше это задание было под номером 16.

Задача (ЕГЭ по информатике, 2019, Москва)

Значение выражения 5³⁶ + 5²⁴ — 25 записали в системе счисления с основанием 5. Сколько цифр «4» содержится в этой записи?

Решение:

Первый способ. (С помощью Питона)

f = 5**36 + 5**24 - 25

s=''

while f>0:
    s = s + str(f%5)
    f = f // 5

print(s.count('4'))

В переменную f записываем функцию. Две звёздочки подряд обозначают возведение в степень. Заводим строчку s, где и будет сформировано число в пятеричной системе.

Сам перевод числа f в пятеричную систему происходит в цикле WHILE.

Записываем остатки от деления на 5 в строку s. Делаем так же, как если бы переводили в ручную. И так же производим само целочисленное деление. Это мы тоже делаем, когда переводим на листке бумаги.

В строке s получается число в пятеричной системе, но в цифры в этой записи стоят в обратном порядке. Ведь, когда мы переводим в ручную, остатки должны записать задом наперёд.

Здесь и не важен порядок цифр, важно количество четвёрок!

С помощью функции count находим количество четвёрок в строке s.

В ответе напишем 22.

Второй способ. (Классический)

Сформулируем главное правило, на которое будем опираться при решении подобного типа задач.

Примеры:

5⁴ (в десятичной системе) — это 10000₅ (в пятеричной системе)
7² (в десятичной системе) — это 100₇ (в семеричной системе)
2⁹ (в десятичной системе) — это 1000000000₂ (в двоичной системе)

Перепишем наше выражение, чтобы все числа были в виде степени представлены.

5³⁶ + 5²⁴ — 5²

Посчитаем 5³⁶ + 5²⁴ в пятеричной системе столбиком, используя основное правило.

Здесь всё просто: ноль прибавить ноль, будет ноль. Единица плюс ноль, будет один.

Теперь от получившегося числа нужно отнять 5² (100₅).

Первые два разряда посчитать легко. Ноль минус ноль, будет ноль.

Третий разряд: из нуля отнять единицу мы не можем, поэтому занимаем у более старших разрядов.

В более старших разрядах тоже нули, поэтому идём до единицы, у которой можно занять. Получается 22 четвёрки.

Вот как было бы, если бы считали в нашей родной десятичной системе счисления в аналогичной ситуации.

Здесь мы считаем в десятичной системе, поэтому получаются девятки. В нашей задаче считали в пятеричной системе, поэтому получаются четвёрки.

В ответе напишем 22 четвёрки.

Ответ: 22

Задача (ЕГЭ по информатике, 2020, Москва)

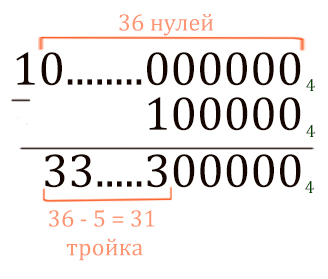
Значение выражения 16⁸ × 4²⁰ — 4⁵ — 64 записали в системе счисления с основанием 4. Сколько цифр «3» содержится в этой записи?

Решение:

Первый способ. (С помощью Питона)

f = 16**8 * 4**20 - 4**5 - 64

s=''

while f>0:
    s = s + str(f%4)
    f = f // 4

print(s.count('3'))

Второй способ. (Классический)

Преобразуем наше выражение. Приведём всё к 4-ам.

16⁸ × 4²⁰ — 4⁵ — 64 =
= (4²)⁸ × 4²⁰ — 4⁵ — 4³ =
= 4¹⁶ × 4²⁰ — 4⁵ — 4³ =
= 4³⁶ — 4⁵ — 4³

Здесь не можем применить технику устного счёта, потому что стоят два минуса. Значит, будем решать с помощью столбиков.

Сначала посчитаем 4³⁶ — 4⁵.

Теперь от этого числа нужно отнять 4³ (1000₄)

Получается 32 тройки.

В последнем вычислении нет ничего сложно. В десятичной системе вы бы легко вычислили в аналогичной ситуации.

Ответ: 32

Задача (Тренировочная)

Укажите через запятую в порядке возрастания все десятичные натуральные числа, не превосходящие 17, запись которых в троичной системе счисления оканчивается на две одинаковые цифры.

Решение:

1) Переведём число 17 в троичную систему.

Получилось 122₃.

2) Теперь выпишем все числа, которые не превосходят 122₃ (Т.е. 122₃ тоже подходит!), запись которых в троичной системе счисления оканчивается на две одинаковые цифры. В троичной системе могут применяться цифры 0, 1, 2.

122₃
122₃
111₃
100₃
22₃
11₃

Теперь переведём эти числа в десятичную систему.

122₃ = 2 × 3⁰ + 2 × 3¹ + 1 × 3² = 17₁₀
111₃ = 1 × 3⁰ + 1 × 3¹ + 1 × 3² = 13₁₀
100₃ = 0 × 3⁰ + 0 × 3¹ + 1 × 3² = 9₁₀
22₃ = 2 × 3⁰ + 2 × 3¹ = 8₁₀
11₃ = 1 × 3⁰ + 1 × 3¹ = 4₁₀

Ответ: 4, 8, 9, 13, 17

Ещё один интересный тип задания номер 14, который вполне может быть на реальном ЕГЭ по информатике 2022.

Задача (Уравнение)

Чему равно наименьшее основание позиционной системы счисления x, при котором 225_x = 405_y?
Ответ записать в виде целого числа.

Решение:

Переведём каждое из чисел 225_x и 405_y в десятичную систему счисления и приравняем, т.к. эти числа равны.

5 × x⁰ + 2 × x¹ + 2 × x² = 5 × y⁰ + 0 × y¹ + 4 × y²

Любое число в нулевой степени — это 1. Значит, 5 × x⁰ = 5 × y⁰ = 5. Эти два выражения равны одному и тому же значению, следовательно, их можно убрать и слева, и справа.

2x + 2x² = 4y²
x + x² = 2y²
x(1 + x) = 2y²

Получили уравнение в целых числах. Слева умножение двух последовательных чисел. Нужно начать подбирать целые числа.

При y = 6 :

x (1 + x) = 2 × 6² = 72 ; Произведение двух последовательных чисел 8 * 9 = 72. Значит, x = 8.

Мы начали проверку с числа 6, потому что у нас в уравнении присутствуют цифра 5. Значит, система счисления может быть минимум с основанием 6.

Получается, что наименьшее значение x равно 8.

В подобных задач нужно знать, что числа обязательно найдутся, нужно их просто хорошо поискать.

Для качественной проработки 14 задания из ЕГЭ по информатике 2022 разберём ещё некоторые задачи.

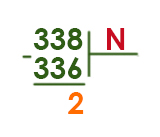
Задача (Основание системы)

Запись числа 338 в системе счисления с основанием N содержит 3 цифры и оканчивается на 2. Чему равно максимально возможное основание системы счисления?

Решение:

В этой задаче применим формулу:

Примером для данной формулы можно взять два разряда в двоичной системе. Максимальное число в двоичной системе равно 11₂. А в десятичной системе это число равно 3₁₀. Т.е. 2² — 1.

338 число будет точно больше, чем двухзначное число с основанием N.

Получается неравенство:

338 > N² — 1
N² < 339

N — положительное целое число. Тогда:

N < √339 ≈ 18
N ≤ 18

Сказано, что число в системе с основанием N оканчивается на 2. Поэтому первый остаток должен быть равен 2!

Будем идти вниз от числа 18 и проверять, на что делится 336.

Число 336 должно делится на N.

Подошло число 16 (16 * 21 = 336!)

Ответ: 16

Продолжаем подготовку к 14 заданию из ЕГЭ по информатике 2022

Задача (На понимание)

Запись числа в девятеричной системе счисления заканчивается цифрой 4. Какой будет последняя цифра в записи этого числа в троичной системе счисления?

Решение:

Подберём такие числа в десятичной системе, которые в остатке при первом делении на 9 дадут 4!

Посмотрим, какой остаток будет при делении этого же числа на 3 при первом делении. Получается 1. Это и будет ответ.

Ответ: 1

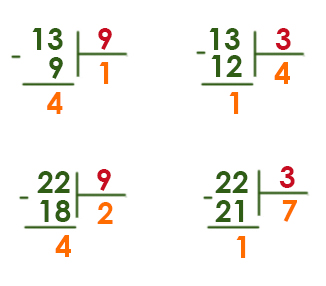
Задача (Закрепление материала)

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.

Решение:

Нужно перебрать все числа от 3 до 23 и определить, какие из них при делении числа 23 дадут остаток 2.

23 : 3 = 7 (ост. 2) +
23 : 4 = 5 (ост. 3) —
23 : 5 = 4 (ост. 3) —
23 : 6 = 3 (ост. 5) —
23 : 7 = 3 (ост. 2) +
23 : 8 = 2 (ост. 7) —
23 : 9 = 2 (ост. 5) —
23 : 10 = 2 (ост. 3) —
23 : 11 = 2 (ост. 1) —
23 : 12 = 1 (ост. 11) —
23 : 13 = 1 (ост. 10) —
23 : 14 = 1 (ост. 9) —
23 : 15 = 1 (ост. —
23 : 16 = 1 (ост. 7) —
23 : 17 = 1 (ост. 6) —
23 : 18 = 1 (ост. 5) —
23 : 19 = 1 (ост. 4) —
23 : 20 = 1 (ост. 3) —
23 : 21 = 1 (ост. 2) +
23 : 22 = 1 (ост. 1) —
23 : 23 = 1 (ост. 0) —

Подходят числа 3, 7, 21.

Здесь можно и написать программу:

for i in range(3, 24):
    if 23%i==2:
        print(i)

Ответ: 3, 7, 21

Задача (Добьём 14 задание из ЕГЭ по информатике 2022)

В некоторой системе счисления записи десятичных чисел 66 и 40 заканчиваются на 1. Определите основание системы счисления.

Решение:

Нужно найти такое число, чтобы числа 66 и 40 при делении на это число давали остаток 1.

Т.е. искомое число должно быть делителем чисел 65 (66-1) и 39 (40-1). У числа 39 не так много делителей: 1, 3, 13, 39

Видим, что число 65 делится на 13 (65 : 13 = 5). Поэтому искомое число равно 13.

Ответ: 13

Задача (Для чемпионов!)

В какой системе счисления выполняется равенство 12 · 13 = 222?
В ответе укажите число – основание системы счисления.

Решение:

Если бы мы находились в десятичной системе, то последней цифрой была бы 6 (2 * 3). Но у нас 2! Т.е. Система счисления меньше или равна 6, т.к. если бы система счисления была больше 6, то у нас была бы 6 последняя цифра.

Шестёрка не «поместилась» в младший разряд, от неё осталось только 2. Остальные 4 единицы ушли в более старший разряд. Если 4 единицы составляют единицу более старшего разряда, то значит, мы находимся в четверичной системе.

Ответ: 4

Задача (Новый тип, Статград окт 2022)

В выражении 1xBAD₁₆ + 2CxFE₁₆ x обозначает некоторую цифру из алфавита шестнадцатеричной системы счисления. Определите наименьшее значение x, при котором значение данного выражения кратно 15. Для найденного x вычислите частное от деления данного выражения на 15 и запишите его в ответе в десятичной системе счисления.

Решение:

Здесь дана сумма чисел, которые написаны в шестнадцатеричной системе счисления.

Мы будем перебирать каждую цифру из шестнадцатеричной системы (0-15) с помощью цикла. Нас будут интересовать те значения x, при котором сумма этих чисел будет делится на 15.

for x in range(0, 16):
    a=13*16**0 + 10*16**1 + 11*16**2 + x*16**3 + 1*16**4
    b=14*16**0 + 15*16**1 + x*16**2 + 12*16**3 + 2*16**4
    if (a+b)%15==0:
        print(x, (a+b)//15)

Чтобы проверить, делится ли данное выражение на 15, переводим оба слагаемых в нашу родную десятичную систему. Переводим стандартным образом, об этом можно прочитать здесь.

В задаче нужно написать для наименьшего найденного значения x результат от деления данной суммы на 15.

Получается 18341

Ответ: 18341

Задача(Новый тип, закрепление)

(Богданов) Операнды арифметического выражения записаны в системе счисления с основанием 17:

9759x₁₇ + 3×108₁₇

В записи чисел переменной x обозначена неизвестная цифра из алфавита 17-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратного 11. Для найденного значения x вычислите частное от деления значения арифметического выражения на 11 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.

Решение:

Решим задание с помощью предыдущего шаблона на языке Python.

for x in range(0, 17):
    a=x*17**0 + 9*17**1 + 5*17**2 + 7*17**3 + 9*17**4
    b=8*17**0 + 0*17**1 + 1*17**2 + x*17**3 + 3*17**4
    if (a+b)%11==0:
        print(x, (a+b)//11)

Ответ: 95306

Задача (Новый тип, две переменные)

(В. Шубинкин) Числа M и N записаны в системах счисления с основаниями 15 и 13 соответственно.

M = 2y23x5₁₅, N = 67x9y₁₃

В записи чисел переменными x и y обозначены допустимые в данных системах счисления неизвестные цифры. Определите наименьшее значение натурального числа A, при котором существуют такие x, y, что M + A кратно N.

Решение:

Принцип решения данной задачи похож на решение 15 задания из ЕГЭ по информатике.

for A in range(1, 5000):
    for x in range(0, 13):
        for y in range(0, 13):   
            M=5*15**0 + x*15**1 + 3*15**2 + 2*15**3 + y*15**4 + 2*15**5
            N=y*13**0 + 9*13**1 + x*13**2 + 7*13**3 + 6*13**4
            if (M+A)%N==0:
                print(A)

Нужно найти A, значит, начинаем перебирать A. Идём от 1, т.к. речь идёт о натуральных числах. Перебираем x и y. Они могут принимать значения из алфавита в 13-ой системе. Берём меньшую, т.к. эти переменные и в первом числе, и во втором одинаковые.

Если выполняется условие задачи, то нам интересно такое A при котором это произошло.

В этой задаче A получается достаточно большим, поэтому перебираем эту переменную до 5000.

Ответ: 1535

На этом всё! Вы прошли чемпионскую тренировку по подготовке 14 задания из ЕГЭ по информатике 2022. Успехов на экзамене!

«В переменную f записываем функцию». В переменную f мы записываем не функцию, а выражение

Господа, вот это я понимаю, по-настоящему чемпионская подготовка. Тут же и язык свой придумали, и решение на нём сделали. Скажите, зачем над змеёй то издеваться? Очень уж режет слух неправильное произношение. «Пайтон» — вот как должно быть. Я бы промолчал, увидев это раз, но видя подобное насилие над словом постоянно — молчать более не могу

Для ласт задачи модно сделать код куда проще и короче
for a in range(1, 10000):
for x in ‘0123456789ABC’:
for y in ‘0123456789ABC’:
M = int(f’2{y}23{x}5′, 15)
N = int(f’67{x}9{y}’, 13)
if (M + a) % N == 0:
print(a)
break

Первое задание, первое решение, очепятка: «В ответе напишем 4»,
вместо: «В ответе напишем 22».

И спасибо Вам за этот сайт!)

Источник

Решение задач ЕГЭ по теме «Системы счисления»

Подписи к слайдам:

Решение задач ЕГЭ
по теме «Системы счисления»

Скалкина С.И., учитель информатики и ИКТ
первой квалификационной категории

Муниципальное бюджетное общеобразовательное учреждение Карсунская средняя школа имени Д.Н. Гусева

Немного теории:

Сколько единиц используется в двоичной записи числа 12F016?

Сколько единиц используется в двоичной записи числа 12F016?

Ответ: 6

2) Укажите наименьшее число, двоичная запись котрого содержит ровно пять значащих нулей и две единицы. Ответ запишите в десятичной системе счисления.

Ответ: 65

3) Сколько единиц в двоичной записи десятичного числа 73?

Ответ: 3

Решение задач ЕГЭ (Часть 1, №1)

1. Сколько единиц в двоичной записи десятичного числа 519?

2. Сколько единиц в двоичной записи восьмеричного числа 17318?

3. Чему равна сумма чисел 138 и 1316? Результат запишите в двоичной системе счисления.

4. Укажите наименьшее четырёхзначное шестнадцатеричное число, двоичная запись которого содержит ровно 5 нулей.

Ответ: 4

Ответ: 7

Ответ: 111102

Ответ: 107F

5. Дано: а=7716, b=1718. Какое число х, записанное в двоичной системе счисления, отвечает неравенству a<x<b?

Ответ:11110002

Весёлая эстафета

Сколько глаз у пиявки? (подсказка 10102).
Сколько вершков в аршине (подсказка: 100002)
Сколько лет спала Спящая красавица из сказки Шарля Перро? (подсказка: 11001002)
Сапоги какого размера носил дядя Степа? (подсказка: 1011012)
Сколько лет было Красной шапочке? (подсказка 10002)

Решение задач ЕГЭ (Часть 1, №16)

Сколько значащих нулей в двоичной записи числа
4512 + 8512 – 2128 – 250

Ответ: 519

2) Решите уравнение: 121x+110=1017
Ответ запишите в троичной системе счисления.

Ответ: 20

1. Значение арифметического выражения: 98 + 35 – 9 записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?

2. Решите уравнение 121x + 110 = 1019. Ответ запишите в десятичной системе счисления.

3. Сколько единиц содержится в двоичной записи значения выражения: 42018 + 22018 – 32?

4. Десятичное число 63 в некоторой системе счисления записывается как 120.Определите основание системы счисления.

Ответ: 3

Ответ: 8.

Ответ: 2014

Ответ: 7

Тренировочный тест

№1. Укажите наименьшее четырёхзначное восьмеричное число, двоичная запись которого содержит 6 единиц.

№ 16. Сколько единиц в двоичной записи числа 42016 – 22018 + 8800 – 80

Ответ: 1037

Ответ: 2395

Рефлексия

присесть на корточки — — невысокая оценка, безразличное отношение;
обычная поза стоя, руки по швам — удовлетворительная оценка, спокойное отношение;
поднять руки вверх, хлопая в ладоши — высокая оценка, восторженное отношение.

Источник

B7 (повышенный уровень, время – 2 мин)

Тема: Кодирование чисел. Системы счисления.

Что нужно знать:

4 3 2 1 0 ← разряды

1 2 3 4 5N = 1·N4 + 2·N3 + 3·N2 + 4·N1 + 5·N0

Пример задания:

Решите уравнение .
Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.

Решение:

удобнее всего перевести все числа в десятичную систему, решить уравнение и результат перевести в шестеричную систему
получаем
уравнение приобретает вид , откуда получаем
переводим 15 в шестеричную систему счисления:
ответ: 23.

Ещё пример задания:

Запись десятичного числа в системах счисления с основаниями 3 и 5 в обоих случаях имеет последней цифрой 0. Какое минимальное натуральное десятичное число удовлетворяет этому требованию?

Решение:

если запись числа в системе счисления с основанием N заканчивается на 0, то это число делится на N нацело
поэтому в данной задаче требуется найти наименьшее натуральное число, которое делится одновременно на 3 и на 5, то есть, делится на 15
очевидно, что это число 15.

Ещё пример задания:

Запись числа 6710 в системе счисления с основанием N оканчивается на 1 и содержит 4 цифры. Укажите основание этой системы счисления N.

Решение:

поскольку запись в системе счисления с основанием N заканчивается на 1, то остаток от деления числа 67 на N равен 1, то есть при некотором целом имеем

следовательно, основание N – это делитель числа 66
с другой стороны, запись числа содержит 4 цифры, то есть
выпишем кубы и четвертые степени первых натуральных чисел, которые являются делителями числа 66:

видим, что из этого списка только для числа N = 3 выполняется условие
таким образом, верный ответ – 3.
можно сделать проверку, переведя число 67 в троичную систему 6710 = 21113

Еще пример задания:

Запись числа 38110 в системе счисления с основанием N оканчивается на 3 и содержит 3 цифры. Укажите наибольшее возможное основание этой системы счисления N.

Решение:

поскольку запись в системе счисления с основанием N заканчивается на 3, то остаток от деления числа 381 на N равен 3, то есть при некотором целом имеем

следовательно, основание N – это делитель числа
с другой стороны, запись числа содержит 3 цифры, то есть
неравенство дает (так как )
неравенство дает (так как )
таким образом, ; в этом диапазоне делителями числа 378 являются числа

наибольшим из приведенных чисел – это 18 (можно было сразу искать подбором наибольший делитель числа 378, начиная с 19 «вниз», на уменьшение)
таким образом, верный ответ – 18.

Еще пример задания:

Общий подход:

Решение (вариант 1, через десятичную систему):

общий вид чисел, которые дают остаток 5 при делении на 16:

где – целое неотрицательное число (0, 1, 2, …)

среди всех таких чисел нужно выбрать те, что меньше или равны 25 («не превосходят 25»); их всего два: 5 (при ) и 21 (при )
таким образом, верный ответ – 5, 21 .

Решение (вариант 2, через четверичную систему, предложен О.А. Тузовой):

переведем 25 в четверичную систему счисления: 25 = 1214, все интересующие нас числа не больше этого значения
из этих чисел выделим только те, которые заканчиваются на 11, таких чисел всего два:
это 114 = 5 и 1114 = 21
таким образом, верный ответ – 5, 21 .

Возможные ловушки и проблемы:

есть риск случайно «забыть» какое-то число или найти «лишнее» (в данном случае – большее 25)
можно сделать ошибки при переводе чисел из четверичной системы в десятичную или вообще «забыть» перевести

Еще пример задания:

Общий подход:

Решение:

итак, нужно найти все целые числа , такие что остаток от деления 23 на равен 2, или (что то же самое)

(*)

где – целое неотрицательное число (0, 1, 2, …);

сложность в том, что и , и неизвестны, однако здесь нужно «играть» на том, что это натуральные числа
из формулы (*) получаем , так что задача сводится к тому, чтобы найти все делители числа 21, которые больше 2
в этой задаче есть только три таких делителя: и
таким образом, верный ответ – 3, 7, 21 .

Возможные ловушки и проблемы:

Еще пример задания:

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31 оканчивается на 11.

Общий подход:

2 1 0 ← разряды

31 = k 1 1N = k·N2 + N1 + N0 = k·N2 + N + 1

4 3 2 1 0 ← разряды

31 = k4 k3 k2 1 1N = k4·N4 + k3·N3 + k2·N2 + N1 + N0

= k·N2 + N + 1

для (из первых трех слагаемых вынесли общий множитель )

Решение:

итак, нужно найти все целые числа , такие что

(**)

где – целое неотрицательное число (0, 1, 2, …);

сложность в том, что и , и неизвестны, однако здесь нужно «играть» на том, что это натуральные числа
из формулы (**) получаем , так что задача сводится к тому, чтобы найти все делители числа 30 и отобрать только те из них, для которых уравнение (**) разрешимо при целом , то есть, – целое число
выпишем все делители числа 30, большие или равные 2: 2, 3, 5, 6, 10, 15, 30
из всех этих делителей только для 2, 3, 5 и 30 значение – целое число (оно равно соответственно 7, 3, 1 и 0)
таким образом, верный ответ – 2, 3, 5, 30.

Еще пример задания:

Укажите, сколько всего раз встречается цифра 2 в записи чисел 10, 11, 12, …, 17 в системе счисления с основанием 5.

Решение (вариант 1):

запишем первое и последнее число в заданном диапазоне в системе счисления с основанием 5:

10 = 205, 17 = 325 .

заметим, что оба они содержат цифру 2, так что, 2 цифры мы уже нашли
между 205 и 325 есть еще числа

215, 225, 235, 245, 305, 315.

в них 5 цифр 2 (в числе 225 – сразу две двойки), поэтому всего цифра 2 встречается 7 раз
таким образом, верный ответ – 7.

Возможные ловушки и проблемы:

нужно не забыть, что в системе счисления с основанием 5 старшая цифра – 4, то есть, вслед за 245 следует 305
помните, что нужно определить не количество чисел, в которых есть двойка, а количество самих двоек
можно не обратить внимание на то, что в числе 225 цифра 2 встречается 2 раза

Решение (вариант 2):

переведем все указанные числа в систему счисления с основанием 5:

10 = 205, 11 = 215, 12 = 225, 13 = 235, 14 = 245, 15 = 305, 16 = 315, 17 = 325 .

считаем цифры 2 – получается 7 штук
таким образом, верный ответ – 7 .

Еще пример задания:

Укажите наименьшее основание системы счисления, в которой запись числа 30 трехзначна.

Решение:

обозначим через неизвестное основание системы счисления, тогда запись числа 30 в этой системе имеет вид

вспомним алгоритм перевода числа из системы счисления с основанием в десятичную систему: расставляем сверху номера разрядов и умножаем каждую цифру на основание в степени, равной разряду:

поскольку запись трехзначная, , поэтому
с другой стороны, четвертой цифры нет, то есть, в третьем разряде – ноль, поэтому
объединяя последние два условия, получаем, что искомое основание удовлетворяет двойному неравенству

учитывая, что – целое число, методом подбора находим целые решения этого неравенства; их два – 4 и 5:

минимальное из этих значений – 4
таким образом, верный ответ – 4 .

Решение (без подбора):

выполним п.1-4 так же, как и в предыдущем варианте решения
найдем первое целое число, куб которого больше 30; это 4, так как

проверяем второе неравенство: , поэтому в системе счисления с основанием 4 запись числа 30 трехзначна
таким образом, верный ответ – 4 .

Еще пример задания:

Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 30, запись которых в системе счисления с основанием 5 начинается на 3?

Решение (вариант 1):

нас интересуют числа от 1 до 30
сначала определим, сколько цифр может быть в этих числах, записанных в системе счисления с основанием 5
поскольку , в интересующих нас числах может быть от 1 до 3 цифр
рассмотрим трехзначные числа, начинающиеся на 3 в системе с основанием 5:

все они заведомо не меньше , поэтому в наш диапазон не попадают;

таким образом, остается рассмотреть только однозначные и двухзначные числа
есть всего одно однозначное число, начинающееся на 3, это 3
общий вид всех двузначных чисел, начинающихся на 3 в системе с основанием 5:

где – целое число из множества {0, 1, 2,3,4} (поскольку система счисления имеет основание 5 и цифр, больших 4, в записи числа быть не может)

используя эту формулу, находим интересующие нас двузначные числа – 15, 16, 17, 18 и 19
таким образом, верный ответ – 3, 15, 16, 17, 18, 19 .

Решение (вариант 2, предложен Сенькиной Т.С., г. Комсомольск-на-Амуре ):

нас интересуют числа от 1 до 30; сначала определим, сколько цифр может быть в пятеричной записи эти чисел
поскольку , в интересующих нас числах может быть не более 2 цифр (все трехзначные пятеричные числа, начинающиеся с 3, больше 30)
есть всего одно однозначное число, начинающееся на 3, это 3
выпишем все пятеричные двузначные числа, которые начинаются с 3, и переведем их в десятичную систему: 305 = 15, 315 = 16, 325 = 17, 335 = 18 и 345 = 19
таким образом, верный ответ – 3, 15, 16, 17, 18, 19 .

Еще пример задания:

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 71 оканчивается на 13.

Решение (1 способ):

Если число в системе с основанием оканчивается на 13, то

, потому что в системах с меньшим основанием нет цифры 3
это число можно представить в виде , где – целое неотрицательное число

определим наибольшее возможное с учетом условия . Из уравнения следует .
очевидно, что чем меньше , тем больше , поэтому значение не превышает

здесь мы подставили – наименьшее допустимое значение

остается перебрать все допустимые значения (от 0 до ), решая для каждого из них уравнение

или равносильное

относительно , причем нас интересуют только натуральные числа

получаем

при :
при : решения – не целые числа
при : и , второе решение не подходит

таким образом, верный ответ: 4, 68.

Решение (2 способ, М.В. Кузнецова и её ученики):

запись числа71 в системе с основанием оканчивается на 13, т.е. в разряде единиц – 3, это значит, что остаток от деления 71 на равен 3, то есть для некоторого целогоимеем

таким образом, искомые основания – делители числа 68; остается выбрать из них те, которые соответствуют другим условиям задачи
среди чисел, оканчивающихся на 13 в системе счисления с основанием ,минимальное – это само число ; отсюда найдем максимальное основание:

так что первый ответ: 68.

остальные числа, окачивающиеся в этой системе на 13, имеют не менее 3-х знаков (,…), т.е. все они больше
поэтому , следовательно,
по условию в записи числа есть цифра 3, поэтому (в системах с основанием ≤ 3 цифры 3 нет)
итак: , и при этом – делитель 68; единственное возможное значение (на 5,6,7 и 8 число 68 не делится)
таким образом, верный ответ: 4, 68.

Возможные ловушки и проблемы:

на шаге 1 нужно вычесть из числа только число единиц, то есть младшую из двух заданных цифр (в примере – 3)
можно забыть рассмотреть двузначное число, записанное заданными в условии цифрами (в примере – 13x ), и пропустить максимальное основание
нужно помнить, что

максимальная цифра на 1 меньше основания системы счисления
100 в системе с основанием p равно p2

Еще пример задания:

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 86 оканчивается на 22.

Решение (1 способ):

Если число в системе с основанием оканчивается на 22, то

, потому что в системах с меньшим основанием нет цифры 2
это число можно представить в виде , где – целое неотрицательное число

определим наибольшее возможное с учетом условия . Из уравнения следует .
очевидно, что чем меньше , тем больше , поэтому значение не превышает

здесь мы подставили – наименьшее допустимое значение

остается перебрать все допустимые значения (от 0 до ), решая для каждого из них уравнение

или равносильное

относительно , причем нас интересуют только натуральные числа

получаем

при :
при : решения – не целые числа
при : и , второе решение не подходит
при : решения – не целые числа

таким образом, верный ответ: 6, 42.

Решение (2 способ, М.В. Кузнецова и её ученики):

запись числа 86 в системе с основанием оканчивается на 22, т.е. в разряде единиц – 2, это значит, что остаток от деления 86 на равен 2, то есть для некоторого целогоимеем

таким образом, искомые основания – делители числа 84; остается выбрать из них те, которые соответствуют другим условиям задачи
среди чисел, оканчивающихся на 22 в системе счисления с основанием ,минимальное – это само число ; отсюда найдем максимальное основание:

так что первый ответ: 42.

остальные числа, окачивающиеся в этой системе на 22, имеют не менее 3-х знаков (,…), т.е. все они больше
поэтому , следовательно,
по условию в записи числа есть цифра 2, поэтому
итак: , и при этом – делитель 84; возможные значения (на 5,8 и 9 число 84 не делится)
переводя число 86 в системы счисления с основаниями , находим, что только для основания 6 запись числа оканчивается на 22 (при делении на 3, 4 и 7 «вторые» остатки не равны 2):

8	6	3			Дальше делить нет смысла	8	6		4			8	6		6			8	6		7
8	4	2	8	3	8	4		2	1	4	8	4		1	4	6	8	4		1	2	7
	2	2	7	9…		2		2	0	5…		2		1	2	2		2			7	1
			1						1						2						5

таким образом, верный ответ: 6, 42.

Еще пример задания:

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 94 начинается на 23.

Решение:

Из условия сразу видно, что искомое основание не меньше 4 (в записи есть цифра 3).
Если запись числа 94 в некоторой системе счисления с основанием двузначна (94 = 23x), то справедливо равенство ; нас интересуют натуральные решения этого уравнения, такие что , таких решений нет.
Предположим, что число четырехзначное. Минимальное допустимое четырехзначное число – 2300x, где . При минимальном основании () оно равно, поэтому запись нужного нам числа имеет не больше трех знаков.
На основании (2) и (3) делаем вывод, что число трехзначное, то есть , где – целое неотрицательное число, такое что .
Максимальное можно определить как решение уравнения (при ); получаем одно из решений – 6,15; поэтому
Если мы знаем , то определится как ; пробуем подставлять в эту формулу , пытаясь получить
Минимальное будет при : , а при получается
Таким образом, верный ответ: 6.

Еще пример задания:

Найти сумму восьмеричных чисел 178 +1708 +17008 +…+17000008, перевести в 16-ую систему счисления. Найдите в записи числа, равного этой сумме, третью цифру слева.

Решение:

Несложно выполнить прямое сложение восьмеричных чисел, там быстро обнаруживается закономерность:

178 + 1708 = 2078

178 + 1708 + 17008 = 21078

178 + 1708 + 17008 + 170008 = 211078

178 + 1708 + 17008 + 170008 + 1700008 = 2111078

178 + 1708 + 17008 + 170008 + 1700008 + 17000008 = 21111078

Переведем последнюю сумму через триады в двоичный код (заменяем каждую восьмеричную цифру на 3 двоичных):

100010010010010001112

Теперь разбиваем цепочку на тетрады (группы из 4-х двоичных цифр), начиная справа, и каждую тетраду представляем в виде шестнадцатеричной цифры

100010010010010001112

8 9 2 4 7

Таким образом, верный ответ (третья цифра слева): 2.

Еще пример задания:

Чему равно наименьшее основание позиционной системы счисления , при котором 225x = 405y? Ответ записать в виде целого числа.

Решение:

Поскольку в левой и в правой частях есть цифра 5, оба основания больше 5, то есть перебор имеет смысл начинать с .
Очевидно, что , однако это не очень нам поможет.
Для каждого «подозреваемого» вычисляем значение и решаем уравнение , причем нас интересуют только натуральные .
Для и нужных решений нет, а для получаем

так что.

Таким образом, верный ответ (минимальное значение ): 8.

Еще пример задания:

Запись числа 3010 в системе счисления с основанием N оканчивается на 0 и содержит 4 цифры. Чему равно основание этой системы счисления N?

Решение (1 способ, подбор):

запись числа 30 в системе с основанием N длиннее, чем в десятичной (4 цифры против двух), поэтому основание N меньше 10
это дает шанс решить задачу методом подбора, переводя в разные системы, начиная с N = 2 до N = 9
переводим:

30 = 111102 = 10103 = …

дальше можно не переводить, поскольку запись 10103 удовлетворяет условию: заканчивается на 0 и содержит 4 цифры
можно проверить, что при N ≥ 4 запись числа 30 содержит меньше 4 цифр, то есть не удовлетворяет условию
Ответ: 3.

Решение (2 способ, неравенства):

запись числа 30 в системе с основанием N содержит ровно 4 цифры тогда и только тогда, когда старший разряд – третий, то есть

первая часть двойного неравенства дает (в целых числах)
вторая часть неравенства дает (в целых числах)
объединяя результаты пп. 2 и 3 получаем, что N = 3
заметим, что условие «оканчивается на 0» – лишнее, ответ однозначно определяется по количеству цифр
Ответ: 3.

Задачи для тренировки^[1]:

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 22 оканчивается на 4.
В системе счисления с некоторым основанием число 12 записывается в виде 110. Укажите это основание.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 39 оканчивается на 3.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.
В системе счисления с некоторым основанием десятичное число 129 записывается как 1004. Укажите это основание.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 40 оканчивается на 4.
В системе счисления с некоторым основанием число десятичное 25 записывается как 100. Найдите это основание.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 27 оканчивается на 3.
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 26, запись которых в троичной системе счисления оканчивается на 22?
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 30, запись которых в четверичной системе счисления оканчивается на 31?
Укажите через запятую в порядке возрастания все десятичные натуральные числа, не превосходящие 17, запись которых в троичной системе счисления оканчивается на две одинаковые цифры?
Укажите, сколько всего раз встречается цифра 3 в записи чисел 19, 20, 21, …, 33 в системе счисления с основанием 6.
Укажите, сколько всего раз встречается цифра 1 в записи чисел 12, 13, 14, …, 31 в системе счисления с основанием 5.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 1.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 63 оканчивается на 23.
Десятичное число, переведенное в восьмеричную и в девятеричную систему, в обоих случаях заканчивается на цифру 0. Какое минимальное натуральное число удовлетворяет этому условию?
В системе счисления с некоторым основанием десятичное число 49 записывается в виде 100. Укажите это основание.
Укажите наименьшее основание системы счисления, в которой запись числа 70 трехзначна.
Укажите наименьшее основание системы счисления, в которой запись числа 50 двузначна.
Сколько значащих цифр в записи десятичного числа 357 в системе счисления с основанием 7?
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием 6 начинается на 4?
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 20, запись которых в системе счисления с основанием 3 начинается на 2?
Какое десятичное число при записи в системе счисления с основанием 5 представляется как 12345?
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101?
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 30 оканчивается на 8.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31 оканчивается на 4.
В системе счисления с некоторым основанием десятичное число 83 записывается в виде 123. Укажите это основание.
В системе счисления с некоторым основанием десятичное число 144 записывается в виде 264. Укажите это основание.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 32 оканчивается на 4.
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 27, запись которых в двоичной системе счисления оканчивается на 110?
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в троичной системе счисления оканчивается на 21?
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 45, запись которых в двоичной системе счисления оканчивается на 1010?
Десятичное число кратно 16. Какое минимальное количество нулей будет в конце этого числа после перевода его в двоичную систему счисления?
В системе счисления с некоторым основанием десятичное число 18 записывается в виде 30. Укажите это основание.
Укажите, сколько всего раз встречается цифра 3 в записи чисел 13, 14, 15, …, 23 в системе счисления с основанием 4.
Укажите, сколько всего раз встречается цифра 2 в записи чисел 13, 14, 15, …, 23 в системе счисления с основанием 3.
В саду 100 фруктовых деревьев – 14 яблонь и 42 груши. Найдите основание системы счисления, в которой указаны эти числа.
Найдите основание системы счисления, в которой выполнено сложение: 144 + 24 = 201.
Найдите основание системы счисления, в которой выполнено умножение: 3·213 = 1043.
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 20, запись которых в системе счисления с основанием 5 оканчивается на 3?
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 100, запись которых в системе счисления с основанием 5 оканчивается на 11?
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 75 оканчивается на 13.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 84 оканчивается на 14.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 61 оканчивается на 15.
Найдите десятичное число x, такое что 20 < x < 30, запись которого в системе счисления с основанием 3 заканчивается на 11.
Запись числа 658 в некоторой системе счисления выглядит так: 311N. Найдите основание системы счисления N.
Запись числа 30 в некоторой системе счисления выглядит так: 110N. Найдите основание системы счисления N.
Запись числа 2B16 в некоторой системе счисления выглядит так: 111N. Найдите основание системы счисления N.
Запись числа 23 в некоторой системе счисления выглядит так: 212N. Найдите основание системы счисления N.
Запись числа 2105 в некоторой системе счисления выглядит так: 313N. Найдите основание системы счисления N.
Укажите наименьшее основание системы счисления, в которой запись числа 50 трехзначна.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 348 оканчивается на 20.
Запись числа 344 в некоторой системе счисления выглядит так: 1A8N. Найдите основание системы счисления N.
К записи натурального числа в восьмеричной системе счисления справа приписали два нуля. Во сколько раз увеличилось число? Ответ запишите в десятичной системе счисления.
Запись числа 281 в системе счисления с основанием N содержит 3 цифры и оканчивается на 1. Чему равно максимально возможное основание системы счисления?
Запись числа 234 в системе счисления с основанием N содержит 3 цифры и оканчивается на 6. Чему равно основание системы счисления?
Запись числа 338 в системе счисления с основанием N содержит 3 цифры и оканчивается на 2. Чему равно максимально возможное основание системы счисления?
Запись числа 256 в системе счисления с основанием N содержит 3 цифры и оканчивается на 4. Чему равно минимально возможное основание системы счисления?
Запись числа 325 в системе счисления с основанием N содержит 3 цифры и оканчивается на 1. Чему равно минимально возможное основание системы счисления?
Запись числа 180 в системе счисления с основанием N содержит 3 цифры и оканчивается на 0. Перечислите в порядке возрастания все возможные основания системы счисления.
Запись числа 280 в системе счисления с основанием N содержит 3 цифры и оканчивается на 0. Перечислите в порядке возрастания все возможные основания системы счисления.
Запись натурального числа в системах счисления с основанием 4 и 6 заканчивается на 0. Найдите минимальное натуральное число, удовлетворяющее этим условиям.
Десятичное число 71 в некоторой системе счисления записывается как «78». Определите основание системы счисления.
Десятичное число 70 в некоторой системе счисления записывается как «64». Определите основание системы счисления.
Десятичное число 57 в некоторой системе счисления записывается как «212». Определите основание системы счисления.
Десятичное число 109 в некоторой системе счисления записывается как «214». Определите основание системы счисления.
Решите уравнение .
Ответ запишите в четверичной системе счисления. Основание системы счисления указывать не нужно.
Решите уравнение .
Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
Решите уравнение .
Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
Решите уравнение .
Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
(http://ege.yandex.ru) Десятичное число 63 в некоторой системе счисления записывается как 120. Определите основание системы счисления.
(http://ege.yandex.ru) Десятичное число 57 в некоторой системе счисления записывается как 212. Определите основание системы счисления.
(http://ege.yandex.ru) В системе счисления с основанием N запись числа 77 оканчивается на 0, а запись числа 29 – на 1. Чему равно число N?
В некоторой системе счисления записи десятичных чисел 56 и 45 заканчиваются на 1. Определите основание системы счисления.
В некоторой системе счисления записи десятичных чисел 68 и 94 заканчиваются на 3. Определите основание системы счисления.
В некоторой системе счисления записи десятичных чисел 41 и 63 заканчиваются на 8. Определите основание системы счисления.
В некоторой системе счисления записи десятичных чисел 56 и 124 заканчиваются на 5. Определите основание системы счисления.
Запись числа 6810 в системе счисления с основанием N оканчивается на 2 и содержит 4 цифры. Чему равно основание этой системы счисления N?
Решите уравнение .
Ответ запишите в троичной системе счисления. Основание системы счисления указывать не нужно.
Запись числа N в системе счисления c основанием 6 содержит две цифры, запись этого числа в системе счисления c основанием 5 содержит три цифры, а запись в системе счисления c основанием 11 заканчивается на 1. Чему равно N? Запишите ответ в десятичной системе счисления.
Запись числа N в системе счисления c основанием 7 содержит две цифры, запись этого числа в системе счисления c основанием 6 содержит три цифры, а запись в системе счисления c основанием 13 заканчивается на 3. Чему равно N? Запишите ответ в десятичной системе счисления.
Решите уравнение .
Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
Решите уравнение .
Ответ запишите в семеричной системе счисления. Основание системы счисления указывать не нужно.

[1] Источники заданий:

Демонстрационные варианты ЕГЭ 2004-2013 гг.
Тренировочные работы МИОО.
Гусева И.Ю. ЕГЭ. Информатика: раздаточный материал тренировочных тестов. — СПб: Тригон, 2009.
Самылкина Н.Н., Островская Е.М. Информатика: тренировочные задания. – М.: Эксмо, 2009.
Якушкин П.А., Лещинер В.Р., Кириенко Д.П. ЕГЭ 2010. Информатика. Типовые тестовые задания. — М: Экзамен, 2010.
Крылов С.С., Лещинер В.Р., Якушкин П.А. ЕГЭ-2010. Информатика. Универсальные материалы для подготовки учащихся / под ред. В.Р. Лещинера / ФИПИ. — М.: Интеллект-центр, 2010.
Якушкин П.А., Ушаков Д.М. Самое полное издание типовых вариантов реальных заданий ЕГЭ 2010. Информатика. — М.: Астрель, 2009.
М.Э. Абрамян, С.С. Михалкович, Я.М. Русанова, М.И. Чердынцева. Информатика. ЕГЭ шаг за шагом. – М.: НИИ школьных технологий, 2010.
Чуркина Т.Е. ЕГЭ 2011. Информатика. Тематические тренировочные задания. — М.: Эксмо, 2010.
Информатика и ИКТ: ЕГЭ-2012. – СПб.: Просвещение, 2012.

Источник

В какой системе счисления число (3375_{10}) будет выглядеть как (1000_{?})?

Стоить заметить, что любое десятичное число A в n-ой степени можно записать как единицу и n нулей в системе счисления с основанием A: (A^{n}_{10}=1underbrace{000…000}_{n}) (_{A})

Тогда (3375_{10}=15^3_{10}), значит в системе счисления с основанием 15 будет выглядеть как (1000_{15}).

Ответ: 15

В какой системе счисления число (121_{10}) будет выглядеть как (100_{?})?

Тогда (121_{10}=11^2_{10}), значит в системе счисления с основанием 11 будет выглядеть как (100_{11}).

Ответ: 11

В какой системе счисления число (2744_{10}) будет выглядеть как (1000_{?})?

Тогда (2744_{10}=14^3_{10}), значит в системе счисления с основанием 14 будет выглядеть как (1000_{14}).

Ответ: 14

В какой системе счисления число (1331_{10}) будет выглядеть как (1000_{?})?

Тогда (1331_{10}=11^3_{10}), значит в системе счисления с основанием 11 будет выглядеть как (1000_{11}).

Ответ: 11

В какой системе счисления число (1024_{10}) будет выглядеть как (100000_{?})?

Тогда (1024_{10}=4^5_{10}), значит в четверичной системе счисления будет выглядеть как (100000_{4}).

Ответ: 4

В какой системе счисления число (6561_{10}) будет выглядеть как (100000000_{?})?

Тогда (6561_{10}=3^8_{10}), значит в троичной системе счисления будет выглядеть как (100000000_{3}).

Ответ: 3

В какой системе счисления число (4096_{10}) будет выглядеть как (10000_{?})?

Тогда (4096_{10}=8^4_{10}), значит в восмеричной системе счисления будет выглядеть как (10000_{8}).

Ответ: 8

Источник