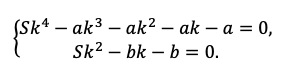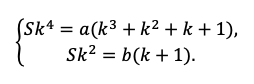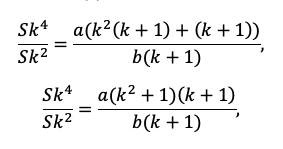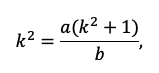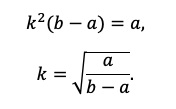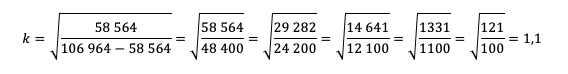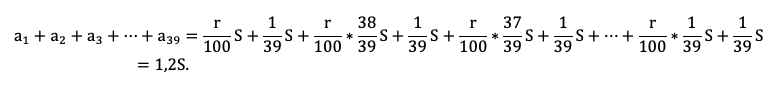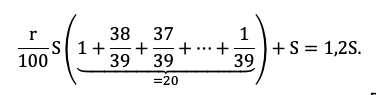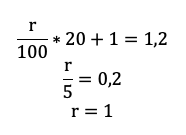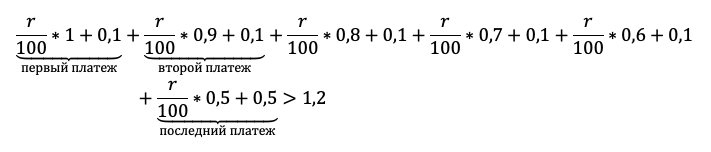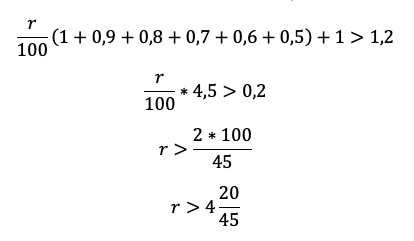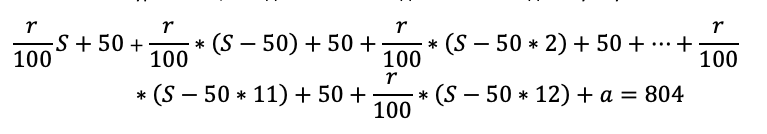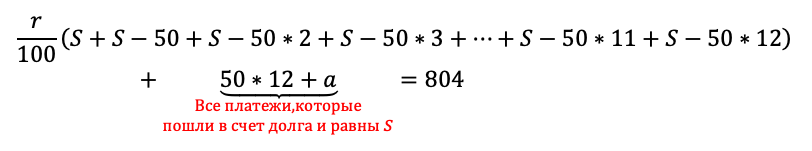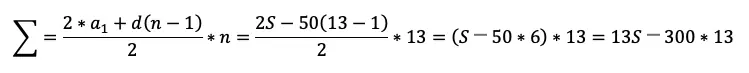Задачи на смешанные платежи егэ

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

В части с развернутым ответом в ЕГЭ по профильной математике есть уникальный номер, к которому школьник почти готов сразу после освоения материала для первых 12-ти заданий. Речь об экономической задаче под номером 17 в ЕГЭ по математике. Конечно, поготовиться придется, но, если повезет с прототипом, баллы можно урвать почти даром!

Прототипы для 17-го номера делятся на три большие группы: 

• банковские задачи, 
• на ценные бумаги,
• задачи на оптимальный выбор. 

В этой статье мы расскажем, как научить ученика структурировать условие любой банковской задачи, как составить по этим данным математическую модель и найти решение. Расскажем, на что обратить внимание ученика, чтобы школьник не потерял баллы из-за неверного оформления.

Главная трудность — школьник плохо понимает условие, ведь с кредитами и вкладами он пока не сталкивался.

• Как работает процент по кредиту?
• На какую сумму начисляется?
• Из каких частей состоит платеж?
• Как уменьшается долг?

На все эти вопросы вам придется ответить. Это отличная возможность показать пользу уроков математики, ведь 17-ый номер — едва ли не самая прикладная задача за весь школьный курс! 

Например, можно рассказать о том, какие бывают образовательные кредиты. Вы в курсе, что их дают с 14 лет, а платеж первые годы может быть ничтожным? Школьник об этом точно не знает.

С чего начать разбор экономической (банковской) задачи в ЕГЭ по математике

Экзамен немного утрирует реальную ситуацию, в жизни кредит работает сложнее. Однако грустно упускать возможность рассказать школьнику что-то из реальности! Если у вас есть опыт с кредитованием, самое время им поделиться. Если нет, то воспользуйтесь нашим:

• Например, расскажите, что клиенту придется сверх купить страховку на случай потери работоспособности, ведь банк не хочет терять прибыль даже если на заемщика кирпич упадет. Ваши ученики знают, как работает страховка?
• Расскажите о механизме аннуитетного платежа: как часть денег банк забирает себе в качестве дохода, то есть на погашение процентов за пользование кредитом; а на вторую часть уменьшает ваш долг. В реальности это разделение считается по специальной формуле, и совсем не в пользу заемщика.
• Например, по нашему опыту, в ипотеке на 10 лет из 20 тысяч ежемесячного платежа на первых порах всего 5 000 рублей идет в счет уменьшения долга, а 15 000 — забирает себе банк! Но каждый раз платеж чуть ребалансируется, и в счет долга идет чуть больше. Так в последних платежах через 10 лет в счет процентов идет буквально пара сотен, а все остальное гасит долг. 

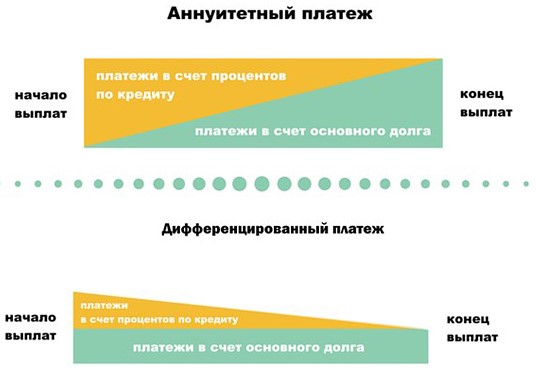
Хорошая новость в том, что в экзаменационных задачах подобной вакханалии не бывает. Долг и проценты или гасятся равномерно, или по заранее известному алгоритму, достаточно просто внимательно прочитать условие.

Еще одно частое упрощение в ЕГЭ — процент там обычно не годовой, а ежемесячный! То есть своим платежом заемщик гасит набежавший за этот месяц процент и уменьшает долг на заданную величину. Удобно.

Мы предлагаем научить школьника упорядочивать данные банковской задачи в ЕГЭ по математике с помощью таблицы. Табличка — не единственный способ решить 17-ый номер, кто-то использует последовательности, кто-то — считает прикладным методом как заправский бухгалтер. Однако наш метод универсален, а значит вы дадите школьнику один алгоритм на все типы банковских задач. Согласитесь, работать с одним алгоритмом проще, чем подбирать разные по ситуации.

Тип 1. Равные платежи

Особенность этого типа заданий в том, что заемщик всегда вносит одинаковые суммы.

В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.

Очевидно, что эта схема должна оказаться у школьника в тетради. Ведь вы же знаете: того, чего нет в тетради, и на уроке-то не было!

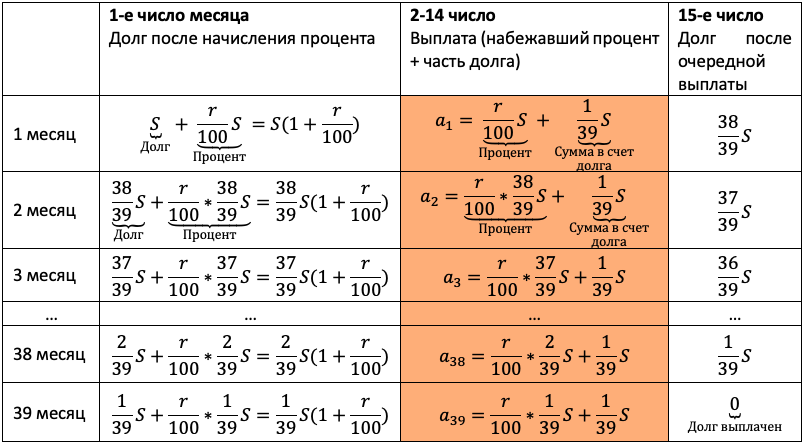
Заполняем всю табличку. Учитываем обе ситуации из условия. Для наглядности каждую выделим жирной рамкой.

Теперь остался еще один непростой шаг — перейти от структурированных данных к математической модели. Дайте ученику возможность увидеть, что уже почти составил ее.

Мы получили два уравнения, которые подсветили в табличке оранжевым. Объединим их в систему и решим!

Напомните выпускнику о культуре вычислений! Порой эти задачи составлены так, что неудачная последовательность действий сделает их нерешаемыми без калькулятора. Потому не надо спешить делать первое попавшееся действие, пусть школьник тренируется думать на пару ходов вперед.

Например, разделим одно уравнение на другое, ведь так мы избавимся от одной неизвестной S:

Наше решение не зависит от суммы кредита, S сокращается. 

По сути, мы получили уравнение с одной неизвестной, ведь платежи a и b знаем из условия. Выразим k:

Пожалуй, все, проще уже некуда. Подставляем значения!   

Тут можно обратить внимание ученика на то, как составители экзамена на самом деле заботятся о нем! Ведь будь задачка хоть чуть-чуть другой, посчитать без калькулятора было бы невозможно.

Вспоминаем, что k=1+r/100, а найти нам надо r.

Ответ: 10%.

Не забудьте после решения расставить акценты в задаче:

Чтобы решить задачу и получить 3 балла, мы:
— Воспользовались простым алгоритмом упорядочивания данных,
— Составили математическую модель,
— Нашли удобный способ решить ее, ВСЕ!
Это и есть алгоритм решения банковской задачи.

Тип 2. Равномерно убывающий долг

В прошлой задаче заемщик платил одинаковую сумму каждый месяц. Тут ему нужно уменьшать долг на одну и ту же величину. То есть за месяц пользования деньгами банк начислил на них процент, клиент теперь должен чуть больше. Своим платежом он оплатит банку проценты, чтобы заем стал таким, как ДО их начисления. А сверху внесет сумму, которая как раз и пойдет на то самое РАВНОМЕРНОЕ уменьшение долга.  

15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
(Считайте, что округления при вычислении платежей не производятся.)

Тут главный элемент в задаче — равномерно убывающий долг. Если мы взяли сумму S на 39 месяцев, и каждый месяц долг должен быть меньше на одинаковую величину, то что это за величина? Пусть правильный ответ 1/39 S даст ученик.

Проиллюстрируйте школьнику, как здорово работает наш алгоритм. Пусть выпускник проговаривает пункты вслух, а вы их выполняйте. Следите, чтобы каждый шаг подопечный фиксировал в тетради:

Продолжаем заполнять табличку. Пусть дальше пробует выпускник, ведь пока сам не попробуешь, не научишься:

Осталось увязать добытую информацию в уравнение или неравенство. Обратите внимание подопечного на то, что ненужных подробностей в задачах ЕГЭ не бывает! Единственная информация в задаче, которую мы до сих пор не использовали — общая сумма выплат. По условию она на 20% больше суммы кредита, то есть равна 1,2S:

Приведем подобные, вынесем общий множитель за скобку:

Решение в итоге снова не зависит от того, какую сумму взяли в долг. Разделим обе части на S и упростим выражение:

Ответ: 1%.

И снова все по нашему алгоритму, ничего нового, кроме него, мы не используем! Не забудьте излучать восторг, иначе школьник не проникнется мощью вашего метода решения.

Тип 3. Долг, убывающий согласно табличке

Задача похожа на прошлую. Разница лишь в том, что кроме процентов нам каждый месяц придется гасить не равную долю долга, а долю согласно таблице.

15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг(в млн рублей)	1	0,9	0,8	0,7	0,6	0,5	0

Найдите наименьшее значение r, при котором общая сумма выплат будет больше 1,2 млн рублей.

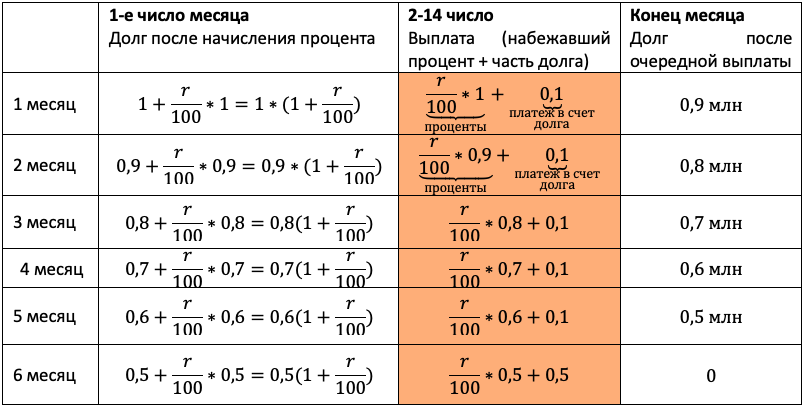
Протестируем нашу универсальную табличку в третий раз, доверьте это непростое занятие школьнику. Пусть процессом командует он! По ответам будет ясно, ловит ли он суть.

Отличие от прошлого типа будет лишь в том, что в третий столбец мы будем записывать не равномерно убывающий долг, а перенесем остаток долга из таблицы условия. Чтобы не таскать по решению нули, считать будем в миллионах:

Чтобы долг убывал согласно табличке, нам снова каждый раз придется гасить набежавшие проценты и первые 5 месяцев добавлять сверху 0,1 млн. После останется погасить весь остаток.

Акцентируйте внимание на механизме погашения, для школьника он не всегда очевиден.

«По условию нам снова дана общая сумма выплат, значит достаточно просуммировать оранжевый столбец, и уравнение готово», — вероятно, подумает школьник. Подловите его! Уравнение в этой задаче — прямой путь потерять балл! Сумма выплат должна быть БОЛЬШЕ 1,2 млн. Отразим это в модели с помощью неравенства:

Подопечный должен быть уверен в каждом символе в бланке ответа. Даже не пригодившиеся промежуточные вычисления с ошибкой приведут к катастрофе.

Приведем подобные и вынесем общие множители за скобку:

Последний шаг – не забыть, что по условию процент должен быть целым и округлить в верную сторону.

Ответ: 5%.

Правильная математическая модель — это суперважно! К ней проверяющие обязательно придерутся.

Тип 4. Погашение кредита в два этапа.

По сути, это та же прошлая задача, но месяцев больше

В 2017-2018 учебном году составителей экзамена посетило вдохновение, на свет родился вот этот тип банковских задач. Школьники были в шоке, и от страха завалили 17-ый номер. Хотя всего-то нужно было догадаться воспользоваться знаниями об арифметической прогрессии и достать из условия одно немного неочевидное дано!

15-го декабря планируется взять кредит в банке на 13 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 12-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 13-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 804 тысячи рублей?

И снова пусть по возможности командует школьник. По крайней мере он уже точно в курсе, что происходит первые 13 месяцев.

Последовательно начисляем процент на остаток долга – считаем выплату – фиксируем остаток долга после выплаты. Сумму кредита возьмем за S.

Научите школьника не спешить с вычислениями. Например, вместо того чтобы написать S-600, мы пишем S-50*12, потому что так удобнее: нам сразу ясно, что речь идет о двенадцатом месяце. Да и потом вычисления будут проще, если мы оставим маленькие числа.

Осталось составить уравнение, и модель готова. В задаче нам снова дали сумму всех выплат:

Как обычно, сгруппируем отдельно слагаемые с r/100, отдельно слагаемые без них:

Вот именно последняя группировка всех платежей в счет долга и оказалась неочевидной. Без нее в задаче остается одна лишняя неизвестная величина, которая рушит все решение.

Осталось привести уравнение к решаемому виду. Для этого надо просуммировать то, что получилось в скобках. Если внимательно приглядеться, то видно, что это сумма арифметической прогрессии:

Посчитаем эту сумму:

Подставляем выражение для суммы в уравнение, заметим, что по условию r=2:

Мы сокращали дробь, пока это было возможно, и в итоге довольно просто получили ответ даже без калькулятора. Ваш подопечный должен научиться также!

Ответ: 700 тысяч.

Зачем использовать формулу суммы прогрессии, если можно посчитать вручную? Все верно, можно. Но это только в данном случае кредит взяли всего на 13 месяцев. А бывают прототипы, когда срок – 21 и больше месяцев. В какой-то момент считать вручную станет совсем долго и неудобно, потому воспользоваться формулой суммы – более универсальный метод.

Чем закончить разбор экономической (банковской) задачи № 17 в ЕГЭ по математике

Чтобы у ученика окончательно сложилась картинка занятия, пробегитесь еще раз по основным выводам:

• Повторите алгоритм заполнения таблицы и решения задачи (да, пятый раз);
• Повторите типы задач и механизм распределения платежа на проценты и долг;
• Напомните, как важно считать культурно и быть уверенным в каждой циферке в бланке;
• Проговорите, что математическая модель должна точно отражать условие задачи.

Как показывает практика, чем больше повторяешь, тем больше шансов, что в голове выпускника останется хоть что-то.

За что дают баллы?

Знание критериев оценивания экономической (банковской) задачи № 17 в ЕГЭ по математике поможетученику чувствовать себя увереннее, ведь выставление баллов — это не какая-то магия и не вредность экспертов. Все правила игры прописаны в нормативных документах.

17-ый номер стоит 3 балла. Чтобы узнать, как их присуждают, мы залезли в методические рекомендации для членов предметных комиссий.

Согласно пояснениям из документа, для получения одного балла мало просто обоснованно составить математическую модель по задаче, надо предложить правильный метод ее анализа. 

Два балла получит школьник, который ошибся в вычислениях или не обосновал появление математической модели в решении. Например, согласно методическим рекомендациям, решение на 2 балла выглядит так:

А вот отсутствие промежуточных вычислений хоть и усложняет проверку, но баллы не снимает.

Идеально выполненная первая часть ЕГЭ по профильной математике принесет школьнику всего 62 тестовых балла. Добавим сюда пару ошибок по невнимательности, и останутся совсем крохи — баллов 50, не больше. Для поступления на бюджет мало, а значит необходимо планировать делать вторую часть! Чем раньше школьник это осознает, тем проще будет с ним работать. А банковская задача поможет получить дополнительные баллы с минимальными усилиями.

Однако кредиты – не единственный прототип 17-го номера, и в следующий раз мы расскажем, как научить школьника решать задачи на оптимальный выбор и ценные бумаги. 

Решение задач на дифференцированные платежи при подготовке к ЕГЭ по математике

1.Дифференцированные платежи

Кредиты играют важную роль в жизни населения со средним достатком. Тем, кто не может позволить себе единовременную оплату из собственных средств при покупке недвижимости или другого дорогостоящего имущества, кредиты просто необходимы.

Какие существуют виды платежей по кредитам?

В чём же разница между аннуитетным и дифференцированным платежами и какой платёж выгоднее?

Дифференцированные платежи

При дифференцированных платежах сумма основного долга, так называемое тело долга, делится равными частями на весь срок платежа, а проценты ежемесячно начисляются на остаток долга. Соответственно, в первый месяц суммы платежей велики, потому что проценты по кредиту существенны.

А к концу срока выплаты будут минимальны. Дифференцированные платежи удобны для тех, у кого доход не носит характер неизменной величины, и через некоторое время может появиться возможность досрочно погасить долг. В этом случае переплата по кредиту будет меньше, чем при аннуитетном расчёте.

Аннуитетные платежи

Отличие аннуитетного платежа от дифференцированного в том, что сумма ежемесячного взноса всегда неизменна, но вот структура этой суммы меняется из месяца в месяц.

Основную часть в первые месяцы составляют проценты по кредиту, а сумма тела долга — минимальна. Таким образом банк страхует риски недополучения прибыли в случае досрочного погашения кредита заёмщиком.

При дифференцированном платеже ежемесячные платежи становятся меньше, сумма основного долга в платеже всегда будет одной и той же. А вот проценты, начисляемые на остаток основного долга, будут уменьшаться по мере выплаты кредита. Ежемесячная сумма основного долга считается следующим образом: сумма кредита делится на количество платежей.

Кредиты с дифференцированными платежами выдавались в Сбербанке до 2011 года, а сейчас выдаются только с аннуитетными.

В подавляющем большинстве случаев банки предлагают своим заемщикам аннуитетную схему погашения задолженности. Однако в некоторых случаях можно выбрать дифференцированный платеж — тип выплаты кредита, при котором размер взносов постепенно уменьшается. Для заемщика пользоваться дифференцированными платежами выгоднее, чем фактически стандартной аннуитетной схемой.

Как рассчитать дифференцированный платеж?

Платеж при дифференцированной схеме делится на две части:

• основную, которая уходит на погашение тела кредита;
• процентную, которая является чистой прибылью банка.

Основную часть платежа высчитать просто по такой формуле:

Платеж =

Так, если заемщик взял в кредит 300 тыс. рублей под 22% годовых на 5 лет, то размер основной части составит:

300000 / 60 = 5000 рублей

Вторая часть платежа — процентная — рассчитывается по такой схеме:

Платеж = остаток основного долга * годовая ставка / 12

Так, проценты за первый месяц пользования кредита составят:

300000 * 0.22 / 12 = 5500 рублей

Путем сложения определяем размер платежа на первый месяц: 5000 + 5500 = 11000 рублей.

Для того, чтобы рассчитать проценты за любой месяц, необходимо узнать остаток задолженности. Если за второй месяц размер общего долга можно узнать путем простого вычитания из 300000 рублей первого платежа в 5000 рублей, то за 10-ый или 25-ый значение можно вычислить по такой схеме:

Остаток долга = общий размер долга — (размер основного платежа * количество прошедших месяцев).

Так, за 10-ый месяц процентная часть будет равна:

(300000 — 5000 * 9) * 0.22 / 12 = 4675

общий размер платежа: 9675 рублей.

За 25-й месяц:

(300000 — 5000 * 24) * 0.22 / 12 = 3300

Общий размер платежа: 8300 рублей.

Как видите, по сравнению с первым месяцем заемщику придется платить на 1700 рублей меньше. Проценты за самый последний месяц будут минимальными:

(300000 — 5000 * 59) * 0.22 / 12 = 91.67

В целом дифференцированную схему погашения кредита используют для небольших займов или при достаточно высоком уровне дохода. Тогда первые платежи не будут столь обременительны для вашего бюджета, а сниженный размер переплат позволит сэкономить и, возможно, потратить высвободившиеся средства для досрочного погашения кредита.

2. Решение задач. 

Рассмотрим решение задач на дифференцированные платежи. Задачи можно найти в любом сборнике для подготовки к ЕГЭ по математике.

Учитывая, что платеж при дифференцированной схеме делится на две части:

основную и процентную, то при решении задач удобно составлять таблицу, в которой основная ежемесячная (ежегодная) часть платежа остается неизменной, а процентная часть меняется.

Решим несколько задач.

№1.

15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r.

Решение.

Пусть S-сумма кредита, r-проценты банку, n=19 (число выплат).

Известно, что долг уменьшается на одну и ту же сумму.

Долг банку:

— это ежемесячные выплаты процентов банку.

Зная, что эти выплаты составляют 30% общей суммы кредита, составим уравнение:

(сумма арифметической прогрессии, где , n=19)

Ответ: 3%.

Примечание.

Выведем формулу для вычисления переплат банку, используя формулу суммы арифметической прогрессии, где

.(формула 1)

Тогда при , r=3

№2.

15-го января планируется взять кредит в банке на 25 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 13% больше суммы, взятой в кредит. Найдите r.

Решение.

Пусть S-сумма кредита, r-проценты банку, n=25 (число выплат).

Известно, что долг уменьшается на одну и ту же сумму. Тогда

Или по формуле (1)      n=25,    ,   r=1%.

Ответ: 1%

№3.

15-го января планируется взять кредит в банке на 2 года. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 25% больше суммы, взятой в кредит. Найдите r.

Решение.

Пусть S-сумма кредита, r-проценты банку, n= 2 года=24месяца (число выплат).

n	Долг	Проценты	Платеж по кредиту (ежемесячный)	Остаток
1	S
2
3
…….
23
24				0

Если общая сумма выплат после полного погашения кредита на 25% больше суммы, взятой в кредит, это означает, что сумма всех ячеек в столбце “Проценты” равна 0,25 от изначального долга (S):

Ответ: 2%

№4.

15 января планируется взять кредит в банке на 24 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Какую сумму следует взять в кредит, чтобы общая сумма выплат после полного погашения равнялась 1 млн рублей?

Решение.

S-сумма кредита, n=24 месяца, r=2%, Sобщ=1млн=1000тыс рублей

Составим таблицу.

n	Долг	Проценты	Платеж по кредиту (ежемесячный)	Остаток
1	S	0,02S
2
3
…….
23
24				0

Sобщ=1млн=1000тыс рублей

Общая сумма платежей состоит из суммы кредита и процентов банку.

Sобщ=S+ 0,02S (. Числа, стоящие в скобках, образуют арифметическую прогрессию.

S+0,02S (, S·(1+0,02·12,5)=1000, S=тыс рублей

Ответ: 800000 руб

№5.

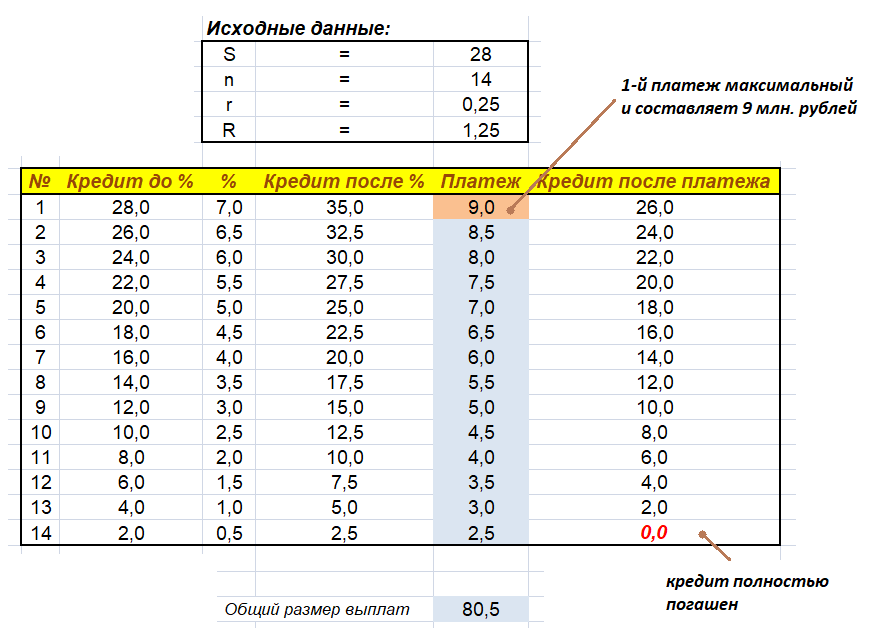
В июле планируется взять кредит в банке на сумму 28 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:

— каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 9 млн рублей?

Решение.

S-сумма кредита, n-целое число лет, r=25%, Sобщ=28млн рублей

Составим таблицу.

n	Долг	Проценты	Платеж	Остаток
1	28млн	0,25·28=7млн
2
…….
n-1
n				0

Наибольший годовой платеж -первый.

7+= 9млн,  n=14

Sобщ=28+ 7 ()=28+7·+·7=80,5млн

Ответ: 80500000 рублей

№6.

15 января планируется взять кредит в банке на 21 месяц. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что на 11-й месяц кредитования нужно выплатить 44,4 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?

n	Долг	Проценты	Платеж по кредиту (ежемесячный)	Остаток
1	S	0,02S
2
………
11
…….
23
24				0

По условию за 11 месяц было выплачено 44,4 тыс.рублей. Составим уравнение

Ответ: 932,4 тыс рублей

№ 7.

15-го января планируется взять кредит в банке на сумму 1300 тысяч рублей на 16 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца с 1-го по 15-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;

— 15-го числа 15-го месяца долг составит 100 тысяч рублей;

— к 15-му числу 16-го месяца кредит должен быть полностью погашен. Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1636 тысяч рублей.

Произведем некоторые вычисления.

1300 тыс-100 тыс=1200тыс.

n	Долг	Проценты	Платеж по кредиту (ежемес)	Остаток
1	1300
2
…….
15
16				0

Общая сумма платежей состоит из суммы кредита и процентов банку.

Ответ: r = 3%

№ 8.

15-го января планируется взять кредит в банке на 11 месяц. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 3 % по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца с 1-го по 10-й долг должен быть на 80 тысяч рублей меньше долга на 15-е число предыдущего месяца;

— к 15-му числу 11-го месяца кредит должен быть полностью погашен;

Какой долг будет 15-го числа 10-го месяца, если общая сумма выплат после полного его погашения составит 1198 тысячи рублей?

Пусть х тыс. рублей будет долг 15-го числа 10-го месяца.

n	Долг	Проценты	Платеж	Остаток
1	800+x
2
…….
10
11				0

Общая сумма платежей состоит из суммы кредита и процентов банку.

Ответ:  тыс. рублей

№ 9.

15-го декабря планируется взять кредит в банке на сумму 1000 тысяч рублей на (n+1) месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца с 1-го по n-й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца;

— 15-го числа n-го месяца долг составит 200 тысяч рублей;

— к 15-му числу (n+1)-го месяца кредит должен быть полностью погашен.
Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1378 тысяч рублей.

Считаем n.

n	Долг	Проценты	Платеж	Остаток
1	1000
2
…….
20
21

Общая сумма платежей состоит из суммы кредита и процентов банку.

.

Числа в скобках образуют арифметическую прогрессию, сумму которой найдем по формуле.

Ответ: %

Не получается успешно решать задачи на дифференцированные платежи из ЕГЭ по математике?

Всем здравствуйте! Меня зовут Александр. Я — профессиональный репетитор по математике, информатике, программированию, базам данных и алгоритмам. Если коротко, то я — матерый технарь.

Одно из генеральных моих направлений — подготовка школьников к успешной сдаче ЕГЭ по математике и информатике. Потратьте буквально $2-3$ минуты собственного времени и познакомьтесь с отзывами моих учеников. Средний балл моих подопечных на официальном экзамене ЕГЭ составляет $91.35$ из $100$ возможных.

Задачи на дифференцированные платежи из ЕГЭ по математике являются одними из моих любимых. Вообще задания из экономического блока мне кажутся очень интересными и познавательными. Поэтому на своих индивидуальных уроках я с большим удовольствием показываю своим ученикам различные эффективные методики их решения.

Существует по-настоящему лишь $2$ способа подготовки на высоченный итоговый балл ЕГЭ по математике:

1. Самоподготовка (автодидактирование).

2. Под началом профессионального репетитора.

Мой контактный номер телефона прописан в шапке данного сайта. Звоните, договаривайтесь о времени проведения и записывайтесь на первый пробный урок.

Условие задачи

В июле планируется взять кредит в банке на сумму (28) миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:

• Каждый январь долг возрастает на (25%) по сравнению с концом предыдущего года.

• С февраля по июнь каждого года необходимо выплатить часть долга.

• В июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платеж составит (9) миллионов рублей?

Решение задачи

Это классическая задача на дифференцированные платежи из ЕГЭ по математике. Почему я так решил? Потому, что есть фраза-маркер, в которой четко дают понять, что размер займа уменьшается равномерно. Вот эта фраза: «В июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года«.

С кредитной программой мы разобрались! Это очень важный момент. Если вы спутаете тип кредитной программы, то гарантировано получите неправильный результат. Именно по этой причине я настоятельно прошу всех выучить свойства и признаки схемы дифференцированных платежей.

Кстати, напомню, что фундаментально кредитная программа бывает двух видов:

• Кредит выплачивается по схеме дифференцированных платежей.

• Кредит выплачивается по схеме аннуитетных платежей.

Давайте введем следующие обозначения:

(S) — размер первоначального кредита	(r) — процентная ставка банка, выраженная в долях	(R = 1 + r) — для удобства расчетов
(n) — общее количество отчетных периодов	(i) — номер текущего отчетного периода	(%_{i}) — размер начисленных банком процентов за конкретный период
(p_{i}) — размер платежа за конкретный период	(P) — общая сумма всех выплат/платежей	(q) — ставка банка, выраженная в процентах

Хочется отметить следующее, что не все выше обозначенные переменные нам потребуются в процессе решении задачи. Но понимать математический смысл вы обязаны каждой из них, если, конечно, не хотите «завалить» экзамен ЕГЭ по математике.

Дальше, давайте рассмотрим под микроскопом следующую фразу: «наибольший годовой платеж составит (9) миллионов рублей«. В этой фразе содержится наиважнейшая информация, и ваша цель — суметь ее расшифровать. Для этого нужно прекрасно понимать, как устроена математическая модель дифференцированных платежей, а также знать свойства этих платежей.

Как известно, в схеме дифференцируемых платежей самый $1$-ый платеж является наибольшим, а самый последний — наименьшим! Значит, когда говорят про наибольший платеж, нужно подразумевать самый $1$-ый платеж.

Из условия вытекает, что:

$S = 28$, млн. руб.

$q = 25%$

$r = frac{q}{100} = 0.25$

$p_{1} = 9$, млн. руб.

Наша задача определить $P$, то есть общий размер всех платежей/выплат!

Важно! Если вы хотите получить максимальный балл за решение задачи на дифференцированные платежи из ЕГЭ по математике, то в своем решении нужно привести вывод соответствуюей математической модели. Поэтому, если плохо знаете принцип работы этой модели — срочно идите ее изучать, зубрить.

Вспомним, что платеж за любой отчетный период формируется из размера начисленных процентов за данный период и равной части первоначального кредита:

$p_{i} = %_{i} + frac{S}{n}$ — размер $i$-го платежа.

Ранее мы выяснили, что из условия задачи нам известен размер $1$-го платежа ($i = 1$). Значит, процентная ставка банка $q$ действует на весь стартовый кредит:

$%_{1} = frac{n}{n} * S * r = S * r = 28 * 0.25 = 7$, млн. рублей. Тогда:

$p_{1} = %_{1} + frac{S}{n} = 7 + frac{28}{n}$.

А размер $1$-го платежа нам задан, он равен $9$ млн. рублей, тогда решим следующее уравнение:

$7 + frac{28}{n} = 9$

$frac{28}{n} = 2$

$2 * n = 28$

$n = 14$.

Оказывается, первоначальный кредит был взят сроком на $14$ лет. При этом все ограничения будут соблюдены. Например, самый наибольший/первый платеж составит $9$ миллионов рублей. Отлично! Идем дальше!

Обратимся к формулам математической модели дифференцируемых платежей и «достанем» наиболее важную из них, а именно формулу, которая позволяет вычислить размер всех платежей:

$P = frac{S * r * (n + 1)}{2} + S$.

Подставим все известные величины в эту формулу и получим ответ. Заметьте, что в этой формуле фигурирует переменная $n$, то есть необходимо знать общее количество отчетных периодов. Ее значение мы нашли на предыдущем шаге ($n = 14$).

$P = frac{28 * 0.25 * (14 + 1)}{2} + 28 = frac{105}{2} + 28 = 52.5 + 28 = 80.5$, млн.руб.

Готово! Результат получен! Да, получилось нецелое значение, но это и не главное. Хотя в большинстве случаев входные данные в задачах на дифференцированные платежи из ЕГЭ по математике подбираются так, чтобы на выходе образовывалось что-то целое.

Но у любознательных старшеклассников может появиться вполне закономерный вопрос: «А правильный ли ответ?«. Очевидно, что, да! Но ведь нужны какие-то гарантии, верно.

Верификацию полученного результата можно произвести арифметическим способом. То есть вы можете пройтись по всем отчетным периодам, вычисляя соответствующие платежи, размер начисленных банком процентов и т.п.

Но на своих индивидуальных занятиях, совместно с учеником, мы проводим верификацию полученных результатов, посредством математического процессора «MS Excel«. Это очень удобный и наглядный вариант проверки решения. Также, построенная таблица обладает хорошим аналитизмом, то есть, анализируя выкладки этой таблицы, становятся понятны многие тонкие моменты, связанные с выплатой кредита.

Данная великолепная таблица доказывает правильность нашего алгебраического решения.

Ответ: 80.5

Выводы

1. Для успешного решения задач на дифференцированные платежи из ЕГЭ по математике нужно знать назубок соответствующую математическую модель. Пока не поймете эту модель, даже не вздумайте пытаться что-то решать из подобного типа заданий.

2. На официальном экзамене, для получения максимального балла за экономическую задачу, в своем решении приводите, в том числе и вывод математической модели. В этом случае ни один эксперт в процессе проверки не сможет «придраться» к вашим математическим выкладкам.

3. Внимательно читайте условие задачи и обращайте особое внимание на фразы-маркеры. Это позволит вам выбрать наиболее эффективный способ решения и не ошибиться в выборе кредитной программы.

4. Решайте задания с применением алгебраического способа, а не арифметического. Хотя оба этих способа уместны, но более профессиональным и продвинутым считается именно алгебраический.

5. И, пожалуй, одно из главных — нужно любить математику.

Примеры условий реальных задач, встречающихся на ЕГЭ по математике

А сейчас я приведу список из нескольких задач на дифференцированные платежи из ЕГЭ по математике. Вы можете попробовать порешать их самостоятельно. Если будут трудности, то переходите по ссылке «Перейти к текстовому решению» и знакомьтесь полноценным моим решением.

Не забывайте о том, что раздел «Финансовая математика» содержит множество других типов задач: аннуитетные платежи, вклады, простые и сложные проценты, акции и т.д. Также зачастую попадаются комбинированные задачи, где происходит смешение моделей. Хотите во всем этом разбираться? Записывайтесь ко мне на частную подготовку!

Все эти задачи на дифференцированные платежи из ЕГЭ по математике решаются достаточно быстро, если вы хорошо знаете, как устроена математическая модель дифференцируемых платежей. Повторю, уже, наверное, раз $10$-ый — разбирайтесь с математической моделью, и будем вам счастье.

Также, время от времени, рекомендую обращаться к этому списку заданий, так как он постоянно обновляется и дополняется, появляются новые условия, а также соответствующие мои математические разборы.

Что-то все равно осталось непонятным? Записывайтесь ко мне на частную подготовку!

Если после прочтения данного материала у вас остались какие-то вопросы, недопонимания, то это некритично, и, даже, вполне логично! Недостаточно пристально рассмотреть одно решение задачи на дифференцированные платежи из ЕГЭ по математике. Нужен комплексный подход!

Я — репетитор-практик, который на своих занятиях, уделяет львиное количество времени конкретным разборам, техникам и эффективным методикам решения. Всевозможной теории полно в глобальной сети Интернет, а экзамен ЕГЭ по математике является практическим, то есть нужно уметь решать, а не знать теоретические изыски.

Мои занятия проходят дистанционно, посредством таких программ, как «Скайп» и «AnyDesk«. Подобный формат взаимодействия репетитора с учеником является очень удобным, позволяет задействовать мультимедийные технологии, а также достаточно недорог.

Я достаточно востребованный и известный репетитор по математике и информатике, поэтому, не откладывайте свое решение в долгий ящик. Действуйте прямо сейчас! И не забывайте, что количество ученических мест ограничено, поэтому, завтра свободных мест уже может и не остаться.