Задачи на сто егэ физика

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Специальную теорию относительности мало кто понимает в полной мере. Тем не менее, решать простейшие задачи по СТО может научиться каждый. Приведем в этой статье несколько примеров задач по специальной теории относительности с решением.

Подпишитесь на наш телеграм, там много полезной и интересной информации. А если хотите получить скидку на заказ, ищите ее на нашем втором канале для клиентов.

Задачи на специальную теорию относительности с решением

Если не знаете, с чего начать решение физических задач, повторите памятку по решению и держите под рукой полезные формулы.

Задача №1 на СТО Эйнштейна

Условие

Чему равна длина космического корабля, движущегося со скоростью 0,9с? Длина покоящегося корабля 100 м.

Решение

Для решения этой простейшей задачи нужно использовать преобразования Лоренца:

l=l01-v2c2l=1001-0,9с2с2=43,5 м

Ответ: 43,5 м

Задача №2 на СТО Эйнштейна

Условие

Ускоритель сообщил радиоактивному ядру скорость 0,4с (0,4 от скорости света в вакууме). В момент вылета из ускорителя ядро выбросило в направлении своего движения β — частицу со скоростью 0,75с относительно ускорителя. Определите скорость частицы относительно ядра. Ответ дать в мегаметрах за секунду.

Решение

Для решения этой задачи нужно использовать релятивистский закон сложения скоростей:

vx=vx’+v1+vx’·vc2

Здесь vx — скорость частицы в системе отсчета, связанной с ускорителем, vx’ — c скорость частицы в системе отсчета, связанной с ядром, v — скорость одной системы отсчета относительно другой.

Тогда скорость частицы относительно ядра будет равна:

vx’=vx-v1-vx·vc2vx’=0,75с-0,4с1-0,75с·0,4сс2=с2=1,5·108 мс=150 М мс

Ответ: 150 М мс.

Задача №3 на СТО Эйнштейна

Условие

На сколько процентов полная энергия протона, вылетающего из ускорителя со скоростью 0,8с, больше его энергии покоя?

Решение

Для решения этой задачи найдем энергию покоя протона W0, его полную релятивистскую энергию W, а затем вычислим их соотошение  ∆WW0, где ∆W=W-W0.

Получаем:

∆WW0=W-W0W0=WW0-1

W0=mc2

W=mc21-v2c2

∆WW0=mc2mc21-v2c2-1=11-v2c2-1

∆WW0=11-0,8с2с2-1=11-0,64-1=0,67

Ответ: полная энергия больше энергии покоя на 67%.

Задача №4 на СТО Эйнштейна

Условие

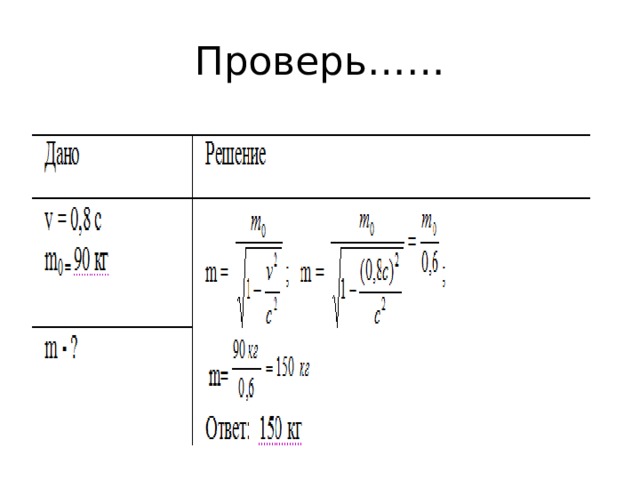
Чему равна будет масса космонавта, движущегося в космическом корабле со скоростью 0,8с? Масса покоящегося космонавта 90 кг.

Решение

Для решения задачи используем преобразования Лоренца для массы:

m=m01-v2c2

m=901-0,8с2с2=900,6=150 кг

Ответ: 150 кг.

Задача №5 на СТО Эйнштейна

Условие

С космического корабля, удаляющегося от Земли со скоростью 0,7с, стартует ракета в направлении движения корабля. Скорость ракеты относительно Земли 0,96с. Чему равна скорость ракеты относительно Земли?

Решение

Обозначим v – скорость движения корабля относительно Земли, v1 – скорость ракеты относительно космического корабля, v2 – скорость ракеты относительно Земли. Тогда v=0,7с, v2=0,96с.

На основании релятивистского закона сложения скоростей имеем:

v2=v1+v1+v1vc2v1+v=v21+v1vc2v1c2+vc2=v2c2+v·v1v1=c2v-v2vv1-c2=c20,7с-0,96с0,7с·0,96с-с2=0,8с

Ответ: 0,8с

Вопросы по теме СТО

Вопрос 1. Что такое специальная теория относительности? Какие задачи она решает?

Ответ. Теория относительности – физическая теория пространства и времени. В частной (специальной) теории относительности рассматриваются только инерциальные системы отсчета. Явления, описываемые теорией относительности, называются релятивистскими (от лат. «относительный») и проявляются при скоростях, близких к скорости света в вакууме (эти скорости тоже принято называть релятивистскими).

Вопрос 2. Сфомулируйте принцип относительности Эйнштейна

Ответ. Принцип относительности Эйнштейна гласит:

«Никакими физическими экспериментами (механическими, электрическими, оптическими) невозможно определить в любой инерциальной системе отсчета, движется ли эта система равномерно и прямо, или она находится в покое».

Не только механические, но и все физические законы одинаковы во всех инерциальных системах отсчета.

Нужно больше вопросов по физике? Загляните в наш блог!

Вопрос 3. В основе специальной теорит относительности лежат два постулата, выдвинутых Эйнштейном. Сформулируйте их.

Ответ. 

1. Первый постулат является естественным обобщением принципа относительности Галилея с механических на все в отсутствие исключения явления природы и может быть сформулирован как утверждение о невозможности наблюдателю, находящемуся в замкнутой системе отсчета, с помощью какого-либо физического (а значит и любого другого) опыта установить, покоится ли его система отсчета или находится в состоянии равномерного прямолинейного движения. 
2. Вторым постулатом Эйнштейна является утверждение о постоянстве скорости света и ее инвариантности во всех системах отсчета. Этот факт неоднократно проверялся в точных экспериментах.

Вопрос 4. Какие выводы делаются из постулатов относительности?

Ответ. На основе сформулированных постулатов Эйнштейна пересматриваются все коренные положения классической механики (кинематики). Понятия одновременности событий, длительности временного промежутка и длины отрезка перестают носить абсолютный характер, становясь зависимыми от выбора системы отсчета, в которой ведется наблюдение.

В рамках специальной теории относительности классическая механика Ньютона является приближением при низких скоростях.

Вопрос 5. В чем смысл преобразований Лоренца?

Ответ. При скоростях, близких к скорости света, преобразования Лоренца приходят на смену классическим преобразованиям Галилея.

Нужна помощь в решении задач по физике и выполнении других заданий? Обращайтесь за ней в профессиональный сервис для учащихся в любое время.

Оглавление

Введение1  

       1   ЕГЭ по физике

 2   Исследование ошибок, допущенных на ЕГЭ в разделе «Элементы СТО»

        Объект исследования: ошибка  при вычислении энергии частицы, движущейся со скоростью близкой к скорости света

     Содержание

      Глава 1  

Основные и вспомогательные знания, формирующие понимание СТО 5

Глава 2

Возможные причины  возникновения ошибки7

       Глава 3

         Методические рекомендации при решении задач на вычисление энергии релятивистской частицы из раздела «Элементы теории относительности».            ………… …………………………………………..….…………………………….11

Литература………………………………………..…..……………………………20

Приложения……………………………………………………………………………………………….21     

 Единый государственный экзамен заставляет учителей, давно работающих в школе, пересматривать методику подготовки выпускников к выпускному экзамену по физике, а начинающих учителей — искать дополнительную методическую литературу, которая помогла бы им правильно выстраивать уроки, чтобы самым рациональным путем  приводить учащихся к успешной сдаче экзамена.

 К сожалению, результаты ЕГЭ этого года и прошлых лет показывают, что и фундаментальные принципы, и законы, и эмпирические закономерности, и частные следствия в среднем усваиваются одинаково. Это означает, что принцип выделения главного при организации учебного процесса не реализуется, небольшое число фундаментальных законов, принципов и идей растворяется в частностях, нет четкого определения статуса изучаемого, основные принципы и закономерности изучаются на тематическом уровне и не обобщаются как общефизические.

За несколько лет проведения ЕГЭ накопились данные, с помощью которых имеется возможность проанализировать результаты решения задач  по разным темам. Анализ типичных ошибок  позволяет   методически грамотно выстроить объяснение тем по каждому из разделов физики и исключить вероятность плохого результата на экзамене у хорошего ученика, так как учитель будет знать заранее,  где и какие акценты необходимо расставить и как методически правильно организовать урок.

Наибольшую тревогу вызывает усвоение основных понятий темы «Элементы СТО»: принцип равноправности ИСО и принцип постоянства скорости света. Результаты выполнения заданий по элементам СТО являются ярким примером ситуации с усвоением наиболее общих принципов физической науки.

Специальная теория относительности (СТО; также частная теория относительности) — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света изучается в школьном курсе физики в 11 классе.

 В силу сложности этой теории, знакомство с ней, при малом количестве часов, становится методически сложным процессом. В специальной теории относительности в пределе малых скоростей  получаются те же следствия, что и в классической механике, с которой учащихся начинают знакомить уже с 7 класса.

 Поэтому, если мы хотим разобраться и выяснить  причины ТИПИЧНЫХ ОШИБОК  при решении учащимися задач по специальной теории относительности на ЕГЭ, то давайте проследим каким образом и какие знания должны были быть изучены и усвоены ими до момента знакомства со специальной теорией относительности.

Цель работы:  провести экскурс в основной материал, расставить  АКЦЕНТЫ,               — на которые нужно обратить внимание учеников, исследовать  типичные ошибки, которые встречаются  при вычислении энергии частицы(тела) раздела «Элементы СТО» и показать методически,  как выстроить объяснение тем, ведущих к максимальному усвоению этого материала.

 Глава 1.  Основные и вспомогательные знания, формирующие понимание СТО

Расчет энергии тела или частицы тела можно встретить в следующих разделах:

• Классическая механика (полная механическая энергия, энергия движущегося тела)
• Молекулярная физика (кинетическая энергия молекулы)
• Термодинамика (внутренняя энергии тела)
• Электродинамика (энергия  движущейся заряженной  частицы)
• Элементы теории относительности (движение (тела) частицы со скоростью близкой к скорости света)

Можно утверждать, что энергию мы вычисляем при изучении любого раздела физики.

Причины возникновения ошибки удобнее рассмотреть, используя хронологию изучения материала с 7 класса. Рассмотрим с помощью таблицы, какие основные и вспомогательные знания формируют наше понимание СТО и энергии в ней.

Глава 2.    Причины возникновения ошибки

В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей.

Идеи и положения СТО, кардинально изменившие представления о пространстве, времени и движении, могут быть поняты только в сравнении с соответствующими классическими воззрениями.

Основные понятия классической механики

• Пространство
• Время
• Материальная точка
• Система отсчета

Согласно классическому определению: движение материальной точки представляет собой процесс непрерывного изменения ее пространственных координат с течением времени относительно фиксированной системы отсчета. Среди множества систем отсчета в классической механике выделяется инерциальная система отсчета.

В инерциальной системе отсчета свободная материальная точка либо покоится, либо движется равномерно и прямолинейно (υ = соnst =0 или υ = соnst ≠ 0). Данное утверждение является и определением ИСО и законом (законом инерции).

В классической механике принимается в качестве фундаментального постулата принцип относительности, гласящий, что все ИСО механики равноценны (эквивалентны). Иначе говоря, любые механические явления протекают одинаково при одинаковых начальных условиях.

первый момент, который готовит учащихся к пониманию СТО — это знание того, что такое инерциальные системы отсчета (ИСО )и понимание  принципа относительности

Из этого принципа, впервые сформулированного вначале 17 в. Г.Галилеем, следуют два важных положения:

1.Любую ИСО можно принять  за неподвижную.

2. Каждая ИСО движется относительно другой ИСО, принятой за неподвижную, со скоростью υ = соnst, т. е. равномерно и прямолинейно.

В ньютоновской  механике введен постулат абсолютности времени: для всех ИСО существует единое, абсолютное время, совпадающее со временем каждой из них:

t =const или ∆t = τ = inv,

где символ «inv» (инвариант, инвариантный- французское слово — неизменяющийся) используется в том смысле, что величина, к которой он относится, абсолютна – одинакова для всех ИСО, не изменяется при переходе от одной из них к другой. Так, если установлено, что τ = 0, т.е. в какой-либо ИСО два события одновременны, то они будут одновременны и относительно любой другой ИСО.

 учащиеся привыкают понимать, что   различные физические величины нужно воспринимать как относительные или как абсолютные

1.2 Законы электродинамики и принцип относительности

После того как во второй половине 19 в. Максвеллом были сформулированы основные законы электродинамики,

С этими законами учащиеся начинают знакомиться с 8 класса, постепенно пополняя свои представления об электромагнитных явлениях, и следует обратить их внимание, что взгляды ученых меняются, а полученные факты и результаты экспериментов заставляют их пересматривать  представление о том или ином явлении. В электродинамике скорость распространения электромагнитных волн в вакууме одинакова по всем направлениям с = 3·108 м/с.  Однако,  с другой стороны, в соответствии с законом сложения скоростей, вытекающим из преобразования Галилея, скорость может равняться с только в одной избранной системе отсчета. В любой другой инерциальной системе отсчета, движущей по отношению к этой избранной системе со скоростью υ, скорость света должна равняться с + υ.

Это означает, что если справедлив обычный закон сложения скоростей, то при переходе из одной инерциальной системы отсчета к другой законы электродинамики должны меняться так, что в этой новой системе отсчета скорость света равнялась не с, а с + υ.

Таким образом, обнаружились определенные противоречия между электродинамикой и механикой Ньютона. Возникшие противоречия пытались решить различными способами.

На этом этапе  учащимся необходимо закрепить понятие, с которым они уже встречались в 9 классе (при изучении Закона всемирного тяготения): границы применимости той или иной теории 

Описываемые специальной теорией относительности отклонения в протекании физических процессов от предсказаний классической механики называют релятивистскими эффектами, а скорости, при которых такие эффекты становятся существенными, — релятивистскими скоростями. В специальной теории относительности рассматриваются только инерциальные системы отсчета, т.е. такие, в которых выполняется закон инерции,  и скорость света в вакууме является универсальной постоянной.

При́нцип соотве́тствия — в методологии науки утверждение, что любая новая научная теория при наличии старой, хорошо проверенной теории находится с ней не в полном противоречии, а даёт те же следствия в некотором предельном приближении (частном случае). 

Принцип соответствия в теории относительности

В специальной теории относительности в пределе малых скоростей  получаются те же следствия, что и в классической механике. Так,преобразования Лоренца переходят в преобразования Галилея, время течёт одинаково во всех системах отсчёта, кинетическая энергия становится равной  и т.д.

   

Глава 3. Методические рекомендации при решении задач на вычисление энергии релятивистской частицы  раздела СТО

Понятно, чтобы приступить к решению задачи (в которой встречается наша ошибка), например на расчет полной и кинетической энергии протона, движущегося со скоростью 0,75с, необходимо ПРОЛОЖИТЬ дорогу к решению через дополнительные задачи, минимизирующие возможность этой ошибки.

1.  «Относительность скорости»

Задача

  По шоссе равномерно движутся в противоположных направлениях два автомобиля с одинаковыми  скоростями 120 км/ч. Определите их относительную скорость?

Решение:

Свяжем с первой частицей неподвижную систему отсчета K, относительно которой она движется со скоростью u. Со второй частицей свяжем систему K ‘, движущуюся вдоль оси x со скоростью v относительно неподвижной системы K в направлении, противоположном оси x, то есть противоположном скорости u.

Используем классический закон сложения скоростей!!!!

ЗАДАЧА №1

 Две частицы движутся в вакууме вдоль прямой навстречу друг другу со скоростями 0,5 с и 0,75 с. Определите их относительную скорость.

Дано:

u = 0,5 с,
v = 0,75 с.
________

u ‘ – ?

Решение

Свяжем с первой частицей неподвижную систему отсчета K, относительно которой она движется со скоростью u. Со второй частицей свяжем систему K ‘, движущуюся вдоль оси x со скоростью v относительно неподвижной системы K в направлении, противоположном оси x, то есть противоположном скорости u.

 Используя релятивистский закон сложения скоростей, и учитывая, что проекция скорости v на ось x отрицательна, !!!

запишем выражение для скорости в неподвижной системе отсчета: 

Отсюда находим относительную скорость частиц u ‘: 

Подставляя численные значения, имеем:

Обратить внимание!!!!

Задачи, в которых два тела двигаются в одном направлении или же в противоположных со скоростями  близкими к скорости света  встречаются сразу две типичные ошибки:

1. Используют классический закон сложения скоростей
2. Даже если написали релятивистский закон сложения скоростей, забывают  учитывать знак.

Уровень С

Две галактики разбегаются от центра Вселенной в противоположных направлениях с одинаковой скоростью 0,70 с относительно центра. С какой скоростью они удаляются друг от друга?

Р е ш е н и е. Для определения относительной скорости галактик υ

12х воспользуемся релятивистским законом преобразования скоростей: 

υ

 х = ( υ12х` + υ0)/ (1 + υ1х υ0`/ с2). (1)

Учтем, что галактики движутся в разные стороны относительно центра Вселенной, υ

1 = υ = 0,70 с и υ2 = — υ = — 070 с. Тогда уравнение (1) примет вид υ = ( υ12` — υ)/ (1 — υ1`υ/ с2). Из данного уравнения находим

υ

12` = 2 υ/ (1 – υ2/с2).

Подставим в формулу числовые значения: υ

12` = 2 ∙ 0,70с/ (1 – 0,70с ∙ 0,70с /с2) ≈ 0,94с. Две галактики удаляются друг от друга со скоростью 0,94 с.

1. Относительность времени или массы, или линейных размеров

Перед следующей задачей  рассмотрите задачу, по нахождению времени движения поезда длиной 150м через тоннель длиной 200м со скоростью 30м/с.

Задача №3
Частица, называемая мезоном, движущаяся со скоростью 0,99с, пролетела в системе отсчета К от места своего рождения до точки распада расстояние 4,7 км. Найдите собственное время жизни мезона.

Р е ш е н и е. В системе К время движения мезона t от точки своего рождения до распада определяется по формуле t = L/υ, (1)

где L — расстояние, пройденное мезоном, υ – скорость движения. Собственное время 

 движения частицы в системе координат, связанной с самой частицей, определяется по формуле: = t. (2)

Из уравнений (1) и (2) находим:

 = (L/υ) .

Подставляя числовые значения, получим 

 = 2,2 ∙ 10-6 с. Собственное время жизни мезона составляет 2,2 ∙ 10-6 с.

Задача №4

Уровень  С

Система К` движется относительно К со скоростью 1,50 ∙ 108 м/с. В начале отсчета времени t = 0, t` = 0 начала О и О` систем совпадали. Координаты центра шара, покоящегося в системе К`, x`= 40м, y`= 20 м, z` = 0. Какими будут координаты центра шара в системе К через 2,00 мкс? 

Р е ш е н и е. В задаче требуется найти координаты центра шара в системе отсчёта К: x, y, z. Согласно преобразованиям Лоренца имеем

x = (x` + υt`)/ 

, (1)

y = y`, (2)

z = z`. (3)

Чтобы определить координату х в системе отсчета К, надо найти собственное время 

 между событиями по часам наблюдателя, находящегося в системе К`  = t, где t – промежуток времени между теми же событиями в системе. Подставим в формулу необходимые данные: = 2 ∙ 10-6= 1,73 ∙ 10-6 с.

Тогда координата х найдем, используя формулу (1):

х = (40 м + 1,50 ∙ 10

8 м/с ∙ 1,73 ∙ 10-6 с )/ 0,87 ≈344 м.Учитывая преобразования Лоренца, имеем y = 20 м , z = 0. Координаты центра шара в системе К такие: х = 344м, y = 20 м , z = 0. 

Обратить внимание!!!

При решении задач на движение со  СКОРОСТЯМИ  БЛИЗКИМИ К СКОРОСТИ СВЕТА  необходимо помнить о релятивистских эффектах

• сокращения линейных размеров,
• замедление времени,
• увеличения массы тела

в движущихся системах отсчета

1.3 Относительность энергии

Задача

А) По шоссе равномерно движутся в противоположных направлениях два автомобиля с одинаковыми  скоростями, относительно системы отсчета, связанной с Землёй. Найти значение кинетической энергии первого тела относительно Земли и второго тела.

Б) Тело начало  движение вертикально вверх со скоростью 15м/с. Определите его полную энергию и кинетическую энергию  через 1 секунду.

Задача №4

Протон движется со скоростью 0,75 с. Определите его энергию покоя, полную энергию и кинетическую энергию.

Дано:

v = 0,75 с,
m = 1,67 • 10–27 кг,
c = 3 • 108 м/с.
E0 – ? E – ? Eк – ?
________

Решение

Энергия покоя протона определяется по формуле Эйнштейна: E0 = mc2.

Полная энергия протона:

В релятивистской механике кинетическая энергия Eк частицы определяется как разность между полной энергией E и энергией покоя E0 этой частицы: Eк = E – E0. Подставляя числовые значения величин, получаем:

E0 = 1,67 • 10–27 кг • (3 • 108)2 м2/с2 = 15 • 10–11 Дж.
E = 2,52 • 10–27 кг • (3 • 108)2 м2/с2 = 22,7 • 10–11 Дж.
Eк = 22,7 • 10–11 Дж – 15 • 10–11 Дж = 7,7 • 10–11 Дж.

Обобщение

Не все поступающие в ВУЗ знают, что механическая энергия и работа являются относительными величинами. В лучшем случае указывается относительный  характер потенциальной энергии.

 Относительность кинетической энергии следует из  формулы для нее:

, где скорость величина относительная, значит кинетическая энергия величина относительная  — на это НАДО ОРАТИТЬ ВНИМАНИЕ уже в 7 классе при знакомстве с кинетической энергией, закрепить в 9 классе и повторить перед введением релятивистской энергией.

Понимание границ применимости :

Чтобы определить какие формулы для  энергии можно применять  при решении задач в разделе СТО, целесообразно еще раз оговорить границы применимости классической физики. Обратить внимание, что классическое выражение для энергии можно использовать при энергетических вычислениях только тогда, когда выполняются два условия:

 а)   скорость рассматриваемого тела мала по сравнению со скоростью света;
б)   массы покоя участвующих в исследуемом процессе тел не изменяются.

Если одно из этих условий не выполнено, то при вычислениях необходимо пользоваться релятивистским выражением энергии :

Er = m0c2/√(1 — v2/c2) = mc2  

Релятивистская энергия. 

Из принципа независимости законов физики в инерциальных системах отсчета, следует, что во всех таких системах должен соблюдаться закон сохранения энергии.

Пусть в инерциальной системе отсчета К тело (или частица) движется со скоростью 

= соnst. Тогда релятивистская энергия Ер, согласно теории относительности, определяется следующим выражением:

Е

р = mc2/.

Как следует из формулы, релятивистская энергия больше собственной энергии этого тела, равной Е = mc

2. Разность между релятивистской энергией движущегося тела и его собственной энергии равна кинетической энергии Ек тела: Ер – Е = Ек.^ Релятивистский импульс. Формула определения релятивистского импульс такова:
р = mυ/.

Из формулы видно, что с увеличением скорости υ релятивистский импульс растет быстрее, чем классический р

к = mυ. Отметим, что классический импульс может быть получен из формулы релятивистского импульса при υ << с.
^ Связь между релятивистским импульсом и релятивистской энергией. Иэ формул определения релятивистских импульса и энергии и исключив скорость, после преобразований получим 
Е2 = m2c4 + р2 c2. (1)
Это соотношение справедливо не только для массовых, но и для безмассовых частиц. Покажем это. На основании выше указанных формул определения релятивистской энергии и релятивистского импульса можно записать Е = рс2/ υ. Тогда энергия частицы, движущаяся со скоростью υ = с, будет равна Е = рс.

Из уравнения (1) получим m

2c4 = Е2 — р2 c2. Но Е = рс, следовательно, m2c4 = 0 или m = 0. Таким образом, мы приходим к выводу, что безмассовые частицы (m = 0) могут двигаться только со скоростью света в вакууме.
Выражение (1) для безмассовой частицы можно записать в виде
Е2 — р2 c2 = m2c4 = 0.

Данное выражение справедливо для любой безмассовой частицы во всех инерциальных системах отсчёта.

Литература:

1. Берков, А.В. и др. Самое полное издание типовых вариантов реальных заданий ЕГЭ 2010, Физика: учебное пособие для выпускников. ср. учеб. заведений   / А.В. Берков, В.А. Грибов. – ООО «Издательство Астрель», 2009. – 160 с.
2. ДЕМОНСТРАЦИОННЫЕ ТАБЛИЦЫ ПО ФИЗИКЕ. КЛАСС!ная физика для любознательных. / http://class-fizika.narod.ru/tabl.htm 
3. Касьянов, В.А. Физика, 11 класс : учебник для общеобразовательных школ / В.А. Касьянов. – ООО «Дрофа», 2004. – 116 с.
4. Мякишев Г.Я. и др. Физика. 11 класс  учебник для общеобразовательных школ   / учебник для общеобразовательных школ Г.Я. Мякишев, Б.Б. Буховцев . –» Просвещение «, 2009. – 166 с.
5. Открытая физика [текст, рисунки]/ http://www.physics.ru
6. Подготовка к ЕГЭ /http://egephizika 
7. Система релятивистских частиц. Дефект массы и энергия связи ядра. Физические основы механики / http://fn.bmstu.ru/phys/bib/physbook/tom1/ch8/texthtml/ch8_7_text.htm 
8. Состав ядра. Ядерные силы. Энергия связи ядра . Портал естественных наук / http://e-science.ru/physics/theory/?t=6 
9. Справочник по физике. Оптика . www. Abitura.com/ http://www.abitura.com/handbook/optic9.html 
10. Федеральный институт педагогических измерений. Контрольные измерительные материалы (КИМ) Физика //[Электронный ресурс]// http://fipi.ru/view/sections/92/docs/ 
11. Энергия Связи и Дефект Массы Ядра . Квантовая Физика. / http://sfiz.ru/page.php?id=124 

Приложение

 Разно уровневые тренировочные вопросы и задачи:

Первый уровень

1. Какие системы отсчета называются инерциальными?
2. Сформулируйте и разъясните содержание первого постулата СТО – принципа относительности Эйнштейна.
3. В чем отличие первого постулата теории относительности в релятивистской физике от принципа относительности в классической физике?
4. Сформулируйте второй постулат СТО.
5. Сформулируйте закон сложения скоростей в классической механике.
6. Напишите релятивистский закон сложения скоростей.
7. Покажите, что классический закон сложения скоростей является частным случаем релятивистского закона сложения скоростей.
8. Может ли электрон двигаться со скоростью, превышающей скорость света в данной среде?
9. Какое время, отсчитанное между событиями, называется собственным?
10. В каких условиях наблюдается эффект замедления времени?
11. Что такое собственная длина стержня? Одинакова ли длина стержня в различных инерциальных системах отсчета? Имеет ли смысл понятие длина стержня вне связи с системой отсчета?
12. Какой стала бы длина тела в направлении вдоль скорости движения относительно неподвижного наблюдателя при v = c?
13. Какое выражение имеет закон релятивистской динамики?
14. По какой формуле определяется релятивистский импульс тела?
15. Что такое энергия покоя тела?
16. В чем состоит универсальный характер взаимосвязи импульса, энергии и массы тела?
17. Нагретая добела железная деталь охлаждена до комнатной температуры. Произошло ли изменение массы детали?

Второй уровень

18. Две космические ракеты движутся по одной прямой в одном направлении со скоростями 0,6 с и 0,8 с относительно неподвижного наблюдателя. Определите скорость удаления второй ракеты от первой по классической и релятивистской формулам сложения скоростей.
19. Две ракеты, снабженные ионными двигателями, приближаются одна к другой с противоположно направленными скоростями, равными 0,80 с и 0,70 с, относительно наблюдателя, покоящегося в некоторой точке на линии их сближения. Определите относительную скорость ракет по законам классической и релятивистской механики.
20. Определите количество лет, прошедших на Земле, если в космическом корабле при скорости его движения относительно Земли, равной 0,80 с, прошло 12 лет.
21. Определите промежуток времени, прошедший за 35 земных лет на звездолете, движущемся относительно Земли со скоростью 0,40 с.
22. Фотонная ракета движется относительно Земли со скоростью 0,60 с. Определите, во сколько раз замедляется ход времени в ракете с точки зрения земного наблюдателя.
23. Определите скорость движения космического корабля относительно Земли, при которой часы на нем идут в четыре раза медленнее, чем на Земле.
24. Собственная длина стержня равна 2,0 м. Определите его длину для наблюдателя, относительно которого стержень перемещается со скоростью 0,98 с, направленной вдоль стержня.
25. Жесткий стержень длиной 1 м измеряется двумя наблюдателями: первый покоится относительно стержня, второй движется вдоль него. Определите скорость движения второго наблюдателя, если измеренная им длина стержня равна 0,50 м.
26. Определите скорость движения космического корабля, если его продольные размеры для земного наблюдателя кажутся в пять раз меньше «истинных».
27. Определите размеры и форму квадратной пластинки с длиной стороны 1 м, которая удаляется от наблюдателя по прямой, параллельной одной из ее сторон, с относительной скоростью 0,80 c. Сравните площади покоящейся и движущейся пластинки.
28. Покажите, что объем куба, движущегося со скоростью v в направлении, параллельном одному из его ребер, равен 
29. Определите импульс электрона, летящего со скоростью 0,98 с.
30. Определите кинетическую энергию электрона при движении его со скоростью 0,75 с по классическим и релятивистским формулам.
31. Определите скорость движения любой частицы вещества, при которой ее кинетическая энергия равна энергии покоя.
32. Определите энергию покоя электрона и нейтрона.
33. Одинакова ли масса сжатой и свободной пружины?
34. Определите изменение массы тела, если полная энергия этого тела возросла на 1 Дж.

35. Определите скорость движения частицы, если ее полная энергия равна E, а энергия покоя E0.
36. Мощность излучения Солнца 3,9 • 1023 кВт. Определите эквивалентное уменьшение массы Солнца за одну секунду при данном излучении.

Третий уровень

37. Мезон, движущийся со скоростью 0,99 с относительно Земли, пролетел от места своего рождения до точки распада расстояние 4,7 км. Определите собственное время жизни мезона и расстояние, которое пролетел бы мезон относительно Земли, если бы релятивистский эффект относительности интервала времени не имел места.
38. Жесткий стержень покоится в подвижной системе отсчета и ориентирован в ней под углом 37° к оси абсцисс. Определите скорость движения этого стержня параллельно оси абсцисс неподвижной системы отсчета, при которой он с   точки зрения неподвижного наблюдателя наклонен к ней под углом 45°.
39. Покажите, что плотность материала куба, движущегося со скоростью v в направлении, параллельном одному из его ребер, равна 
40. Определите скорость движения тела, если его плотность возросла на 10 %.
41. Определите скорость движения стержня, при которой релятивистское сокращение его длины составит 20 %.
42. Определите угол между диагоналями квадрата при его движении со скоростью 0,90 с в направлении, параллельном одной из сторон.
43. Определите скорость и кинетическую энергию, которая должна быть сообщена космическому кораблю массой 104 кг, чтобы его часы по возвращении на Землю показывали вдвое меньшее время, чем часы на Земле.
44. Определите работу, совершаемую однородным электрическим полем при разгоне электрона от скорости 0,980 c до 0,999 c.
45. Протон, имеющий начальную скорость 0,9 c, попадает в однородное электрическое поле и, двигаясь вдоль линии напряженности, полностью теряет свою скорость. Определите разность потенциалов двух точек, между которыми перемещался протон.
46. Определите скорость и импульс частицы массой m, если ее кинетическая энергия равна удвоенной энергии покоя.
47. Какую ускоряющую разность потенциалов должен пройти протон, чтобы его полная энергия стала в одиннадцать раз больше энергии покоя?
48. Находящаяся в озере вода объемом 2•106 м3, нагрелась на 5 °С. Определите эквивалентное изменение массы.
49. На 1 м2 поверхности, перпендикулярной направлению солнечных лучей около Земли, но вне ее атмосферы, приходит ежесекундно примерно 1,4 кДж энергии излучения Солнца. На какое время хватит массы водорода на Солнце, чтобы поддерживать это излучение? Расстояние от Солнца до Земли около 1,5 • 108 км, масса Солнца 2 • 1030 кг, количество водорода составляет 75 % по массе.

Четвертый уровень

50. Электрон испускается под углом 37° к оси x со скоростью 0,5 с. Определите абсолютное значение и направление скорости этого электрона относительно инерциальной системы, движущейся со скоростью с (рис. 3). 
51. Стержень собственной длиной l0 движется в лаборатории поступательно так, что вектор его скорости v образует угол j со стержнем. Определите длину стержня в лабораторной системе отсчета.
52. В лабораторной системе отсчета (K-система) движется стержень со скоростью 0,98 с. По измерениям, произведенным к K-системе, его длина оказалась равной 1,08 м, а угол, который он составляет с осью x, равным 78,7°. Определите собственную длину стержня в K ‘-системе, связанной со стержнем, и угол, который он составляет с осью x ‘.
53. Частица массой m0, двигаясь со скоростью 0,8 c, испытывает неупругое столкновение с покоящейся частицей той же массы. Определите скорость и энергию покоя составной частицы, которая образовалась в результате соударения.

Ответы

2. Все инерциальные системы отсчета эквивалентны в отношении любых физических процессов. Система отсчета, движущаяся с постоянной скоростью относительно данной ИСО, также есть ИСО, поэтому, кроме исходной, имеется множество других ИСО.
8. Может, но его скорость все равно меньше скорости света в вакууме.
10. Эффект замедления времени наблюдается только в тех системах отсчета, которые движутся друг относительно друга со скоростями, близкими к скорости света в вакууме.
11. Собственной длиной стержня l0 называется длина стержня в системе отсчета, относительно которой он покоится; длина стержня в различных системах отсчета неодинакова. Не имеет.
12. Из формулы следует, что при v ® c, l ® 0, следовательно, при v = с длина тела стала бы равной нулю, что невозможно.
15. Энергия покоя тела – это внутренняя энергия тела.
17. Да, произошло, на величину Dm = Q/c2, где Q – количество теплоты, отданное деталью окружающей среде при ее охлаждении.
18. 0,2с; 0,385с.
19. 1,5с; 0,96с.
20. 20 лет.
21. 32 года.
22. 1,25.
23. 2,9 • 108 м/с.
24. 0,4 м.
25. 0,866с.
26. 2,94 •108 м/с.
27. Прямоугольник со сторонами 1 м и 0,6 м. Площадь уменьшилась на 0,4 м2.
29. 1,34 • 10–21 кг • м/с.
30. 2,3 • 10–14 Дж; 4 • 10–14 Дж.
31. 0,866с =  2,596•108 м/с. 
32. 0,51 МэВ;  939,6 МэВ.
33. Масса сжатой пружины больше, чем свободной, на величину Dm =kx2/2c2 , где k – коэффициент упругости, Dx – удлинение пружины.
34. 11,1 • 10–18 кг.
35. 
36. 4,4 • 106 т.
37. 2,21 мкс; 665 м.
38. 0,66с.
40. 0,42с.
41. 0,6с.
42. 47°.
43. 260 000 км/с; 9 • 1020 Дж.
44. 8,9 • 106 эВ.
45. 1,216 • 109 В.
46. 0,943с; 2,83mc.
47. 9,4 • 109 В.
48. 4,67 • 10–4 кг.
49. 14 400 млрд лет.
50. 0,325с; 67,3°.
51. b =v/c .
52. 1,5 м; 45°.

53. 0,5547с; 2,3m0.

1. Тип 18 № 25667 

Протон массой m движется
в ускорителе со скоростью, близкой к скорости света, имея энергию E =  эВ.

Определите скорость протона. Ответ
дайте в мегаметрах в секунду.

2. Тип 18 № 25668 

Время жизни некоторой частицы в системе
отсчета, связанной с ней, равно 31 нс. Частица движется относительно
неподвижного наблюдателя со скоростью 0,95с. Масса частицы равна 3·10⁻²⁶ кг.
Чему равно время жизни частицы в системе отсчета, связанной с
наблюдателем? Ответ дайте в наносекундах, округлив до целых.

3. Тип 18 № 25669 

Собственное время жизни частицы отличается
в 2 раза по сравнению с временем жизни по неподвижным часам. Масса частицы
равна 1·10^-10 кг. Чему равна полная энергия движущейся
частицы? Ответ выразите в мегаджоулях.

4. Тип 18 № 25670 

Собственное время жизни частицы отличается
в 2 раза по сравнению с временем жизни по неподвижным часам. Масса частицы
равна 1·10^-10 кг. Какую часть скорость частицы составляет от
скорости света? Ответ округлите до сотых.

5. Тип 18 № 25671 

Время жизни некоторой частицы в системе
отсчета, связанной с ней, равно 31 нс. Частица движется относительно
неподвижного наблюдателя со скоростью 0,95с. Масса частицы равна 3·10^-26 кг.
Чему равна полная энергия частицы? Ответ запишите в наноджоулях,
округлив до десятых.

6. Тип 18 № 25672 

Синхротрон – кольцевой циклический
ускоритель заряженных частиц, в котором частицы двигаются по круговой орбите.
Электрону, который ускоряется подобным образом сообщили энергию 1 МэВ. Чему
равна скорость электрона? Ответ дайте в мегаметрах в секунду.

7. Тип 18 № 25673 

Синхротрон – кольцевой циклический
ускоритель заряженных частиц, в котором частицы двигаются по круговой орбите.
Электрону, который ускоряется подобным образом сообщили энергию 1 МэВ. Чему
равна полная энергия электрона? Ответ запишите в мегаэлектрон-вольтах,
округлив до сотых.

8. Тип 18 № 25674 

Протон движется в вакууме со скоростью
0,65с. Чему равна энергия покоя протона? Ответ запишите в
джоулях, умножив на , округлив до
десятых.

9. Тип 18 № 25675 

Протон движется в вакууме со скоростью
0,65с. Чему равна полная энергия протона? Ответ запишите в
джоулях, умножив на , округлив до
целых.

10. Тип 18 № 25676 

Собственное время жизни частицы отличается
в 3 раза по сравнению с временем жизни по неподвижным часам. Масса частицы
равна 3·10^-12 кг. Чему равна скорость частицы? Ответ
дайте в мегаметрах в секунду, округлив до целых.

11. Тип 18 № 25677 

В ядре Солнца осуществляется
протон-протонная термоядерная реакция, в результате которой из четырёх протонов
образуется гелий-4. При этом известно, что мощность излучения Солнца составляет
3,83·10²⁶ Вт.

На сколько уменьшается масса Солнца
ежесекундно? Ответ дайте в мегатоннах, округлив до десятых.

12. Тип 18 № 25678 

Неизвестная частица движется в ускорителе
со скоростью, близкой к скорости света. Кинетическая энергия и энергия покоя
этой частицы соответственно равны E_к = 6·10^-12 Дж
и E₀ = 9·10^-12 Дж. Чему равна
скорость частицы? Ответ запишите в метрах в секунду, деленных на , округлив до
десятых.

13. Тип 18 № 25679 

Время жизни некоторой частицы в системе
отсчета, связанной с ней, равно 31 нс. Частица движется относительно
неподвижного наблюдателя со скоростью 0,9с. Масса частицы равна 3·10^-26 кг.
Чему равна полная энергия частицы? Ответ выразите в джоулях, умножив
на и округлив до
десятых.

14. Тип 18 № 25680 

Собственное время жизни частицы отличается
в 3 раза по сравнению с временем жизни по неподвижным часам. Масса частицы
равна 3·10^-12 кг. Чему равна полная энергия частицы? Ответ
запишите к килоджоулях.

15. Тип 18 № 25681 

Неизвестная частица движется в ускорителе
со скоростью, близкой к скорости света. Кинетическая энергия и энергия покоя
этой частицы соответственно равны E_к = 15·10^-10 Дж
и E₀ = 5·10^-10 Дж. Чему равна
полная энергия частицы? Ответ дайте в наноджуолях.

16. Тип 18 № 25682 

Время жизни некоторой частицы в системе
отсчета, связанной с ней, равно 31 нс. Частица движется относительно
неподвижного наблюдателя со скоростью 0,9с. Масса частицы равна 3·10^-26 кг.
Определите время жизни частицы в системе отсчета, связанной с
наблюдателем. Ответ дайте в наносекундах, округлив до десятых.

17. Тип 18 № 25683 

Неизвестная частица движется в ускорителе
со скоростью, близкой к скорости света. Кинетическая энергия и энергия покоя
этой частицы соответственно равны E_к = 15·10^-10 Дж
и E₀ = 5·10^-10 Дж. Чему равна
скорость движения частицы? Ответ дайте в метрах в секунду, разделив
на  и
округлив до десятых.

18. Тип 18 № 25684 

Протон движется в вакууме со скоростью
0,65с. Чему равна кинетическая энергия протона? Ответ дайте в
наноджоулях, округлив ответ до сотых.

19. Тип 18 № 25685 

Протон движется в вакууме со скоростью 0,8с.
Чему равна кинетическая энергия протона? Ответ дайте в наноджоулях,
округлив до десятых.

20. Тип 18 № 25686 

Две частицы в вакууме летят навстречу друг
другу со скоростями 0,5c. Расстояние между частицами составляет l  =  10 м.
Через какое время произойдет соударение? Ответ дайте в наносекундах,
округлив до целых.

21. Тип 18 № 25687 

Протон движется в вакууме со скоростью 0,8с.
Чему равна полная энергия протона? Ответ дайте в наноджоулях, округлив
до сотых.

22. Тип 18 № 25688 

Протон движется в вакууме со скоростью
0,65с. Чему равна полная энергия движущейся частицы? Ответ дайте
в наноджоулях, округлив до десятых.

23. Тип 18 № 25689 

Синхротрон  — кольцевой циклический
ускоритель заряженных частиц, в котором частицы двигаются по круговой орбите.
Электрону, который ускоряется подобным образом, сообщили энергию 0,1 МэВ. Чему
равна скорость движения электрона? Дайте ответ в метрах в секунду,
разделив на  и
округлив до десятых.

24. Тип 18 № 25690 

Две частицы в вакууме летят навстречу друг
другу со скоростями 0,7c. Расстояние между частицами составляет l  =  100 м.
Через какое время произойдет соударение частиц? Ответ дайте в
наносекундах, округлив до целых.

25. Тип 18 № 25691 

Протон движется в вакууме со скоростью 0,8с.
Чему равна полная энергия протона? Ответ дайте в наноджоулях, округлив
ответ до сотых.

26. Тип 18 № 25692 

Две частицы в вакууме летят навстречу друг
другу со скоростями 0,5c. Чему равно отношение относительной скорости
частиц к скорости света в вакууме?

27. Тип 18 № 25693 

Две частицы в вакууме летят навстречу друг
другу со скоростями 0,7c. Найдите отношение относительной скорости
частиц к скорости света в вакууме. Ответ запишите, округлив до сотых.

28. Тип 18 № 25694 

Синхротрон  — кольцевой циклический
ускоритель заряженных частиц, в котором частицы двигаются по круговой орбите.
Электрону, который ускоряется подобным образом, сообщили энергию 0,1 МэВ. Чему
равна полная энергия частицы? Ответ дайте в мегаэлектрон-вольтах,
округлив до сотых.

---

Основы СТО. Подготовка к ЕГЭ (презентация).

Целевая аудитория: для 11 класса

Автор: Попова И.А.
Место работы: МОУ СОШ № 30 г. Белово
Добавил: rina

© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

---

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

---

Фотографии предоставлены

МЕТОДЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ ПО СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

В разработке рассмотрены основные вопросы специальной теории относительности. Приведены методические указания по решению типовых задач ЕГЭ. Предназначено для учащихся 11 класса.

Решение задач

Релятивистская механика

11 класс

Задача №1

• .Чему равна длина космического корабля, движущегося со скоростью 0,8 с. Длина покоящегося корабля 100 м. 

Образец решения

Задача №2

• С какой скоростью должна двигаться частица (тело), чтобы его масса увеличилась в 3 раза?
• Ответ : 0,94 с

Задача №3

•   Чему равна будет масса космонавта, движущегося в космическом корабле со скоростью 0,8с? Масса покоящегося космонавта 90 кг.

Проверь……

Задача №4

С космического корабля, удаляющегося от Земли со скоростью 0,7с, стартует ракета в направлении движения корабля. Скорость ракеты относительно Земли 0,96с. Чему равна скорость ракеты относительно Земли?

Проверь……

ЗАДАЧА №5

Длина линейки, неподвижной относительно земного наблюдателя, 2 м. Какова длина этой линейки, движущейся относительно его со скоростью, равной 0.5 скорости света? Скорость света принять равной 3*10 8 м/с.

Ответ: 1.74 м

ЗАДАЧА №6

Какой промежуток времени пройдет на звездолете, движущемся относительно Земли со скоростью, равной 0.4 скорости света, за 25 земных лет. Скорость света принять равной

3*10 8 м/с.

Ответ: 23 года

ЗАДАЧА №7

С какой скоростью должен двигаться космический корабль относительно Земли, чтобы часы на нем шли в 4 раза медленнее, чем на Земле? Скорость света принять равной 3*10 8 м/с.

Ответ: 2.9*10 8 м/с

Задания ЕГЭ №18

• РЕШЕНИЕ ЗАДАНИЙ С САЙТА «РЕШУ ЕГЭ»