Задачи на тела вращения с решениями в егэ 11 класс

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

По теме: методические разработки, презентации и конспекты

1. Радиус основания цилиндра 2 м, а высота 3 м. Найдите диагональ осевого сечения.

РЕШЕНИЕ

2. Осевое сечение цилиндра квадрат, площадь которого Q. Найдите площадь основания цилиндра.

РЕШЕНИЕ

3. Высота цилиндра 6 см, радиус основания 5 см. Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4 см от нее.

РЕШЕНИЕ

4. Высота цилиндра 8 дм, радиус основания 5 дм. Цилиндр пересечен плоскостью так, что в сечении получился квадрат. Найдите расстояние от этого сечения до оси.

РЕШЕНИЕ

5. Высота цилиндра 6 дм, радиус основания 5 дм. Концы отрезка АВ, равного 10 дм, лежат на окружностях обоих оснований. Найдите кратчайшее расстояние от него до оси.

РЕШЕНИЕ

6. В равностороннем цилиндре (диаметр равен высоте цилиндра) точка окружности верхнего основания соединена с точкой окружности нижнего основания.

РЕШЕНИЕ

7. В цилиндр вписана правильная шестиугольная призма. Найдите угол между диагональю ее боковой грани и осью цилиндра, если радиус основания равен высоте цилиндра.

РЕШЕНИЕ

8. Высота цилиндра 2 м. Радиус основания 7 м. В этот цилиндр наклонно вписан квадрат так, что все вершины его лежат на окружностях оснований. Найдите сторону квадрата.

РЕШЕНИЕ

9. Радиус основания конуса 3 м, высота 4 м. Найдите образующую L

РЕШЕНИЕ

10. Образующая конуса l наклонена к плоскости основания под углом 30°. Найдите высоту.

РЕШЕНИЕ

11. Радиус основания конуса R. Осевым сечением конуса является прямоугольный треугольник. Найдите его площадь.

РЕШЕНИЕ

12. В равностороннем конусе (осевое сечение правильный треугольник) радиус основания R. Найдите площадь сечения, проведенного через две образующие, угол между которыми равен α.

РЕШЕНИЕ

13. Высота конуса 20, радиус его основания 25. Найдите площадь сечения, проведенного через вершину, если расстояние от него до центра основания конуса равно 12.

РЕШЕНИЕ

14. Радиус основания конуса R, а образующая наклонена к плоскости основания под углом α. Через вершину конуса проведена плоскость под углом φ к его высоте. Найдите площадь полученного сечения.

РЕШЕНИЕ

15. Конус пересечен плоскостью, параллельной основанию, на расстоянии d от вершины. Найдите площадь сечения, если радиус основания конуса r, а высота h

РЕШЕНИЕ

16. Высота конуса h. На каком расстоянии от вершины надо провести плоскость, параллельную основанию, чтобы площадь сечения была равна половине площади основания

РЕШЕНИЕ

17. Через середину высоты конуса проведена прямая, параллельная образующей l. Найдите длину отрезка прямой, заключенной внутри конуса.

РЕШЕНИЕ

18. Образующая конуса 13 см, высота 12 см. Конус пересечен прямой, параллельной основанию, расстояние от нее до основания равно 6 см, а до высоты 2 см. Найдите отрезок прямой, заключенный внутри конуса.

РЕШЕНИЕ

19. Радиусы оснований усеченного конуса 3 м и 6 м, высота 4 м. Найдите образующую.

РЕШЕНИЕ

20. Радиусы оснований усеченного конуса R и r, образующая наклонена к основанию под углом 45°. Найдите высоту Н.

РЕШЕНИЕ

21. Образующая усеченного конуса равна 2a и наклонена к основанию под углом 60°. Радиус одного основания вдвое больше радиуса другого основания. Найдите радиусы.

РЕШЕНИЕ

22. Радиусы оснований усеченного конуса 3 дм и 7 дм, образующая 5 дм. Найдите площадь осевого сечения.

РЕШЕНИЕ

23. Площади оснований усеченного конуса 4 дм2 и 16 дм2, через середину высоты проведена плоскость, параллельная основаниям. Найдите площадь сечения.

РЕШЕНИЕ

24. Площадь оснований усеченного конуса M и m. Найдите площадь среднего сечения, параллельного основаниям.

РЕШЕНИЕ

25. У пирамиды все боковые ребра равны. Докажите, что она является вписанной в некоторый конус.

РЕШЕНИЕ

26. В конусе даны радиус основания R и высота H. Найдите ребро вписанного в него куба.

РЕШЕНИЕ

27. В конусе даны радиус основания R и высота H. В него вписана правильная треугольная призма, у которой боковые грани квадраты Найдите ребро призмы.

РЕШЕНИЕ

28. Полушар и вписанный в него конус имеют общее основание и общую высоту. Через середину высоты проведена плоскость, параллельная основанию. Докажите, что площадь сечения, заключенного между боковой поверхностью конуса и поверхностью полушара. равна половине площади основания.

РЕШЕНИЕ

29. Шар, радиус которого 41 дм, пересечен плоскостью на расстоянии 9 дм от центра. Найдите площадь сечения.

РЕШЕНИЕ

30. Через середину радиуса шара проведена перпендикулярная ему плоскость. Как относится площадь полученного сечения к площади большого круга

РЕШЕНИЕ

31. Радиус шара R. Через конец радиуса проведена плоскость под углом 60° к нему. Найдите площадь сечения.

РЕШЕНИЕ

32. Радиус земного шара R. Чему равна длина параллели, если ее широта 60°?

РЕШЕНИЕ

33. Город N находится на 60° северной широты. Какой путь совершает этот пункт в течение 1 ч. вследствие вращения Земли вокруг своей оси

РЕШЕНИЕ

34. На поверхности шара даны три точки. Прямолинейные расстояния между ними 6 см, 8 см, 10 см. Радиус шара 13 см. Найдите расстояние от центра до плоскости, проходящей через эти точки.

РЕШЕНИЕ

35. Диаметр шара 25 см. На его поверхности даны точка А и окружность, все точки которой удалены (по прямой) от А на 15 см. Найдите радиус этой окружности.

РЕШЕНИЕ

36. Радиус шара 7 см. На его поверхности даны две равные окружности, имеющие общую хорду длиной 2 см. Найдите радиусы окружностей, зная, что их плоскости перпендикулярны.

РЕШЕНИЕ

37. Дан шар радиуса R. Через одну точку его поверхности проведены две плоскости: первая касательная к шару, вторая под углом 30° к первой. Найдите площадь сечения.

РЕШЕНИЕ

38. Имеется тело, ограниченное двумя концентрическими шаровыми поверхностями (полый шар). Докажите, что его сечение плоскостью, проходящей через центр, равновелико сечению, касательному к внутренней шаровой поверхности.

РЕШЕНИЕ

39. Шар радиуса R касается всех сторон правильного треугольника со стороной а. Найдите расстояние от центра шара до плоскости треугольника

РЕШЕНИЕ

40. Стороны треугольника 13 см, 14 см и 15 см. Найдите расстояние от плоскости треугольника до центра шара, касающегося всех сторон треугольника. Радиус шара 5 см.

РЕШЕНИЕ

41. Диагонали ромба 15 см и 20 см. Шаровая поверхность касается всех его сторон. Радиус шара 10 см. Найдите расстояние от центра шара до плоскости ромба.

РЕШЕНИЕ

42. Через касательную к поверхности шара проведены две взаимно перпендикулярные плоскости, пересекающие шар по кругам радиусов r1 и r2 Найдите радиус шара R.

РЕШЕНИЕ

43. Шар радиуса R вписан в усеченный конус. Угол наклона образующей l к плоскости нижнего основания конуса равен α. Найдите радиусы оснований и образующую усеченного конуса.

РЕШЕНИЕ

44. Два равных шара радиуса R расположены так, что центр одного лежит на поверхности другого. Найдите длину линии l, по которой пересекаются их поверхности.

РЕШЕНИЕ

45. Радиусы шаров 25 дм и 29 дм, а расстояние между их центрами 36 дм. Найдите длину линии l, по которой пересекаются их поверхности.

РЕШЕНИЕ

46. Найдите радиус шара, описанного около куба с ребром а.

РЕШЕНИЕ

47. Докажите, что центр шара, описанного около правильной пирамиды, лежит на ее оси.

РЕШЕНИЕ

48. Докажите, что центр шара, вписанного в правильную пирамиду, лежит на ее высоте.

РЕШЕНИЕ

49. Найдите радиус шара, описанного около правильного тетраэдра с ребром a

РЕШЕНИЕ

50. В правильной четырехугольной пирамиде сторона основания равна a, а плоский угол при вершине равен α. Найдите радиусы вписанного и описанного шаров.

РЕШЕНИЕ

51. В шар радиуса R вписана правильная треугольная пирамида с плоскими углами α при ее вершине. Найдите высоту пирамиды.

РЕШЕНИЕ

52. Правильная n-угольная призма вписана в шар радиуса R. Ребро основания призмы равно а. Найдите высоту призмы при: 1) n = 3; 2) n = 4; 3) n = 6.

РЕШЕНИЕ

53. Сторона основания правильной n-угольной пирамиды равна а, двугранный угол при основании равен φ. Найдите радиус шара, вписанного в пирамиду.

РЕШЕНИЕ

54. Найдите радиус шара, описанного около правильной n-угольной пирамиды, если сторона основания равна a, а боковое ребро наклонено к плоскости основания под углом α.

РЕШЕНИЕ

ТЕЛА ВРАЩЕНИЯ

РЕШЕНИЕ ЗАДАЧ

Основные формулы

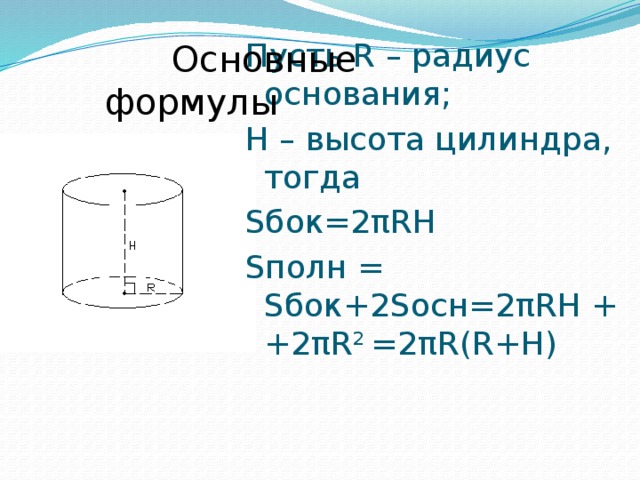
Пусть R – радиус основания;

H – высота цилиндра, тогда

Sбок=2πRH

Sполн = Sбок+2Sосн=2πRH + +2πR 2 =2πR(R+H)

Основные формулы

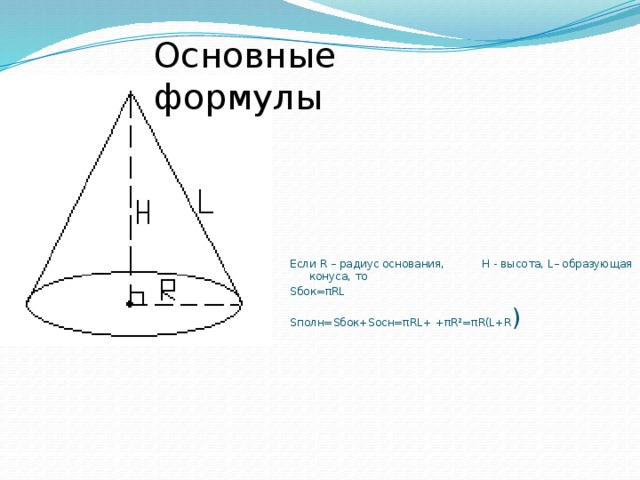
Если R – радиус основания, H — высота, L– образующая конуса, то

Sбок=πRL

Sполн=Sбок+Sосн=πRL+ +πR²=πR(L+R )

Усеченный прямой конус

h – высота усеченного конуса ; R и R1 – радиусы его верхнего и нижнего оснований; l – его образующая

Формулы:

Основные формулы

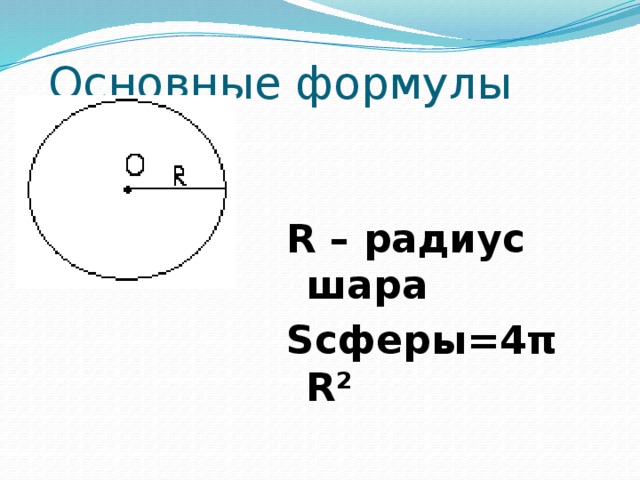
R – радиус шара

Sсферы=4πR²

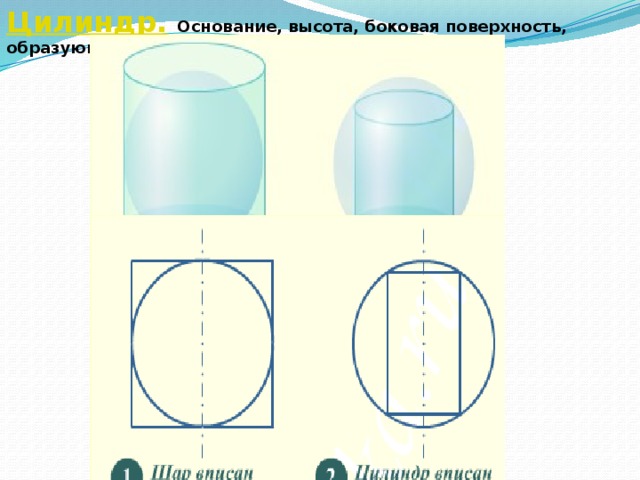
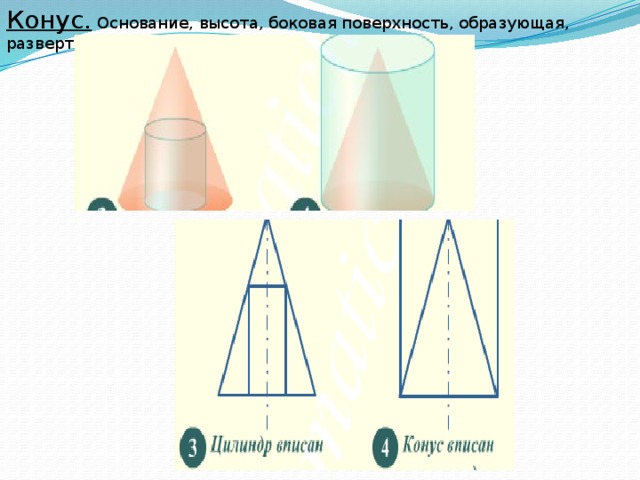
Цилиндр.   Основание, высота, боковая поверхность, образующая, развертка

Конус.   Основание, высота, боковая поверхность, образующая, развертка

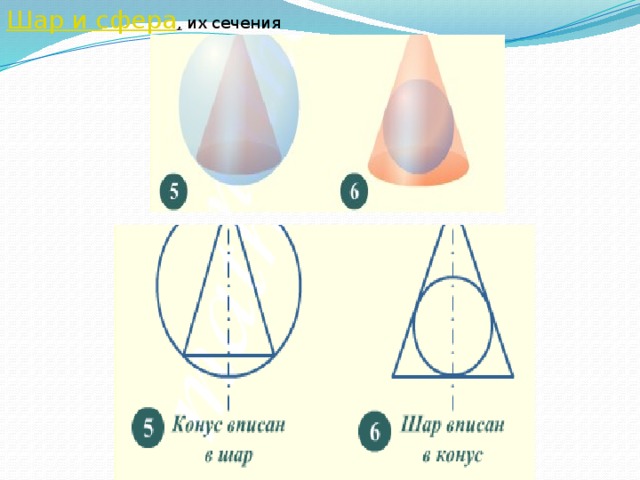
Шар и сфера ,   их сечения

Задача 1.

Шар вписан в цилиндр. Площадь поверхности шара равна 111.

Найдите площадь полной поверхности цилиндра.

Решение.

Площадь полной поверхности цилиндра находим по формуле  S ц  = 2 πrh  + 2 πr 2 .

Из рисунка (1) для плоского

сечения видно, что радиус

основания цилиндра ( r ) равен

радиусу вписанного шара ( R ),

а его высота ( h ) равна диаметру

шара (удвоенному радиусу).

Поэтому  S ц  = 2 πR ·2 R  + 2 πR 2  = 6 πR 2 . Величину  πR 2  найдем из формулы поверхности шара  S ш  = 4 πR 2 . Следовательно,  πR 2  =  S ш  / 4 = 111/4. Окончательно находим  S ц  = 6·111 / 4 = 333/2 = 166,5.

Ответ:  166,5

Задача 2

В шар, площадь поверхности которого равна 100π, вписан цилиндр. Найти высоту цилиндра, если радиус его основания равен 4.

Дополним чертеж осевого сечения радиусом шара и расставим буквы для обозначения отрезков.  Площадь поверхности шара  S ш  = 4 πR 2  = 100π. Отсюда  R 2  = 25 и  R  = 5. В треугольнике  OAB :  OA  =  x  — половина искомой высоты цилиндра;  AB  = 4 — радиус основания цилиндра;  OB  = 5 — радиус шара.  По теореме Пифагора: x 2  + 4 2  = 5 2  ,

x 2  = 25 − 16 = 9;  x  = 3.  h  = 6.

Ответ:  6

Задача 3

Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 3√2. Найдите площадь боковой поверхности конуса.

  l  2  =  h  2  +  r  2 По условию задачи  h  =  r , следовательно  l  2  =  r  2  +  r  2 ;    l  2  = 2 r  2 ;     l  = √2· r . Площадь боковой поверхности цилиндра  S ц  = 2 πrh  = 2 πr  2 . Площадь боковой поверхности конуса  S к  =  πrl  =  πr ·√2· r  = √2 πr  2 ; т.е. площадь боковой поверхности цилиндра в √2 раз больше площади боковой поверхности конуса. Окончательно  S к  = 3√2 / √2 = 3/ Ответ:  3 A C B » width=»640″

Воспользуемся чертежом осевого сечения, расставим буквы для обозначения отрезков:  AC  =  h  — высота конуса и цилиндра,  CB  =  r  — радиус оснований конуса и цилиндра,  AB  =  l  — образующая цилиндра.

Из треугольника  ABC  по теореме Пифагора: AB 2  =  AC 2  +  CB 2  ==  l  2  =  h  2  +  r  2 По условию задачи  h  =  r , следовательно  l  2  =  r  2  +  r  2 ;    l  2  = 2 r  2 ;     l  = √2· r . Площадь боковой поверхности цилиндра 

S ц  = 2 πrh  = 2 πr  2 . Площадь боковой поверхности конуса  S к  =  πrl  =  πr ·√2· r  = √2 πr  2 ;

т.е. площадь боковой поверхности цилиндра в √2 раз больше площади боковой поверхности конуса. Окончательно  S к  = 3√2 / √2 = 3/ Ответ:  3

A

C

B

Задача 4

Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна 7√2. Найдите радиус сферы.

Так как по условию задачи центр сферы находится в центре основания конуса, то основание конуса, в свою очередь, является диаметральным сечением сферы. Т.о. на плоском чертеже отрезок  AB  является диаметром окружности, и ∠ ACB  = 90° как вписанный угол, опирающийся на её диаметр.

Пусть  l  = 7√2 — образующая конуса,  R  — радиус сферы. Тогда в прямоугольном треугольнике  ABC   AC  =  BC  =  l  — катеты,  AB  = 2 R  — гипотенуза. По теореме Пифагора AB 2  =  AC 2  +  BC 2 ; (2 R ) 2  =  l  2  +  l  2 ; 4 R  2  =  l  2  +  l  2  = 2 l  2 ;   4 R  2  = 2(7√2_) 2 ; 4 R  2  = 2·49·2 = 4·49;    R  2  = 49;   R  = 7.

Ответ:  7

Задача 5

Найти площадь поверхности шара, описанного около конуса, у которого радиус основания   2/√π, а высота   1/√π.

Пусть  R  — радиус сферы. Поскольку  СD  — диаметр окружности осевого сечения, то  СH  +  HD  = 2 R . Воспользуемся свойством пересекающихся хорд окружности, чтобы найти длину отрезка  HD  =  x .

DH·HС = AH·HC; x ·  1/√π =   2/√π ·  2/√π; Преобразуя, получим  х  =   4/√π.  2 R  =   1/√π +   4/√π =  5/√π;    R  =  5/2√π. Площадь сферы  S  = 4π R 2  = 4π·25/4π = 25.

Ответ:  25

Задача 5

В шар вписан конус, образующая которого равна диаметру основания. Найти отношение полной поверхности этого конуса к поверхности шара.

Пусть образующая конуса ( AC  =  BC ) равна  a . Тогда по условию задачи диаметр конуса ( AB ) тоже равен  a . То есть, треугольник  ABC  — равносторонний.

Чтобы найти радиус шара ( R ), используем формулу, связывающую длину стороны равностороннего треугольника и радиус описанной около него окружности.

Радиус основания конуса  r  =  a /2 (половина диаметра).

Площадь полной поверхности конуса S к  = π r ( r  +  l ) = π· a /2·( a /2 +  a ) = 3π a 2 /4.

Площадь поверхности шара S ш  = 4π R 2  = 4π· a 2 ·(√3/3) 2  = 4π a 2 /3.

Их отношение

S к / S ш  = 3π a 2 /4/4π a 2 /3 =  9/16 = 0,5625.

Ответ:  0,5625

ЗАДАНИЕ НА ДОМ

№ 616

Задачи ЕГЭ (распечатка)

Цилиндры, сферы и конусы: будем вписывать их в другие объекты, будем рассекать их различными плоскостями, отыскивать углы наклона этих сечений к основанию или их площади.

Задача 1.

В правильную шестиугольную пирамиду, боковое ребро которой равно 10, а высота равна 6, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.

Так как сфера касается всех граней, то точки касания обязательно лежат на апофемах граней. Нарисуем пирамиду в разрезе, причем разрез пройдет по апофемам противолежащих граней. Тогда сечение – треугольник MSN, а сечение сферы – вписанная в этот треугольник окружность. Разберемся, отрезки каких длин в этом сечении присутствуют. Так как высота пирамиды 6, а боковое ребро 10, найдем длину отрезка :

Так как основание пирамиды составлено из правильных треугольников, то длина равна ребру основания. Теперь можем определить длину апофемы:

Основание треугольника сечения составлено из двух одинаковых отрезков, которые равны высоте треугольника , например. Так как это правильный треугольник со стороной 8, то высота этого треугольника равна , а длина MN тогда .

Итак, теперь мы знаем стороны треугольника сечения : , .
Определим радиус вписанной в него окружности.

Как известно, радиус вписанной окружности можно определить через площадь:


Теперь, зная радиус, можно найти и площадь поверхности сферы:

Ответ:

Задача 2.

Радиус основания конуса равен 6, а его высота равна 8. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 4. Найдите расстояние от центра основания конуса до плоскости сечения.

Образующую конуса можно найти из осевого сечения по теореме Пифагора.

Отрезок OP – высота треугольника . В треугольнике MON стороны равны 4, 6 и 6, определим его площадь по формуле Герона и затем найдем высоту:

Полупериметр треугольника MON равен 8, площадь:


Искомое расстояние – высота треугольника , проведенная к SP.
Определим высоту сечения SP.

По теореме Пифагора

Площадь треугольника SOP:

Наконец, искомое расстояние:

Ответ:

Задача 3.

В правильную четырёхугольную пирамиду, боковое ребро которой равно 10, а высота равна 6, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.

Так как сфера касается всех граней, то точки касания обязательно лежат на апофемах граней. Нарисуем пирамиду в разрезе, причем разрез пройдет по апофемам противолежащих граней. Тогда сечение – треугольник SQP, а сечение сферы – вписанная в этот треугольник окружность. Разберемся, отрезки каких длин в этом сечении присутствуют. Так как высота пирамиды 6, а боковое ребро 10, найдем длину отрезка :

Тогда равна , так как треугольник — равнобедренный и прямоугольный, имеет острые углы по , тригонометрические функции которых хорошо известны:

Определим длину апофемы грани:

В треугольнике SQP стороны: ,
Определим радиус вписанной в него окружности.



Как известно, радиус вписанной окружности можно определить через площадь:


Теперь, зная радиус, можно найти и площадь поверхности сферы:

Ответ:

Задача 4.

Радиус основания конуса с вершиной равен 6, а длина его образующей равна 9. На окружности основания конуса выбраны точки и , делящие окружность на две дуги, длины которых относятся как 1:5. Найдите площадь сечения конуса плоскостью .

Длины дуг окружности пропорциональны центральным углам, поэтому , . Таким образом, поскольку радиус основания конуса равен 6, то треугольник MON правильный и длина хорды . Далее просто пользуемся формулой Герона для определения площади сечения:

Ответ:

Задача 5.

Две параллельные плоскости, расстояние между которыми 2, пересекают шар. Одна из плоскостей проходит через центр шара. Отношение площадей сечений шара этими плоскостями равно 0,84. Найдите радиус шара.

Площадь сечения шара плоскостью – окружность. Площадь окружности

Большая окружность проходит через центр сферы, поэтому ее радиус – радиус сферы R.
Тогда отношение площадей:


Рассмотрим треугольник . В нем , , .
Это прямоугольный треугольник, поэтому


Или

Тогда:

Получили уравнение:




Ответ:

20 февраля 2022

В закладки

Обсудить

Жалоба

Объёмы тел вращения

В данной методической разработке приведены формулы и разобраны примеры решения традиционных задач на вычисление объёмов тел вращения.

obemy-tel-vraschenija.docx
obemy-tel-vraschenija.pdf

Задача №1

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 36 см³.

Задача №2

Высота одного цилиндра вдвое больше высоты второго цилиндра, но его радиус в два раза меньше радиуса второго цилиндра. Найти отношение их объёмов

Задача №3

Найти объем 25м цилиндрической трубы (полого цилиндра), если внешний радиус равен 50см, диаметр стенок равен 10см.

Задача №4

Объём конуса равен 36, а его высота равна 12. Найдите радиус основания конуса.

Задача №5

Объём конуса равен 24 см³. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объём меньшего конуса.

Задача №6

Диаметр основания конуса равен 16, а длина образующей — 17. Найдите объем конуса.

Задача №7

Радиусы оснований усечённого конуса равны 4 и 12, а образующая равна 10. Вычислить объем усечённого конуса.

Задача №8

Внутренний диаметр полого шара равен 8 см, а толщина стенок равна 2 см. Найдите объем материала, из которого сделан шар.

Задача №9

Прямоугольная трапеция с основаниями 11см и 17 см и высотой 12 см вращается около прямой, проходящей через вершину острого угла перпендикулярно основаниям. Hайдите объем полученного тела вращения.

Задача №10
Прямоугольный треугольник с катетами 20 см и 15 см вращается вокруг гипотенузы . Найти объём полученного тела вращения.

Задания для самостоятельного решения.

1. Даны две кружки цилиндрической формы. Первая кружка в полтора раза ниже второй, а вторая вдвое шире первой. Во сколько раз объём второй кружки больше объёма первой?

2. Однородный шар диаметром 3 см имеет массу 162 грамма. Чему равна масса шара, изготовленного из того же материала, с диаметром 2 см? Ответ дайте в граммах.

3. Осевое сечение конуса равносторонний треугольник, сторона которого равна 12 см. Найдите объём конуса.

4. Найти объем тела, полученного в результате вращения прямоугольного треугольника вокруг гипотенузы, если катеты равны 3см и 4 см.

5. Прямоугольная трапеция с основанием 5 см и 8 см и высотой 4 см вращается около большего основания. Найдите объем тела вращения.

Автор: Барсукова Наталья Александровна.

Зачет   «Тела вращения»

1 вариант

№13
ЕГЭ, база

1)     
Радиус ос­но­ва­ния
цилиндра равен 2, вы­со­та равна 3. Най­ди­те площадь бо­ко­вой поверхности
цилиндра, де­лен­ную на π.

2)     
Площадь бо­ко­вой поверхности ци­лин­дра
равна 2π, а диа­метр основания равен 1. Най­ди­те высоту цилиндра.

3)     
Площадь боковой поверхности цилиндра
равна 2π, а высота равна 1. Найдите диаметр основания.

4)     
Во сколь­ко раз уве­ли­чит­ся пло­щадь бо­ко­вой
по­верх­но­сти конуса, если его об­ра­зу­ю­щую уве­ли­чить в 3 раза?

5)     
Высота ко­ну­са равна 4, а диа­метр
основания — 6. Най­ди­те образующую конуса.

6)     
Площадь боль­шо­го круга шара равна 3. Най­ди­те
площадь по­верх­но­сти шара.

7)     
Даны два шара с ра­ди­у­са­ми 3 и 1. Во
сколь­ко раз пло­щадь поверхности пер­во­го шара боль­ше площади по­верх­но­сти
второго?

№16
ЕГЭ, база

     
Площадь осевого сечения цилиндра равна 4.
Найдите площадь боковой поверхности цилиндра, деленную на π.

9)     
Длина окружности основания конуса равна 3,
образующая равна 2. Найдите площадь боковой поверхности конуса.

10) Куб
вписан в шар радиуса . Найдите объем куба.

11)  Около
шара опи­сан цилиндр, пло­щадь поверхности ко­то­ро­го равна 18. Най­ди­те
площадь по­верх­но­сти шара.

12)  Около
конуса описана сфера (сфера содержит окружность основания конуса и его
вершину). Центр сферы находится в центре основания конуса. Радиус сферы
равен . Найдите образующую
конуса.

Дополнительно: (№13 ЕГЭ, профиль)

13) 
В цилиндре
образующая перпендикулярна плоскости основания. На окружности одного из
оснований цилиндра выбраны точки А и В, а на
окружности другого основания — точки В₁ и С₁,
причем ВВ₁ — образующая цилиндра, а отрезок АС₁ пересекает
ось цилиндра.

а)
Докажите, что угол АВС₁ прямой.

б)
Найдите угол между прямыми ВВ₁ и АС₁,
если АВ = 6, ВВ₁ = 15, В₁С₁ = 8.

Зачет   «Тела вращения»

2 вариант

№13
ЕГЭ, база

1)     
Радиус основания цилиндра
равен 7, высота равна 10. Найдите площадь боковой поверхности цилиндра,
деленную на π .

2)     
Длина
окруж­но­сти основания ци­лин­дра равна 3. Пло­щадь боковой по­верх­но­сти
равна 6. Най­ди­те высоту цилиндра.

3)      Площадь
бо­ко­вой поверхности ци­лин­дра равна 40π а диа­метр основания равен
5. Най­ди­те высоту цилиндра.

4)      Во сколько
раз уменьшится площадь боковой поверхности конуса, если радиус его основания
уменьшится в 1,5 раза, а образующая останется прежней?

5)     
Высота конуса равна 4, а
длина образующей — 5. Найдите диаметр основания конуса.

6)     
Во сколь­ко раз уве­ли­чит­ся
площадь по­верх­но­сти шара, если ра­ди­ус шара уве­ли­чить в 2 раза?

7)     
Даны два
шара. Диа­метр пер­во­го шара в 8 раз боль­ше диа­мет­ра второго. Во сколь­ко
раз пло­щадь по­верх­но­сти пер­во­го шара боль­ше пло­ща­ди по­верх­но­сти
второго?

№16
ЕГЭ, база

     
Радиус ос­но­ва­ния
цилиндра равен 26, а его об­ра­зу­ю­щая равна 9. Сечение, па­рал­лель­ное оси
цилиндра, уда­ле­но от неё на расстояние, рав­ное 24. Най­ди­те площадь этого
сечения.

9)     
Длина окружности основания
конуса равна 8, образующая равна 8. Найдите площадь боковой поверхности конуса.

10) Куб вписан в шар радиуса .
Найдите объем куба.

11) 
Около шара описан цилиндр,
площадь поверхности которого равна 45. Найдите площадь поверхности шара.

12)  Около
конуса описана сфера (сфера содержит окружность основания конуса и его
вершину). Центр сферы находится в центре основания конуса. Радиус сферы
равен . Найдите образующую
конуса.

Дополнительно: (№13 ЕГЭ, профиль)

13) В цилиндре образующая перпендикулярна плоскости основания.
На окружности одного из оснований цилиндра выбраны точки А и В,
а на окружности другого основания — точки В₁ и С₁,
причем ВВ₁ — образующая цилиндра, а отрезок АС₁ пересекает
ось цилиндра.

а) Докажите, что угол АВС₁ прямой.

б) Найдите площадь боковой
поверхности цилиндра, если AB = 20, BB₁ = 15, B₁C₁ = 21.