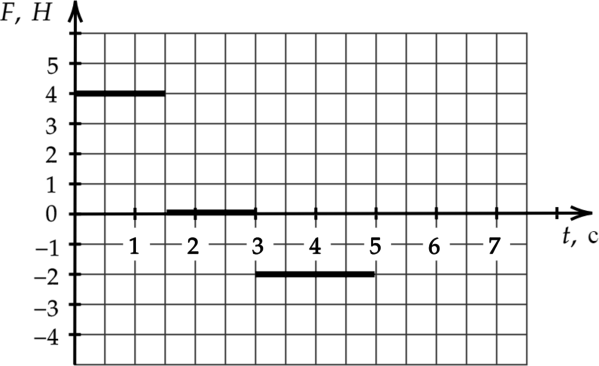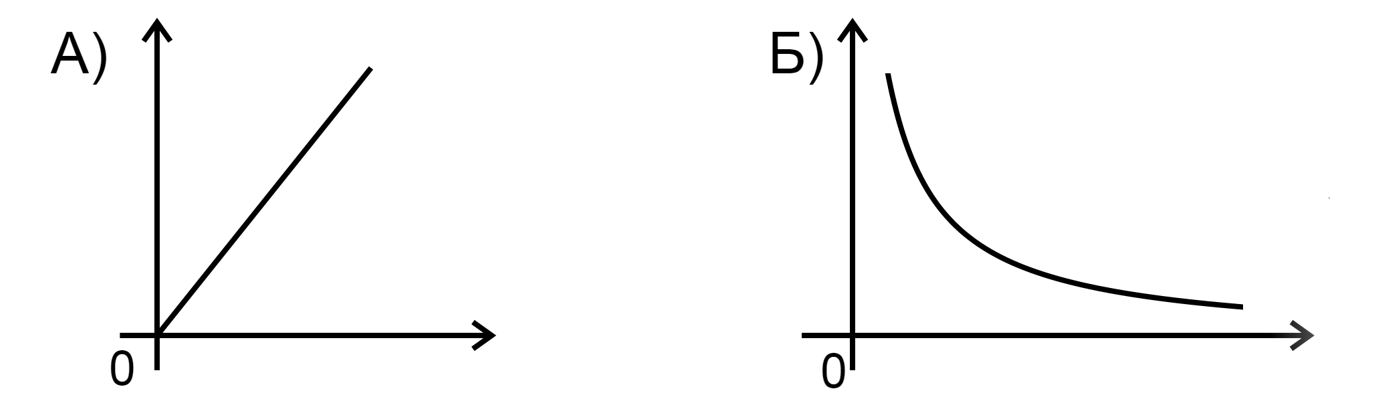Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
2
Задания Д28 C1 № 703
Массивный брусок движется поступательно по горизонтальной плоскости под действием постоянной силы, направленной под углом к горизонту. Модуль этой силы
Коэффициент трения между бруском и плоскостью
Модуль силы трения, действующей на брусок равен 2,8 Н. Чему равна масса бруска? Ответ приведите в килограммах.
3
Задания Д28 C1 № 704
Брусок массой движется поступательно по горизонтальной плоскости под действием постоянной силы, направленной вверх под углом
к горизонту. Модуль этой силы
Модуль силы трения, действующей на брусок равен 2,8 Н. Чему равен коэффициент трения между бруском и плоскостью? Ответ с точностью до первого знака после запятой.
4
Задания Д28 C1 № 705
Брусок массой движется поступательно по горизонтальной плоскости под действием постоянной силы F, направленной под углом
к горизонту. Коэффициент трения между бруском и плоскостью
Модуль силы трения, действующей на брусок равен 2,8 Н. Чему равен модуль силы F? Ответ приведите в ньютонах.
5
Задания Д28 C1 № 706
Коэффициент трения резины колес автомобиля об асфальт равен 0,4. При скорости движения водитель, во избежание аварии, должен придерживаться радиуса поворота, не меньшего, чем? Ответ приведите в метрах.
Пройти тестирование по этим заданиям
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
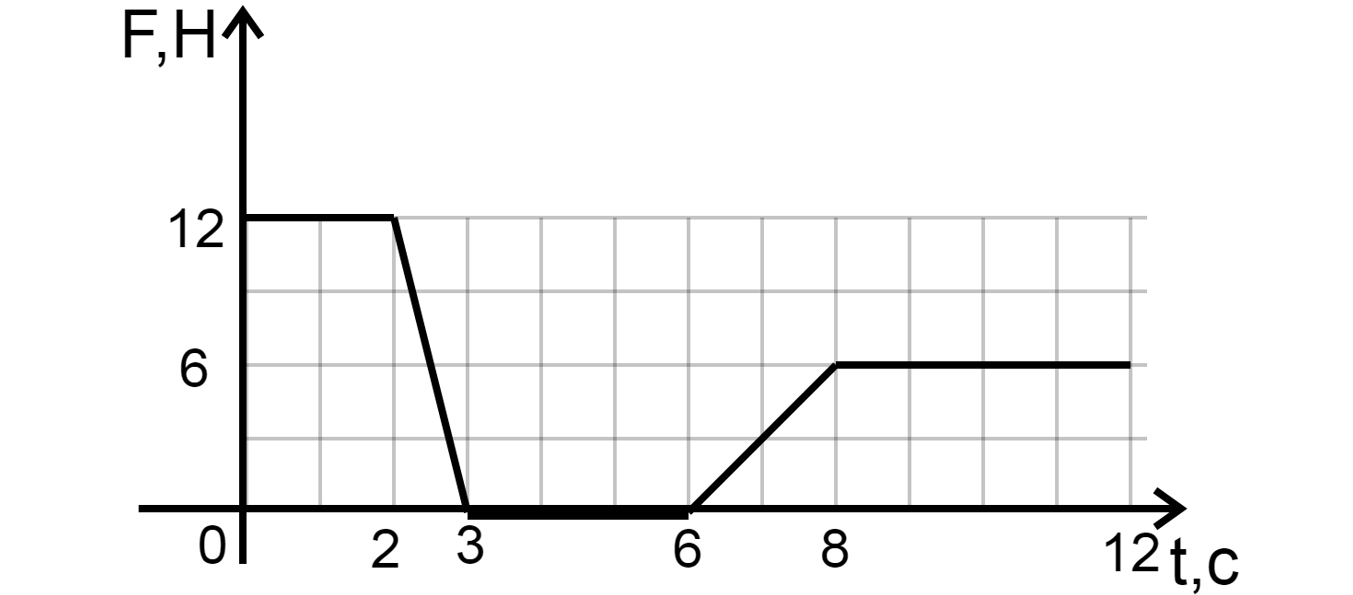
Мяч массой (m=1{,}5) кг движется вдоль горизонтальной оси (Ox) под действием горизонтальной силы (F). В начальный момент времени тело покоилось. График зависимости силы (F) от времени (t) изображён на рисунке. Чему равен импульс мяча в конце 4 секунды? (Ответ дайте в кг(cdot)м/с)
Воспользуемся законом изменения импульса: [sum F=frac{Delta p}{Delta t}] Тогда же, если сила постоянна, то импульс мы можем найти по следующей формуле: [p=F_1(t_2 — t_1) + F_2(t_3 — t_2) + F_3 (t_4 — t_3) = 4 cdot (1{,}5 — 0) + 0 cdot (3 — 1{,}5) + (-2) cdot (4 — 3) = 4 text{ кг$cdot$м/с}]
Ответ: 4
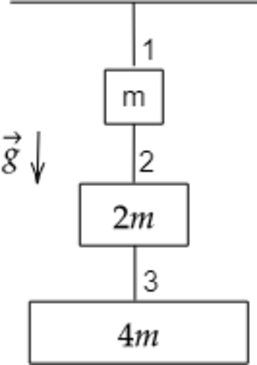
Три бруска массами m, 2m и 4m с помощью невесомых нерастяжимых нитей 1, 2 и 3 соеденены между собой и подвешены к потолку (см. рисунок). Система находится в равновесии. Чему равно отношение модулей сил натяжения нитей 1 и 3?
Масса, которая действует на нерастяжимую нить 1: [m_1=m+2m+4m] [m_1=7m] Масса, которая действует на нерастяжимую нить 3: [m_3=4m] На бруски действуют сила тяжести и сила натяжения нити. По 2 закону Ньютона: [T=mg] Сила натяжения нити для нити 1: [T_1=m_1g] [T_1=7mg] Сила натяжения нити для нити 3: [T_3=m_3g] [T_3=4mg] Тогда отношение модулей сил натяжения нитей 1 и 3: [frac{T_1}{T_3}=dfrac{7mg}{4mg}=1,75]
Ответ: 1,75
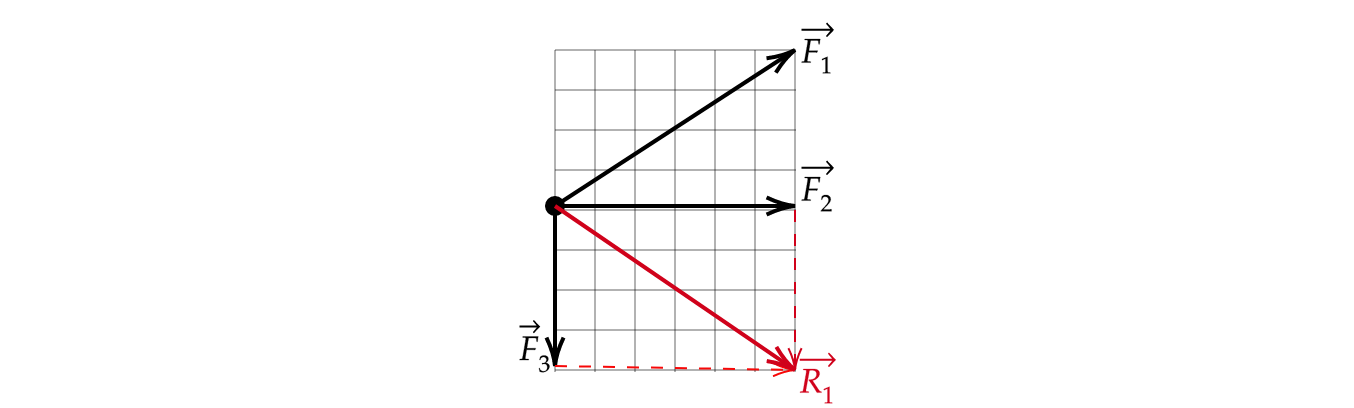
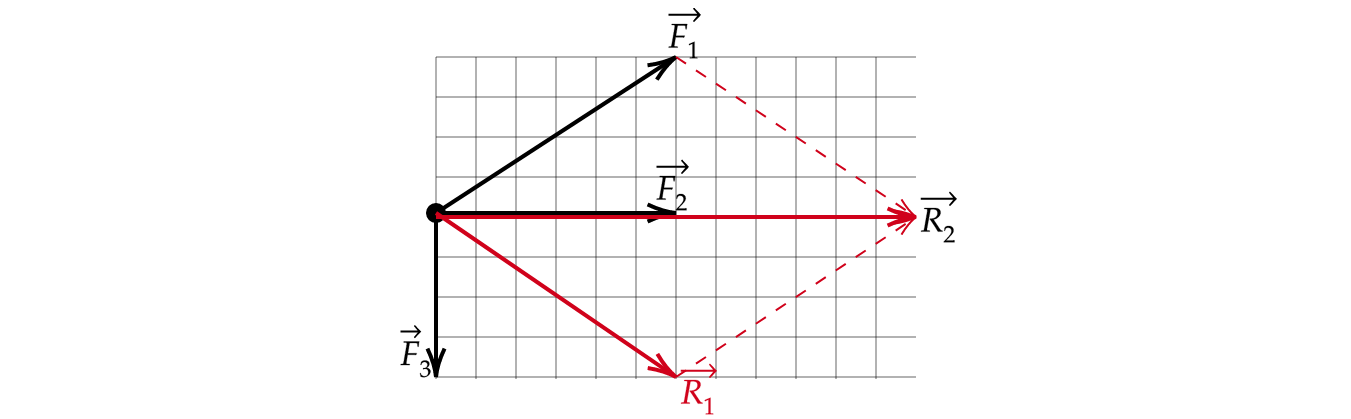
К телу было приложено две силы под углом (90^{circ}) друг к другу. Известно, что равнодействующая этих сил равна (F_text{равн}=10) Н, а одна из приложенных сил равна (F_1=6) Н. Чему равен модуль второй силы (F_2)?
Равнодействующая двух сил – это сумма двух сил: [vec{F}_text{равн}=vec{F}_1+vec{F}_2] Вспомним, что равнодействующая двух сил – это величина результирующего вектора. Изобразим силы на рисунке, воспользовавшись правилом параллелограмма: 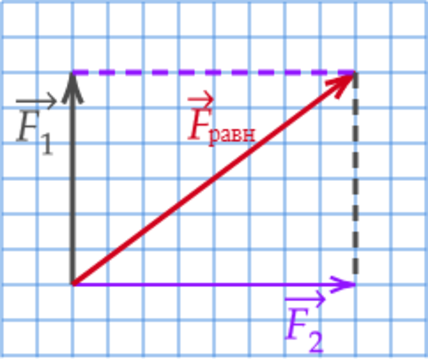
Ответ: 8
К телу было приложено две силы (F_1) и (F_2). Под действием одной силы (F_1) тело двигалось с ускорением (a_1=8) м/с(^2). Под действием другой силы, направленной противоположно силе (F_1), ускорение тела равно (a_2=5) м/с(^2). С каким ускорением тело будет двигаться при одновременном действии сил (F_1) и (F_2)? Ответ дайте в метрах в секундах в квадрате.
Рассмотрим действие силы (F_1) на тело. Спроецируем все силы, действующие на тело на ось (ox). Тогда, по 2-ому закону Ньютона: [F_1=ma_1] Аналогично с (F_2): [F_2=ma_2] Рассмотрим одновременное действие сил (F_1) и (F_2). Спроецируем все силы, действующие на тело на ось (ox). Тогда, по 2-ому закону Ньютона: [F_1-F_2=ma_3] Подставим (F_1) и (F_2) из предыдущих выражений, получаем: [ma_1-ma_2=ma_3] Разделим все выражение на (m), получим: [a_1-a_2=a_3] Подставим исходные значения: [a_3=8text{ м}text{$/c^2$}-5text{ м}text{$/c^2$}=3text{ м}text{$/c^2$}]
Ответ: 3
На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Определите модуль равнодействующей этих сил.

Складываем силы по правилу параллелограма (параллельно переносим каждую из сил в конец другой) и находим, что равнодействующая равна 3 Н.
Ответ: 3
На тело массой 2 кг действует сила 60 Н. Найдите ускорение тела “Основная волна 2020”
По второму закону Ньютона: [F=ma Rightarrow a=dfrac{F}{m}=dfrac{60text{ Н}}{2text{ кг}}=30text{ м/с$^2$}]
Ответ: 30
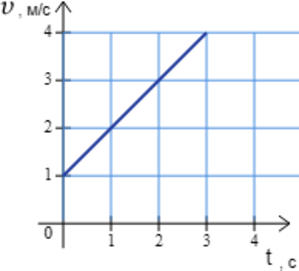
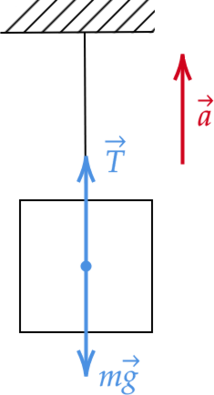
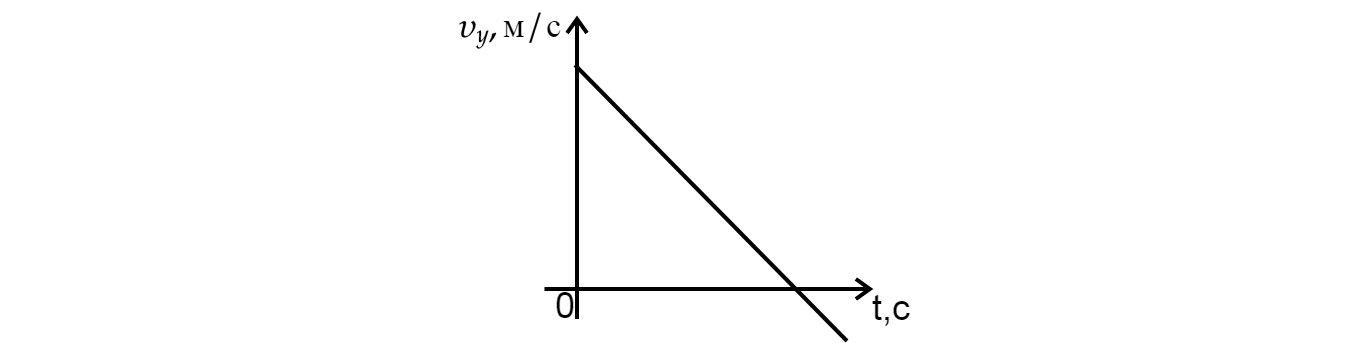
Ящик поднимают с помощью веревки вертикально вверх. На рисунке приведена зависимость проекции скорости (bfupsilon) ящика на ось, направленную вертикально вверх, от времени (t). Определите массу ящика, если известно, что сила натяжения веревки в течение подъёма равна 275 Н. Ответ выразите в кг.
Заметим(из графика), что скорость груза меняется линейно, следовательно тело движется с ускорением равным: [a=dfrac{upsilon-upsilon_{0}}{t}=dfrac{4text{ м/c$^2$}-1text{ м/c$^2$}}{3text{ c}}=1text{ м/c$^2 $}] Изобразим все силы, действующие на тело:
Спроецируем силы на ось (Oy) и воспользуемся 2 законом Ньютона: [T-mg=ma] [m(g+a)=T] [m=frac{T}{(g+a)}] Подставим в полученную формулу исходные значения: [m=dfrac{275text{ H}}{10text{ м/c$^2$}+1text{ м/c$^2$}}=25text{ кг }]
Ответ: 25

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Обучающие задания ЕГЭ по физике на тему «Динамика», с ответами — теория и практика
- 30.09.2013
Специально подобранные задания с учётом специфики КИМов ЕГЭ. К каждому заданию прилагается поясняющий комментарий, который помогает понять и разобрать задание. С этим материалом вы сможете безупречно изучить раздел физики «Динамика» и хорошо сдать егэ.
Все задания в конце файла содержат ответы.
Дополнительный материал по теме «Динамика»:
- Теория
- Обучающие задания
- Практические задания
- Контрольная работа
Смотреть в PDF:
Или прямо сейчас: Скачайте в pdf файле.
Материалы для подготовки к ЕГЭ по физике. Динамика.
Динамика (теория)
Сила () – векторная физическая величина, являющаяся количественной характеристикой действия одного тела на другое (или частей одного и того же тела).
Сила характеризуется: 1. модулем
2. направлением
3. точкой приложения
Равнодействующая (результирующая) сила (Σ) – сила, которая оказывает на тело такое же действие, как и несколько одновременно действующих сил, т.е. геометрическая сумма сил.
Σ = ++ … +
Инерция – явление сохранения скорости тела при отсутствии действия на него других тел (т.е. покой или прямолинейное равномерное движение)
Инерциальные системы отсчёта – системы отсчёта, относительно которых тело движется равномерно прямолинейно или покоится, если на него не действуют другие тела.
Инертность – свойство тел, характеризующее их способность сопротивляться изменению их скорости под воздействием силы.
Масса — мера инертности тел.
Механические силы.
1. Сила всемирного тяготения – сила, с которой все тела притягиваются друг к другу.
Природа – гравитационная.
Направление – вдоль линии, соединяющей центры тел.
Закон всемирного тяготения – все тела притягиваются друг к другу с силой, модуль которой прямо пропорционален произведению их масс и обратно пропорционален квадрату расстояния между ними. m1 m2
где m1, m2 – массы взаимодействующих тел,|F1| = |F2|
R – расстояние между их центрами,
G – гравитационная постоянная, G = 6,6710-11 R
Пределы применимости: 1. материальные точки.
2. однородные шары.
3. однородный шар большого радиуса и тело.
Сила тяжести – сила, с которой планета притягивает к себе
окружающие тела. h
Fтяж –частный случай закона всемирного тяготения
Природа – гравитационная.
Точка приложения – центр масс тела.
Направление – вертикально вниз (к центру Земли). Fтяж = mg
g – ускорение свободного падения, g =9,8 м/с2 ≈ 10 м/с2- для всех тел!
; — на поверхности планеты (Земли)
; — на высоте h от поверхности планеты (Земли),
где m – масса тела, M – масса планеты (Земли)
h – высота тела над поверхностью планеты (Земли)
Движение спутника вокруг планеты (Земли).
Fт =mац
h
R— 1-ая космическая скорость (старт с поверхности планеты)
Мm uз = 7,9
Rорб uh = ,гдеRорб. = R + h
2. Вес тела – сила, с которой тело давит на опору или растягивает подвес.
Природа – электромагнитная.
Точка приложения – опора или подвес.
Направление – противоположное силе реакции опоры
или силе натяжения нити.
= — (Р = N) — по третьему закону Ньютона
P = mgP = m(g+a) ↓↑ P = m(g-a)↑↑P = 0
если =const- направлено вверх- направлено вниз=
опора – горизонтальна,ац невесомость
подвес – вертикален ац
3. Сила упругости – сила, которая возникает при деформациях тела.
Природа – электромагнитная.
Точка приложения – тело.
Направление – противоположное направлению смещения частиц при деформации.
При упругих деформациях выполняется закон Гука – сила упругости, возникающая при деформации тела, прямо пропорциональна величине деформации и направлена против смещения частиц при деформации. Fупр l0 х
Fупр = —kx |x| = |l – l0|
|Fупр| = k|x|l
х – величина деформации. х
где k – коэффициент жесткости. [k] =
k ~ ,где s – площадь поперечного сечения жгута или троса.
Соединение пружин.
Последовательное
Параллельное
Колебание тела
k1k2
=++ … +
(х = х1 + х2 + … + хn)
k1
k2
k = k1+k2+ … + kn
F = F1 + F2 + … + Fn
k1k2
k = k1+k2
Виды сил упругости:
а) сила реакции опоры — перпендикулярна поверхности опоры.
б) сила натяжения нити — направлена вдоль нити (подвеса).
4. Силы трения – сила, возникающая при попытке перемещения одного тела по поверхности другого тела или при относительном движении тел.
Причины возникновения:
— шероховатости и неровности соприкасающихся поверхностей;
— межмолекулярное притяжение (прилипание поверхностей).
Природа – электромагнитная.
Приложена к обоим соприкасающимся телам.
Направление – вдоль поверхностей соприкасающихся тел, против скорости движения.
Виды сухого трения.
трение покоя
трение скольжения
трение качения
Fтр.покоя – сила трения, возникающая при движении соприкасающихся тел относительно друг друга, направленная вдоль поверхностей соприкосновения, что препятствует относительному движению тел.
Fтр.покоя = Fтяги , пока uотн.= 0
Fтр.покоя макс = µN – максимальное значение Fтр.покоя
Fтр.скольж. – сила трения, действующая между соприкасающимися телами, движущимися относительно друг друга.
Fтр.скольж= µN , где µ — коэффициент трения скольжения.Fтр.скольж ≈ Fтр.пок.max
Fтр не зависит от площади соприкасающихся поверхностей.
Еслиtgα = µ- скольжение
Fтр.кач. – сила, возникающая, когда одно тело катится по поверхности другого.
Fтр.скольж. » Fтр.кач.
Жидкое трение Fтр.жид. – сила трения, возникающая, когда тело движется соприкасаясь с жидкостью или газом.
Fтр.жид.« Fтр.сухое , т.к. в жидкости и газе нет силы трения покоя.
Fтр.жид. зависит от: размеров и формы тела, свойств среды, скорости относительного движения
5. Сила Архимеда
FA =ρжgVт
Законы Ньютона.
I законНьютона
II законНьютона
III законНьютона
Когда тело движется равномерно прямолинейно или покоится?
— если сумма действующих на тело сил равна нулю или силы отсутствуют.
если++ … +=0,( Σ =0),
то= constили = 0
Когда тело движется с ускорением?
— если действующие на тело силы не скомпенсированы.
Ускорение тела прямо пропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе.
=m= ++ … +
Особенности II закон Ньютона:
1. Для любых сил.
2. Сила причина ускорения и определяет ускорение.
3. Вектор сонаправлен с вектором Σт.е.↑↑
— Тело движется прямолинейно, если Σ= const по направлению.
— Тело движется по окружности, если Σ^
— Тело движется криволинейно при α ≠0и α ≠ 90°
Как взаимодействуют два тела?
Силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению.
= —
1)
2)SNNS
3)
Особенности III закон Ньютона:
1. Силы возникают только парами.
2. Силы одной природы.
3. Силы не уравновешивают друг друга, т.к. приложены к разным телам.
Границы применимости законов Ньютона: — для инерциальных систем отсчёта
— дляu « с
— для макроскопических тел
Алгоритм решения задач по теме «Динамика».
- Сделать чертеж по плану:
- Опора (если есть)
- Тело.
- Силы.
- Ускорение (если есть)
- Оси координат (х вдоль ).
- Проанализировать состояние объекта: покой, равномерное прямолинейное движение или равноускоренное движение. В зависимости от этого записать I или II закон Ньютона, описывающий условие данной задачи в векторной форме.
- Сделать проекции этого выражения на оси.
- Записать систему уравнений, добавив в неё при необходимости формулу силы трения или уравнения кинематики.
- Решить систему уравнений относительно неизвестной.
Далее вы найдете тренировочные задания по теме «Динамика» и ответы к этим заданиям.
1. После спуска с сортировочной горки железнодорожная платформа массой 9000 кг имела скорость 2 м/с и двигалась до полной остановки в течение 10с. Какова равнодействующая всех сил, действовавших на платформу?
Решение:
2. Лыжник массой 80 кг в конце спуска с горы приобрёл скорость 12 м /с и продолжал двигаться по горизонтальной поверхности. Через сколько времени он остановится, если сила трения, действующая на него, равна 16 Н ?
Решение:
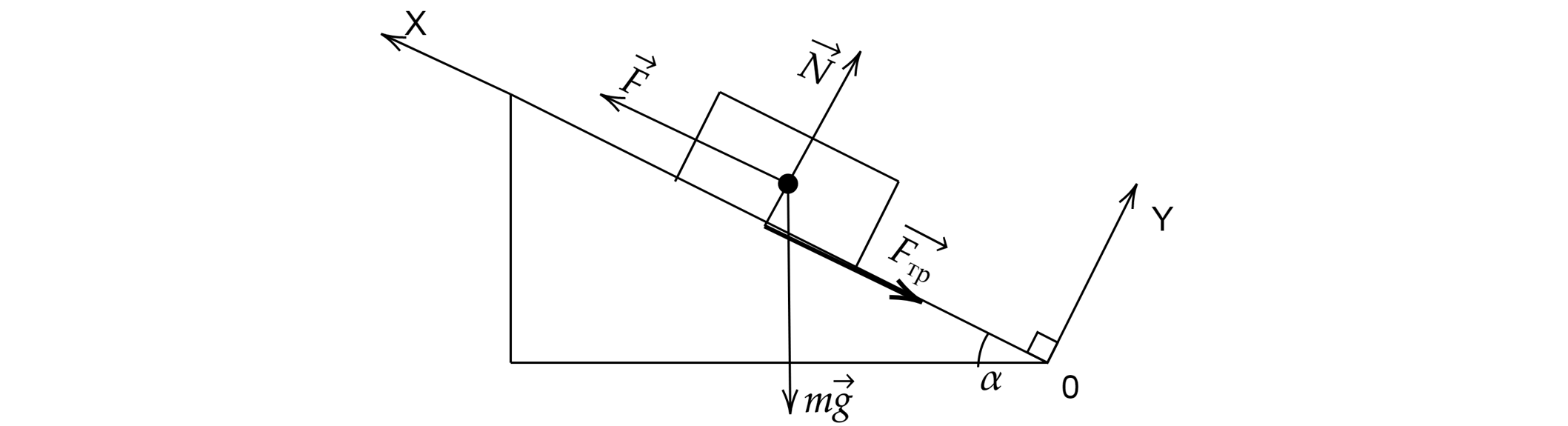
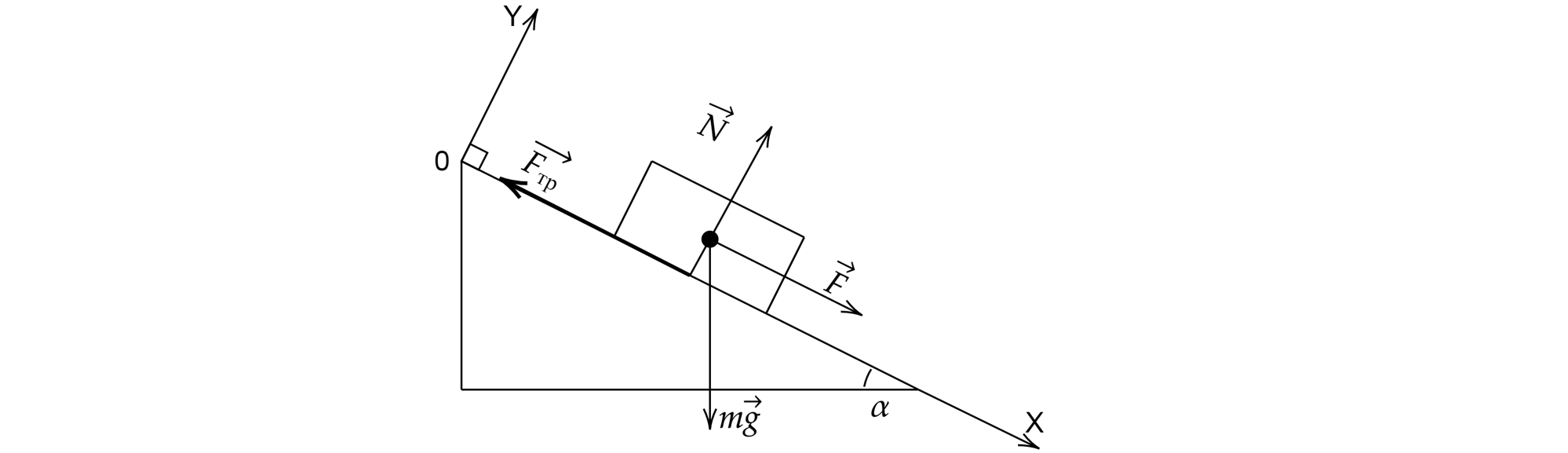
3. Брусок массой m тянут по полу с постоянной скоростью, действуя на него силой F, направленной под углом α к направлению движения. Ускорение свободного падения g. Чему равна вертикальная составляющая силы Fy с которой пол действует на брусок?
Решение:
Ответ:
4. Тело поднимают вверх по наклонной плоскости, прикладывая к нему горизонтальную силу, величина которой вдвое больше действующей на тело силы тяжести. Высота наклонной плоскости 3 м, её длина 5 м. Найдите ускорение тела, если коэффициент трения равен 0,2
Запишем второй закон Ньютона в проекции на направление плоскости в направлении действия силы F.
ma = Fcosα − mgsinα − Fmp,
где
Fmp = μN = μmgcosα + Fsinα.
Тогда
ma = Fcosα − mgsinα − μ(mgcosα + Fsinα). (1)
Учтем, что по условию задачи F = 2mg, а sinα = h/l, а cosα = √(l2 − h2)/l, подставляя в уравнение (1) и сокращая на массу, получим
a = 2g√(l2 − h2)/l − gh/l − μ(g√(l2 − h2)/l + 2gh/l).
Рассчитаем ускорение
a = 2•10•√(52 − 32)/5 − 10•3/5 − 0,2•(10•√(52 − 32)/5 + 2•10•3/5) = 6 м/с2.
Ответ: a = 6 м/с2.
Замечания: при решении задач такого типа, возможно проще будет, если мы рассчитаем отдельно sinα = 3/5 = 0,6 и cosα = √(52 − 32)/5 = 0,8. Тогда уравнение второго закона будет проще
ma = 0,8F − 0,6mg − μ(0,8mg + 0,6F)
или
a = 16 − 6 − 0,2(8 + 12) = 6 м/с2.
5. Вверх по наклонной плоскости высотой 9 м и длиной 15 м пущена шайба. Коэффициент трения равен 0,5. Найдите ускорение шайбы. В ответе укажите абсолютную величину ускорения.
На рисунке шайба движется вверх по наклонной плоскости. Ускорение шайбе сообщают приложенные к ней силы: сила тяжести и сила взаимодействия шайбы с плоскостью, которую для удобства разложим на две составляющие: силу трения и реакцию опоры. Запишем уравнение второго закона Ньютона в проекции на оси x и y:
ma = mgsinα + Fmp и 0 = N – mgcosα
С учетом того, что сила трения скольжения равна
Fmp = μN = μmgcosα,
получим
a = gsinα + μgcosα.
Где sinα = h/l = 0,6, а cosα = √(1 – (h/l) 2) = 0,8.
Вычислим
a = 10•0,6 + 0,5•10•0,8 = 10 м/с2.
Ответ: a = 10 м/с2.
6.По наклонной плоскости скользит с ускорением a = 1 м/с2 брусок массой m = 200 г. С какой силой F нужно прижимать брусок перпендикулярно наклонной плоскости, чтобы он начал двигаться равномерно? Коэффициент трения бруска о наклонную плоскость μ = 0,1.
Запишем уравнение второго закона Ньютона в проекции на направление осей x и y при движении с ускорением a:
ma = mgsinα − Fmp и 0 = N − mgcosα.
С учетом того, что сила трения скольжения равна
Fmp = μN = μmgcosα,
получим
ma = mgsinα − μmgcosα. (1)
При равномерном движении, силы вдоль направления движения по наклонной плоскости, компенсируют друг друга
mgsinα = Fmp = μ(mgcosα + F);. (2)
Сделаем замену (2) в (1)
ma = μ(mgcosα + F) − μmgcosα.
Откуда ma = μF и F = maμ.
Вычислим F = 0,2•1•0,1 = 2 Н.
Ответ: F = 2 Н.
7.На столе лежит деревянный брусок массой М = 2 кг, к которому привязана нить, перекинутая через блок, укрепленный на краю стола. К свободному концу нити подвешен груз массой m = 1 кг, вследствие чего брусок движется с ускорением а = 0,6 м/с2. Каковы будут ускорения груза и бруска, а также натяжение нити, если вся система будет: а) подниматься с ускорением а = 2,2 м/с2; б) опускаться с тем же по модулю ускорением?
Решение.
Запишем уравнение второго закона Ньютона
mg − μMg = (m + M)a. (1)
а) Если переносное ускорение системы a1, относительное ao, то уравнение второго закона Ньютона для груза имеет вид:
T − mg = m(a1 − ao), (2)
для бруска:
T − μN = Mao, (3)
и
N − Mg = Ma1. (4)
Модуль полного ускорения груза
aг = a1 − ao, (5)
бруска
aб = √{ao2 + a12}. (6)
Из уравнений (1) − (6) находим:
aг ≈ 1,46 м/с2; aб ≈ 2,3 м/с2; Т = 11,2 H.
б) aг ≈ 2,66 м/с2; aб ≈ 2,24 м/с2; Т ≈ 7 H.
8. С помощью прочного троса груз равноускоренно поднимают с поверхности земли вертикально вверх. Через Δt = 5,0 с после начала подъема груз уже находился на высоте h = 15 м, продолжая движение. Сила тяги подъемного механизма к этому моменту времени, когда тело достигло высоты h = 15 м, совершила работу А = 8,4 кДж. Определите массу поднимаемого груза.
Решение.
На груз действует сила тяги и сила тяжести.
По второму закону Ньютона
ma = Fтяг + mg. (векторно)
В проекции на вертикальную ось
ma = Fтяг − mg.
Откуда сила тяги
Fтяг = ma + mg.
Работа силы тяги
A = Fтягh = m(a + g)h. (1)
Из кинематики определим ускорение
h = aΔt2/2, a = 2h/Δt2. (2)
Из (1) выражаем искомую массу груза и подставляем ускорение из (2)
m = A/((2h/Δt2 + g)h).
Подставим численные значения
m = 8400/((2•15/52 + 10) × 15) = 50 (кг).
Ответ: масса поднимаемого груза 50 кг.
9. Брусок массой m = 2,0 кг движется без начальной скорости по горизонтальной поверхности под действием силы, модуль которой F = 10 Н, направленной параллельно этой поверхности. Коэффициент трения между бруском и поверхностью μ = 0,20. Через какой промежуток времени Δt, модуль скорости у тела станет равным v = 30 м/с.
Решение:
По второму закону Ньютона, ускорение получаемое телом есть результат приложенных к нему сил (равнодействующей силы).
Результирующая сила равна разности приложенной силы F и силы трения. Сила тяжести и реакция опоры направлены перпендикулярно к направлению движения тела.
a = (F − Fmp)/m = (F − μmg)/m. (1)
Воспользуемся уравнением скорости v = vo + at, при vo = 0, v = at. Искомое время t = v/a. После подстановки (1) получим
t = mv/( F – μmg).
После подстановки численных значений, имеем
t = 2•30/(10 − 0,2•2,0•10) = 10 (c).
Ответ: t = 10 c.
10. С какой минимальной силой нужно тянуть за веревку, чтобы равномерно перемещать сани массой m = 10 кг по горизонтальному асфальту, если коэффициент трения скольжения μ = 0,7?
Решение.
Запишем уравнения движения санок в проекциях на горизонтальное и вертикальное направления:
где α − угол между веревкой и горизонтом, а сила трения Fmp = μN.
Из написанной выше системы уравнений найдем силу натяжения веревки
Теперь проанализируем зависимость силы F от угла α. Санки будут двигаться равномерно, если горизонтальная составляющая силы реакции веревки Fcosα равна силе трения Fmp. Для обеспечения минимальности силы F веревку, казалось бы, надо тянуть горизонтально, так как в этом случае sinα = sin0° = 0. C другой стороны, желательно, чтобы угол α был побольше, так как в этом случае за счет увеличения вертикальной составляющей Fsinα, стремящейся приподнять санки, уменьшается их давление на опору и, соответственно, уменьшается сила трения. Таким образом, на результат влияют два конкурирующих фактора.
Представим зависимость F(α) в виде графика.
Из графика видно, что исследуемая функция имеет минимум. Для нахождения значений αmin и Fmin воспользуемся аналитическим методом. Функция F(α) минимальна, если знаменатель максимален. Обозначим его буквой y, найдем производную y по α и приравняем ее к нулю:
y/ = −sinα + μcosα = 0.
Отсюда, обозначив соответствующий угол αo, получим
tgαo = μ; αo = 35°.
Тогда
Используя соотношения
найдем искомую величину
11.На рисунке изображены три силы, которые подействовали на тело массой 1 кг, покоящееся в инерциальной системе отсчета. Если одна клеточка соответствует силе 10 Н, то тело тело будет двигаться … с модулем ускорением …
1) по направлению силы F2, 10 м/с2; 2) по направлению силы F3, 5 м/с2;
3) по направлению силы F1, 10 м/с2; 4) против направления силы F2, 10 м/с2;
5) тело будет покоится, 0 м/с2.
Решение.
Разложим вектора сил на направления осей x и y. Обратим внимание на то, что вдоль оси х, результирующая сил равна
Вдоль оси y результирующая сил равна
В результате действия трех сил тело будет двигаться по направлению оси x, т.е. по направлению силы F2, с ускорением равным
Выбираем правильным ответ 1) по направлению силы F2, 10 м/с2.
Тема 6.
Механика (установление соответствия)
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
механика (установление соответствия)
6.01Кинематика
6.02Динамика
6.03Законы сохранения в механике
6.04Статика
6.05Гидростатика
6.06Механические колебания и волны
Решаем задачи
Показать ответ и решение
А) Линейная скорость равна:
Б)
На шайбу действует сила трения и сила упругости пружины. Сила трения равна:
где
– сила реакции опоры.
Длина нерастянутой пружины равна , тогда сила упругости пружины равна:
При
этом и сила упругости и сила трения направлены в центр траектории, так как сила упругости пытается
вернуть пружины в нерастянутое положение, а сила трения препятствует вылету шайбы с поверхности
диска, следовательно, равнодействующая сила равна:
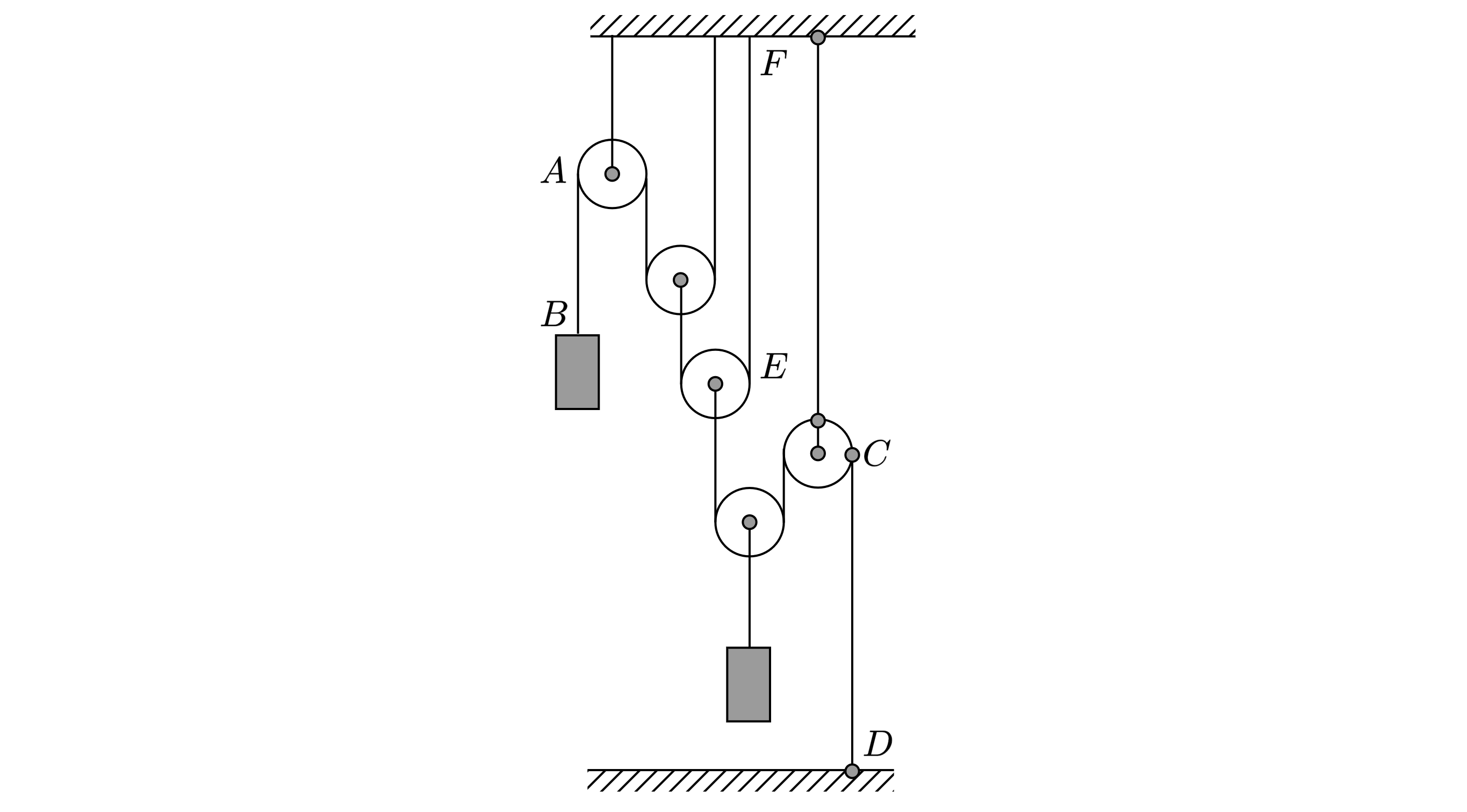
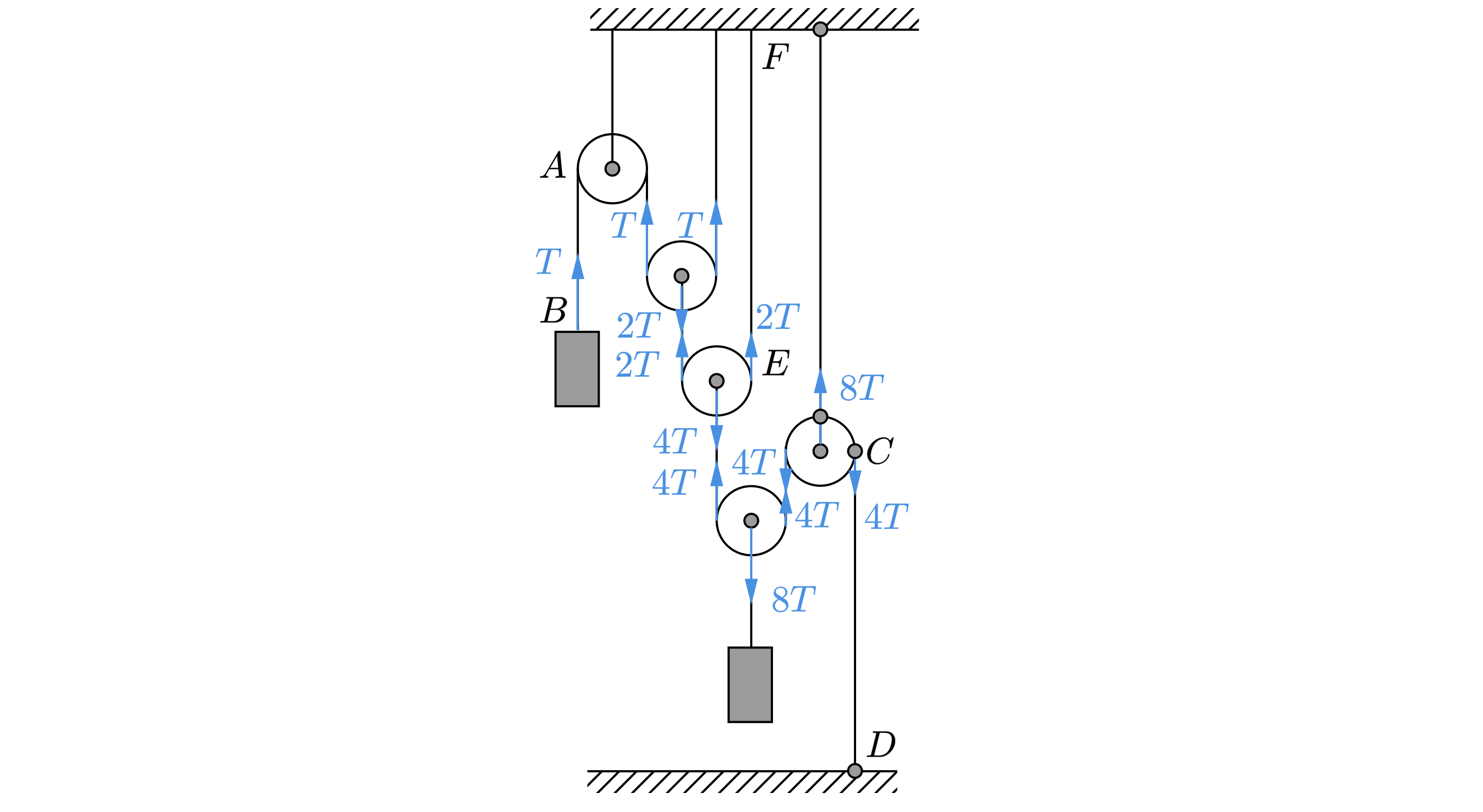
С помощью системы невесомых блоков на невесомых и нерастяжимых нитях уравновешены два груза
(см. рисунок). Модуль силы натяжения участка нити AB равен T. Установите соответствие между
модулями сил натяжения и участками нитей.
Показать ответ и решение
Так как блоки невесомы, то сумма сил действующих на каждый блок должна быть равна нулю,
тогда
Для участка –
, а для участка
–
.
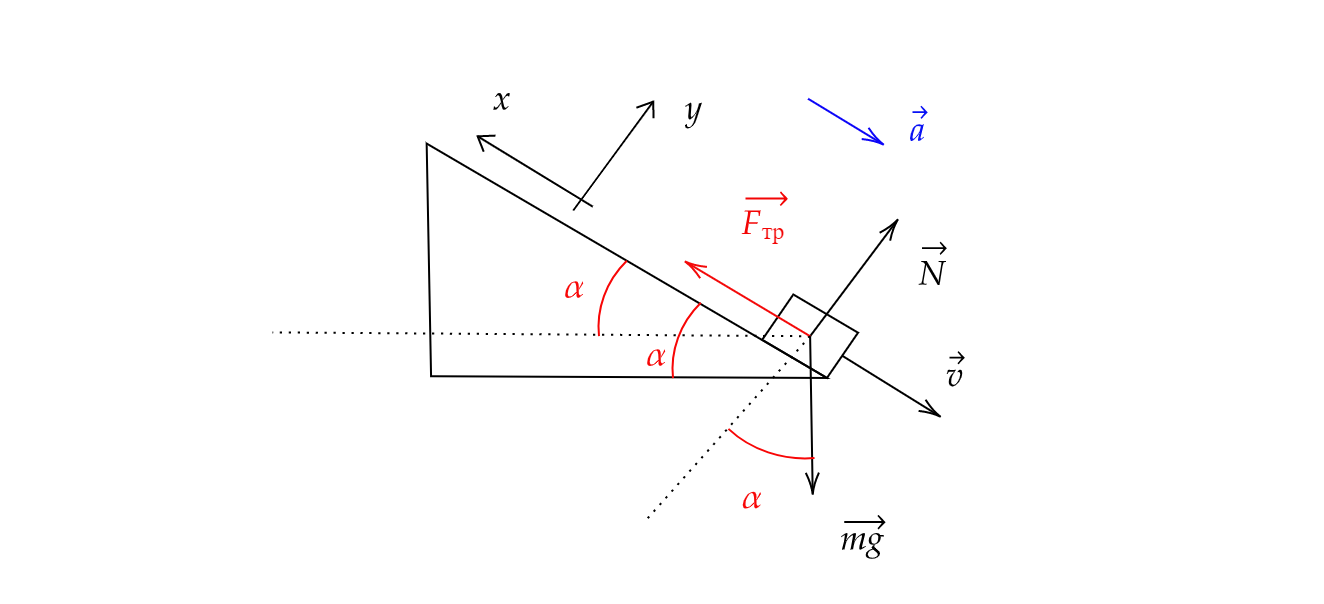
Брусок массой соскальзывает с закреплённой шероховатой поверхности наклонной плоскости с
углом при основании. Коэффициент трения между бруском и наклонной плоскостью равен
,
модуль скорости бруска возрастает. Сопротивлением воздуха пренебречь.
Установите соответствие между физическими величинами и формулами, при помощи
которых их можно вычислить. К каждой позиции первого столбца подберите соответствующую
позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими
буквами.
Показать ответ и решение
Запишем второй закон Ньютона
Спроецируем его на оси и
:
Так
как тело движется, то сила трения равна максимально возможной и равняется
А —
4
Из уравнения на ось найдем ускорение:
Б —
2
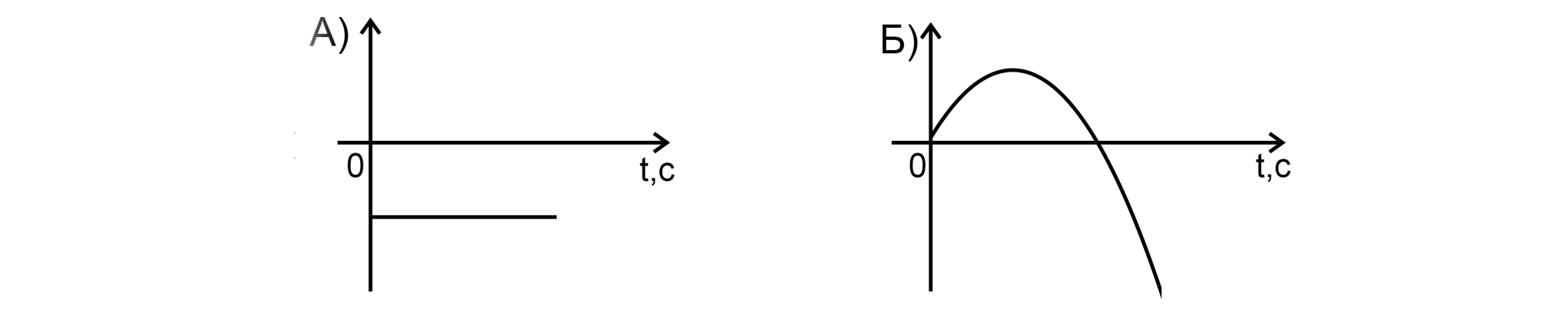
Мальчик кинул мячик так, что координата мячика по оси с течением времени
менялась по
закону: (все величины выражены в СИ).
Установите соответствие между графиками зависимости и величинами, зависимости которых от
времени они могут изображать. К каждой позиции первого столбца подберите соответствующую
позицию из второго. В ответ укажите последовательность цифр.
ГРАФИКИ:
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ:
1) Проекция перемещения тела,
2) Модуль равнодействующей всех сил,
3) Проекция ускорения,
4) Проекция скорости тела,
Показать ответ и решение
1) Основное уравнение кинематики
где
— начальная координата,
— проекция скорости на
,
— проекция ускорения на
.
2) Перемещение тела можно найти как разность начальной и конечной координат мячика:
Так
как это квадратное уравнение относительно переменной t, то его график — парабола, у которой ветви
вниз, ведь перед стоит минус. При чём в момент времени
координата по оси
равна нулю.
Это соответствует графику Б Б — 1.
3) Из уравнения видно, что проекция ускорения
график её зависимости от
времени — прямая, проходящая ниже нуля и параллельная
. Этому соответствует график А
А — 3.
4) Модуль равнодействующих всех сил равен:
Значит, график зависимости равнодействующей от времени
будет выглядеть так:
5) Так как скорость — это производная координаты по времени, то:
Значит, график зависимости проекции скорости на от времени будет выглядеть так:
Автомобиль движется вдоль оси , при этом его координата изменяется с течением времени в
соответствии с формулой (все величины выражены в СИ).
Установите соответствие между графиками и физическими величинами, зависимости которых от
времени эти графики могут представлять.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите
в таблицу выбранные цифры под соответствующими буквами.
1)
проекция скорости автомобиля
2) проекция перемещения автомобиля
3) проекция ускорения автомобиля
4) модуль равнодействующей сил, действующих на автомобиль.
Тело массой 200 г движется вдоль оси , при этом его координата изменяется во времени в
соответствии с формулой (все величины выражены в СИ). Установите соответствие
между физическими величинами и формулами, выражающими их изменения во времени. К каждой
позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу
выбранные цифры под соответствующими буквами.
Демоверсия 2021
Показать ответ и решение
А) Скорость – это первая производная от координаты:
Б)
Ускорение это производная от скорости
Сила
по определению равна
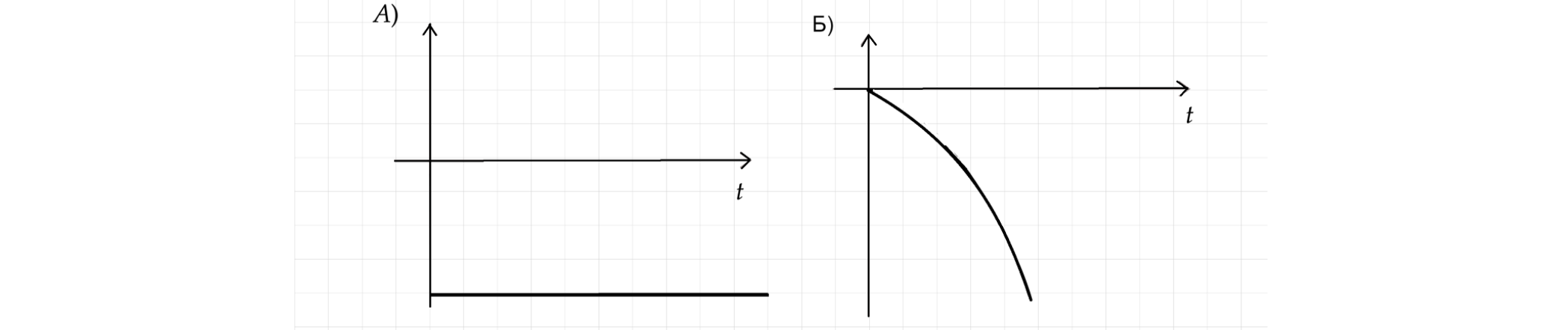
Тело массой кг движется под действием некоторых сил На рисунке приведён график
зависимости результирующей всех сил от времени
. Определите по графику ускорение тела в
период времени от 0 с до 2 с и от 3 с до 6 с.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца. В ответ
укажите последовательность цифр.
Показать ответ и решение
По второму закону Ньютона результирующая всех сил F равна:
Запишем это уравнение для первого и второго случаев соответственно:
Посчитаем нужные нам ускорения:
Спутник вращается вокруг Земли на расстояние . Масса спутника –
, а масса Земли –
,
–
гравитационная постоянная. Чему равны потенциальная энегия спутника и его скорость
?
К каждой позиции первого столбца подберите соответствующую позицию из второго. В ответ
укажите последовательность цифр.
Показать ответ и решение
1) Потенциальная энергия спутника массой , летающего на расстояние
от планеты определяется
формулой:
А — 1
2) На спутник действует сила гравитации. По второму закону Ньютона:
где — ускорение спутника, при чём так как он движется по окружности, то:
Б — 2
Грузик подвесили к лёгкой пружинке, прикреплённой к потолку. Система находится в равновесии. На
рисунках изображены графики зависимости некоторых физических величин от других величин.
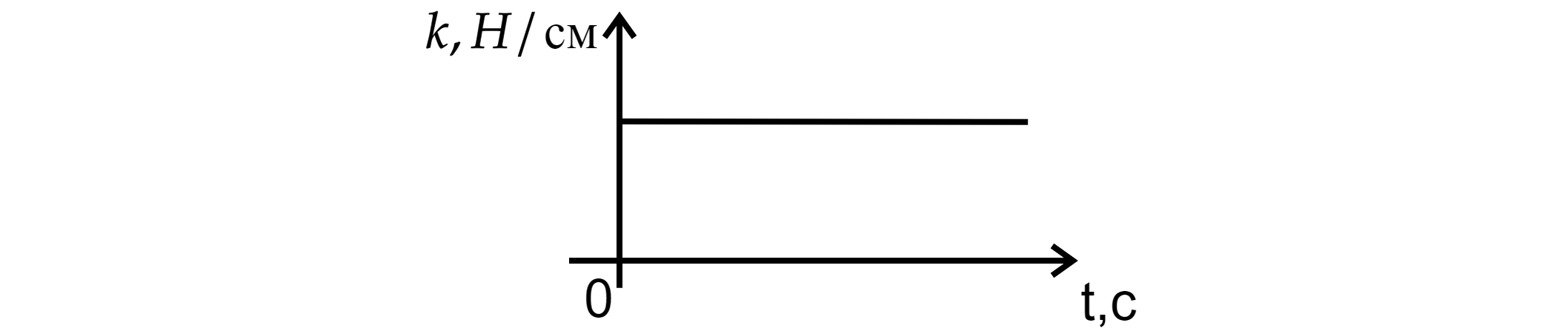
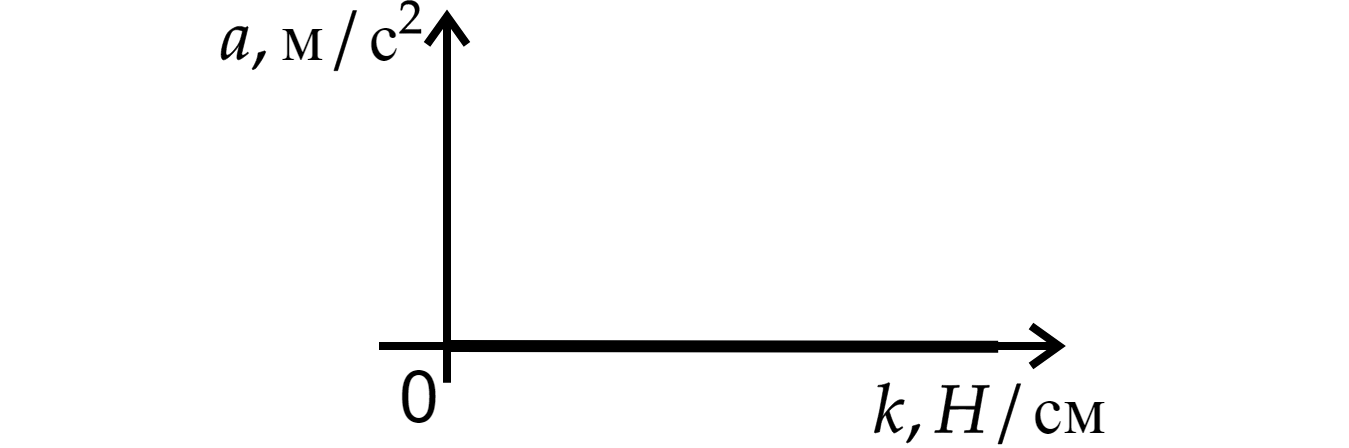
Определите, какие зависимости могут изображать эти графики?
К каждой позиции из первого столбца подберите соответствующую позицию из второго. В ответ
укажите последовательность цифр
ГРАФИКИ:
ЗАВИСИМОСТИ:
1) Растяжение пружинки от жёсткости,
2) Жёсткость пружинки от времени,
3) Ускорение тела от жёсткости пружинки,
4) Сила упругости от растяжения пружинки,
Показать ответ и решение
1) По закону Гука сила уругости равна:
Значит, график зависимоти – гипербола, что соответсвует графику Б
Б –
1
2) Время никак не влияет на жёсткость пружины (это видно из закона Гука, п.1), следовательно,
график зависимости – прямая, параллельная оси Ох.
3) Так как система в равновесии, то ускорения у грузика нет, при любых значениях жёсткости
ускорение .
4) По закону Гука сила упругости равна:
Значит, сила F зависит от растяжения линейно, что соответствует графику А
А —
4.
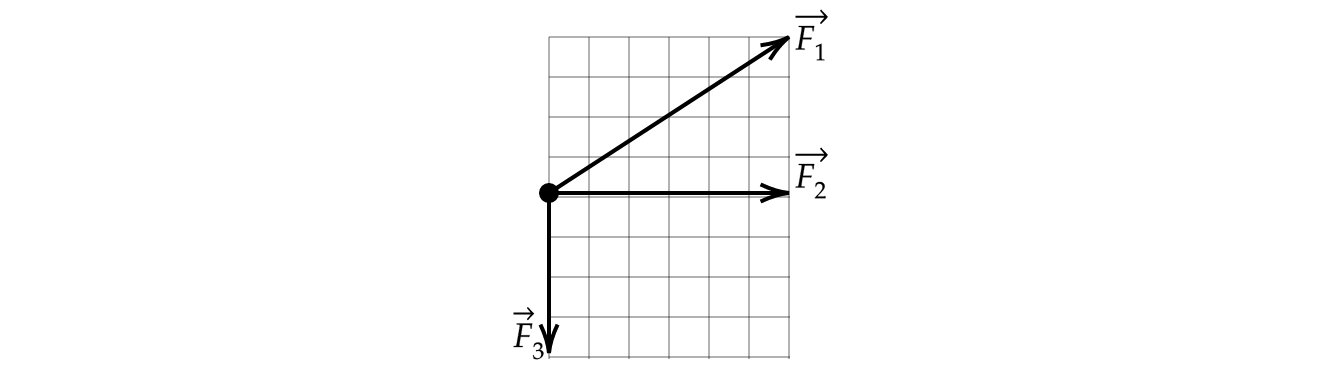
На рисунке изображены векторы, которые приложены к одному точечному телу. Сторона клетки равна
1 Н. Найдите равнодействующую всех сил и ускорение тела
, если его масса
кг. (все силы
находятся в одной плоскости)
Каждой позиции первого столбца подберите соответствующую позицию из второго столбцa, в ответ
укажите последовательность цифр.
Показать ответ и решение
А – 1
Равнодействующая всех сил равна векторной сумме всех сил. Найдём равнодействующую сил
и
:
Теперь найдём равнодействующую сил
и
:
По рисунку видно, что H.
Б – 3
По второму закону Ньютона:
Мальчик тянет равномерно санки массой сначала вниз по горке, а потом – вверх с постоянной силой.
Угол наклона плоскости к горизонту . Коэффициент трения горки о санки равен
.
Определите, по каким формулам можно найти силу , с которой тянет мальчик вверх и
вниз?
Каждой позиции первого столбца подберите соответствующую позицию из второго столбца, в ответ
укажите последовательность цифр.
Показать ответ и решение
А – 1
Рассмотрим силы, действующие на санки:
По второму закону Ньютона:
Спроецируем на оси и
:
По определению сила трения равна:
Отсюда:
Б – 3
Рассмотрим силы, действующие на санки:
По второму закону Ньютона:
Спроецируем на оси и
:
По определению сила трения равна:
Отсюда:
Предлагаю решение нескольких задач из книги «Отличник ЕГЭ. Физика. Решение сложных задач». Возможно, в дальнейшем на сайте появятся и решения других задач из этой книги. Задачи интересные, и все как одна «решабельные», то есть никаких подвохов в них нет.
Задача 1.
Шайба, брошенная вдоль наклонной плоскости, скользит по ней, двигаясь вверх, а затем движется вниз. График зависимости модуля скорости шайбы от времени дан на рисунке. Найти угол наклона плоскости к горизонту.
К задаче 1
Так как график составлен из двух отрезков прямых, то ускорение шайбы постоянно на обоих отрезках. Определим его. При движении вверх скорость шайбы изменилась с 6 м/с до 0 за 4 с, следовательно, ускорение равно м/с
. На пути вниз скорость шайбы с нуля доросла до 4 м/с за 4 с, следовательно, ускорение равно
м/с
.
К задаче 1 — движение вверх
К задаче 1 — движение вниз
Реакция опоры при движении шайбы равна
От реакции опоры напрямую зависит сила трения. Запишем уравнение по второму закону Ньютона для движения шайбы вверх (сразу учтем, что ускорение отрицательно, поскольку шайба тормозит):
Запишем уравнение по второму закону Ньютона для движения шайбы вниз:
Складывая уравнения, имеем:
Откуда
Ответ: .
Задача 2.
Два шарика одинакового диаметра, имеющие массы г и
г, связаны между собой легкой нерастяжимой нитью, длина которой значительно превышает диаметр шариков. Шарики сбросили с достаточно большой высоты. Спустя некоторое время после этого вследствие сопротивления воздуха скорость падения шариков стала постоянной. Найти натяжение нити Т при установившемся падении шариков. Ускорение свободного падения
м/с
.
К задаче 2
Шарики при падении «выстроятся»: снизу расположится более тяжелый, за ним «потянется» более легкий. «Потянется» в прямом смысле, посредством нити.
Для первого шарика уравнение для установившегося движения:
Для второго шарика:
Складывая, имеем:
Подставим в любое уравнение полученную силу сопротивления:
Ответ: Н.
Задача 3.
Два одинаковых груза массой кг связаны между собой нитью, перекинутой через блок с неподвижной осью. На один из грузов кладут перегрузок массой
кг. С какой силой Р будет давить перегрузок на груз
? Массой блока и нити, а также трением в оси блока пренебречь, нить считать нерастяжимой‚ ускорение свободного падения принять равным
м/с
.
К задаче 3
Запишем уравнение по второму закону для груза с перегрузком:
Для груза без перегрузка:
Из второго уравнения имеем :
Подставим в первое:
Теперь, зная ускорение, легко отыщем силу давления перегрузка на груз:
Ответ: .
Задача 4.
В системе, показанной на рисунке, грузы массами кг и
кг прикреплены к концам невесомой нерастяжимой нити. На такой же нити, один конец которой закреплен, а другой прикреплен к грузу массой
, висит подвижный блок. К оси этого блока на легких нерастяжимых нитях подвешен груз массой
кг. Отрезки нитей, не лежащие на блоках, вертикальны. Пренебрегая трением и массой блоков, найти модуль и направление ускорения груза
. Ускорение свободного падения принять равным
м/с
.
К задаче 4
Это одна из задач, решение которых строится на факте нерастяжимости нити. Именно этот факт будет важен, так как решение будем основывать на том, что сумма путей, пройденных грузами, постоянна, и максимально равна длине нити. Пусть координаты грузов по оси
,
и
соответственно. Пусть в некоторый момент времени их координаты стали
,
и
. Путь, пройденный телом 1:
А нить при этом «сократилась» на .
Путь, пройденный телом 2:
А нить при этом «сократилась» на .
Путь, пройденный телом 3:
А нить при этом «удлинилась» на .
Запишем пути, пройденные телами, через их ускорения:
Можно записать, что
Следовательно, ускорения тел 2 и 3 одинаковы, , а у тела 1 тогда
.
Теперь можно перейти к динамике. Запишем уравнения по второму закону Ньютона для всех тел. При этом обратим внимание, что разные участки нити будут по-разному натянуты. Это происходит из-за наличия груза 2, он является своеобразным «перегрузком»:
Силы
Перейдем везде к ускорению , ведь оно – искомое:
Из последнего уравнения
А из первого
Тогда, подставляя все во второе, получим:
«Минус» указывает направление ускорения: оно направлено вверх, против .
Ответ: м/с
, направлено вверх.
Задача 5.
Через гладкий блок, закрепленный на гладкой неподвижной наклонной плоскости, составляющей с горизонтом угол , перекинута легкая нерастяжимая нить. Один конец нити прикреплен к бруску массой
кг, лежащему на плоскости, а свисающий конец пропущен через узкое отверстие в грузе массой
кг, как показано на рисунке. Если одновременно отпустить брусок и груз, нить будет проскальзывать через отверстие с постоянным ускорением
м/с
относительно груза. Найти силу
натяжения нити. Ускорение свободного падения принять равным
м/с
.
К задаче 5
Запишем уравнение по второму закону для обоих грузов:
Теперь определимся с ускорениями: так как нить проскальзывает относительно груза , то
Тогда, подставляя силу натяжения нити, имеем:
Теперь можно определять силу натяжения:
Ответ: Н
Задача 6.
Маленькую шайбу массой г запустили со скоростью
м/с в направлении по касательной к внутренней поверхности находящейся в невесомости сферы массой
г и радиусом
м. Найдите модуль силы, действующей на шайбу со стороны сферы. Трение отсутствует, сфера вначале покоилась.
По закону сохранения импульса
Если перейти в систему отсчета «сфера», то скорость шайбы в ней будет равна
Известно, что при движении по окружности угловая скорость такого движения равна , следовательно,
Угловая скорость через период:
Период – время одного оборота:
Следовательно,
Аналогично
Теперь можем найти, с какой силой шайба будет давить на сферу:
Ответ: Н.
Задача 7.
На горизонтальном диске на расстоянии см от оси лежит маленькая шайба. Диск медленно раскручивают так, что его угловая скорость равномерно возрастает со временем. Через время
с после начала раскручивания шайба начала скользить по диску. Найти коэффициент трения шайбы о диск, если за время
диск сделал
оборотов.
К задаче 7
Сила трения удерживает шайбу от соскальзывания. Однако диск разгоняется, следовательно, есть тангенциальное ускорение, и скорость шайбы растет, что вызывает рост нормального ускорения. Наконец, общее ускорение становится столь большим, что сила, им обусловленная, превышает силу трения, и шайба соскальзывает.
Условие соскальзывания
Где .
Выясним, каковы нормальное и тангенциальное ускорения.
Скорость шайбы растет и становится равной к моменту соскальзывания. Угловая скорость становится равной
за то же время. Тогда
Путь, пройденный телом – пять кругов – равен .
Угловая скорость определяет, какой угол преодолело тело за промежуток времени. У нас пять кругов, следовательно, тело прошло радиан за время
, тогда
Нормальное ускорение тела
В свою очередь, полное ускорение равно
Тогда
Ответ: .
2 комментария
Никита
✉️
26.01.2019 20:10:12
добрый вечер, в задаче № 3 в разделе сложных задач по динамике, я думаю что формула силы давления в данном случае будет иметь вид P= m*(g+a), а не P= m*(g-a) , так как ускорение груза с перегрузом будет направлено вниз . Если я не прав, прошу объяснить в чем моя ошибка.
Анна Валерьевна
✨
27.01.2019 12:26:31
[latexpage]
Конечно, ускорение направлено вниз. Поэтому для перегрузка можно записать
$$ma=mg-N$$
Или
$$N=mg-ma=m(g-a)$$
По третьему закону сила реакции опоры равна силе, с которой перегрузок давит на груз.