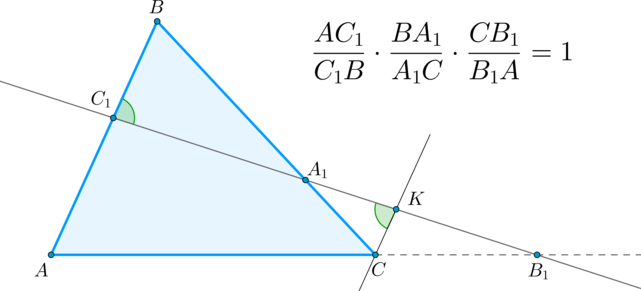
(blacktriangleright) Теорема Менелая: пусть прямая пересекает треугольник в точке (C_1) на стороне (AB), в точке (A_1) на стороне (BC) и в точке (B_1) на продолжении стороны (AC). Тогда имеет место следующее соотношение:
Доказательство: Проведем через точку (C) прямую параллельно (AB). Пусть она пересечет (A_1B_1) в точке (K). Тогда по двум углам (triangle A_1BC_1sim triangle A_1KC Rightarrow)
(dfrac{C_1B}{CK}=dfrac{BA_1}{A_1C}) или (dfrac{BA_1cdot CK}{A_1Ccdot C_1B}=1 (*))
Т.к. (triangle AB_1C_1sim triangle CKB_1 Rightarrow )
(dfrac{CK}{AC_1}=dfrac{B_1C}{AB_1}), откуда (CK=dfrac{B_1Ccdot
AC_1}{AB_1})
Подставив последнее равенство в ((*)) и сгруппировав множители, получим требуемое равенство.
(blacktriangleright) Теорема, обратная теореме Менелая: пусть в треугольнике точка (B_1) лежит на продолжении стороны (AC), а точки (A_1, C_1) — на сторонах (BC) и (AB) соответственно. Тогда, если выполнено равенство [dfrac{AB_1}{B_1C}cdot dfrac{CA_1}{A_1B}cdot dfrac{BC_1}{C_1A}=1,] то точки (A_1, B_1, C_1) лежат на одной прямой.
Доказательство: Предположим, что эти три точки не лежат на одной прямой. Тогда прямая (A_1B_1) пересечет сторону (AB) в точке (C_2), отличной от точки (C_1). Тогда по теореме Менелая для точек (A_1, B_1, C_2) будет выполнено равенство:
(dfrac{AB_1}{B_1C}cdot dfrac{CA_1}{A_1B}cdot
dfrac{BC_2}{C_2A}=1)
Сравнивая это равенство с равенством из условия, получим, что (dfrac{BC_2}{C_2A}=dfrac{BC_1}{C_1A}),
то есть точки (C_1) и (C_2) поделили отрезок (AB) в одинаковом соотношении. Значит, эти точки совпадут.
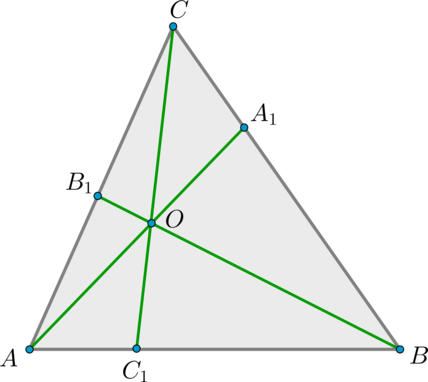
Теорема Чевы: пусть на сторонах треугольника (ABC) выбраны точки (A_1in BC, B_1in AC, C_1in AB). Отрезки (AA_1, BB_1, CC_1) пересекаются в одной точке тогда и только тогда, когда выполнено равенство [{large{dfrac{AB_1}{B_1C}cdot dfrac{CA_1}{A_1B}cdot
dfrac{BC_1}{C_1A}=1}}]
Доказательство:
1) Докажем, что из пересечения отрезков следует данное равенство:
Применим теорему Менелая для (triangle ABB_1) и прямой (CC_1):
(dfrac{AC_1}{C_1B}cdot dfrac{BO}{OB_1}cdotdfrac{B_1C}{CA}=1)
Применим теперь теорему Менелая для (triangle BB_1C) и прямой (AA_1):
(dfrac{BA_1}{A_1C}cdot dfrac{CA}{AB_1}cdot dfrac{B_1O}{OB}=1)
Перемножив полученные два равенства, получим:
(dfrac{AB_1}{B_1C}cdotdfrac{CA_1}{A_1B}cdotdfrac{BC_1}{C_1A}=1)
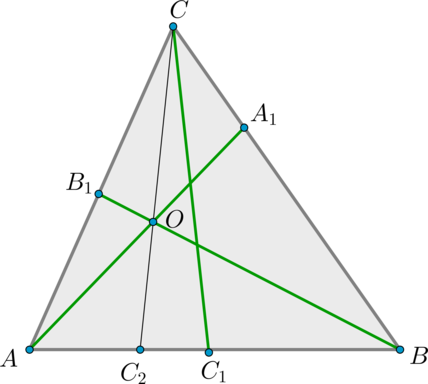
2) Докажем, что из данного равенства следует, что отрезки пересекутся в одной точке:
Предположим, что отрезок (CC_1) не проходит через точку (O). Тогда проведем отрезок (CC_2) через точку (O). Т.к. три отрезка (AA_1,
BB_1, CC_2) пересеклись в одной точке, то для них верно:
(dfrac{AB_1}{B_1C}cdotdfrac{CA_1}{A_1B}cdotdfrac{BC_2}{C_2A}=1)
Сравнивая полученное равенство с равенством из условия, заключаем, что
(dfrac{BC_2}{C_2A}=dfrac{BC_1}{C_1A}), т.е. точки (C_1) и (C_2) поделили отрезок (AB) в одинаковом отношении. Это возможно только в том случае, когда эти точки совпадают, т.е. (C_1=C_2).
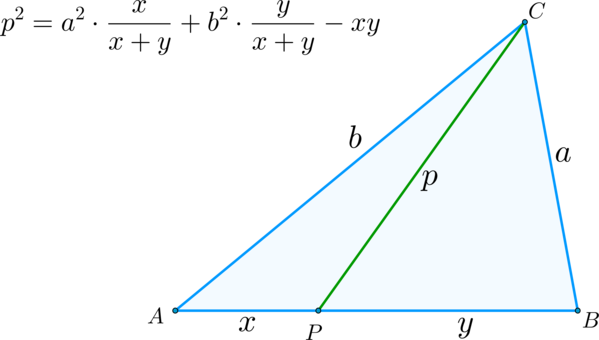
(blacktriangleright) Теорема Стюарта: пусть в треугольнике на стороне (AB) отмечена точка (P).
Тогда, если (CP=p, AP=x,
BP=y,AC=b, BC=a), верно следующее соотношение:
Доказательство: Рассмотрим (triangle ABC): по теореме косинусов имеем
(a^2=b^2+(x+y)^2-2b(x+y)cos angle A Rightarrow cosangle
A=dfrac{b^2+(x+y)^2-a^2}{2b(x+y)})
Рассмотрим (triangle ACP):
(p^2=b^2+x^2-2bxcos angle A Rightarrow cosangle
A=dfrac{b^2+x^2-p^2}{2bx})
Следовательно: (dfrac{b^2+x^2-p^2}{2bx}=dfrac{b^2+(x+y)^2-a^2}{2b(x+y)}
Rightarrow dfrac{b^2+x^2-p^2}{x}=dfrac{b^2+(x+y)^2-a^2}{x+y}), откуда получаем равенство из условия.
(blacktriangleright) С помощью теоремы Стюарта выводятся формулы нахождения биссектрис и медиан треугольника:
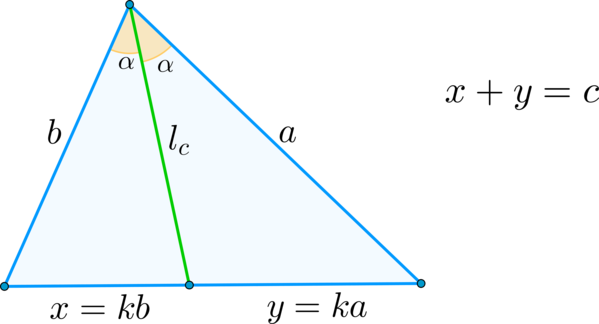
I. Если (l_c) — биссектриса, проведенная к стороне (c) и разбивающая эту сторону на отрезки (x) и (y), а (a,b) — две другие его стороны, то [{large{l^2_c=ab-xy}}]
Действительно, т.к. (l_c) — биссектриса, то она делит сторону (c) на отрезки, пропорциональные прилежащим сторонам, т.е.
(dfrac{x}{y}=dfrac{b}{a})
Следовательно, можно принять (x=kb, y=ka), где (k) — этот коэффициент пропорциональности.
Запишем теорему Стюарта:
(l^2_c=a^2cdot dfrac x{x+y}+b^2cdot dfrac
y{x+y}-xy=dfrac{a^2kb}{k(a+b)}+dfrac{b^2ka}{k(a+b)}-xy=dfrac{kab(a+b)}{k(a+b)}-xy=ab-xy)
II. Если (m_c) — медиана, проведенная к стороне (c) треугольника, а (a,b) — две другие его стороны, то [{large{m^2_c=dfrac{2a^2+2b^2-c^2}4}}]
Действительно, т.к. (m_c) — медиана, то (x=y). Подставив это в равенство Стюарта, получим формулу вычисления медианы треугольника.
Слайд 1
Проектно –исследовательская работа : « Полезные формулы для вычисления чевиан треугольника » Номинация: Геометрическая миниатюра Работу выполнили: Уртаев Эдуард Плиева Камилла ученики 8 класса МКОУ СОШ с. Н.Батако Научный руководитель: Гагиева А.О.
Слайд 2
Цели исследования: Сбор и систематизация общих формул для нахождения замечательных элементов треугольника. Сведение результатов таблицу. Актуальность исследования: Полученные формулы можно применять при решении любых заданий школьного курса, прикладных задач, в том числе при сдаче ЕГЭ и ОГЭ. Предмет исследования широко применяется во многих научных дисциплинах: физике, черчении, моделировании и т.д.
Слайд 3
ВВЕДЕНИЕ Геометрия начинается с треугольника. В школьном курсе ученик получает знания, позволяющие ему из трёх известных элементов треугольника найти оставшиеся три – «решить» треугольник. Однако полученных знаний порой не хватает для рационального решения задач не только в дальнейшей школьной программе, но на экзаменах ОГЭ и ЕГЭ , не говоря уже о собственных научных проектах учащихся, например по физике. В задачах на метрические соотношения в треугольнике часто приходится одну из вершин треугольника соединять с некоторой точкой противоположной стороны или её продолжением и вычислять длину отрезка, соединяющего вершину треугольника с этой точкой. Для всех подобных задач можно указать очень простой и в то же время общий способ решения, основанный на предложении, содержащем одно из самых общих свойств треугольника. Это предложение известно под названием теоремы Стюарта. Эта теорема значительно упрощает решение многих задач на вычисление сторон, медиан и биссектрис треугольника. Мы решили собрать формулы для нахождения элементов треугольника, часто встречающихся в задачах, таких как расстояние между ними, медиана, биссектриса, высота или любая другая чевиана .
Слайд 4
Содержание: 1. Формулы высоты треугольника 2. Формулы высоты из прямого угла в прямоугольном треугольнике 3. Формулы высоты, медианы, биссектрисы равнобедренного треугольника 4. Теорема Стюарта 4.1 Длина биссектрисы, проведенной из прямого угла на гипотенузу. 4.2 Длина биссектрисы, проведенной из острого угла на катет 4.3 Формулы биссектрисы в произвольном треугольнике 4.4 Формулы медианы произвольного треугольника 4.5 Формулы медианы прямоугольного треугольника 4.6 Задачи Заключение Использованная литература
Слайд 5
Чевиана — это любой отрезок в треугольнике, один конец которого является вершиной треугольника, а другой конец лежит на противоположной вершине стороне. Медианы, высоты и биссектрисы являются специальными случаями чевиан . а,в,с — чевианы треугольника MNK в а с M N K
Слайд 6
Формулы высоты треугольника H — высота треугольника a — сторона, основание b , c — стороны β , γ — углы при основании p — полупериметр, p= ( a+b+c )/2 R — радиус описанной окружности S — площадь треугольника Формула длины высоты через сторону и угол Формула длины высоты через стороны и радиус, описанной окружности Формула длины высоты через стороны
Слайд 7
Формулы высоты из прямого угла в прямоугольном треугольнике H — высота из прямого угла a , b — катеты с — гипотенуза c 1 , c 2 — отрезки полученные от деления гипотенузы, высотой α , β — углы при гипотенузе Формула длины высоты через стороны Формула длины высоты через гипотенузу и острые углы Формула длины высоты через катет и угол
Слайд 8
Формулы высоты, медианы, биссектрисы равнобедренного треугольника L — высота = биссектриса = медиана a — равные стороны треугольника b — основание α — равные углы при основании β — угол образованный равными сторонами
Слайд 9
Теорема Стюарта: Квадрат любой чевианы равен отношению суммы произведения квадратов боковых сторон на несмежные с ними отрезки основания к длине основания без произведения этих отрезков
Слайд 10
Теорема Стюарта Если даны треугольник ABC и на его основании BC точка D , лежащая между точками B и C , то имеет место равенство:
Слайд 11
Длина биссектрисы, проведенной из прямого угла на гипотенузу: L — биссектриса, отрезок ME , исходящий из прямого угла (90 град) a , b — катеты прямоугольного треугольника с — гипотенуза α — угол прилежащий к гипотенузе Формула длины биссектрисы через катеты, ( L ): Формула длины биссектрисы через гипотенузу и угол, ( L ):
Слайд 12
Длина биссектрисы, проведенной из острого угла на катет: L — биссектриса, отрезок ME , исходящий из острого угла a , b — катеты прямоугольного треугольника с — гипотенуза α, β — углы прилежащие к гипотенузе Формулы длины биссектрисы через катет и угол, ( L ): Формула длины биссектрисы через катет и гипотенузу, ( L ):
Слайд 13
Формулы биссектрисы в произвольном треугольнике L — биссектриса a , b — стороны треугольника с — сторона, на которую опущена биссектриса d , e — отрезки полученные делением биссектрисы γ — угол ABC , разделенный биссектрисой пополам p — полупериметр, p = ( a+b+c )/2 Длина биссектрисы через две стороны и угол между ними Длина биссектрисы через полупериметр и стороны Длина биссектрисы через три стороны Длина биссектрисы через стороны и отрезки d , e
Слайд 14
Формулы медианы произвольного треугольника M — медиана, отрезок |AO| c — сторона на которую ложится медиана a , b — стороны треугольника γ — угол CAB Формула длины медианы через три стороны Формула длины медианы через две стороны и угол между ними
Слайд 15
Формулы медианы прямоугольного треугольника M — медиана R — радиус описанной окружности O — центр описанной окружности с — гипотенуза a , b — катеты α — острый угол CAB Формула длины через катеты Формула длины через катет и острый угол
Слайд 16
Задача №1 В равнобедренном треугольнике основание и боковая сторона равны соответственно 5 см и 20 см. Найдите биссектрису угла при основании. Решение: Длину биссектрисы найдем по формуле: а=с=20см, в=5см, р= (20+20+5):2=22,5см в=5 с=20 а=20 L
Слайд 17
Задача №2 В равнобедренном треугольнике с боковой стороной 4 см, проведена медиана к боковой стороне. Найдите основание, если медиана равна 3 см. Решение: Применим теорему Стюарта: 3 4 m 2 2
Слайд 18
Задача №3 Основание треугольника равно 20 см, медианы боковых сторон равны 18 и 24 см. Найти площадь треугольника. Решение: Применим 20 18 24 А В С Д Р
Слайд 19
Задача №4 . Сторона AB треугольника ABC равна 3, BC =2 AC , E — точка пересечения продолжения биссектрисы CD данного треугольника с описанной около него окружностью, DE =1. Найти сторону AC . Решение:
Слайд 20
Вывод: Теорема Стюарта расширяет возможности решения задач по нахождению элементов треугольника, даёт возможность творчества при решении задач, учит видеть и находить связь между элементами треугольника.
Слайд 21
Заключение Исследовательская работа была интересной и в будущем мы хотим продолжить эту работу , чтобы найти другие формулу для упрощения вычислительной работы при решении геометрических задач.
Слайд 22
Литература: Из опыта проведения внеклассной работы по математике в средней школе. Сборник статей. Под редакцией П. В. Стратилатова. Москва — 1955. Г. И. Глейзер. История математики в школе. 9–10 класс. Москва «Просвещение». 1983 Московский государственный университет им. Ломоносова. Математика. И. Н. Сергеев, И. И. Мельников, С. Н. Олехник , Задачи вступительных экзаменов (1993–1997). Москва 1998. О. П. Зеленяк , Решение задач по планиметрии. Технология алгоритмического подхода на основе задач-теорем. Киев, Москва, ДМК, Пресс, 2008 П. С. Моденов , Экзаменационные задачи по математике с анализом их решения, Москва «Книга по требованию». Н. Рыбкина «Сборник задач по геометрии для 6–9 классов средней школы», часть I, Планиметрия, «Просвещение», 1964. http://www.problems.ru Л. С. Атанасян и др , Геометрия: Доп.главы к шк.учеб.9кл.: Учебное пособие для учащихся шк . и кл . с углубл . изуч ..математики. М.: Просвещение, 1997.
Библиографическое описание:
Помелов, Н. В. Теорема Стюарта и применение её для решения задач / Н. В. Помелов, О. Г. Верещагина, В. А. Суровцева. — Текст : непосредственный // Юный ученый. — 2016. — № 2 (5). — С. 67-73. — URL: https://moluch.ru/young/archive/5/266/ (дата обращения: 11.03.2023).
Теорем и задач, которые вошли в учебники геометрии довольно много. Некоторые из них заслуживают определённого внимания, так как обладают некоторой общностью и могут помочь в сложных заданиях ЕГЭ.
Формулы, позволяющие определить медианы и биссектрисы треугольника по заданным сторонам треугольника, являются частными случаями более общей формулы, которая является основой теоремы Стюарта (Мэтью Стюарт, шотландский астроном и математик, 1717–1785гг.).
Теорема Стюарта названа по имени доказавшего её английского математика М. Стюарта и опубликовавшего её в труде «Некоторые общие теоремы» (1746, Эдинбург). Теорему сообщил Стюарту его учитель Р. Симпсон, который опубликовал эту теорему лишь в 1749 г. Она применяется для нахождения медиан и биссектрис треугольников.
Теорема Стюарта: три точки А, В и С лежат на одной прямой, причем точка В лежит между А и С, тогда и только тогда, когда для любой точки плоскости М выполняется равенство
МА2 * ВС + МС2 * АВ — МВ2 * СА = АВ * ВС * СА
Или другая формулировка: Произведение квадрата расстояния от точки, лежащей на стороне треугольника, до противоположной вершины на длину этой стороны равно сумме квадратов оставшихся сторон на несмежные с ними отрезки первой стороны без произведения этих отрезков на длину основания.
AD2*BC = AB2*CD + AC2*BD — BC*BD*CD

Дано: ΔABC, DЄBC
Доказать:AB²DC
AC²
BD
AD²
BC
BC
DC
BD
Доказательство:
Рассмотрим ΔABC:
По теореме косинусов AC²AB²
BC²
2AB
BC
cosB,
откуда cosB.
Следовательно:
По свойству пропорции:
AB²BD
BC²
BD
AC²
BD
AB²
BC
BD²
BC
AD²
BC
Преобразуем данное выражение:
AB²BD
BC²
BD
AB²
BC
BD²
BC
AC²
BD
AD²
BC
AB² (BC
BD)
BC
BD (BC
BD)
AC²
BD
AD²
BC
Так как BCBD=DC, то
AB²
DC
BC
BD
DC
AC²
BD
AD²
BC
Умножим обе части на (-1) и выполним переносы из одной части в другую:
AB²DC
AC²
BD
AD²
BC
BC
DC
BD
Теорема доказана. [8]
Полученное равенство словами можно сформулировать следующим образом:
Произведение квадрата одной стороны треугольника на не прилежащий к ней отрезок второй стороны плюс произведение квадрата третьей стороны на не прилежащий к ней отрезок второй стороны минус произведение квадрата внутреннего отрезка на вторую сторону, равняется произведению второй стороны на её отрезки, отсекаемые внутренним отрезком. [8]
Предлагаем самостоятельно доказать теорему Стюарта используя:
а) метод координат;
б) векторы;
в) используя формулы для площадей треугольников;
г) геометрический подход.
Применение теоремы Стюарта при доказательстве теорем стереометрии
Если прямая образует с двумя пересекающимися прямыми в точке их пересечения прямые углы, то она перпендикулярна ко всякой прямой, которая проходит в плоскости, содержащей эти две прямые, через точку их пересечения.
Доказательство этой теоремы, данное Евклидом, длинное и сложное. Более простое доказательство с помощью Т.Стюарта представил А.Лежанр. Посмотреть его можно в [2. с.98].
Применение теоремы Стюарта к вычислению длин некоторых линий треугольника [8]
Следствие 1: если отрезок AD — медиана треугольника АВС, тогда
Следствие 2: если отрезок AD –биссектриса внутреннего угла А треугольника АВС, р — полупериметр треугольника АВС, тогда
Следствие 3: если отрезок AD –биссектриса внешнего угла А треугольника АВС, р — полупериметр треугольника АВС, тогда
Примеры решения задач
- В равнобедренном треугольнике с боковой стороной 4 см, проведена медиана к боковой стороне. Найдите основание, если медиана равна 3 см.
Дано: АВС-равнобедренный треугольник, АД-медиана к боковой стороне
АВ=ВС=4см, АД=3см
Найти: основание АС
Решение: применяя следствие из Т.Стюарта для медианы треугольника получаем
, подставляем данные
.
Откуда АС=
Ответ. Основание равно .
-
Медианы проведенные к катетам прямоугольного треугольника, равны
и
. Найдите гипотенузу треугольника.
Дано: АВС — прямоугольный треугольник (угол С=90°).
Медиана, проведенная из угла А ma= , а медиана из угла В mв=
.
Найти: длину гипотенузы АВ.
Решение: Пусть катет напротив угла А ВС=2а (медиана делит его на равные отрезки, равные по а), а катет напротив угла В АС=2в (медиана делит его на равные отрезки, равные по в). Длина гипотенузы равна с. Применяем дважды Т.Стюарта для каждой медианы:
и
.
По Т.Пифагора для треугольника АВС получаем: .
Записываем три уравнения в систему и решаем её. Получаем, что АВ=10.
Ответ. Гипотенуза равна 10.
- В прямоугольном треугольнике радиус описанной окружности равен 15 см, радиус вписанной окружности — 6 см. Найдите стороны треугольника.
Дано: АВС — прямоугольный треугольник (угол С=90°). R=15см, r =6см.
Найти: стороны треугольника АВС.
Решение: Так как АВС — прямоугольный треугольник, то гипотенуза АВ=2R, значит АВ=30см.
Обозначим стороны АС=в, ВС=а, АВ=с.
1) В прямоугольном треугольнике для радиуса вписанной окружности справедливо равенство:
Так как r = 6см, а = 30 см, следовательно а+в = 42 (1)
2) В прямоугольном треугольнике медиана, проведенная из вершины прямого угла равна половине гипотенузы (по свойствам прямоугольного треугольника). А по следствию из Т.Стюарта СО — медиана треугольника АВС равна . Так как СО = 15см, а=30см, следовательно
= 900 (2)
3) Записываем уравнения (1) и (2) в систему:
. Решив её получаем а=24, в=18 или а=18, в=24.
Ответ. Стороны треугольника 18см, 24см, 30см.
- В равнобедренном треугольнике основание и боковая сторона равны соответственно 5 см и 20 см. Найдите биссектрису угла при основании.
Дано: АВС — равнобедренный треугольник (АВ = ВС), АА1 — биссектриса угла А.
АВ = ВС =20см, АС=5см.
Найти: длину биссектрисы АА1.
Решение: по следствию из Т. Стюарта , гдер — полупериметр. р = (20+20+5)/2 = 22,5. Тогда АА1 = 30см.
Ответ. Биссектриса угла при основании равна 30 см.
- Основание треугольника равно 20см, медианы боковых сторон равны 18 и 24см. Найти площадь треугольника.
Дано: АВС — треугольник (ВС — основание). ВВ1, СС1 — медианы.
ВВ1=18см, СС1=24см.
Найти: площадь треугольника АВС.
Решение:
- по следствию из Т. Стюарта
или
(1).
Аналогично или
(2).
Из уравнений (1) и (2) составляем систему: 
Решая её получаем ,
-
Найдем площадь треугольника по формуле Герона
, гдер — полупериметр.
. Тогда
= … =
= 4*см2
Ответ. Площадь треугольника 4*см2.
- Две стороны треугольника равны соответственно 6см и 8см. Известно, что медианы, проведенные к этим сторонам перпендикулярны. Найдите третью сторону треугольника.
Дано: АВС — треугольник. ВВ1, СС1 — медианы. ВВ1 ┴ СС1, АВ=6см, АС=8см.
Найти: длину стороны ВС.
Решение: 1) Пусть медианы пересекаются в точке О. Тогда ОВ1=х см, ВО=2х см, ОС1=у см, СО=2у см. Треугольник ОВС — прямоугольный, тогда по Т. Пифагора 4х2+4у2=ВС2(1).
2) Применяем следствие из Т. Стюарта для медианы:
или
или 36х2=8+2ВС2(2);
или
или 36у2=92+2ВС2(3).
Из уравнений (1), (2) и (3) составляем систему и, решив её, получаем, что ВС=2.
Ответ. Длина третьей стороны равна 2.
- Докажите, что сумма квадратов медиан треугольника равна трем четвертям суммы квадратов его сторон.
Дано: АВС — треугольник. АА1, ВВ1, СС1 — медианы.
Доказать: АА12 + ВВ12 + СС12 = (АВ2 + ВС2 + АС2).
Доказательство: Применяем следствие из Т. Стюарта для медианы:
или
;
или
;
или
.
Тогда после сложения получаем:
АА12 + ВВ12 + СС12 = =
=(АВ2 + ВС2 + АС2).
-
В треугольнике ABC сторона AB равна 21, биссектриса BD равна 8
, а отрезок DC равен 8. Найти периметр треугольника ABC.
Дано: АВС — треугольник. BD — биссектриса, АВ=21, BD =8, DC=8.
Найти: периметр треугольника ABС.
Решение: Пусть AD=х; BC=a.
По теореме Стюарта AB2DC+BC2
AD
BD2
AC=AD
DC∙AC.
Тогда
212∙8+a2∙х−2∙(8+х) =8х(8+х)
По свойству биссектрисы имеем: , откуда а =
212∙8+()2∙х−
2∙(8+х) =8х(8+х)
Разделим обе части уравнения на 8 и умножим на х, получим:
441х+3528−56х2−448х=х3+8х2, х3+64х2+7х−3528=0, (х−7)(х2+71х+504)=0
х−7=0 или х2+71х+504=0
х1=7 D=5041−2016=3025; =55
х2 ==−63 не удовлетворяет условию задачи
х3=8 не удовлетворяет условию задачи
а =24
P = AC+BC+AB=15+24+21=60
Ответ. Периметр треугольника равен 60.
-
В треугольнике КРМ стороны КР=5, РМ=
, а медиана РО=3
. Найдите площадь треугольника КРМ.
Дано: КРМ — треугольник. РО — медиана. КР=5, РМ=, РО=3
.
Найти: площадь треугольника КРМ.
Решение: 1) Применяем следствие из Т. Стюарта для медианы
Откуда КМ=2.
Применяя формулу Герона получаем что S=3.
Ответ. Площадь треугольника равна 3.
-
Сторона AB треугольника ABC равна 3, BC
2AC, E
точка пересечения продолжения биссектрисы CD данного треугольника с описанной около него окружностью, DE=1. Найти сторону AC.
Решение задачи представлено на [8]
-
Найти периметр прямоугольного треугольника, катеты которого относятся как 3:4, а длина биссектрисы прямого угла равна 24
.
Решение задачи представлено в [6].
-
В треугольнике ABC стороны АВ=18см и АС=15см, а биссектриса АЕ=4
см. Найдите периметр треугольника АВС.
Дано: АВС — треугольник АЕ — биссектриса угла А.
АВ =18см, АС=15см.
Найти: периметр треугольника АВС.
Решение: по следствию из Т. Стюарта , гдер — полупериметр. Тогда
. Откуда ВС = 11см. Тогда P = AC+BC+AB=15+18+11=44(см)
Ответ. Периметр треугольника равен 44см.
-
Площадь треугольника ABC равна 20
. Стороны АВ=8 и АС=14. Найти медиану ВМ треугольника АВС.
Дано: АВС — треугольник ВМ — медиана.
АВ =8, АС=14, .
Найти: длину медиану ВМ.
Решение: Пусть ВС=х, применяя формулу Герона получаем что . Откуда получаем 2 случая:
1) ВС =.
По следствию из Т.Стюарта: . Подставляя и преобразовывая получим, что ВМ=
.
2) ВС =.
По следствию из Т.Стюарта: . Подставляя и преобразовывая получим, что ВМ= 5.
Ответ. Медиана ВМ треугольника равна или 5.
Задачи, рекомендуемые для самостоятельного решения
- Биссектриса AL1 пересекает вписанную в треугольник ABC окружность в точках Е и Т. Какой из отрезков больше: АЕ или ТL1?
- Докажите, что если биссектрисы треугольник ABC точкой J делятся в одном отношении, то треугольник ABC -равносторонний.
- Сторона ВС треугольника ABC есть среднее арифметическое сторон АВ и АС. Докажите, что прямая МJ (точка М — центр тяжести треугольника, J — точка пересечения биссектрис) параллельна стороне ВС.
-
Доказать, что медиана треугольника меньше полусуммы сторон, ее заключающих, и больше разности между этой полусуммой и половиной третьей стороны.
- В равнобедренном треугольнике высота, проведенная из вершины равна 12см, а основание относится к боковой стороне как 4: 3. Найдите радиус вписанной окружности.
-
В треугольнике АВС медиана АМ равна среднему пропорциональному двух его сторон АС = b, АВ = с, т. е. АМ =
.Докажите, что
.
Вывод:Теорема Стюарта расширяет возможности решения задач по нахождению элементов треугольника, даёт возможность творчества при решении задач, учит видеть и находить связь между элементами треугольника.
Литература:
- Из опыта проведения внеклассной работы по математике в средней школе. Сборник статей. Под редакцией П. В. Стратилатова. Москва — 1955.
- Г. И. Глейзер. История математики в школе. 9–10 класс. Москва «Просвещение». 1983 Московский государственный университет им. Ломоносова. Математика.
- И. Н. Сергеев, И. И. Мельников, С. Н. Олехник, Задачи вступительных экзаменов (1993–1997). Москва 1998.
- О. П. Зеленяк, Решение задач по планиметрии. Технология алгоритмического подхода на основе задач-теорем. Киев, Москва, ДМК, Пресс, 2008
- П. С. Моденов, Экзаменационные задачи по математике с анализом их решения, Москва «Книга по требованию».
- Н. Рыбкина «Сборник задач по геометрии для 6–9 классов средней школы», часть I, Планиметрия, «Просвещение», 1964.
- http://www.problems.ru
- Л. С. Атанасян и др, Геометрия: Доп.главы к шк.учеб.9кл.: Учебное пособие для учащихся шк. и кл. с углубл. изуч..математики. М.: Просвещение, 1997.
Основные термины (генерируются автоматически): ABC, BCBD, BDAD, прямоугольный треугольник, Площадь треугольника, медиана, сторона треугольника, треугольник, периметр треугольника, сторона.
��������: 1 [����� �����: 3]
������ 54717 [������� �������] |
���������: 4 ������: 8,9 |
����� D ����������� �� ������� BC ������������ ABC. ��������,
���
AB2 . DC + AC2 . BD — AD2 . BC = BC . DC . BD.
������� $AC$ ������������ $ABC$ �������� ��������� ���������� � ����� $K$, � ��������������� ������������ � ����� $L$. ����� $P$ – �������� ������ ��������� ���������� �� ���������� ������������� � $AC$. ��������, ��� ����������� � ������ $K$ � $L$ � ��������� ���������� ������������ $BKL$ ������������ �� ��������� ���������� ������������ $ABC$. ��������, ��� ������ $AB$ � $BC$ �������� ���������� $PKL$.
� ������������ ABC M – ����� ����������� ������, I – ����� ��������� ����������, A1 � B1 – ����� ������� ���� ���������� �� ��������� BC � AC, G – ����� ����������� ������ AA1 � BB1. ��������, ��� ���� CGI ������ ����� � ������ �����, ����� GM || AB.
��������: 1 [����� �����: 3]
В данной публикации мы рассмотрим одну из основных теорем евклидовой геометрии – теорему Стюарта, получившую такое название в честь английского математика М. Стюарта, доказавшего ее. Также подробно разберем пример решения задачи для закрепления представленного материала.
- Формулировка теоремы
- Применение теоремы
- Пример задачи
Формулировка теоремы
Дан треугольнике ABC. На его стороне AC взята точка D, которая соединена с вершиной B. Примем следующие обозначения:
- AB = a
- BC = b
- BD = p
- AD = x
- DC = y
Для данного треугольника справедливо равенство:
Применение теоремы
Из теоремы Стюарта можно вывести формулы для нахождения медиан и биссектрис треугольника:
1. Длина биссектрисы
Пусть lc – это биссектриса, проведенная к стороне c, которая делится на отрезки x и y. Две другие стороны треугольника примем за a и b. В этом случае:
2. Длина медианы
Пусть mc – это медиана, опущенная на сторону c. Две другие стороны треугольника обозначим как a и b. Тогда:
Пример задачи
Дан треугольник ABC. На стороне AC, равной 9 см, взята точка D, которая делит сторону так, что AD в два раза длиннее DC. Длина отрезка, соединяющего вершину B и точку D, составляет 5 см. При этом образованный треугольник ABD является равнобедренным. Найдите оставшиеся стороны треугольника ABC.
Решение
Изобразим условия задачи в виде чертежа.
AC = AD + DC = 9 см. Отрезок AD длиннее DC в два раза, т.е. AD = 2DC.
Следовательно, 2DC + DC = 3DC = 9 см. Значит, DC = 3 см, AD = 6 см.
Т.к. треугольник ABD – равнобедренный, и сторона AD равна 6 см, значит равными являются AB и BD, т.е. AB = 5 см.
Остается только найти BC, выведя формулу из теоремы Стюарта:
Подставляем в данное выражение известные нам значения:
Таким образом, BC = √52 ≈ 7,21 см.
5 февраля 2018
В закладки
Обсудить
Жалоба
Какие геометрические факты можно использовать на ЕГЭ без доказательства?
Начнём с того, что для ЕГЭ не нужны сколько-нибудь редкие теоремы, особенно где-нибудь на шпаргалке.
Нужно уметь применять всем знакомые факты, видеть рисунок и решать больше задач. Но вопрос из заголовка задают очень часто, и ответить на него нужно. Естественно, все сотни признаков и свойств, что есть в вашем школьном учебнике можно использовать. Но как насчет более редких фактов: что можно применять без доказательства, а что нет? Точный ответ: любые факты из школьных учебников, рекомендованных минобром на 2017-2018 год.
Ну а вот заветный список того, что мне все-таки удалось обнаружить в соответствующих учебниках:
→ Теорема Менелая (Атанасян. Геометрия 7-9 классы)
→ Теорема Чевы (Атанасян. Геометрия 7-9 классы)
→ Теорема Птолемея (Мерзляк. Геометрия 8 класс)
→ Прямая Эйлера (Мерзляк. Геометрия 8 класс)
→ Теорема об окружности Эйлера (Бутузов. Геометрия 8 класс)
→ Формула медианы треугольника (Шарыгин. Геометрия 7-9 классы)
→ Формула биссектрисы треугольника (Шарыгин. Геометрия 7-9 классы)
→ Теорема о четырех замечательных точках трапеции (Шарыгин. Геометрия 7-9 классы)
Формулу радиуса вневписанной окружности используйте. Каноническое уравнение эллипса — да пожалуйста! Ключевые формулы метода координат для задачи №14, опять же, есть
Но если здесь есть коллеги по цеху, которые могут уточнить еще несколько популярных вопросов насчет непопулярной теории — черкните, буду признателен! Вот интересующие факты: формула Брахмагупты, теорема Стюарта, формула Эйлера для расстояния между центрами вписанной и описанной окружностями треугольника, понятие определителя квадратной матрицы.
Ну и еще раз в заключение. Вероятность того, что задача ЕГЭ не решается без экзотики, равна нулю (такие события называются невозможными). Вероятность того, что вам вообще попадется конфигурация, для которой актуальна, например, теорема о девяти точках окружности, приблизительно равна 0,015. Вероятность того, что школьник в целом знает что-то «запрещенное», приблизительно равна, не кидайтесь камнями, 0,000037.
Источник: vk.com/wildmathing
Автор: Потапова Фэимэ Фагимовна
Должность: учитель математики
Учебное заведение: ГБОУ СОШ №4 имени Жака-Ива Кусто
Населённый пункт: Санкт-Петербург
Наименование материала: статья
Тема: Теоремы планиметрии,используемые при решении задач повышенной сложности в заданиях ОГЭ и ЕГЭ.
Раздел: полное образование
Три теоремы планиметрии, используемые
при решении задач
п
овышенной сложности в заданиях ОГЭ и ЕГЭ.
Потапова Фэимэ Фагимовна
ГБОУ СОШ №4-Кусто
2018-2019уч.год
1. Теорема Стюарта и параметры треугольников
1
Теорем и задач, которые вошли в учебники геометрии довольно много. Некоторые
из них заслуживают определённого внимания, так как обладают некоторой общностью и
могут помочь в сложных заданиях ЕГЭ.
Формулы, позволяющие определить медианы и биссектрисы треугольника по
заданным сторонам треугольника, являются частными случаями более общей формулы,
которая является основой теоремы Стюарта (Мэтью Стюарт, шотландский астроном и
математик , 1717-1785). Рассмотрим треугольник АВС (см.
рис.), в котором АВ = с, ВС = а, ВК = х, АК = p, КС = q,
АС = b. Задача состоит в том, чтобы по заданным четырём
параметрам – а, с, p, q – определить отрезок ВК.
Воспользуемся известным равенством для векторов
,
,
:
, из которого после возведения в квадрат
получаем выражение
. С другой стороны,
.
Таким образом, после подстановки и некоторых преобразований, можно получить
формулу для определения отрезка ВК:
.
Тот же результат можно получить, если записать теорему косинусов для
треугольников АВК и АВС, выбрав общий угол А.
Рассмотрим частные случаи этой формулы.
1). Пусть ВК является медианой. Тогда
и имеем формулу для расчета медиан
.
2).
Пусть ВК является биссектрисой.
Тогда
и получаем формулу для
биссектрисы
.
3). Если ВК – отрезок в равнобедренном треугольнике, то в этом случае
,
где а – боковая сторона треугольника.
Следующие формулы для биссектрисы являются необходимым дополнением к
решению треугольников.
2
Формула
легко получается из простого
соотношения
(все
обозначения
соответствуют рис.).
Формула для биссектрисы, выраженная через три
стороны
треугольника,
получается
после
ряда
преобразований.
Так
как
,
откуда
, то первую формулу для биссектрисы легко преобразовать в
следующую:
. Таким образом, имеем
.
Учитывая, что
, получаем ещё ряд полезных соотношений:
,
включая и уже полученный ранее результат
.
Формула для медианы, полученная ранее, также
выводится из других источников. Например, следует
из
известного
равенства
для
параллелограмма
, если в нём принять
,
(см. рис.). В результате
получаем следующее выражение
.
Этот же результат можно получить, применяя теорему косинусов для треугольников ABC
и AOC, выбрав общий угол ОАС.
2. Теорема Чевы. Пересечение высот в треугольнике.
В обязательный минимум содержания основных образовательных программ профильного
уровня по геометрии входят известные теоремы планиметрии: теорема Чевы и теорема
Менелая.
Но
эти
теоремы
интересны
ещё
и
своими
следствиями.
Прежде обратимся к самой теореме Чевы
(Джованни Чева, итальянский математик, 1648-1734).
3
Теорема Чевы
Если на сторонах АВ, ВС, СА треугольника АВС (см. рис.) взяты соответственно
точки С
1
, А
1
, В
1
, то отрезки АА
1
, ВВ
1
, СС
1
пересекаются в одной точке тогда и только
тогда, когда
(*)
В основе доказательства прямой теоремы лежат следующие соображения. Пусть отрезки
пересекаются в точке О,
тогда
. При выводе был использован принцип
равных отношений:
.
Таким образом, имеем:
,
,
. Перемножая эти
выражения, получаем соотношение (*).
В обратной теореме на сторонах треугольника взяты точки С
1
, А
1
, В
1
так, что выполняется
равенство (*). Пусть точка
. Проведём
, которая пересекается с
в
точке
. По доказанному выше, имеем равенство:
.
Поделив оба выражения друг на друга почленно, окончательно приходим к выводу, что
, т.е. точки
и
делят сторону
в одном и том же отношении, что
означает совпадение этих точек и исходные отрезки пересекаются в одной точке.
Воспользовавшись этим результатом, докажем теперь теорему о пересечении чевиан.
Теорема о пересечении чевиан
Чевианы в треугольнике АВС точкой пересечения О делятся в отношении
, считая от вершины.
Имеем, с одной стороны:
и
. Откуда следует, что:
. С другой стороны, получаем такой же результат
из другого условия:
. Таким образом, утверждение
теоремы доказано.
4
Рассмотрим частные случаи этой формулы. В случае медиан получаем классический
результат:
или
.
В случае пересечения биссектрис следует учесть, что
и
. Таким
образом, имеем:
.
Рассмотрим подробнее задачу о пресечении высот, так как здесь возможны две
конфигурации.
1.
Случай остроугольного треугольника (см. рис.).
При пересечении высот следует учесть, что каждый
отрезок
можно записать через высоты и
углы
треугольника.
А
именно,
.
В результате
окончательно получаем
. Конечно, данный результат можно получить и
другим путём, не используя теорему о чевианах. Однако, такой подход наиболее
оптимален.
2.
Случай тупоугольного треугольника (см. рис.).
Воспользуемся
формулой,
полученной
выше:
.
Из рисунка следует, что
или
.
5