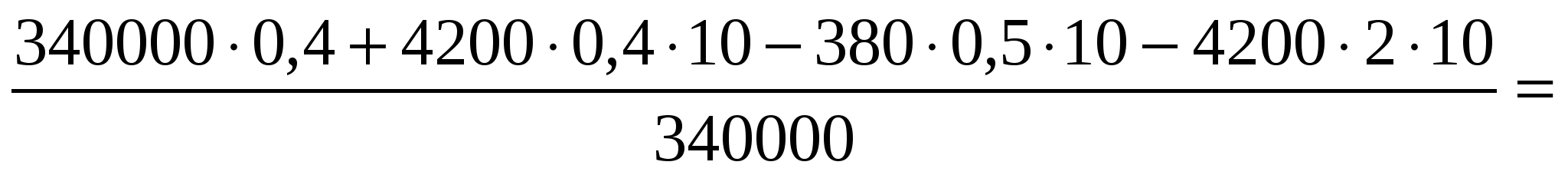Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
В эксперименте установлено, что при температуре воздуха в комнате 29 °C на стенке стакана с холодной водой начинается конденсация паров воды из воздуха, если снизить температуру стакана до 27 °C. По результатам этих экспериментов определите абсолютную и относительную влажность воздуха. Для решения задачи воспользуйтесь таблицей. Поясните, почему конденсация паров воды в воздухе может начинаться при различных значениях температуры. Давление и плотность насыщенного водяного пара при различной температуре показано в таблице:
|
7 |
9 |
11 |
12 |
|
14 |
15 |
16 |
19 |
21 |
23 |
25 |
27 |
29 |
40 |
60 |
|
|
10 |
11 |
13 |
14 |
15 |
16 |
17 |
18 |
22 |
25 |
28 |
32 |
36 |
40 |
74 |
200 |
|
|
7,7 |
8,8 |
10,0 |
10,7 |
11,4 |
12,11 |
12,8 |
13,6 |
16,3 |
18,4 |
20,6 |
23,0 |
25,8 |
28,7 |
51,2 |
130,5 |
2
В калориметре находился 1 кг льда. Чему равна первоначальная температура льда, если после добавления в калориметр 20 г воды, имеющей температуру 20 °C, в калориметре установилось тепловое равновесие при ? Теплообменом с окружающей средой и теплоемкостью калориметра пренебречь.
4
В калориметре находился 1 кг льда. Какой была температура льда, если после добавления в калориметр 15 г воды, имеющей температуру 20 °C, в калориметре установилось тепловое равновесие при –2 °C? Теплообменом с окружающей средой и теплоемкостью калориметра пренебречь.
5
В 2012 году зима в Подмосковье была очень холодной, и приходилось использовать системы отопления дачных домов на полную мощность. В одном из них установлено газовое отопительное оборудование с тепловой мощностью 17,5 кВт и КПД 85%, работающее на природном газе — метане Сколько пришлось заплатить за газ хозяевам дома после месяца (30 дней) отопления в максимальном режиме? Цена газа составляла на этот период 3 рубля 30 копеек за 1 кубометр газа, удельная теплота сгорания метана 50,4 МДж/кг. Можно считать, что объём потреблённого газа измеряется счётчиком при нормальных условиях. Ответ округлите до десятков рублей.
Пройти тестирование по этим заданиям
Егэ физика задачи на уравнение теплового баланса
Репетитор
по физике
Репетитор
по физике
Репетитор
по алгебре
Репетитор
по физике
Задачи на определение температуры смеси
(Задачи на уравнение теплового баланса) .
Задача 1. (Температура смеси)
Смешали (m_<хол>=1 кг ) холодной воды при температуре (t_<хол>=10^0C ) и горячую воду при температуре (t_<гор>=90^0C .) Температура смеси при этом оказалась равна ( 50^0 C . )
Какова масса горячей воды?
Показать ответ Показать решение Видеорешение
Составим уравнение теплового баланса:
Разделим на (40) обе части уравнения:
Разделим на (c ) обе части уравнения:
Задача 2. (Температура смеси)
Смешали (m_х=1 кг ) холодной воды при температуре (t_х=10^0C ) и горячую воду при температуре (t_г=90^0C .) Температура смеси при этом оказалась равна (Theta=50^0 C . )
Какова масса горячей воды?
Показать ответ Показать решение Видеорешение
Составим уравнение теплового баланса:
Задача 3. (Температура смеси)
Смешали (m_1=2 кг ) холодной воды при температуре (t_1=5^0C ) и горячую воду при температуре (t_2=95^0C .) Температура смеси при этом оказалась равна (Theta=80^0 C . )
Какова масса горячей воды?
Показать ответ Показать решение Видеорешение
Решение задач на теплообмен с использованием уравнения теплового баланса (методические рекомендации)
Разделы: Физика
Пособие рекомендовано учащимся, желающим получить практические навыки в решении задач на теплообмен, и может быть полезным для учителей и абитуриентов.
При соприкосновении тел, имеющих разные температуры, между этими телами происходит теплообмен. С точки зрения молекулярно-кинетической теории, это объясняется так: молекулы более нагретого тела имеют большую кинетическую энергию, чем молекулы тела, менее нагретого. При “столкновениях” молекул соприкасающихся тел происходит процесс выравнивания их средних кинетических энергий. Молекулы более нагретого тела теряют часть своей кинетической энергии, при этом нагретое тело будет остывать. Кинетическая энергия молекул холодного тела возрастает, поэтому температура этого тела будет увеличиваться. В конечном итоге кинетические энергии молекул обоих тел сравняются, и температуры тел станут одинаковыми. На этом теплообмен прекращается.
Энергию, которую тело получает или отдаёт в процессе теплообмена, называют количеством теплоты (Q).
Количество теплоты, как и все другие виды энергии, измеряется в системе СИ в Джоулях: [Q] = Дж. (Здесь и в дальнейшем единицы измеряются в системе СИ.)
Нагревание или охлаждение
При нагревании или охлаждении тела количество теплоты, поглощаемое или выделяемое им, рассчитывается по формуле:
(t2 – t1) – разность температур тела,° С (или К);
с – удельная теплоёмкость вещества, из которого состоит тело,
Удельная теплоёмкость вещества – это количество теплоты, которое нужно сообщить одному килограмму данного вещества, чтобы увеличить его температуру на 1° С (или это количество теплоты, которое выделяет один килограмм данного вещества, остывая на 1° С).
Значения удельных теплоемкостей других веществ можно найти в справочниках, а также в школьном учебнике или задачнике.
При нагревании тела его внутренняя энергия увеличивается. Это требует притока энергии к телу от других тел. Значит, оно поглощает некоторое количество теплоты, принимая его от других тел, участвующих в теплообмене.
При охлаждении тела его внутренняя энергия уменьшается. Поэтому остывающее тело отдаёт кому-либо некоторое количество теплоты.
Обычно конечную температуру, установившуюся в результате теплообмена, обозначают греческой буквой 
В формуле (1) произведение cm для каждого конкретного тела есть величина постоянная. Её называют теплоёмкостью тела и обозначают С:
Размерность теплоемкости: 
Теплообмен между телами, имеющими одинаковые температуры, не происходит, даже если контактируют вещества, находящиеся в разных агрегатных состояниях. Например, при температуре плавления (0° С) лёд и вода могут находиться бесконечно долго, при этом количество льда и количество воды останутся неизменными. Аналогично ведут себя пар и жидкость, находящиеся при температуре кипения. Теплообмен между ними не происходит.
Плавление или кристаллизация
Если при нагревании тела его температура достигнет температуры плавления, то начинает происходить процесс перехода этого вещества из твердого состояния в жидкое. При этом идут изменения в расположении и характере взаимодействия молекул. Температура при плавлении не изменяется. Это означает, что средние кинетические энергии молекул жидкости и твердого тела при температуре плавления одинаковы. Однако внутренняя энергия тела при плавлении возрастает за счет увеличения энергии взаимодействия молекул. Количество теплоты, поглощаемое телом при плавлении, рассчитывается по формуле

где m – масса тела, кг;

При кристаллизации, наоборот, внутренняя энергия тела уменьшается на величину 
Удельная теплота плавления показывает, сколько энергии нужно сообщить одному килограмму данного вещества, взятого при температуре плавления, чтобы полностью превратить его при этой температуре в жидкость (или сколько энергии выделяет 1 кг жидкости, взятой при температуре кристаллизации, если вся она при этой температуре полностью превратится в твёрдое тело).
Удельную теплоту плавления любого вещества можно найти в справочниках. Для льда же
Температура плавления у каждого вещества своя. Её также можно найти в справочниках. Важно подчеркнуть, что температура плавления вещества равна температуре кристаллизации этого же вещества. У льда tпл = 0° С.
Кипение или конденсация
При достижении жидкостью температуры кипения начинает происходить другой фазовый переход – кипение, при котором расстояния между молекулами значительно увеличиваются, а силы взаимодействия молекул уменьшаются. Вся подводимая к жидкости теплота идет на разрыв связей между молекулами. При конденсации пара в жидкость, наоборот, расстояния между молекулами значительно сокращаются, а силы взаимодействия молекул увеличиваются. Для кипения жидкости энергию к жидкости нужно подводить, при конденсации пара энергия выделяется. Количество теплоты, поглощаемое при кипении или выделяемое при конденсации, рассчитывается по формуле:
где m – масса тела, кг; L – удельная теплота парообразования,
Удельная теплота парообразования показывает, сколько энергии нужно сообщить одному килограмму жидкости, взятой при температуре кипения, чтобы при этой температуре полностью превратить её в пар (для конденсации: сколько энергии выделяет один килограмм пара, взятого при температуре конденсации, полностью превращаясь в жидкость).
При одинаковом давлении температура кипения и температура конденсации одного и того же вещества одинаковы.
Температуры кипения и удельные теплоты парообразования также можно найти в справочниках. Для воды же они соответственно равны: рис. 9 (при нормальном атмосферном давлении).
Уравнение теплового баланса
Тела, участвующие в теплообмене, представляют собой термодинамическую систему. Термодинамическая система называется теплоизолированной, если она не получает энергию извне и не отдаёт её; теплообмен происходит только между телами, входящими в эту систему. Для любой теплоизолированной системы тел справедливо следующее утверждение: количество теплоты, отданное одними телами, равно количеству теплоты, принимаемому другими телами.
Это утверждение описывает частный случай закона сохранения и превращения энергии в применении к процессу теплообмена. А формула (5) является одним из видов уравнения теплового баланса.
При решении задач с помощью данного вида уравнения теплового баланса в формуле (1) в качестве t2 следует брать большую температуру, а в качестве t1 – меньшую. Тогда разность (t2 – t1) будет положительна и всё произведение cm(t2–t1) также будет положительным. Все теплоты, отданные и полученные, будут положительными.
Уравнение теплового баланса можно записать и в таком виде:
где n – количество тел системы.
Алгебраическая сумма всех количеств теплоты (поглощенных и выделенных) в теплоизолированной системе равна нулю.
Q1, Q2, …, Qn – это теплоты, поглощаемые или выделяемые участниками теплообмена. Очевидно, что в этом случае какие-то теплоты должны быть положительны, а какие-то – отрицательны. При записи уравнения теплового баланса в виде (6) всегда t2 – конечная температура, а t1 – начальная.
Если тело нагревается, то разность (t2 – t1) положительна и все произведение cm(t2 – t1) положительно. То есть Q > 0 тогда, когда теплота к данному телу подводится.
А если t2 0; если тело выделяет энергию (кристаллизация, конденсация), то Q
 |
Проведём анализ:
Вода и калориметр находились в тепловом равновесии, поэтому они имели одинаковую температуру: t1 = t2 = 20° С. При опускании в воду с температурой 20° С свинцового тела с температурой 90° С между водой и свинцом будет происходить теплообмен. Свинец будет остывать, а вода — нагреваться. В этом же процессе участвует и калориметр, который, как и вода, будет тоже нагреваться. |
 |
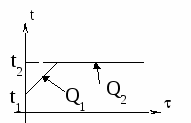
Изменение температур тел с течением времени удобно изображать на графике зависимости t(t ).
Отрезок АВ соответствует графику изменения температуры свинцового тела. Стрелка, идущая от него, показывает, что, остывая, свинец выделяет энергию Q3. |
| Два параллельных отрезка СВ соответствуют графикам изменения температур калориметра и воды. Стрелки, идущие к ним, показывают, что для нагревания калориметра и воды требуется энергия Q1 и Q2, которую они поглощают. | |
| Решим задачу с использованием уравнения теплового баланса в виде (5):
|
Решим задачу с использованием уравнения теплового баланса в виде (6):
Ответ: Вода нагреется до 24° С.
Предлагаю читателю самостоятельно сделать проверку размерности.
Егэ физика задачи на уравнение теплового баланса
В эксперименте установлено, что при температуре воздуха в комнате 29 °C на стенке стакана с холодной водой начинается конденсация паров воды из воздуха, если снизить температуру стакана до 27 °C. По результатам этих экспериментов определите абсолютную и относительную влажность воздуха. Для решения задачи воспользуйтесь таблицей. Поясните, почему конденсация паров воды в воздухе может начинаться при различных значениях температуры. Давление и плотность насыщенного водяного пара при различной температуре показано в таблице:
Водяной пар в воздухе становится насыщенным при температуре 27 °C. Следовательно, давление р водяного пара в воздухе равно давлению насыщенного пара при температуре 27 °C, из таблицы 36 гПа.
Абсолютная влажность равна плотности водяных паров. Первое состояние: насыщенный пар при 27 °C. Второе: пар при 29
°C. Пар охлаждается от 29 до 27 °C изобарически, поэтому
Давление насыщенного водяного пара при температуре 29 °C равно 40 гПа. Относительной влажностью воздуха
называется отношение:
Пусть — абсолютная влажность воздуха при температуре 29 °C равно, а
— плотность насыщенных водяных паров при этой температуре. Относительную влажность можно рассчитать как отношение
откуда
Конденсация паров воды происходит при условии равенства давления водяного пара, имеющегося в воздухе, давлению насыщенного водяного пара при данной температуре воздуха. Давление насыщенного водяного пара зависит от температуры. Поэтому при разной плотности водяного пара в воздухе температура начала конденсации пара (точка росы) оказывается различной.
Приведённое решение неверно. В условии нигде не сказано, что можно считать водяной пар идеальным газом, а стало быть уравнение Менделеева-Клайперона даёт неточный результат. Относительная влажность по другому определяется через отношение абсолютной влажности к плотности водяных паров при данной температуре, следовательно мы можем взять значение для абсолютной влажности при 29 градусах непосредственно из таблицы — она равна плотности насыщенных паров при 27 градусах, т.е. 25,8 г/куб. м.
Немного изменили решение. Но при изменении температуры при постоянном давлении меняется (хоть и незначительно) относительная влажность. Поэтому нельзя сказать, что искомая относительная влажность равна плотности насыщенного парам при 27 °С. Составителям следовало бы взять разницу температур побольше.
В аналогичной задаче 2930 принцип нахождения абсолютной влажности описан верно, в данной задаче — нет
Это решение верное и ответ получится такой же. В задаче 2930 более очевидный переход.
В калориметре находился 1 кг льда. Чему равна первоначальная температура льда, если после добавления в калориметр 20 г воды, имеющей температуру 20 °C, в калориметре установилось тепловое равновесие при ? Теплообменом с окружающей средой и теплоемкостью калориметра пренебречь.
Количество теплоты, необходимое для нагрева льда, находящегося в калориметре, до температуры t:
Количество теплоты, отдаваемое водой при охлаждении ее до :
Количество теплоты, выделяющееся при отвердевании воды при :
Количество теплоты, вьделяющееся при охлаждении льда, полученного из воды, до температуры t:
Уравнение теплового баланса:
Объединяя (1)—(5), получаем:
Ответ:
Почему количество теплоты, выделяющееся при отвердевании воды равно Q=Lm (L- лямбда)? Если я не ошибаюсь, то отвердевание это кристаллизация и формула будет Q=-Lm.
Знак не имеет особого значения. Просто нужно писать данное слагаемое в «правильную часть» теплового баланса, то есть правильно указывать, куда переходит данная энергия.
В калориметре находился лед при температуре Какой была масса
льда, если после добавления в калориметр
воды, имеющей температуру
и установления теплового равновесия температура содержимого калориметра оказалась равной
причем в калориметре была только вода?
Количество теплоты, полученное при нагреве льда, находящегося в калориметре, до температуры :
(1).
Количество теплоты, полученное льдом при его таянии при
(2).
Количество теплоты, отданное водой при охлаждении её до
(3).
Уравнение теплового баланса: (4).
Объединяя (1)—(4), получаем:
Ответ:
В калориметре находился 1 кг льда. Какой была температура льда, если после добавления в калориметр 15 г воды, имеющей температуру 20 °С, в калориметре установилось тепловое равновесие при –2 °С? Теплообменом с окружающей средой и теплоемкостью калориметра пренебречь.
Количество теплоты, необходимое для нагревания льда, находящегося в калориметре, до температуры t:
(1)
Количество теплоты, отдаваемое водой при охлаждении её до 0 °С:
(2)
Количество теплоты, выделяющейся при отвердевании воды при 0 °С:
(3)
Количество теплоты, выделяющейся при охлаждении льда, полученного из воды, до температуры t:
(4)
Уравнение теплового баланса:
(5)
Объединяя формулы (1)—(5), получаем
Ответ:
Почему в уравнении (3) удельная теплота плавления взята с плюсом? Т.к. идёт процесс, обратный плавлению, она должна быть с минусом.
Я бы Вам посоветовал забыть про этот знак минус в формуле, лучше все считать положительным, просто понимать, куда перетекает тепло. Писать тепловой баланс в виде: .
Это полностью эквивалентно балансу в виде
А почему в уравнении (2) , при расчете температуры мы вычитаем 0 , не -2 ?
То что происходит с 15 г воды можно представить в виде трёх процессов: а) вода охлаждается до 0 °С, б) замерзает (превращается в лёд) и в) лёд охлаждается до –2 °С.
Уравнение (2) описывает процесс (а).
В 2012 году зима в Подмосковье была очень холодной, и приходилось использовать системы отопления дачных домов на полную мощность. В одном из них установлено газовое отопительное оборудование с тепловой мощностью 17,5 кВт и КПД 85%, работающее на природном газе — метане Сколько пришлось заплатить за газ хозяевам дома после месяца (30 дней) отопления в максимальном режиме? Цена газа составляла на этот период 3 рубля 30 копеек за 1 кубометр газа, удельная теплота сгорания метана 50,4 МДж/кг. Можно считать, что объём потреблённого газа измеряется счётчиком при нормальных условиях. Ответ округлите до десятков рублей.
Метан имеет молярную массу Согласно уравнению Клапейрона — Менделеева, плотность метана
при нормальных условиях (температура
давление
) равна
Удельная теплота сгорания метана в пересчёте на кубометр газа равна КПД газового отопительного оборудования
а тепловая мощность установки
поэтому мощность, выделяющаяся при сгорании газа, равна
Таким образом, за месяц (30 суток по 86400 секунд) потребление энергии составит
Объём потребленного за месяц газа будет равен а его стоимость равна
Ответ: хозяевам пришлось заплатить за месяц отопления дома газом 4960 рублей.
источники:
http://urok.1sept.ru/articles/103594
http://phys-ege.sdamgia.ru/test?theme=307
Разделы сайта
Рекомендую
Тепловой баланс
Задача 517 из задачника Бендрикова и др.
Задача 517 из задачника Бендрикова и др.
Задача. Два металлических шара радиусами 10 см с одинаковыми массами, один из которых откачан, а другой заполнен кислородом при давлении МПа, вносят в камеру, через которую идёт поток водяного…
Тепловой баланс: задачки ненулевого уровня, продолжение.
Решаем сложные задачи на тепловой баланс. Сложность примерно соответствует 30-й задаче ЕГЭ, или простой олимпиаде.
Задача 1.
В закрытом медном калориметре массой 600 г находится 1,0 кг измельченного льда при температуре C. В калориметр впустили 200…
10.12.2020 06:12:01 | Автор: Анна
|
|
Тепловой баланс — задачки ненулевого уровня.
Решаем сложные задачи на тепловой баланс. Сложность примерно соответствует 30-й задаче ЕГЭ, или простой олимпиаде.
Задача 1.
После опускания в воду, имеющую температуру C, тела, нагретого до …
08.12.2020 07:47:01 | Автор: Анна
|
|
Тепловой баланс. 10 класс, подготовка к олимпиадам.

Продолжаем подготовку к олимпиадам. Здесь для вас собраны задачи на тепловой баланс. Очень многие содержат графики, а с графиками «дружат» не все. Давайте тренироваться, чтобы «дружить».
Задача 1.
На рисунке представлен график зависимости температуры от…
24.12.2019 06:36:49 | Автор: Анна
|
|
Подготовка к олимпиадам: графические задачи на тепловой баланс, 8 класс.

В задачах на тепловой баланс иногда часть информации дана в виде графика, и нужно уметь эту информацию извлечь из такой графической формы и перевести в числовую, такую, которую можно использовать для расчетов.
Задача 1.
В небольшой чайник налита доверху теплая вода при температуре
01.08.2018 08:14:14 | Автор: Анна
|
|
Подготовка к олимпиадам: мощность теплопередачи-1
Продолжаем подготовку к олимпиадам. Сегодня закрепляем тему «мощность теплопередачи». Формулы мы будем использовать те же, это и классические формулы теплового баланса, и формулы для определения мощности теплопередачи, которые вы найдете в прошлой статье.
Задача 1.
Для работы паровой установки расходуется
26.07.2018 15:07:31 | Автор: Анна
|
|
Подготовка к олимпиадам: мощность теплопередачи, 8 класс.

Продолжаем подготовку к олимпиадам. Сегодня рассматриваем тему «мощность теплопередачи». Задачи интересные, и в школе эту тему не дают, заимствованы на «Фоксфорде» — спасибо составителям за удовольствие от решения.
Мощность теплопередачи – количество теплоты, отданное системой за время
24.07.2018 13:41:47 | Автор: Анна
|
|
Подготовка к олимпиадам: тепловой баланс, 8 класс.

Продолжаем подготовку к олимпиадам. Рассматриваем тему «тепловой баланс». Тут мы познакомимся с интересным, иногда очень эффективным способом решать задачи – виртуальным тепловым банком, в котором можно как временно занять теплоты, чтобы нагреть (виртуально) все компоненты системы, так и наоборот, охладить все компоненты, и излишек тепла…
08.07.2018 15:16:47 | Автор: Анна
|
|
Подготовка к олимпиадам: тепловой баланс, 8 класс.
Продолжаем подготовку к олимпиадам. Тема сегодняшней статьи – тепловой баланс. Начнем, как обычно, с более простых задач, и потом перейдем к тем, что посложнее.
Задача 1.
Цилиндрическое ведро с кипятком поставлено на лед. Температура льда …
28.06.2018 08:34:45 | Автор: Анна
|
|
Тепловой баланс. Подготовка к олимпиадам.
Эти задачи я использовала при подготовке к олимпиаде семи- и восьмиклассников. Также можно решать их для подготовки к ЕГЭ, для более глубокого проникновения в тему.
Задача 1.
На дне глубокой шахты лежало 700 кг льда при температуре …
24.03.2018 14:02:01 | Автор: Анна
|
|
Задачи вступительного экзамена в Академическую гимназию СПбГУ по физике (прошлых лет)

В статье приведен типовой вариант задания вступительных испытаний по физике в Академическую гимназию СПбГУ, в класс физико-математического направления. Задачи разбиты по уровням сложности, есть очень непростые для среднего школьника.
Часть А.
Задача 1.
На рисунке приведен график зависимости скорости от времени для тела, движущегося прямолинейно. В…
06.06.2017 15:22:24 | Автор: Анна
|
|
Тепловой баланс
Задача 1.
Сколько нужно килограммов льда, чтобы охладить воду в ванне от до ? Объем воды 100 л. Температура льда .
Тепло от воды передается льду и он тает. Потом получившаяся при…
09.03.2016 10:32:57 | Автор: Анна
|
|
Тепловое равновесие
1. В термос с большим количеством льда при температуре заливают 0,5 кг воды при температуре . При установлении теплового равновесия в сосуде расплавится лед массой
1) 90 г …
08.08.2014 14:16:32 | Автор: Анна
|
|
Фазовые переходы: плавление, парообразование, кристаллизация.

Что нам понадобится знать и помнить для решения задач таких типов? То, что температура плавления и кристаллизации — одинаковы, и температура тела остается постоянной в течение всего процесса плавления (кристаллизации), и точно так же температура парообразования и конденсации равны, и температура жидкости в течение данных…
05.08.2014 20:01:12 | Автор: Анна
|
|
Теплообмен и тепловое равновесие

1. Тело А находится в тепловом равновесии с телом С, а тело В не находится в тепловом равновесии с телом С. Найдите верное утверждение.
1) температуры тел A и C не одинаковы
2) температуры тел A, C и B одинаковы
3) тела A и B находятся в тепловом равновесии
4) температуры тел A и B не одинаковы
Если тело А в тепловом равновесии с телом С, то у…
03.08.2014 10:15:33 | Автор: Анна
|
|
Внутренняя энергия, теплоемкость и количество теплоты.

1. Имеются два кубика одинаковой массы, сделанные из разных материалов, причем удельная теплоемкость вещества первого кубика больше удельной теплоемкости вещества второго кубика. Первоначальная температура кубиков одинаковая. Если сообщить кубикам одинаковое количество теплоты, то можно утверждать:
1) кубики нагреются до одинаковой температуры
2) первый кубик нагреется до более высокой…
29.07.2014 10:14:13 | Автор: Анна
|
|
Последние записи
Облако меток
Архивы
Физика — это область естествознания, наука, которая
изучает наиболее фундаментальные закономерности, определяющие общую структуру и
эволюцию материального мира. Являясь одним из трех китов, на которых зиждется
современная система мироустройства, физика, является наукой о природе в самом
широком понимании этого слова! Кроме того, что она изучает материальные и
энергетические параметры организации вселенной, она также ставит перед собой
задачи пояснения и логического обоснования фундаментальных взаимодействий в
природе, управляющих движением материи.
Умение решать физические задачи – одно из свойств
человеческого интеллекта. С помощью решения задач обобщаются знания о
конкретных объектах и явлениях, создаются и решаются проблемные ситуации,
формируются практические умения и навыки, обобщаются знания из истории, науки и
техники, формируются такие качества личности, как целеустремленность,
настойчивость, аккуратность, внимательность, дисциплинированность, развиваются
эстетические чувства, формируются творческие способности. В период ускорения
научно – технического прогресса на каждом рабочем месте необходимы умения
ставить и решать задачи науки и техники. Поэтому целью физического образования
является формирование умений работать со школьной учебной физической задачей.
Основная цель, которая ставится при решении задач,
заключается в том, чтобы учащиеся глубже поняли физические закономерности,
научились разбираться в них и применять их к анализу физических явлений, к
практическим вопросам.
Типы задач по физике
Глобально
все задачи можно разделить на 2 основные группы:
1.
Базовые
(физические) задачи – задачи, в которых нужно определить физический закон или
физическое явление и применить соответствующую формулу.
2.
Комбинированные
задачи – задачи, в которых нужно применить законы из нескольких разделов
физики.
По
содержанию физические задачи разделяют прежде всего на задачи по механике,
молекулярной физике, электродинамике. Такое деление условно, так как часто в
условии используются сведения из нескольких разделов физики. Данный вид задач
часто применяется на экзаменах по физике.
Далее
различают задачи с :
а) абстрактным
содержанием (Какую максимальную скорость может развить велосипед движущийся по
окружности радиуса r, если коэффициент трения покоя равен k?). такие задачи
используются при повторении материала, особенно при подготовки к экзаменам.
б) конкретным
содержанием, указав конкретное значение r и k получим задачу с конкретным
содержанием.
Такие задачи дают
связь с действительностью, жизненным опытом учащихся.
Познавательный
интерес только тогда имеет прочную основу для своего развития, когда учителю и
ученикам будет понятна связь между содержанием учебного материала и его
назначением в жизни. Очень важно понимать для чего, зачем мы изучаем те или
иные явления природы и насколько велико их значение в развитии цивилизации.
Качественные
задачи появились около 200 лет назад. Главная особенность качественной задачи
состоит в том, что в ней внимание учащихся акцентируется на объяснении
физических явлений, свойств тел, вещества, изучаемых процессов. Цель их не
формальное закрепление полученных на уроках знаний и механическое заучивание
физических терминов и формул, а разносторонний анализ явлений, законов природы,
технических достижений.
В
качественной задаче по физике для разрешения ставится проблема, связанная с
качественной стороной физического явления. Решается такая задача или путем
логических умозаключений, базирующихся на законах физики, или графически, или
экспериментально в условиях лабораторных исследований. Математические действия
при решении задачи обычно не применяются. В качественной задаче ставится такой
вопрос, ответ на который ученик должен составить сам, синтезируя данные условия
задачи и свои знания по физике. Метод решения таких задач можно назвать
аналитико-синтетическим методом. Центр тяжести в таких задачах переносится на
логическое решение, которое осуществляется на основе применения физических
законов, соотношений между физическими величинами, известных фактов.
Все физические
задачи, независимо от раздела, можно решить, выполняя определённые шаги,
которые назовём
«Алгоритм
решения задач по физике»
1. Внимательно
прочитайте задачу.
2. Запишите в
«Дано» все данные и правильно запишите искомую величину.
3. Сделайте
перевод единиц в СИ, если это необходимо.
4. Сделайте
чертёж или схему, если это необходимо.
5. Напишите
формулу или закон, по которым находится искомая величина.
6. Запишите
дополнительные формулы, если это необходимо. Сделайте математические
преобразования.
7. Подставьте
цифровые значения в окончательную формулу. Вычислите ответ. Проанализируйте
его.
8. Запишите ответ.
9. Похвалите себя.
Алгоритм
решения задач очень хорошо помогает отработать навыки применения базовых знаний
по конкретным темам и разделам физики. Это является основным инструментом
учителя и учащегося при подготовке к итоговой аттестации в форме ОГЭ и ЕГЭ.
Алгоритм
решения задач на «Газовые законы»:
1.
Проанализировать условие задачи: выяснить, сколько состояний газа
рассматривается в задаче.
2.
Записать краткое условие задачи в единицах СИ.
3.
Записать параметры p,V и T, характеризующие каждое состояние газа. Определить
какой процесс произошёл.
4.
Записать уравнение закон Клапейрона — Менделеева для данных состояний.
5.
Вывести формулу для расчёта искомой величины.
6.
Вычислить значение искомой величины.
7.
Проконтролировать размерность и ответ.
Алгоритм
решения задач на «Основы термодинамики»
1.
Проанализировать условие задачи: проверить систему тел на замкнутость;
определить, какие тела участвуют в теплообмене.
2. Записать
краткое условие задачи в единицах СИ.
3. Определить для
каждого тела, какие процессы с ним происходят при теплообмене.
4. Записать для
каждого процесса формулу для вычисления количества теплоты, выделенной или
поглощённой.
5. Составить
уравнение теплового баланса.
6. Вывести формулу
для расчёта искомой величины.
7. Вычислить
значение искомой величины.
8.
Проконтролировать размерность и ответ.
Значение
качественных задач трудно переоценить. Они способствуют углублению и
закреплению теоретических знаний учащихся. Приближая изучаемую теорию к
окружающей жизни, они усиливают интерес к предмету, способствует развитию
наблюдательности.
Метод
решения этих задач, заключающийся в построении логических умозаключений,
основанных на физических законах, служит прекрасной школой мышления,
вырабатывает четкое понимание сущности физических явлений и их закономерностей,
учит учащихся применять знания на практике. Эти задачи прививают любознательность,
желание узнать, почему так происходит, умение ставить проблему и, что не менее
важно решать ее. В последние годы количество качественных задач в материалах
ОГЭ и ЕГЭ повышается.
Литература:
Алгоритм решения
задач по физике — http://www.tutoronline.ru/blog/algoritm-reshenija-zadach-po-fizike
ЕГЭ —
http://4ege.ru/fizika/51877-algoritm-resheniya-zadach-po-fizike.html
Качественные
задачи в курсе физики —
http://nsportal.ru/shkola/fizika/library/2013/11/03/kachestvennye-zadachi-v-kurse-fiziki
Решение задач и
физический эксперимент в школьном курсе физики —
http://portal.snauka.ru/2013/03/863
Физика – наука о природе —
http://www.all-fizika.com/article/index.php?id_article=656
Муниципальное
общеобразовательное учреждение «Средняя общеобразовательная школа №16 села
Томузловского Буденновского района» Ставропольского края
Решение
задач по термодинамике
(Доклад
на РМО по физике)
Работу
подготовила
учитель
физики
МОУ
СОШ№16 с.Томузловского
Поделякина
Т.В.
2017
год
В данной разработке содержатся задачи для 9 -11 классов на составление уравнения теплового баланса аналогичные материалам ЕГЭ и ОГЭ, составленные в соответствии с Программой общеобразовательных учреждений по физике.
Задачи содержат решение и ответ. Материал поможет учащимся закрепить и систематизировать знания по данной теме при подготовке к ОГЭ и ЕГЭ.
©
Трусов Александр Анатольевич
Трусов Александр Анатольевич
Понравилось? Сохраните и поделитесь:
По кнопке ниже вы можете скачать методическую разработку «Решение задач на теплообмен с использованием уравнения теплового баланса» категории «ЕГЭ по физике» бесплатно. Будем благодарны, если вы оставите отзыв или посмотрите еще другие материалы на нашем сайте. Характеристики документа: «задачи».
Загрузка началась…
Понравился сайт? Получайте ссылки
на лучшие материалы еженедельно!
Подарок каждому подписчику!
Задачи на количество теплоты с решениями
Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».
Название величины |
Обозначение |
Единица измерения |
Формула |
Масса |
m |
кг |
|
Температура |
t |
°С |
|
Удельная теплоемкость |
c |
Дж/кг•°С |
|
Количество теплоты |
Q |
Дж |
|
1 г = 0,001 кг; 1 т = 1000 кг; 1 кДж = 1000 Дж; 1 МДж = 1000000 Дж
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?
При решении задачи нужно учесть, что оба тела — и котёл, и вода — будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С — 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.
Задача № 2.
Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.
Задача № 3.
Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?
Задача № 4.
В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь
Задача № 5.
На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?
Задача № 6.
По графику определите удельную теплоёмкость образца, если его масса 50 г.
Задача № 7.
Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?
Задача № 8.
Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?
Задача № 9.
Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?
Задача № 10.
Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?
Задача № 11.
а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух?
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)
Задача № 12.
ОГЭ
Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой mв = 300 г, а температура tв = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды св = 4200 Дж/(кг К).
Задача № 13.
В теплоизолированном сосуде сначала смешивают три порции воды 100 г, 200 г и 300 г с начальными температурами 20 °C, 70 °C и 50 °C соответственно. После установления теплового равновесия в сосуд добавляют новую порцию воды массой 400 г при температуре 20 °C. Определите конечную температуру в сосуде. Ответ дайте в °C, округлив до целого числа. Теплоёмкостью калориметра пренебрегите.
Решение.
Ответ: 39 °С.
Задача № 14. (повышенной сложности)
Стальной шарик радиусом 5 см, нагретый до температуры 500 ˚С, положили на лед, температура которого 0 ˚С. На какую глубину погрузится шарик в лед? (Считать, что шарик погрузился в лед полностью. Теплопроводностью шарика и нагреванием воды пренебречь.)
Дано: R = 0,05 м; t1 = 500 ˚С; t2 = 0 ˚С;
ρ1 (плотность стали) = 7800 кг/м3.;
ρ2 (плотность льда) = 900 кг/м3.
c (удельная теплоемкость стали) = 460 Дж/кг •˚С,
λ (удельная теплота плавления льда) = 3,3 • 105 Дж/кг,
Найти: h – ?
Краткая теория для решения Задачи на количество теплоты.
Конспект урока «Задачи на количество теплоты».
Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»
Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».
Уравнение теплового баланса. Пособие Самарина
При соприкосновении тел, имеющих разные температуры, между этими телами происходит теплообмен. С точки зрения молекулярно-кинетической теории, это объясняется так: молекулы более нагретого тела имеют большую кинетическую энергию, чем молекулы тела, менее нагретого. При «столкновениях» молекул соприкасающихся тел происходит процесс выравнивания их средних кинетических энергий. Молекулы более нагретого тела теряют часть своей кинетической энергии, при этом нагретое тело будет остывать. Кинетическ…
Поделитесь с коллегами:
Лицей естественных наук г. Кирова
Г.Г. Самарин
Решение задач на теплообмен
с использованием уравнения теплового баланса
(методические рекомендации)
Киров
2002
ББК 74.204.2
С 17
Печатается по решению редакционно-издательского совета Лицея естественных наук г. Кирова
Рецензент: К.А. Коханов, кандидат педагогических наук, старший преподаватель кафедры дидактики физики Вятского государственного гуманитарного университета, заместитель заведующего кафедрой дидактики физики.
С 17 Самарин Г.Г. Решение задач на теплообмен с использованием уравнения теплового баланса: Методические рекомендации. — Киров: Издательство Лицея естественных наук, 2002. — 35 с.
Пособие рекомендовано учащимся, желающим получить практические навыки в решении задач на теплообмен, и может быть полезным для учителей и абитуриентов.
© Лицей естественных наук, 2002
© Г.Г. Самарин, 2002
При соприкосновении тел, имеющих разные температуры, между этими телами происходит теплообмен. С точки зрения молекулярно-кинетической теории, это объясняется так: молекулы более нагретого тела имеют большую кинетическую энергию, чем молекулы тела, менее нагретого. При «столкновениях» молекул соприкасающихся тел происходит процесс выравнивания их средних кинетических энергий. Молекулы более нагретого тела теряют часть своей кинетической энергии, при этом нагретое тело будет остывать. Кинетическая энергия молекул холодного тела возрастает, поэтому температура этого тела будет увеличиваться. В конечном итоге кинетические энергии молекул обоих тел сравняются, и температуры тел станут одинаковыми. На этом теплообмен прекращается.
Энергию, которую тело получает или отдаёт в процессе теплообмена, называют количеством теплоты (Q).
Количество теплоты, как и все другие виды энергии, измеряется в системе СИ в Джоулях: [Q] = Дж.
Нагревание или охлаждение
При нагревании или охлаждении тела количество теплоты, поглощаемое или выделяемое им, рассчитывается по формуле:
Q = сm(t2 — t1), (1)
где m — масса тела, кг;
(t2 — t1) — разность температур тела,С (или К);
с — удельная теплоёмкость вещества, из которого состоит тело,
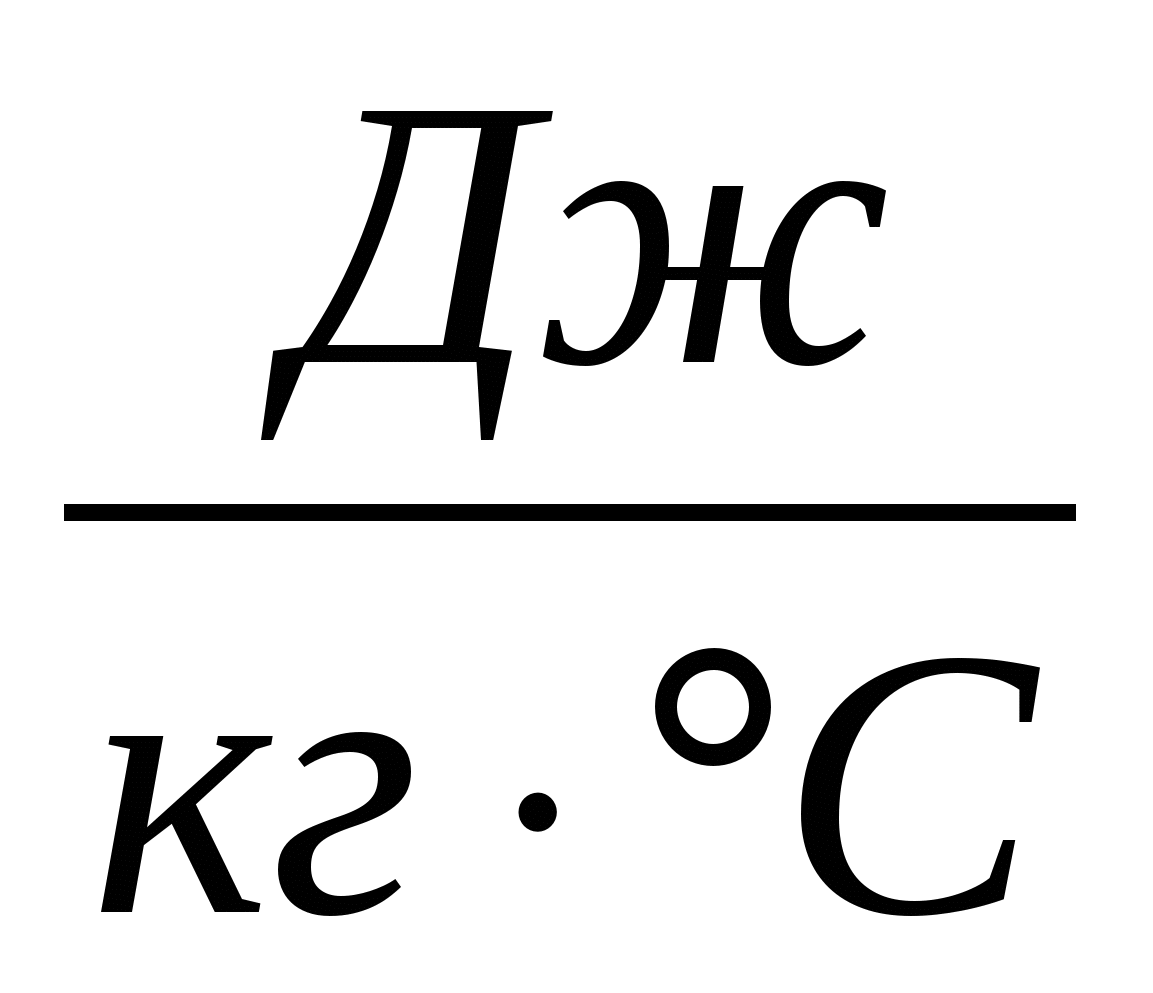
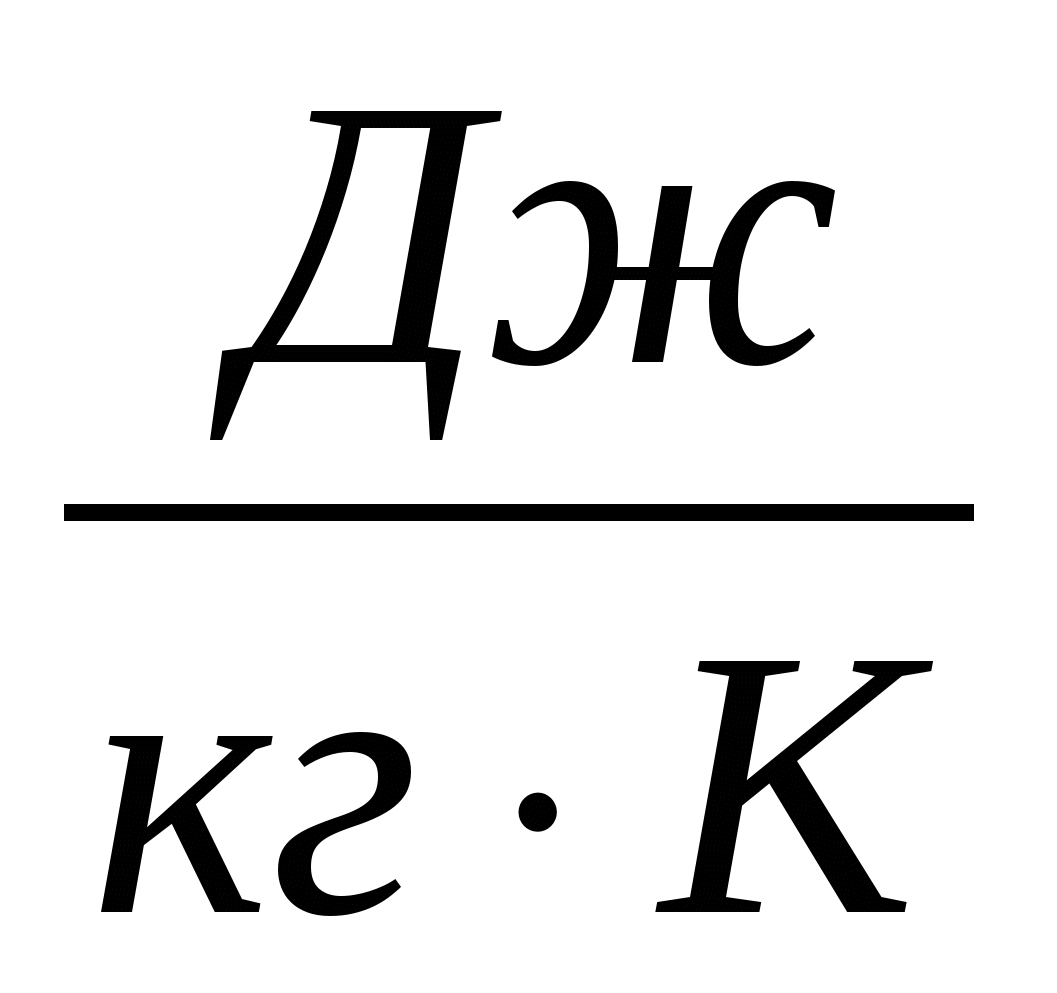
Удельная теплоёмкость вещества — это количество теплоты, которое нужно сообщить одному килограмму данного вещества, чтобы увеличить его температуру на 1С (или это количество теплоты, которое выделяет один килограмм данного вещества, остывая на 1С).
Например, Своды = 4200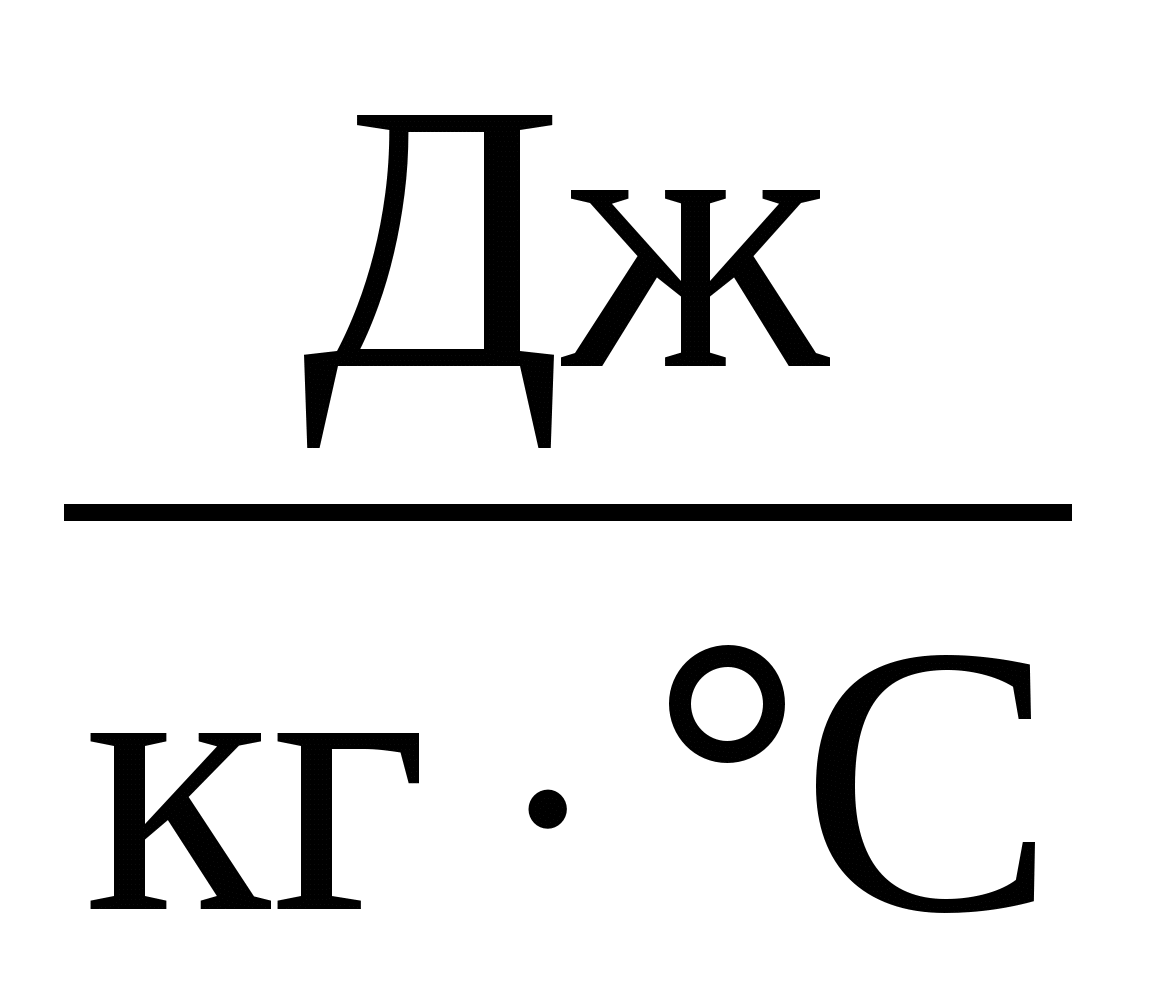
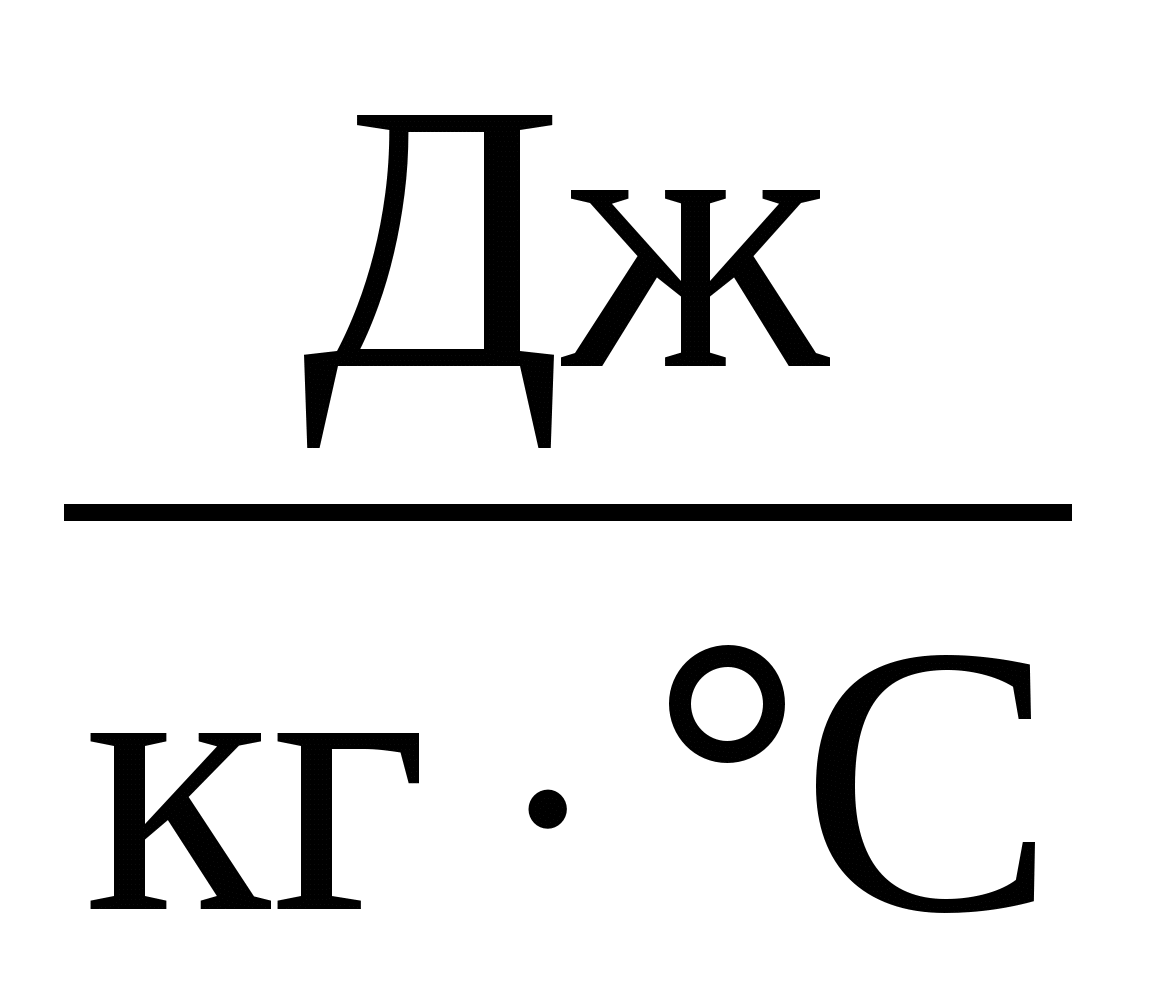
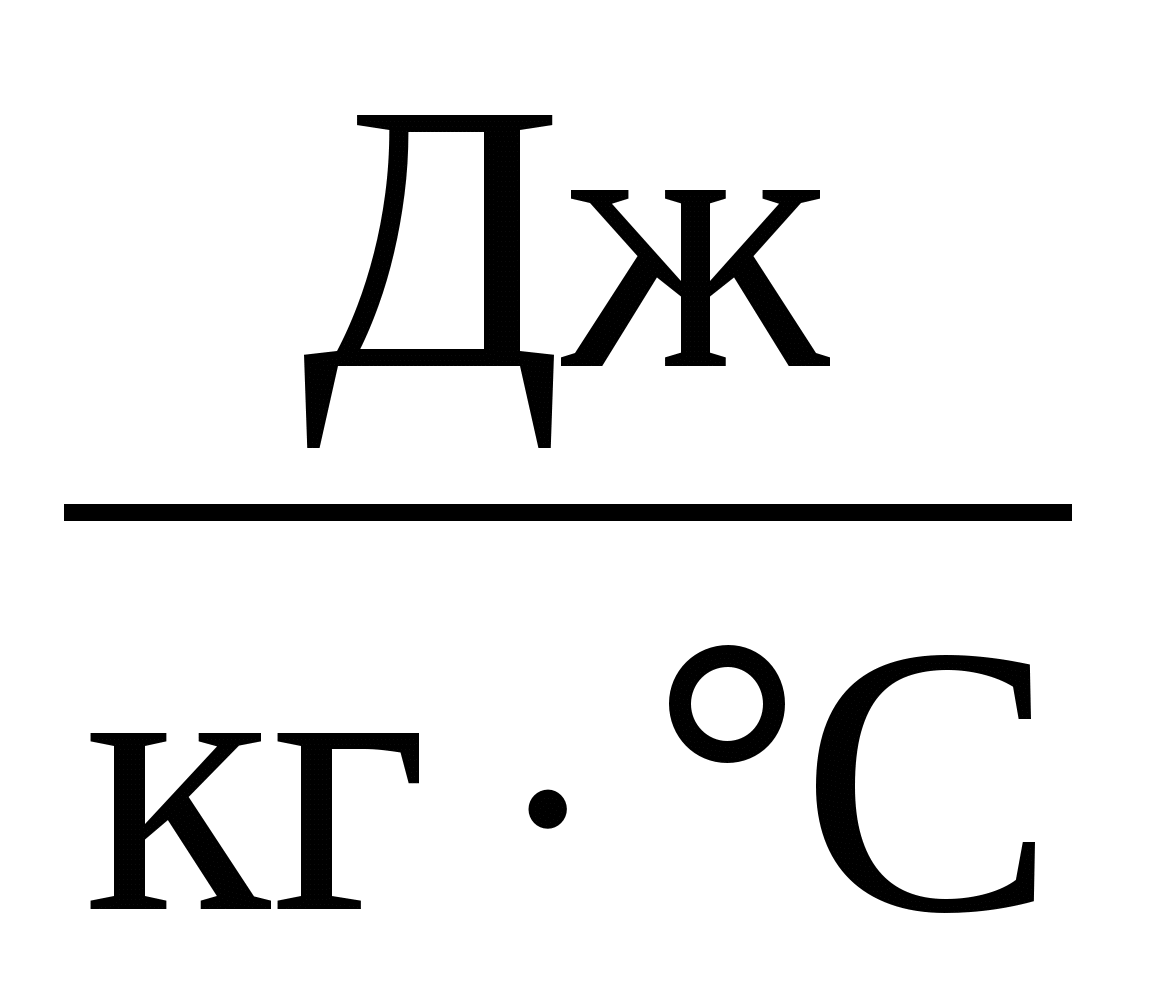
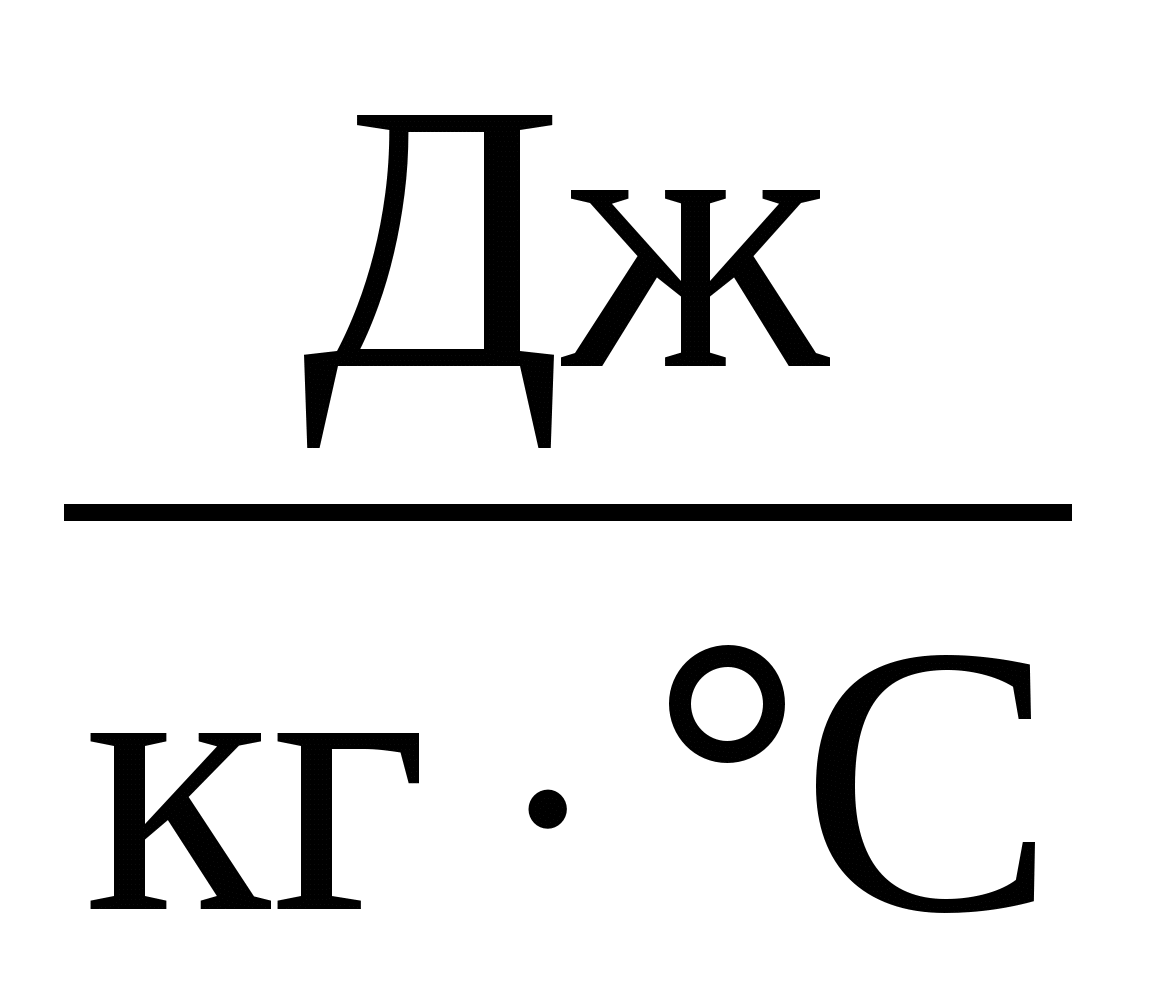
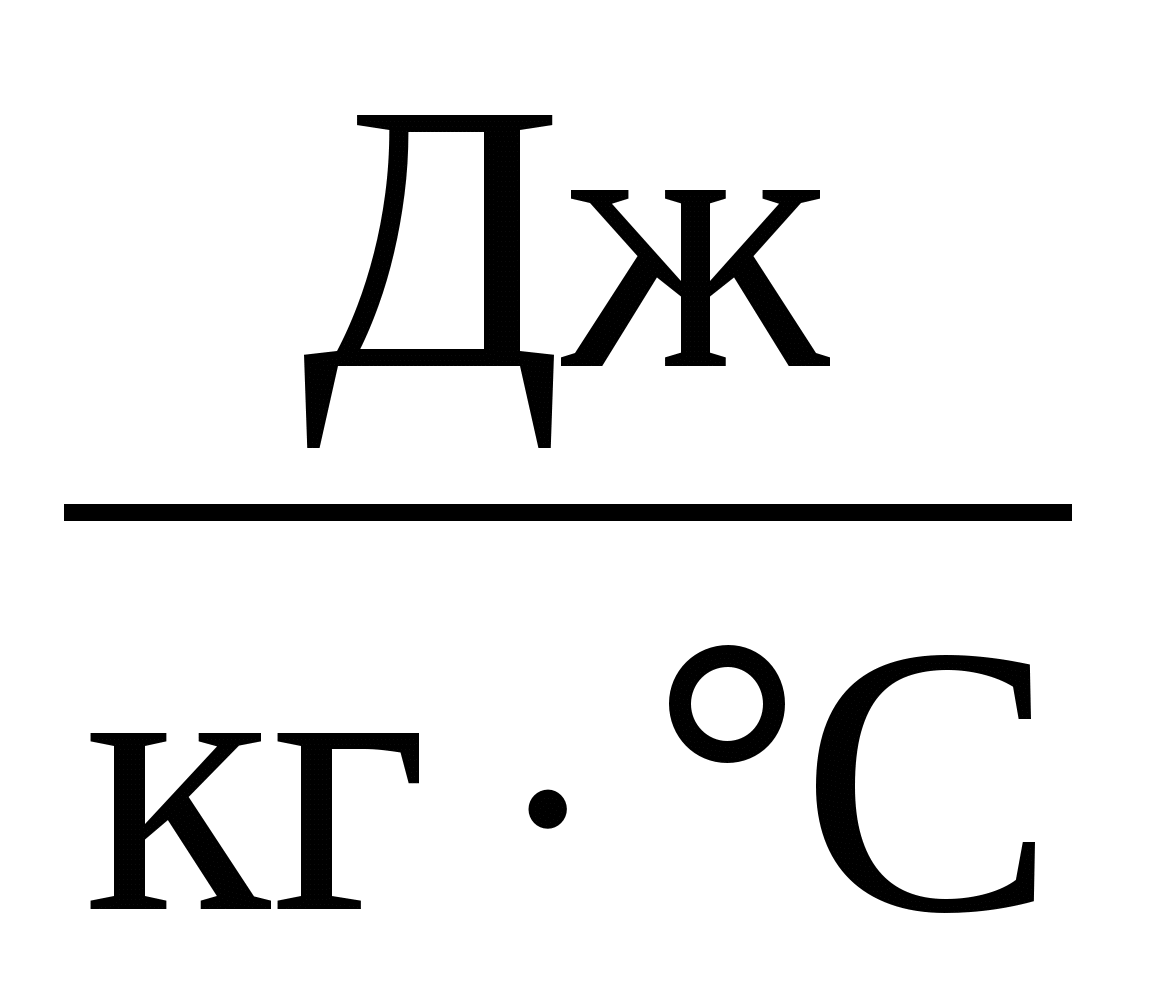
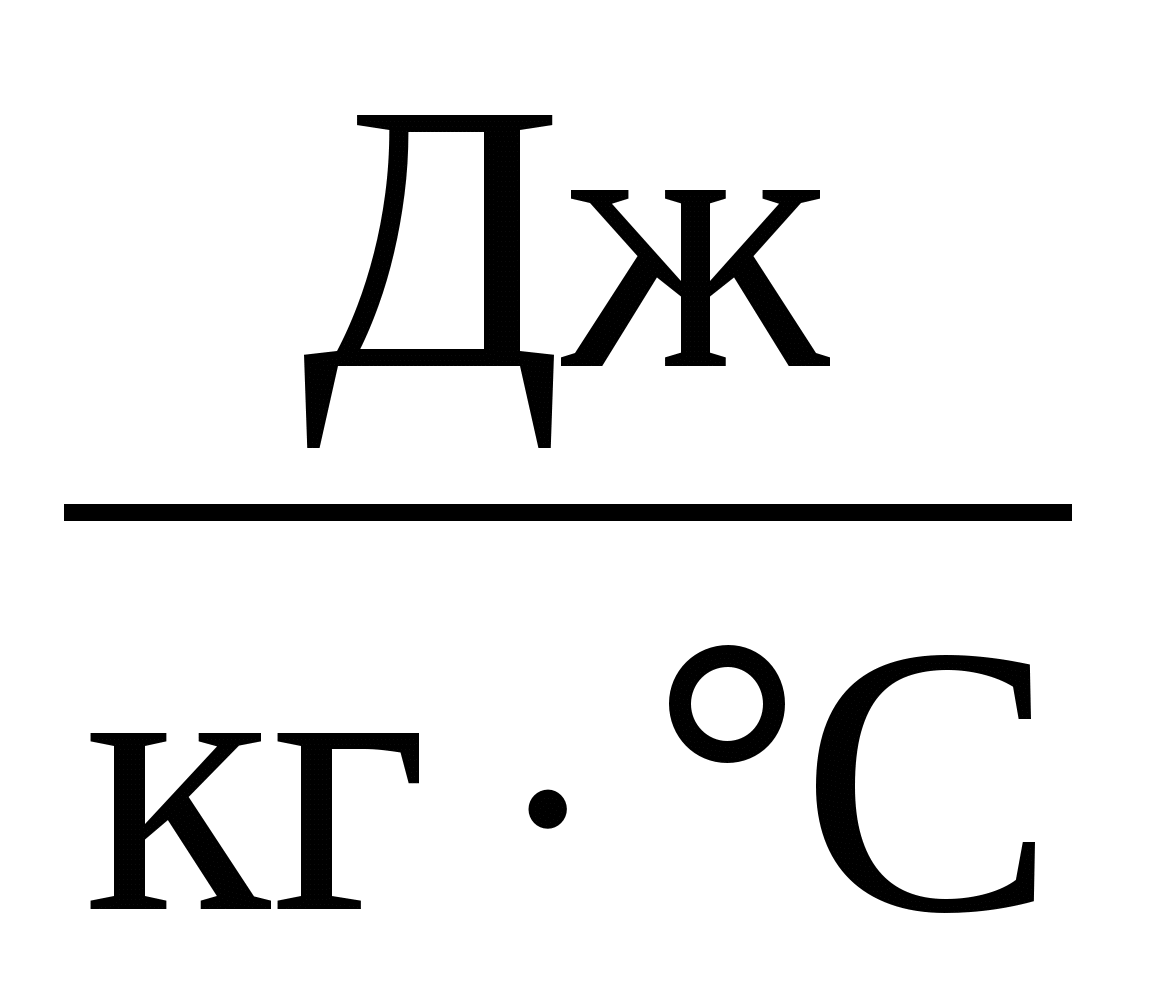
Значения удельных теплоемкостей других веществ можно найти в справочниках, а также в школьном учебнике или задачнике.
При нагревании тела его внутренняя энергия увеличивается. Это требует притока энергии к телу от других тел. Значит, оно поглощает некоторое количество теплоты, принимая его от других тел, участвующих в теплообмене.
При охлаждении тела его внутренняя энергия уменьшается. Поэтому остывающее тело отдаёт кому-либо некоторое количество теплоты.
Обычно конечную температуру, установившуюся в результате теплообмена, обозначают греческой буквой (тэта).
В формуле (1) произведение cm для каждого конкретного тела есть величина постоянная. Её называют теплоёмкостью тела и обозначают С:
C = cm.(2)
Размерность теплоемкости: [С] = 
Теплообмен между телами, имеющими одинаковые температуры, не происходит, даже если контактируют вещества, находящиеся в разных агрегатных состояниях. Например, при температуре плавления (0С) лёд и вода могут находиться бесконечно долго, при этом количество льда и количество воды останутся неизменными. Аналогично ведут себя пар и жидкость, находящиеся при температуре кипения. Теплообмен между ними не происходит.
Плавление или кристаллизация
Если при нагревании тела его температура достигнет температуры плавления, то начинает происходить процесс перехода этого вещества из твердого состояния в жидкое. При этом идут изменения в расположении и характере взаимодействия молекул. Температура при плавлении не изменяется. Это означает, что средние кинетические энергии молекул жидкости и твердого тела при температуре плавления одинаковы. Однако внутренняя энергия тела при плавлении возрастает за счет увеличения энергии взаимодействия молекул. Количество теплоты, поглощаемое телом при плавлении, рассчитывается по формуле
Q = m(3),
где m — масса тела, кг;
— удельная теплота плавления, 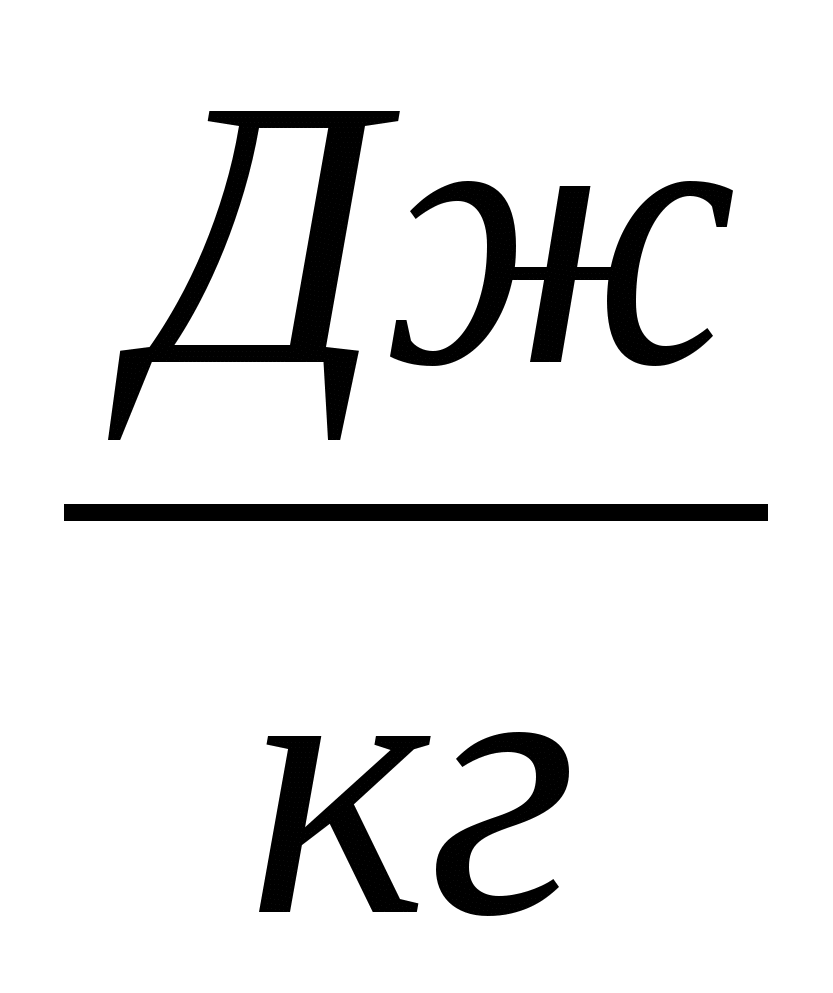
При кристаллизации, наоборот, внутренняя энергия тела уменьшается на величину Q = m, и эта теплота данным телом выделяется. Она поглощается другими телами, участвующими в теплообмене.
Удельная теплота плавления показывает, сколько энергии нужно сообщить одному килограмму данного вещества, взятого при температуре плавления, чтобы полностью превратить его при этой температуре в жидкость (или сколько энергии выделяет 1 кг жидкости, взятой при температуре кристаллизации, если вся она при этой температуре полностью превратится в твёрдое тело).
Удельную теплоту плавления любого вещества можно найти в справочниках. Для льда же = 3,4105 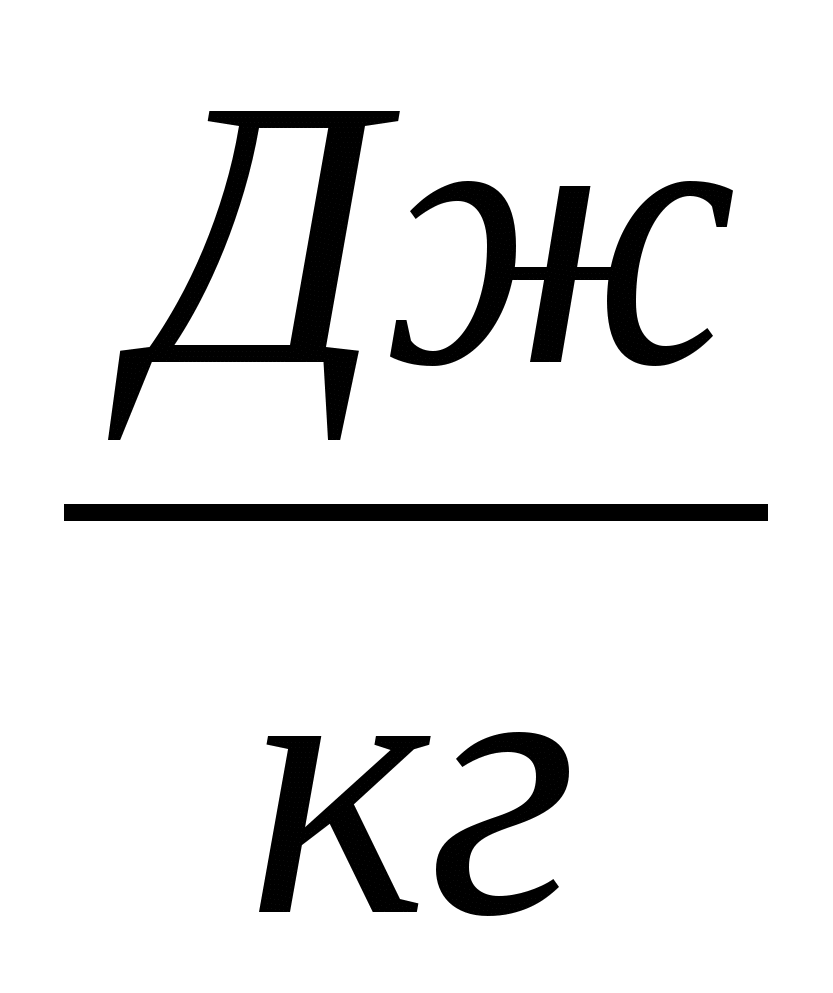
Температура плавления у каждого вещества своя. Её также можно найти в справочниках. Важно подчеркнуть, что температура плавления вещества равна температуре кристаллизации этого же вещества. У льда tпл = 0С.
Кипение или конденсация
При достижении жидкостью температуры кипения начинает происходить другой фазовый переход — кипение, при котором расстояния между молекулами значительно увеличиваются, а силы взаимодействия молекул уменьшаются. Вся подводимая к жидкости теплота идет на разрыв связей между молекулами. При конденсации пара в жидкость, наоборот, расстояния между молекулами значительно сокращаются, а силы взаимодействия молекул увеличиваются. Для кипения жидкости энергию к жидкости нужно подводить, при конденсации пара энергия выделяется. Количество теплоты, поглощаемое при кипении или выделяемое при конденсации, рассчитывается по формуле:
Q = Lm (4),
где m — масса тела, кг;
L — удельная теплота парообразования, 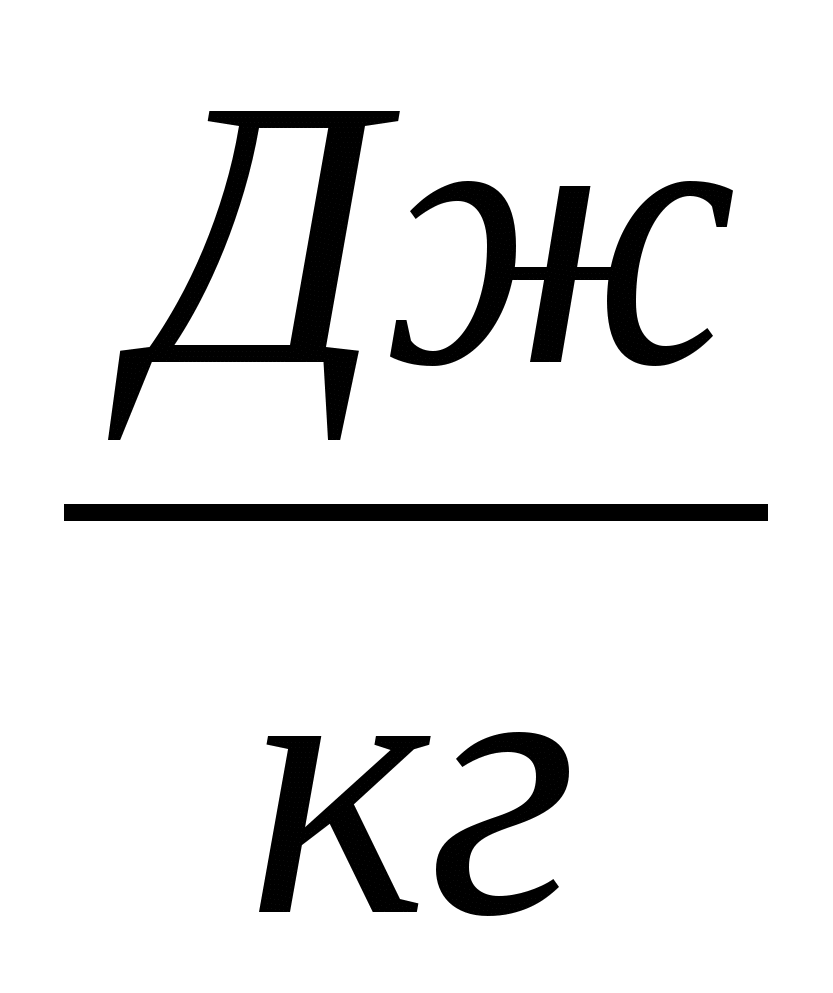
Удельная теплота парообразования показывает, сколько энергии нужно сообщить одному килограмму жидкости, взятой при температуре кипения, чтобы при этой температуре полностью превратить её в пар (для конденсации: сколько энергии выделяет один килограмм пара, взятого при температуре конденсации, полностью превращаясь в жидкость).
При одинаковом давлении температура кипения и температура конденсации одного и того же вещества одинаковы.
Температуры кипения и удельные теплоты парообразования также можно найти в справочниках. Для воды же они соответственно равны: tкип = 100С, L = 2,3106 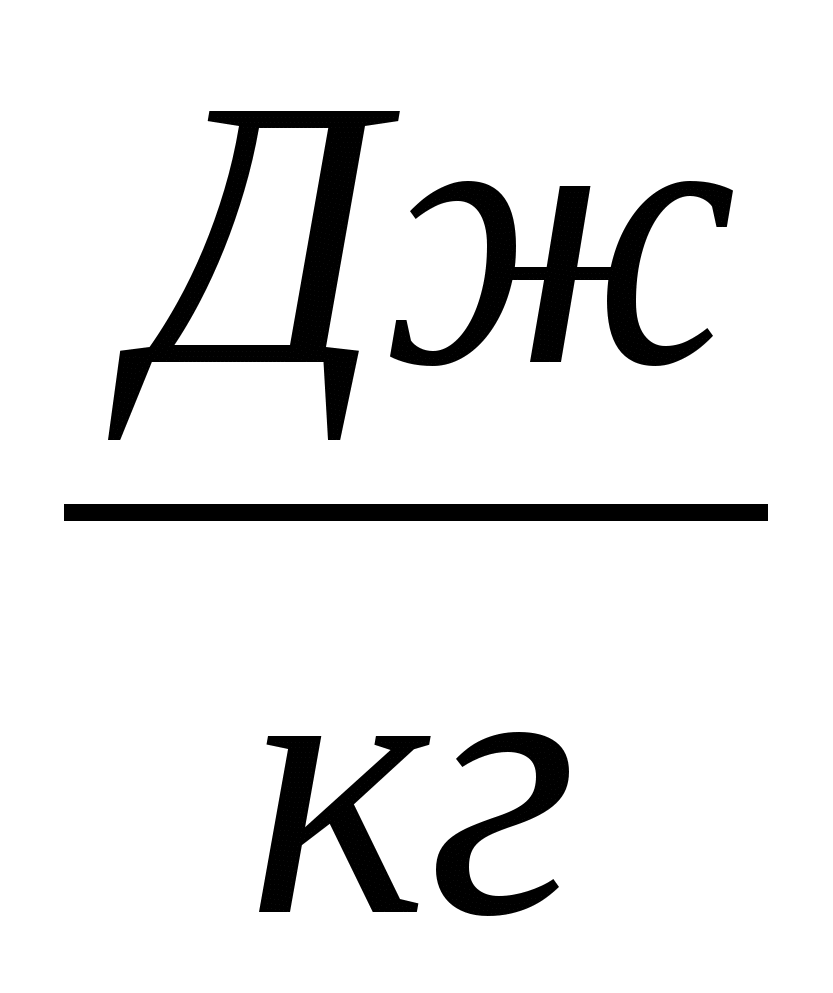
Уравнение теплового баланса
Тела, участвующие в теплообмене, представляют собой термодинамическую систему. Термодинамическая система называется теплоизолированной, если она не получает энергию извне и не отдаёт её; теплообмен происходит только между телами, входящими в эту систему. Для любой теплоизолированной системы тел справедливо следующее утверждение: количество теплоты, отданное одними телами, равно количеству теплоты, принимаемому другими телами.
Qотд. = Qполуч.(5)
Это утверждение описывает частный случай закона сохранения и превращения энергии в применении к процессу теплообмена. А формула (5) является одним из видов уравнения теплового баланса.
При решении задач с помощью данного вида уравнения теплового баланса в формуле (1) в качестве t2 следует брать большую температуру, а в качестве t1 — меньшую. Тогда разность (t2 — t1) будет положительна и всё произведение cm(t2-t1) также будет положительным. Все теплоты, отданные и полученные, будут положительными.
Уравнение теплового баланса можно записать и в таком виде:
Q1+ Q2+…+ Qn= 0,(6)
Где n — количество тел системы.
Алгебраическая сумма всех количеств теплоты (поглощенных и выделенных) в теплоизолированной системе равна нулю.
Q1, Q2, …, Qn — это теплоты, поглощаемые или выделяемые участниками теплообмена. Очевидно, что в этом случае какие-то теплоты должны быть положительны, а какие-то — отрицательны. При записи уравнения теплового баланса в виде (6) всегда t2 — конечная температура, а t1 — начальная.
Если тело нагревается, то разность (t2 — t1)положительна и все произведение cm(t2 — t1) положительно. То есть Q > 0 тогда, когда теплота к данному телу подводится.
А если t2 < t1 (тело остывает), то разность (t2 — t1) отрицательна, то есть Q < 0. В этом случае тело энергию выделяет.
Если при фазовом переходе энергия к телу подводится (плавление, кипение), то Q > 0; если тело выделяет энергию (кристаллизация, конденсация), то Q < 0.
В принципе уравнения (5) и (6) равносильны. Результат решения задачи не зависит от того, каким видом уравнения пользуемся. Выбор способа решения — за читателем.
Применим уравнение теплового баланса для решения ряда задач.
Задача 1
В медном калориметре массой 100 г находится 1 кг воды при температуре 20С. В воду опускают свинцовую деталь массой 2 кг, имеющую температуру 90С. До какой температуры нагреется вода? Потерями теплоты пренебречь.
Решение
m
с1= 380 Дж/(кг0С)
t2 = 20С
m2 = 1 кг
с2=4200 Дж/(кг0С)
m3 = 2 кг
с3= 140 Дж/(кг0С)
t3 = 90С

Проведём анализ:
Вода и калориметр находились в тепловом равновесии, поэтому они имели одинаковую температуру: t1 = t2 = 20С.
При опускании в воду с температурой 20С свинцового тела с температурой 90С между водой и свинцом будет происходить теплообмен. Свинец будет остывать, а вода — нагреваться. В этом же процессе участвует и калориметр, который, как и вода, будет тоже нагреваться.
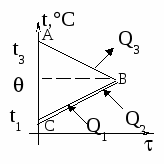
Изменение температур тел с течением времени удобно изображать на графике зависимости t().
Отрезок АВ соответствует графику изменения температуры свинцового тела. Стрелка, идущая от него, показывает, что, остывая, свинец выделяет энергию Q3.
Два параллельных отрезка СВ соответствуют графикам изменения температур калориметра и воды. Стрелки, идущие к ним, показывают, что для нагревания калориметра и воды требуется энергия Q1 и Q2, которую они поглощают.
Решим задачу с использованием уравнения теплового баланса в виде (5):
Q1 + Q2 = Q3,
c1m1( t1) + c2m2( t2) = c3m3(t3 ).
Выражаем температуру :
= 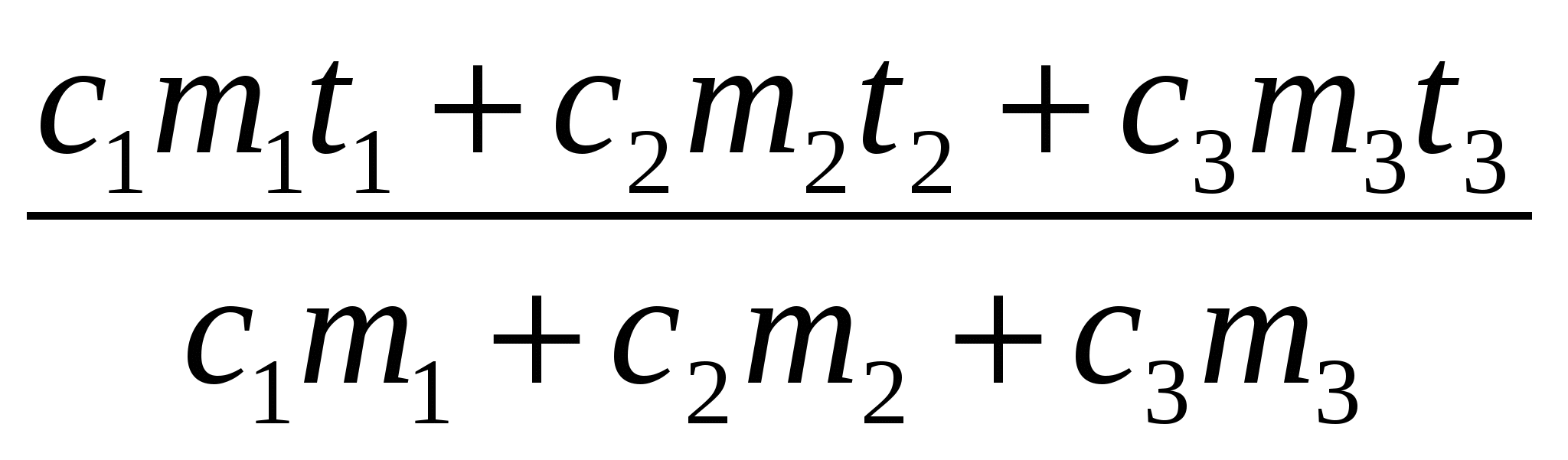
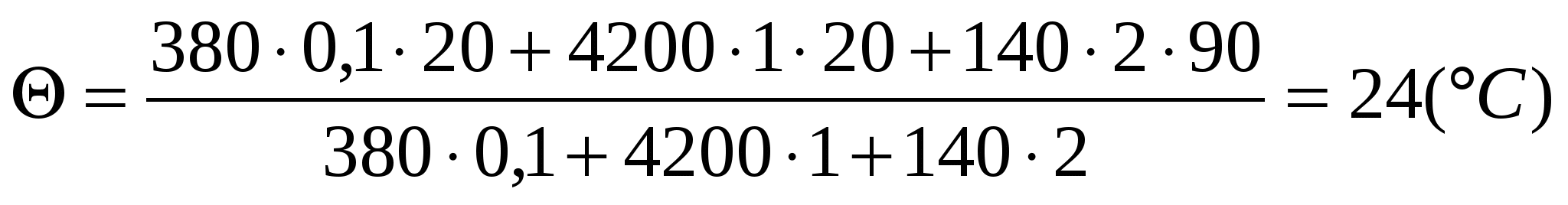
Решим задачу с использованием уравнения теплового баланса в виде (6):
Q1 + Q2 + Q3 = 0,
c1m1( t1) + c2m2( t2) + c3m3( t3) = 0.
= 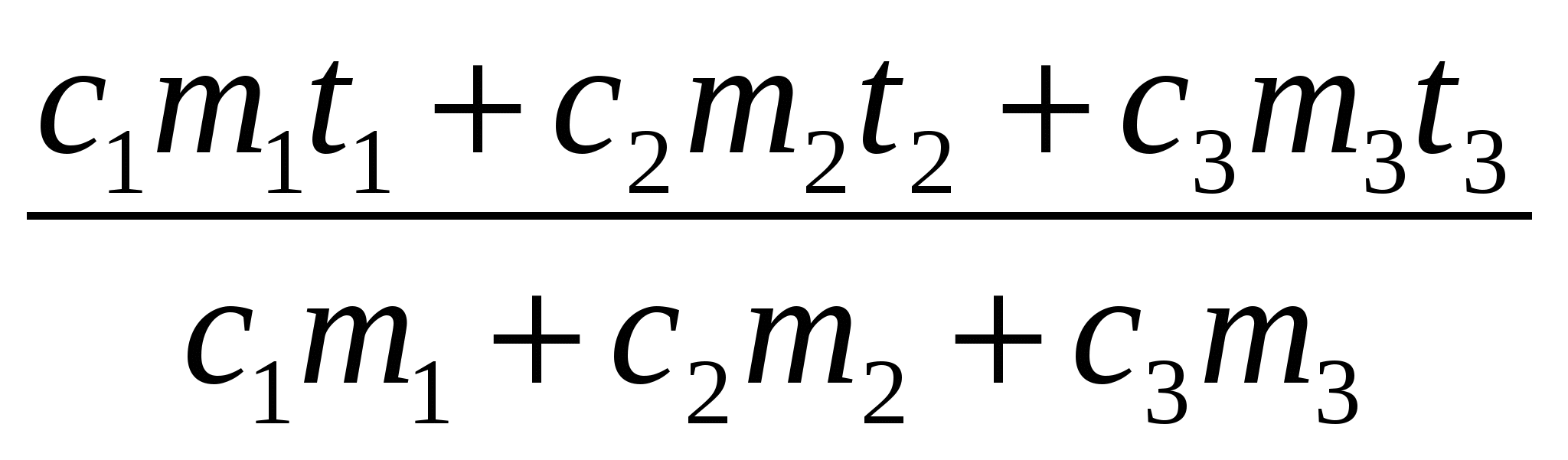
Ответ: Вода нагреется до 24 С.
Предлагаю читателю самостоятельно сделать проверку размерности.
Задача 2
Т
ри пластины: медную, имеющую массу m1 = 1 кг и температуру t1 = 100С, железную (m2 = 1,2 кг, t2 = 150С) и алюминиевую (m3 = 0,8 кг, t3 = 80С) сложили вплотную (см рис). Какую температуру будут иметь пластины, когда теплообмен прекратится? Потерями теплоты в окружающую среду пренебречь.
m1 = 1 кг
с1= 380 Дж/(кг0С)
t1 = 100С
m2 = 1,2 кг
с2= 460 Дж/(кг0С)
t2 = 150С
m3 = 0,8 кг
с3= 920 Дж/(кг0С)
t3 = 80С
Решение
Решим задачу с помощью уравнения теплового баланса в виде (5).
1 . Не трудно догадаться, что в результате теплообмена самая горячая пластина остынет, а самая холодная нагреется. Итак, мы знаем, что будет происходить с железной и алюминиевой пластинами: железная будет остывать, алюминиевая — нагреваться.
. Не трудно догадаться, что в результате теплообмена самая горячая пластина остынет, а самая холодная нагреется. Итак, мы знаем, что будет происходить с железной и алюминиевой пластинами: железная будет остывать, алюминиевая — нагреваться.
Мысленно соединим сначала эти две пластины и найдём температуру t, которой они при этом достигнут:
Q2 = Q3
c2m2(t2 t) = c3m3(t t3)
t = 
?
t = 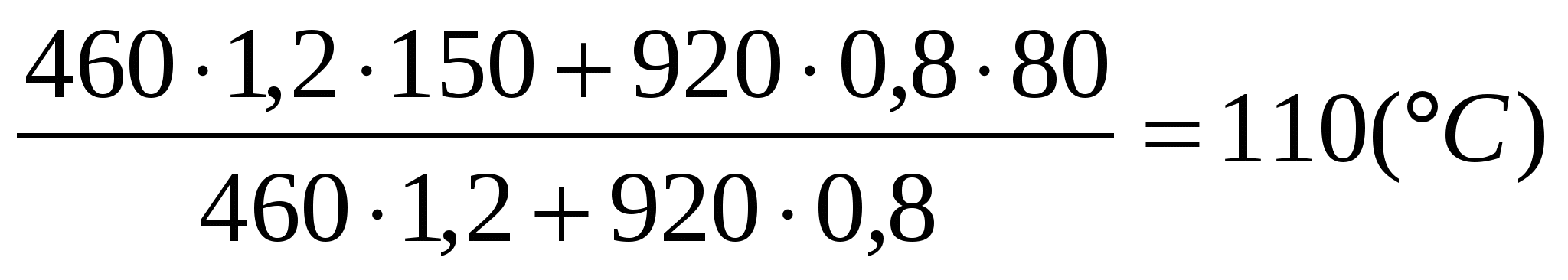
2. Теперь медная пластина вступает в теплообмен с железной и алюминиевой. Медная будет нагреваться от температуры t1 до температуры , а железная и алюминиевая — остывать от температуры t до температуры . Тогда:
Q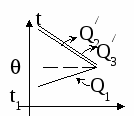
c1m1( t1) = (c2m2 + c3m3)(t ),
c1m1 — c1m1t1 = (c2m2 + c3m3)t — (c2m2 + c3m3)
= 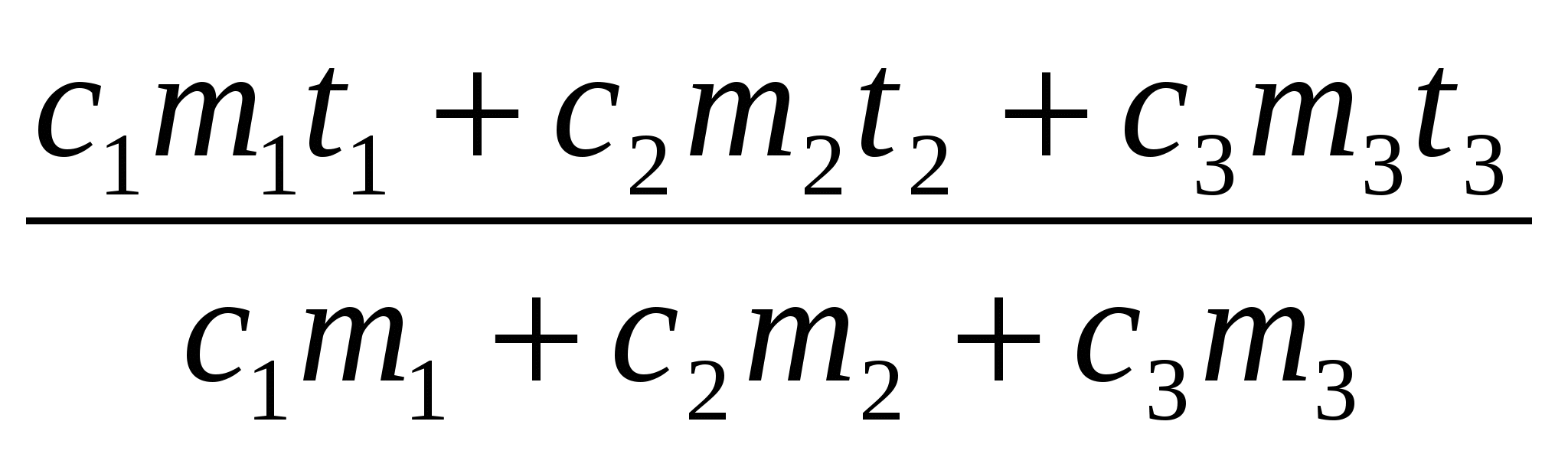
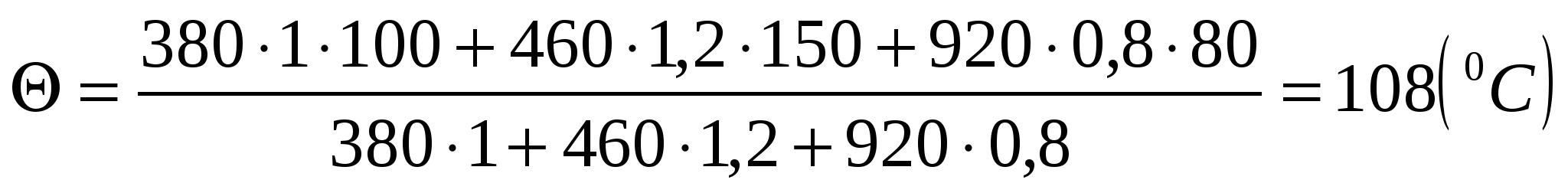
3. Решим задачу, применив уравнение теплового баланса в виде (6):
Q1 + Q2 + Q3 = 0,
c1m1( t1) + c2m2( — t2) + c3m3( t3) = 0,
= 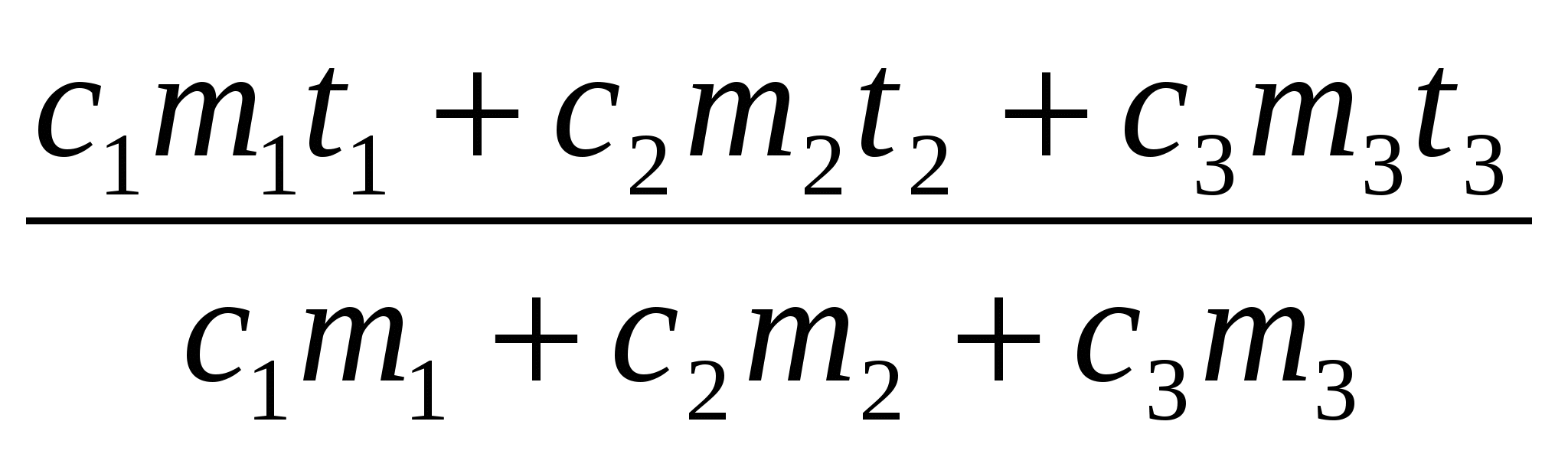
Ответ: Пластины будут иметь температуру 108 С.
Как видим, второй способ оказался и в данном случае более рациональным. Однако, первый способ зачастую оказывается более понятным, особенно при наличии фазовых переходов. Поэтому в дальнейшем автор будет придерживаться первого способа решения задач. Желательно, чтобы читатель пробовал решать их и вторым способом.
Задача 3
В железном ведре массой 1,2 кг находится 5 кг воды при температуре 20С. Сколько льда температурой —10С надо положить в ведро, чтобы температура воды понизилась до 12С? Теплообменом с окружающей средой пренебречь.
m1 = 1,2 кг
с1=460 Дж/(кг0С)
m2 = 5 кг
с2=4200 Дж/(кг0С)
t1 = t2 = 20С
t3 = 10С
с3=2100 Дж/(кг0С)
t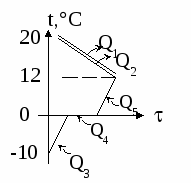
= 12С
Решение
Известна конечная температура, Значит, анализ ситуации довольно прост: вода и ведро будут остывать, не испытывая фазовых переходов, отдавая теплоты Q1 и Q2, а лёд сначала будет нагреваться до температуры плавления t4, поглощая теплоту Q3, затем плавиться,
поглощая теплоту Q4, а затем вода, образовавшаяся из льда, будет нагреваться до конечной температуры , поглощая теплоту Q5.
Так как иных участников теплообмена нет, то можно так записать уравнение теплового баланса:
Q1 + Q2 = Q3 + Q4 + Q5.
(c1m1 + c2m2)(t1 ) =
= c3m3(t4 t3) + m3 + c2m3( t4)
m3 — ?
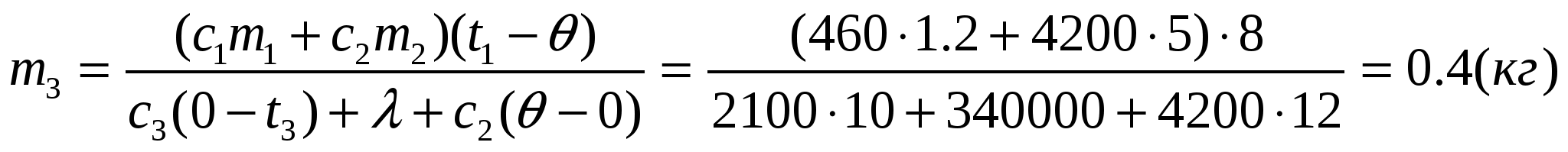
Ответ: Потребуется 0,4 кг льда.
Задача 4
В алюминиевую кастрюлю массой 200 г, содержащую 3 кг воды при 20С, поместили стальную деталь массой 0,5 кг, нагретую до 500С. При этом часть воды выкипела, а оставшаяся вода нагрелась до 22С. Сколько воды выкипело?

m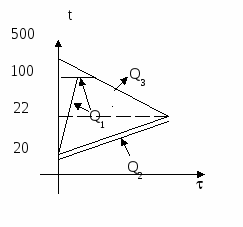
с1=4200Дж/(кгС)
m2 = 0,2 кг
с2 =920 Дж/(кгС)
t1 = t2 = 20С
= 22С
m3 = 0,5 кг
с3 = 460 Дж/(кг0С)
t3 = 500С
L = 2,3106 Дж/кг
Решение
-
Стальная деталь, не претерпевая фазовых переходов, остыла от 500С до 22С, выделив при этом количество теплоты
Q3 = c3m3(t3 ).
2. Часть воды массой m0 нагрелась до температуры кипения (100оС) и выкипела. При этом была поглощена теплота
Q1 = c1m0(100 t1) + Lm0.
3. Оставшаяся в кастрюле вода массой (m1 m0) и сама кастрюля массой m2 нагрелись от 200С до 22С. При этом была поглощена теплота
Q2 = c1(m1 m0)( t1) + c2m2( t1).
m0 — ?
4. Так как потерь тепла нет, то записываем уравнение теплового баланса:
Q1 + Q2 = Q3,
c1m0(100 t1) + Lm0 + c1(m1 m0)( t1) +
+ c2m2( t2) = c3m3(t3 ).
5. Решая это уравнение, находим m0:
m0 = 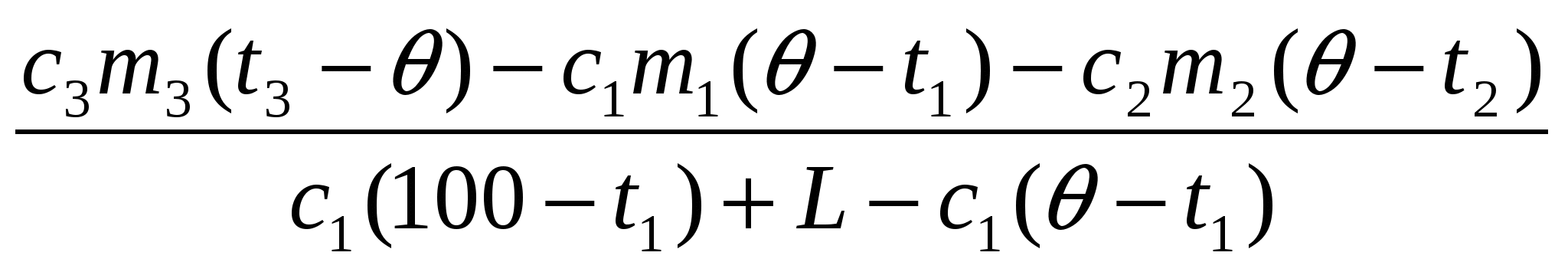
m0 = 
Ответ: Выкипело 32 г воды.
Задача 5
Комок мокрого снега массой 400 г опустили в медный таз массой 500 г, содержащий 2 кг воды при температуре 20С. После установления теплового равновесия температура воды в тазу стала 10С. Сколько воды было в комке снега?
m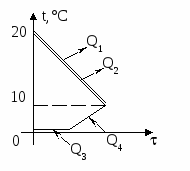
= 3,4105 Дж/кг
t1 = t2 = 20С
t3 = 0С
m1 = 0,5 кг
с1 = 380 Дж/(кг0С)
m2 = 2 кг
с2=4200Дж/(кг0С)
= 10С
Решение
1. Медный таз и вода находятся в тепловом равновесии. Поэтому 20С — их общая температура. При остывании от 20С до 10С ни медь, ни вода фазовых превращений не испытывают. При этом они отдают суммарную теплоту:
Q1 + Q2 = c1m1(t1 ) + c2m2(t2 ).
2. Мокрый снег — это снег, содержащий воду. Значит, снег и вода находятся в тепловом равновесии. Это возможно только при температуре фазового перехода, то есть при 0С.
mв — ?
Итак, начальная температура мокрого снега 0С.
3. На пути к температуре 10С снег массой m3-mв будет сначала таять. Для этого требуется теплота Q3 = (m3 mв). А затем вся вода массой m3 будет нагреваться от 0С до 10С. Для этого ей надо получить количество теплоты Q4 = c2m3( t3).
4. Так как нет потерь тепла, то можно написать уравнение теплового баланса:
Q1 + Q2 = Q3 + Q4,
с1m1(t1 ) + c2m2(t2 ) = (m3 mв) + c2m2( t3).
5. Решая это уравнение, находим mв:
mв = 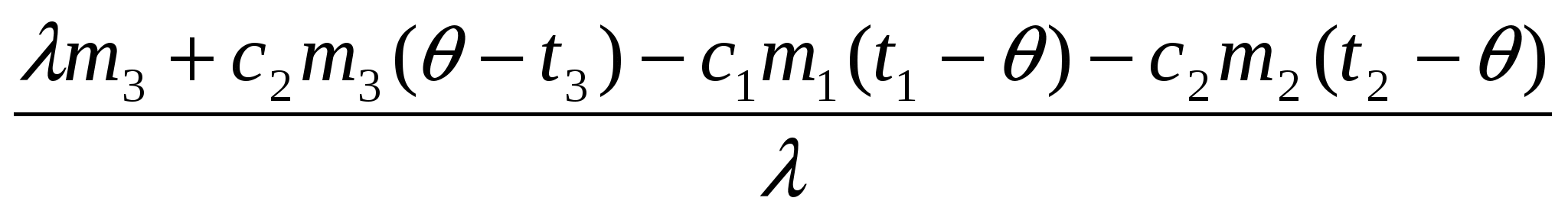
mв = 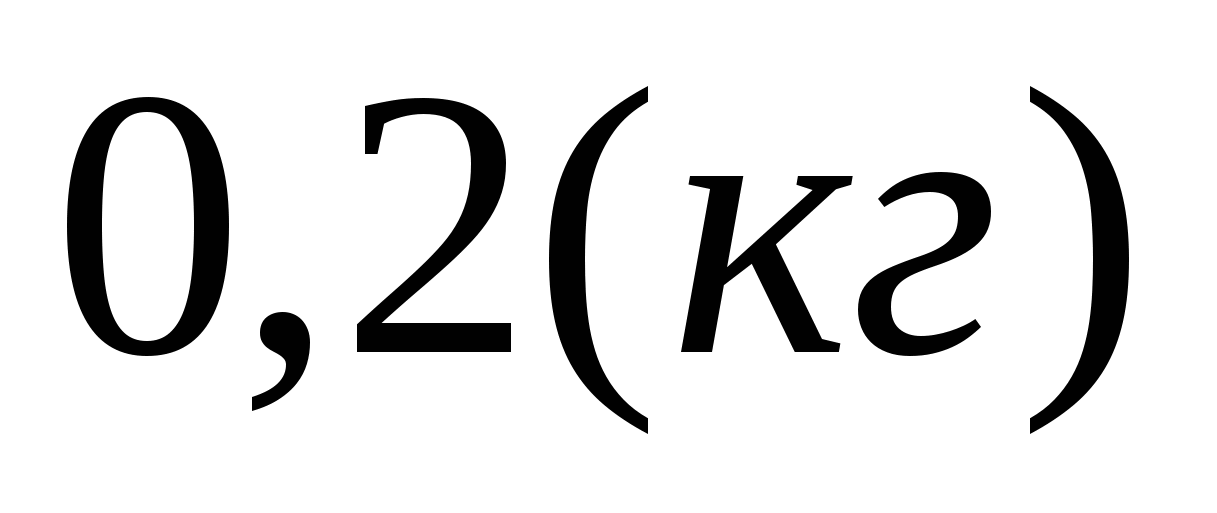
Ответ: В комке мокрого снега было 0,2 кг воды.
Задача 6
В холодную воду массой 2 кг, имеющую температуру 10С, находящуюся в кастрюле, влили 3 кг горячей воды при температуре 80С. До какой температуры нагреется холодная вода, если известно, что 25% теплоты, отданной горячей водой, пошло на нагревание кастрюли? Какова теплоемкость кастрюли?
M1 = 2 кг
t1 = 10С
m2 = 3 кг
t2 = 80С
1=0,25 (25%)
Решение
Так как 25% теплоты отданы кастрюле, то 75% теплоты пошло на нагревание холодной воды. Значит, можно говорить о КПД процесса нагревания холодной воды:
2 = 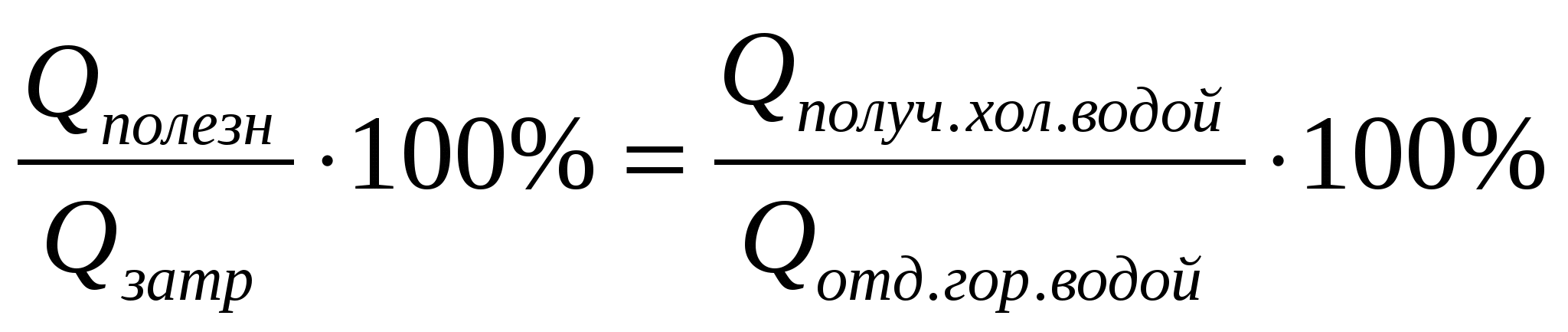
Здесь Qполез — теплота, идущая на нагревание холодной воды: Qполез = c1m1( t1);
Qзатр — теплота, отданная горячей водой: Qзатр = c2m2(t2 ).
Удельные теплоты с1 холодной и с2 горячей воды равны.
2 = 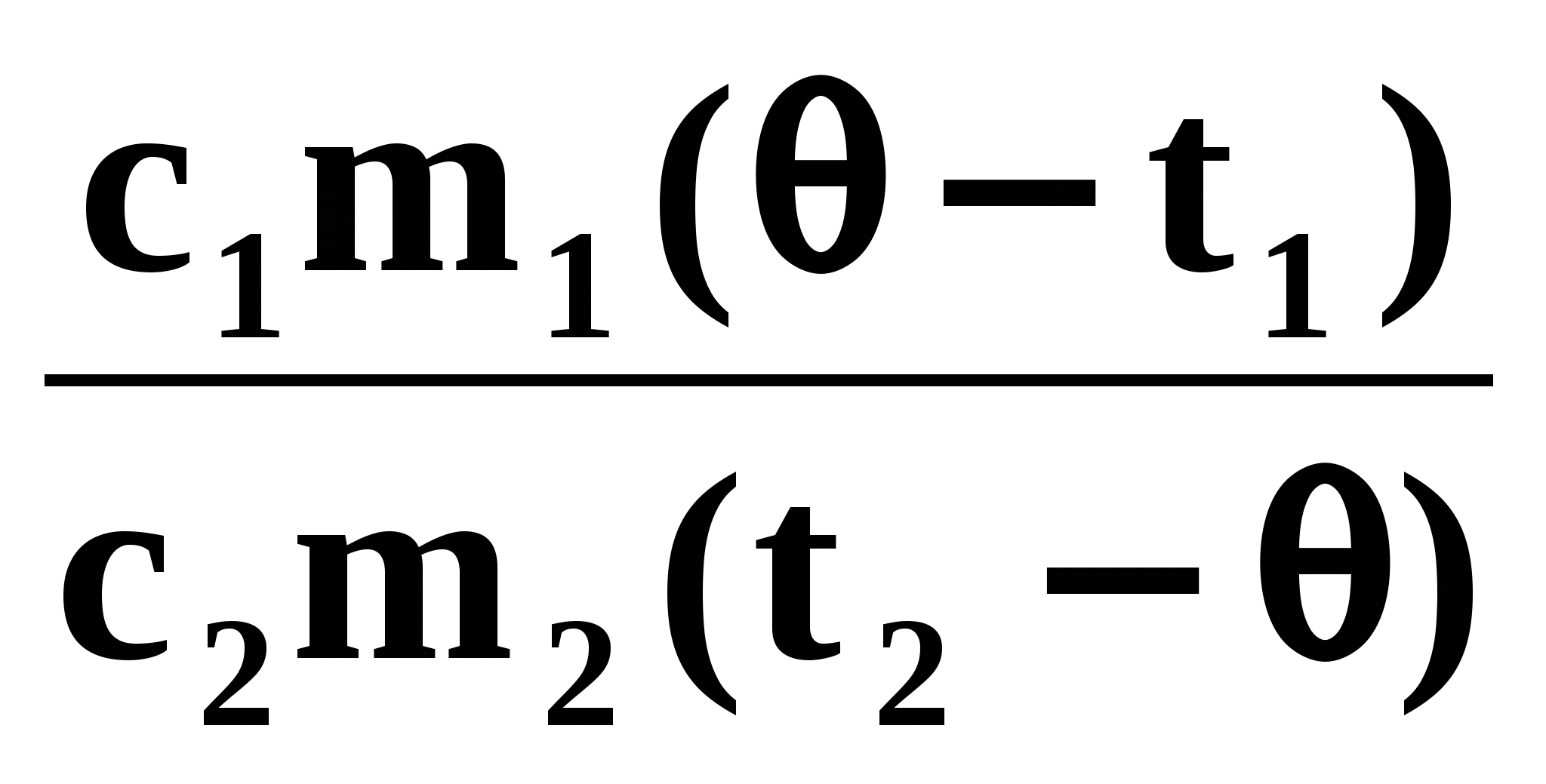
2m2t2 2m2 = m1 m1t1,
?
С ?
= 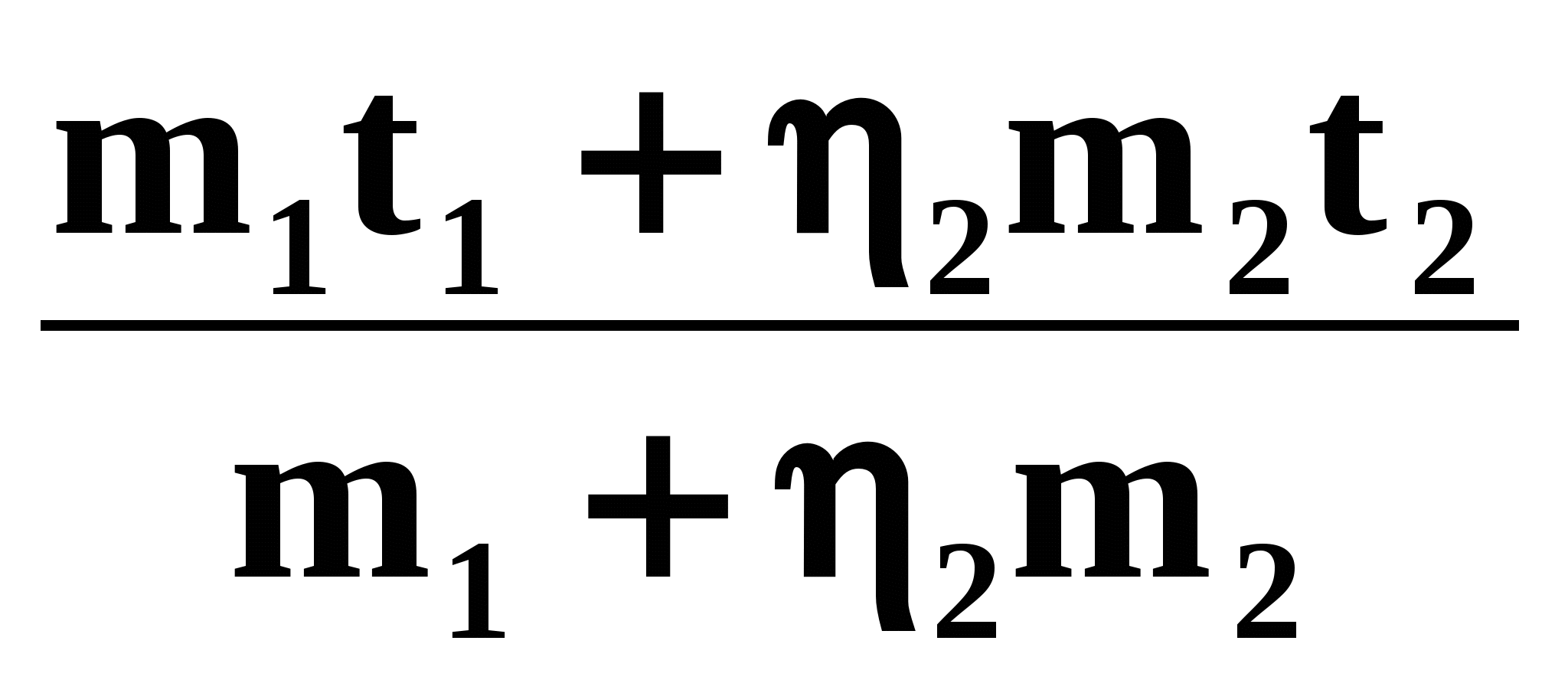
= 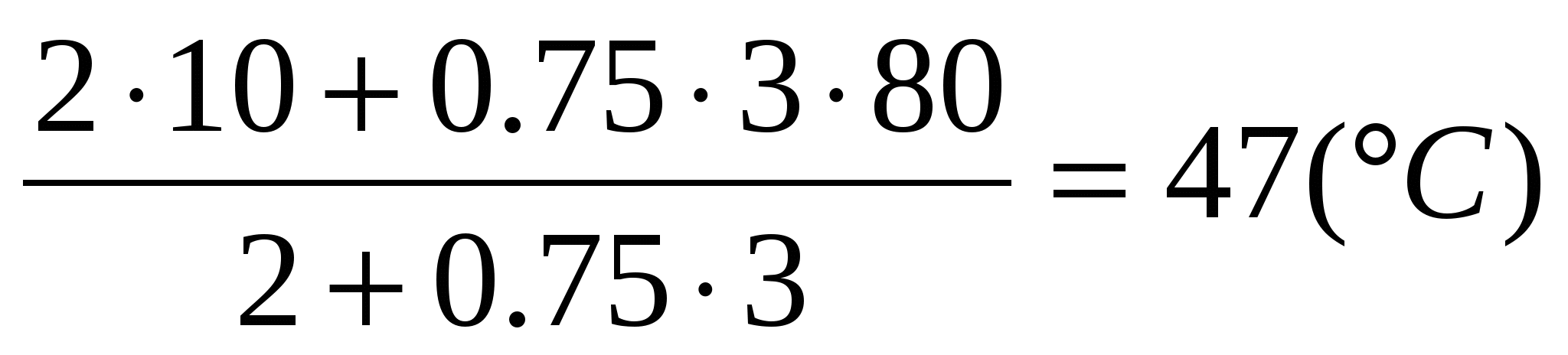
Так как 25% теплоты, отданной горячей водой, пошло на нагревание кастрюли, то можно говорить и о КПД процесса нагревания кастрюли:
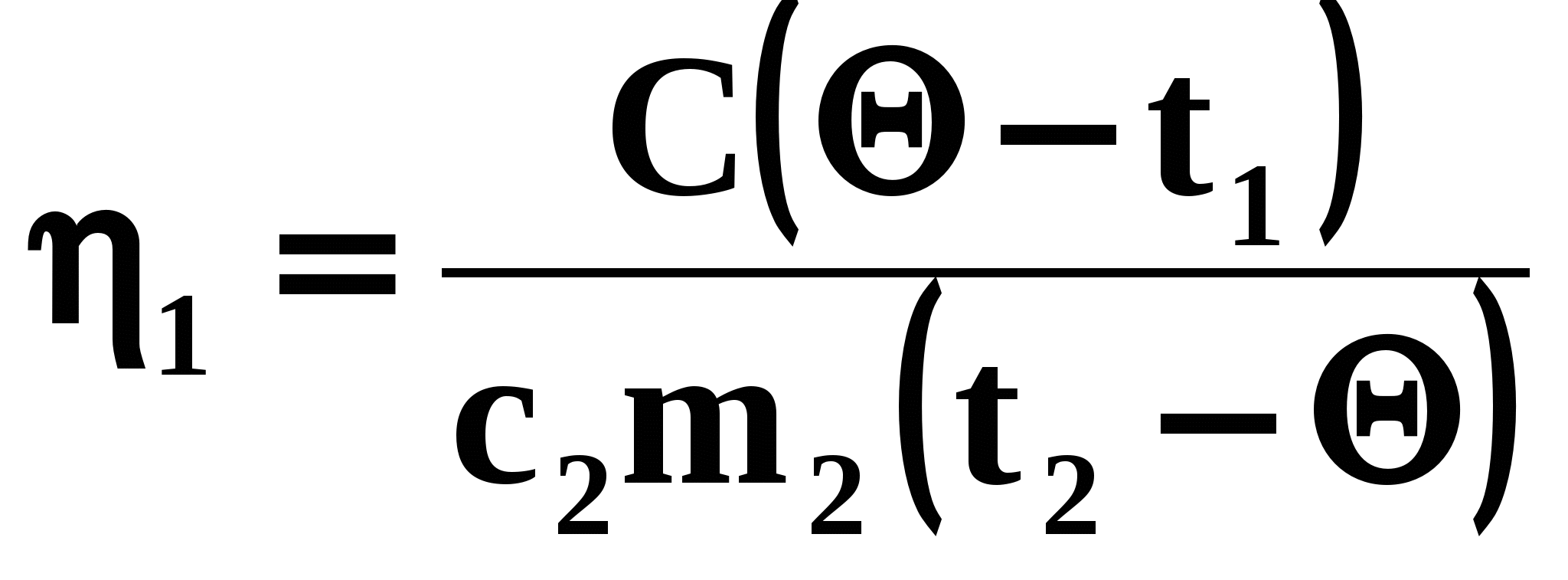
откуда: 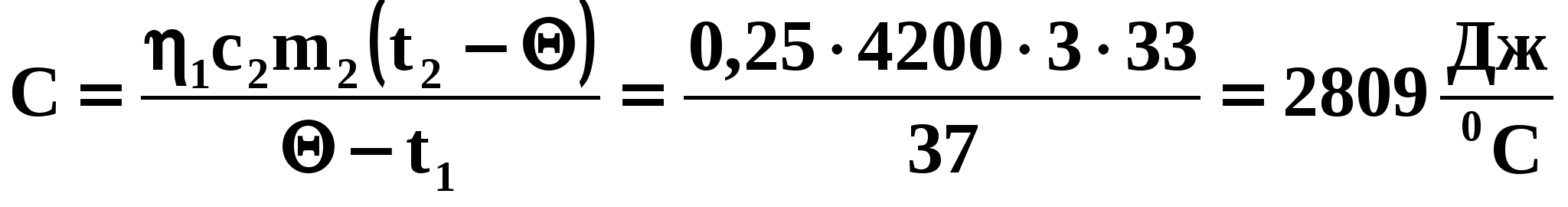
Ответ: Холодная вода нагреется до температуры 47С. Теплоемкость кастрюли 2809 Дж/0С.
Задача 7
Сколько керосина нужно сжечь, чтобы превратить в пар 1 кг льда, взятого при температуре 40С? КПД нагревательного устройства равен 60%, удельная теплота сгорания керосина 46 МДж/кг.
m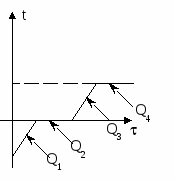
t1 = 40С
с1 =2100Дж/(кг0С)
= 3,4105 Дж/кг
с2 =4200Дж/(кг0С)
L = 2,3106 Дж/кг
= 0,6 (60%)
q = 46106 Дж/кг
Решение
1. Изобразим на графике t() процессы: нагревание льда, плавление льда, нагревание получившейся из льда воды, кипение этой воды. Для осуществления каждого из этих процессов необходим подвод теплоты. Теплоту выделяет керосин в процессе сгорания (на графике не показано).
2. Применим формулу КПД нагревателя:
= 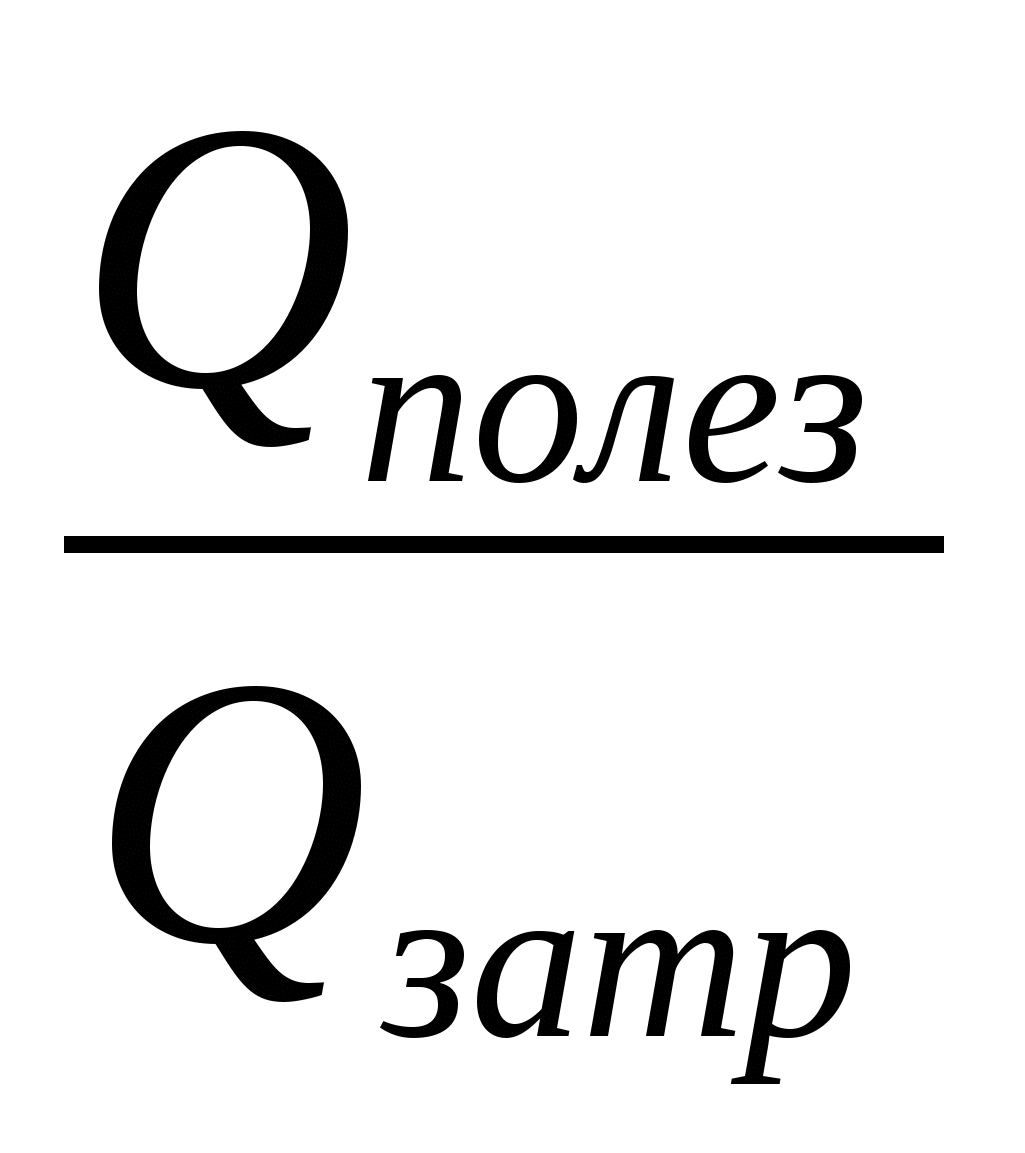
Здесь Qполез = Q1 + Q2 + Q3 + Q4 =
= m1[c1(0 t1) + + c2(100 0) + L],
а Qзатр = qm2.
Получаем: = 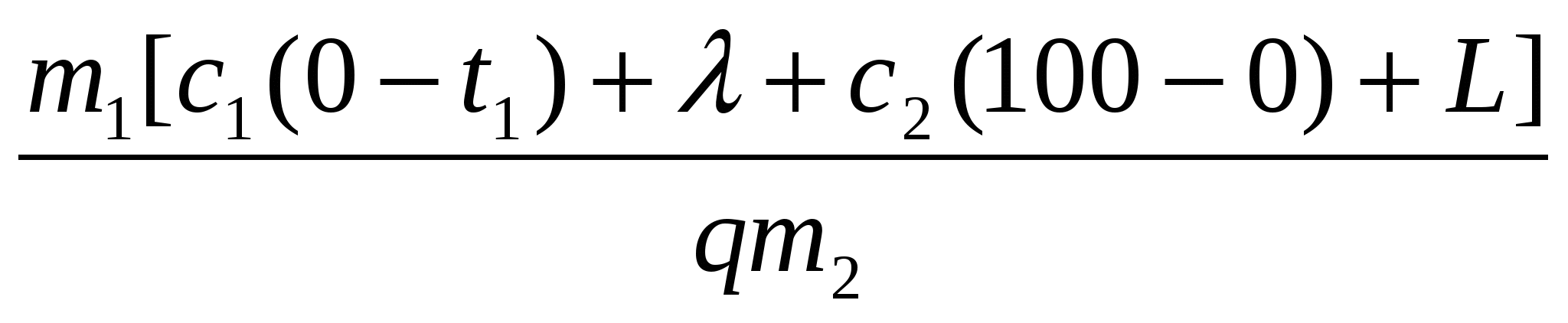
откуда: m2 = 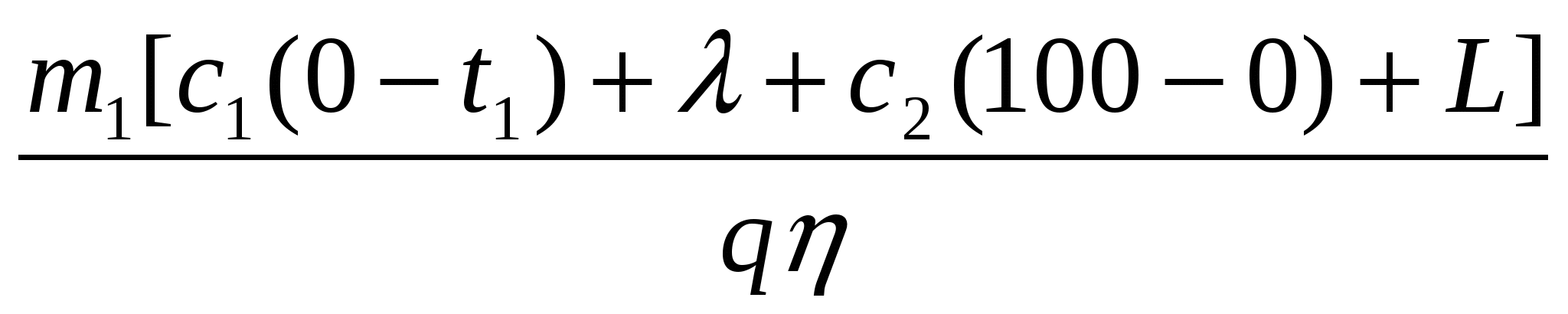
m2 = 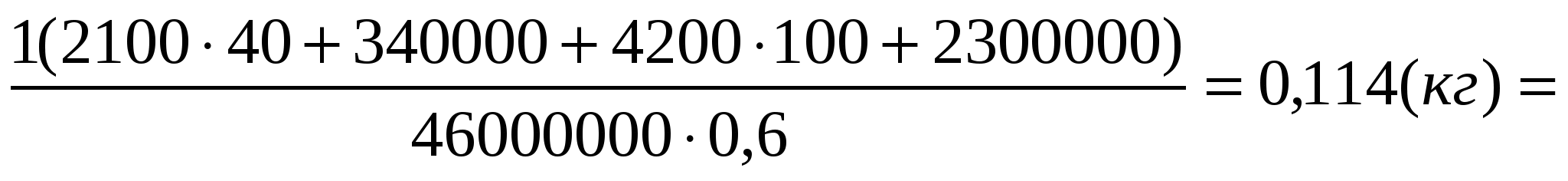
= 114 г
m2 — ?
Ответ: Нужно сжечь 114 г керосина.
Задача 8
Сколько водяного пара, имеющего температуру 120С, надо впустить в калориметр, содержащий 800 г льда при температуре 20С, чтобы температура образовавшейся воды оказалась 20С? Теплоёмкостью калориметра пренебречь.
m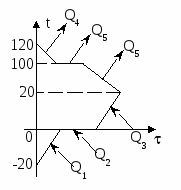
t1 = 20С
с1 = с2 = 2100
Дж/(кг0С)
t2 = 120С
с3 =4200Дж/(кг0С)
= 20С
Решение
1. Так как теплоемкостью калориметра можно пренебречь, то систему лед — пар можно считать теплоизолированной: теплообмен происходит только между паром и льдом.
2. Получают теплоту тела:
-
лёд, нагреваясь от -200С до температуры плавления: Q1 = c1m1(0 t1);
-
лёд, превращаясь в воду при температуре плавления: Q2 = m1;
-
вода, образовавшаяся из льда, нагреваясь от 0С до 20С: Q3 = с3m1( 0).
3. Отдают теплоту тела:
-
пар, остывая от 120С до температуры конденсации: Q4 = c2m2(t2 100);
-
пар, превращаясь в воду при 100С: Q5 = Lm2;
-
вода, образовавшаяся из пара, остывая от 100С до 20С: Q6 = c3m2(100 ).
4. Других участников теплообмена нет, поэтому записываем уравнение теплового баланса:
Q1 + Q2 + Q3 = Q4 + Q5 + Q6,
c1m1(0 — t1) + m1 + c3m1( 0) = c2m2(t2 100) + + Lm2 + c3m2(100 ),
m2-?
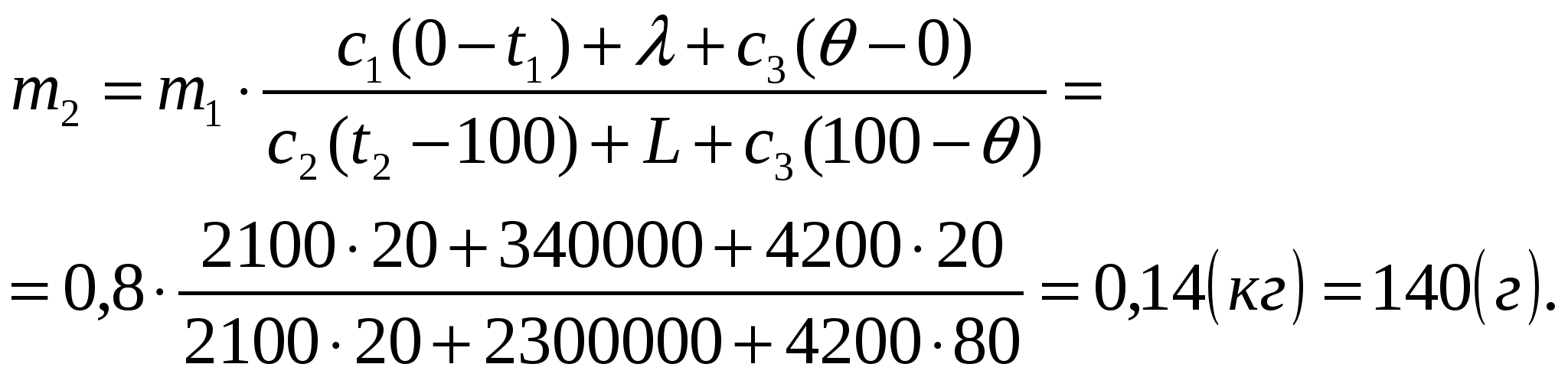
Ответ: Потребуется 140 г водяного пара.
Часто при решении задач можно встретиться со следующей проблемой. В теплообмене участвуют вещества, находящиеся в различных агрегатных состояниях, и конечная температура теплообмена не известна. Тогда уравнение теплового баланса сразу написать не удастся, так как его вид зависит от того, в каких агрегатных состояниях будут находиться конечные продукты. В этом случае последовательность решения задачи немного изменяется. Сначала нужно сделать предварительные расчеты: сколько теплоты выделит или поглотит каждое вещество в предполагаемом процессе, сравнить эти теплоты и сделать вывод о том, в каких агрегатных состояниях будут находиться продукты теплообмена. И только после этого можно записывать уравнение теплового баланса. Такие задачи значительно сложнее задач, в которых конечная температура известна. Рассмотрим ряд таких задач.
Задача 9
В калориметр, содержащий воду массой 0,5 кг при температуре 25С, впускают водяной пар массой 50 г при температуре 120С. Какая температура установится в калориметре, если его теплоёмкость 1200 Дж/оС?
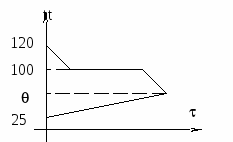
m1 = 0,5 кг
с1 =4200 Дж/(кг0С)
t1 = 25С
m2 = 0,05 кг
t2 = 120С
c2=2100 Дж/(кг0С)
С = 1200 Дж/0С
L = 2,3106 Дж/кг
Решение
1. Если в конечном итоге весь пар остынет от 120С до 100С, затем сконденсируется в воду, затем образовавшаяся из
пара вода остынет от 100С до , то в калориметре будет находиться вода при температуре , а уравнение теплового баланса примет вид:
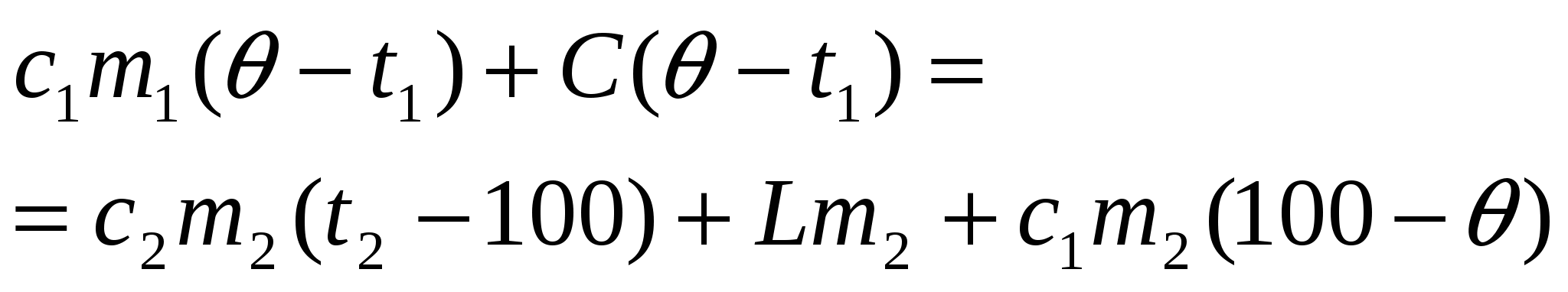
-?

2. Если пар остынет от 120С до 100С, а сконденсируется не весь, то в калориметре будет находиться смесь воды и пара при температуре 100С, а уравнение теплового баланса будет таким:

Здесь m— масса сконденсировавшегося пара.
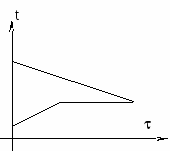
3. Пар может остыть от 120С до 100С, а вода и калориметр уже нагреются до 100С, и при этом часть воды даже выкипит. В калориметре будет смесь пара и воды при температуре 100С.
Уравнение теплового баланса будет иметь вид:

Каким из трёх уравнений пользоваться?
Cделаем предварительные расчёты. Вычислим:
а) сколько теплоты нужно для того, чтобы нагреть воду и калориметр от 25С до 100С:
Q1 = c1m1(100 t1) + C(100 t1) = 42000,575+120075 = 247500 (Дж).
б) сколько теплоты выделится, если весь пар остынет от 120С до 100С: Q2 = c2m2(t2 100) =21000,0520 = 2100 (Дж).
в) сколько теплоты выделится, если весь пар сконденсируется в воду при температуре 100С:
Q3 = Lm2 = 23000000,05 = 115000 (Дж).
Выделяющаяся теплота Q2 + Q3 = 2100 Дж + 115000 Дж = 117100 Дж при охлаждении пара и его конденсации меньше теплоты, которая требуется для нагревания «холодной» воды и калориметра. Значит, чтобы вода вместе с калориметром смогла нагреться до 100С, ей нужно больше энергии, чем может отдать пар, остывая и конденсируясь. Поэтому 117100 Дж пар отдаст, став при этом «горячей» водой при 100С, а «холодная» вода при этом до 100С ещё не нагреется. Тогда в калориметре будут одновременно находиться сконденсировавшаяся из пара вода при 100С и подогретая «холодная» вода. В результате дальнейшего теплообмена «горячая» вода остынет, а «холодная» нагреется. И в итоге в калориметре будет вода, температура которой ниже 1000С, но выше 250С.
Уравнение теплового баланса будет иметь вид (1):
c1m1( t1) + C( t1) = c2m2(t2 100) + Lm2 + c1m2(100 ), откуда
c1m1 c1m1t1 + С Сt1 = 117100 + c1m2100 c1m2.
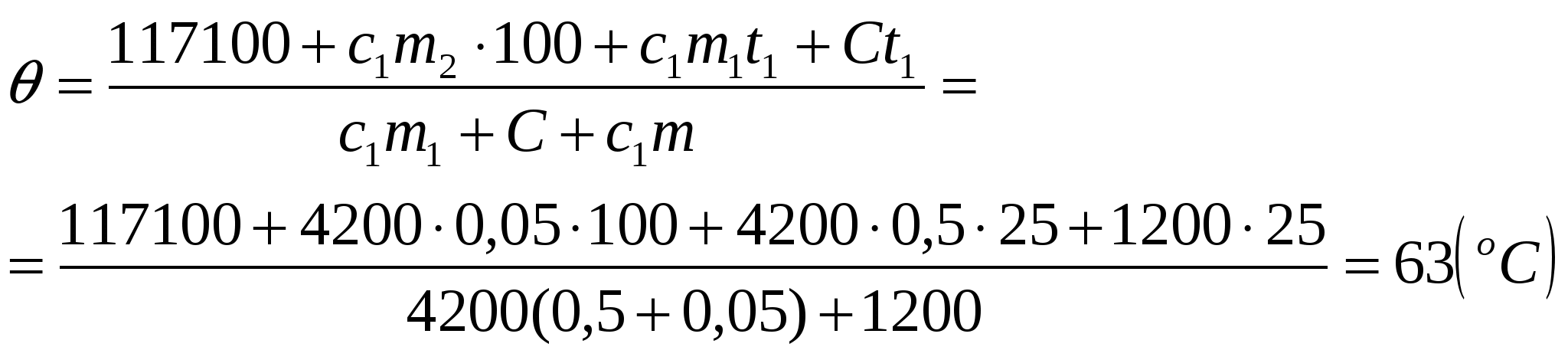
Ответ: В калориметре установится температура 63С.

Задача 10
В калориметре находится вода массой 0,8 кг при температуре 20С. В воду опустили 2 кг льда при температуре 30С. Что будет в калориметре после того, как теплообмен прекратится? Теплоёмкостью калориметра пренебречь.
m
с1=4200 Дж/(кг0С)
t1 = 20С
m2 = 2 кг
t2 = 30С
c2=2100 Дж/(кг0С)
= 3,4105 Дж/кг
Решение
Рассмотрим варианты решения:
1. Вода остынет от 20С до 0С, затем эта вода замёрзнет и станет льдом при температуре 0С, затем лёд, образовавшийся из воды, остынет до температуры (см. график).
А опущенный в воду лёд только нагреется от температуры 30С до температуры . В калориметре будет находиться лёд при температуре .
Уравнение теплового баланса запишется так:
c1m1(t1 0) + m1 + c2m1(0 ) = c2m2( t2).
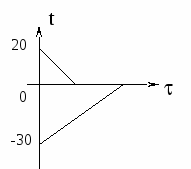
2. Вода остынет от 20С до 0С, часть её замёрзнет и станет льдом при 0С, остальная — останется водой при 0С. Лёд при этом нагреется от 30С до 0С (см. график). И тогда в калориметре будет находиться смесь воды со льдом при температуре 0С. Уравнение теплового баланса запишется так:
c
3. Вода остынет от 20С до 0С. Лёд при этом нагреется от 30С до 0С, затем частично или полностью расплавится и станет водой при 0С. В калориметре будет смесь воды и льда при температуре 0С. Уравнение теплового баланса запишется так:
c1m1(t1 0) = c2m2(0 t2) + m, где m масса превратившегося в воду льда.
4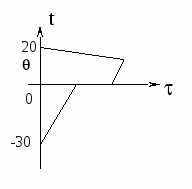
c1m1(t1 ) = c2m2(0 t2) + m2 + c1m2( 0).
Проведем численный анализ ситуации. Сколько теплоты:
а) выделит вода при остывании от 20С до 0С:
Q1 = c1m1(t1 0) = 42000,820 = 67200 (Дж);
б) выделит вода при превращении в лед при 0С:
Q2 = m1 = 3400000,8 = 272000 (Дж);
в) нужно получить льду, чтобы нагреться от 30С до 0С:
Q3 = c2m2(0 t2) = 2100230 = 126000 (Дж);
г) нужно получить льду, чтобы полностью расплавиться при температуре 0С:
Q4 = m2 = 3400002 = 680000 (Дж).
Получаем: чтобы весь лёд нагрелся от 30С до 0С, ему нужно передать 126000 Дж теплоты, а вода при этом, остывая от 20С до 0С, может дать только 67200 Дж. Значит, лёд эти 67200 Дж у воды «возьмет», но ему ещё не будет хватать Q = 126000 Дж 67200 Дж = 58800 Дж, чтобы нагреться до 0С. Он их «возьмёт» у превращающейся в лед воды (если бы вода полностью превратилась в лед, то она бы выделила 272000 Дж, а это больше, чем «нужно» льду):
Q = m m = Q/ = 58800/340000 0,2 (кг), где
m это масса воды, обратившейся в лёд при температуре 0С.
Как только лёд нагреется до 0С, теплообмен между льдом и водой прекратится, так как они будут иметь одинаковые температуры.
Итак, получили: вода остынет до 0С, часть её (а именно m = 0,2 кг) замёрзнет и станет льдом при 0С, а лёд нагреется до 0С. И в результате в калориметре будет находиться смесь воды и льда при 0С. При этом масса воды будет равна:
mв = m1 m= 0,8 кг 0,2 кг = 0,6 кг,
а масса льда равна: mл = m2 + m = 2 кг + 0,2 кг = 2,2 кг.
Ответ: В калориметре при 0С находится смесь воды (0,6 кг) и льда (2,2 кг).
Задача 11
В калориметр, содержащий 1 кг льда при 20С, впускают 200 г водяного пара при 120С. Что будет в калориметре, когда теплообмен прекратится? Теплоёмкостью калориметра пренебречь.
m1 = 1 кг
с1 = c2 = 2100 Дж/(кг0С)
t1 = 20С
m2 = 0,2 кг
t2 = 120С
L = 2,3106 Дж/кг
= 3,4105 Дж/кг
с3 =4200Дж/(кг0С)
Решение
1. Вычислим, сколько теплоты нужно получить льду, чтобы нагреться от 20С до 0С:
Q1 = c1m1(0 t1) = 2100120 = 42000 (Дж);
2. Вычислим, сколько теплоты нужно получить льду, чтобы при 0С растаять:
Q1 = m1 = 3400001 = 340000 (Дж);
3. Вычислим, сколько теплоты нужно получить воде, образующейся из льда, чтобы нагреться от 0С до 100С:
Q1 = c3m1(100 0) = 42001100 = 420000 (Дж);
4. Найдем, сколько теплоты выделит пар, остывая от 120С до 100С:
Q2 = c2m2(t2 100) = 21000,220 = 8400 (Дж);
5. Найдем, сколько теплоты выделит пар, конденсируясь в воду при 100С:
Q2 = Lm2 = 23000000,2 = 460000 (Дж);
6. Рассчитаем, сколько теплоты может выделить вода, образовавшаяся из пара, остывая от 100С до 0С:
Q2 = c3m3(100 0) = 42000,2100 = 84000 (Дж).
— ?
mв — ?
mл — ?
Проведем анализ ситуации:
а) льду надо получить 42000 Дж, чтобы нагреться от 20С до 0С, а пар, остывая от 120С до 100С, может отдать только 8400 Дж. Значит, лёд «возьмёт» у пара 8400 Дж, но ещё не нагреется до 0С. Льду не достает еще 42000 Дж — 8400 Дж = 33600 Дж, чтобы нагреться до 0С;
б) недостающая энергия может быть получена от конденсации пара. Пар будет конденсироваться при 100С и выделит при этом 460000 Дж. Лёд за счёт этого сначала нагреется до 0С, а затем будет плавиться. Для этого ему нужна энергия: 33600 Дж + 340000 Дж = 373600 Дж. Это меньше, чем выделит пар, превращаясь в воду;
в) значит, лед растает и станет водой при 0С. А у пара еще «останется» 460000 Дж — 373600 Дж = 86400 (Дж). Но этого не хватит, чтобы вода, образующаяся из льда, нагрелась до 100С. Но на сколько-то она все же нагреется. Поэтому можно сделать вывод: в калориметре будет находиться только вода. Она будет состоять из воды, образованной из льда, и воды, образованной из пара. Её масса: mв = m1 + m2 = 1,2 кг.
Конечную температуру воды будем искать из уравнения теплового баланса:
c1m1(0 t1) + m1 + c3m1( 0) =c2m2(t2 100) + Lm2 + c3m3(100 ).
Используем результаты сделанных ранее вычислений:
c3m1( 0) c3m2(100 ) = 86400,
c3m1 c3m2100 + c3m2 = 86400,
= 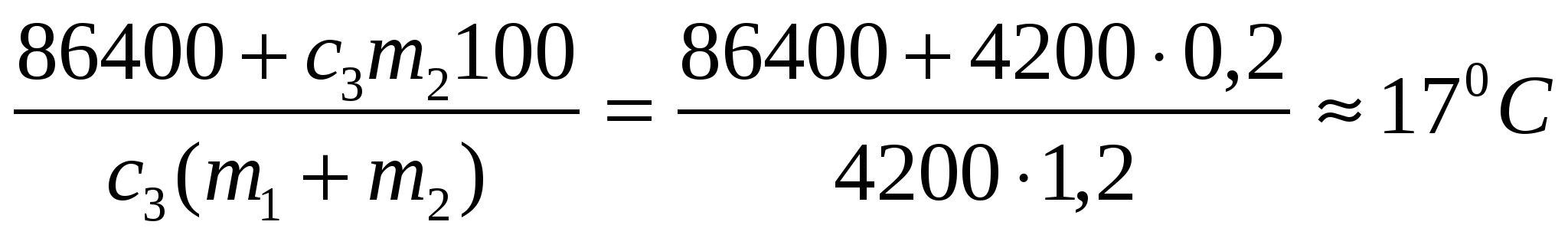
Ответ: В калориметре будет находиться 1,2 кг воды при температуре 17С.
Иногда в задачах говорится о веществах, находящихся при указанных температурах в таких агрегатных состояниях, которые не соответствуют указанной температуре. Например, перегретая жидкость — жидкость, находящаяся при температуре выше температуры кипения (при обычном давлении); переохлаждённая жидкость — жидкость, находящаяся при температуре ниже температуры замерзания, но остающаяся ещё жидкостью. Такое возможно в условиях, когда нет центров парообразования или центров кристаллизации. При малейшем возмущении эти вещества самопроизвольно и очень быстро переходят в то агрегатное состояние, которое соответствует указанной температуре. В таких веществах энергия, необходимая для того или иного процесса, заключена в самом веществе. При решении подобных задач строить графики нет необходимости.
Задача 12
Колбу , содержащую 120 г перегретой воды при температуре 118С и нормальном атмосферном давлении, слегка встряхивают, отчего происходит бурное вскипание воды. Сколько воды останется в колбе? Теплоёмкостью колбы и теплообменом с окружающей средой пренебречь.
m = 0,12 кг
t1 = 118С
t2 = 100С
с = 4200 Дж/(кг0С)
L = 2,3106 Дж/кг
Решение
Обозначим: m1 — масса выкипевшей воды.
Q1 = Lm1 — энергия, необходимая для превращения в пар воды массой m1. Этот переход обычно происходит при 100С. а вся вода находится при температуре 118С.
Значит, вся вода остывает до 100С, выделяя при этом теплоту Q2 = cm(t1 t2). Эта теплота и поглощается выкипающей водой.
Уравнение теплового баланса: Q1 = Q2
Lm1 = cm(t1 t2) m1 = m
m — m1 = m — m

= 0,12(1 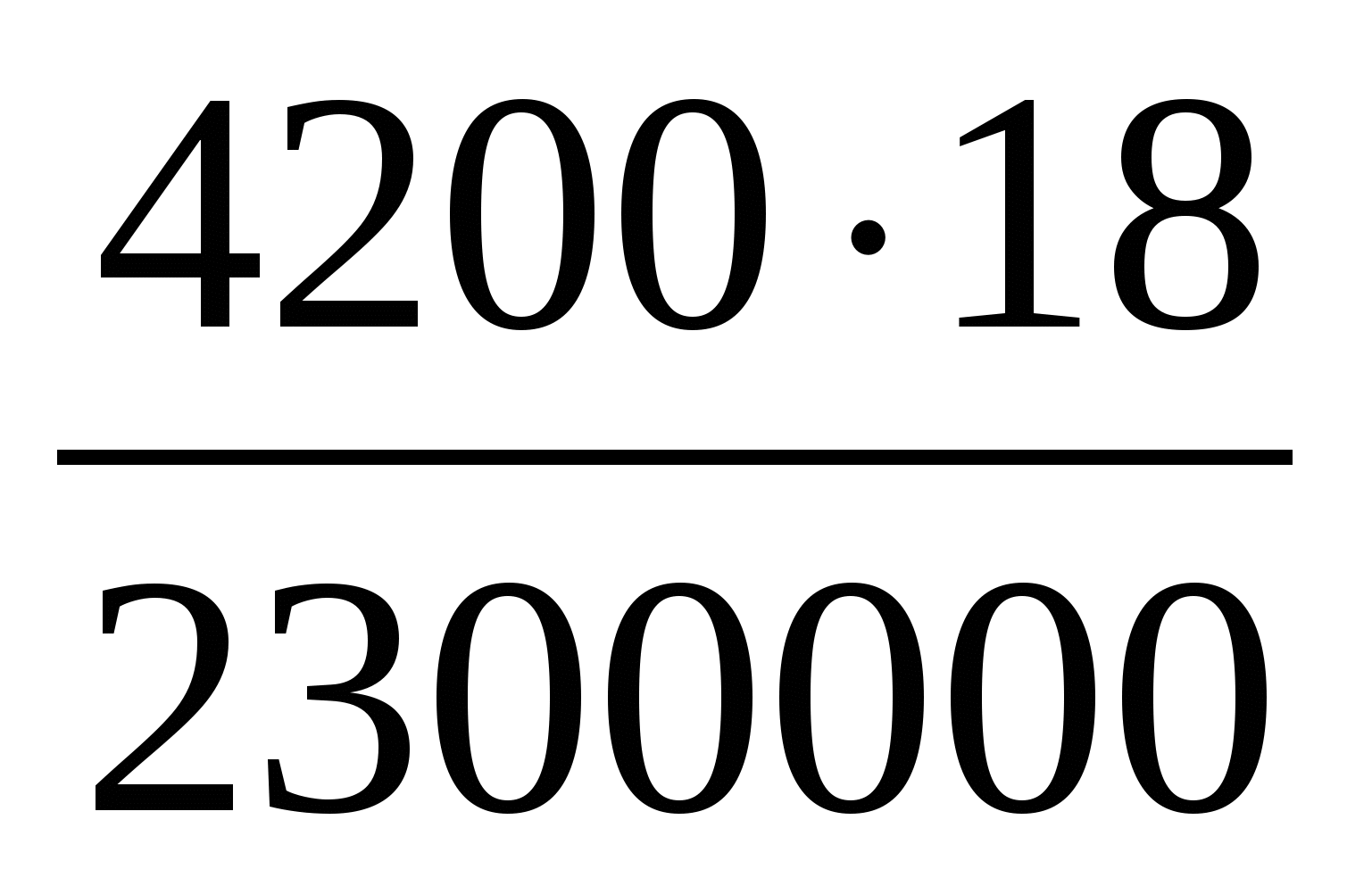
(m — m1) — ?
Ответ: В колбе останется 116 г воды.
Задача 13
Пробирку, содержащую 100 г воды, переохлаждённой до температуры 10С, слегка встряхивают, отчего вода превращается в лёд с температурой 0С. Какова масса образовавшегося льда? Теплоёмкость пробирки мала.
m = 0,1 кг
с =4200 Дж/(кг0С)
= 3,4105 Дж/кг
t1 = 10С
t2 = 0С
Решение
Вся вода нагревается от 10С до 0С, получая энергию Q за счёт того, что часть воды при этом превращается в лёд с температурой 0С и выделяет при этом энергию Q1.
m1 — ?
Получается, что вся вода нагревается за счет теплоты, выделяющейся при кристаллизации своей части. Поэтому:
Q = Q1,
cm(t2 t1) = m1,
m1 = 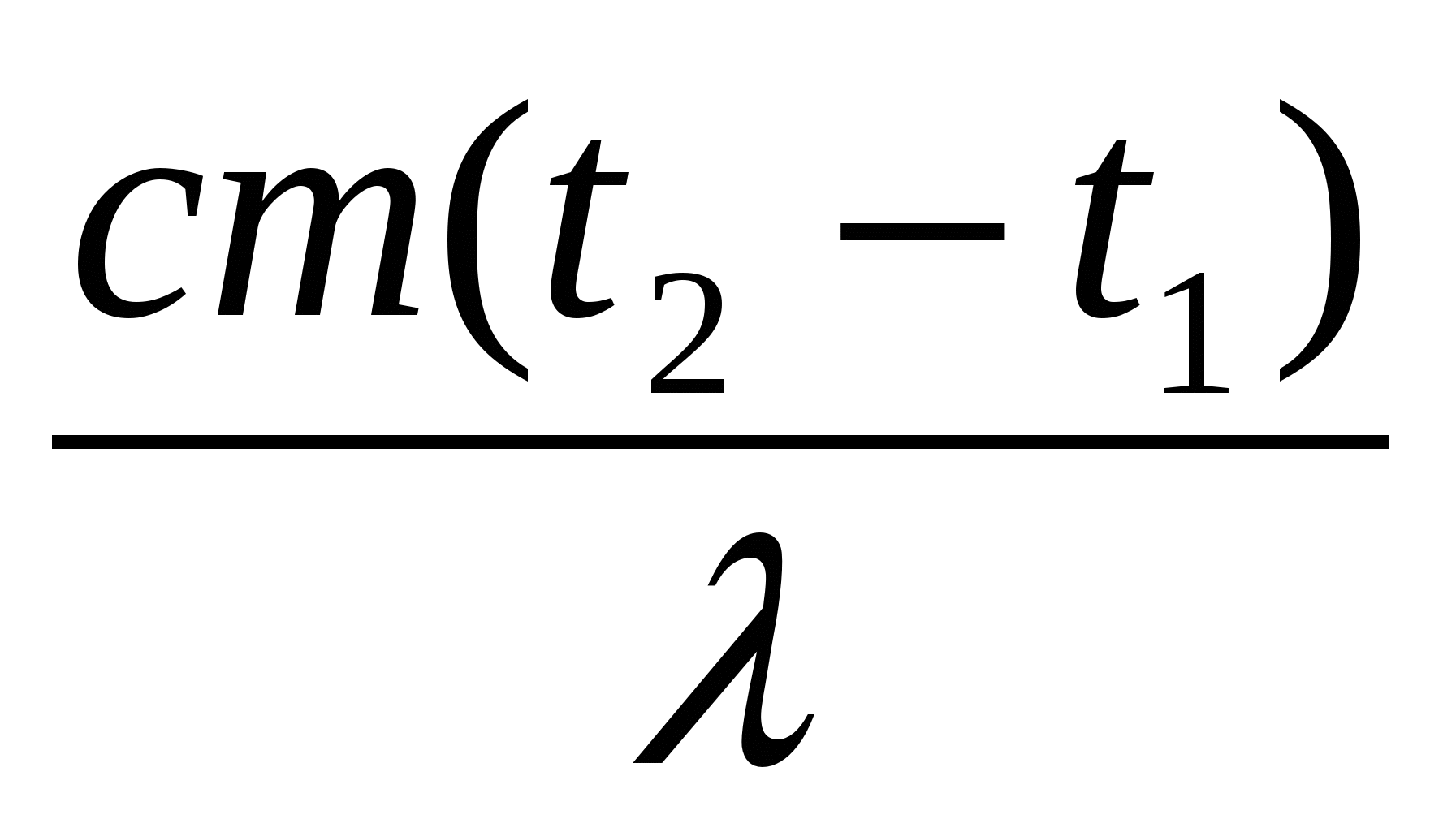
m1 = 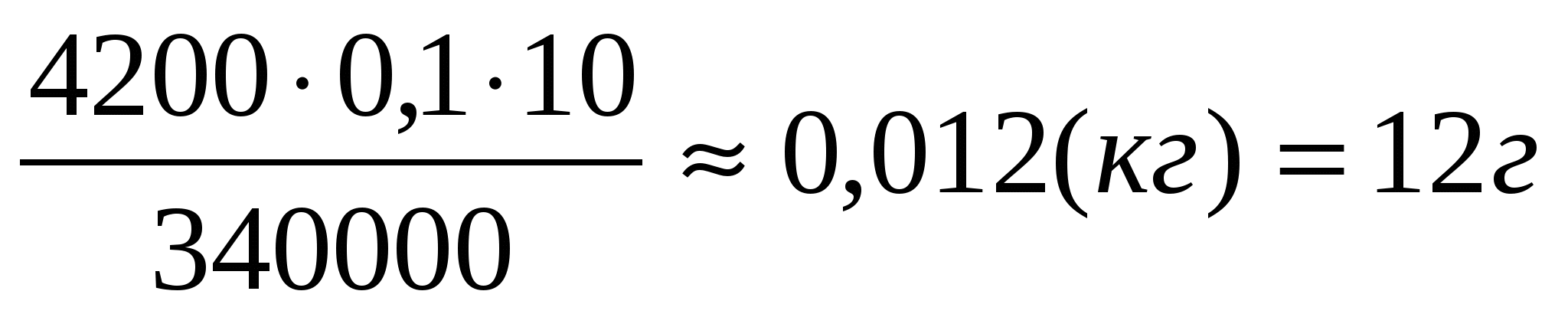
Ответ: Масса образовавшегося льда равна 12 г.
Задачи для самостоятельного решения
-
Для приготовления ванны ёмкостью 100 л смешали холодную воду, имеющую температуру 12С, и горячую, имеющую температуру 72С. Сколько той и другой воды надо взять, чтобы температура воды в ванне была 36С?
-
Когда в 2 кг воды, находящейся в калориметре при 20С, опустили алюминиевое тело массой 0,8 кг, имеющее температуру 100С, температура воды поднялась до 25С. Определить теплоёмкость калориметра.
-
В 2 кг воды, имеющей температуру 20С, опустили сначала медное тело массой 2 кг, имеющее температуру 80С. После того, как температура перестала меняться, в воду опустили железное тело массой 3 кг, имеющее температуру 20С. Какой после этого стала температура воды? Теплоёмкостью сосуда пренебречь.
-
После опускания в воду, имеющую температуру 100С, тела с температурой 20С, установилась общая температура 80С. Какой станет температура воды, если, не вынимая первого тела, в нее опустить ещё два таких же тела, имеющих температуру 20С?
-
В чайник налили воду при температуре 200С и поставили на электроплитку. Через 13 минут вода закипела. Через какое время половина воды выкипит?
-
Для того, чтобы на спиртовом нагревателе, с КПД 70%, нагреть до кипения 1,4 кг воды и половину ее превратить в пар, израсходовали 100 г спирта. Какова начальная температура воды? Удельная теплота сгорания спирта 29106 Дж/кг.
-
В калориметре находится лёд массой 500 г при температуре 0С. В калориметр впускают водяной пар температурой 100С. Сколько воды окажется в калориметре, когда весь лёд растает, а температура образовавшейся воды будет равна 0С?
-
В калориметр, содержащий 400 г воды и 200 г льда при 0С, впустили водяной пар с температурой 100С. Сколько пара было впущено в калориметр, если в калориметре установилась температура 20С? Теплоёмкость калориметра 1000 Дж/0С.
-
В сосуд теплоёмкостью 1000 Дж/0С, содержащий 5 кг воды при температуре 20С, положили лёд, имеющий температуру 40С. Температура образовавшейся смеси оказалась равна 2С. Сколько льда было положено в сосуд?
-
В алюминиевом калориметре массой 200 г находится кусок льда с температурой 20С. В калориметр впустили водяной пар, имеющий температуру 100С. Когда температура калориметра стала равна 20С, измерили массу его содержимого. Она оказалась равной 400 г. Найти массу льда, находящегося в калориметре, и массу сконденсировавшегося пара.
-
В калориметр, содержащий 3 кг воды при температуре 20С, опустили 2 кг льда, имеющего температуру 10С. Что будет в калориметре, когда теплообмен прекратится? Теплоемкостью калориметра пренебречь.
-
В калориметр, содержащий 1 кг льда и 800 г воды при 0С впускают 100 г водяного пара при 100С. Что будет в калориметре, когда теплообмен прекратится? Теплоемкостью калориметра пренебречь.
-
В калориметре находится вода массой 600 г при температуре 5С. К ней долили ещё 300 г воды с температурой 10С и положили 600 г льда с температурой 60С. Что будет в калориметре после того, как теплообмен прекратится? Теплоемкостью калориметра пренебречь.
-
В теплоизолированном медном сосуде массой 400 г находятся 2 кг льда при температуре 10С. В сосуд помещают 400 г водяного пара при температуре 110С. Что будет в сосуде после того, как теплообмен прекратится?
-
В колбе находятся 200 г воды при температуре 0С. Откачиванием паров всю воду в колбе заморозили. Сколько получилось льда?
Ответы и решения
-
60 л холодной и 40 л горячей воды.
t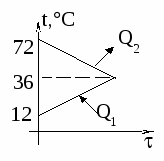
t2 = 72С
= 36С
V = 100 л
Решение
Q1 = cm1( t1) — теплота, которую получит холодная вода, нагреваясь от 12С до 36С;
Q2 = c(m m1)(t2 ) — теплота, которую отдаст горячая вода, остывая от 72С до 36С,
V1 — ?
V2 — ?
Q1 = Q2,
cm1( t1) = c(m m1)(t2 ),
m1( t1) + m1(t2 ) = m(t2 ),
V1( t1 + t2 ) = V (t2 ),
V1 = V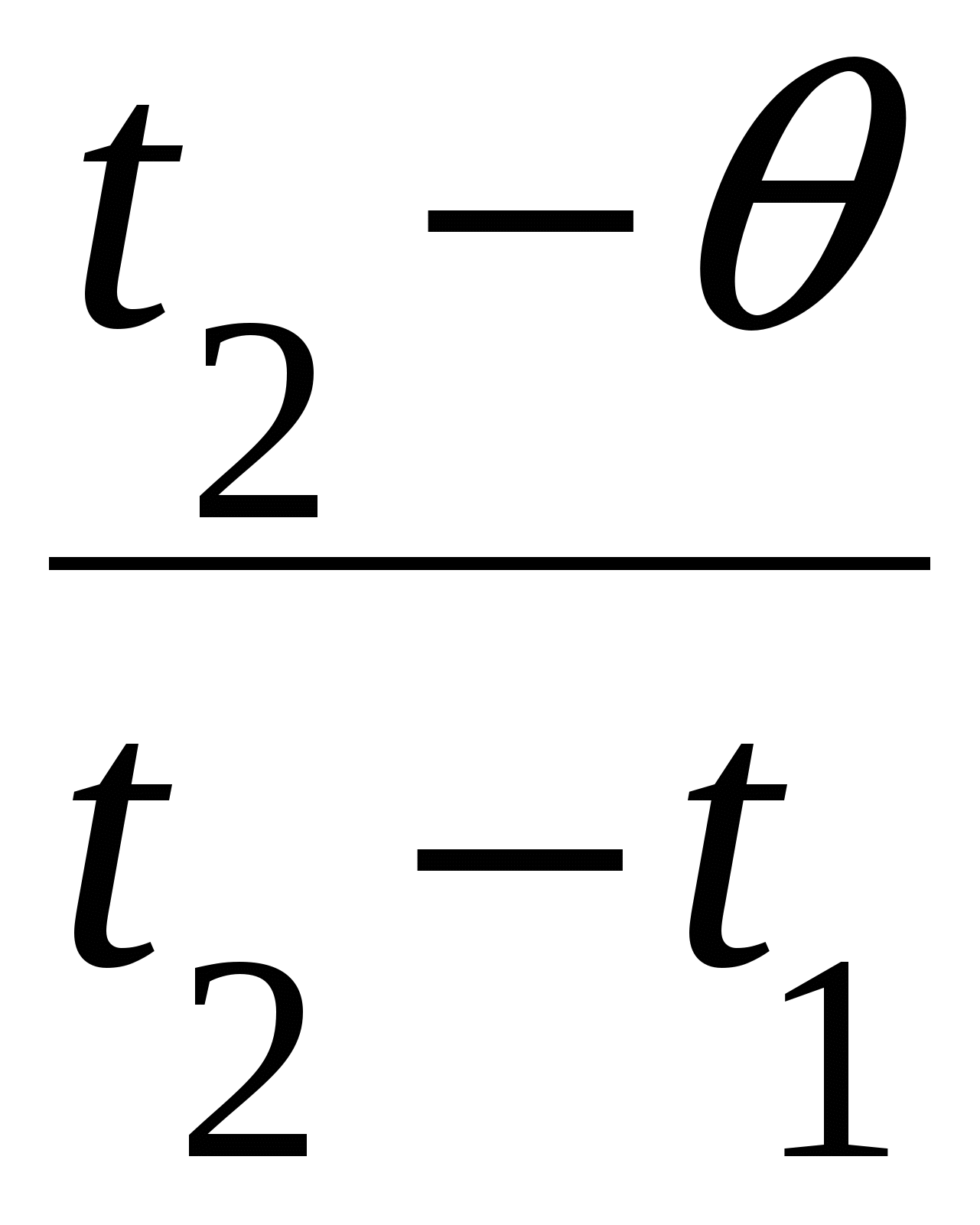
V1 = 100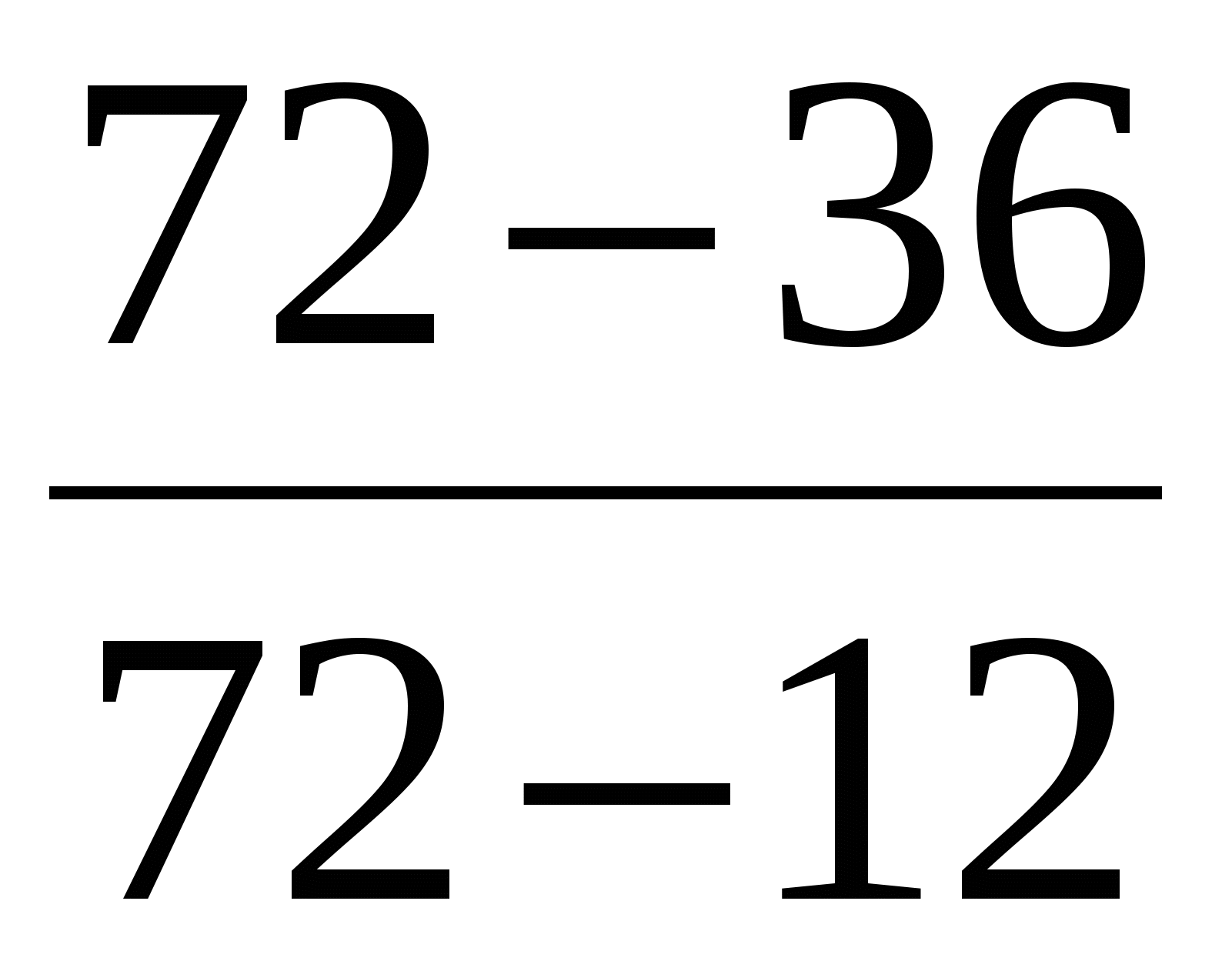
V2 = V V1 = 100 — 60 = 40 (л).
2. 2640 .
m
t1 = 20С
с1=4200 Дж/(кг0С)
m2 = 0,8 кг
t2 = 100С
с2 = 920 Дж/(кг0С)
= 25С_______
Ск — ?
Решение
Q2 = Q + Q1, где
Q2 — теплота, отданная алюминиевым телом;
Q1 — теплота, полученная водой,
Q теплота, полученная калориметром.
c2m2(t2 ) = (Cк + c1m1)( t1),
Cк = 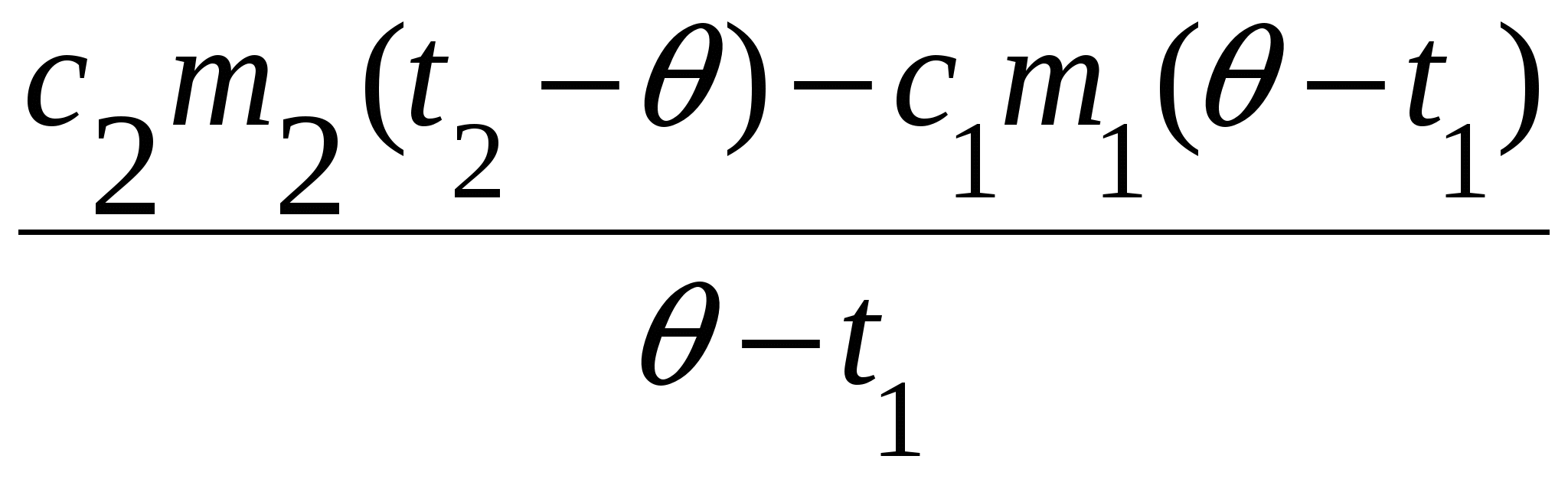
Cк = 
3. 190С.
m1 = 2 кг
c1=4200 Дж/(кг0С)
t1 = 20С
m2 = 2 кг
c2 = 380 Дж/(кг0С)
t2 = 80С
m3 = 3 кг
c3 = 460 Дж/(кг0С)
t3 = 20С
Решение
Здесь удобнее пользоваться уравнением теплового баланса в виде (6), так как при решении этим способом последовательность опускания в воду тел не важна:
Q1 + Q2 + Q3 = 0,
c1m1( t1) + c2m2( t2) + c3m3( t3) = 0,
= 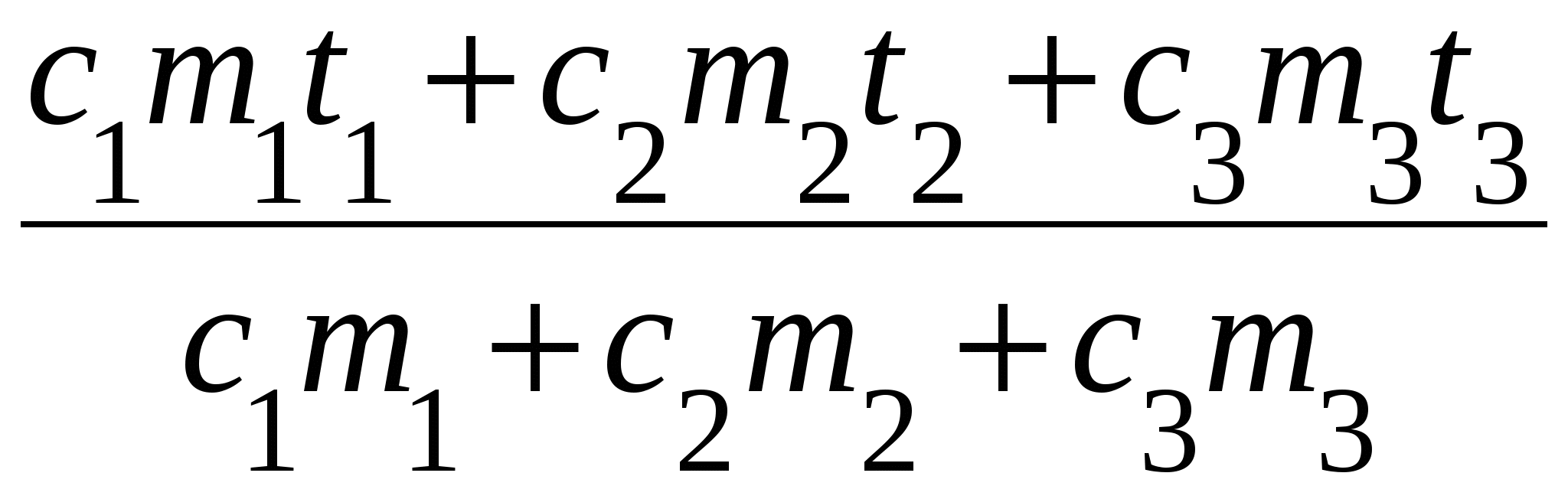

— ?
4. 53С
С1— теплоёмкость воды;
t1 = 100С
С2— теплоёмкость тела;
t2 = 20С
t3 = 80С
Решение
-
При опускании в воду с температурой t1 первоготела:
С1(t1 t3) = С2(t3 t2). (1)
-
При опускании в воду с температурой t2 сразу трех тел:
С1(t1 t4) = 3С2(t4 t2). (2)
-
Делим уравнение (1) на уравнение (2) и получаем:
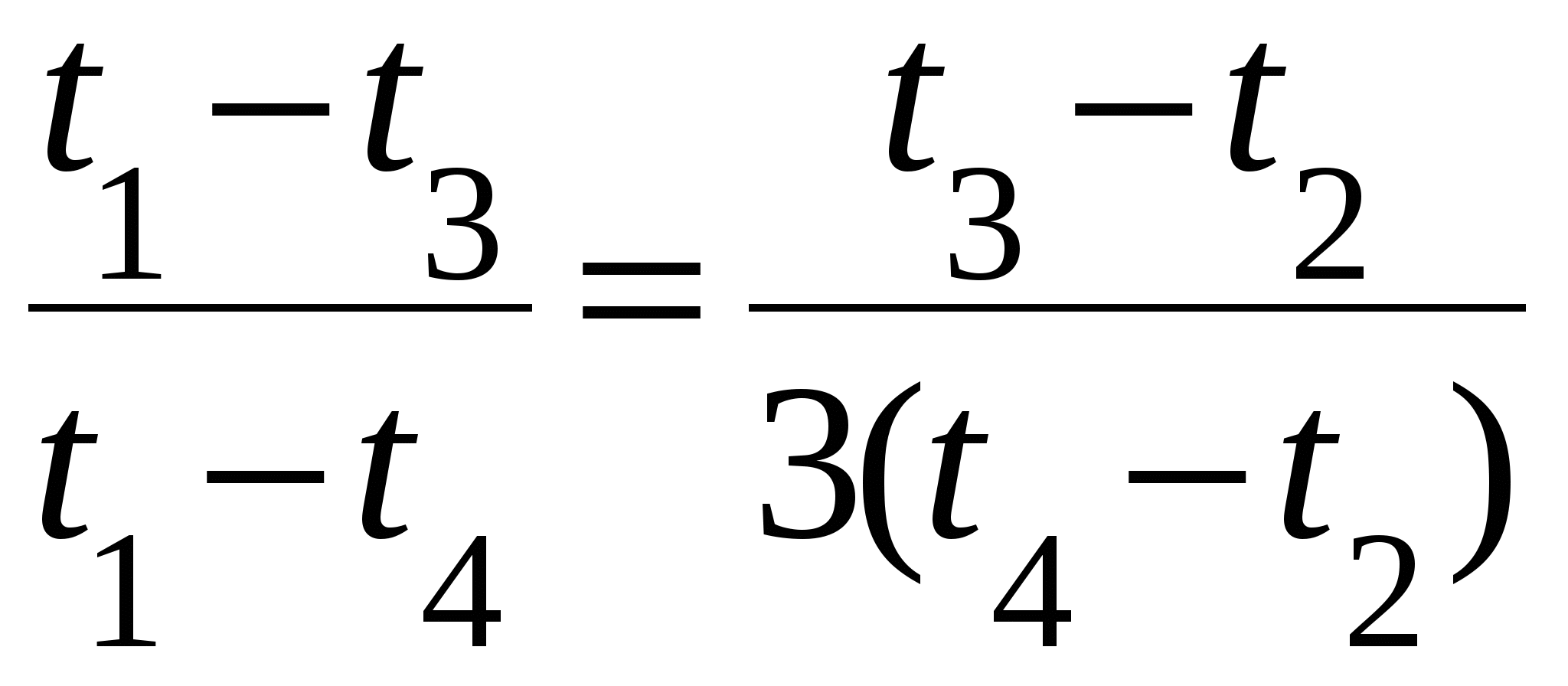
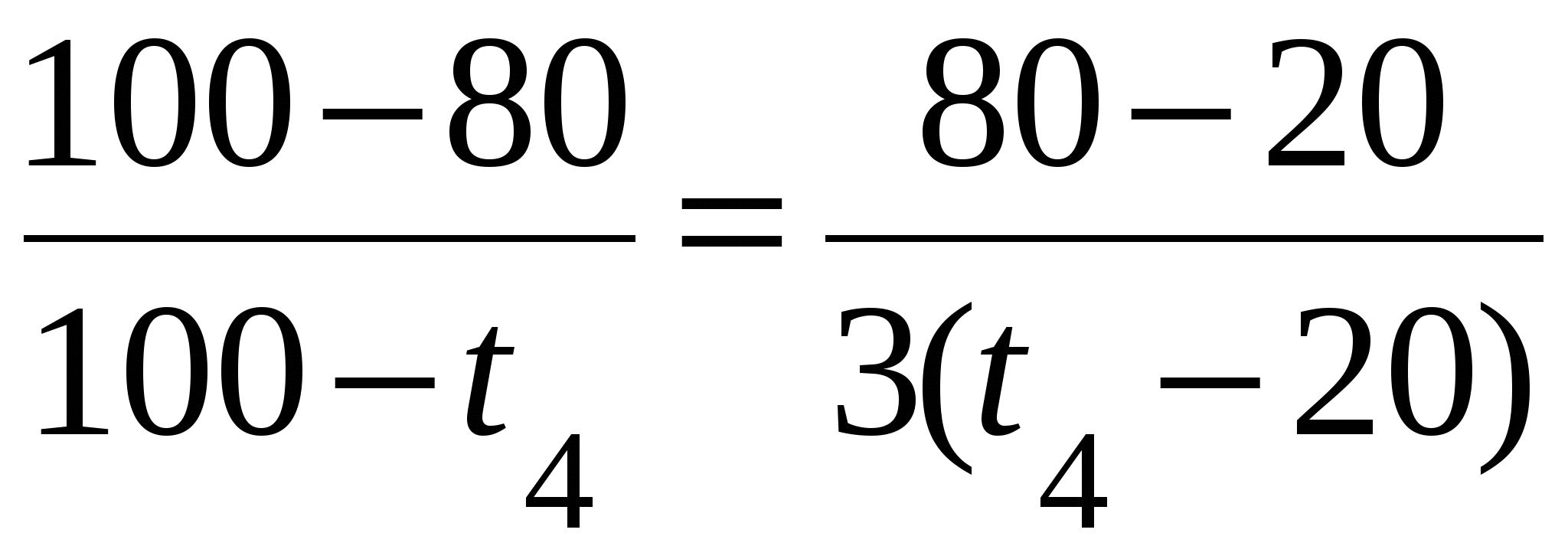
Решая это уравнение, находим, что : t4 53 С.
t4 — ?
-
44,5 мин.
1 = 13 мин
t1 = 20С
t2 = 100С
m2 = m1/2
с = 4200 Дж/(кг0С)
L = 2,3106 Дж/кг
2 — ?
Решение
Мощность электроплитки подразумеваем постоянной. Поэтому:
,
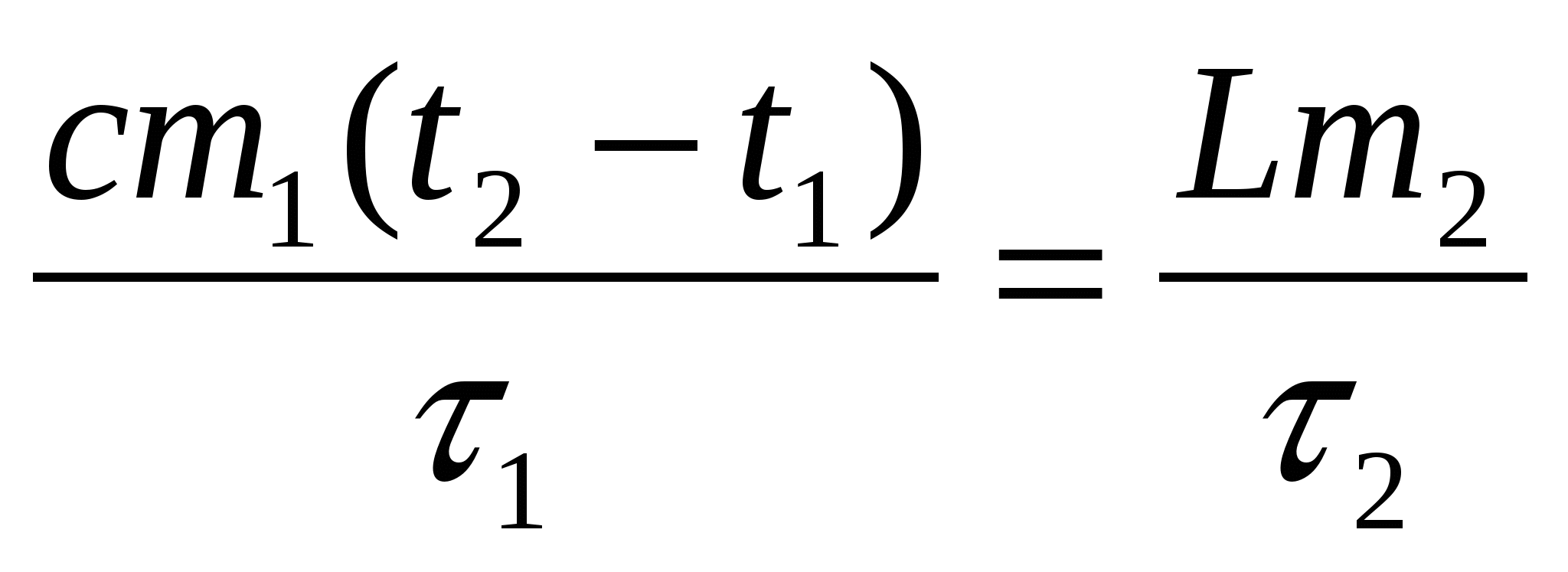
откуда:
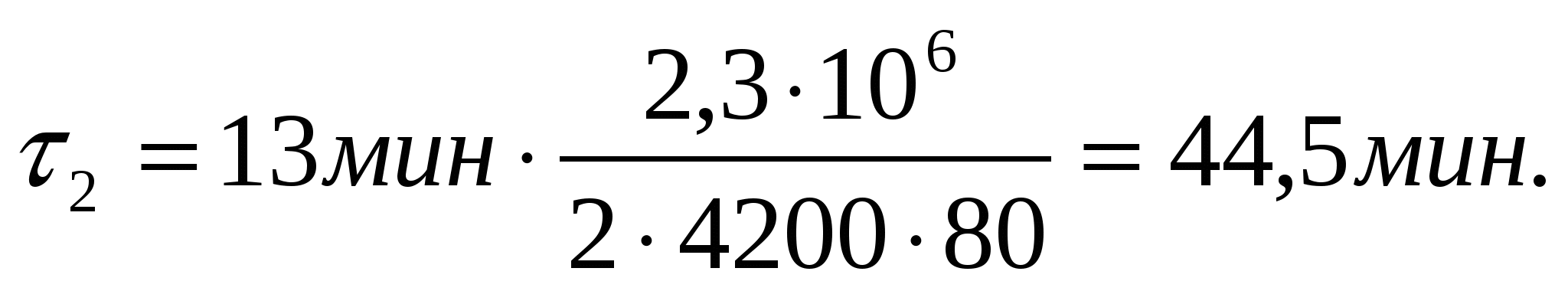
6. 29С
m1 = 1,4 кг
с1=4200 Дж/(кг0С)
t2 = 100С
= 0,7
m2 = 0,1 кг
q = 29106 Дж/кг
Решение
= 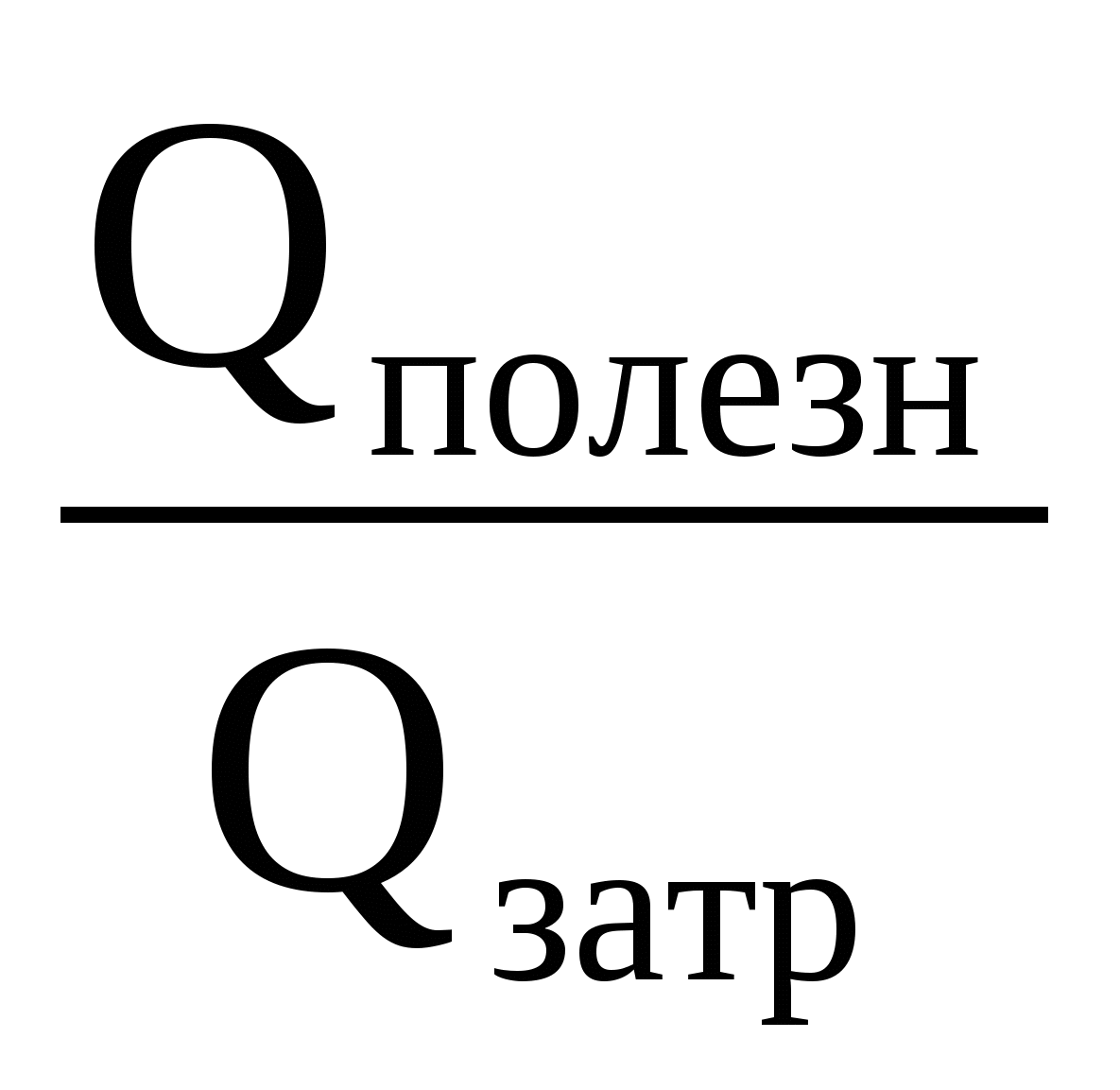
Qполез = Q1 + Q2 =
= cm1(t2 t1) + L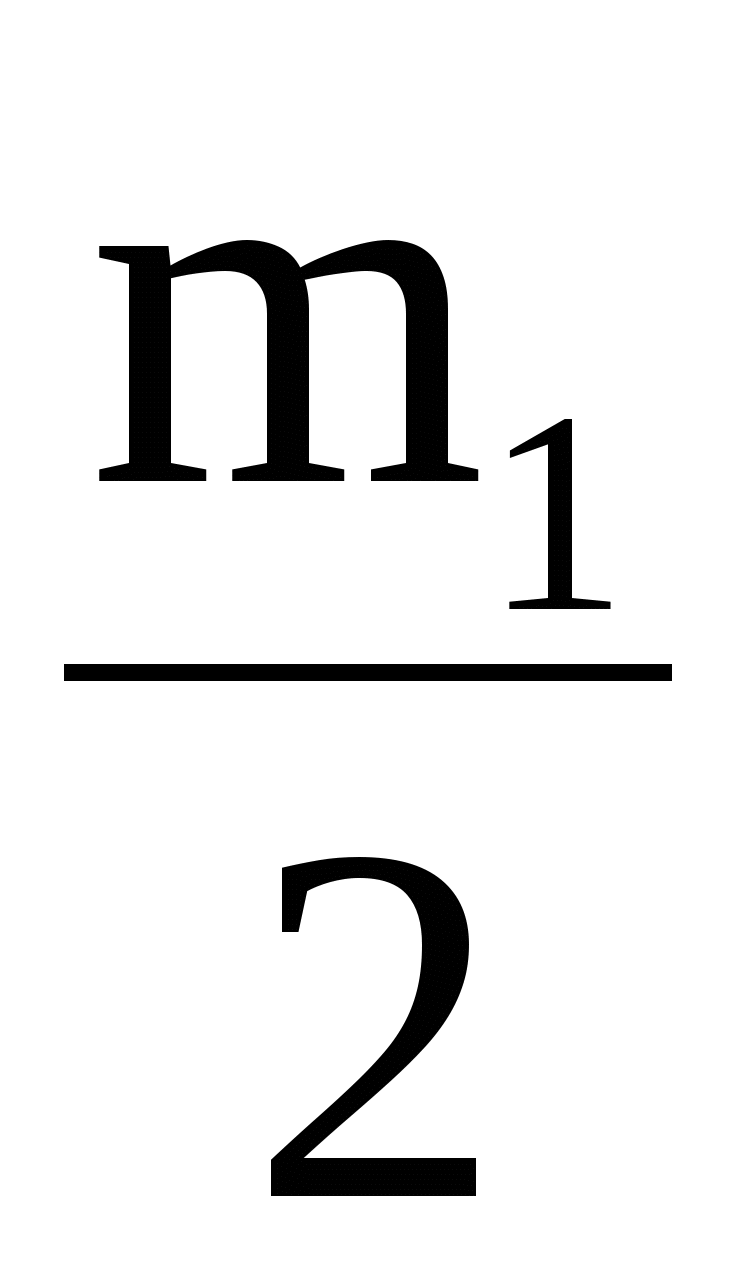
Qзатр = qm2.
Тогда = 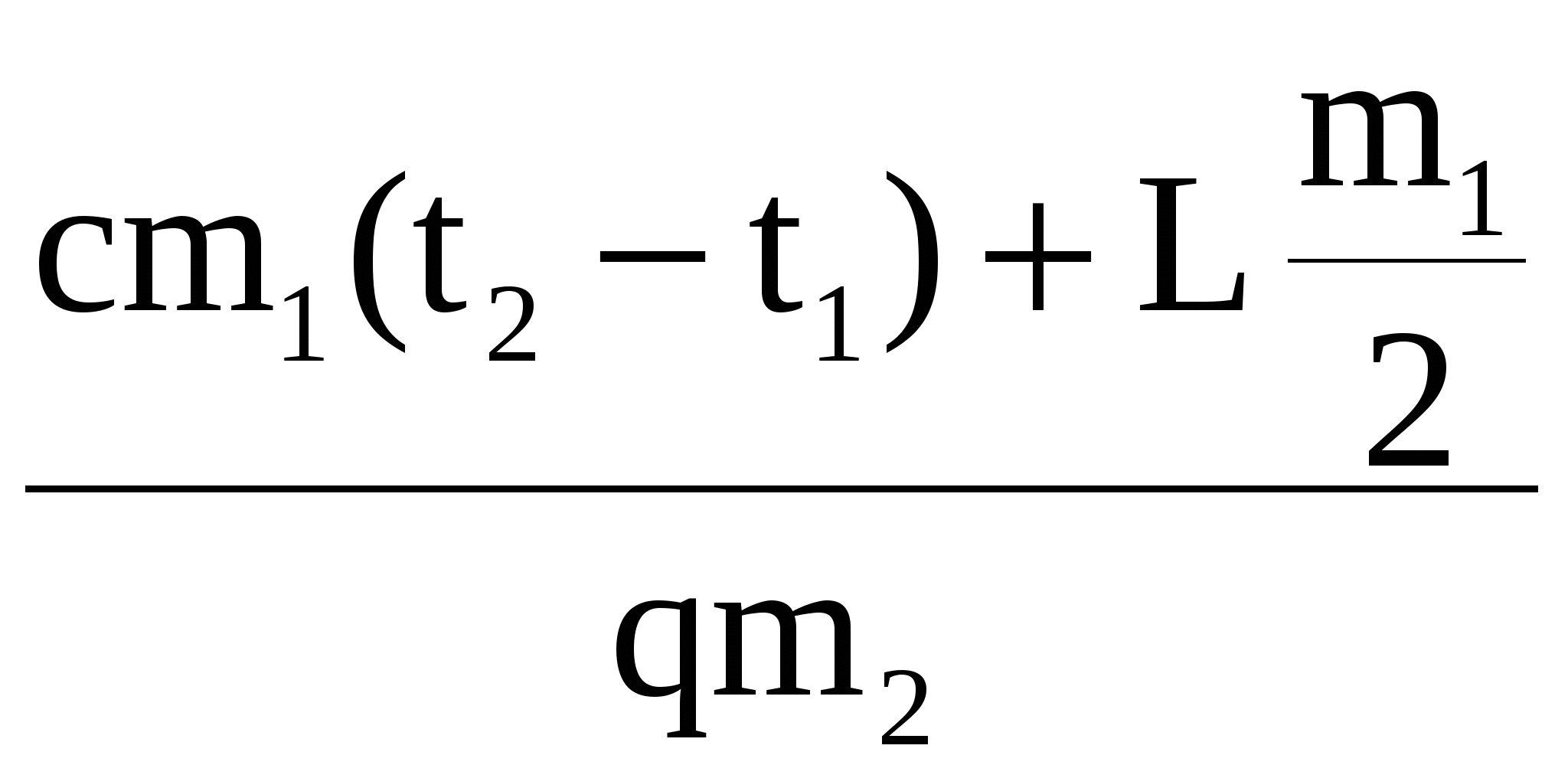
t1-?
Выражаем t1: t1 = t2 — 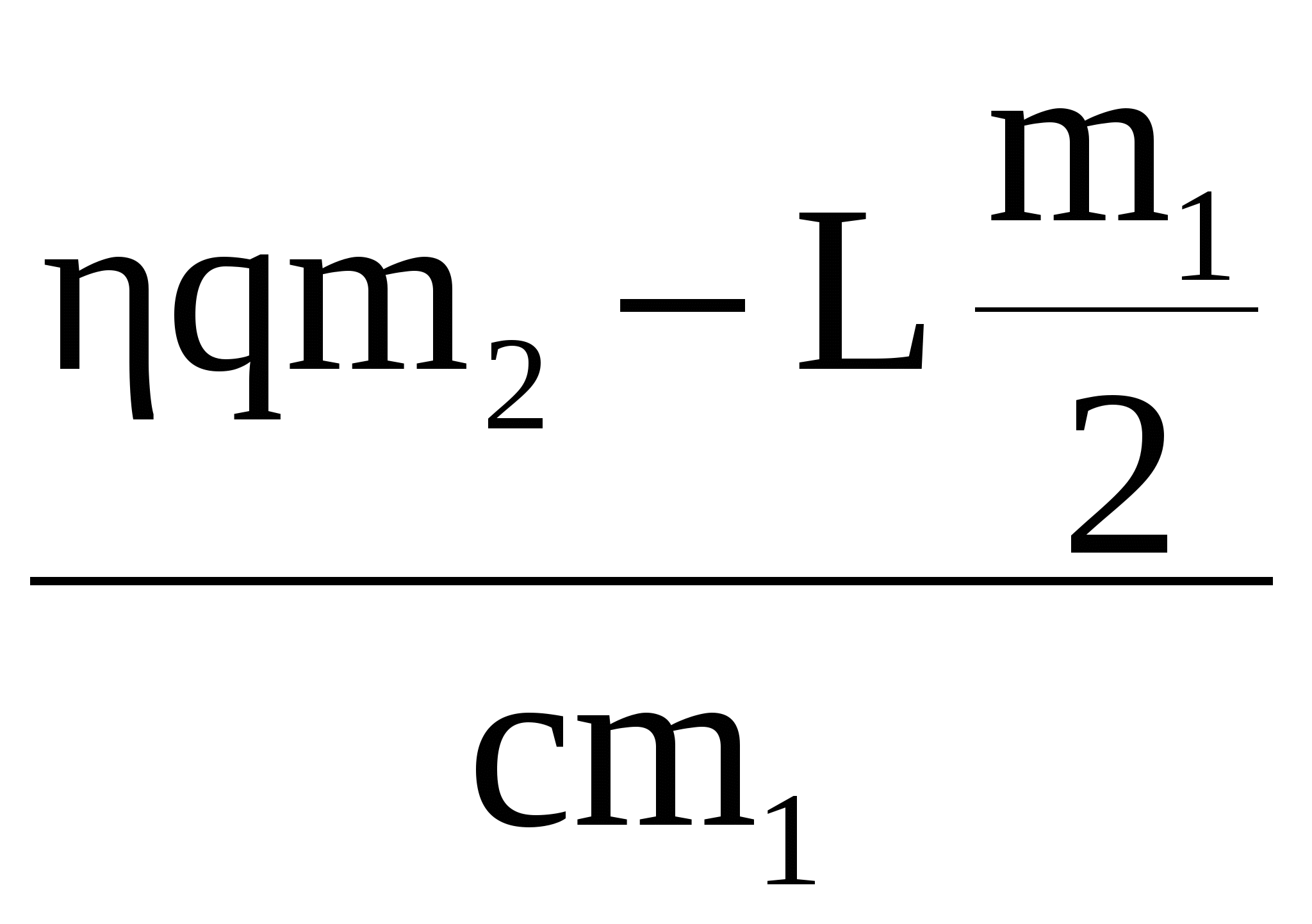
t1 = 100 — 
7. 563 г.
m1 = 0,5кг
= 3,4105 Дж/кг
t1 = 0С
с = 4200 Дж/(кг0С)
L = 2,3106 Дж/кг
t2 = 100С
Р
t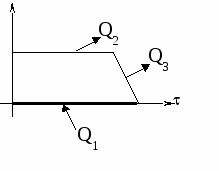
Q1 = Q2 + Q3,
m1 = Lm2 + cm2(t2 t1),
m2 = 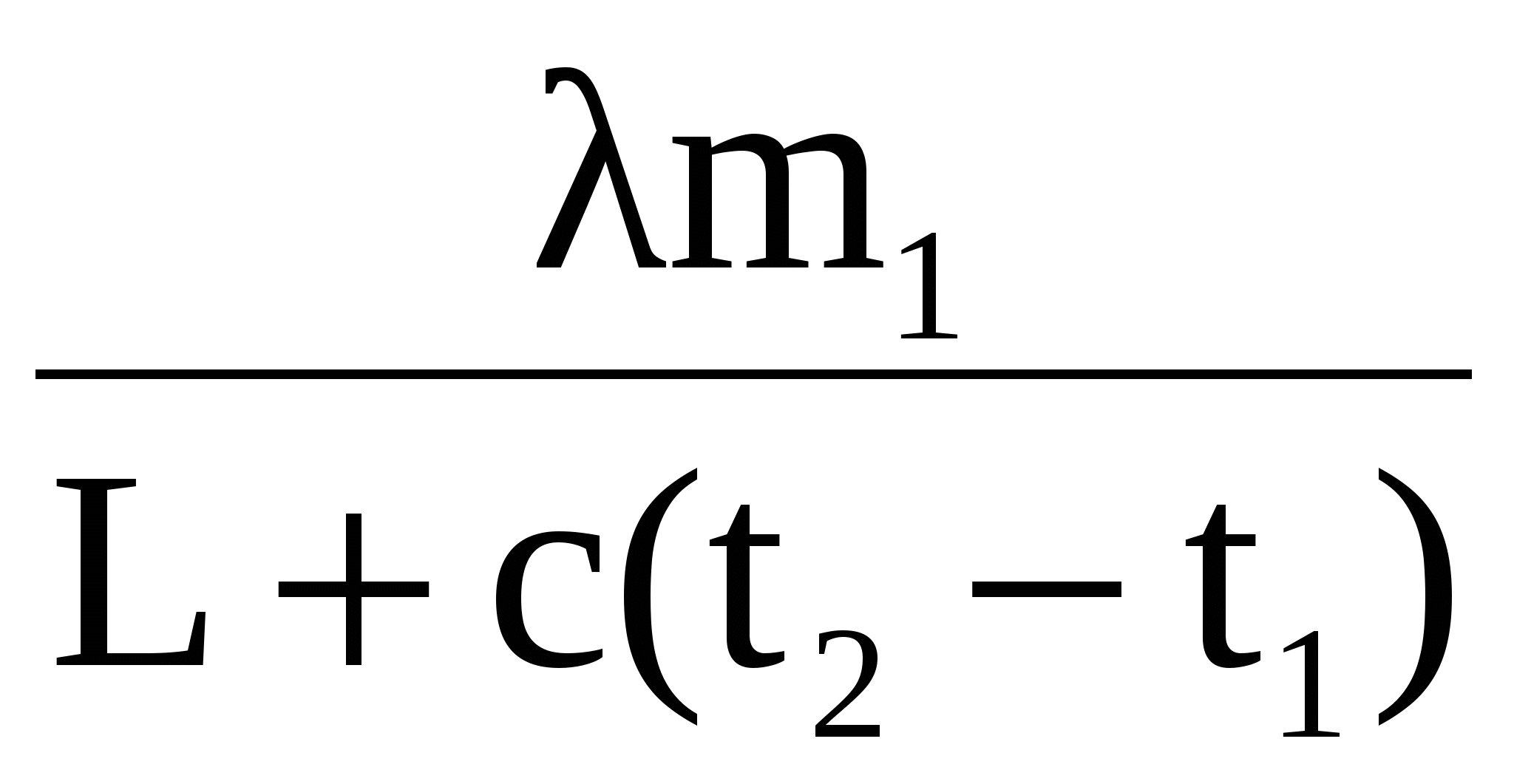
m2 = 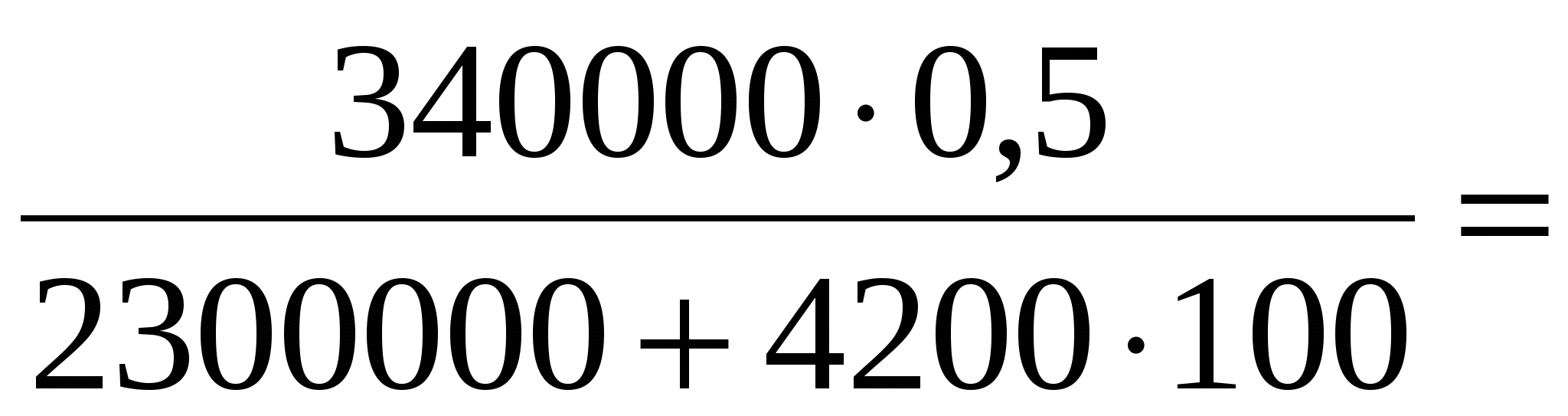
m — ?
= 0,063 (кг) = 63 г
В итоге: m= m1 + m2 = 500 +63 = 563 (г).
-
65 г
m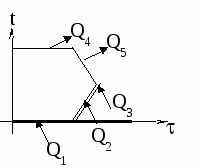
m2 = 0,2 кг
= 3,4105 Дж/кг
t1 = 0С
c =4200Дж/(кг0С)
t2 = 100С
L = 2,3106 Дж/кг
= 20С
C = 1000 Дж/0С
Решение
Q1 + Q2 + Q3 = Q4 + Q5,
m2 + c(m1 + m2)(0 t1) +
+ C( t1) =
= Lm3 + cm3(t2 ),
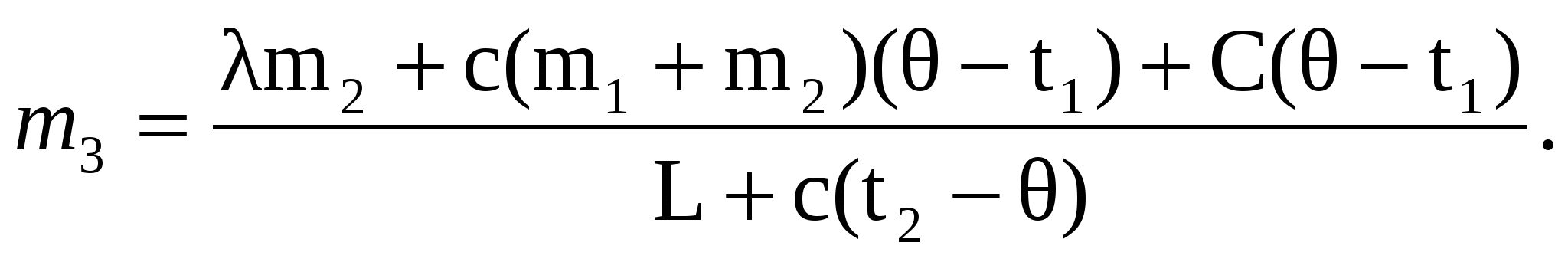
m3 = 
m3 — ?
-
27,1 кг.
C = 1000 Дж/0С
m1 = 5 кг
c1=4200 Дж/(кг0С)
t1 = 20С
t2 = 40С
c2=2100 Дж/(кг0С)
= 3,4105 Дж/кг
= 2С
Решение
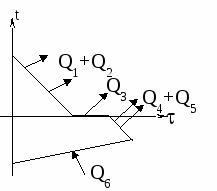
Q1 + Q2 + Q3 + Q4 + Q5 = Q6,
Q2 + Q4 = C(t1 ) — теплота, отданная калориметром;
Q1 + Q3 + Q5 =
c1m1(t1 0) + m1 + c2m1(0 ) — теплота, отданная водой;
Q6 = c2m2( t2) — теплота, принятая льдом.
m2 — ?
Тогда m2 = 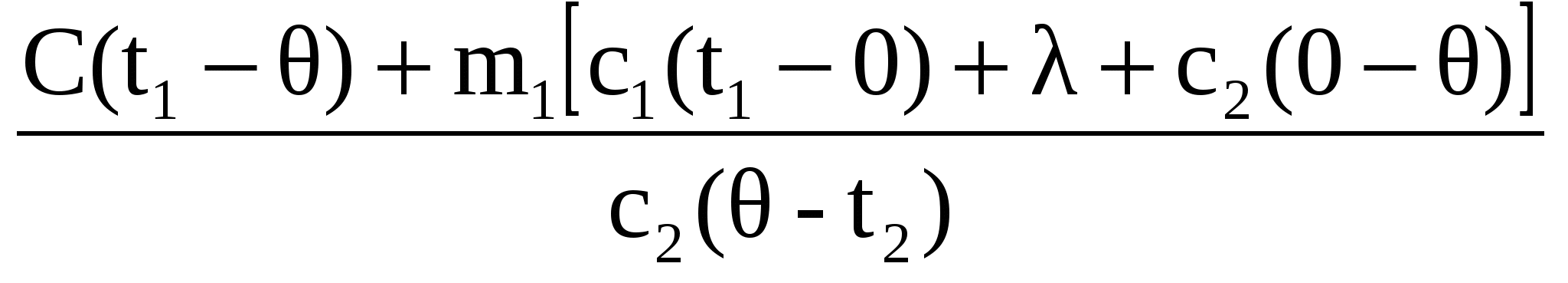
m2 = 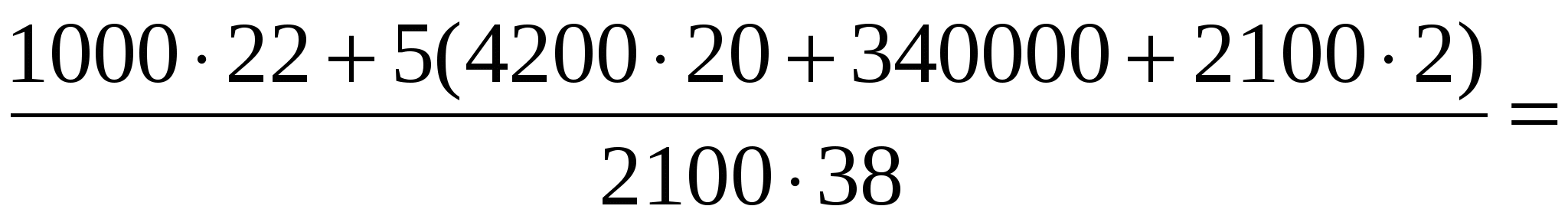
10. 340 г льда и 60 г пара.
с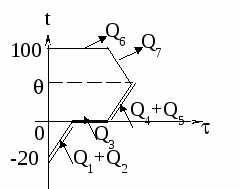
m1 = 0,2 кг
t1 = t2 = 20С
c2=2100 Дж/(кг0С)
t3 = 100С
L = 2,3106 Дж/кг
= 3,4105 Дж/кг
c3=4200 Дж/(кг0С)
= 20С
m = 0,4 кг
Решение
Q1 + Q2 + Q3 + Q4 + Q5 =
= Q6 + Q7.
Q2, Q3, Q4 — теплоты, полученные льдом;
Q1, Q5 — теплоты, полученные калориметром;
Q6, Q7 — теплоты, отданные паром.
c1m1( t1) + c2m2(0 t2) + m2 + c3m2( 0) =
= L(m m2) + c3(m m2)(100 ),
Масса льда:
m2 — ? m3 — ?
m2 = 
m2 = 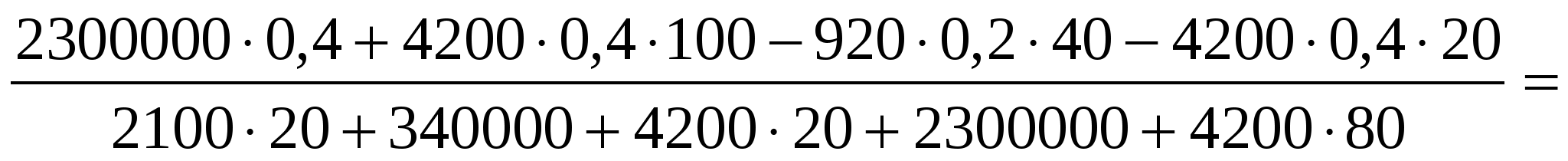
Масса пара: m3 = m — m2 = 0,4 кг — 0,34 кг = 0,06 кг.
11. Смесь, состоящая из 1,4 кг льда и 3,6 кг воды при температуре 00С.
m1 = 3 кг
t1 = 20С
c1= 4200 Дж/(кг0С)
m2 = 2 кг
t2 = 10С
c2= 2100 Дж/(кг0С)
= 3,4105 Дж/кг
Решение
1. Q1 = c1m1(t1 0) = 4200320 = 252000 (Дж) — может отдать вода, остывая от 20С до 0С.
2. Q2 = c2m2(0 t2) = 2100210 = 42000 (Дж) — нужно льду, чтобы нагреться от -10С до 0С.
3. Q3 = m2 = 3400002 = 680000 (Дж) — нужно льду, чтобы полностью расплавиться.
4. Q1 Q2 < Q3 — значит, у воды не хватит энергии, чтобы расплавить весь лёд.
m1 — ?
m2 — ?
— ?
Вывод: лёд растает не весь, и в калориметре будет находиться смесь воды со льдом при температуре 0С.
Сколько растает льда?
m = Q1 Q2 m = 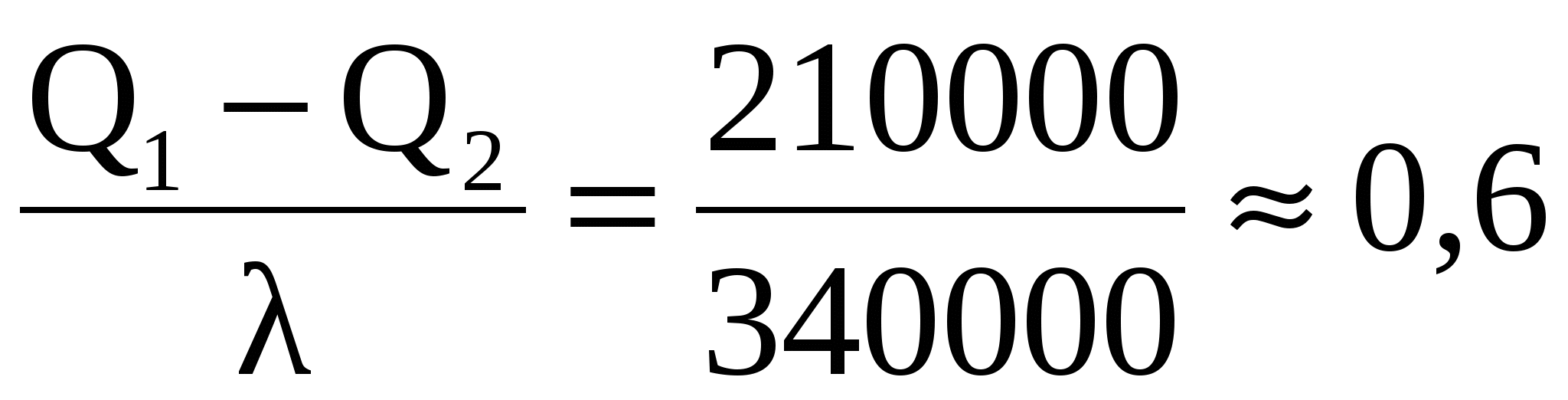
Тогда останется льда: m2 = m2 m = 2 кг — 0,6 кг = 1,4 кг.
Масса воды: m1 = m1 + m = 3 кг + 0,6 кг = 3,6 кг
12. 0,2 кг льда и 1,7 кг воды при температуре 00С.
m1 = 1 кг
m2 = 0,8 кг
t1 = t2 = 0С
= 3,4105 Дж/кг
c = 4200 Дж/(кг0С)
m3 = 0,1 кг
t3 = 100С
L = 2,3106 Дж/кг
Решение
1. Q1 = m1 = 3400001 = 340000 (Дж) — нужно льду, чтобы полностью растаять при 00С.
2. Q2 = Lm3 = 23000000,1 = 230000 (Дж) — может отдать пар, конденсируясь при 1000С в воду.
3. Q3 = cm3(t3 t1) = 42000,1100 = 42000 (Дж) — может отдать пар, остывая от 1000С до 00С. 4. Q2 + Q3 = 230000 + 42000 = 272000 (Дж) Q1.
Поэтому лёд растает не весь, пар весь сконденсируется, а образовавшаяся из него вода остынет до 0С.
— ?
m1 - ?
m2 — ?
Сколько льда растает?
m = Q2 + Q3 m = 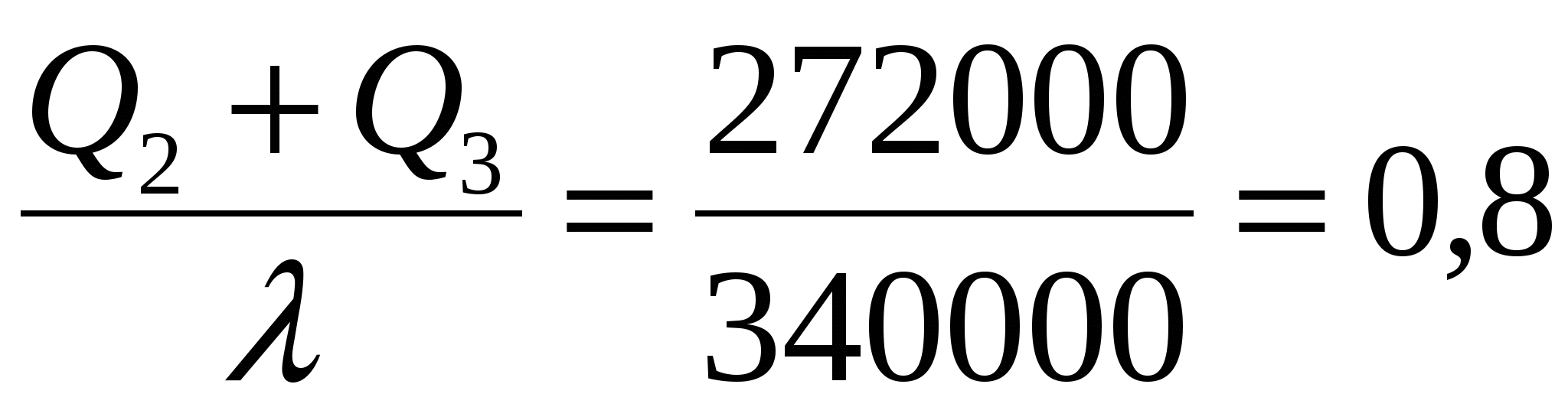
В калориметре останется льда: m1 = m1 m = 1 кг — 0,8 кг = 0,2 кг .
Масса воды: m2 = m2 + m+ m3 = (0,8 + 0,8 + 0,1) кг = 1,7 (кг)
Полученная смесь находится при температуре 0С.
13. Смесь воды (750 г) и льда (750 г) при 00С.
m1 = 0,6 кг
c1= 4200 Дж/(кг0С)
t1 = 5С
m2 = 0,3 кг
t2 = 10С
m3 = 0,6 кг
t3 = 600С
с2= 2100 Дж/(кг0С)
= 3,4105 Дж/кг
Решение
1. Q1 = c1m1(t1 0) = 42000,65 = 12600 (Дж) — выделят 600 г воды, остывая от 5С до 0С.
2. Q2 = c1m2(t2 0) = 42000,310 = 12600 (Дж) — выделят 300 г воды, остывая от 10С до 0С.
Q1 + Q2 = 25200 Дж.
3. Q3 = c2m3(0 t3) = 21000,660 = 75600 (Дж) — нужно льду, чтобы нагреться от -60С до 0С.
Q3 Q1 + Q2 вся вода остынет до 0С, а лёд ещё при этом не нагреется до 0С.
Q = Q3 (Q1 + Q2) = 75600 — 25200 = 50400 (Дж). Нагреваясь до 0С, лед «приморозит» к себе часть воды m:
— ?
mводы — ?
mльда — ?
m = Q m = 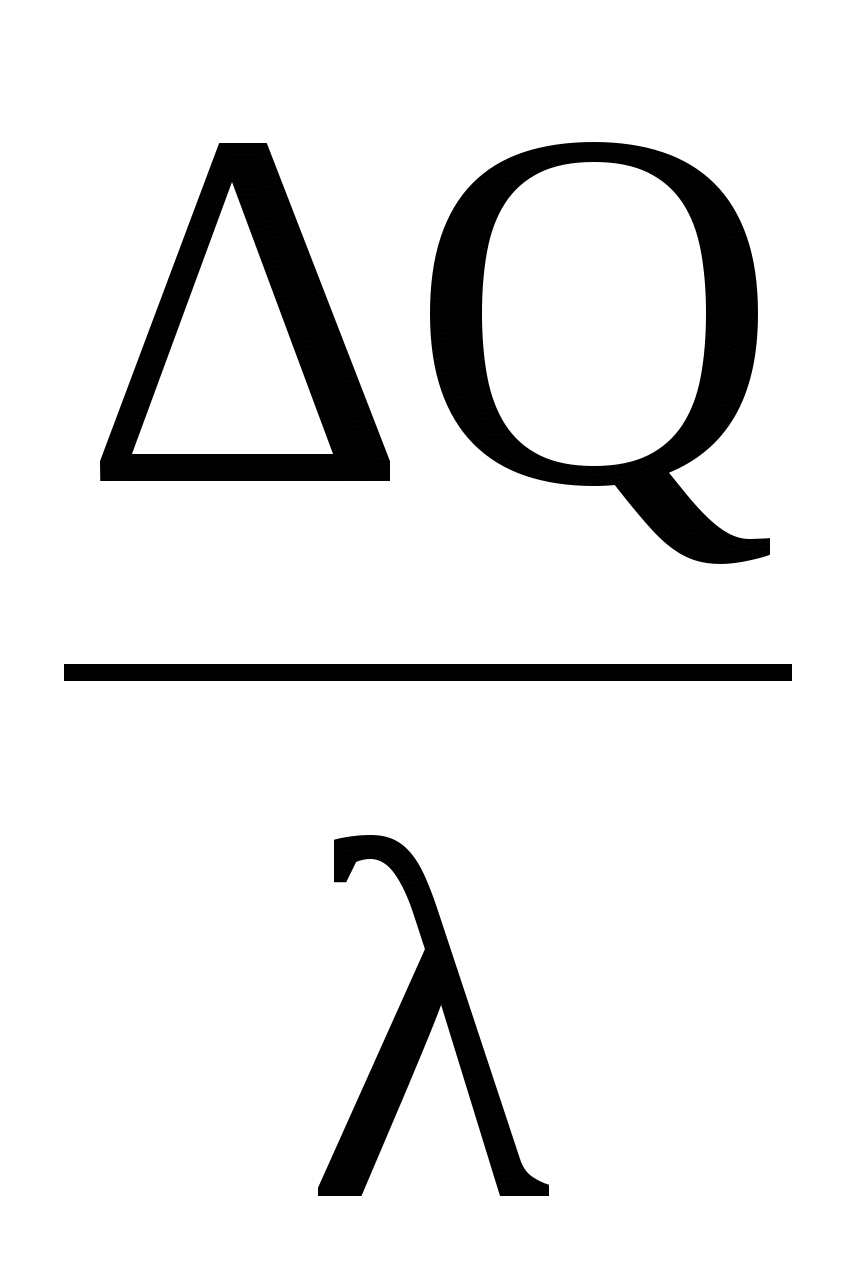
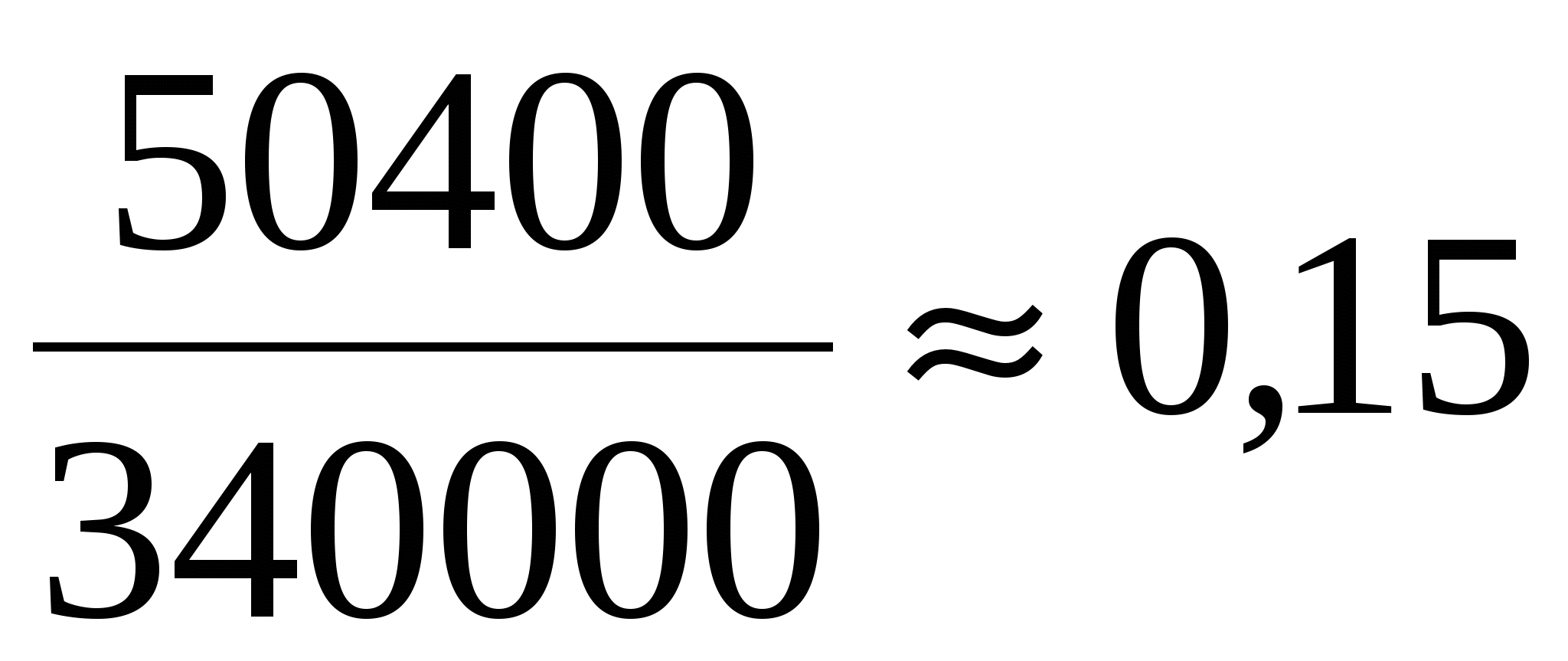
Итак, в калориметре будет находиться смесь воды со льдом при температуре 0С:
mводы = m1 + m2 m = 0,6 + 0,3 0,15 = 0,75 (кг),
mльда = m3 + m = 0,6 + 0,15 = 0,75 (кг)
14. 2,4 кг воды при температуре 360С.
m1 = 0,4 кг
c1 = 380 Дж/(кг0С)
m2 = 2 кг
c2= 2100 Дж/(кг0С)
t1 = t2 = 10С
= 3,4105 Дж/кг
m3 = 0,4 кг
t3 = 110С
с3= 2100 Дж/(кг0С)
L = 2,3106 Дж/кг
c4= 4200 Дж/(кг0С)
Решение
1. Q1 = c1m1(0 t1) = 3800,410 = 1520 (Дж) — нужно получить медному сосуду, чтобы нагреться от -10С до 0С.
2. Q2 = c2m2(0 t1) = 2100210 = 42000 (Дж) — нужно получить льду, чтобы он нагрелся от
10С до 0С.
3. Q3 = m2 = 3400002 = 680000 (Дж) — нужно получить льду, чтобы растаять и стать водой при 0С.
Q1 + Q2 + Q3 = 723520 (Дж) — нужно получить сосуду и льду, чтобы в сосуде при 0С была вода.
4. Q4 = c3m3(t3 100) = 21000,410 = 8400 (Дж) — может отдать пар, остывая от 110С до 100С.
5. Q5 = Lm3 = 23000000,4 = 920000 (Дж) — может отдать пар, конденсируясь в воду при 1000С.
— ?
m — ?
Q4 + Q5 = 8400 + 920000 = 928400 (Дж) — может отдать пар, превращаясь в пар с температурой 100С;
Q = (Q4 + Q5) (Q1 + Q2 + Q3) = 928400 — 723520 = 204880 (Дж) — столько энергии останется у пара, когда он станет водой при 1000С, (лед при этом превратится в воду при 0С).
Проверим, хватит ли этой энергии, чтобы вода, образовавшаяся из льда, нагрелась вместе с сосудом от 0С до 100С?
Q6 = (c1m1 + c2m2)(100 0) = (3800,4 + 42002)100 = 855200 (Дж).
Это больше, чем 204880 Дж. Значит, вода, образовавшаяся из льда, нагреется не до 100С. Найдем, до какой температуры нагреются вода и сосуд:
Q1 + Q2 + Q3 + (c1m1 + c4m2)( 0) = Q4 + Q5 + c4m3(100 ),
c1m1 + c4m2 + c4m3 = c4m3100+ 204880,
= 
15. 174 г.
m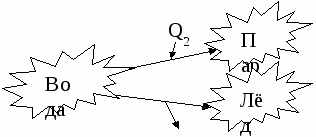
= 3,4105 Дж/кг
L = 2,3106 Дж/кг
Решение
m
Q11 — ?
Q1 = m1 — энергия, которая выделяется при замерзании воды массой m1.
Q2 = L(m — m1) — энергия, которая необходима для превращения оставшейся воды в пар.
Q1 = Q2,
m1 = L(m m1)
m1 = m
m1 = 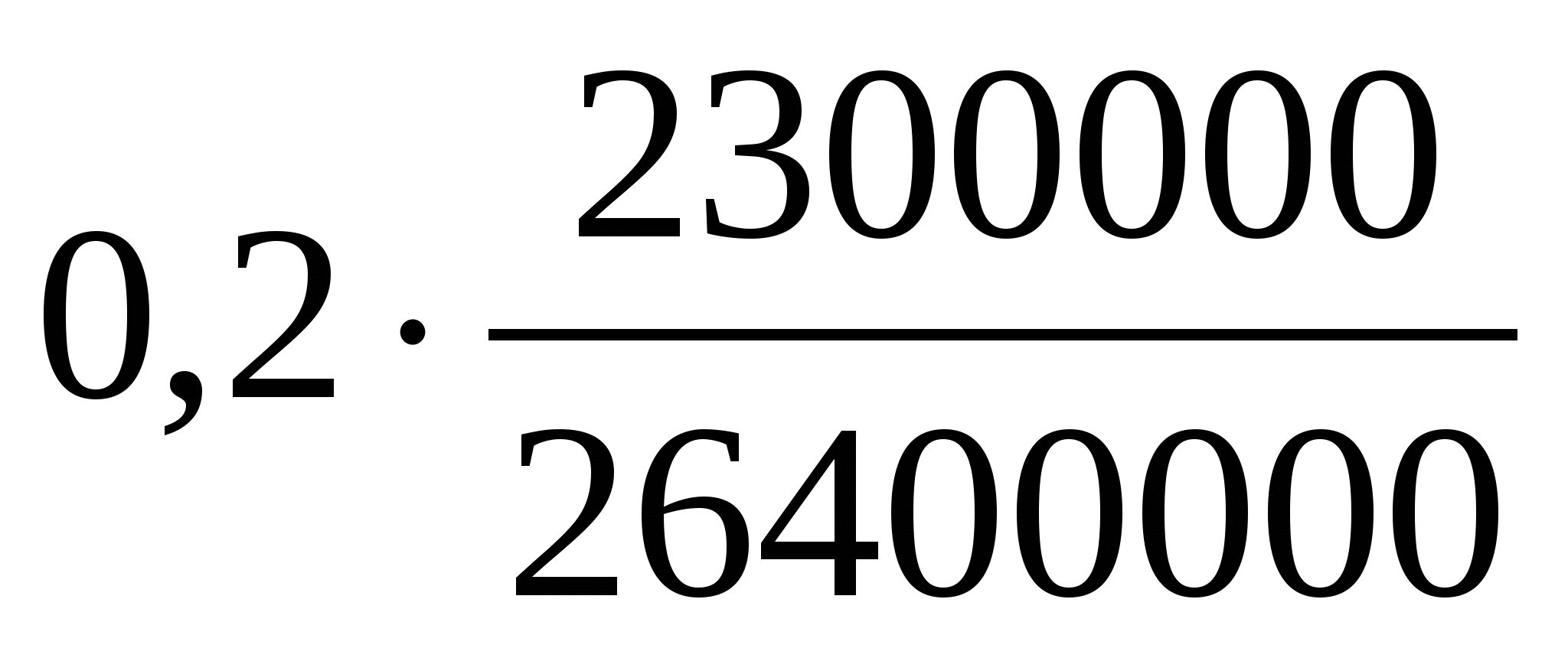
Учебное издание
Самарин Григорий Геннадьевич
Решение задач на теплообмен с использованием уравнения теплового баланса
(методические рекомендации)
Редактор — Г. Д. Попырина
Компьютерная верстка — К. В. Маренин
Подписано в печать:
Бумага типографская
Условных печатных листов — 2,25
Тираж — 100 экз.
Заказ —
Цена договорная.
Лицей естественных наук
610006, г. Киров, ул. Возрождения, 6
Здесь и в дальнейшем единицы измеряются в системе СИ.
В этой и последующих задачах потерями теплоты в калориметре пренебречь.











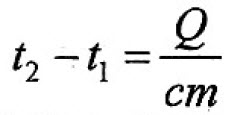
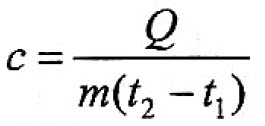







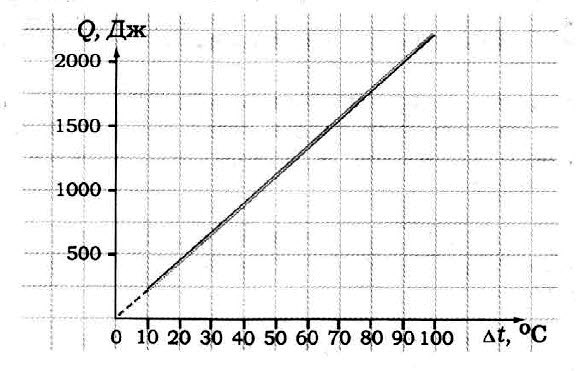


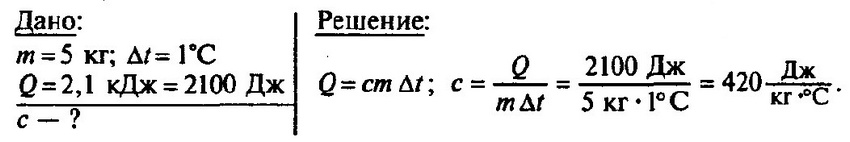








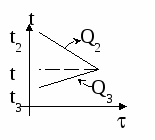 . Не трудно догадаться, что в результате теплообмена самая горячая пластина остынет, а самая холодная нагреется. Итак, мы знаем, что будет происходить с железной и алюминиевой пластинами: железная будет остывать, алюминиевая — нагреваться.
. Не трудно догадаться, что в результате теплообмена самая горячая пластина остынет, а самая холодная нагреется. Итак, мы знаем, что будет происходить с железной и алюминиевой пластинами: железная будет остывать, алюминиевая — нагреваться.