Задачи на трапецию егэ математика профиль - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

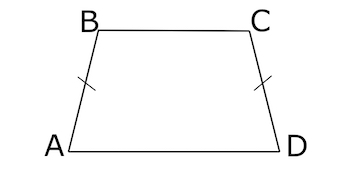
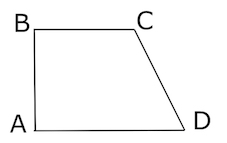
Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.

Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен Найдите боковую сторону.

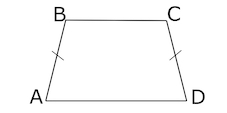
Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен Найдите меньшее основание.

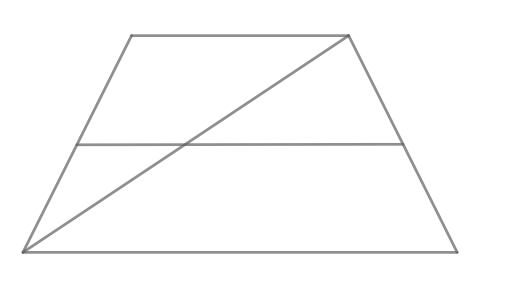
Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен Найдите высоту трапеции.

Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 39. Тангенс острого угла равен Найдите большее основание.

Пройти тестирование по этим заданиям

Источник

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Трапеция»

Открытый банк заданий по теме трапеция. Задания B6 из ЕГЭ по математике (профильный уровень)

Производная и первообразная функции

Задание №1067

Тип задания: 6
Тема:
Трапеция

Условие

Большее основание равнобедренной трапеции равно 24. Боковая сторона равна 7. Синус острого угла равен frac{sqrt{33}}{7}. Найдите меньшее основание.

Показать решение

Решение

Рассмотрим равнобедренную трапецию ABCD, в которой BC и AD — основания, AD = 24, AB = CD = 7. Проведём высоты CK и BH. BCKH — прямоугольник, BC = KH.

Треугольник ABH прямоугольный, cos A = frac{AH}{AB}. Вычислим cos A= sqrt{1-sin^2A}= sqrt{1-left (frac{sqrt{33}}{7}right)^2}= frac47. AH= ABcos A= 7cdotfrac47= 4. Треугольники ABH и DCK равны по гипотенузе и острому угу, откуда AH=KD=4, BC=24-4-4=16.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1065

Тип задания: 6
Тема:
Трапеция

Условие

Площадь треугольника МРЕ равна 68, KT — средняя линия, параллельная стороне MP. Найдите площадь трапеции MPTK.

Показать решение

Решение

S_{MPTK}=S_{MPE}-S_{KTE}. KT — средняя линия, параллельная стороне MP, поэтому K и T — середины сторон и ET=frac12EP, KE=frac12 EM.

triangle MPE sim triangle KTE по двум углам: angle E — общий, MP parallel KT Rightarrow angle MPE= angle KTE. S_{KTE}= frac14S_{MPE}= frac{68}{4}= 17. S_{MPTK}= 68-17= 51.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1064

Тип задания: 6
Тема:
Трапеция

Условие

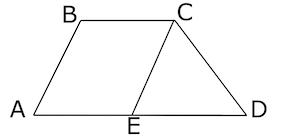
Площадь треугольника АВС равна 76, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.

Показать решение

Решение

S_{ABED}=S_{ABC}-S_{CDE}. DE — средняя линия, параллельая стороне AB, поэтому D и E — середины сторон.

CD=frac12CA, CE=frac12CB, S_{ABC} =frac12CAcdot CBsin C,

S_{CDE}= frac12CDcdot CEsin C= frac12cdotfrac12CAcdotfrac12CBsin C= frac14cdotfrac12CAcdot CBsin C= frac14 S_{ABC}= frac{76}{4}=19

S_{ABED}= S_{ABC}-S_{CDE}= 76-19=57.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1061

Тип задания: 6
Тема:
Трапеция

Условие

Основания равнобедренной трапеции равны 10 и 90, а её боковые стороны равны 41. Найдите площадь трапеции.

Показать решение

Решение

Рассмотрим равнобедренную трапецию ABCD, в которой BC = 10, AD = 90 — основания, AB = CD = 41.

Проведём высоты CP и BH. BCPH — прямоугольник, BC = PH = 10. Прямоугольные треугольники ABH и DCP равны по гипотенузе и катету (AB = CD, BH = CP), тогда AH = PD = (90 — 10) : 2 = 40.

Треугольник ABH прямоугольный, BH = sqrt{41^2-40^2} = 9.

Площадь трапеции равна S = frac{BC+AD}{2}cdot BH= frac{10+90}{2}cdot 9= 450.

Ответ

450

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №895

Тип задания: 6
Тема:
Трапеция

Условие

Основания равнобедренной трапеции равны 15 и 43. Косинус острого угла трапеции равен 0,7. Найдите боковую сторону.

Показать решение

Решение

Рассмотрим равнобедренную трапецию ABCD, в которой BC=15, AD=43 — основания, AB=CD.

Проведём высоты CK и BH. BCKH — прямоугольник, BC=KH=15. Треугольники ABH и DCK равны по гипотенузе и острому углу, откуда AH=KD=(43-15):2=14. Треугольник ABH прямоугольный, cos A=frac{AH}{AB}. Боковая сторона трапеции AB=AH:cos A=14:0.7=20.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №888

Тип задания: 6
Тема:
Трапеция

Условие

Найдите площадь прямоугольной трапеции, основания которой равны 16 и 22, большая боковая сторона составляет с основанием угол 45^{circ}.

Показать решение

Решение

Рассмотрим прямоугольную трапецию ABCD с основаниями BC=16 и AD=22, angle A=90^{circ}, angle D=45^{circ}. Проведём высоту CH. ABCH — прямоугольник, BC=AH=16, тогда HD=22-16=6.

Треугольник CDH прямоугольный и равнобедренный (т.к. angle CHD=90^{circ}, angle HCD=45^{circ}=angle D). HD=HC=6.

Площадь трапеции S=frac{BC+AD}{2}cdot CH=frac{16+22}{2}cdot6=114.

Ответ

114

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №297

Тип задания: 6
Тема:
Трапеция

Условие

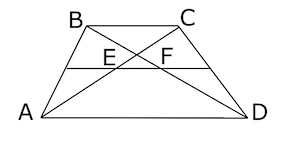
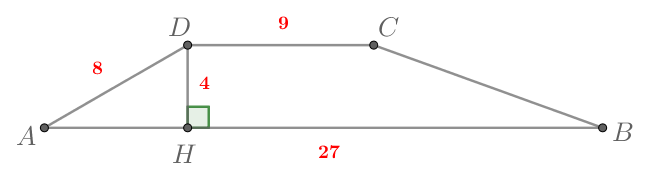
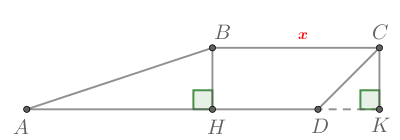
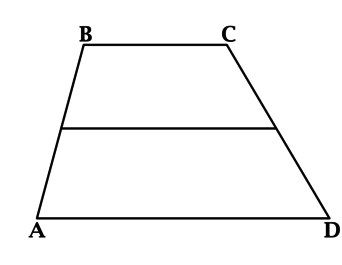
Основания равнобедренной трапеции равны 9 и 53. Тангенс острого угла равен frac{6}{11}. Найдите высоту трапеции.

Показать решение

Решение

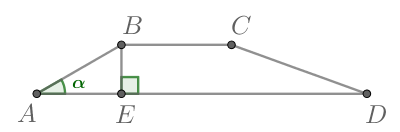
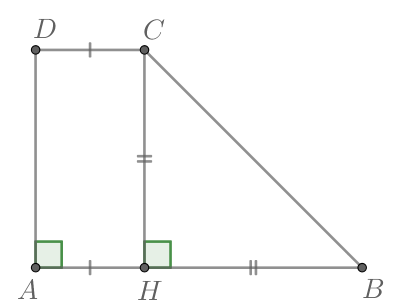
Рассмотрим рисунок:

BKperp AD и CMperp AD, тогда AK=MD=frac{53-9}{2}=22.

frac{BK}{AK}=tgangle BAK=frac{6}{11}, поэтому BK=AKcdotfrac{6}{11}=22cdotfrac{6}{11}=12.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №293

Тип задания: 6
Тема:
Трапеция

Условие

Основания прямоугольной трапеции имеют длины 4 и 8. Ее большая сторона с основанием образуют угол равный 45^{circ}. Найдите площадь трапеции.

Показать решение

Решение

Пусть CH — высота трапеции ABCD. Тогда в прямоугольном треугольнике CHD острый угол CHD = 45^{circ}. Значит, этот треугольник равнобедренный, то есть CH=DH=AD-BC=8-4=4.

Тогда S_{ABCD}=frac{AD+BC}{2}cdot CH=frac{8+4}{2}cdot4=24.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник

25
Июл 2013

Категория: 01 Геометрия

01. Трапеция

2013-07-25
2022-09-11

Задача 1. Основания равнобедренной трапеции равны и Боковые стороны равны Найдите синус острого угла трапеции.

Решение: + показать

Задача 2. Большее основание равнобедренной трапеции равно Боковая сторона равна Синус острого угла равен $frac{sqrt5}{3}.$ Найдите меньшее основание.

Решение: + показать

Задача 3. Основания равнобедренной трапеции равны и Тангенс острого угла равен $frac{11}{13}$ . Найдите высоту трапеции.

Решение: + показать

Задача 4. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна $70^{circ}$ ? Ответ дайте в градусах.

Решение: + показать

Задача 5. Найдите среднюю линию трапеции, если ее основания равны и

Решение: + показать

Задача 6. Средняя линия трапеции равна а меньшее основание равно Найдите большее основание трапеции.

Решение: + показать

Задача 7. Основания трапеции равны и Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

Решение: + показать

Задача 8. Основания трапеции равны и Найдите отрезок, соединяющий середины диагоналей трапеции.

Решение: + показать

Задача 9. В равнобедренной трапеции основания равны и острый угол равен $60^{circ}$ . Найдите ее периметр.

Решение: + показать

Задача 10. Основания трапеции равны и боковая сторона равна Площадь трапеции равна Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ дайте в градусах.

Решение: + показать

Задача 11. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного отсекает треугольник, периметр которого равен Найдите периметр трапеции.

Решение: + показать

Задача 12. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины и Найдите среднюю линию этой трапеции.

Решение: + показать

Задача 13. Основания трапеции относятся как а средняя линия равна Найдите меньшее основание.

Решение: + показать

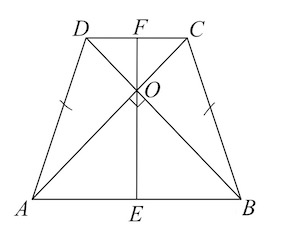
Задача 14. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна Найдите ее среднюю линию.

Решение: + показать

Задача 15. Найдите площадь прямоугольной трапеции, основания которой равны и большая боковая сторона составляет с основанием угол $45^{circ}.$

Решение: + показать

Задача 16. Основания равнобедренной трапеции равны и а ее периметр равен Найдите площадь трапеции.

Решение: + показать

Задача 17. Найдите среднюю линию трапеции , если стороны квадратных клеток равны .

Решение: + показать

Вы можете пройти тест по теме «Трапеция»

Автор: egeMax |

комментариев 14

Печать страницы

Источник

Тема 1.

Геометрия на плоскости (планиметрия)

Трапеция и ее свойства

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

геометрия на плоскости (планиметрия)

1.01Треугольник: внутренние и внешние углы

1.02Треугольник: высота, биссектриса, медиана

1.03Треугольник: задачи на подобие

1.04Прямоугольный треугольник и теорема Пифагора

1.05Треугольник: площадь и периметр

1.06Параллелограмм и его свойства

1.07Параллелограмм и свойство его биссектрисы

1.08Прямоугольник и его свойства

1.09Ромб и его свойства

1.10Квадрат и его свойства

1.11Трапеция и ее свойства

1.12Равнобедренная трапеция

1.13Окружность: центральный и вписанный углы

1.14Окружность: углы, образованные хордами, секущими, касательными

1.15Окружность: отрезки хорд, секущих, касательных

1.16Окружность: описанная около многоугольника

1.17Окружность: вписанная в многоугольник или угол

1.18Длина окружности или дуги и площадь круга или сектора

1.19Правильный шестиугольник и его свойства

1.20Площадь многоугольника: различные формулы

1.21Внешние углы многоугольника и тригонометрия

1.22Решение треугольника и других фигур с помощью тригонометрии

1.23Теорема синусов и теорема косинусов

1.24Координатная плоскость

1.25Векторы: сложение, вычитание, координаты

1.26Задачи на клетчатой бумаге

Решаем задачи

Один из углов прямоугольной трапеции равен ∘
113 . Найдите меньший угол этой трапеции. Ответ дайте в градусах.

Показать ответ и решение

В трапеции сумма углов, прилежащих боковой стороне, равна ∘
180 , то есть если один из таких углов равен ∘
113 , то другой
равен

Оставшиеся два угла равны ∘
90 , так как трапеция — прямоугольная. Тогда меньший угол равен ∘
67 .

В трапеции ABCD известно, что ∘
∠BDA = 14 и ∘
∠BDC = 106. Найдите угол ABD. Ответ дайте в
градусах.

Показать ответ и решение

Трапеция равнобедренная, то есть

∘ ∘ ∘
∠BAD = ∠CDA = ∠BDA + ∠BDC = 106 + 14 = 120

По сумме углов треугольника ABD имеем:

∘ ∘ ∘ ∘ ∘
∠ABD = 180 − ∠BAD − ∠ADB = 180 − 120 − 14 = 46

Основания трапеции равны 3 и 9, а высота равна 5. Найдите среднюю линию этой трапеции.

Показать ответ и решение

Средняя линия трапеции равна полусумме оснований, то есть равна

1 12
2(3 +9)= 2-= 6

Основания трапеции равны 10 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее
диагоналей.

Показать ответ и решение

Пусть

Так как — средняя линия трапеции, и — средние линии треугольников ADC и ACB соответственно.
Значит,

EO = 1DC = 1⋅10= 5
2 2

1 1
OF = 2 AB = 2 ⋅11 =5,5

Больший из этих отрезков равен 5,5.

Средняя линия трапеции равна 20. Одна из диагоналей трапеции делит среднюю линию в отношении 1 к 4. Найдите большее
основание трапеции.

Основания трапеции равны 6 и 8. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее
диагоналей.

Показать ответ и решение

Для начала найдем длину средней линии трапеции: она равна полусумме оснований, то есть

6+ 8
-2-- =7

Так как — средняя линия трапеции ABCD , то и при этом — середина AD.

Тогда в треугольнике ADB отрезок параллелен основанию и при этом проходит через середину стороны AD.
Значит, — средняя линия треугольника ADB и

EO = 1AB = 4
2

Тогда

Следовательно, наибольший из отрезков равен 4.

Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции,
прилежащий к данной боковой стороне. Ответ выразите в градусах.

Показать ответ и решение

Опустим высоту на AD. В прямоугольном треугольнике ABE катет напротив угла равен

Запишем площадь трапеции, чтобы найти sinα

1 2SABCD
SABCD = 2(AD + BC )⋅BE ⇒ BE = AD-+-BC-= 4

Тогда

sin α= BE- = 0,5 ⇒ α= 30∘
8

Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол ∘
150. Найдите
площадь трапеции.

Показать ответ и решение

Пусть ∘
∠ABC =150 , тогда из параллельности ∘
∠DAB = 30 . Опустим высоту на AD. В прямоугольном треугольнике
ABE катет напротив угла в 30∘ равен половине гипотенузы

1
BE = 2AB = 3,5

Тогда площадь трапеции

Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в
градусах.

Показать ответ и решение

Опустим высоту на основание трапеции. ABCE — прямоугольник и Тогда

Запишем площадь трапеции, чтобы найти длину высоты CE :

1 2S 2⋅64
SABCD = 2(BC + AD )⋅CE ⇒ CE = BC-A+BCADD- = 12+-4 = 8

Получили, что Тогда треугольник CDE — прямоугольный с равными катетами, значит, его острый угол
равен 45∘.

Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием
угол 45∘.

Показать ответ и решение

Опустим высоту на основание трапеции. ABCE — прямоугольник и Тогда

Треугольник CDE — прямоугольный с углом в ∘
45 , следовательно, он равнобедренный и Тогда площадь
трапеции

Показать ответ и решение

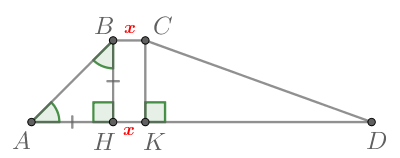
Рассмотрим треугольники ABC и ACD :

Тогда треугольники ABC и ACD подобны по пропорциональности двух сторон и равенству углов между ними, следовательно,
их площади относятся как квадрат коэффициента подобия:

( )2
SABC-= BC- = 1 ⇒ SACD = 4 ⋅SABC = 8
SACD AC 4

Таким образом,

Основания трапеции равны и боковая сторона равна Площадь трапеции равна 72. Найдите острый угол трапеции,
прилежащий к данной боковой стороне. Ответ дайте в градусах.

Показать ответ и решение

Пусть AD = 8. Проведем

Тогда площадь трапеции равна

AB-+DC-- 27-+9-
72= 2 ⋅DH = 2 ⋅DH ⇒ DH = 4

Рассмотрим прямоугольный △ADH. Так как катет равен половине гипотенузы AD, то угол DAH равен
30∘.

Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

Основания прямоугольной трапеции равны и Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в
градусах.

Показать ответ и решение

Проведем высоту CH.

Тогда ADCH — прямоугольник, следовательно,

Площадь трапеции равна

AB-+-DC- 4+-12
64 = 2 ⋅CH = 2 ⋅CH ⇒ CH =8

Заметим, что мы получили, что Тогда △CHB равнобедренный, значит, углы при основании равны, то есть
Так как сумма острых углов в прямоугольном треугольнике равна 90∘, то

∘ ∘
∠B =∠HBC =90 :2 = 45

Одно из оснований трапеции в 5 раз меньше ее средней линии. Во сколько раз это основание меньше другого основания
трапеции?

Показать ответ и решение

Обозначим меньшее основание трапеции за большее — за Тогда — длина средней линии трапеции. Так как средняя
линия равна полусумме оснований, то

Следовательно, меньшее основание в 9 раз меньше большего основания.

В трапеции боковые стороны равны и 12√5, угол при меньшей боковой стороне равен 135∘. Найдите отношение меньшего
основания к большему, если площадь трапеции равна 156.

Если задача допускает несколько вариантов ответа, внесите в бланк меньший из них.

Показать ответ и решение

Рассмотрим трапецию ABCD, где и проведем в ней высоты и CK. При этом
трапеция может выглядеть двумя разными способами.

1 способ.

Заметим, что △ABH — прямоугольный и равнобедренный, тогда

BH = AH = AB√- = 1√2-= 6√2
2 2

Значит, из прямоугольного △DCK можно найти KD :

√- √ - √-------- √-
KD2 = CD2 − CK2 = (12 5)2− (6 2)2 = 648 ⇒ KD = 9⋅9 ⋅4 ⋅2= 18 2

Т.к. площадь трапеции равна 156 , то имеем следующее уравнение:

√ - √ -
6--2+-18-2+-x+-x ⋅6√2 = 156 ⇒ x =√2
2

Тогда

√- √-
BC :AD = ( 2):(25 2)= 1:25

2 способ.

В этом случае, поступая аналогично первому способу, находим

CK = DK = BH = 6√2-
√ -
AH =18 2
√ - √- √ -
AD = 18 2+ x− 6 2= 12 2+ x

Из уравнения 12√2+ x+ x √-
156 = -----2-----⋅6 2 находим √ -
x =7 2.

Значит,

Т.к. то в ответ пойдет

В трапеции ABCD Найдите модуль разности острых углов трапеции.

Показать ответ и решение

△BCD — равнобедренный, следовательно,

∘
∠CBD = ∠CDB =20
∠BAD = 180∘ − ∠ABD − ∠CBD = 180∘− 100∘− 20∘ = 60∘
∘ ∘ ∘
∠ADC = 180 − 140 = 40

Тогда

∘ ∘ ∘ ∘
|∠ADC − ∠BAD |=|40 − 60|= |− 20|= 20

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ Профиль №3. Трапеция

ЕГЭ Профиль №3. Трапецияadmin2022-07-27T23:39:15+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №3. Трапеция

Задача 1. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.

Ответ

ОТВЕТ: 0,96.

Задача 2. Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен (frac{5}{7}). Найдите боковую сторону.

Ответ

ОТВЕТ: 21.

Задача 3. Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен (frac{{2sqrt {10} }}{7}). Найдите меньшее основание.

Ответ

ОТВЕТ: 22.

Задача 4. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен (frac{5}{{11}}). Найдите высоту трапеции.

Ответ

ОТВЕТ: 10.

Задача 5. Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 39. Тангенс острого угла равен (frac{{13}}{8}). Найдите большее основание.

Ответ

ОТВЕТ: 71.

Задача 6. Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.

Ответ

ОТВЕТ: 0,4.

Задача 7. Основания трапеции равны 8 и 34, площадь равна 168. Найдите ее высоту.

Ответ

ОТВЕТ: 8.

Задача 8. Основание трапеции равно 13, высота равна 5, а площадь равна 50. Найдите второе основание трапеции.

Ответ

ОТВЕТ: 7.

Задача 9. Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции.

Ответ

ОТВЕТ: 15.

Задача 10. Средняя линия трапеции равна 12, площадь равна 96. Найдите высоту трапеции.

Ответ

ОТВЕТ: 8.

Задача 11. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.

Ответ

ОТВЕТ: 160.

Задача 12. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.

Ответ

ОТВЕТ: 30.

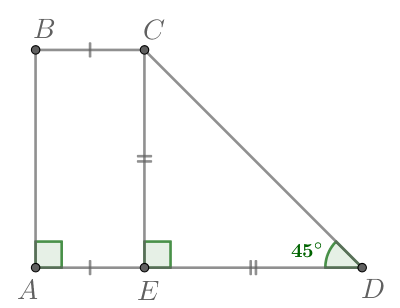
Задача 13. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45°.

Ответ

ОТВЕТ: 16.

Задача 14. Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах.

Ответ

ОТВЕТ: 45.

Задача 15. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

Ответ

ОТВЕТ: 160.

Задача 16. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции. Ответ ОТВЕТ: 5.
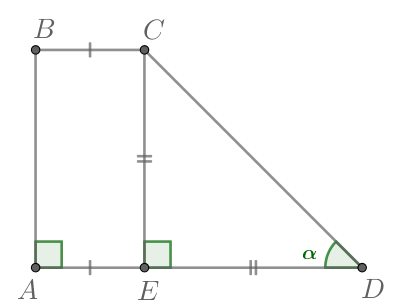
Задача 17. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол . Найдите площадь трапеции. Ответ ОТВЕТ: 42.
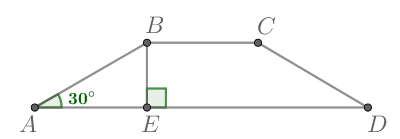
Задача 18. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах. Ответ ОТВЕТ: 30.
Задача 19. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах. Ответ ОТВЕТ: 115.
Задача 20. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции. Ответ ОТВЕТ: 38.
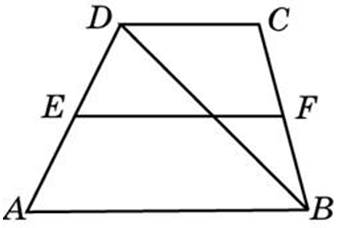
Задача 21. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей. Ответ ОТВЕТ: 5.
Задача 22. В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними. Найдите меньшее основание. Ответ ОТВЕТ: 15.
Задача 23. В равнобедренной трапеции основания равны 12 и 27, острый угол равен . Найдите ее периметр. Ответ ОТВЕТ: 69.
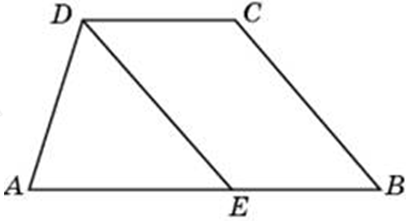
Задача 24. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции. Ответ ОТВЕТ: 23.
Задача 25. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции. Ответ ОТВЕТ: 10.
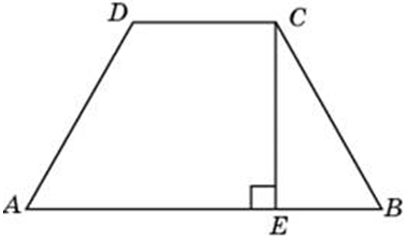Задача 26. Основания равнобедренной трапеции равны 15 и 9, один из углов равен . Найдите высоту трапеции. Ответ ОТВЕТ: 3.
Задача 27. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции. Ответ ОТВЕТ: 0,5.
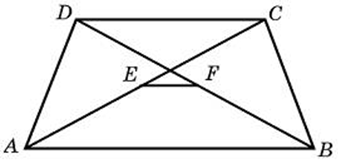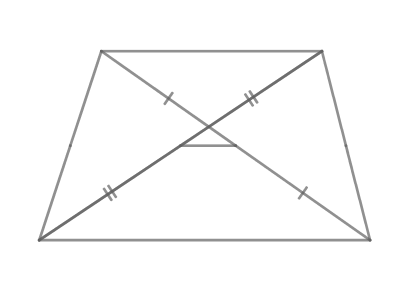
Задача 28. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию. Ответ ОТВЕТ: 12.
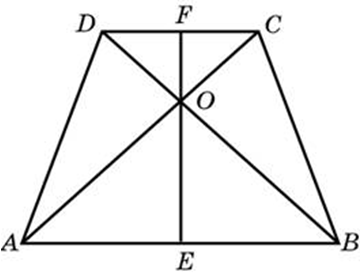Задача 29. Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону. Ответ ОТВЕТ: 5.

Источник

3. Геометрия на плоскости (планиметрия). Часть I

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

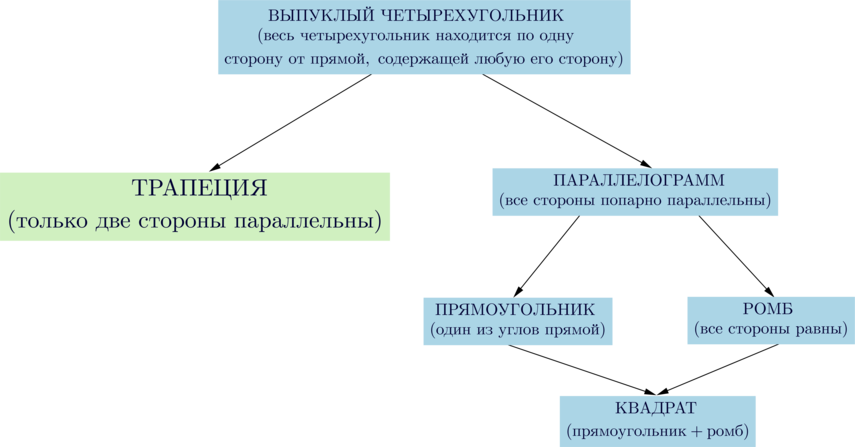
Произвольная трапеция

Сумма внутренних углов любого четырехугольника равна (360^circ).

Свойства трапеции:

(blacktriangleright) Сумма углов при боковой стороне равна (180^circ).

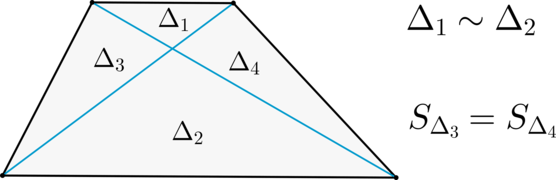
(blacktriangleright) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.

(blacktriangleright) Средняя линия трапеции – отрезок, соединяющий середины боковых сторон. Средняя линия параллельна основаниям и равна их полусумме.

Площадь трапеции

Площадь трапеции равна произведению полусуммы оснований на высоту.

Задание
1

#3091

Уровень задания: Равен ЕГЭ

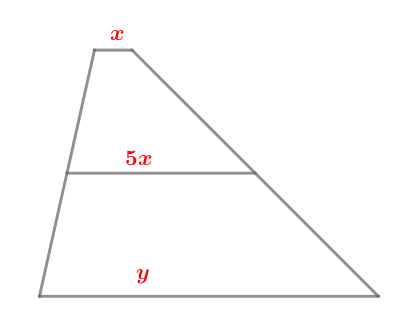
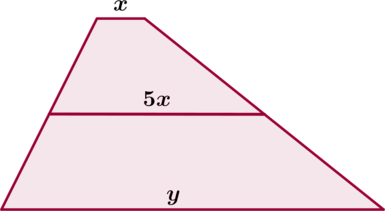
Одно из оснований трапеции в (5) раз меньше ее средней линии. Во сколько раз оно меньше другого основания трапеции?

Обозначим меньшее основание трапеции за (x), большее – за (y). Тогда (5x) – длина средней линии трапеции. Так как средняя линия равна полусумме оснований, то [x+y=2cdot 5xquadLeftrightarrowquad y=9x.] Следовательно, меньшее основание в 9 раз меньше большего.

Ответ: 9

Задание
2

#1694

Уровень задания: Равен ЕГЭ

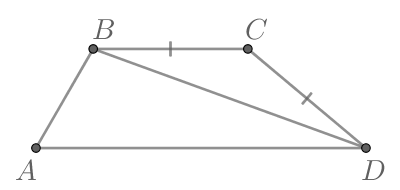
В трапеции (ABCD): (CD = BC), (angle BCD = 140^circ), (angle ABD = 100^circ). Найдите модуль разности острых углов трапеции.

Ответ: 20

Задание
3

#290

Уровень задания: Равен ЕГЭ

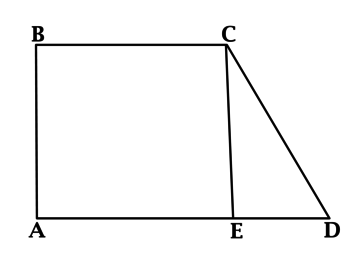
В трапеции (ABCD) с основаниями (BC = 5) и (AD = 2cdot BC) проведена высота (BE). Найдите отношение площади трапеции к длине этой высоты.

Площадь трапеции равна произведению полусуммы оснований на высоту. Полусумма оснований трапеции (ABCD) равна (0,5(5 + 2cdot 5) = 7,5). Площадь трапеции (ABCD) равна (7,5 BE), тогда (dfrac{S_{ABCD}}{BE} = 7,5).

Ответ: 7,5

Задание
4

#292

Уровень задания: Равен ЕГЭ

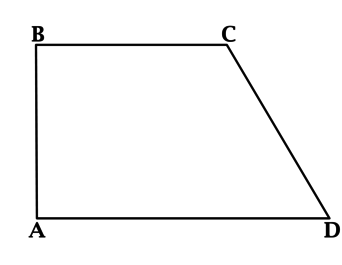
В трапеции (ABCD) с основаниями (BC = 4) и (AD > BC) угол (A) – прямой. Известно, что (CD = 6), (angle D = 60^{circ}). Найдите среднюю линию трапеции (ABCD).

Из точки (C) опустим высоту (CE). В прямоугольном треугольнике (CDE): (angle ECD = 30^{circ}). В прямоугольном треугольнике катет, лежащий против угла в (30^{circ}) равен половине гипотенузы, тогда (DE = 0,5cdot CD = 3). При этом (ABCE) – прямоугольник, (AE = BC = 4), тогда (AD = AE + ED = 4 + 3 = 7).

В трапеции средняя линия равна полусумме оснований. (0,5(BC + AD) = 0,5(4 + 7) = 5,5), значит, длина средней линии равна (5,5).

Ответ: 5,5

Задание
5

#293

Уровень задания: Равен ЕГЭ

В трапеции (ABCD) средняя линия составляет (dfrac{4}{5}) одного из оснований. Найдите отношение длины другого основания к длине средней линии.

Средняя линия трапеции равна полусумме оснований. Полусумма оснований трапеции (ABCD) составляет (0,8) одного из оснований, тогда сумма оснований трапеции (ABCD) составляет (2cdot 0,8 = 1,6) этого основания, обозначим его за (AD). Тогда (BC + AD = 1,6AD), откуда (BC = 0,6AD). Средняя линия равна (0,8AD), тогда отношение длины основания (BC) к длине средней линии равно (0,6 : 0,8 = 0,75).

Ответ: 0,75

Задание
6

#294

Уровень задания: Равен ЕГЭ

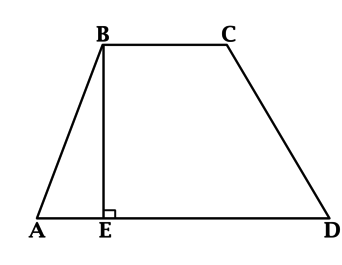
Основания (AD) и (BC) трапеции (ABCD) равны соответственно (20) и (12), одна из боковых сторон равна (10), площадь трапеции (ABCD) равна (80). Найдите острый угол трапеции (ABCD), который образует эта боковая сторона с одним из оснований. Ответ дайте в градусах.

Пусть (AB = 10), (BE) – перпендикуляр к (AD), точка (E) лежит на (AD).

Площадь трапеции равна произведению полусуммы оснований на высоту, тогда (80 = 0,5(20 + 12)cdot BE).

(BE = 5 = 0,5cdot AB). Треугольник (ABE), – прямоугольный, причём (BE = 0,5cdot AB), тогда угол, лежащий против катета (BE), равен (30^{circ}).

(angle BAE = 30^{circ}) – единственный острый угол трапеции (ABCD), который образует (AB) с одним из оснований.

Ответ: 30

Задание
7

#1693

Уровень задания: Равен ЕГЭ

В трапеции (ABCD) диагонали пересекаются в точке (O). Площадь (triangle AOD) относится к площади (triangle ODC), как (8:3). В каком отношении состоит меньшее основание (BC) трапеции (ABCD) к большему основанию (AD)?

Высота, опущенная из вершины (D) на сторону (AO) в (triangle AOD) и на сторону (OC) в (triangle ODC) будет одной и той же. Значит, (frac{S_{triangle DOC}}{S_{triangle AOD}} = frac{OC}{AO} = frac{BC}{AD} = frac{3}{8} = 0,375).

Ответ: 0,375

Всем выпускникам, которые готовятся к сдаче ЕГЭ по математике, будет полезно освежить в памяти тему «Произвольная трапеция». Как показывает многолетняя практика, планиметрические задачи из этого раздела вызывают у многих старшеклассников определенные сложности. При этом решить задачи ЕГЭ на тему «Произвольная трапеция» требуется при прохождении и базового, и профильного уровня аттестационного испытания. Следовательно, уметь справляться с подобными упражнениями должны все выпускники.

Как подготовиться к экзамену?

Большинство планиметрических задач решаются путем классических построений. Если в задаче ЕГЭ требуется найти, к примеру, площадь трапеции, изображенной на рисунке, стоит отметить на чертеже все известные параметры. После этого вспомните основные теоремы, относящиеся к ним. Применив их, вы сможете найти правильный ответ.

Чтобы подготовка к экзамену была действительно эффективной, обратитесь к образовательному порталу «Школково». Здесь вы найдете весь базовый материал по темам «Произвольная трапеция или «Равнобедренная трапеция», который поможет вам успешно сдать ЕГЭ. Основные свойства фигуры, формулы и теоремы собраны в разделе «Теоретическая справка».

«Прокачать» навыки решения задач выпускники смогут также на нашем математическом портале. В разделе «Каталог» представлена большая подборка соответствующих упражнений разного уровня сложности. Перечень заданий наши специалисты регулярно обновляют и дополняют.

Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник