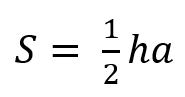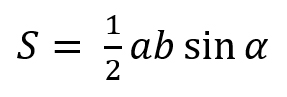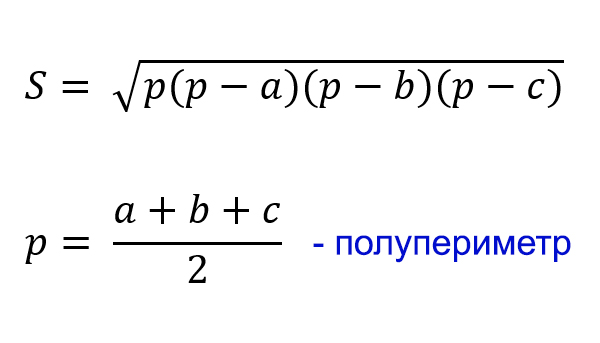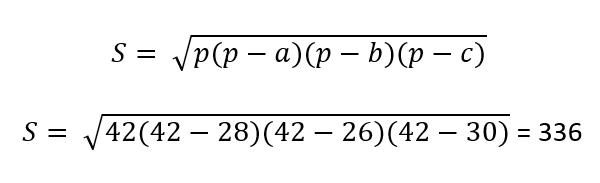СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Треугольники общего вида
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 1 № 27591
Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30°.
Аналоги к заданию № 27591: 55255 55257 55303 530817 530892 55259 55261 55263 55265 55267 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
2
Тип 1 № 27592
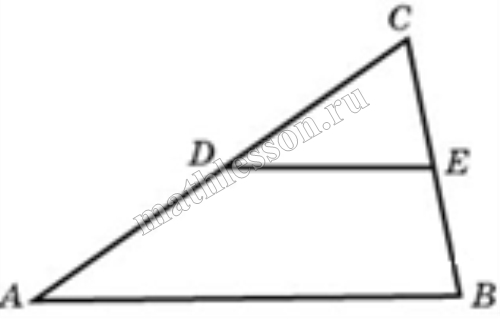
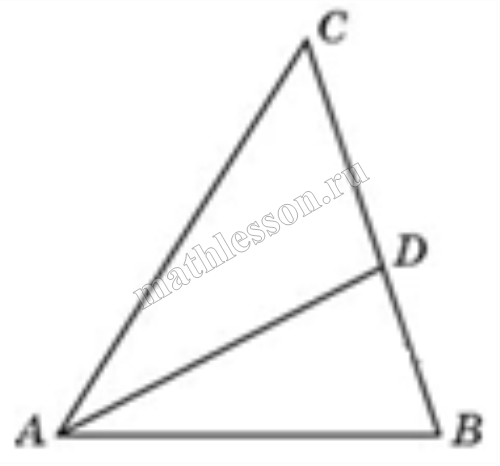
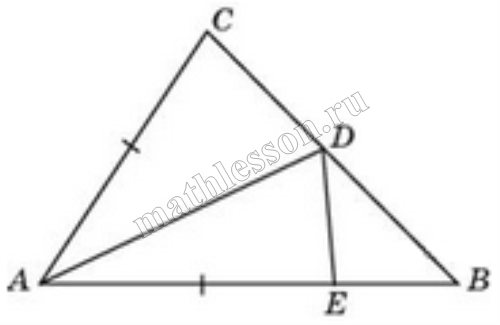
Площадь треугольника ABC равна 4, DE — средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.
Аналоги к заданию № 27592: 55305 55353 549312 55307 55309 55311 55313 55315 55317 55319 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
3
Тип 1 № 27623
У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?
Аналоги к заданию № 27623: 56755 56801 56805 513617 56757 56759 56761 56763 56765 56767 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
4
Тип 1 № 27743
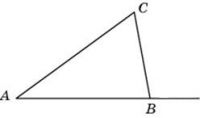
В треугольнике ABC угол A равен
внешний угол при вершине B равен
Найдите угол
Ответ дайте в градусах.
Аналоги к заданию № 27743: 46035 46089 505144 505165 46037 46039 46041 46043 46045 46047 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.1 Величина угла, градусная мера угла
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
5
Тип 1 № 27752
Углы треугольника относятся как 2 : 3 : 4. Найдите меньший из них. Ответ дайте в градусах.
Аналоги к заданию № 27752: 46705 46707 46709 46711 46713 46715 46717 46719 46721 46723 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.1 Величина угла, градусная мера угла
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
ЕГЭ Профиль №3. Треугольник общего вида
Скачать файл в формате pdf.
ЕГЭ Профиль №3. Треугольник общего вида
| Задача 1. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30°.
Ответ
ОТВЕТ: 24. |
| Задача 2. Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE.
Ответ
ОТВЕТ: 1. |
| Задача 3. У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?
Ответ
ОТВЕТ: 6. |
| Задача 4. В треугольнике ABC угол A равен 40°, внешний угол при вершине B равен 102°. Найдите угол C. Ответ дайте в градусах.
Ответ
ОТВЕТ: 62. |
| Задача 5. Углы треугольника относятся как . Найдите меньший из них.
Ответ
ОТВЕТ: 40. |
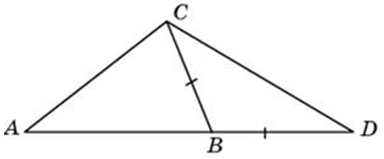
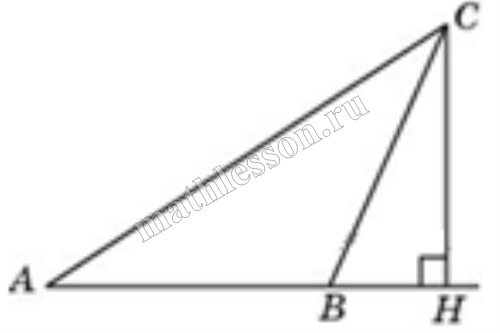
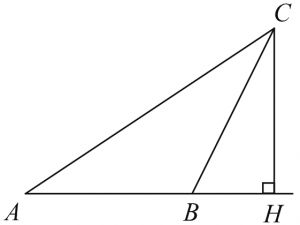
| Задача 6. В треугольнике ABC угол A равен 30°, угол В — тупой, CH — высота, угол BCH равен 22°. Найдите угол ACB. Ответ дайте в градусах.
Ответ
ОТВЕТ: 38. |
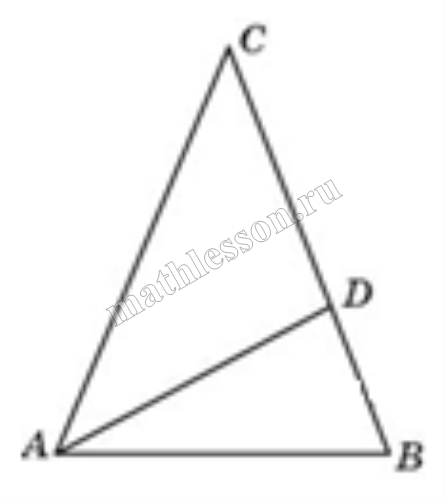
| Задача 7. В треугольнике ABC AD — биссектриса, угол C равен 50°, угол CAD равен 28°. Найдите угол B. Ответ дайте в градусах.
Ответ
ОТВЕТ: 74. |
| Задача 8. В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах.
Ответ
ОТВЕТ: 52. |
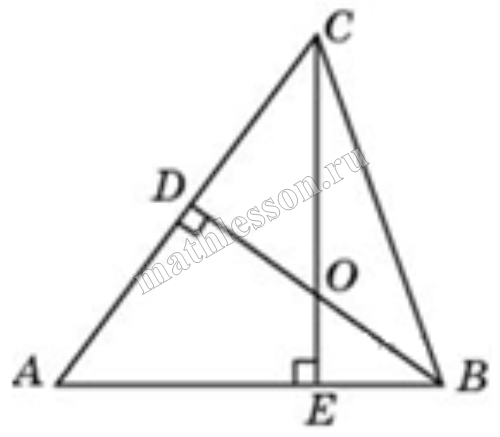
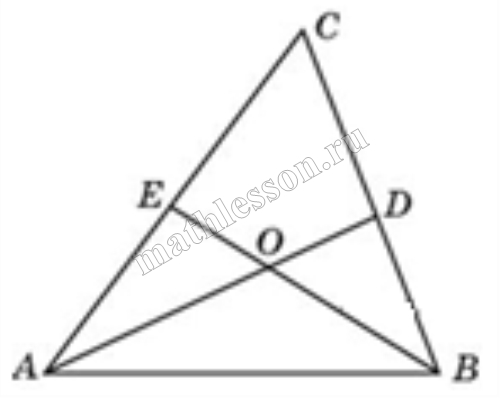
| Задача 9. В треугольнике ABC угол A равен 72°, а углы B и C — острые. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.
Ответ
ОТВЕТ: 108. |
| Задача 10. Два угла треугольника равны 58° и 72°. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
Ответ
ОТВЕТ: 130. |
| Задача 11. В треугольнике ABC угол C равен 58°, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах. |
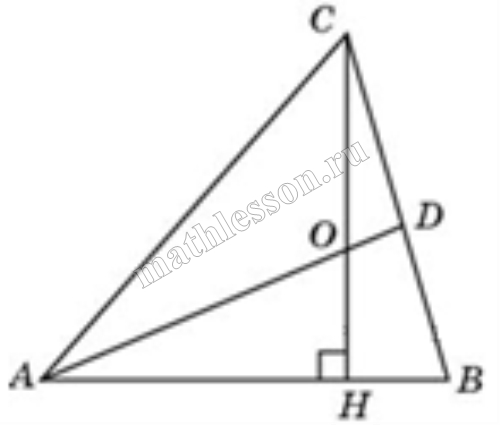
| Задача 12. В треугольнике ABC CH — высота, AD — биссектриса, O — точка пересечения CH и AD, угол BAD равен 26°. Найдите угол AOC. Ответ дайте в градусах. |
| Задача 13. В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах. |
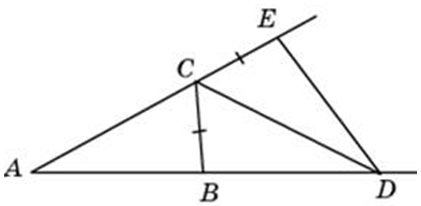
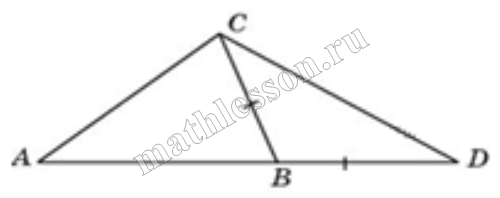
| Задача 14. В треугольнике ABC угол A равен 44°, угол C равен 62°. На продолжении стороны AB отложен отрезок BD = BC. Найдите угол D треугольника BCD. Ответ дайте в градусах.
|
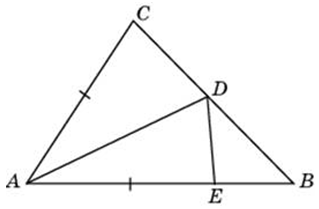
| Задача 15. В треугольнике ABC угол B равен 45°, угол C равен 85°, AD — биссектриса, E — такая точка на AB, что AE = AC. Найдите угол BDE. Ответ дайте в градусах.
|
| Задача 16. В треугольнике ABC угол A равен 30°, угол B равен 86°, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE = CB. Найдите угол BDE. Ответ дайте в градусах.
|
| Задача 17. В треугольнике ABC угол A равен 60°, угол B равен 82°. AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах. |
| Задача 18. В треугольнике ABC угол A равен 60°, угол B равен 82°. AD, BE и CF — высоты, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах. |
| Задача 19. Площадь треугольника ABC равна 12. DE – средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED. |
Привет! Это первая статья посвящённая ЕГЭ по математике профильного уровня.
В ней речь пойдёт о задачах на площадь треугольника.
Вспомним основные формулы для площади треугольника.
Формулы для площади треугольника
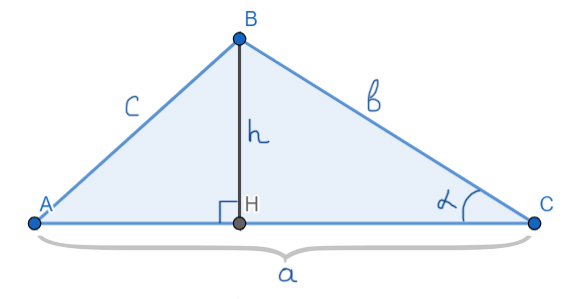
Основная формула:
Площадь треугольника равна половине произведения основания на высоту.
Запасная формула:
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Формула Герона:
Решение задач
Приступим к тренировочным задачам задания №1 из ЕГЭ по математике профильного уровня на площадь треугольника.
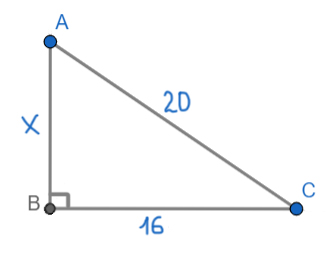
Задача (Прямоугольный треугольник)
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 16 и 20.
Решение:
Здесь можно воспользоваться основной формулой для нахождения площади прямоугольного треугольника. Но важно знать, что любой катет — это и есть высота прямоугольного треугольника.
Таким образом, высота будет, к примеру, сторона AB. Тогда основанием будет сторона ВС.
Найдём сторону АВ по теореме Пифагора.
x2 + 162 = 202
x2 = 400 — 256 = 144
x = 12
Тогда площадь будет равна:
S = 0,5 * 12 * 16 = 6 * 16 = 96
Ответ: 96
Задача (Прямоугольный треугольник, закрепление)
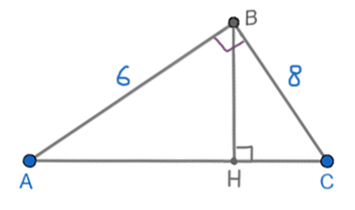
Катеты прямоугольного треугольника равны 6 и 8. Найдите высоту, проведённую к гипотенузе.
Решение:
Найдём гипотенузу по теореме Пифагора.
AC2 = AB2 + BC2
AC2 = 62 + 82 = 100
AC = 10
Мы в прошлой задаче выяснили, что площадь прямоугольного треугольника можно найти, как половину произведения его катетов. А с другой стороны, исходя из основной формулы, площадь равна половине произведения высоты ВН и основания (гипотенузы AC).
S = 0,5*AB*BC = 0,5*BH*AC
BH = AB*BC / AC = 6*8 / 10 = 4,8
Ответ: 4,8
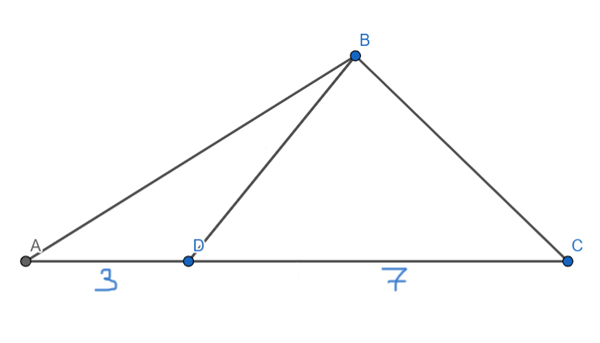
Задача (Три треугольника, одна высота)
На стороне AC треугольника ABC отмечена точка D так, что AD=3, DC=7. Площадь треугольника ABC равна 100. Найдите площадь треугольника BCD.
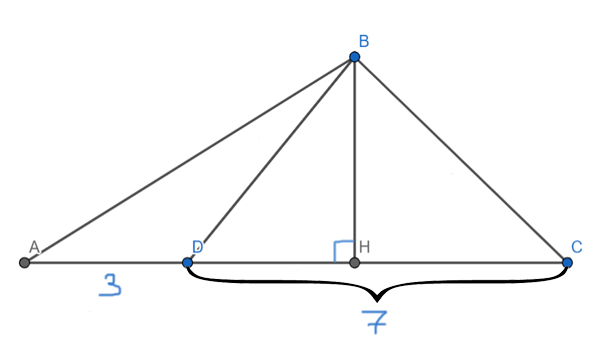
Решение:
Проведём в треугольнике ABC высоту BH. Оказывается, что ВН является высотой и для треугольника ABD, и для треугольника DBC, и для треугольника ABC.
Применим основную формулу для треугольника ABC и найдём высоту BH.
SABC = 0,5 * AC *BH
SABC = 0,5 * 10 * BH = 100
BH = 100 / (0,5*10) = 20
Теперь применим основную формулу, чтобы найти площадь треугольника BCD.
SDBC = 0,5 * DC * BH
SDBC = 0,5 * 7 * 20 = 70
Ответ: 70
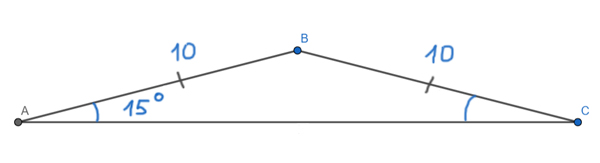
Задача (Запасная формула)
В равнобедренном треугольнике ABC (AB = BC) угол при основании равен 15°. Боковая сторона равна 10. Найдите площадь треугольника ABC.
Решение:
Здесь удобно использовать запасную формулу. Мы знаем две боковые стороны треугольника. Остаётся найти синус угла между ними.
Мы знаем, что углы при основании равны в равнобедренном треугольнике. Поэтому
∠ABC + ∠ВАС + ∠BCA = 180°
∠ABC = 180° — ∠ВАС — ∠BCA
∠ABC = 180° — 15° — 15° = 150°
Синус угла 150° известен. Он равен sin(150°) = sin(30°) = 0,5. Тогда
S = 0,5 * AB*BC * sin(∠ABC)
S = 0,5 * 10*10 * 0,5 = 25
Ответ: 25
Задача (Треугольники в ромбе)
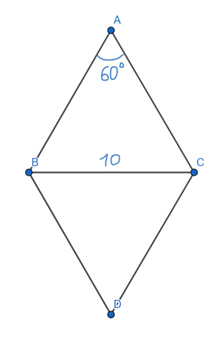
Найдите площадь ромба, если один из его углов равен 60°, а меньшая диагональ равна 10. В ответе запишите число, делённое на √3.
Решение:
Меньшая диагональ будет находится напротив угла 60°, т.к. второй угол у ромба будет 120°, и напротив этого угла будет находится большая диагональ.
Рассмотрим треугольник ВАС. Мы знаем, что у ромба все стороны равны, поэтому треугольник ВАС равносторонний. Ведь, ВА = АС ⇒ ∠ABC = ∠ACB. Тогда
∠ABC + ∠ACB + ∠BAC = 180°
x = ∠ABC = ∠ACB
x + x + 60° = 180°
2x = 120°
x = 60°
Значит, треугольник ВАС равносторонний. Следовательно, BA = AC = CB = 10.
Чтобы найти площадь ромба, можно разбить его на два одинаковых треугольника: BAC и BDC. Эти два треугольника равны по трём сторонам (BA = AC = CD = DB, BC — общая).
Площадь треугольника BAC легко найти по запасной формуле, ведь две стороны мы знаем, и синус угла между ними тоже известен.
SBAC = 0,5 * BA * AC * sin(60°)
SBAC = 0,5 * 10 * 10 * (√3/2)
SBAC = 25 * √3
Площадь ромба будет равна
SBACD = 2 * SBAC = 2 * 25 * √3 = 50 * √3
В ответе нужно указать число, делённое на √3.
Ответ: 50
Задача (Решаем задачу двумя способами)
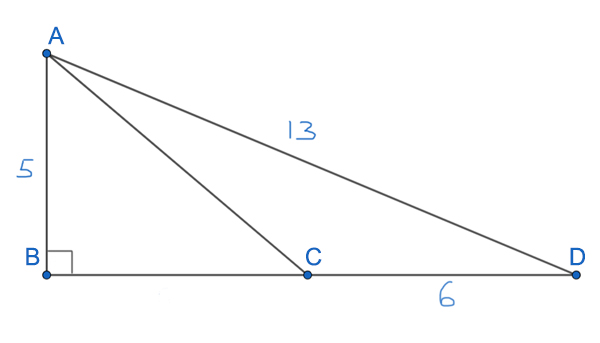
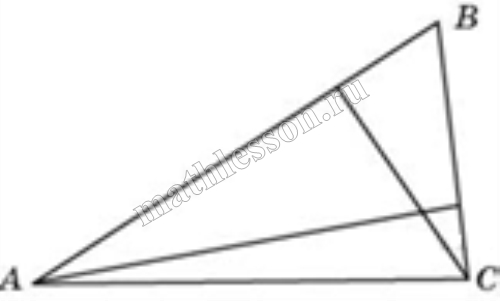
На рисунке AB ⊥ BD, AB = 5, AD = 13 и CD = 6. Найдите площадь треугольника CAD.
Решение:
Первый способ (основная формула)
Нам известна высота треугольника CAD, AB=5. Нам известно основание, на которое она опущена, это CD=6. Применим основную формулу для площади треугольника.
SCAD = ½ * AB * CD
SCAD = ½ * 5 * 6 = 15
Второй способ (запасная формула)
В прямоугольном треугольнике ABD найдём синус ∠BDA.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
sin(∠BDA) = AB/AD = 5/13
Теперь воспользуемся запасной формулой для треугольника CAD.
SCAD = ½ * CD * DA * sin(∠BDA)
SCAD = ½ * 6 * 13 * (5/13) = 15
Ответ: 15
Задача (Формула Герона)
Найдите площадь треугольника, стороны которого равны 28, 26, 30.
Решение:
Решим по формуле Герона.
Найдём полупериметр.
p=(28+26+30)/2 = 42
Тогда
Ответ: 336
На этом всё! Сегодня мы повторили основные формулы для нахождения площади треугольника и порешали задачи на эту темы. Всем удачи!
Задание 861
|
Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30°. |
|
Ответ: 24
Задание 862
|
Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE. |
|
Ответ: 1
Задание 863
|
У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне? |
|
Ответ: 6
Задание 864
|
В треугольнике ABC угол A равен 40°, внешний угол при вершине B равен 102°. Найдите угол C. Ответ дайте в градусах. |
|
Ответ: 62
Задание 865
|
В треугольнике ABC угол A равен 30°, CH — высота, угол BCH равен 22°. Найдите угол ACB. Ответ дайте в градусах. |
|
Ответ: 38
Задание 866
|
В треугольнике ABC AD — биссектриса, угол C равен 50°, угол CAD равен 28°. Найдите угол B. Ответ дайте в градусах. |
|
Ответ: 74
Задание 867
|
В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах. |
|
Ответ: 52
Задание 868
|
В треугольнике ABC AC = BC, AD — высота, угол BAD равен 24°. Найдите угол C. Ответ дайте в градусах. |
|
Ответ: 48
Задание 869
|
В остроугольном треугольнике ABC угол A равен 65°. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах. |
|
Ответ: 115
Задание 870
|
Два угла треугольника равны 58° и 72°. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах. |
|
Ответ: 130
Задание 871
|
В треугольнике ABC угол C равен 58°, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах. |
|
Ответ: 119
Задание 872
|
В треугольнике ABC CH — высота, AD — биссектриса, O — точка пересечения CH и AD, угол BAD равен 26°. Найдите угол AOC. Ответ дайте в градусах. |
|
Ответ: 116
Задание 873
|
В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах. |
|
Ответ: 36
Задание 874
|
В треугольнике ABC угол A равен 44°, угол C равен 62°. На продолжении стороны AB за точку B отложен отрезок BD, равный стороне BC. Найдите угол D треугольника BCD. Ответ дайте в градусах. |
|
Ответ: 37
Задание 875
|
В треугольнике ABC угол B равен 45°, угол C равен 85°, AD — биссектриса, E — такая точка на AB, что AE = AC. Найдите угол BDE. Ответ дайте в градусах. |
|
Ответ: 40
В треугольнике (ABC) угол (C) равен 90°, (AB=40), (AC=4sqrt{51}). Найдите (sin A).
В треугольнике ABC угол C равен 90°, AC=9, BC=12. Найдите sin A.
В треугольнике ABC угол A равен 14°, внешний угол при вершине B равен 91°. Найдите угол C. Ответ дайте в градусах.
Найдите (cos{A}), если известно, что (AB = 10), (CB = sqrt{19}).
В треугольнике (ABC), изображенном на рисунке, угол (A) равен 30°, (CH) — высота, угол (BCH) равен 39°. Найдите угол (ACB). Ответ дайте в градусах.
В треугольнике ABC угол C равен 90°, BC=3√15, AB=12. Найдите sin∠B.
В треугольнике ABC угол A равен 36°, внешний угол при вершине C равен 106°. Найдите угол B. Ответ дайте в градусах.
В треугольнике ABC угол C равен 88°, стороны AC и BC равны. Найдите угол A. Ответ дайте в градусах.
В треугольнике ABC стороны AC и BC равны, угол C равен 134°, угол CBD – внешний. Найдите угол CBD. Ответ дайте в градусах.
В треугольнике ABC угол A равен 30°, CH – высота, угол BCH равен 39°. Найдите угол ACB. Ответ дайте в градусах.
Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.
1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике $АВС$ для острого угла $В$:
$sinB={AC}/{AB};$
$cosB={BC}/{AB};$
$tgB={AC}/{BC};$
$ctgB={BC}/{AC}.$
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
$sin BOA=sin BOC;$
$cos BOA=-cos BOC;$
$tg BOA=-tg BOC;$
$ctg BOA=-ctg BOC.$
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Площадь прямоугольного треугольника равна половине произведения его катетов
$S={AC∙BC}/{2}$
Пример:
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√{91}$. Найдите косинус внешнего угла при вершине $В$.
Решение:
Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то
$cosABD=-cosABC$
Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:
$cosABC={ВС}/{АВ}$
Катет $ВС$ мы можем найти по теореме Пифагора:
$ВС=√{10^2-√{91}^2}=√{100-91}=√9=3$
Подставим найденное значение в формулу косинуса
$cos ABC = {3}/{10}=0,3$
$cos ABD = — 0,3$
Ответ: $-0,3$
Пример:
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sinA={4}/{5}, AC=9$. Найдите $АВ$.
Решение:
Распишем синус угла $А$ по определению:
$sinA={ВС}/{АВ}={4}/{5}$
Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.
Применим теорему Пифагора, чтобы отыскать $«х»$
$АС^2+ВС^2=АВ^2$
$9^2+(4х)^2=(5х)^2$
$81+16х^2=25х^2$
$81=25х^2-16х^2$
$81=9х^2$
$9=х^2$
$х=3$
Так как длина $АВ$ составляет пять частей, то $3∙5=15$
Ответ: $15$
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
$CD^2=DB∙AD$
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
$CB^2=AB∙DB$
$AC^2=AB∙AD$
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
$AC∙CB=AB∙CD$
Равнобедренный треугольник — это такой треугольник, у которого две стороны равны. Равные стороны называются боковыми. Третья сторона называется основанием.
Свойства:
1. В равнобедренном треугольнике углы при основании равны.
2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
3. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
4. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
5. Углы, противолежащие равным сторонам равнобедренного треугольника, всегда острые.
6. В равнобедренном треугольнике:
— биссектрисы, проведенные из вершин при основании, равны;
— высоты, проведенные из вершин при основании, равны;
— медианы, проведенные из вершин при основании, равны.
7. Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане, проведенных к основанию.
8. Вписанная окружность точкой касания делит основание пополам.
Внешним углом треугольника называется угол, смежный с каким-либо углом этого треугольника.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.
$∠BCD$ — внешний угол треугольника $АВС$.
$∠BCD=∠A+∠B$
Теорема Пифагора.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$.
Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом ($ctg$) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
Пример:
В прямоугольном треугольнике $АВС$ для острого угла $В$:
$sinB={AC}/{AB};$
$cosB={BC}/{AB};$
$tg B={AC}/{BC};$
$ctg B={BC}/{AC}$.
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
$sin BOA=sin BOC;$
$cos BOA= — cos BOC;$
$tg BOA= — tg BOC;$
$ctg BOA= — ctg BOC.$
Пример:
В треугольнике $ABC$ $AB=BC, AH$ — высота, $AC=34, cos ∠BAC=0.15$. Найдите $CH$.
Решение:
Так как треугольник $АВС$ равнобедренный, то $∠A=∠С$ (как углы при основании)
Косинусы равных углов равны, следовательно, $cos∠BAC=cos∠ВСА=0.15$
Рассмотрим прямоугольный треугольник $АНС$.
Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Распишем косинус $∠НСА$ (он же $∠ВСА$) по определению:
$cos∠НСА={НС}/{АС}={НС}/{34}=0.15$
Из последнего равенства найдем $НС$, для этого $0.15$ представим в виде обыкновенной дроби и воспользуемся свойством пропорции:
${НС}/{34}={15}/{100}$
$НС={34·15}/{100}=5.1$
Ответ: $5.1$
Теорема Менелая:
Если на сторонах $ВС, АВ$ и продолжении стороны $АС$ треугольника $АВС$ за точку $С$ отмечены соответственно $А_1,С_1,В_1$, лежащие на одной прямой, то
${АС_1}/{С_1 В}·{ВА_1}/{А_1 С}·{СВ_1}/{В_1 А}=1$
Теорема синусов.
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ}={c}/{sinγ}=2R$, где $R$ — радиус описанной около треугольника окружности.
Пример:
В треугольнике $АВС$ $ВС=16, sin∠A={4}/{5}$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.
Решение:
Воспользуемся теоремой синусов:
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности
${ВС}/{sinA}=2R$
Далее подставим числовые данные и найдем $R$
${16·5}/{4}=2R$
$R={16·5}/{4·2}=10$
Ответ: $10$
Теорема косинусов.
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
$a^2=b^2+c^2-2·b·c·cosα.$
Треугольники общего вида.
Основные свойства треугольников:
- Сумма всех углов в треугольнике равна $180°$.
- В равнобедренном треугольнике углы при основании равны.
- В равнобедренном треугольнике высота, проведенная к основанию, одновременно является медианой и биссектрисой.
- В равностороннем треугольнике все углы по $60°$.
- Внешний угол треугольника равен сумме двух углов, не смежных с ним.
- Средняя линия треугольника параллельна основанию и равна его половине.
$MN$ — средняя линия, так как соединяет середины соседних сторон.
$MN$ // $AC$, $MN = {AC}/{2}$
Биссектриса — это линия, которая делит угол пополам.
Свойства биссектрисы:
- В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
- Три биссектрисы в треугольнике пересекаются в одной точке, эта точка является центром вписанной в треугольник окружности.
- Биссектрисы смежных углов перпендикулярны.
- В треугольнике биссектриса угла делит противоположную сторону на отрезки, отношение которых такое же, как отношение сторон треугольника, между которыми эта биссектриса прошла.
${AB}/{AC}={BA_1}/{A_1C}$
Медиана — это линия, проведенная из вершины треугольника к середине противоположной стороны.
Свойства медиан:
1. Медиана делит треугольник на два равновеликих треугольника, т.е. на два треугольника, у которых площади равны.
$S_1=S_2$
2. Медианы пересекаются в одной точке и этой точкой делятся в отношении два к одному, считая от вершины.
3. В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы и радиусу описанной около этого треугольника окружности.
Высота в треугольнике — это линия, проведенная из вершины треугольника к противоположной стороне под углом в 90 градусов.
$BB_1$ — высота
Свойства высот:
1. Три высоты (или их продолжения) пересекаются в одной точке.
2. Угол между высотами в остроугольном треугольнике равен углу между сторонами, к которым эти высоты проведены.
3. Высоты треугольника обратно пропорциональны его сторонам:
$h_a:h_b:h_c={1}/{a}:{1}/{b}:{1}/{c}$
Прямоугольный треугольник и его свойства:
В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
1. Сумма острых углов в прямоугольном треугольнике равна 90 градусов.
2. Катет прямоугольного треугольника, лежащий напротив угла в 30 градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
3. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности (R)
4. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями которых являются катеты данного треугольника.
$CD=AC=CB=R$
5. В прямоугольном треугольнике радиус вписанной окружности равен: $r={a+b-c}/{2}$ , где $а$ и $b$ – это катеты, $с$ – гипотенуза.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$AC^2+BC^2=AB^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Тригонометрические тождества:
1. Основное тригонометрическое тождество:
$sin^2x+cos^2x=1$
2. Связь между тангенсом и косинусом одного и того же угла:
$1+tg^2x={1}/{cos^{2}x}$
3. Связь между котангенсом и синусом одного и того же угла:
$1+ctg^{2} x={1}/{sin^{2} x}$
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ} ={c}/{sinγ} =2R$, где $R$ — радиус описанной около треугольника окружности.
Пример:
В треугольнике $АВС ВС=16, sin∠A={4}/{5}$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.
Решение:
Воспользуемся теоремой синусов:
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности
${ВС}/{sinA} =2R$
Далее подставим числовые данные и найдем $R$
${16·5}/{4}=2R$
$R={16·5}/{4·2}=10$
Ответ: $10$
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
$a^2=b^2+c^2-2·b·c·cosα;$
$b^2=a^2+c^2-2·a·c·cosβ;$
$c^2=b^2+a^2-2·b·a·cosγ.$
Формулы площадей треугольника:
- ${a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$
- $S={a·b·sinα}/{2}$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
Задачи егэ с треугольниками
Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30°.
Площадь треугольника равна половине произведения его сторон на синус угла между ними. Поэтому
Площадь треугольника ABC равна 4, DE — средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.
Средняя линия отсекает от треугольника подобный ему с коэффициентом подобия Площади подобных фигур относятся как квадрат коэффициента подобия. Тогда
У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?
Выразим площадь двумя способами:
Тогда,
В треугольнике ABC угол A равен внешний угол при вершине B равен
Найдите угол
Ответ дайте в градусах.
Внешний угол треугольника равен сумме несмежных с ним углов этого треугольника. Поэтому
Задания по теме «Треугольник общего вида»
Открытый банк заданий по теме треугольник общего вида. Задания B6 из ЕГЭ по математике (профильный уровень)
Задание №1063
Условие
Найдите площадь треугольника, две стороны которого равны 6 и 14 , а угол между ними равен 30^<circ>.
Решение
Площадь треугольника можно найти как половину произведения двух его сторон на синус угла между ними. В заданном треугольнике площадь S= frac12cdot6cdot14cdotsin30^<circ>= 21.
Ответ
Задание №894
Условие
В тупоугольном треугольнике ABC AC=BC=50, AH — высота, CH=40. Найдите cos ACB.
Решение
angle ACB=180^<circ>-angle ACH, поэтому cosangle ACB=-cosangle ACH=-frac.
По условию CH=40, AC=50.
Ответ
Задание №889
Условие
В треугольнике ABC угол A равен 48^<circ>, угол C равен 62^<circ>. На продолжении стороны AB за точку B отложен отрезок BD , равный стороне BC . Найдите угол D треугольника BCD . Ответ дайте в градусах.
Решение
Угол CBD является внешним углом треугольника ABC и равен сумме двух углов треугольника, не смежных с ним. Найдём угол CBD .
angle CBD = angle A + angle C = 48^<circ>+62^<circ>= 110^<circ>. Треугольник BCD равнобедренный, его углы при основании равны: angle D=angle DCB. Сумма углов треугольника равна 180^<circ>. Тогда angle D = (180^<circ>-110^<circ>):2=35^<circ>.
ЕГЭ для VIP
Подготовке к ЕГЭ
ЕГЭ по математике Профиль. Задание 3
ЕГЭ по математике Профиль. Задание 3: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
ЕГЭ Профиль. Задание № 3
АЛГОРИТМ ВЫПОЛНЕНИЯ
Задание № 3 рассчитано на умение использовать геометрические понятия и теоремы для решения практических задач, связанных с нахождением геометрических величин (длин, углов, площадей).
Задание состоит из текстовой задачи и рисунка. Необходимо внимательно прочитать текст, решить задачу и записать результат в поле ответа в тексте работы и бланк ответов. Если в итоге получилась обыкновенная дробь, её нужно перевести в десятичную.
Чтобы успешно справиться с данным заданием, нужно повторить определения и свойства плоских фигур:
- треугольники:
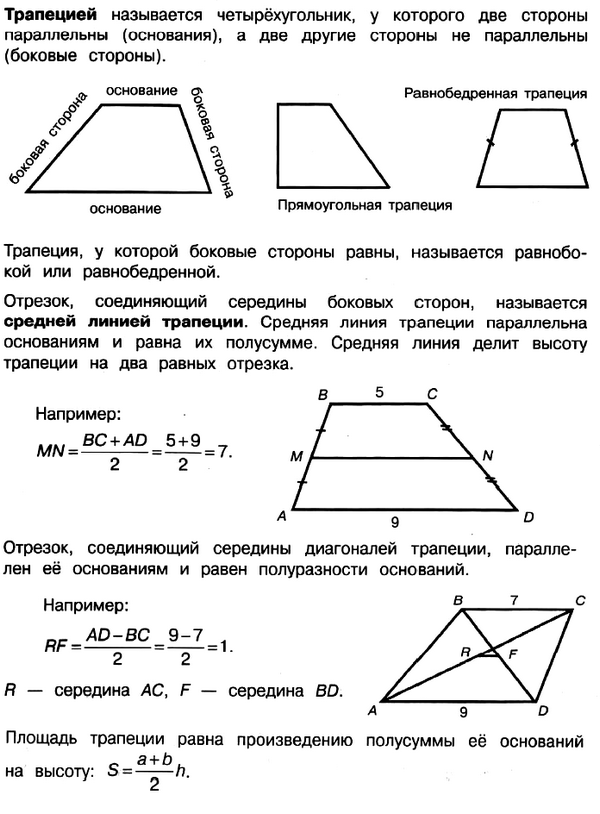
- четырёхугольники, в частности параллелограмм, прямоугольник, ромб, квадрат, трапеция;
- многоугольники, в частности правильные многоугольники;
- окружность и круг, описанные и вписанные в многоугольник окружности;
- площади треугольника, параллелограмма, трапеции, круга, сектора.
План выполнения:
- Внимательно прочитайте задачу.
- При необходимости выполните на чертеже дополнительные построения.
- Выполните арифметические вычисления.
- Запишите полученное число в поле ответа КИМ и бланк ответов № 1.
Задачи на Прямоугольные треугольники
При подготовке следует повторить значение синуса, косинуса и тангенса основных углов; отношения между сторонами прямоугольника; теорему Пифагора.
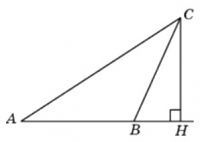
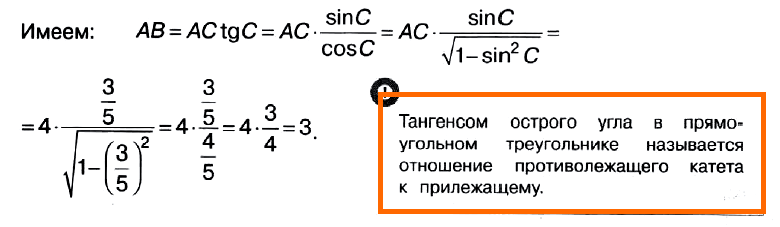
Задача № 3 (1). В треугольнике АВС угол А равен 90°, АС = 4, sin C = 3/5. Найдите АВ.
Решение:
Ответ: 3.
Задача № 3 (2). В треугольнике АВС угол С равен 90°, CD – высота, АВ = 5, tg B = 1/2. Найдите BD.
Решение: 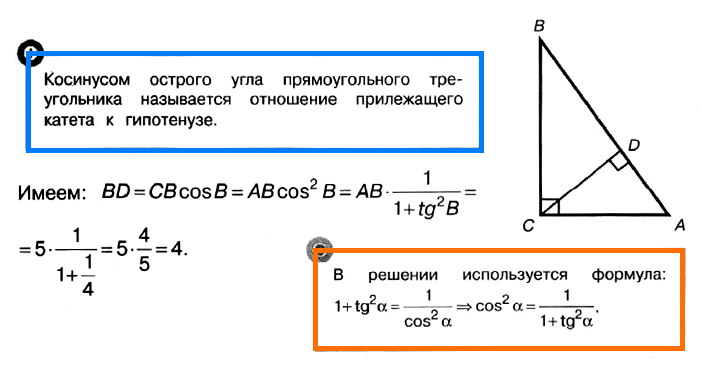
Ответ: 4.
Задачи на Равнобедренные треугольники
Задача № 3 (3). В треугольнике АВС АС = ВС = 10, sin А = 3/5. Найдите АВ.
Решение: 
Ответ: 16.
Задача № 3 (4). В треугольнике АВС АС = ВС = 25, sin BAC = 3/5. Найдите высоту АН.
Решение: 
Ответ: 24.
Задача № 3 (5). В тупоугольном треугольнике АВС АС = ВС = 6, высота АН = 3. Найдите sin АСВ.
Решение: 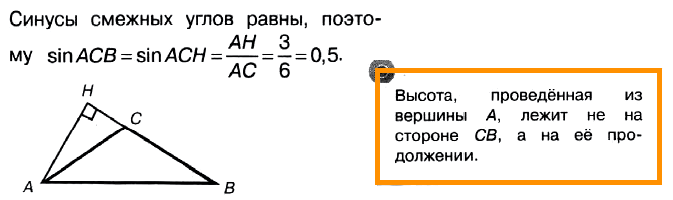
Ответ: 0,5.
Задачи на Разносторонние треугольники
Задача № 3 (6). Площадь треугольника АВС равна 8. DE — средняя линия CDE.
Решение: 
Ответ: 2.
Задача № 3 (7). В треугольнике АВС угол С равен 60°, AD и BE — биссектрисы, пересекающиеся в точке О. Найдите угол АОВ. Ответ дайте в градусах.
Решение: 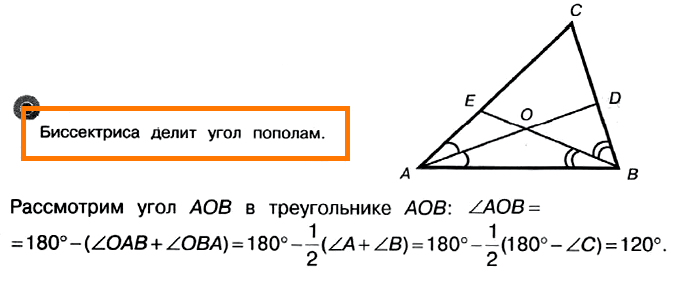
Ответ: 120.
Задачи на Параллелограммы
Задача № 3 (8). Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.
Решение: 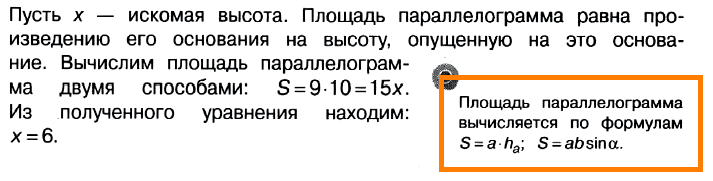
Ответ: 6.
Задачи на Трапецию
Задача № 3 (9).
Решение: 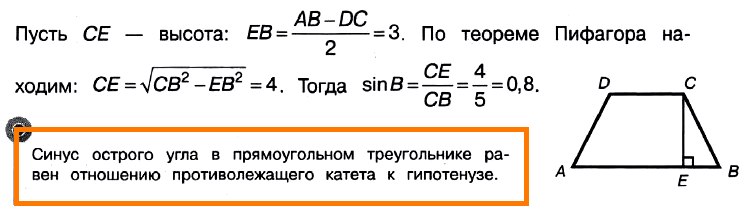
Ответ: 0,8.
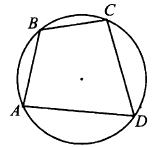
Задачи на Центральные и вписанные углы
При подготовке нужно повторить свойства центральных и вписанных углов, понятия хорды, касательной и секущей к окружности; знать правила нахождения величин центральных и вписанных углов, дуг окружностей.
Задача № 3 (10). Найдите угол АСВ, если вписанные углы ADB и DAE опираются на дуги окружности, градусные величины которых равны соответственно 158° и 38°. Ответ дайте в градусах.
Решение: 
Ответ: 60.
Задачи на Вписанные и описанные окружности
Задача № 3 (11). В четырёхугольник ABCD вписана окружность, АВ = 4, CD = 6. Найдите периметр четырёхугольника ABCD.
Решение: 
Ответ: 20.
Задача № 3 (12).
Решение: 
Ответ: 1.
Тренировочные задания с самопроверкой
№ 3.1. Стороны АВ, ВС, CD и AD четырёхугольника ABCD стягивают дуги описанной окружности, градусные величины которых равны соответственно 75°, 63°, 93°, 129° (см. рис.). Найдите угол BCD. Ответ дайте в градусах.
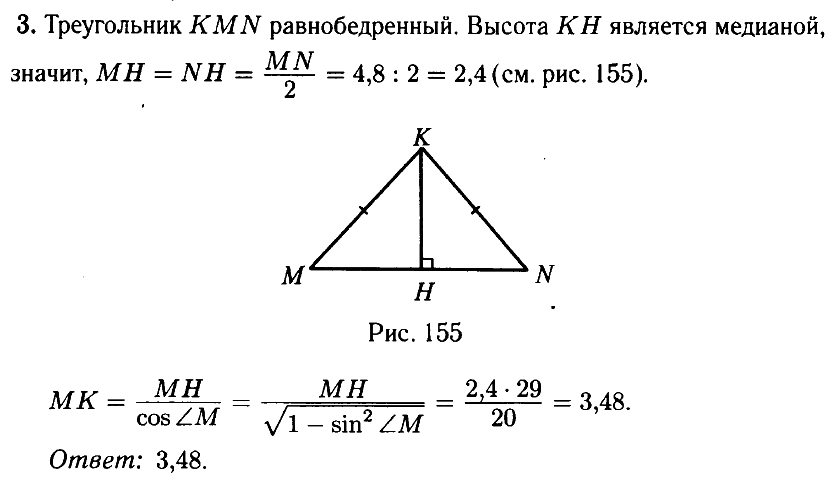
№ 3.2. В треугольнике MNK известно, что МК = NK, MN = 4,8, sin М = 21/29 (см. рис.). Найдите МК. 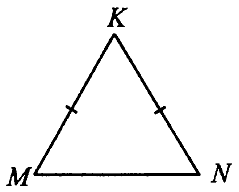
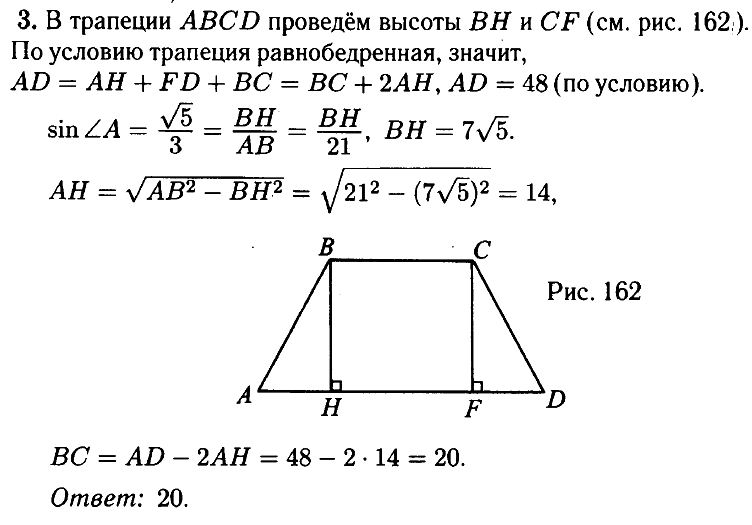
№ 3.3. Большее основание равнобедренной трапеции равно 48. Боковая сторона равна 21. Синус острого угла равен √5/3 (см. рис.). Найдите меньшее основание. 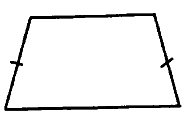
№ 3.4. В треугольнике АВС известно, что АС = ВС, высота ВН равна 9, АВ = 3√13 (см. рис.). Найдите tg АВС. 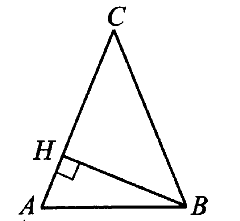
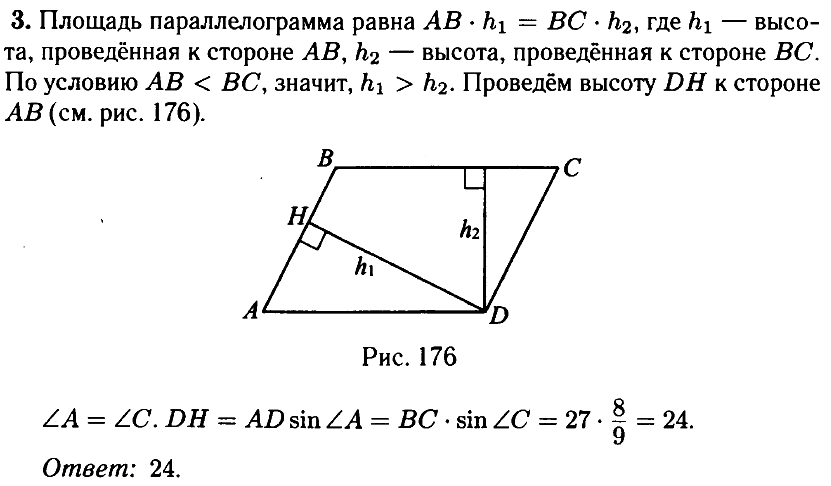
№ 3.5. В параллелограмме ABCD известно, что АВ = 18, ВС = 27, sin ∠C = 8/9 (см. рис.). Найдите большую высоту параллелограмма. 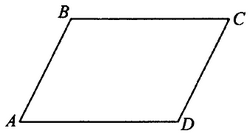
Вы смотрели: ЕГЭ по математике Профиль. Задание 3: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
источники:
http://academyege.ru/theme/treugolnik-obshchego-vida.html
http://egevip.ru/egje-po-matematike-profil-zadanie-3/