Задачи на ттп в егэ - Помощь в подготовке к экзаменам и поступлению

Всего: 124 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Основанием пирамиды SABC является правильный треугольник, длина стороны которого равна Основанием высоты, опущенной из вершины S, является точка О, лежащая внутри треугольника ABC. Расстояние от точки О до стороны АС равно 1. Синус угла OBA относится к синусу угла OBC как 2:1. Площадь грани SAB равна

а)  Найдите объем пирамиды.

б)  Найдите расстояние от точки А до плоскости SBC.

Источник: А. Ларин. Тренировочный вариант № 262.

В правильной треугольной призме ABCA₁B₁C₁ сторона основания равна 12, а боковое ребро AA₁ равно На рёбрах AB и B₁C₁ отмечены точки K и L, соответственно, причём AK  =  B₁L  =  3. Точка M  — середина ребра A₁C₁. Плоскость γ параллельна ребру AC и содержит точки K и L.

а)  Докажите, что прямая BM перпендикулярна плоскости γ.

б)  Найдите расстояние от точки C до плоскости γ.

Источник: ЕГЭ — 2016 по математике. Основная волна 06.06.2016. Вариант 3 (C часть)

Дана правильная треугольная призма ABCA₁B₁C₁ со стороной основания 12 и высотой 3. Точка K  — середина BC, точка L лежит на стороне A₁B₁ так, что В₁L  =  5. Точка М  — середина A₁C₁. Через точки K и L проведена плоскость таким образом, что она параллельна прямой AC.

а)  Докажите, что указанная выше плоскость перпендикулярна прямой MB.

б)  Найдите объем пирамиды с вершиной в точке В, у которой основанием является сечение призмы плоскостью.

Источник: ЕГЭ — 2016. Основная волна 06.06.2016. Центр

Сечением прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ плоскостью α содержащей прямую BD₁ и параллельной прямой AC, является ромб.

а)  Докажите, что грань ABCD  — квадрат.

б)  Найдите угол между плоскостями α и BCC₁, если AA₁  =  6, AB  =  4.

Источник: ЕГЭ по математике 31.03.2017. Досрочная волна.

Основанием прямого параллелепипеда ABCDA₁B₁C₁D₁ является ромб ABCD, сторона которого равна а угол ВАD равен 60°.

а)  Докажите, что прямые AC_1 и BD перпендикулярны.

б)  Найдите расстояние от точки А до прямой C₁D₁, если известно, что боковое ребро данного параллелепипеда равно 8.

Прямоугольник ABCD и цилиндр расположены таким образом, что AB  — диаметр верхнего основания цилиндра, а CD лежит в плоскости нижнего основания и касается его окружности, при этом плоскость прямоугольника наклонена к плоскости основания цилиндра под углом 60°.

а)  Докажите, что ABCD  — квадрат.

б)  Найдите длину той части отрезка BD, которая находится снаружи цилиндра, если радиус цилиндра равен

Дан правильный треугольник ABC. Точка D лежит вне плоскости ABC,

а)  Докажите, что прямые AD и BC перпендикулярны.

б)  Найдите расстояние между прямыми AD и BC, если AC  =  6.

Источник: ЕГЭ по математике 28.03.2022. Досрочная волна. Москва. Вариант 1, Задания 13 ЕГЭ–2022

Правильную четырехугольную пирамиду пересекает плоскость, проходящая через вершину основания перпендикулярно противоположному боковому ребру. Площадь получившегося сечения в два раза меньше площади основания пирамиды. Найдите отношение длины высоты пирамиды к длине бокового ребра.

Источник: А. Ларин: Тренировочный вариант № 32.

В правильной треугольной пирамиде SABC точка E  — середина ребра AC, точка P  — середина ребра SВ.

а)  Докажите, что прямая РЕ делит высоту SH пирамиды в отношении 1:3.

б)  Найдите тангенс угла между прямой РЕ и плоскостью АSС, если известно, что SA=10.

Источник: А. Ларин. Тренировочный вариант № 263.

В прямом круговом цилиндре проведена образующая NN₁, точка N лежит в нижнем основании. Отрезок KM₁ пересекает ось цилиндра, а точки K и M₁ лежат на окружностях нижнего и верхнего основания соответственно.

а)   Докажите, что треугольник KNM₁ прямоугольный.

б)  Найдите расстояние от точки N до прямой KM₁, если KN  =  9, N₁M₁  =  20.

Источник: Пробный вариант ЕГЭ по математике 18.03.21 Санкт-Петербург. Вариант №2, А. Ларин. Тренировочный вариант № 348.

Вне плоскости правильного треугольника ABC расположена точка D, причем

а)  Докажите, что прямые AD и BC перпендикулярны.

б)  Найдите расстояние между этими прямыми, если AB  =  2.

Источник: ЕГЭ по математике 28.03.2022. Досрочная волна, Задания 13 ЕГЭ–2022

Дана правильная треугольная пирамида DABC с вершиной D. Сторона основания пирамиды равна высота равна

а)  Докажите, что сечение, проходящее через середину бокового ребра BD и точки М и Т (середины ребер АС и AВ соответственно), является прямоугольником.

б)  Найдите расстояние от середины бокового ребра BD до прямой МТ.

В правильной четырёхугольной призме АВСDА₁В₁С₁D₁ сторона АВ основания равна 6, а боковое ребро АА₁ равно На ребрах BC и C₁D₁ отмечены точки К и L соответственно, причём ВК = 4, C₁L  =  5. Плоскость γ параллельна прямой BD и содержит точки К и L.

а)  Докажите, что прямая AC₁ перпендикулярна плоскости γ.

б)  Найдите расстояние от точки B₁ до плоскости γ.

Источник: Задания 14 (С2) ЕГЭ 2016, ЕГЭ по математике 06.06.2016. Основная волна. Юг (C часть).

В основании треугольной пирамиды SABC лежит прямоугольный треугольник ABC с прямым углом C. Основание высоты SO этой пирамиды является серединой ребра AB.

а)  Докажите, что SA  =  SC.

б)  Найдите угол между плоскостями SAC и ABC, если AC  =  16, AB  =  20, SA  =  26.

Источник: ЕГЭ по математике 07.06.2021. Основная волна. Санкт-Петербург, Москва, другие города. Вариант 359 (C часть), Задания 14 ЕГЭ–2021

Все рёбра правильной треугольной призмы ABCA₁B₁C₁ имеют длину 6. Точки M и N— середины рёбер AA₁ и A₁C₁ соответственно.

а)  Докажите, что прямые BM и MN перпендикулярны.

б)  Найдите угол между плоскостями BMN и ABB₁.

Источник: Демонстрационная версия ЕГЭ—2016 по математике. Профильный уровень., Демонстрационная версия ЕГЭ—2018 по математике. Профильный уровень., Демонстрационная версия ЕГЭ—2020 по математике. Профильный уровень.

Основание ABCD призмы   — трапеция с основаниями AB  =  2CD.

а)  Докажите BA_1D_1 проходит через середину бокового ребра CC_1.

б)  Найдите угол между боковым ребром AA_1 и этой плоскостью, если призма прямая, трапеция ABCD прямоугольная с прямым углом при вершине B, а BC  =  CD и

Источник: А. Ларин. Тренировочный вариант № 314. (Часть C)

Все рёбра правильной треугольной призмы ABCA₁B₁C₁ имеют длину 12. Точки M и N— середины рёбер AA₁ и A₁C₁ соответственно.

а)  Докажите, что прямые BM и MN перпендикулярны.

б)  Найдите угол между плоскостями BMN и ABB₁.

Дана правильная пирамида PABCD с вершиной в точке Р. Через точку В перпендикулярно прямой DP проведена плоскость Ω, которая пересекает DP в точке К.

а)  Докажите, что прямые ВК и АС перпендикулярны.

б)   Найдите площадь сечения пирамиды плоскостью Ω, если известно, что сторона основания пирамиды равна 6 и высота пирамиды равна 6.

Источник: А. Ларин: Тренировочный вариант № 205.

В окружность нижнего основания цилиндра с высотой 2 вписан правильный треугольник ABC со стороной В окружность верхнего основания вписан правильный треугольник A₁B₁C₁ так, что он повернут относительно треугольника ABC на угол 60°.

а)  Докажите, что четырехугольник ABB₁C₁  — прямоугольник.

б)  Найдите объем многогранника ABCA₁B₁C₁.

Источник: А. Ларин. Тренировочный вариант № 284.

а)  Докажите, что SA  =  SC.

б)  Найдите угол между плоскостями SAC и ABC, если AB  =  30, SC  =  17, СB  =  24.

Источник: ЕГЭ по математике 07.06.2021. Основная волна. Санкт-Петербург, Москва, другие города. Вариант 358 (часть С), Задания 14 ЕГЭ–2021

Всего: 124 1–20 | 21–40 | 41–60 | 61–80 …

Источник

8. Геометрия в пространстве (стереометрия)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Теорема о трех перпендикулярах

Необходимые факты:

(blacktriangleright) Определение: прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой из этой плоскости.

(blacktriangleright) Признак перпендикулярности прямой и плоскости: если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.

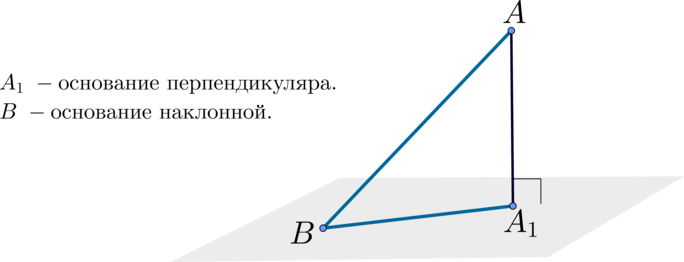
(blacktriangleright) Наклонная (к плоскости) (AB) – отрезок прямой, не перпендикулярной плоскости, один из концов которого лежит на плоскости (основание наклонной).

(blacktriangleright) Перпендикуляр (к плоскости) (AA_1) – отрезок прямой, перпендикулярной плоскости, один из концов которого лежит на плоскости (основание перпендикуляра).

(blacktriangleright) Проекция наклонной (BA_1) – отрезок, соединяющий основания перпендикуляра и наклонной.

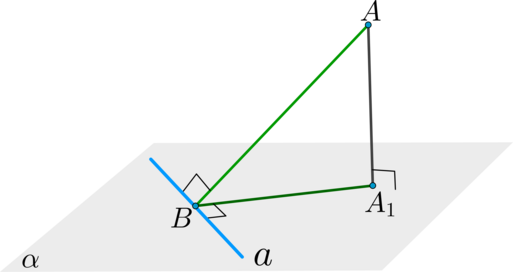
Теорема о трех перпендикулярах (ТТП):

Пусть в плоскости (alpha) через основание наклонной (BA) (т. (B,)) проведена прямая (a). Если эта прямая перпендикулярна проекции (BA_1) этой наклонной, то она перпендикулярна и самой наклонной.

(AA_1perp alpha; ain alpha.) Если (aperp BA_1), то (aperp
BA).

Обратная ТТП:

Пусть в плоскости через основание наклонной проведена прямая. Если эта прямая перпендикулярна наклонной, то она перпендикулярна и проекции этой наклонной.

(AA_1perp alpha; ain alpha.) Если (aperp BA), то (aperp
BA_1).

Задание
1

#2870

Уровень задания: Равен ЕГЭ

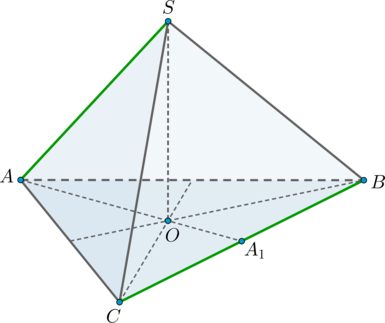
Пусть (SABC) – правильная треугольная пирамида с вершиной (S). Найдите угол между (AS) и (BC). Ответ дайте в градусах.

Так как пирамида правильная, то высота пирамиды (SO) падает в точку пересечения медиан основания. Пусть (AA_1) – медиана основания. Тогда (AO) – проекция наклонной (AS) на плоскость основания. Так как (AO) – часть (AA_1), а (AA_1perp BC) (медианы правильного треугольника являются также и высотами), то по теореме о трех перпендикулярах ((SOperp (ABC), AOperp BC,)) наклонная (AS) перпендикулярна (BC). Следовательно, (angle (AS, BC)=90^circ).

Ответ: 90

Задание
2

#2871

Уровень задания: Равен ЕГЭ

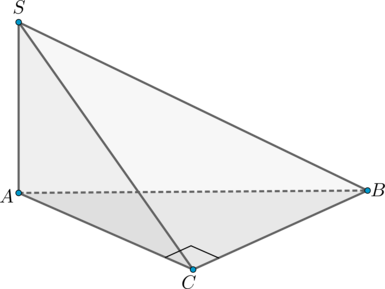
Дана пирамида (SABC) с высотой (SA). Известно, что в основании лежит прямоугольный треугольник с прямым углом (C). Найдите угол между ребрами (SC) и (BC). Ответ дайте в градусах.

Так как (SA) – высота пирамиды, то (SAperp (ABC)). Заметим, что (AC) – проекция наклонной (SC) на плоскость (ABC). Так как (ACperp
BC), то по теореме о трех перпендикулярах (SCperp BC), следовательно, угол между (SC) и (BC) равен (90^circ).

Ответ: 90

Задание
3

#2872

Уровень задания: Равен ЕГЭ

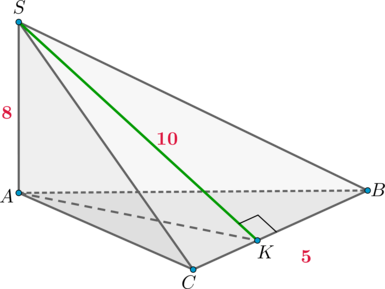
Дана пирамида (SABC) с высотой (SA=8). Известно, что (SK) равно (10) и перпендикулярно (BC=5), причем (K) лежит на (BC). Найдите площадь треугольника (ABC).

Так как (SA) – высота пирамиды, то (SAperp (ABC)). Заметим, что (AK) – проекция наклонной (SK) на плоскость (ABC). Так как (SKperp
BC), то по теореме о трех перпендикулярах (AKperp BC), следовательно, [S_{triangle ABC}=dfrac12AKcdot BC.] Треугольник (SAK) прямоугольный, следовательно, по теореме Пифагора [AK=sqrt{SK^2-SA^2}=6.] Следовательно, [S_{triangle ABC}=dfrac12cdot 6cdot 5=15.]

Ответ: 15

Задание
4

#2874

Уровень задания: Равен ЕГЭ

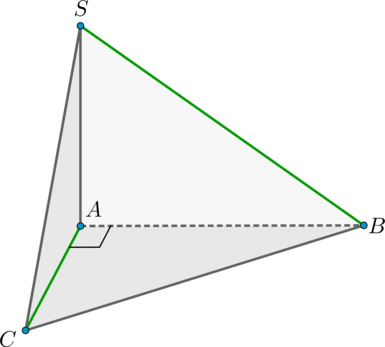
Дана пирамида (SABC) с высотой (SA), в основании которой лежит прямоугольный треугольник с прямым углом (A). Найдите угол между прямыми (SB) и (AC). Ответ дайте в градусах.

Так как (SA) – высота пирамиды, то (SAperp (ABC)). Заметим, что (AB) – проекция наклонной (SB) на плоскость (ABC). Следовательно, по теореме о трех перпендикулярах (так как (SAperp(ABC), ABperp
AC,)) наклонная (SB) перпендикулярна (AC), то есть угол между ними равен (90^circ).

Ответ: 90

Задание
5

#2873

Уровень задания: Сложнее ЕГЭ

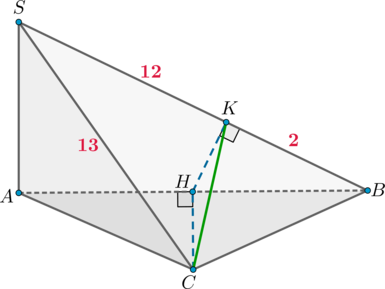
Дана пирамида (SABC) с высотой (SA). (H) – такая точка на (AB), что (CHperp AB). (K) – такая точка на (SB), что (HKperp SB), причем (SC=13), (SK=12), (KB=2). Найдите площадь треугольника (SBC).

Так как (SA) – высота пирамиды, то (SAperp (ABC)). Следовательно, (SA) перпендикулярно любой прямой из ((ABC)), значит, (SAperp CH). Тогда (CH) перпендикулярна двум пересекающимся прямым (SA) и (AB) из плоскости (SAB), значит, (CHperp (SAB)).
Заметим, что тогда (HK) – проекция наклонной (CK) на эту плоскость. Значит, по теореме о трех перпендикулярах (CKperp SB).
По теореме Пифагора из (triangle SCK):[CK=sqrt{SC^2-SK^2}=5.] Следовательно, [S_{triangle SBC}=dfrac12CKcdot SB=dfrac12cdot
5cdot 14=35.]

Ответ: 35

Задание
6

#2705

Уровень задания: Сложнее ЕГЭ

Из точки (N) на плоскость прямоугольника (ABCD) опустили перпендикуляр (NB). Известно, что (AD = 7), (NA = 24). Найдите (ND).

Так как (NB) – перпендикуляр к плоскости ((ABCD)), то (AB) – проекция (NA) на (ABCD). Так как (ABCD) – прямоугольник, то (AD) перпендикулярна (BA), следовательно по теореме о трех перпендикулярах (AD) перпендикулярна (NA) и треугольник (NAD) – прямоугольный.

По теореме Пифагора [AD^2 + NA^2 = ND^2,] откуда (ND^2 = 625), тогда (ND = pm 25). Так как длина – неотрицательна, то (ND = 25).

Ответ: 25

Задание
7

#936

Уровень задания: Сложнее ЕГЭ

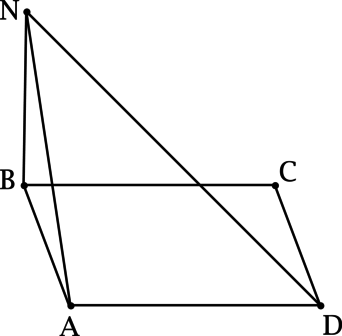
Отрезки (AB) и (CD) перпендикулярны, отрезки (DC) и (NC) перпендикулярны. Отрезки (AB) и (NC) перпендикулярны, (AD : AB) как (1 : 2). Найдите [dfrac{angle AND}{angle ANB} = ,?]

Так как (NC) перпендикулярен (DC) и (AB), причём (DC) и (AB) пересекаются, то (NC) перпендикулярен плоскости ((ABC)). Тогда (DC) – проекция (ND) на ((ABC)), но (DC) перпендикулярен (AB), следовательно, по теореме о трех перпендикулярах (ND) перпендикулярен (AB).

Так как (AD : AB) как (1 : 2), то (D) – середина (AB), тогда (ND) в треугольнике (ANB) является медианой и высотой, следовательно, треугольник (ANB) – равнобедренный и [angle AND = dfrac{1}{2}angle ANBqquadRightarrowqquaddfrac{angle AND}{angle ANB} = dfrac{1}{2}.]

Ответ: 0,5

Как правильно применить теорему о трех перпендикулярах в задачах, которые ежегодно встречаются в ЕГЭ? С приближением аттестационного испытания этот вопрос становится все более актуальным для учащихся старших классов общеобразовательных школ.

О том, как правильно применяется теорема о трех перпендикулярах в задачах ЕГЭ и как научиться оперативно справляться с подобными заданиями, вы узнаете, посетив образовательный портал «Школково». Наши специалисты подготовили весь необходимый базовый материал. Благодаря доступному изложению информации, учащиеся с любым уровнем подготовки смогут научиться правильно решать задачи с применением теоремы о трех перпендикулярах в ЕГЭ. Ознакомиться с теоретическим материалом вы можете, посетив раздел «Теоретическая справка».

После этого, чтобы лучше закрепить изученную информацию и попрактиковаться, например, в нахождении двугранного угла, предлагаем вам выполнить соответствующие задания. Сделать это можно в режиме онлайн, находясь в любом городе. Чтобы посмотреть подборку задач, перейдите в раздел «Каталог».

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

Ваш е-мэйл

Заполните, если хотите получить ответ

Оцените наш проект

Источник

Тема 2.

Геометрия в пространстве (стереометрия)

Теорема о трех перпендикулярах

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

геометрия в пространстве (стереометрия)

2.01Теорема о трех перпендикулярах

2.02Угол между прямыми

2.03Угол между прямой и плоскостью

2.04Угол между плоскостями и двугранный угол

2.05Пирамида

2.06Правильная и прямоугольная пирамиды

2.07Призма

2.08Правильная и прямая призмы

2.09Параллелепипед как частный случай призмы

2.10Прямоугольный параллелепипед

2.11Куб как частный случай прямоугольного параллелепипеда

2.12Конус

2.13Цилиндр

2.14Сфера и шар

2.15Комбинированные тела: их объемы и площади поверхностей

2.16Отношение площадей поверхностей и отношение объемов тел

2.17Вписанные и описанные тела

Решаем задачи

Показать ответ и решение

√ ----2------2
CK = SC − SK = 5.

Следовательно,

Показать ответ и решение

S△ABC = 1AK ⋅ BC.
2

Треугольник SAK прямоугольный, следовательно, по теореме Пифагора

√ ------------
AK = SK2 − SA2 = 6.

Следовательно,

1
S△ABC = -⋅ 6 ⋅ 5 = 15.
2

Источник

Предмет: геометрия

Класс: 10

Учитель: Дружинина Татьяна Алексеевна

Школа: МБОУ «Октябрьская школа-гимназия»

Тип урока: урок совершенствования знаний, умений и
навыков.

Тема: Решение задач на применение теоремы о трех
перпендикулярах (ТТП), на угол между прямой и плоскостью.

Цели урока

Образовательная: закрепить изученный материал на практике,
обосновать необходимость теоремы о трех перпендикулярах при решении задач на
доказательство и задач, требующих найти численное или буквенное значение
какого-либо элемента. Учить умению читать чертеж, умению объяснять,
комментировать упражнения в виде цельного связного рассказа.

Развивающая: способствовать развитию общения,
аналитико-синтетического мышления, смысловой памяти и внимания.

Воспитательная: способствовать развитию творческой
деятельности учащихся, потребности к самообразованию.

Ход урока.

Организационный
момент.
Сообщение
темы и цели урока.
Проверка
домашнего задания. Актуализация опорных знаний и умений учащихся.

1) один ученик
готовит у доски доказательство теоремы о трех перпендикулярах

2) один ученик
готовит у доски домашнюю задачу

3) весь класс
работает по карточкам устно

4) слушаем
ответы учащихся (по необходимости комментируем)

Упражнения по образцу и в сходных условиях с
целью выработки умений безошибочного применения знаний.

Решение
задач по готовым чертежам (карточки) с краткой записью в тетрадях задачи на
применение ТТП.

Решение
упражнений с переносом знаний в новые условия.

Работа в парах с последующим
обсуждением задач у доски

I уровень

II уровень

III уровень

6. Рефлексия.

Учащимся
предлагается поочередно ответить на вопрос: Какие теоретические знания вы
применяли при решении задач на уроке?

7. Подведение итогов урока

8. Домашнее задание
и инструктаж

Источник

1.

Урок геометрии в 10 классе
Тема: Решение задач по
теме «Теорема о трёх
перпендикулярах»

2.

Цель: сформировать навык
применения теоремы о трех
перпендикулярах к решению задач.

3.

Отрезок АD перпендикулярен к плоскости равнобедренного
треугольника АВС. Известно, что АВ = АС = 5 см, ВС = 6 см, АD = 12
см.
Найдите расстояния от концов отрезка АD до прямой ВС.
№149 (дом.)
D
П-Р
В
12
П-я
А
N 6
5
С
BC AN
П-я
TTП
BC DN
Н-я
АN и DN – искомые расстояния

4.

Дано: ABCD – прямоугольник,
АK (АВС), KD = 6 см,
KВ = 7 см, KС = 9 см.
Найдите ρ (K, (АВС)), ρ (АK, CD).
№ 150
K
A
D
B
C
Решение
1. ρ (K, (АВС)) = АK.
3. Δ KВС – прямоугольный.
CB = 4√2 см.
2. AK ( ABC )
4. Δ AKD – прямоугольный.
AB CB
KB CB. AK = 2 см.
AB проекция
5. ρ (АK, CD) = АD; AD = 4√2
KB наклонная
см.

5.

II. Устная работа.
A
B
α
a΄
C
a
1. Верно ли утверждение:
«Если прямая,
принадлежащая плоскости,
перпендикулярна проекции
наклонной на эту
плоскость, то она
перпендикулярна и самой
наклонной»?
(Верно.) Обоснуйте ответ.

6.

II. Устная работа.
A
B
α
a΄
C
2. Верно ли утверждение:
«Если прямая
перпендикулярна проекции
наклонной, то эта прямая
перпендикулярна
наклонной»?
a
(Неверно.) Какое условие теоремы о трех перпендикулярах здесь
не выполняется?
Прямая не принадлежит плоскости.

7.

II. Устная работа.
Установите по рисункам положение прямых а и b.
F
F
a
b
B
A
a
b
B
C
D
АВСД – прямоугольник
ВF (АВС)
A
C
D
АВСД – прямоугольник
ВF (АВС)

8.

II. Устная работа.
Установите по рисункам положение прямых а и b.
F
F
a
b
C
B
A
АВСД – ромб
ВF (АВС)
D
a
b
B
A
АВСД – ромб
ВF (АВС)
C
D

9.

III. Решение задач.
D
1.
α
A
D
2.
30°
60°
B
C
Дано: А = 30°; АВС = 60°,
DB АВС.
Докажите, что СD АС.
B
A
α
C
Дано: ВАС = 40°, АСВ = 50°,
AD
АВС.
Докажите, что СВ BD.

10.

III. Решение задач.
K
3.
4.
M
B
D
A
α
C
1) Дано: МА (АВС), АВ = АС,
CD = BD.
Докажите, что MD ВС
2) Дано:МА (АВС), BD = CD,
MD ВС.
Докажите, что АВ = АС.
F
α
A
D
B
E
C
Дано: АЕ и CF – высоты,
ВK АВС.
Докажите, что KD АС.

11.

IV. Решение задач.

12.

IV. Решение задач.

Источник

Урок геометрии. 10 класс

Учебник: Л.С. Атанасян, В.Ф. Бутузов и др. «Геометрия, 10 – 11»

Тема урока: Решение задач на применение теоремы о трёх перпендикулярах

Цели урока: совершенствовать умения учащихся применять теоретические знания к решению задач на доказательство и вычисления, развивать пространственное воображение, развивать умение строить аргументированное и логически верное решение задачи, способствовать дальнейшему развитию навыков самоконтроля.

Ход урока

I. Устная работа.

Учащимся предлагаются для решения задачи по готовым чертежам (задачи на слайдах), при этом учитель просит, чтобы ученики прежде всего сформулировали условие задачи.

1. Дано: АО = 4,

p – касательная к окружности,

АВ – наклонная к α, АВ = 5

Доказать: АВ

Найти: r

2. Дано: М

Доказать:

3. Дано:

Доказать:

4. Дано:

ВК – медиана и высота ∆ АВС

Доказать:

Определить вид ∆ АМС В С

II. На каждой парте лежит лист с задачами (на лицевой стороне – задачи, решение которых будет разбираться со всеми учащимися, на обратной стороне – задачи для самостоятельной работы):

Учитель предлагает учащимся в течение 15 минут самостоятельно решить 4 задачи:

1. Дано: ВК – высота ∆ АВС М

АВ = 7, ВС = 3

, МВ = 4

АМ = , СМ = 5 В С

Доказать:

2. Дано: , МВ = 3 К

МА = МС = 5, А

АК = КС,

Найти расстояние от точки М до АС.

3. Дано: ∆ АВС, , Д

Доказать:

4. Дано: ∆ АВС, , В А

Найти:

Далее проводится проверка и обсуждение решения задач со всеми учащимися класса

Решение задач:

№ 1

∆ МВС – прямоугольный, так как (4² + 3² = 5²), следовательно
∆ МВА – прямоугольный, так как (4² + 7² = ), следовательно
Из 1) и 2) следует, что МВ – перпендикуляр к плоскости АВС.
МК – наклонная к плоскости АВС, ВК – её проекция, , следовательно . Тогда прямая АС перпендикулярна двум пересекающимся прямым МК и ВК плоскости МВК, т.е.

Что и требовалось доказать.

№ 2

Так как , и . Тогда ∆ АВМ = ∆СВМ по катету и гипотенузе (МВ – общий катет, МА = МС по условию), следовательно АВ = СВ =
∆АВС: АВ = СВ = 4, , ВК – медиана, высота и биссектриса, следовательно ∆АВК – прямоугольный с гипотенузой 4 и острым углом ,

ВК = 2

ВК – проекция МК на плоскость (АВС), , следовательно , т.е. МК – расстояние от точки М до АС.
∆ МВК – прямоугольный ().

Ответ: расстояние от точки М до АС равно

№ 3

1) , ДС – наклонная к плоскости АВС, АС – её проекция, (по условию), тогда , ∆ ДСВ – прямоугольный,

2) ∆ АВС – прямоугольный по условию,

3) ∆ ДАВ – прямоугольный (),

4) , что и требовалось доказать.

№ 4

Используем формулу, доказанную в задаче № 3, cos ∠ДВС = cos ∠ДВА ∙ cos ∠АВС

cos∠ДВС = , ∠ ДВС =

Ответ:

III. Проверочная работа. Учащимся предлагается решить одну из задач, представленных на обратной стороне листа, по выбору.

Задачи для самостоятельного решения:

Уровень 1

Через вершину В прямоугольника АВСД проведен перпендикуляр МВ к плоскости прямоугольника. Определите вид ∆ АМД и найдите его площадь, если стороны прямоугольника АВ = 3 и АД = 8, а ВМ = 4. (Ответ: 20)
Из вершины равностороннего треугольника АВС восставлен перпендикуляр АД к плоскости треугольника. Найдите расстояние от точки Д до стороны ВС, если

АД = 13, ВС = 6. (Ответ: 14)

Уровень 2

К плоскости треугольника из центра вписанной в него окружности восставлен перпендикуляр длиной 3. Найдите расстояние от конца этого перпендикуляра до сторон треугольника, если длины сторон треугольника 13, 14 и 15 (Ответ: 5)
Точка М лежит вне плоскости ромба АВСД на равном расстоянии от его сторон. Найдите расстояние от проекции точки М на эту плоскость до сторон ромба, если сторона ромба равна 12, а острый угол (Ответ: 6)

Уровень 3

Катеты прямоугольного треугольника равны 18 и 32. Из точки М, делящей гипотенузу пополам, восставлен к плоскости треугольника перпендикуляр МК, равный 12. Найдите расстояние от точки К до каждого катета. ( Ответ: 20 и 15)
Через вершину А прямоугольного треугольника АВС в прямым углом В проведён перпендикуляр АД к плоскости треугольника. Найдите длину наклонной ДС, если её проекция равна ℓ, , . (Ответ: ℓ)

IV. Домашнее задание: п. 20, № 204, 206

Источник