Задачи на урожайность егэ

Задание 17 ЕГЭ по математике (профиль). Задачи на оптимальный выбор. Фермер и два поля

Задача 1. (№ 513292)

У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 500 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором — 500 ц/га.

Фермер может продавать картофель по цене 5 000 руб. за центнер, а свёклу — по цене 8 000 руб. за центнер. Какой наибольший доход может получить фермер?

Решение.

Составим таблицу:

	Картофель (5000 руб. за 1 ц)	Свёкла (8000 руб. за 1 ц)
	Общая площадь	Засеянная площадь	Урожайность, ц/га	Общая площадь	Засеянная площадь	Урожайность, ц/га
1-е поле	10	10 – х	500	10	х	300
2-е поле	10	–	300	10	10	500

1) Продавать свёклу более выгодно, поэтому второе поле, где ее урожайность выше, следует засадить только свёклой.

Она принесет доход 10 га · 500 ц/га · 8 000 руб./ц = 40 млн. руб.

2) Прибыль с 1-го поля составляет:

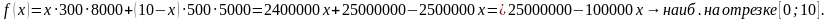
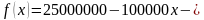
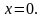
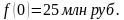
Так как линейная убывающая функция, то наибольшее значение функция достигает при

Общая прибыль: 40 + 25 = 65 (млн. руб.)

Ответ: 65 млн. рублей.

Примечание. Приведем ещё одно решение:

Доход с 1 га картофеля на первом поле: 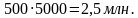  руб.

Доход с 1 га картофеля на втором поле: 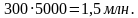   руб.

Доход с 1 га свеклы на первом поле: 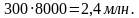  руб.

Доход с 1 га свеклы на втором поле: 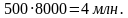  руб.

Таким образом, первое поле выгодно полностью засадить картофелем, а второе — свёклой. Суммарно получаем:

руб.

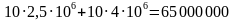
Задания для самостоятельного решения:

1. (№ 513296)

У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 400 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором — 400 ц/га.

Фермер может продавать картофель по цене 10 000 руб. за центнер, а свёклу — по цене 11 000 руб. за центнер. Какой наибольший доход может получить фермер?

Ответ: 84 млн. руб.

2. (№ 515785)

У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 300 ц/га, а на втором — 200 ц/га. Урожайность свёклы на первом поле составляет 200 ц/га, а на втором — 300 ц/га.

Фермер может продавать картофель по цене 10 000 руб. за центнер, а свёклу — по цене 13 000 руб. за центнер. Какой наибольший доход может получить фермер?

Ответ: 69 млн. рублей.

3. (№ 517184)

У фермера есть два поля, каждое площадью 8 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 350 ц/га, а на втором — 200 ц/га. Урожайность свёклы на первом поле составляет 250 ц/га, а на втором — 300 ц/га.

Фермер может продавать картофель по цене 2500 руб. за центнер, а свёклу — по цене 3000 руб. за центнер. Какой наибольший доход может получить фермер?

Ответ: 14,2 млн. рублей.

4. (№ 517222)

У фермера есть два поля, каждое площадью 15 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 400 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 250 ц/га, а на втором — 400 ц/га.

Фермер может продавать картофель по цене 2000 руб. за центнер, а свёклу — по цене 3000 руб. за центнер. Какой наибольший доход может получить фермер?

Ответ: 30 млн. рублей.

Задача 1.

У
фермера есть два поля, каждое площадью 10 гектаров. На каж­дом поле можно
выращивать картофель и свеклу, поля можно де­лить между этими культурами в
любой пропорции. Урожайность картофеля на первом поле составляет , а на втором – .
Урожайность свеклы на первом поле составляет , а на
втором – .

Фермер
может продавать картофель по цене  руб. за
центнер, а свеклу – по цене руб. за центнер.
Какой наибольший доход может получить фермер?

Решение:

На
первом поле пусть (га) занимает картофель.
Доход от него определяем:

 руб.

Доход
от свеклы на первом поле

 (руб.)

На
втором поле на картофель выделяем  (га). Тогда
доход от него:

 (руб.)

Доход
от свеклы на втором поле:

 (руб.)

Общий
доход:

;

.

если , а .

Окончательно
 руб.

Задачу
можно решить из соображений здравого смысла.

Так
как урожайность на первом поле выше у картофеля, то все первое поле засевается
им. А на втором поле выше урожайность у свеклы. Тогда:

 руб.

Ответ:
 руб.

Задача 2.

31
декабря 2014 года Василий взял в банке некоторую сумму в кредит под годовых. Схема выплаты кредита следующая –
31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму
долга (то есть увеличивает долг на ), затем Василий
переводит в банк 3 696 300 рублей. Какую сумму взял Василий в банке, если он
выплатил долг двумя равными плате­жами (то есть за два года)?

Решение:

Если
– сумма кредита, то через год останется

 руб.

А
через два года:

,

.

Ответ:
6330000 руб.

Задача 3.

В
двух шахтах добывают алюминий и никель. В первой шахте имеется  рабочих, каждый из которых готов
трудиться часов в день. При этом один рабочий за час
добывает кг алюминия или кг никеля. Во второй шахте имеется  рабочих, каждый из которых готов
трудиться  часов в день. При этом один рабо­чий за
час добывает кг алюминия или кг никеля. Обе шахты поставляют
добытый металл на завод, где для нужд промышленности производится сплав
алюминия и никеля, в кото­ром на кг алюминия
приходится кг никеля. При этом шахты
договариваются между собой вести добычу металлов так, чтобы завод мог
произвести наибольшее количество сплава. Сколько ки­лограммов сплава при таких
условиях ежедневно сможет произве­сти завод?

Решение:

Пусть
рабочих добывают в первой шахте алюминий.
Его масса

(кг).

Тогда
никеля (кг).

Во
второй шахте алюминия добывается в день рабочими:
(кг).

Никеля
добывается: (кг).

По
условию на кг алюминия приходится  кг никеля.

Тогда:

Получаем

.

Масса
сплава равна:

,

,

,

.

Выражение
максимально, если

 (кг).

Ответ:
 (кг).

Задача 4.

15-го
января планируется взять кредит в банке на 18 месяцев. Ус­ловия его возврата
таковы:

—
1-го числа каждого месяца долг возрастает на по
сравнению с концом предыдущего месяца;

— 
со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

—
15-го числа каждого месяца долг должен быть на одну и ту же величину меньше
долга на 15-е число предыдущего месяца.

Сколько
процентов от суммы кредита составляет общая сумма де­нег, которую нужно
выплатить банку за весь срок кредитования?

Решение:

Предположим,
что  – сумма кредита,  –
разница в долге на 15-е число месяца.

Представим
выплаты в виде таблицы:

№ п/п	На 1-е число месяца	На 15-е число месяца
1	–
2	1,02
3	1,02
4	1,02
5	1,02
–	–	–
18	1,02
19	1,02

.

Чтобы
найти сумму денег, которую нужно выплатить банку за весь срок кредитования , необходимо
сложить разность строк, начиная со второй.

,

.

Ответ:
119%

Задача 5.

В
двух областях есть по  рабочих, каждый из которых
готов тру­диться по  часов в сутки на добыче
алюминия или никеля. В первой области один рабочий за час добывает кг алюминия или  кг никеля. Во второй области для
добычи  кг алюминия в день требуется  человеко-часов труда, а для добычи  кг никеля в день требуется  человеко-часов труда.

Обе
области поставляют добытый металл на завод, где для нужд промышленности
производится сплав алюминия и никеля, в кото­ром на  кг
алюминия приходится  кг никеля. При этом
области договариваются между собой вести добычу металлов так, чтобы завод мог
произвести наибольшее количество сплава. Сколько ки­лограммов сплава при таких
условиях ежедневно сможет произве­сти завод?

Решение:

Предположим,
что  человек в первой области добывают
алюминий, тогда его масса равна (кг), а никеля (кг)

Во
второй области:

Общая
масса алюминия  (кг), никеля (кг)

Массу
обоих металлов выражаем по формуле:

По
условию задачи в сплаве на  кг алюминия
приходится  кг никеля:

,

,

,

,

,

,

,
где ,

.

Найдем
производную :

,

.

Найдем
критическое значение из условия .

,

,

(кг).

кг

Максимальное
значение массы металлов

 кг

Ответ:
кг

Задача 6.

Тимофей
хочет взять в кредит 1,1 млн рублей. Погашение кредита происходит раз в год
равными суммами (кроме, может быть, послед­ней) после начисления процентов.
Ставка процента годовых. На какое минимальное
количество лет может Тимофей взять кредит, чтобы ежегодные выплаты были не
более 270 тысяч рублей?

Решение:

Расчеты
ведем по формуле для нахождения остатка

, где –
сумма  долга.

Распишем
выплаты в виде таблице

№ п/п	Перед выплатой (млн руб.)	После выплаты (млн руб.)
1	1,21	0,94
2	0,94	0,764
3	0,764	0,5704
4	0,5704	0,35744
5	0,35744	0,123184
6	0,123184	–

Таким
образом, на погашение долга потребуется 6 лет

Ответ:
6 лет.

Задача 7.

31
декабря 2014 года Олег взял в банке некоторую сумму в кредит под некоторый
процент годовых. Схема выплаты кредита следующая – 31 декабря каждого
следующего года банк начисляет проценты на оставшуюся сумму долга (то есть
увеличивает долг на %), затем Олег переводит
очередной транш. Если он будет платить каждый год по 328 050 рублей, то
выплатит долг за 4 года. Если по 587 250 рублей, то за 2 года. Найдите .

Решение:

Пусть
 – сумма, взятая в кредит

 – выплачиваемый  транш, если долг
выплачивается 4 года

– выплачиваемый  транш, если долг
выплачивается 2 года

Выплата
долга в течение 4 лет:

1.    
Через 1 год: .

2.    
Через 2
года: .

3.    
Через 3
года:

,

.

4.    
Через 4
года: .

Обозначаем

.

При
выплате по второй схеме:

С
учетом замены:

,

,

,

,

,

Ответ:

Задача 8.

В
двух областях есть по 90 рабочих, каждый из которых готов трудиться по 5 часов
в сутки на добыче алюминия или никеля. В первой области один рабочий за час
добывает кг алюминия или  кг никеля. Во второй области для
добычи х кг алюминия в день требуется х²
человеко-часов труда, а для добычи у кг ни­келя в день требуется у²
человеко-часов труда.

Для
нужд промышленности можно использовать или алюминий, или никель, причём  кг алюминия можно заменить  кг никеля. Какую наибольшую массу
металлов можно добыть в двух областях суммарно для нужд промышленности?

Решение:

В
соответствии с условием задачи, наиболее выгодно в первой области добывать
алюминий. Тогда общий объем часов

человеко-часов.

Соответственно,
добытый алюминий в первой области

 кг.

Рассмотрим
вторую область. По условию:

Следовательно,

Общая
масса металла добытого во второй области

,

где ; .

Находим
производную

Находим
критические значения  из условия

Итак,
алюминия добывают

 кг, а никеля  кг.

Во
второй области наибольшая масса добытых металлов:

 кг.

А
в обеих областях:

 кг.

Ответ:
наибольшая масса добытых металлов  кг.

Задача 9.

За
время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в
размере  в ме­сяц, затем ,
потом  и, наконец, в
месяц. Известно, что под действием каждой новой процентной ставки вклад
находился целое число месяцев, а по истечении срока хранения первоначальная
сумма вклада увеличилась на . Определите срок
хранения вклада.

Решение:

Предположим,
что под в месяц вклад хранился  месяцев, под  – месяцев, под – месяцев,  под  – месяцев.

  – натуральные числа.

S – первоначальная сумма вклада.

1.    
Через  месяцев будет
сумма:

;

2.    
Далее через  месяцев:

;

3.    
Через месяцев:

4.    
Через  месяцев:

.

По
условию задачи

.

Итак:

.

.

.

	(1)
(2)
(3)
(4)

Удвоим
уравнение (4) и сложим с уравнением (1) и сложим уравнения (2) и (3).

Получим:

Сложив
эти два уравнения имеем:

        

Из (4):

      

Из (2):

          

         .

Подставим
все в уравнение (1):

,

,

,

(месяца),

(месяца),

(месяца),

(месяца),

 (месяцев).

Ответ:12
месяцев или 1 год

Задача 10.

Папа
Карло выстрогал Буратино и отправил его в школу, дав ему на букварь несколько
деревянных рублей, не более 30 штук. Буратино продал все рубли коллекционерам
по 150 сольдо за каждый. Пять сольдо он сунул себе за щеку, не более трех
закопал на поле Чудес, а на оставшиеся купил хлеба по цене 51 сольдо за
корочку. Сколько корочек хлеба купил Буратино?

Решение:

Обозначим
– количество рублей, – количество корочек хлеба, – количество закопанных сольдо.

Для
 выполняется
условие ; учтем, что  натуральные числа и . Составим уравнение по условию:

1.    
Если , то

,

,

,

,

.

a)    
если , а – условию задачи удовлетворяет;

b)   
 

 –
не
подходит

2.    
,

,

.

a)      
.

.

 –
нецелое.

b)     
.

.

 – нецелое
и больше 30.

3.    
,

,

.

a)      
.

 – нецелое

b)     
.

– нецелое и больше
30.

Условию
задачи удовлетворяет только .
Тогда количество корочек .

Ответ:
44 корочки хлеба.

Задача 11.

В
Шестьляндии в обращении находятся денежные купюры номиналом 1 рубль, 6 рублей и
36 рублей. Банком, в котором содер­жится неограниченный запас купюр каждого
вида, 14 купюрами выдана некоторая сумма, меньшая 200 рублей. Найти эту сумму,
если известно, что меньшим числом купюр выдать ее невозможно.

Решение:

 – количество
купюр достоинством 1 рубль,

 – количество
купюр достоинством 6 рублей,

 – количество
купюр достоинством 36 рублей.

Из
условия задачи следует:

Из
условия, что меньше чем 14 купюр быть не может, следует, что:

 так как

, то .

При
, имеем .

При
, будет .

При
, получаем , что не
соответствует условию задачи.

Рассмотрим
варианты:

1.   ,

,

,

2.   ,

,

,

3.   ,

,

,

 – подходит.

Ответ:
174 рубля.

Задачи для самостоятельной работы

Задача 1.

В
двух областях есть по 100 рабочих, каждый из которых готов трудиться по 10
часов в сутки на добыче алюминия или никеля. В первой области один рабочий за
час добывает кг алюминия или  кг никеля. Во второй области для
добычи кг алюминия в день требуется  человеко-часов труда, а для добычи  кг ни­келя в день требуется  человеко-часов труда.

Обе
области поставляют добытый металл на завод, где для нужд промышленности
производится сплав алюминия и никеля, в кото­ром на  кг
алюминия приходится  кг никеля. При этом
области договариваются между собой вести добычу металлов так, чтобы завод мог
произвести наибольшее количество сплава. Сколько ки­лограммов сплава при таких
условиях ежедневно сможет произве­сти завод?

Задача 2.

15-го
января планируется взять кредит в банке на сумму 2,4 млн рублей на 24 месяца.
Условия его возврата таковы:

—
1-го числа каждого месяца долг возрастает на  по
сравнению с концом предыдущего месяца;

—
со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

—
15-го числа каждого месяца долг должен быть на одну и ту же величину меньше
долга на 15-е число предыдущего месяца. Какую сумму нужно выплатить банку за
первые 12 месяцев?

Задача 3.

У
фермера есть два поля, каждое площадью 10 гектаров. На каж­дом поле можно
выращивать картофель и свеклу, поля можно де­лить между этими культурами в
любой пропорции. Урожайность картофеля на первом поле составляет  ц/га, а на втором –  ц/га. Урожайность свеклы на первом
поле составляет  ц/га, а на втором –  ц/га.

Фермер
может продавать картофель по цене 10 000 руб. за центнер, а свеклу – по цене 13
000 руб. за центнер. Какой наибольший доход может получить фермер?

Задача 4.

В
двух областях есть по 250 рабочих, каждый из которых готов трудиться по 5 часов
в сутки на добыче алюминия или никеля. В первой области один рабочий за час
добывает  кг алюминия или  кг никеля. Во второй области для
добычи кг алюминия в день требуется   человеко-часов труда, а для добычи  кг ни­келя в день требуется  человеко-часов труда.

Для
нужд промышленности можно использовать или алюминий, или никель, причём  кг алюминия можно заменить  кг никеля. Какую наибольшую массу
металлов можно добыть в двух областях суммарно для нужд промышленности?

Задача 5.

Техническая
реконструкция предприятия была проведена в четыре этапа. Каждый из этапов продолжал­ся
целое число месяцев и сопровождался падением производст­ва. Ежемесячное падение
производства составило на первом этапе , на
втором – , на третьем – и на
четвертом – в месяц. По окончании реконструкции
первоначальный объем производства на предприятии сократился на . Определите продолжительность периода
реконструкции.

Задача 6.

Купил
Роман раков, вчера – мелких, по цене 510 рублей з штуку, а сегодня – по 990, но
очень крупных. Всего на раков он истратил 25200 рублей, из них переплаты из-за
отсутствия сдачи в сумме составили от 160 до 200 рублей. Сколько Роман купил
раков вчера и сколько сегодня?

Задача 7.

В
Семиземье в обращении находятся монеты трех видов: брон­зовые рубли, серебряные
монеты достоинством 7 рублей и золотые монеты достоинством 49 рублей. Из казны,
в которой содержится неограниченный запас монет каждого вида, 17 монетами
выдана некоторая сумма, меньшая 300 рублей. Найти эту сумму, если из­вестно,
что меньшим числом монет выдать ее невозможно.

12
Май 2016

16 Задание (2022)

В задании №17 в ЕГЭ по профильной математике, вместо ожидаемой текстовой задачи на кредиты, иногда встречаются оптимальный выбор. Этот вид задач считается более сложным по сравнению с кредитами. Чтобы хорошо подготовиться к экзамену, нужно научиться их решать.

Тут требуется умение искать наибольшие и наименьшие значения функции, обычно зависящей от нескольких переменных. Эти переменные, как правило, связаны дополнительными условиями.

Вам обязательно понадобится умение искать производные и исследовать функции на экстремумы. Нужно знать, что такое ограниченные, возрастающие и убывающие функции. Если вы умеете решать 12-й и 7-й номера из ЕГЭ, то вам повезло – все необходимое для решения инструменты уже у вас в руках. А те, кто не умеет считать производные, то настоятельно рекомендуем сначала разобраться с первой частью экзамена и только потом переходить на более сложные задачи, такие, как №17.

Основной подход к решению заключается в следующем. Необходимо составить функцию, задающую нужную зависимость – если нужно найти максимальную или минимальную прибыль, значит это должна быть функция, описывающая прибыль, если нужен максимальный выпуск продукции на заводе, значит функция должна задавать количество продукции выпускаемой заводом, нужно найти оптимальное расстояние – наша функция будет описывать расстояние. Внимательно, функция может зависеть сразу от нескольких переменных. После того, как вы смогли записать функцию, нам предстоит ее исследовать.

На самом деле, тут нет какой-то сухой теории, которую можно прочить и научиться решать задачи на оптимальный выбор. Поэтому давайте учиться на примерах. Сначала разберем простые, поймем алгоритм решения, а потом перейдем к более сложным, которые могут встретиться на экзамене.

Пример 1

Пусть у Василия есть завод, который выпускает спичечные коробки. Расходы на производство одного коробка 1 руб, а продает он их за 5 руб. В итоге с каждого коробка Василий получает прибыль 4 руб. Давайте разберемся, сколько нужно производить коробков, чтобы прибыль была наибольшей, если (Х) работников завода может производить в месяц ( N=-left(x-10right)^{2}+500) коробков.

И так, согласно условию задачи, если на заводе Х работников, то они производят ( N=-left(x-10right)^{2}+500) коробков.

А какая прибыль (P) с такого количества? Ответ очевиден, нужно просто прибыль (4 руб) с одного коробка умножить на количество произведенных коробков: ( P=4*(-left(x-10right)^{2}+500)).

Давайте посмотрим при каком количестве работников прибыль Василия будет максимальна. Или другими словами при каком (Х) будет наибольшим (Р). Такое задание часто встречается в 12-м номере ЕГЭ, нужно просто исследовать нашу зависимость прибыли ( P=4*(-left(x-10right)^{2}+500)) от (Х) и найти экстремумы.

Напомню, что функция принимает наибольшее или наименьшее значения в точках, где ее производная равна 0. Значит ищем производную от (Р) и приравниваем к 0.

$${P}^{’}=(4*(-left(x-10right)^{2}+500))^{‘}= 4cdotleft(-2right)cdotleft(x-10right)$$

Приравниваем (0):

$$4cdotleft(-2right)cdotleft(x-10right)=0$$

И ищем (Х), при котором производная равна (0):

$$ X=10.$$

Что мы такое нашли? При этом значении (Х) (количестве рабочих) прибыль будет либо максимальна, либо минимальна. Это точка экстремума, а какая именно, мы пока не знаем.

Давайте это определим. Напоминаю, если производная отрицательная, то функция убывает, если положительна, то возрастает. Если подставить значения меньшее (10) в нашу производную, например (1):

$$ 4cdotleft(-2right)cdotleft(x-10right) = 4cdotleft(-2right)cdotleft(1-10right)=4*18=72$$

Значение производной получилось больше 0:

$$ {P(x<10)}^{‘}>0$$

Значит при (Х<10) функция возрастает, а при (Х>10) убывает. А значит (Х=10) – это максимум. Мы получили, что максимальная прибыль будет, если на производстве будет задействовано всего 10 рабочих. Как так может быть? Казалось бы, чем больше рабочих, тем больше продукции выпускает завод, а значит и больше прибыль. Но в реальной жизни все не так просто – размеры завода ограничены, и если там будет слишком много людей, то они просто будут мешать друг другу делать свою работу, в результате выпуск продукции начнет снижаться или поднимутся расходы на производство.

Вернемся к задаче, а какая будет максимальная прибыль? Просто подставим (Х=10) в функцию для прибыли:

$$ P=4*(-left(x-10right)^{2}+500)= 4*(-left(10-10right)^{2}+500)=4*500=2000 руб. $$

Только что мы решили первую задачу на оптимальный выбор.

Разберем следующий пример:

Пример 2

Пусть опять у нас есть завод, на котором расходы на производство (y) автомобилей составляет (Q=0,5y^2+y+7) миллионов рублей в месяц. Если продавать каждый автомобиль за (S) тысяч рублей, то при продаже всех произведенных за месяц автомобилей завод получит доход (S*y), а заработает на этом прибыль (доходы минус расходы) — (S*y-Q). Какую наименьшую цену продажи (S) нужно установить, чтобы за 3 месяца завод получил прибыль 75 миллионов рублей?

Первым делом давайте составим функцию, описывающую зависимость прибыли от количества произведенной продукции и цены продажи, которую мы должны установить. Сразу 2 неизвестные!

И так, чтобы посчитать прибыль (P(y,S)), зависящую от (у) и (S), нам нужно стоимость продажи одного автомобиля (S) умножить на количество проданных машин (у), получим общий доход, и вычесть все расходы (Q), которые мы понесли при производстве (в условии, кстати, это написано — подсказка):

$$P(x,S)=S*y-Q=S*y-(0,5*y^2+y+7)=-0,5y^2+(S-1)y-7$$

Проанализируем полученное выражение. Это квадратный многочлен. Если построить график относительно (у), то это уравнение параболы. Как анализировать квадратные многочлены, можно посмотреть тут.

Так как коэффициент перед (y^2) отрицательный, то ветки параболы направлены вниз. То есть, наибольшее значение нашей функции будет в вершине параболы. Можно по известным формулам найти вершину и значение функции и в ней, это и будет максимальное значение. А можно пойти по старому пути, как в примере 1, и посчитать производную. Число (S) будем считать просто за константу, то есть берем производную относительно (у):

$$ {P(x,S)}^{’}={(-0,5y^2+(S-1)y-7)}^{’}=-y+S-1; $$

Приравниваем производную нулю, чтобы найти точки экстремума:

$$-y+S-1=0;$$
$$y=S-1;$$

Так как график исходной функции парабола с ветками вниз, то это точка максимума функции (P(x,S)). Подставим (y=S-1) в нашу функцию:

$$ P(x,S)=-0,5*y^2+(S-1)y-7=-0,5(S-1)^2+(S-1)(S-1)-7=frac{(S-1)^2}{2}-7; $$

Мы получили — какую максимальную прибыль мы можем заработать в зависимости от (S). Другими словами, подставляя различные значения стоимости автомобиля в нашу функцию, получим максимальную прибыль при данной стоимости продажи.

По условию задачи общая прибыль за 3 месяца должна быть не меньше чем 75 миллионов рублей. Запишем это в виде неравенства:

$$ {3*P(S)}_{max}=3*frac{(S-1)^2}{2}-7 ge 75; $$

Осталось только решить это неравенство:

$$(S-1)^2ge64;$$
$$(S-9)(S+7)ge0;$$

(S) отрицательным быть не может, что это тогда за бизнес, где цена продаваемой продукции отрицательна. А значит при (S ge9) прибыль завода будет больше 75 миллионов рублей.

Пример 3

Решим задачу на оптимизацию расстояния:

Два мотоциклиста подъезжают к перекрестку по двум перпендикулярным дорогам. Первый едет со скоростью 40 км/ч и до перекрестка ему осталось ехать 5 км, а скорость второго 30км/ч и ехать до перекрестка 3 км. Через какое время расстояние между мотоциклистами будет наименьшим?

Для решения задачи нам понадобится теорема Пифагора, ведь мотоциклисты едут по взаимно перпендикулярным дорогам, а значит расстояние между ними — это гипотенуза прямоугольного треугольника, а катеты – это расстояния от каждого мотоциклиста до перекрестка.

Пусть мотоциклисты уже находятся в пути (t) часов. Тогда первый проедет расстояние:

$$S=v*t=40t;$$

До перекрестка осталось ехать

$$S_1=5-40t;$$

А второму:

$$S_2=3-30t;$$

Мы получили прямоугольный треугольник с катетами (S_1) и (S_2). По теореме Пифагора выведем функцию, задающую расстояние между мотоциклистами:

$$L=sqrt{(5-40t)^2+(3-30t)^2}=sqrt{25-400t+1600t^2+9-180t+900t^2}=sqrt{2500t^2-580t+34};$$

Согласно условию задачи, нужно найти такое время (t), чтобы расстояние (L) было наименьшим. Для этого опять возьмем производную и исследуем функцию (L) на экстремум:

$$ {L}^{’}=frac{1}{2*sqrt{2500t^2-580t+34}}*(5000*t-580); $$

Приравниваем нулю:

$$5000*t-580=0;$$
$$t=frac{580}{5000}=frac{29}{250} часа;$$

Так как при (t) меньшем этого числа производная функции отрицательна, а при большем – положительна, то получаем точку минимума и, что расстояние между мотоциклистами будет наименьшим через (frac{29}{250}) часа, это и требовалось найти.

Если бы в задаче нас попросили еще найти это расстояние, то нужно подставить (t=frac{29}{250}) в функцию расстояния (L):

$$L(t=frac{29}{250})=sqrt{(5-40*frac{29}{250})^2+(3-30*frac{29}{250})^2}=(frac{3}{5})км$$

Что такое задачи на оптимизацию?

Задача на оптимизацию — в математике задача
нахождения экстремума(минимума или максимума)целевой функции вне которой
области определения. В самых простых задачах на оптимизацию мы имеем дело с
двумя величинами, одна из которых зависит от другой, причем надо найти такое
значение 2-ой величины, при котором первая принимает свое наилучшее в данных
условиях значение.

Как решать задачи на оптимизацию?

Задачи на оптимизацию решают по обычной схеме
из трех этапов  математического моделирования:

1) составление
математической модели;

2) работа с
математической моделью;

3) ответ на вопрос
задачи.

Первый этап.
Составление математической модели.

1) Проанализировав
условия задачи, выделите оптимизируемую величину (О.В.),
т. е. величину, о наибольшем или наименьшем значении которой идет речь.
Обозначьте ее буквой y.

2) Одну из
участвующих в задаче неизвестных величин, через которую сравнительно нетрудно
выразить О.В.,примите ее за независимую переменную (Н.П.)
и обозначьте ее буквой x. Установите реальные границы изменения Н.П.,
т. е. область определения для искомой О.В.

3) Исходя из
условий задачи, выразите y через x. Математическая модель задачи
представляет собой функцию  y = f(x) с областью определения X,
которую нашли на втором шаге.

Второй этап. Работа
с математической моделью

На втором этапе для функции y=f(x), x ϵ X
найдите y_наим. или y_наиб.в зависимости от того, что
требуется найти в условии задачи.

Третий этап. Ответ
на вопрос задачи. Здесь следует дать
конкретный ответ на вопрос задачи, опираясь на результаты, полученные на этапе
работы с моделью

За­да­ние 17 № 508236. В 1-е клас­сы по­сту­па­ет 45 че­ло­век: 20 маль­чи­ков и 25 де­во­чек.
Их рас­пре­де­ли­ли по двум клас­сам: в одном долж­но по­лу­чить­ся 22 че­ло­ве­ка,
а в дру­гом ― 23. После рас­пре­де­ле­ния по­счи­та­ли про­цент де­во­чек в каж­дом
клас­се и по­лу­чен­ные числа сло­жи­ли. Каким долж­но быть рас­пре­де­ле­ние
по клас­сам, чтобы по­лу­чен­ная сумма была наи­боль­шей?

За­да­ние
17 № 513301. В двух об­ла­стях есть по 160 ра­бо­чих,
каж­дый из ко­то­рых готов тру­дить­ся по 5 часов в сутки на до­бы­че алю­ми­ния
или ни­ке­ля. В пер­вой об­ла­сти один ра­бо­чий за час до­бы­ва­ет 0,1 кг алю­ми­ния
или 0,1 кг ни­ке­ля. Во вто­рой об­ла­сти для до­бы­чи x кг алю­ми­ния в
день тре­бу­ет­ся x² че­ло­ве­ко-часов труда, а для до­бы­чи у
кг ни­ке­ля в день тре­бу­ет­ся у² че­ло­ве­ко-часов труда.

Для нужд про­мыш­лен­но­сти можно
ис­поль­зо­вать или алю­ми­ний, или ни­кель, причём 1 кг алю­ми­ния можно за­ме­нить
1 кг ни­ке­ля. Какую наи­боль­шую массу ме­тал­лов можно за сутки сум­мар­но до­быть
в двух об­ла­стях?

Слайд 1

Финансовые задачи на оптимальный выбор ( № 17 ЕГЭ профильного уровня) Подготовила : Быкова М.Г. , учитель математики МКОУ Купреевской СОШ

Слайд 2

Задача №1 У фермера есть два поля, каждое площадью 10 га. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 500 ц /га , а на втором – 300 ц /га . Урожайность свёклы на первом поле составляет 300 ц /га , а на втором – 500 ц /га . Фермер может продавать картофель по цене 5 000 р / ц , а свёклу – по цене 8 000 р / ц . Какой наибольший доход может получить фермер? Решение 1 поле Площадь Урожай Выручка картофель (10 — х ) га 500 ц / га 500*5000* (10 — х ) = 25 000 000 – 2 500 000х рублей свёкла х га 300 ц / га 300*8000* х = 2 400 000х рублей Всего 25 000 000 – 2 500 000х +2 400 000 = 25 000 000 – 100 000х 2 поле Площадь Урожайность Выручка картофель 300 ц / га свёкла 10 га 500 ц / га 10*500*8000 = 40 000 000 рублей

Слайд 3

Выручка 25 000 000 – 100 000х будет наибольшей если х = 0. Следовательно выручка с 1 поля равна 25 000 000 рублей. Наибольший доход = 40 000 000 + 25 000 000 = 65 000 000 рублей Ответ : 65 000 000 рублей В двух областях работают по 160 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,1 кг алюминия или 0,3 кг никеля. Во второй области для добычи x кг алюминия в день требуется x 2 человеко-часов труда, а для добычи у кг никеля в день требуется y 2 человеко-часов труда. Для нужд промышленности можно использовать или алюминий, или никель, причём 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно добыть в двух областях суммарно для нужд промышленности? Задача №2

Слайд 4

1 область Кол-во раб 160 чел 5 час / сутки доб . за час Al Ni 0 , 1 кг 0 , 3 кг 160*5*0 ,3=240 кг 2 область Кол-во раб 160 чел 5 час / сутки Al Ni x кг треб . x 2 чел / часов у кг треб. y 2 чел / часов m чел ( 160- m) чел X 2 = 5m y 2 = 5*(160-m) Масса доб . металла X=√ 5 m Y=√5(160-m) f(m)= √5m +√5(160-m) f(80)= 20 + 20 = 40 кг f`(m)=0 √ (800-5m) — √5m= 0 10m=800 m=80 Общая масса доб.металла = 240 + 40 = 280 кг. Ответ : 280 кг.

Слайд 5

В двух шахтах добывают алюминий и никель. В первой шахте имеется 20 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1 кг алюминия или 2 кг никеля. Во второй шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 2 кг алюминия или 1 кг никеля. Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод? Задание № 3 Al Ni Кол- во раб. Кол- во мет . Кол- во раб. Кол- во мет . 1 шахта х 5x 20 — x 2*5*(20-x)= 200-10x 2 шахта y 2*5*y = 10y 100 — y 1*5*(100-y) = 500 – 5y Всего 5 x+10y 200-10x+500-5y =700 – 10x -5y

Слайд 6

5x+10y = 2 (700-10x-5y) 5x+10y +20x+10y = 1400 25x+20y = 1400│: 5 5x +4y = 280 x=56 – 4/5y y = 70 – 5/4x СПЛАВ = 3 (700 -10 x – 5y ) = 2100 – 30x -15y СПЛАВ = 2100 – 30 (56 – 4/5y) – 15y = 2100 – 1680 +24y -15y = 420 + 9y При x = 0, у будет max. y = 70 Сплав = 420 + 9 *70 = 1050 кг. Ответ : 1050 кг.

Слайд 7

Задание №4 Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 30 квадратных метров и номера «люкс» площадью 40 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 940 квадратных метров. Предприниматель может определить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 4000 рублей в стуки, а номер «люкс» — 5000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель? Кол-во Площадь(кв.м) Стоимость в сутки стандартные X 30 4000 люкс y 40 5000 30 x + 40y ≤ 940 4000x+5000y 30 x + 40y ≤ 940 │: 10 3x +4y ≤ 94 S = 4000x+5000y = 1000 (4x +5y) S зависит от (4 x + 5y ) S = 4 x + 5y x = 0,25S -1, 25 y 3 (0,25S – 1,25y) +4y ≤ 94 0,75S – 3,75y + 4y ≤ 94 0,75S +0,25y≤94 0,75S ≤ 94 – 0,25y

Слайд 8

При у=0 31 стандартный номер 31* 4000 = 124000 рублей При y = 1 30 стандартных номеров и 1 люкс 30*4000 + 1*5000 = 125000 рублей При y = 2 28 стандартных номеров и 2 люкса 28*4000 +2* 5000 = 122000 рублей Ответ : 125000 рублей

Слайд 9

Задание №5 Производство x тыс. единиц продукции обходится в q = 0,5 x 2 + x + 7 млн рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет px − q . При каком наименьшем значении p через три года суммарная прибыль составит не менее 75 млн рублей? Решение Затраты q = 0,5 x 2 + x + 7 Прибыль px − q px — 0,5 x 2 — x — 7 0,5 x 2 + x (p — 1) – 7 X=-b/2a x = — (p-1)/2*(-0,5) x = p – 1 Y = — 0,5 (p-1) 2 + (p-1) 2 — 7 = 0,5 (p-1) 2 — 7 за 1 год за 3 года : 3 * (0,5 (p-1) 2 — 7 )≥ 75 (0,5 (p-1) 2 — 7 ) ≥ 75 : 3 0,5 (p-1) 2 — 7 ≥ 25 0,5 (p-1) 2 ≥ 32 (p-1) 2 ≥ 64 (p – 9)(p+7) ≥ 0 p≥ 9 Ответ : 9 тыс.руб

Слайд 10

СПАСИБО ЗА ВНИМАНИЕ!!!