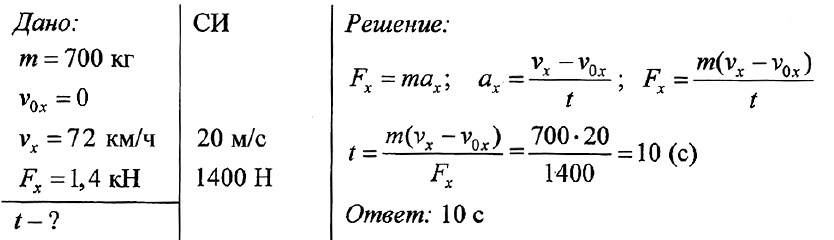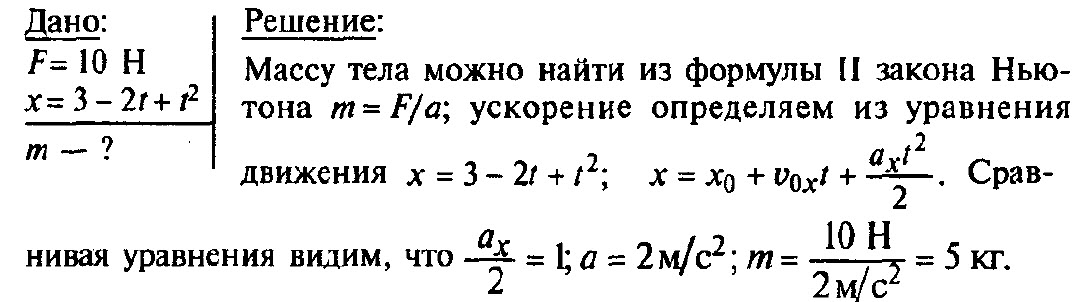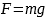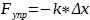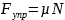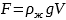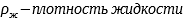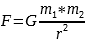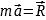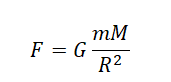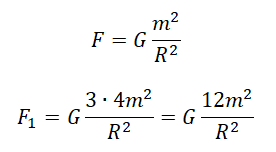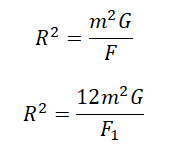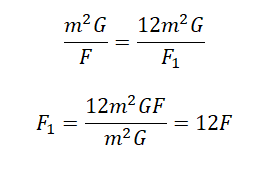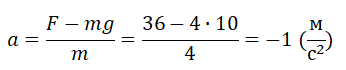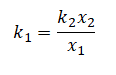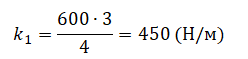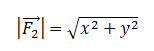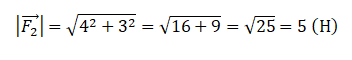Задачи на второй закон ньютона егэ

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

ЕГЭ11
ФИЗИКА Задание №2  Второй закон Ньютона. Равнодействующая сил.

№1На полу
лифта, разгоняющегося вверх с постоянным ускорением  1м/с2 лежит груз
массой 5 кг.  Каков вес этого груза? Ответ выразите в ньютонах.

№2 Четыре одинаковых кирпича массой 3 кг
каждый сложены в стопку (см. рисунок). На сколько увеличится сила N действующая со стороны горизонтальной опоры на 1-й
кирпич, если сверху положить ещё один такой же кирпич? Ответ выразите в
ньютонах.

№3Материальная точка массой 2 кг движется
вдоль горизонтальной оси Ox под действием горизонтальной
силы F. В начальный момент времени тело покоилось. График
зависимости силы F от времени t изображён на
рисунке. Чему равен импульс материальной точки в конце второй секунды? (Ответ
дайте в кг·м/с.)

№4Тело массой 2 кг движется вдоль оси Ox.
На рисунке представлен график зависимости проекции скорости υx этого тела от
времени t. Чему равен модуль проекции силы F_x,
действующей на это тело в течение первой секунды? (Ответ дайте в ньютонах.)

№5Точечное тело движется по гладкой
горизонтальной поверхности под действием постоянной горизонтальной силы,
направленной вдоль оси Ox. Известно, что проекция импульса этого
тела на указанную ось изменяется со временем по закону:  Чему равен модуль силы, действующей на это тело? (Ответ дайте в ньютонах.)

№6Точечное тело массой 0,5 кг свободно
движется по гладкой горизонтальной плоскости параллельно оси Ox со
скоростью V = 4 м/с (см. рисунок, вид сверху). В момент
времени t = 0, когда тело находилось в точке A, на
него начинает действовать сила  F модуль
которой равен 1 Н. Чему равна координата этого тела по оси Ох в
момент времени t = 4 с? (Ответ дайте в метрах.)

№7

№8
Лифт массой 800 кг, закрепленный на
тросе, поднимается вертикально вверх. На рисунке изображен график зависимости
модуля скорости  лифта v от
времени t Чему равна сила натяжения троса? Ответ
выразите в ньютонах. Ускорение свободного падения примите равным 10 м/с².

№9 На тело, находящееся на горизонтальной
плоскости, действуют три горизонтальные силы (см. рисунок, вид сверху). Каков
модуль равнодействующей этих сил, если F1=1H (Ответ дайте в ньютонах и округлите до
десятых.)

№10Под действием одной силы F₁ тело
движется с ускорением 4 м/с². Под действием другой силы F₂,
направленной противоположно силе F₁, ускорение тела
равно 3 м/с². С каким ускорением тело будет двигаться при
одновременном действии сил F₁ и F₂?
(Ответ дайте в метрах в секундах в квадрате.)

№11На рисунке представлены три вектора сил, лежащих
в одной плоскости и приложенных к одной точке. Масштаб
рисунка таков, что сторона одного квадрата сетки соответствует модулю силы
1 H. Определите модуль вектора равнодействующей трех векторов сил. (Ответ
дайте в ньютонах.)

№12Тело массой 6 кг движется вдоль оси Ox.
В таблицу приведена зависимость проекции

скорости v_x этого тела
от времени t. Считая равнодействующую всех сил, приложенных к телу,
постоянной, определите, чему равна проекция этой равнодействующей на ось Ox.
(Ответ дайте в ньютонах.)

№13Тележка массой 0,1 кг удерживается на наклонной плоскости с
помощью нити (см. рисунок).

Чему равна сила натяжения нити? (Ответ дайте в
ньютонах.)

№14 К бруску массой m₁ = 5 кг,
находящемуся на закреплённой наклонной шероховатой плоскости, приложена
сила F = 10 Н, направленная вдоль плоскости, как показано
на рисунке. При этом брусок движется вверх с ускорением. На какую величину
изменится ускорение бруска, если, не изменяя модуля и направления силы  заменить
брусок на другой — из того же материала, но массой m₂ = 0,4 m₁? Ответ выразите в м/с².

Ответы:

1	2	3	4	5	6	7	8	9	10
55	2	30	1	8	4	17	5	7840	500
11	12	13	14
3,2	5	1	10

Задачи на Законы Ньютона с решениями

Формулы, используемые на уроках «Задачи на Законы Ньютона с решениями».

Название величины	Обозначение	Единица измерения	Формула
Масса	m	кг	m = Fx / ax
Ускорение (проекция на ось х)	ax	м/с2
Сила (проекция на ось х)	Fx	Н	Fx = m ax

---

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

---

Задача № 1.
 Какое ускорение приобретет тело массой 500 г под действием силы 0,2 Н?

---

Задача № 2.
 Сила 30 Н сообщает телу ускорение 0,4 м/с. Какая сила сообщит тому же телу ускорение 2 м/с² ?

---

Задача № 3.
 Какую скорость приобретает тело массой 3 кг под действием силы, равной 9 Н, по истечении 5 с?

---

Задача № 4.
 Сколько времени потребуется автомобилю массой 700 кг, чтобы разогнаться из состояния покоя до скорости 72 км/ч, если сила тяги двигателя 1,4 кН?

---

Задача № 5.
 Поезд массой 500 т, трогаясь с места, через 25 с набрал скорость 18 км/ч. Определите силу тяги.

---

Задача № 6.
 Под действием постоянной силы, равной 10 Н, тело движется прямолинейно так, что зависимость координаты тела от времени описывается уравнением х = 3 — 2t + t2. Определите массу тела.

---

Задача № 7.
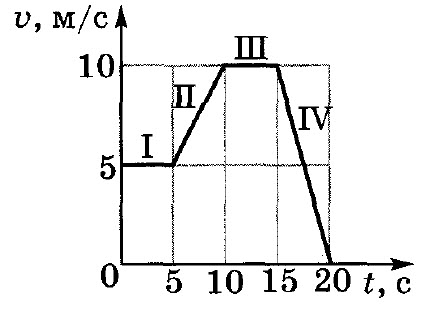
 Скорость тела массой 2 кг изменяется со временем так, как представлено на графике рисунка.

Найдите силу, действующую на каждом этапе этого движения. Определите по графику, на каком этапе движения тело прошло наибольший путь.

---

Задача № 8. (повышенной сложности)
 Начальная скорость тела, находящегося в точке А, равна нулю. В течение 8 с на тело действует постоянная сила. Затем направление силы изменяется на противоположное, а модуль остается прежним. Через какое время от начала движения тело вернется в точку А?

Ответ: через 27 с.

---

Задача № 9. (повышенной сложности)
 Самолет массой 14 т, пройдя по взлетной полосе путь 600 м, приобретает необходимую для отрыва от поверхности Земли скорость 144 км/ч. Считая движение равноускоренным, определите время разгона, ускорение и силу, сообщающую самолету это ускорение.

---

Задача № 10.
  ОГЭ
 Вагон массой m = 20 т движется равнозамедленно с ускорением а = 0,3 м/с² и начальной скоростью v₀ = 54 км/ч. Найти силу торможения, действующую на вагон, время его движения до полной остановки и путь, пройденный за это время.

---

Задача № 11.
   ЕГЭ
 Два тела массами m₁ = 1 кг и m₂ = 2 кг, находящиеся на гладкой горизонтальной поверхности, связаны нерастяжимой нитью. Ко второму телу в горизонтальном направлении приложена сила F = 10 Н. Найти ускорение а, с которым движутся оба тела, и силу Т натяжения нити.

---

Пояснения для решения задачи на Законы Ньютона с решениями.

Раздел механики, изучающий законы Ньютона, называется динамикой. Если при изучении кинематики рассматривается вопрос: как тело движется (равномерно, равноускоренно и т. д.), то динамика дает ответ: почему тело движется так, а не иначе.

I закон Ньютона говорит о состоянии покоя или равномерного прямолинейного движения.

Если . Существуют такие системы отсчета, относительно которых тело сохраняет свою скорость неизменной, если на него не действуют другие тела (или их действие скомпенсировано), (или равнодействующая всех сил, действующих на тело, равна нулю).

II закон Ньютона говорит о движении тела с ускорением.

Если 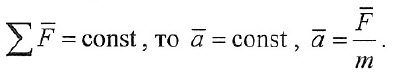Если на тело действует постоянная сила (или несколько сил), то тело движется с постоянным ускорением. Причем ускорение тела прямо пропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе. Вектор ускорения сонаправлен с вектором равнодействующей сил.

При решении простых задач, где на тело действует только одна сила, можно применять формулу сразу. Если же на тело действует несколько сил, то нужно делать чертеж и геометрическим путем определять направление равнодействующей сил.

III закон Ньютона говорит о взаимодействии тел.

Силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению.

Особенности сил:

1. Силы появляются парами.
2. Силы одной природы.
3. Силы приложены к разным телам, поэтому не могут уравновешивать друг друга.

Например, Земля притягивает к себе тело массой 1 кг с силой 9,8 Н. Камень точно с такой же силой притягивает к себе Землю. Однако ускорения эти тела приобретают различные, так как у них разные массы. Камень получает большое ускорение вследствие своей малой массы, а Земля получает мизерное ускорение вследствие своей огромной массы.

Задачи на Законы Ньютона повышенной сложности — это задачи на движение тела под действием нескольких сил: по наклонной плоскости, движение связанных тел и т. д.

---

Это конспект по теме «ЗАДАЧИ на Законы Ньютона с решениями». Выберите дальнейшие действия:

• Перейти к теме: ЗАДАЧИ на применение Закона всемирного тяготения
• Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
• Вернуться к списку конспектов по Физике.
• Проверить свои знания по Физике.

Предлагаю решение нескольких задач из книги «Отличник ЕГЭ. Физика. Решение сложных задач». Возможно, в дальнейшем на сайте появятся и решения других задач из этой книги. Задачи интересные, и все как одна «решабельные», то есть никаких подвохов в них нет.

Задача 1.

Шайба, брошенная вдоль наклонной плоскости, скользит по ней, двигаясь вверх, а затем движется вниз. График зависимости модуля скорости шайбы от времени дан на рисунке. Найти угол наклона плоскости к горизонту.

Так как  график составлен из двух отрезков прямых, то ускорение шайбы постоянно на обоих отрезках. Определим его. При движении вверх скорость шайбы изменилась с 6 м/с до 0 за 4 с, следовательно, ускорение равно м/с. На пути вниз скорость шайбы с нуля доросла до 4 м/с за 4 с, следовательно, ускорение равно м/с.

Реакция опоры при движении шайбы равна

От реакции опоры напрямую зависит сила трения. Запишем уравнение по второму закону Ньютона для движения шайбы вверх (сразу учтем, что ускорение отрицательно, поскольку шайба тормозит):

Запишем уравнение по второму закону Ньютона для движения шайбы вниз:

Складывая  уравнения, имеем:

Откуда

Ответ: .

Задача 2.

Два шарика одинакового диаметра, имеющие массы г и г, связаны между собой легкой нерастяжимой нитью, длина которой значительно превышает диаметр шариков. Шарики сбросили с достаточно большой высоты. Спустя некоторое время после этого вследствие сопротивления воздуха скорость падения шариков стала постоянной. Найти натяжение нити Т при установившемся падении шариков. Ускорение свободного падения м/с .

Шарики при падении «выстроятся»: снизу расположится более тяжелый, за ним «потянется» более легкий. «Потянется» в прямом смысле, посредством нити.

Для первого шарика уравнение для установившегося движения:

Для второго шарика:

Складывая, имеем:

Подставим в любое уравнение полученную силу сопротивления:

Ответ: Н.

Задача 3.

Два одинаковых груза массой кг  связаны между собой нитью, перекинутой через блок с неподвижной осью. На один из грузов кладут перегрузок массой кг. С какой силой Р будет давить перегрузок на груз ? Массой блока и нити, а также трением в оси блока пренебречь, нить считать нерастяжимой‚ ускорение свободного падения принять равным м/с.

Запишем уравнение по второму закону для груза с перегрузком:

Для груза без перегрузка:

Из второго уравнения имеем :

Подставим в первое:

Теперь, зная ускорение, легко отыщем силу давления перегрузка на груз:

Ответ: .

Задача 4.

В системе, показанной на рисунке, грузы массами кг и кг прикреплены к концам невесомой нерастяжимой нити. На такой же нити, один конец которой закреплен, а другой прикреплен к грузу массой ,  висит подвижный блок. К оси этого блока на легких нерастяжимых нитях подвешен груз массой кг. Отрезки нитей, не лежащие на блоках, вертикальны. Пренебрегая трением и массой блоков, найти модуль и направление ускорения груза .  Ускорение свободного падения принять равным м/с.

Это одна из задач, решение которых строится на факте нерастяжимости нити. Именно этот факт будет важен, так как решение будем основывать на том, что сумма путей, пройденных грузами, постоянна, и максимально равна длине нити. Пусть координаты грузов по оси , и соответственно. Пусть в некоторый момент времени их координаты стали , и . Путь, пройденный телом 1:

А нить при этом «сократилась» на .

Путь, пройденный телом 2:

А нить при этом «сократилась» на .

Путь, пройденный телом 3:

А нить при этом «удлинилась» на .

Запишем пути, пройденные телами, через их ускорения:

Можно записать, что

Следовательно, ускорения тел 2 и 3 одинаковы, , а у тела 1 тогда .

Теперь можно перейти к динамике. Запишем уравнения по второму закону Ньютона для всех тел. При этом обратим внимание, что разные участки нити будут по-разному натянуты. Это происходит из-за наличия груза 2, он является своеобразным «перегрузком»:

Перейдем везде к ускорению , ведь оно – искомое:

Из последнего уравнения

А из первого

Тогда, подставляя все во второе, получим:

«Минус» указывает направление ускорения: оно направлено вверх, против .

Ответ: м/с, направлено вверх.

Задача 5.

Через гладкий блок, закрепленный на гладкой неподвижной наклонной  плоскости, составляющей с горизонтом угол , перекинута легкая нерастяжимая нить. Один конец нити прикреплен к бруску массой кг, лежащему на плоскости, а свисающий конец пропущен через узкое отверстие в грузе массой кг, как показано  на рисунке. Если одновременно отпустить брусок и груз, нить будет проскальзывать через отверстие с постоянным ускорением м/с относительно груза. Найти силу натяжения нити. Ускорение свободного падения принять равным м/с.

Запишем уравнение по второму закону для обоих грузов:

Теперь определимся с ускорениями: так как нить проскальзывает относительно груза , то

Тогда, подставляя силу натяжения нити, имеем:

Теперь можно определять силу натяжения:

Ответ: Н

Задача 6.

Маленькую шайбу массой г запустили со скоростью м/с в направлении по касательной к внутренней поверхности находящейся в невесомости сферы массой г и радиусом м. Найдите модуль силы, действующей на шайбу со стороны сферы. Трение отсутствует, сфера вначале покоилась.

По закону сохранения импульса

Если перейти в систему отсчета «сфера», то скорость шайбы в ней будет равна

Известно, что при движении по окружности угловая скорость такого движения равна  , следовательно,

Угловая скорость через период:

Период – время одного оборота:

Следовательно,

Аналогично

Теперь можем найти, с какой силой шайба будет давить на сферу:

Ответ: Н.

Задача 7.

 На горизонтальном диске на расстоянии см от оси лежит маленькая шайба. Диск медленно раскручивают так, что его угловая скорость равномерно возрастает со временем. Через время с после начала раскручивания шайба начала скользить по диску. Найти коэффициент трения шайбы о диск, если за время диск сделал оборотов.

Сила трения удерживает шайбу от соскальзывания. Однако диск разгоняется, следовательно, есть тангенциальное ускорение, и скорость  шайбы растет, что вызывает рост нормального ускорения. Наконец, общее ускорение становится столь большим, что сила, им обусловленная, превышает силу трения, и шайба соскальзывает.

Условие соскальзывания

Где .

Выясним, каковы нормальное и тангенциальное ускорения.

Скорость шайбы растет и становится равной к моменту соскальзывания. Угловая скорость становится равной за то же время. Тогда

Путь, пройденный телом – пять кругов – равен .

Угловая скорость определяет, какой угол преодолело тело за промежуток времени. У нас пять кругов, следовательно, тело прошло радиан за время , тогда

Нормальное ускорение тела

В свою очередь, полное ускорение равно

Тогда

Ответ: .

2 комментария

Из последних КИМов ЕГЭ по физике следует, что задание 2 относится к разделу «Динамика» и может содержать расчетные задачи по следующим темам: «Законы Ньютона, закон всемирного тяготения, закон Гука, сила трения».

Основные формулы, которые необходимо знать для успешного решения задания 2.

Сила тяжести		m — масса тела g=10 м/с2 – ускорение свободного падения
Сила упругости		Δx – удлинение пружины k – коэффициент жесткости пружины
Сила трения		µ — коэффициент трения N – сила реакции опоры
Сила Архимеда (выталкивающая сила)		V – объём погруженной части тела g=10 м/с2 – ускорение свободного падения
Сила притяжения между телами (закон Всемирного тяготения)		G = 6,67*10-11 Н*м2/кг2 – гравитационная постоянная m1 и m2 — массы взаимодействующих тел r – расстояние между телами
Второй закон Ньютона		m – масса тела R – равнодействующая всех сил, действующих на тело a – ускорение, с которым движется тело под действием этих сил

Алгоритм решения

При решении задач из раздела «Динамика» желательно придерживаться следующего алгоритма решения:

1. Сделать рисунок, на котором указать вектора всех сил, действующих на тело.

2. Если тело двигается с ускорением, указать направление этого ускорения. Если тело покоится или двигается равномерно, его ускорение a=0.

3. Составить уравнение движения (второй закон Ньютона) для рассматриваемого тела в его векторном виде.

3. Выбрать систему координат и спроецировать полученное уравнение на выбранные оси координат.

4. Расшифровать неизвестные величины, вошедшие в уравнение движения.

5. Решить полученную систему уравнений.

Задание 2
– это расчётные задачи базового уровня сложности, и для решения некоторых из них этот алгоритм будет чересчур подробным и перегруженным, так как их можно решить и без вспомогательного рисунка или даже без записи второго закона Ньютона. Это касается, например, заданий, в которых на тело действует только одна сила. Но привычка решать задания по приведенному выше алгоритму поможет ученикам успешно справиться с расчетными задачами по разделу «Динамика» повышенного и высокого уровней сложности – такие задания могут стоять в ЕГЭ под номерами 25 и 29.

Ответом на задание 2 является число, именно его нужно вписать в бланк ответов 1, не указывая единицы измерения.

Примеры решения с разбором

Пример решения 2 задания по физике (ЕГЭ-2019)

Пружина жёсткостью 2*10⁴
Н/м одним концом закреплена в штативе. На какую величину она растянется под действием силы 400 Н?

Ответ: ___________________________ см.

Решение:

Сделаем чертёж

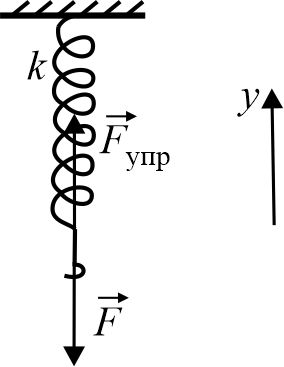
Пружина под действием силы F
привели в растянутое состояние. Кроме растягивающей силы F
и силы упругости
, стремящейся вернуть пружину в нерастянутое состояние, больше никакие силы на нее не действуют.

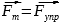
Запишем проекции сил на вертикальную ось Oy

F=F_упр

По закону Гука, сила упругости F_упр = k
*Δx, следовательно,

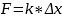
k
— коэффициент жёсткости пружины, Δx
– её удлинение.

Выразим величину растяжения пружины

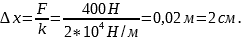
Ответ: 2

Пример решения 2 задания по физике (ЕГЭ – 2020. Вариант 1 досрочного ЕГЭ)

Тело движется по горизонтальной плоскости. Нормальная составляющая силы воздействия тела на плоскость равна 40 Н, сила трения равна 10 Н. Определите коэффициент трения скольжения.

Ответ: _______ .

Решение:

Силу трения можно найти по формуле

F_тр= µN,

где N – сила реакции опоры, или по-другому нормальная составляющая силы воздействия тела на плоскость.

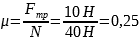
Ответ: 0,25.

Пример решения 2 задания по физике (ЕГЭ – 2020. Демонстрационный вариант)

Два одинаковых маленьких шарика массой m каждый, расстояние между центрами которых равно r, притягиваются друг к другу с силами, равными по модулю 0,2 пН. Каков модуль сил гравитационного притяжения двух других шариков, если масса каждого из них равна 2m, а расстояние между их центрами равно 2r?

Ответ: _______ пН.

Решение:

По закону Всемирного тяготения шары массами m₁и m₂, находящиеся друг от друга на расстоянии r,
притягиваются друг к другу с силой

.

В первом случае

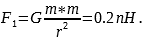
Во втором случае

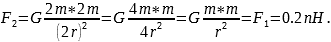
Ответ: 0,2

Пример решения 2 задания по физике (ЕГЭ – 2019. Демонстрационный вариант)

По горизонтальному полу по прямой равномерно тянут ящик, приложив к нему горизонтальную силу 35 Н. Коэффициент трения скольжения между полом и ящиком равен 0,25. Чему равна масса ящика?

Ответ _______ кг.

Решение:

Сделаем чертёж, на котором обозначим все силы, действующие на тело.

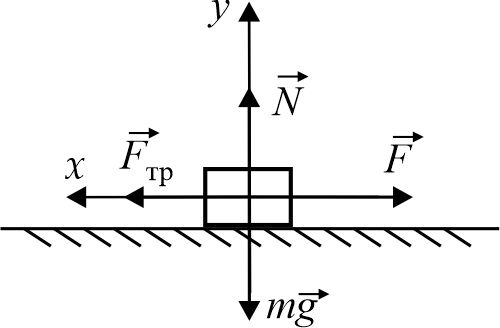
По второму закону Ньютона, равнодействующая всех сил, действующих на тело, будет равна нулю, так как по условию задачи тело движется равномерно, то есть ускорение тела a=0.

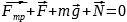
Запишем это в проекциях на оси Ox и Oy

Ox: F_тр
– F = 0,

Oy: N — m g=0.

Откуда N = mg, следовательно,

F_тр = µ N = µ mg.

Масса тела

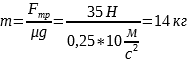
Ответ: 14

Пример решения 2 задания по физике (ЕГЭ – 2018)

К пружине подвесили груз массой 150 г, вследствие чего пружина удлинилась на 1 см. Чему будет равно удлинение этой пружины, если к ней подвесить груз 450 г?

Ответ: __________ см.

Решение:

Переведём единицы измерения физических величин в систему СИ

m₁ = 150 г = 0,15 кг, m₂ = 450 г = 0,45 кг, Δx=1 см = 0,01 м.

Сделаем чертёж, на котором обозначим все силы, действующие на тело.

На тело действует сила тяжести (F_т
= mg), направленная вертикально вниз, и сила упругости со стороны пружины (F_упр
= k Δx), направленная вертикально вверх.

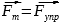
В проекции на вертикальную ось Oy.

F_т
=F_упр

mg = kΔx (1)

k
— коэффициент жёсткости пружины, Δx
– её удлинение.

Найдём, чему равен коэффициент жёсткости пружины

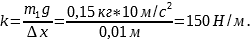
Выразим из выражения (1) удлинение пружины во втором случае

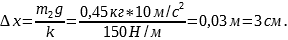
Ответ: 3

Во втором задании ЕГЭ по физике необходимо решить задачу на законы ньютона или связанную с действием сил. Ниже мы приводим теорию с формулами, которые необходимы для успешного решения задач по этой тематике.

Задание EF17569

Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Чему равен модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами такое же, как и в первом случае, а массы звёзд равны 3m и 4m?

а) 7F

б) 9F

в) 12F

г) 16F

---

Алгоритм решения

1.Записать закон всемирного тяготения.

2.Применить закон всемирного тяготения для первой и второй пары звезд.

3.Из каждого выражения выразить расстояние между звездами.

4.Приравнять правые части уравнений и вычислить силу притяжения между второй парой звезд.

Решение

Закон всемирного тяготения выглядит так:

Примерим этот закон для первой и второй пары звезд:

Выразим квадраты радиусов, так как они в обоих случаях одинаковые:

Приравняем правые части выражений и выразим силу притяжения во втором случае:

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18738

Человек массой 80 кг с сумкой весом 100 Н стоит неподвижно на полу. Сила давления подошв его ботинок на пол равномерно распределена по площади 600 см². Какое давление человек оказывает на пол?

---

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Выполнить решение в общем виде.

3.Вычислить искомую величину, подставив исходные данные.

Решение

Запишем исходные данные:

• Масса человека: m = 80 кг.

• Вес сумки, которую держит человек: P_c = 100 Н.

• Площадь соприкосновения подошвы ботинок с полом: S = 600 кв. см.

600 кв. см = 600/10000 кв. м = 0,06 кв. м

Давление — это отношение силы к площади, на которую она действует. В данном случае на площадь действует сила, равная сумме силы тяжести человека и веса сумки:

F = mg + P_c

Поэтому давление, оказываемое человеком с сумкой на пол, равно:

P=mg+PCS=80·10+1000,06=15000 (Па)

Ответ: 15000

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF19052

Кирпич массой 4 кг лежит на горизонтальной кладке стены, покрытой раствором, оказывая на неё давление 1250 Па. Какова площадь грани, на которой лежит кирпич? Ответ запишите в квадратных сантиметрах.

---

Алгоритм решения

1.Записать исходные данные.

2.Выполнить решение в общем виде.

3.Вычислить искомую величину, подставив исходные данные.

Решение

Запишем исходные данные:

• Масса кирпича: m = 4 кг.

• Давление, оказываемое кирпичом на раствор: P = 1250 Па.

Площадь можно выразить из формулы давления твердого тела. Она будет равна:

S=FP

В данном случае под силой будет подразумеваться сила тяжести кирпича. Поэтому:

S=mgP=4·101250=0,032 (м2)=320 (см2)

Ответ: 320

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17624

Подъёмный кран поднимает груз с постоянным ускорением. На груз со стороны каната действует сила, равная по величине 8⋅10³ H. На канат со стороны груза действует сила, которая:

а) 8∙10³ Н

б) меньше 8∙10³ Н

в) больше 8∙10³ Н

г) равна силе тяжести, действующей на груз

---

Алгоритм решения

1.Сформулировать третий закон Ньютона.

2.Применить закон Ньютона к канату и грузу.

3.На основании закона сделать вывод и определить силу, которая действует на канат со стороны груза.

Решение

Третий закон Ньютона формулируется так:

«Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны».

Математически он записывается так:

F_A = –F_B

Если на груз со стороны каната действует некоторая сила, то и груз действует на канат с этой силой, которая называется весом этого груза, или силой натяжения нити. Следовательно, груз действует на канат с силой 8∙10³ Н.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF22586

Мальчик медленно поднимает гирю, действуя на неё с силой 100 Н. Гиря действует на руку мальчика с силой:

а) больше 100 Н, направленной вниз

б) меньше 100 Н, направленной вверх

в) 100 Н, направленной вниз

г) 100 Н, направленной вверх

 

---

Алгоритм решения

1.Записать исходные данные.

2.Сделать чертеж, иллюстрирующий ситуацию.

3.Записать второй закон Ньютона в векторной форме.

4.Записать второй закон Ньютона в виде проекций.

5.Вычислить силу, с которой гиря действует на руку мальчика.

Решение

Запишем исходные данные: мальчик поднимает гирю вверх с силой F = 100 Н.

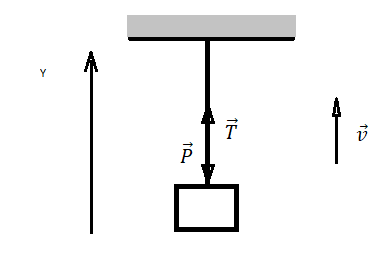
Сделаем рисунок. В данном случае рука мальчика выступает в роли подвеса. Так как мальчик поднимает гирю медленно, можно считать, что он поднимает ее равномерно (равнодействующая всех сил равна нулю). Выберем систему координат, направление оси которой совпадает с направлением движения руки и гири.

На руку (подвес) действуют только две силы. Поэтому второй закон Ньютона выглядит следующим образом:

P + T = 0

Запишем этот же закон в проекции на ось ОУ:

–P + T = 0

Отсюда:

P = T

Следовательно, на руку мальчика действует вес гири, который по модулю равен силе, с которой мальчик действует на эту гирю.

Внимание! Существует второй способ решения задачи через третий закон Ньютона. Согласно ему, тела действуют друг на друга с силами, равными по модулю, но противоположными по направлению.

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17555

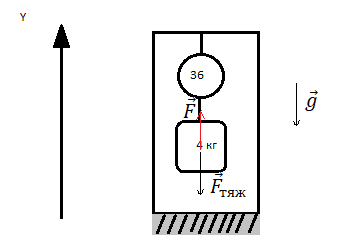
Груз массой 4 кг подвешен к укреплённому в лифте динамометру. Лифт начинает спускаться с верхнего этажа с постоянным ускорением. Показания динамометра при этом равны 36 Н. Чему равно и куда направлено ускорение лифта?

а) 1 м/с², вниз

б) 1 м/с², вверх

в) 9 м/с², вниз

г) 9 м/с², вверх

---

Алгоритм решения

1.Записать исходные данные.

2.Сделать чертеж с указанием известных сил, действующих на груз, их направлений и выбором системы координат.

3.Определить, какая сила действует на тело.

4.Записать второй закон Ньютона в векторной форме.

5.Записать второй закон Ньютона в виде проекций на оси.

6.Выразить из формулы проекцию ускорения лифта и рассчитать ее.

7.По знаку проекции ускорения лифта определить, в какую сторону оно направлено.

Решение

Запишем исходные данные:

• Масса груза равна: m = 4 кг.

• Показания динамометра во время спуска: F = 36 Н.

Сделаем чертеж:

Направление силы, действующей на тело, обратно силе, которую оказывает тело на подвес в виде динамометра. Поэтому сила F равна по модулю весу тела во время спуска, но направлена противоположно ему (вверх). Направление ускорения лифта пока остается неизвестным.

Второй закон Ньютона в векторной форме:

F + mg = ma

Второй закон Ньютона в виде проекции сил на ось ОУ:

F – mg = ma

Выразим отсюда ускорение лифта и вычислим его, подставив известные данные:

Перед проекцией ускорения стоит знак «–». Это значит, что оно направлено противопроложно оси ОУ (т.е. вниз).

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17589

Система отсчёта, связанная с Землёй, считается инерциальной. В этом случае систему отсчёта, связанную с самолётом, можно считать инерциальной, если самолёт движется:

а) равномерно и прямолинейно, набирая высоту

б) с постоянным ускорением по горизонтали

в) равномерно, выполняя поворот

г) по взлетной полосе при взлете

---

Алгоритм решения

1. Сформулировать первый закон Ньютона об инерциальных системах отсчета.
2. На основании закона сделать вывод, при каких условиях система отсчета, связанная с самолетом, может считаться инерциальной.
3. Проанализировать все 4 ситуации, приведенные в вариантах ответа.
4. Выбрать тот вариант, который описывает ситуацию, не противоречащую условию, выведенному в шаге 2.

Решение

Первый закон Ньютона формулируется так:

«Существуют такие системы отсчета, называемые инерциальными, относительно которых тела движутся равномерно и прямолинейно или находятся в состоянии покоя, если на них не действуют другие тела или их действие компенсировано».

Чтобы система отсчета, связанная с самолетом, была инерциальной, она должна быть неподвижной или двигаться относительно Земли — инерциальной системы отсчета — равномерно и прямолинейно.

Когда самолет движется равномерно и прямолинейно, набирая высоту, самолет движется с собственным ускорением, которое компенсируется ускорением свободного падения. И это единственный верный ответ, так как:

• Самолет, двигаясь с постоянным ускорением по горизонтали, движется неравномерно, что противоречит условию.
• Самолет, двигаясь равномерно во время поворота, движется непрямолинейно (с центростремительным ускорением).
• Самолет, двигаясь по взлетной полосе при взлете, движется прямолинейно, но неравномерно, так как он разгоняется из состояния покоя.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17484

Тело массой m скользит по шероховатой наклонной опоре с углом α к горизонту (см. рисунок). На него действуют 3 силы: сила тяжести mg, сила упругости опоры N и сила трения F_тр. Если скорость тела не меняется, то модуль равнодействующей сил F_тр и mg равен:

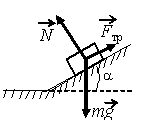
а) N cosα

б) N

в) N sinα

г) mg + F_тр

---

Алгоритм решения

1. Запись второго закона Ньютона в векторном виде.
2. Вывод формулы равнодействующей силы трения и силы тяжести.
3. Нахождение модуля равнодействующей силы трения и силы тяжести.

Решение

Записываем второй закон Ньютона в векторном виде с учетом того, сто скорость тела не меняется (ускорение равно 0):

N + mg + F_тр = 0

Отсюда равнодействующая силы трения и силы тяжести равна:

mg + F_тр = –N

Следовательно, равнодействующая силы трения и силы тяжести направлена противоположно силе реакции опоры, но равна ей по модулю. Отсюда:

|mg + F_тр| = N

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18489

Кубик массой 1 кг покоится на гладком горизонтальном столе, сжатый с боков пружинами (см. рисунок). Первая пружина сжата на 4 см, а вторая сжата на 3 см. Жёсткость второй пружины k₂ = 600 Н/м. Чему равна жёсткость первой пружины k₁?

---

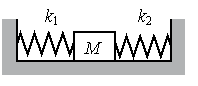
Алгоритм решения

1. Записать исходные данные.
2. Записать закон Гука.
3. Применить закон Гука к обеим пружинам.
4. Применить третий закон Ньютона.
5. Выразить жесткость первой пружины.
6. Вычислить искомую величину.

Решение

Запишем исходные данные:

• Сжатие первой пружины x₁ — 4 см.
• Сжатие второй пружины x₂ — 3 см.
• Жесткость второй пружины k₂ — 600 Н/м.

Запишем закон Гука:

F_упр = kx

Применим этот закон к обеим пружинам:

F_упр1 = k₁x₁

F_упр2 = k₂x₂

Силы упругости обеих пружин уравновешены, так как тело между ними покоится. Согласно третьему закону Ньютона:

F_упр1 = F_упр2

Отсюда:

k₁x₁ = k₂x₂

Выразим отсюда жесткость первой пружины:

Подставим известные данные и вычислим:

Внимание! В данном случае переводить единицы измерения в СИ не нужно. Отношение длин постоянно независимо от выбранной единицы измерения.

Ответ: 450

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18548

На тело действуют две силы: F₁ и F₂. По силе F₁ и равнодействующей двух сил F = F₁ + F₂ найдите модуль второй силы (см. рисунок).

---

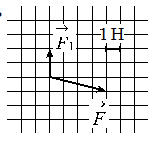
Алгоритм решения

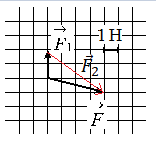
1. Изобразить на рисунке второй вектор с учетом правил сложения векторов.
2. Записать геометрическую формулу для расчета модуля вектора по его проекциям.
3. Выбрать систему координат и построить проекции второй силы на оси ОХ и ОУ.
4. По рисунку определить проекции второй силы на оси.
5. Используя полученные данные, применить формулу для расчета вектора по его проекциям.

Решение

Построим вектор второй силы. Его начало должно совпадать с концом вектора первой силы, а его конец — с концов равнодействующей этих сил. Этот вывод следует из сложения векторов правилом треугольника.

Модуль вектора равен корню из суммы квадратов его проекций на оси ОХ и ОУ:

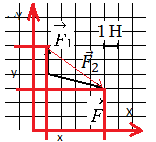
Выберем систему координат и построим проекции второй силы на оси ОХ и ОУ:

Согласно рисунку, проекция второй силы на ось ОХ равна: x = 4 (Н). Ее проекция на ось ОУ равна: y = 3 (Н).

Подставим известные данные в формулу и вычислим модуль вектора второй силы:

Ответ: 5

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17520

Две упругие пружины растягиваются силами одной и той же величины F. Удлинение второй пружины Δl₂ в 2 раза меньше, чем удлинение первой пружины Δl₁. Жёсткость первой пружины равна k₁, а жёсткость второй k₂ равна…

а) 0,25k₁

б) 2k₁

в) 0,5k₁

г) 4k₁

---

Алгоритм решения

1. Записать исходные данные.
2. Записать закон Гука.
3. Применить закон Гука к обеим пружинам.
4. Выразить величину жесткости второй пружины.

Решение

Записываем исходные данные:

• Первая и вторая пружины растягиваются под действием одной и той же силы. Поэтому: F₁ = F₂ = F.
• Удлинение первой пружины равно: Δl₁ = 2l.
• Удлинение второй пружины вдвое меньше удлинения первой. Поэтому: Δl₂ = l.

Закон Гука выглядит следующим образом:

F = k Δl

Применим закон Гука для обеих пружин:

F₁ = k₁ Δl₁

F₂ = k₂ Δl₂

Так как первая и вторая силы равны, можем приравнять правые части выражений. Получим:

k₁ Δl₁ = k₂ Δl₂

Перепишем выражение с учетом значения удлинений первой и второй пружин:

k₁ 2l = k₂ l

«l» в левой и правой частях выражения взаимоуничтожаются, отсюда жесткость второй пружины равна:

k₂ = 2k₁

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор | оценить

Силы в природе, законы Ньютона. Закон всемирного тяготения, закон Гука, сила трения

В. З. Шапиро

Второе задание ЕГЭ по физике проверяет знания по разделу «Динамика». Это задание базового уровня сложности, без возможности выбора ответа. Для его решения необходимо знать законы Ньютона, формулы, которые выражают силу тяжести, силу всемирного тяготения, силу упругости, вес тела, силу трения, силу реакции опоры на горизонтальной поверхности и на наклонной плоскости. Во многих задачах применяется одна и та же формула, но в различных ситуациях. Как правило, необходимо составить и решить систему из двух уравнений.

Применение закона всемирного тяготения

Необходимая теория: Сила тяготения

1. Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Во сколько раз больше будет модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами в два раза больше, а массы звёзд равны 2m и 3m?

Ответ: в _________________________ раз(а).

В этой задаче необходимо записать формулу закона всемирного тяготения для двух случаев:

(1).

(2).

Разделив (2) на (1), получим:

Ответ: в 1,5 раза.

Подобные задачи проверяют знания основных физических формул. Их необходимо записать в общем виде и в случае, когда происходит изменение какой-либо физической величины. Полученную систему уравнений решаем любым удобным способом. Задания такого типа часто встречаются в различных разделах курса физики.

Применение II закона Ньютона

Необходимая теория: Второй и третий законы Ньютона

2. На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Сторона клетки соответствует 1 Н. Определите модуль равнодействующей сил, приложенных к телу.

Равнодействующая сила равна геометрической сумме сил, приложенных к телу.

Следующий шаг – найти сумму проекций сил на оси OX и OY.

Сумма проекций сил на ось OX равна:

Сумма проекций сил на вертикальную ось равна:

По теореме Пифагора, модуль равнодействующей силы определяется:

 Ответ: 2 Н.

Секрет решения: Многие задачи по динамике требует прочных знаний по геометрии. Теорема Пифагора, а также соотношения в прямоугольном треугольнике являются обязательными инструментами для тех, кто собирается сдавать экзамен по физике.

Применение формулы силы упругости (закон Гука)

Необходимая теория: Сила упругости

3. Подвешенная к потолку пружина под действием силы 5 Н удлинилась на 10 см. Чему равно удлинение этой пружины под действием силы 8 Н?

Ответ: ___________________________ см.

Запишем формулу закона Гука для двух случаев:

(1)

(2)

Разделим (2) на (1).

(м).

Ответ: 16 см.

Задача решается стандартным применением физической формулы для двух случаев. Обратите внимание на единицы измерения, которые требуются в ответе.

Применение формул для силы реакции опоры и силы трения

Необходимая теория: Сила трения

4. Тело движется по горизонтальной плоскости. Нормальная составляющая силы воздействия тела на плоскость равна 40 Н, сила трения равна 10 Н. Определите коэффициент трения скольжения.

Ответ: ___________________________.

Общая формула для силы трения имеет вид:

 где N  — сила реакции опоры.

Отсюда коэффициент трения можно выразить 

Проведем расчет: 

Ответ: 0,25.

Секрет решения: Помним, что коэффициент трения находится в интервале от 0 до 1. Это поможет вам более уверенно решать задачи на расчет коэффициента трения.