Задачи на вычисление площади криволинейной трапеции егэ - Помощь в подготовке к экзаменам и поступлению

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Первообразная функции»

Открытый банк заданий по теме первообразная функции. Задания B7 из ЕГЭ по математике (профильный уровень)

Геометрические фигуры на плоскости: вычисление величин с использованием углов

Геометрические фигуры в пространстве: нахождение длины, площади, объема

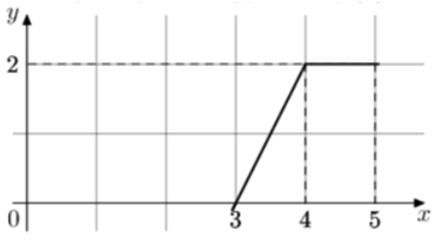
Задание №1164

Тип задания: 7
Тема:
Первообразная функции

Условие

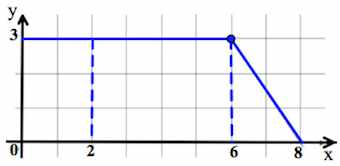
На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(9)-F(5), где F(x) — одна из первообразных функции f(x).

Показать решение

Решение

По формуле Ньютона-Лейбница разность F(9)-F(5), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=9 и x=5. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 4 и 3 и высотой 3.

Её площадь равна frac{4+3}{2}cdot 3=10,5.

Ответ

10,5

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1158

Тип задания: 7
Тема:
Первообразная функции

Условие

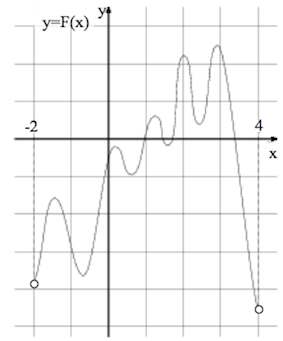
На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-3; 4].

Показать решение

Решение

Согласно определению первообразной выполняется равенство: F'(x)=f(x). Поэтому уравнение f(x)=0 можно записать в виде F'(x)=0. Так как на рисунке изображён график функции y=F(x), то надо найти те точки промежутка [-3; 4], в которых производная функции F(x) равна нулю. Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 7 (четыре точки минимума и три точки максимума).

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

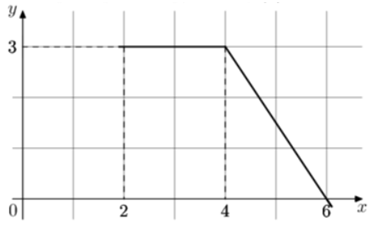
Задание №1155

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(5)-F(0), где F(x) — одна из первообразных функции f(x).

Показать решение

Решение

По формуле Ньютона-Лейбница разность F(5)-F(0), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=5 и x=0. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 5 и 3 и высотой 3.

Её площадь равна frac{5+3}{2}cdot 3=12.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1149

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 4). Пользуясь рисунком, определите количество решений уравнения f (x)=0 на отрезке (-3; 3].

Показать решение

Решение

Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 5 (две точки минимума и три точки максимума).

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

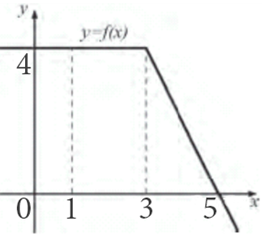
Задание №1146

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображен график некоторой функции y=f(x). Функция F(x)=-x^3+4,5x^2-7 — одна из первообразных функции f(x).

Найдите площадь заштрихованной фигуры.

Показать решение

Решение

Заштрихованная фигура является криволинейной трапецией, ограниченной сверху графиком функции y=f(x), прямыми y=0, x=1 и x=3. По формуле Ньютона-Лейбница её площадь S равна разности F(3)-F(1), где F(x) — указанная в условии первообразная функции f(x). Поэтому S= F(3)-F(1)= -3^3 +(4,5)cdot 3^2 -7-(-1^3 +(4,5)cdot 1^2 -7)= 6,5-(-3,5)= 10.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

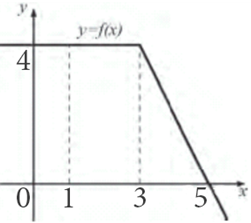
Задание №907

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график некоторой функции y=f(x). Функция F(x)=x^3+6x^2+13x-5 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.

Показать решение

Решение

Заштрихованная фигура является криволинейной трапецией, ограниченной графиком функции y=f(x) и прямыми y=0, x=-4 и x=-1. По формуле Ньютона-Лейбница её площадь S равна разности F(-1)-F(-4), где F(x) — указанная в условии первообразная функции f(x).

Поэтому S= F(-1)-F(-4)= (-1)^3+6(-1)^2+13(-1)-5-((-4)^3+6(-4)^2+13(-4)-5)= -13-(-25)=12.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №307

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображен график некоторой функции y=f(x). Функция F(x)=x^3+18x^2+221x-frac12 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.

Показать решение

Решение

По формуле Ньютона-Лейбница S=F(-1)-F(-5).

F(-1)= (-1)^3+18cdot(-1)^2+221cdot(-1)-frac12= -204-frac12.

F(-5)= (-5)^3+18cdot(-5)^2+221cdot(-5)-frac12= -125+450-1105-frac12= -780-frac12.

F(-1)-F(-5)= -204-frac12-left (-780-frac12right)= 576.

Ответ

576

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №306

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображен график некоторой функции y=f(x).Пользуясь рисунком, вычислите F(9)-F(3), где F(x) — одна из первообразных функции f(x).

Показать решение

Решение

F(9)-F(3)=S, где S — площадь фигуры, ограниченной графиком функции y=f(x), прямыми y=0 и x=3,:x=9. Рассмотрим рисунок ниже.

Данная фигура — трапеция с основаниями 6 и 1 и высотой 2. Ее площадь равна frac{6+1}{2}cdot2=7.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №104

Тип задания: 7
Тема:
Первообразная функции

Условие

На координатной плоскости изображен график функции y=f(x). Одна из первообразных этой функции имеет вид: F(x)=-frac13x^3-frac52x^2-4x+2. Найдите площадь заштрихованной фигуры.

Показать решение

Решение

На рисунке видно, что заштрихованная фигура ограничена по оси абсцисс точками −4, −1, а по оси ординат графиком функции: f(x). Значит площадь фигуры мы можем найти с помощью разности значений первообразных в точках −4 и −1, по формуле определенного интеграла:

intlimits_{-4}^{-1}f(x)dx=F(-1)-F(-4)

Подставим значение первообразной из условия и получим площадь фигуры:

F(-1)-F(-4)=

=frac13-frac52+4+2-frac{64}{3}+frac{80}{2}-16-2=

=-frac{63}{3}+frac{75}{2}-12=-21+37,5-12=4,5

Ответ

4,5

Задание №103

Тип задания: 7
Тема:
Первообразная функции

Условие

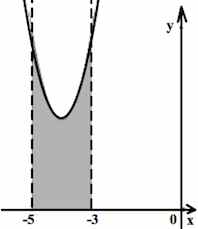
Первообразная y=F(x) некоторой функции y=f(x) определена на интервале (−16; −2). Определите сколько решений имеет уравнение f(x) = 0 на отрезке [−10; −5].

Показать решение

Решение

Формула первообразной имеет следующий вид:

f(x) = F'(x)

По условию задачи нужно найти точки, в которых функция f(x) равна нулю. Принимая во внимание формулу первообразной, это значит, что, нужно найти точки, в которых F'(x) = 0, то есть те точки, в которых производная от первообразной равна нулю.

Мы знаем, что производная равна нулю в точках локального экстремума, т.е. функция имеет решения в тех точках, в которых возрастание F(x) сменяется убыванием и наоборот.

На отрезке [−10; −5] видно что это точки: −9; −7; −6. Значит уравнение f(x) = 0 имеет 3 решения.

Ответ

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

Сайты, меню, вход, новости

Каталог заданий.
Первообразная

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

На рисунке изображён график функции y  =  F(x)  — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x)  =  0 на отрезке [−2; 4].

Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 2.

На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x)  — одна из первообразных функции f(x).

Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 1., Пробный экзамен по математике Санкт-Петербург 2014. Вариант 1.

На рисунке изображён график функции y = f(x). Функция   — одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.

На рисунке изображён график некоторой функции y = f(x). Функция   — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.

Пройти тестирование по этим заданиям

Источник

Задания по теме «Площадь криволинейной трапеции»

Учитель математики

высшей квалификационной категории

МОУ Левобережной СОШ г.Тутаева

Борисова Елена Леонидовна

Пример 1

Найти площадь плоской фигуры, ограниченной линиями , .

Решение: Сначала нужно выполнить чертеж. Вообще говоря, при построении

чертежа в задачах на площадь нас больше всего интересуют точки

пересечения линий. Найдем точки пересечения параболы и прямой

. Это можно сделать двумя способами. Первый способ – аналитический.

Решаем уравнение:

Значит, нижний предел интегрирования , верхний предел интегрирования

Гораздо выгоднее и быстрее построить линии поточечно, при этом пределы

интегрирования выясняются как бы «сами собой». Возвращаемся к нашей

задаче: рациональнее сначала построить прямую и только потом параболу.

Выполним чертеж:

А теперь рабочая формула: Если на отрезке некоторая непрерывная

функция больше либо равна некоторой непрерывной функции , то

площадь фигуры, ограниченной графиками данных функций и прямыми ,

, можно найти по формуле:

В рассматриваемом примере очевидно, что на отрезке парабола

располагается выше прямой, а поэтому из необходимо вычесть

Завершение решения может выглядеть так:

Искомая фигура ограничена параболой сверху и прямой

снизу.

На отрезке , по соответствующей формуле:

Ответ:

Пример 2

Вычислить площадь фигуры, ограниченной линиями , , ,

Решение: Сначала выполним чертеж:

Фигура, площадь которой нам нужно найти, заштрихована синим цветом

(внимательно смотрите на условие – чем ограничена фигура!). Но на практике

по невнимательности нередко возникает «глюк», что нужно найти площадь

фигуры, которая заштрихована зеленым цветом!

Этот пример еще полезен и тем, что в нём площадь фигуры считается с

помощью двух определенных интегралов. Действительно:

1) На отрезке над осью расположен график прямой ;

2) На отрезке над осью расположен график гиперболы .

Совершенно очевидно, что площади можно (и нужно) приплюсовать, поэтому:

Ответ:

Пример 3

Вычислить площадь фигуры, ограниченной

линиями: у = 4х – х

, у = 5, х = 3.

Решение:

= 2, у

= 4

= S

ОАВД

– S

ОСД

прям.

ОСД

= F(3) – F(0), где F(x) первообразная для

функции f(х) = 4х – х

F(х)= ; S

ОСД

= 15 – 9 = 6.

Ответ: 6.

Пример 4

Вычислить площадь фигуры, ограниченной линиями ,

Решение:

Представим уравнения в «школьном» виде , и выполним

поточечный чертеж:

Из чертежа видно, что верхний предел у нас «хороший»: .

Но чему равен нижний предел?! Понятно, что это не целое число, но какое?

Может быть ? Но где гарантия, что чертеж выполнен с идеальной

точностью, вполне может оказаться что . Или корень. А если мы вообще

неправильно построили график?

В таких случаях приходиться тратить дополнительное время и уточнять

пределы интегрирования аналитически.

Найдем точки пересечения прямой и параболы .

Для этого решаем уравнение:

Действительно, .

Дальнейшее решение тривиально, главное, не запутаться в подстановках и

знаках, вычисления здесь не самые простые.

На отрезке , по соответствующей формуле:

Ответ:

Пример 5

Вычислить S фигуры, ограниченной линиями у = (х + 2)

, х = 0, у = 0.

Решение:

АОВ – криволинейный треугольник или криволинейная трапеция. (рис 10.)

S = F(0) – F(-2) =

F(x) = x

+4x+4; F(x) =

S =

Ответ:

Пример 6

Найти S фигуры, ограниченной параболой у = х

+ 1 и прямой у = х + 3.

Решение:

Построим в одной системе координат графики данных функций.

1) у = х

+ 1, х

= 0, у

= 0.

2) у = х + 3

3) х

+ 1 = х + 3

= 1, х

=2.

= S

1АВСД

– S

2АВmСД

тр.АВСД

АВmСД

= F(2) – F(-1), F(x) = , S = 6

= S

– S

= 4,5.

II способ.

АВСД

= F(2) – F(-1), F(x) = .

Ответ: S

= 4,5.

Пример 7:

Найдите 3 четверти площади фигуры,

ограниченной параболой, заданной уравнением

у = – х

+4х—3 и осью абсцисс.

Решение:

1) х

=2, у

2) – х

+4х—3=0 х

=3, х

Функция неотрицательна на [1;3]

F(x) = S

= F(3) – F(1) =

3) Умножим S

на . S

иск.

Ответ: 1

Пример 8

Найти S фигуры, ограниченной линиями f

(x) = x

; f

(x) = 2x – x

Решение:

1) Схематично изобразим данную фигуру (рис.

12)

(x) = – x

+ 2x

= , у

= 1

2) Найдем абсциссы точек пересечения этих линий

= 2x – x

– 2х = 0

х = 0, х = 1

3) Найдем площадь фигуры

(x) = x

–

= F(1) – F(0) =

(x) = ; S

= .

4) S

= S

– S

= .

Ответ: S

= .

Пример 9

Вычислить S фигуры, ограниченной линиями:

у=х

+1, у=0, х=0, х=2.

Решение:

F(x) =

S = F(2) – F(0) = 16/4 + 2 – 0/4 + 0 = 6

Ответ: 6.

Пример 10

Вычислить площадь фигуры, ограниченной линиями , , и осью

Это пример для самостоятельного решения. Полное решение и ответ в конце

урока.

Что делать, если криволинейная трапеция расположена под осью ?

Решение:

Выполним чертеж:

На отрезке график функции расположен над осью , поэтому:

Ответ:

Примечание: В задачах на нахождение площадей преподаватели часто

требуют записывать ответ не только точно, но и, в том числе,

приближенно.

Пример 11 : Найти площадь фигуры, ограниченной линиями ,

.Решение:

Выполним чертеж:

На отрезке , по соответствующей формуле:

Ответ:

Пример 12:

Найти площадь фигуры, ограниченной линиями , .

Решение:

Выполним чертеж.

На отрезке , по соответствующей формуле:

Ответ:

Используемые ресурсы:

1. https://infourok.ru/samostoyatelnaya-rabota-po-teme-neopredelenniy-

integral-klass-761699.html

2. http://festival.1september.ru/articles/566339/

3. http://school-collection.edu.ru/catalog/rubr/8a790bee-ba9d-4b2b-9c3a—

6e370cc2df5b/113019/?

4. ЕГЭ: 4000 задач с ответами по математике. Все задания «Закрытый сегмент».

Базовый и профильный уровни /И.В.Ященко, И.Р.Высоцкий, А.В.Забелин и др.;

под редакцией И.В.Ященко. – М.: Издательство «Экзамен», 2016. – 640 с. (Серия

«Банк заданий ЕГЭ»)

5. Математика. ЕГЭ – 2013: экспресс – курс для подготовки к экзамену/ Дмитрий

Гущин. – М, : Издательский дом «Учительская газета», 2013. – 256 с.

(Библиотечка «Учительской газеты». Готовимся к ЕГЭ с лучшими учителями

России

Источник

Содержание:

Примеры с решением

Рассмотрим функцию , которая непрерывна на отрезке и принимает на этом промежутке неотрицательные значения. Фигуру, ограниченную графиком функции и прямыми , и , называют криволинейной трапецией.

На рисунке 26.1 приведены примеры криволинейных трапеций.

Рассмотрим теорему, которая позволяет вычислять площади криволинейных трапеций.

Теорема 26.1.

Площадь криволинейной трапеции, ограниченной графиком функции и прямыми , и , можно вычислить по формуле

где — любая первообразная функции на отрезке .

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Доказательство. Рассмотрим функцию , где , которая определена таким правилом.

Если , то ; если , то — это площадь криволинейной трапеции, показанной штриховкой на рисунке 26.2.

Докажем, что для всех .

Пусть — произвольная точка отрезка и — приращение аргумента в точке , Ограничимся рассмотрением случая, когда (случай, когда , рассматривают аналогично).

Имеем:

Получаем, что — это площадь криволинейной трапеции, заштрихованной на рисунке 26.3.

На отрезке как на стороне построим прямоугольник, площадь которого равна (рис. 26.4). Длины сторон этого прямоугольника равны и , где — некоторая точка промежутка . Тогда Отсюда

Если , то .

Возможно вам будут полезны данные страницы:

Поскольку функция непрерывна в точке , то . Отсюда, если , то

Имеем

Поскольку — произвольная точка области определения функции , то для любого выполняется равенство . Получили, что функция является одной из первообразных функции на отрезке .

Пусть — некоторая первообразная функции на отрезке . Тогда по основному свойству первообразной можно записать

где — некоторое число.

Имеем:

По определению функции искомая площадь криволинейной трапеции равна . Следовательно,

Примеры с решением

Пример 1.

Найдите площадь фигуры, ограниченной графиком функции и прямыми , и

Решение:

На рисунке 26.5 изображена криволинейная трапеция, площадь которой требуется найти.

Одной из первообразных функции на отрезке является функция Тогда

Пример 2.

Найдите площадь фигуры, ограниченной графиком функции и прямой .

Решение:

График функции пересекает прямую в точках и (рис. 26.6). Тогда фигура, площадь которой требуется найти, является криволинейной трапецией, ограниченной графиком функции и прямыми

Одной из первообразных функции на отрезке является функция Тогда

Определение. Пусть — первообразная функции на промежутке , числа и , где , принадлежат промежутку . Разность называют определенным интегралом функции на отрезке .

Определенный интеграл функции на отрезке обозначают (читают: «интеграл от до эф от икс де икс»). Следовательно,

где — произвольная первообразная функции на промежутке .

Например, функция является первообразной функции на промежутке . Тогда для произвольных чисел и , где , можно записать:

Заметим, что значение разности не зависит от того, какую именно первообразную функции выбрали. Действительно, каждую первообразную функции на промежутке можно представить в виде , где — некоторая постоянная. Тогда

Равенство (1) называют формулой Ньютона—Лейбница. Следовательно, для вычисления определенного интеграла по формуле Ньютона-Лейбница надо:

найти любую первообразную функции на отрезке ;
вычислить значение первообразной в точках и ;
найти разность .

При вычислении определенных интегралов разность обозначают

Используя такое обозначение, вычислим, например, Имеем:

Пример 3.

Вычислите

Решение:

Имеем:

Если функция имеет первообразную на отрезке и , то из формулы Ньютона-Лейбница следует такое свойство определенного интеграла:

Действительно,

Если каждая из функций и имеет первообразную на отрезке , то, используя теоремы 25.1 и 25.2, можно доказать (сделайте это самостоятельно) такие свойства определенного интеграла:

где — некоторое число.

Формула Ньютона-Лейбница позволяет установить связь между определенным интегралом и площадью криволинейной трапеции, ограниченной графиком функции и прямыми , и ().

Используя теорему 26.1, можно записать:

Заметим, что в этой формуле рассматриваются непрерывные функции , которые на отрезке принимают только неотрицательные значения. Однако определенный интеграл можно использовать для вычисления площадей более сложных фигур.

Рассмотрим непрерывные на отрезке функции и такие, что для всех выполняется неравенство

Покажем, как найти площадь фигуры , ограниченной графиками функций и и прямыми и (рис. 26.7).

Перенесем фигуру вверх на единиц так, чтобы полученная фигура находилась выше оси абсцисс (рис. 26.8). Фигура ограничена графиками функций и и прямыми , .

Поскольку фигуры и имеют равные площади, то искомая площадь равна разности

где — площадь криволинейной трапеции, ограниченной графиком функции и прямыми , и (рис. 26.9, а);

— площадь криволинейной трапеции, ограниченной графиком функции и прямыми , и (рис. 26.9, б).

Таким образом, используя свойства определенного интеграла, можем записать:

Следовательно, если функции и непрерывны на отрезке и для всех выполняется неравенство то площадь фигуры, ограниченной графиками функций и и прямыми и , можно вычислить по формуле

Пример 4.

Найдите площадь фигуры, ограниченной графиками функций и

Решение:

На рисунке 26.10 изображена фигура, площадь которой требуется найти.

Решив уравнение , устанавливаем, что графики функций и пересекаются в двух точках с абсциссами и .

Тогда искомая площадь

Лекции:

Экспонента, натуральные логарифмы и гиперболические функции
Непрерывная случайная величина
Математическое ожидание и дисперсия случайной величины
Исследование функции: пример решения
Понятие функции. Теория пределов
Элементарные функции комплексного переменного. Дробно-рациональные функции
Равномерная сходимость функционального ряда
Критерий Сильвестра
Преобразования в пространстве и на плоскости
Площадь поверхности подобных фигур

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

Алгебра 10-11 класс. Площадь криволинейной трапеции

Алгебра 10-11 класс. Площадь криволинейной трапецииadmin2022-11-04T14:15:40+03:00

Скачать файл в формате pdf.

Алгебра 10-11 класс. Площадь криволинейной трапеции

Задача 1. На рисунке изображён график некоторой функции (y = fleft( x right)) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите (Fleft( 5 right) — Fleft( 3 right)), где (Fleft( x right))— одна из первообразных функции (fleft( x right)). Ответ ОТВЕТ: 3.
Задача 2. На рисунке изображён график некоторой функции (y = fleft( x right)) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите (Fleft( 6 right) — Fleft( 2 right)), где (Fleft( x right))— одна из первообразных функции (fleft( x right)). Ответ ОТВЕТ: 9.
Задача 3. На рисунке изображен график некоторой функции (y = fleft( x right)). Пользуясь рисунком, вычислите определенный интеграл (intlimits_1^5 {fleft( x right)} ,dx) Ответ ОТВЕТ: 12.
Задача 4. На рисунке изображен график некоторой функции (y = fleft( x right)). Пользуясь рисунком, вычислите определенный интеграл (intlimits_2^5 {fleft( x right)} ,dx) Ответ ОТВЕТ: 8.
Задача 5. На рисунке изображён график некоторой функции (y = fleft( x right)). Функция (Fleft( x right) = frac{2}{3}{x^3} + 20{x^2} + 201x — frac{6}{{13}}) — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры. Ответ ОТВЕТ: 9.
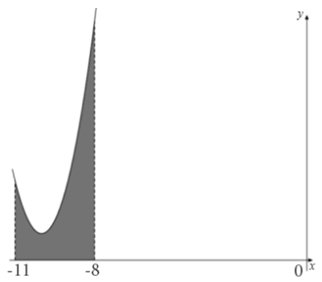Задача 6. На рисунке изображён график некоторой функции (y = fleft( x right)). Функция (Fleft( x right) = — frac{1}{{12}}{x^3} — frac{3}{2}{x^2} — frac{{27}}{4}x — frac{3}{4}) — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры. Ответ ОТВЕТ: 9.
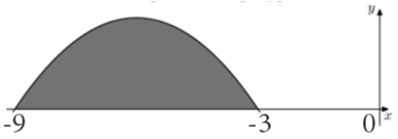Задача 7. Вычислите площадь фигуры ограниченной линиями (y = {x^3},,,y = 0,,,x = 2) Ответ ОТВЕТ: 4.
Задача 8. Вычислите площадь фигуры ограниченной линиями (y = {x^3} + 2,,,y = 0,,,x = 2,,,x = 3) Ответ ОТВЕТ: 18,25.
Задача 9. Вычислите площадь фигуры ограниченной линиями (y = — {x^2} + 9x — 18,,,y = 0) Ответ ОТВЕТ: 4,5.
Задача 10. Вычислите площадь фигуры ограниченной линиями (y = — {x^2} + 9,,,y = 0) Ответ ОТВЕТ: 36.

Задача 11. Вычислите площадь фигуры ограниченной линиями (y = frac{1}{{{x^2}}},,,y = 0,,,x = — 4,,,x = — 2)

Ответ

ОТВЕТ: 0,25.

Задача 12. Вычислите площадь фигуры ограниченной линиями (y = — sqrt x ,,,y = 0,,,x = 9,,,x = 36)

Ответ

ОТВЕТ: 126.

Задача 13. Вычислите площадь фигуры ограниченной линиями (y = sin 2x,,,y = 0,,,x = 0,,,x = frac{pi }{2})

Ответ

ОТВЕТ: 1.

Задача 14. Вычислите площадь фигуры ограниченной линиями (y = frac{1}{{{{cos }^2}x}} + frac{2}{pi },,,,y = 0,,,,x = 0,,,,x = frac{pi }{4})

Ответ

ОТВЕТ: 1,5.

Задача 15. Вычислите площадь фигуры ограниченной линиями (y = sqrt x ,,,y = — 2x,,,x = 9)

Ответ

ОТВЕТ: 99.

Задача 16. Вычислите площадь фигуры ограниченной линиями (y = — sqrt x ,,,y = {x^2},,,x = 9)

Ответ

ОТВЕТ: 261.

Задача 17. Вычислите площадь фигуры ограниченной линиями (y = {e^{2x}},,,y = 0,,,,x = ln 2,,,,x = ln 6)

Ответ

ОТВЕТ: 16.

Задача 18. Вычислите площадь фигуры ограниченной линиями (y = frac{1}{x},,,y = 0,,,,x = e,,,,x = {e^3})

Ответ

ОТВЕТ: 2.

Задача 19. Вычислите площадь фигуры ограниченной линиями (y = — {x^2} + 2x + 3,,,y = 3 — x)

Ответ

ОТВЕТ: 4,5.

Задача 20. Вычислите площадь фигуры ограниченной линиями (y = 1 — {x^2},,,y = — x — 1)

Ответ

ОТВЕТ: 4,5.

Задача 21. Вычислите площадь фигуры ограниченной линиями (y = — {x^2} + 2,,,y = {x^2} — 2x — 2)

Ответ

ОТВЕТ: 9.

Задача 22. Вычислите площадь фигуры ограниченной линиями (y = {x^2} — 4x + 3,,,y = — {x^2} + 6x — 5)

Ответ

ОТВЕТ: 9.

Задача 23. Найдите площадь фигуры, ограниченной графиком функции (y = {x^3}) и касательной, проведенной к ней в точке (left( { — 1;, — 1} right))

Ответ

ОТВЕТ: 6,75.

Задача 24. Найдите площадь фигуры, ограниченной графиком функции (y = {x^3} — 3x) и касательной, проведенной к ней в точке (left( { — 1;,2} right))

Ответ

ОТВЕТ: 6,75.

Задача 25. Вычислите (frac{1}{pi }intlimits_0^4 {sqrt {4x — {x^2}} dx} ), используя геометрический смысл определенного интеграла

Ответ

ОТВЕТ: 2.

Задача 26. Вычислите (frac{1}{pi }intlimits_{ — 1}^0 {sqrt { — 2x — {x^2}} dx} ), используя геометрический смысл определенного интеграла

Ответ

ОТВЕТ: 0,25.

Задача 27. Вычислите (intlimits_0^3 {left| {,x — 2,} right|dx} ), используя геометрический смысл определенного интеграла

Ответ

ОТВЕТ: 2,5.

Задача 28. Вычислите (intlimits_0^4 {left| {,left| {,x — 2,} right| — 1,} right|dx} ), используя геометрический смысл определенного интеграла

Ответ

ОТВЕТ: 2.

Источник

10
Авг 2013

Категория: 07 Производная, ПО

07. Первообразная

2013-08-10
2022-09-11

Задача 1. На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите , где — одна из первообразных функции .

Решение: + показать

Задача 2. На рисунке изображён график некоторой функции . Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.

Решение: + показать

Задача 3. На рисунке изображён график некоторой функции . Функция $F(x)=-frac{4}{9}x^3-frac{34}{3}x^2-frac{280}{3}x-frac{18}{5}$ — одна из первообразных функции . Найдите площадь закрашенной фигуры.

Решение: + показать

Задача 4. На рисунке изображён график функции – одной из первообразных некоторой функции , определённой на интервале . Пользуясь рисунком, определите количество решений уравнения на отрезке .

Решение: + показать

Загляните –> + показать

Вы можете пройти тест «Первообразная»

Автор: egeMax |

комментариев 7

Источник

Алгебра и начала математического анализа, 11 класс

Урок №23.Площадь криволинейной трапеции. Интеграл и его свойства.

Перечень вопросов, рассматриваемых в теме

1) Нахождение определенного интеграла

2) Нахождение площади криволинейной трапеции с помощью формулы Ньютона – Лейбница

3) Решение задач, с помощью формулы Ньютона – Лейбница

Формула Ньютона – Лейбница

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

ОрловаЕ. А., СеврюковП. Ф., СидельниковВ. И., СмоляковА.Н.Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b].

Отрезок [a;b] называют основанием этой криволинейной трапеции

формула Ньютона – Лейбница

Если в задаче требуется вычислить площадь криволинейной трапеции, то ответ всегда будет положительный. Если требуется, используя чертеж, вычислить интеграл, то его значение может быть любым(зависит от расположения криволинейной трапеции).

Примеры и разбор решения заданий тренировочного модуля

№1.Найти площадь криволинейной трапеции, изображенной на рисунке