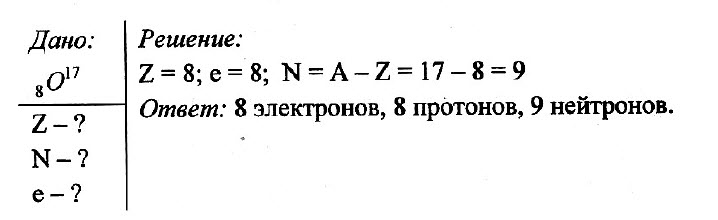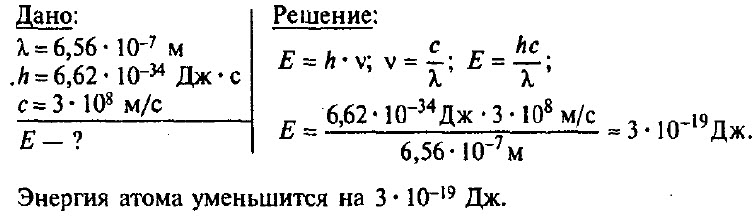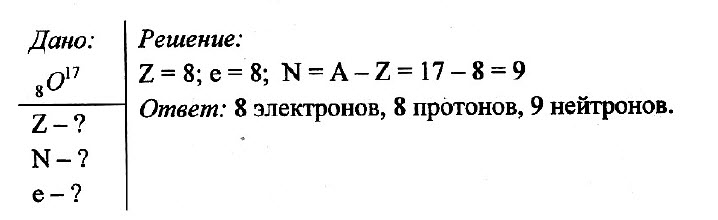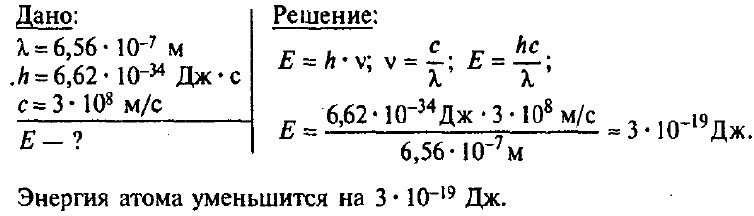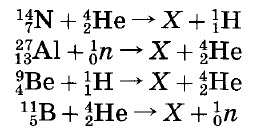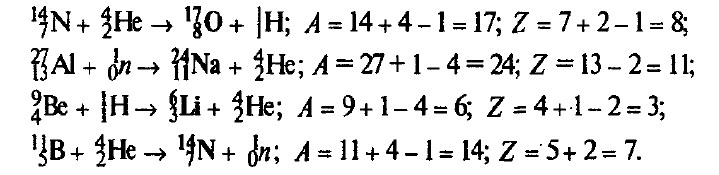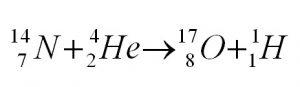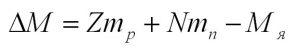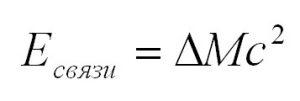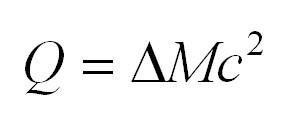Задачи на ядерные реакции егэ - Помощь в подготовке к экзаменам и поступлению

Каталог заданий.
Ядерная физика

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Задания Д32 C3 № 3035

-мезон массой распадается на два -кванта. Найдите модуль импульса одного из образовавшихся -квантов в системе отсчета, где первичный -мезон покоится.

Раздел кодификатора ФИПИ/Решу ЕГЭ: 5.1.2 Фотоны. Энергия фотона. Импульс фотона

Решение

Сообщить об ошибке · Помощь

Задания Д32 C3 № 3050

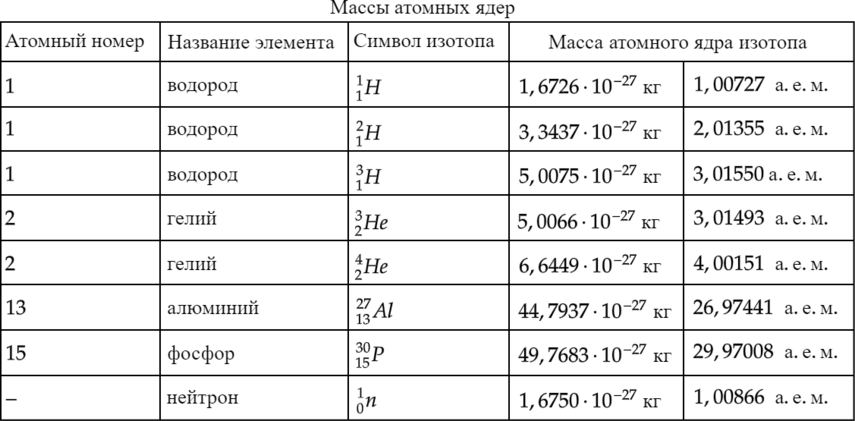
Используя таблицу масс атомных ядер, вычислите энергию, освобождающуюся при синтезе 1 кг гелия из изотопов водорода  — дейтерия и трития:

Массы атомных ядер

Атомный номер	Название элемента	Символ изотопа	Масса атомного ядра изотопа
1	водород
1	водород
1	водород
2	гелий
2	гелий
13	алюминий
15	фосфор
—	нейтрон

Раздел кодификатора ФИПИ/Решу ЕГЭ: 5.3.2 Энергия связи нуклонов в ядре. Ядерные силы, 5.3.6 Ядерные реакции. Деление и синтез ядер

Решение

1 комментарий · Сообщить об ошибке · Помощь

Задания Д32 C3 № 3051

Используя таблицу масс атомных ядер, вычислите энергию, освобождающуюся при осуществлении ядерной реакции:

Массы атомных ядер

Атомный номер	Название элемента	Символ изотопа	Масса атомного ядра изотопа
—	нейтрон
1	водород
1	водород
1	водород
2	гелий
2	гелий
13	алюминий
15	фосфор

Решение

Сообщить об ошибке · Помощь

Задания Д32 C3 № 3052

Определите, ядро какого изотопа X освобождается при осуществлении ядерной реакции:

Используя таблицу масс атомных ядер, вычислите энергию, освобождающуюся при осуществлении этой ядерной реакции.

Атомный номер	Название элемента	Символ изотопа	Масса атомного ядра изотопа
1	водород
1	водород
1	водород
2	гелий
2	гелий
13	алюминий
15	фосфор

Решение

Сообщить об ошибке · Помощь

Задания Д32 C3 № 3053

Определите, какая частица X образуется при осуществлении ядерной реакции: Используя таблицу масс атомных ядер, вычислите энергию, освобождающуюся при осуществлении этой ядерной реакции.

Массы атомных ядер

Атомный номер	Название элемента	Символ изотопа	Масса атомного ядра изотопа
1	водород
1	водород
1	водород
2	гелий
2	гелий
13	алюминий
15	фосфор

Решение

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник

Задачи на Состав атома и ядерные реакции с решениями

Формулы, используемые на уроках «Задачи на Состав атома, ядерные реакции и энергия связи атомного ядра».

Название величины	Обозначение	Единица измерения	Формула
*Масса протона*	m_p	а.е.м	m_p = 1,00728
*Масса нейтрона*	m_n	а.е.м	m_n = 1,00867
*Число протонов*	Z
*Число нейтронов*	N
*Масса ядра*	M_я	а.е.м
*Дефект масс*	Δm	а.е.м, кг	Δm = (Zm_p + Nm_n) – M_я
*Энергия связи ядра*	ΔE₀	Дж	ΔE₀ = Δmc²
*Скорость света*	c	м/с	c = 3•10⁸

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
Определите число электронов, протонов и нейтронов в атоме кислорода ₈O¹⁷.

Задача № 2.
В результате α-pacnada ядро некоторого элемента превратилось в ядро радона ₈₆Rn²²². Что это был за элемент?

Задача № 3.
На сколько уменьшилась энергия атома, если при переходе из одного энергетического состояния в другое атом излучил свет длиной волны 6,56 • 10^–7 м?

Задача № 4.
В какое ядро превращается торий после трех последовательных α-распадов?

Ответ:

Задача № 5.
В какое ядро превращается сурьма после четырех β-распадов?

Ответ:

Задача № 6.
Каким образом можно осуществить давнюю мечту алхимиков средневековья — превратить ртуть в золото?

Задача № 7.
Определите дефект масс и энергию связи ядра атома .

Ответ: 3,18 • 10^–27 кг; 28,6 • 10^–11 Дж.

Задача № 8.
Выделяется или поглощается энергия при следующей ядерной реакции: ?

Ответ: энергия поглощается.

Задача № 9.
Вычислите энергию связи ядра лития ₃Li⁷. Масса ядра равна 7,01436 а.е.м.

Задача № 10.
Определите неизвестный продукт X каждой из ядерных реакций:

Решение:

Краткая теория для решения Задачи на Состав атома и ядерные реакции.

Алгоритм решения задачи на расчет энергии связи атомного ядра:
1. Определить количество протонов и нейтронов в ядре атома.
2. Вычислить дефект масс в атомных единицах массы.
3. Перевести атомные единицы массы в килограммы: 1 а.е.м. = 1,6605•10^-27 кг.
4. Вычислить энергию связи; ответ записать в стандартном виде.

Важные замечания:
1. Вычисления сложные, поэтому лучше их производить с помощью микрокалькулятора.
2. В ходе вычисления дефекта масс нельзя ничего округлять, иначе дефект масс обратится в ноль. Округлить можно только результат.

Это конспект по теме «ЗАДАЧИ на Состав атома и ядерные реакции». Выберите дальнейшие действия:

Перейти к теме: ЗАДАЧИ на
Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
Вернуться к списку конспектов по Физике.
Проверить свои знания по Физике.

Источник

Ядерная физика. Планетарная модель атома. Нуклонная модель ядра. Ядерные реакции.

В. З. Шапиро

Задание 19 ЕГЭ по физике посвящено темам: «Физика атома», «Физика атомного ядра». Задание относится к базовому уровню. Чтобы его решить, нужно уметь работать с Периодической системой элементов Д. И. Менделеева, определять количество протонов, нейтронов, записывать уравнения ядерных реакций.

На рисунке представлен фрагмент Периодической системы элементов Д. И. Менделеева. Под названием каждого элемента приведены массовые числа его основных стабильных изотопов. При этом нижний индекс около массового числа указывает (в процентах) распространённость изотопа
в природе.

Укажите число протонов и число нейтронов в ядре самого распространённого стабильного изотопа калия.

Число протонов	Число нейтронов

Необходимая теория:

Строение атома

Используя периодическую систему Д. И. Менделеева, можно определить атомную массу калия. Из двух предложенных изотопов надо выбрать самый распространенный – это калий с атомной массой 39. Так как порядковый номер определяет количество протонов (19), то для нахождения числа нейтронов надо вычесть из атомной массы количество протонов.

N_нейтр.= 39 — 19 = 20

Число протонов	Число нейтронов
19	20

Секрет решения. Задачи по данной теме являются одними из самых простых. Но и здесь можно допустить ошибку, если невнимательно прочитать условие. Например, можно неправильно выбрать самый распространенный (или менее распространенный) стабильный изотоп химического элемента.

2. Ядро бериллия может захватить гамма-квант, в результате чего происходит ядерная реакция ${}^9_4{Be}+{}^0_0gamma to {}^A_ZX+{}^1_0n$ с образованием ядра химического элемента $_{Z}^{A}textrm{X}$ Каковы заряд образовавшегося ядра Z (в единицах элементарного заряда) и его массовое число A?

Заряд числа Z	Массовое число ядра A

Необходимая теория:

Ядерные реакции

При написании ядерных реакций сумма верхних индексов в левой части уравнения должна быть равна сумме верхних индексов в правой части уравнения. То же самое относится и к нижним индексам. Это правило основано на выполнении законов сохранения заряда и массы. Проведем расчет.

Z = 4 – 0 = 4; A = 9 – 1 = 8.

Заряд ядра Z	Массовое число ядра A
4	8

Секрет решения. При написании ядерных реакций, кроме закономерностей, описанных в решении, надо знать массовые и зарядовые числа некоторых частиц:

нейтрон $_{0}^{1}textrm{n}$

протон $_{1}^{1}textrm{p}$ или $_{1}^{1}textrm{H}$ (ядро атома водорода);

α-частица $_{2}^{4}textrm{He}$ (ядро атома гелия)

электрон $_{-1}^{0}textrm{e}.$

Указанные значения масс и зарядов частиц надо знать наизусть. Только это вызывает трудности при написании ядерных реакций.

3. Сколько протонов и сколько нейтронов содержится в ядре $_{17}^{35}textrm{Cl}.$

Число протонов	Число нейтронов

Необходимая теория:

Строение атома

Нижний индекс химического элемента определяет порядковый номер, заряд ядра и количество протонов. Для ядра $_{17}^{35}textrm{Cl}$ количество протонов равно 17. Количество нейтронов определяется разницей массового и зарядового чисел.

N_нейтр.= 35 – 17 = 18

Число протонов	Число нейтронов
17	18

Секрет решения. Важно знать, что суммарное количество протонов и нейтронов определяют массу атома. Электроны, безусловно, влияют на массу, но незначительно. Массу электронов необходимо вычитать из общей массы атома при расчетах энергии связи атомного ядра.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 19 ЕГЭ по физике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.03.2023

Источник

32. Электродинамика. Квантовая физика (расчетная задача)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Ядерные реакции. Энергия связи

Используя таблицу масс атомных ядер, вычислите энергию, освобождающуюся при синтезе 1 кг гелия из изотопов водорода — дейтерия и трития: [^2_1H+^3_1Hrightarrow ^4_2He+^1_0n]
Ответ дайте разделив его на (10^{14})

Выход (Delta E) ядерной реакции синтеза ядер гелия из ядер дейтерия и трития вычислим по формуле деффекта массы: [Delta E=Delta mc^2] [Delta m=m_{_1^2H}+m_{_1^3H}-m_{_1^4H}-m_n]
Найдем деффект массы (Delta m) ядерной реакции: [Delta m=2,01355+3,01550-4,00151-1,00866=0,01888text{ a.e. м}]
или: [Delta m=(3,3437+5,0075-6,6449-1,6750)cdot 10^{-27}text{ кг}=3,13cdot 10^{-29}text{ кг}]
Используя переводной коэффициент получим энергетический выход ядерной реакции: [Delta E=0,01888 cdot 931,5text{ МэВ}approx=17,6text{ МэВ}]
Или Умножим массу на вкадрат скорости света, получим энергетический выход ядерной реакции: [Delta E=3,13cdot 10^{-29}cdot 9cdot 10^{16}text{ Дж}=2,817cdot 10^{-12}text{ Дж}]
Найдем число (N) ядер в 1 кг гелия: [N=dfrac{m}{m_{He}}=dfrac{1text{ кг}}{6,6449cdot 10^{-27}text{ кг}}=approx 1,5cdot 10^{26}]
Количество энергии освободившееся при синтезе: [E=Delta Ecdot Napprox17,6cdot 1,6cdot 10^{-13}cdot 1,5 cdot 20^{26}approx 4,2cdot 10^{14}text{ Дж}]
или [E=Delta Ecdot Napprox 2,817cdot 10^{-12}cdot 1,5cdot 20^{26}approx 4,2cdot 10^{14}text{ Дж}]

Ответ: 4,2

При взрыве атомной бомбы освобождается энергия (8,3cdot10^{16}) Дж. Эта энергия получается в основном за счет деления ядер урана 238. При делении одного ядра урана 238 освобождается 200 МэВ, масса ядра равна примерно 238 а. е. м. Вычислите массу ядер урана, испытавших деление при взрыве, и суммарный дефект массы.

Масса (m) ядер урана, испытавших деление при взрыве: [m=Nm_0]
Число (N) ядер равно: [N=dfrac{E}{Delta E}]
Тогда значение массы: [m=Nm_0=dfrac{Ecdot M_0}{Delta E}=] [=dfrac{8,3cdot10^{16} cdot 238 cdot 1,66 cdot 10^{-27}}{200cdot 1,6 cdot 10^{-13} }approx 10^3text{ кг}]
Найдем деффект массы (Delta m) ядерной реакции: [Delta E=Delta mc^2]
выразим (Delta m): [Delta m=dfrac{E}{c^2}] [Delta m=dfrac{8,3cdot 10^{16}}{9cdot 10^{16}}approx 0,92text{ кг}]

Ответ: 0,92

Находящееся в однородном магнитном поле с индукцией (B = 5) Тл ядро покоящегося нейтрального атома испытывает (alpha)-распад, в результате которого рождается ион нового элемента массой (M = 50) а.е.м. Его траектория лежит в плоскости, перпендикулярной направлению магнитного поля, и представляет собой дугу окружности радиуса (R = 5) см. Найти выделившуюся при (alpha)-распаде энергию (Delta E), считая, что она целиком переходит в кинетическую энергию продуктов реакции. Ответ дайте, разделив его на (10^(-13)).

Поскольку исходный атом неподвижен и выделившаяся при реакции энергия (Delta E) целиком переходит в кинетическую энергию продуктов реакции, то из законов сохранения импульса и энергии следуют равенства [mupsilon=MV,] [dfrac{mupsilon^2}{2}+dfrac{MV^2}{2}=Delta E,]
Где (upsilon) и (V)–скорости (alpha)–частицы и иона после распада.
Исключая из этих равенств (upsilon), получаем, что [Delta E=dfrac{M(M+m)}{2m}cdot V^2.]
Из закона сохранения заряда следует, что модуль заряда иона равен заряду (alpha)–частицы. По второму закону Ньютона уранвение движения иона с магнитном поле под действием силы Лоренца имеет вид [dfrac{MV^2}{R}=qVB]
Подставляя (V=dfrac{qBR}{M}) в найденное выражение для (Delta E), получаем [Delta E=dfrac{(qBR)^2(M+m)}{2Mm}approx 5,2cdot 10^{-13}text{ Дж}]

Ответ: 5,2

При радиоактивном распаде ядра (^{226}_{88}Ra) вылетает (alpha)-частица. Известно, что в образце радия массой 1 мг каждую секунду распадаются (3,7 cdot 10^7) ядер. (alpha)-частицы вылетающие из этого образца за 2 часа, имеют суммарную энергию 205 мДж. Какую энергию имеет каждая (alpha)-частица? Ответ приведите в кэВ с точностью (pm100)кэВ.

Пусть (E_0) – энергия одной (alpha)-частицы, (N) – число распадов ядер в секунду, а, значит, и число (alpha)-частиц, вылетающих из образца за одну секунду. Суммарная энергия вылетевших (alpha)-частиц: [E=E_0 N t] [E_0=frac{E}{Nt}=frac{205cdot10^{-3}}{3,7 cdot 10^7cdot7200}=0,77 cdot10^{-12}text{ Дж}=4800 text{ кэВ}]

Ответ: 4800

Пренебрегая кинетическими энергиями и суммарным импульсом бериллия и гелия в ядерной реакции [^9_4Be+^4_2Herightarrow ^{12}_6C+_0^1n] определить кинетические энергии (E_C) и (E_n) углерода и нейтрона, считая, что вся выделяющаяся в реакции энергия (Delta E) практически равна (E_C +E_n.)
В ответ запишите разность между полученными значениями, разделив, на (10^{-14})

В соответсвии с закономи сохранении энергии сумма масс до реакции равна сумме масс после реакции плюс дефект массы (Delta m), связанный с выделяющейся или поглощающейся энергией (Delta E) соотношением [Delta E=|Delta m|cdot c^2]
Используя данные таблицы, получим: [Delta m=m_{Be}+m_{alpha}-m_{C}-m_{n}=9,01219+4,00260-12,00000-1,00867=0,00612text{ а.е. м.},]
где (m_{alpha})– масса образовавшейся (alpha)–частицы (ядра (_2^4He)). Поскольку (delta m)>0, в реакции происходит выделение энергии [Delta E=(m_{Be}+m_{alpha}-m_{C}-m_{n})cdot c^2.]
По условию суммарный импульс бериллия и гелия равен нулю, поэтому суммарный импульс углерода и нейтрона [p_C+p_n=0.]
Суммарная кинетическая энергия бериллия и гелия по условию также равна нулю, следовательно, вся выделяющаяся в реакции энергия [Delta E=E_C+E_n,] где [E_C=p^2_C/2m_Ctext{ и } E_n=p^2_n/2m_n]
–кинетическая энергия углерода и нейтрона
Отсюда получаем : [E_n=dfrac{m_n(m_{Be}+m_{alpha}-m_{C}-m_{n})cdot c^2}{m_C+m_n}=dfrac{1,00867cdot 0,00612}{12,00000+1,00867}cdot 1,66cdot 10^{-27}cdot(3cdot10^8)^2approx7cdot 10^{-14}text{ Дж}] [E_C=dfrac{m_c(m_{Be}+m_{alpha}-m_{C}-m_{n})cdot c^2}{m_C+m_n}=dfrac{12cdot 0,00612}{12,00000+1,00867}cdot 1,66cdot 10^{-27}cdot(3cdot10^8)^2approx 8,4cdot 10^{-13} text{ Дж}] [84-7=77]

Ответ: 77

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Задачи на Состав атома и ядерные реакции с решениями

Формулы, используемые на уроках «Задачи на Состав атома, ядерные реакции и энергия связи атомного ядра».

Название величины	Обозначение	Единица измерения	Формула
*Масса протона*	m_p	а.е.м	m_p = 1,00728
*Масса нейтрона*	m_n	а.е.м	m_n = 1,00867
*Число протонов*	Z
*Число нейтронов*	N
*Масса ядра*	M_я	а.е.м
*Дефект масс*	Δm	а.е.м, кг	Δm = (Zm_p + Nm_n) – M_я
*Энергия связи ядра*	ΔE₀	Дж	ΔE₀ = Δmc²
*Скорость света*	c	м/с	c = 3•10⁸

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1. Определите число электронов, протонов и нейтронов в атоме кислорода ₈O¹⁷.

Задача № 2. В результате α-pacnada ядро некоторого элемента превратилось в ядро радона ₈₆Rn²²². Что это был за элемент?

Задача № 3. На сколько уменьшилась энергия атома, если при переходе из одного энергетического состояния в другое атом излучил свет длиной волны 6,56 • 10^–7 м?

Задача № 4. В какое ядро превращается торий после трех последовательных α-распадов?

Ответ:

Задача № 5. В какое ядро превращается сурьма после четырех β-распадов?

Ответ:

Задача № 6. Каким образом можно осуществить давнюю мечту алхимиков средневековья — превратить ртуть в золото?

Задача № 7. Определите дефект масс и энергию связи ядра атома .

Ответ: 3,18 • 10^–27 кг; 28,6 • 10^–11 Дж.

Задача № 8. Выделяется или поглощается энергия при следующей ядерной реакции: ?

Ответ: энергия поглощается.

Задача № 9. Вычислите энергию связи ядра лития ₃Li⁷. Масса ядра равна 7,01436 а.е.м.

Задача № 10. Определите неизвестный продукт X каждой из ядерных реакций:

Решение:

Краткая теория для решения Задачи на Состав атома и ядерные реакции.

Это конспект по теме «ЗАДАЧИ на Состав атома и ядерные реакции». Выберите дальнейшие действия:

Перейти к теме: ЗАДАЧИ на
Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
Вернуться к списку конспектов по Физике.
Проверить свои знания по Физике.

Источник

Атомная
физика

Квантовая
физика

Методические
рекомендации к решению задач части С

Фотоны.
Постулаты Бора.

№ 1.Монохроматический пучок параллельных лучей создается
источником,
который за время Δt = 8·10^-4 с излучает N = 5·10¹⁴
фотонов.
Фотоны падают по нормали на площадку S = 0,7 см² и создают давление
p = 1,5·10^-5 Па.
При этом 40% фотонов отражается, а 60% поглощается.
Определите длину волны излучения.
Решение:

№
3.
Электромагнитное излучение с длиной волны λ = 3,3·10 ^-7м используется
для нагревания воды массой 1 кг. Сколько времени потребуется для
нагревания воды на Δt^o = 10 ^оС,
если источник за 1 с излучает N = 10²⁰ фотонов? Считать, что излучение полностью поглощается
водой.

Решение. Теплота нагревания воды Q = mc_вΔt ^o, энергия излучения U = hνNt. Излучение полностью поглощается
водой, следовательно, m c_вΔt ^o = hνNt, t = mc_вΔt ^o/hνN. ν = с/ λ.

t = mc_вΔt ^o λ /hсN = 1 · 4200 · 10 · 3,3 · 10^-7/
6,6 · 10 ^-34· 3 ·10⁸·10²⁰ =
4200/6 = 700 (с).

№ 4. На рисунке изображены несколько энергетических уровней
электронной оболочки атома и указаны длины волн фотонов, излучаемых и
поглощаемых при переходах с одного уровня на другой. Чему равна минимальная
длина длина волны фотонов, излучаемых при переходе с одного уровня нр другой,
если λ_1-3 = 400 нм, λ_2-4 = 500 нм, λ_3-2
= 600 нм?

Решение.
Согласно
постулату Бора энергия фотона hν = E₄ – E₁ . Из рисунка видно,
что Е_4-1= Е_2-4 + Е_1-3–
Е_2-3.

hν=hc/ λ. hc/ λ_{4-1 =}hc/ λ_2-4 + hc/ λ_1-3– hc/ λ_2-3.

1/ λ_4-1= 1/ λ_2-4 + 1/ λ_1-3– 1/
λ_2-3 = 1/500 + 1/ 400 – 1/600 = 34/12000, λ_4-1= 352
(нм).

№5.

Реши самостоятельно.

№ 1. Препарат активностью А = 1,7 ·10¹¹
частиц в секунду помещён в медный контейнер массой 0,5
кг. На сколько повысилась температура контейнера за 1 час, если известно, что
данное радиоактивное вещество испускает альфа-частицы энергией Е₁=
5,3 МэВ. Считать, что энергия всех альфа-частиц полностью переходит во
внутреннюю энергию контейнера. Теплоёмкостью препарата и теплообменом с
окружающей средой пренебречь.

№ 2. Образец, содержащий радий, за 1 с
испускает 3,7⋅10¹⁰ α-частиц, обладающих импульсом 1,0⋅10^–19 кг⋅м/с. За какое время выделится энергия 100
Дж? Масса α-частиц равна 6,7⋅10^–27 кг. Энергией отдачи ядер, γ-излучением
и релятивистскими эффектами пренебречь.

№ 3.

На рисунке представлены энергетические уровни

электронной оболочки атома и указаны
частоты

фотонов, излучаемых и поглощаемых при

переходах между этими уровнями. Какова
частота ν₂₄, если ν₁₃= 7·10¹⁴ Гц, ν₃₂
= 3·10¹⁴ Гц, а при переходе с уровня Е₄ на уровень Е₁излучаются фотоны длиной волны λ = 360 нм?

№ 4. На рисунке изображены
энергетические уровни атома и указаны длины волн фотонов, излучаемых и
поглощаемых при переходах с одного уровня на другой. Экспериментально
установлено, что минимальная длина волны для фотонов, излучаемых при
переходах между этими уровнями, равна λ₀ = 250 нм. Какова величина
λ₁₃, если λ₃₂ = 545 нм, λ₂₄ = 400 нм?

№ 5. Мощность излучения лазерной указки с длиной волны 600нм
равна 2мВт. Определите число фотонов, излучаемых указкой за 1с.

№6. Неподвижная
пылинка массой 0,1мг освещается импульсом
лазерного света с длиной волны $lambda = 0,63 cdot 10^{ - 6} ,!$ 0,63мкм. Определите число поглощённых
пылинкой фотонов, если она в результате действия света приобрела скорость 1мм/с.

№7. Электрон,
имеющий импульс p = 2•10^–24
кг•м/с, сталкивается с покоящимся протоном, образуя атом
водорода в состоянии с энергией E_n
(n = 2). В процессе образования атома излучается фотон. Найдите
частоту ν этого фотона, пренебрегая кинетической энергией атома. Уровни энергии
электрона в атоме водорода задаются формулой E_n = -(13.6/n²) эВ,
где n = 1, 2, 3.

№8. Покоящийся
атом излучает фотон с энергией 16,32•10^-19 Дж в
результате перехода электрона из возбуждённого состояния в основное. Атом в
результате отдачи начинает двигаться поступательно в противоположном
направлении с кинетической энергией 8,81•10^-27 Дж.
Найдите массу атома. Скорость атома считать малой по сравнению со скоростью
света.

№ 9. В сосуде находится разреженный атомарный водород. Атом
водорода в основном состоянии (Е₁
= — 13,6 эВ) поглощает фотон с частотой 3,7•10¹⁵ Гц.
С какой скоростью v
движется вдали от ядра электрон, вылетевший из атома в результате ионизации?
Энергией теплового движения атомов водорода пренебречь.

№ 10.В сосуде находится разреженный атомарный водород. Атом
водорода в основном состоянии (Е₁
= — 13,6 эВ) поглощает фотон с частотой 3,7•10¹⁵ Гц.
С какой скоростью v
движется вдали от ядра электрон, вылетевший из атома в результате ионизации?
Энергией теплового движения атомов водорода пренебречь

Уравнение Эйнштейна для
фотоэффекта.

№ 1. В вакууме
находятся два покрытых кальцием электрода, к которым подключен конденсатор
ёмкостью С. При длительном освещении катода светом с длиной волны λ=100нм
фототок, возникший вначале, прекращается, а на конденсаторе появляется заряд q
= 9,6•10^-10 Кл. Работа выхода электрона из кальция А=4,42•10^-19
Дж. Определите ёмкость конденсатора С.

Решение.
Напряжение на конденсаторе U будет равно задерживающей разности потенциалов U_з,
которое можно найти из уравнения Эйнштейна для фотоэффекта: hν = A_вых+Е_к, Е_к=еU_з, V=c/λ, т.е. v=3 ·10⁸/10^-7=3·10¹⁵Гц.
Тогда
, Отсюда:

1/1,6·10^-19(6,63·10^—34·3·1015-4,42·10^-19)=9,6В.

Находим емкость конденсатора:

9,6•10^-10/9,6=10^-10Ф.

№ 2. Уровни энергии электрона в
атоме водорода задаются формулой

эВ, где n = 1, 2, 3,
…

При переходе из состояния Е₂ в состояние Е₁ атом
испускает фотон.
Поток таких фотонов падает на поверхность фотокатода.
Запирающее напряжение для фотоэлектронов, вылетающих с поверхности фотокатода U_зап
= 7,4 В.
Какова работа выхода А_вых фотоэлектронов с поверхности фотокатода?

Решение.

Энергия фотона:
hν = E₂ — E₁ .
Уравнение Эйнштейна для фотоэффекта: hν = A_вых —
eU_зап.

Е₁=-13,6/1²=-13,6эВ,
Е₂=-13,6/2²=-3,4эВ, Е₂-Е₁=-10,2эВ=-16,32·10^-19Дж.

Отсюда
A_вых =(E₂ — E₁) —
eU_зап , А_вых= -16,32·10^-19Дж+1,6·10^-19·7,4=4,54,5·10^–19
Дж

Ответ: А_вых ≈ 4,5·10^–19 Дж ≈ 2,8
эВ.

№3.
Уровни энергии электрона в
атоме водорода задаются формулой

, где n = 1, 2, 3, … . При переходе
атома из состояния Е₂в
состояние Е₁ атом испускает фотон. Попав на поверхность
фотокатода,                                         фотон выбивает
фотоэлектрон. Длина волны света, соответствующая                                         красной
границе фотоэффекта для материала поверхности
фотокатода,                                                 λкр = 300 нм. Чему максимальная возможная скорость
фотоэлектронов?

Решение:

№5.

Решение.

Реши самостоятельно
№ 1. В сосуде находится разрежённый атомарный
водород. Атом водорода в основном состоянии (Е₁ = – 13,6 эВ)
поглощает фотон и ионизуется. Электрон, вылетевший из атома в результате
ионизации, движется вдали от ядра со скоростью 1000 км/с. Какова
частота поглощённого фотона? Энергией теплового движения атомов водорода
пренебречь.

№
2.
В
двух опытах по фотоэффекту металлическая пластинка облучалась светом с длинами
волн соответственно λ₁=350 нм. и λ₂=540 нм.
Максимальные скорости фотоэлектронов в первом и во втором опытах отличались в 2
раза. Какова работа выхода с поверхности металла?

№
3. Для увеличения яркости изображения слабых источников
света используется вакуумный прибор – электронно-оптический преобразователь. В
этом приборе фотоны, падающие на катод, выбивают из него фотоэлектроны, которые
ускоряются разностью потенциалов U = 15000 В и бомбардируют
флюоресцирующий экран, рождающий вспышку света при попадании каждого электрона.
Длина волны падающего на катод света λ₁=820 нм, а
света, излучаемого экраном, λ₂= 410 нм. Во
сколько раз N прибор увеличивает число фотонов, если 1
фотоэлектрон рождается при попадании на катод в среднем k = 10 фотонов?
Работу выхода электронов принять равной 1эВ. Считать, что энергия
падающих на экран электронов переходит в энергию света без потерь.

№
4. Уровни энергии электрона в атоме водорода задаются
формулой E_n = -13,6/n² эВ, где n =1, 2, 3, … . При переходе
атома из состояния E₂ в состояние E₁, атом испускает
электрон. Попав на поверхность фотокатода, фотон выбивает фотоэлектрон. Длина
волны света, соответствующая красной границе фотоэффекта для материала
поверхности фотокатода равна 300 нм. Чему равна максимальная возможная
скорость фотоэлектронов?

№
5.
Фотокатод облучают светом длиной волны λ₁=
300нм. Красная граница фотоэффекта для вещества фотокатода λ₂= 450 нм. Какое напряжение между анодом и катодом нужно создать,
чтобы фототок прекратился?

№6.Уровни энергии
электрона в атоме водорода задаются формулой

, где n = 1, 2, 3, … . При переходе
атома из состояния Е₂в                                        состояние
Е₁ атом испускает фотон. Попав на поверхность фотокатода,
фотон выбивает фотоэлектрон. Длина волны света, соответствующая                                               красной
границе фотоэффекта для материала поверхности фотокатода,
λкр = 300 нм. Чему максимальная возможная скорость
фотоэлектронов?

№ 7.Какова максимальная скорость электронов, выбиваемых из металлической пластины светом с длиной волны λ = 3•10^-7 м, если красная граница фотоэффекта λ_кр = 540 нм?
№8. Фотоны, имеющие энергию 5 эВ, выбивают электроны с поверхности металла. Работа выхода электронов из металла равна 4,7 эВ. Какой импульс приобретает электрон при вылете с поверхности металла?
№ 9. В вакууме находятся два покрытых кальцием электрода, к которым подключен конденсатор емкостью С = 8000 пФ. При длительном освещении катода светом c частотой ν = 10¹⁵ Гц фототок, возникший вначале, прекращается. Работа выхода электронов из кальция А = 4,42•10^-19 Дж. Какой заряд q при этом оказывается на обкладках конденсатора?
№ 10. Фотокатод, покрытый кальцием (работа выхода 4,42•10^-19 Дж), освещается светом с длиной волны 300 нм. Вылетевшие из катода электроны попадают в однородное магнитное поле с индукцией 8,3•10^-4 Тл перпендикулярно линиям индукции этого поля. Каков максимальный радиус окружности, по которой движутся электроны

Закон радиоактивного распада.

№ 2.Активность препарата ³²P равна 2 мкКи.
Сколько весит такой препарат?
Решение.

Закон радиоактивного распада: N(t) = N₀e^-λt,где N₀
— количество радиоактивных ядер в произвольно выбранный начальный момент
времени t = 0, N(t) — количество радиоактивных ядер, не распавшихся к
моменту времени t, λ — постоянная распада (вероятность распада в единицу
времени). λN — активность (интенсивность излучения) радиоактивного препарата,
измеряется в Ки, 1 Ки = 3.7·10¹⁰ распадов/с. T_1/2
— период полураспада данного ядра (время, в течение которого количество
радиоактивных ядер уменьшается в два раза) равен для ³²P
14.5 суток. Период полураспада T_1/2 связан с постоянной распада
λ соотношением T_1/2 = ln 2/λ.
Количество ядер в образце массой m грамм

где N_A — число Авогадро, A — массовое число. Активность
препарата

тогда его масса будет

7.1·10^-12 г.

№ 3.
Определить период полураспада радиоактивного изотопа, если 5/8 начального
количества ядер этого изотопа распалась за время t = 849 c.

Решение.

Используя
закон радиоактивного распада , найдем

Прологарифмировав
последнее выражение , найдем .
Тогда период полураспада

мин.

№ 4. Природный уран состоит на из
изотопа U
и на —
из .
По современным представлениям, все элементы тяжелее железа образовались при
взрывах сверхновых звёзд, а после этого из получившихся газопылевых облаков
возникли звёзды следующего «поколения», в частности, Солнце и планеты Солнечной
системы. По-видимому, в этих выбросах всех изотопов урана было примерно
поровну. Оцените, сколько лет назад произошёл тот выброс вещества, из которого
сформировалась наша Земля. Период полураспада, то есть время, в течение
которого число атомов данного изотопа уменьшается в 2 раза, для равно
лет,
а для —
лет.

Решение                                                                                                                                                Обозначим
количество атомов каждого изотопа непосредственно после взрыва сверхновой звезды
через N₀. Тогда
через время T₁ после
взрыва количество атомов стало
равно N₀/2, через
время 2Т₁ — стало равно N₀/2²
,
и так далее. Очевидно, что через время t=nT₁ после
взрыва, равное периодам
полураспада ,
количество атомов этого изотопа стало равно N₁=N₀/2ⁿ .                                                                                                        Аналогично,
за то же самое время t=rT₂, равное периодам
полураспада ,
количество атомов данного изотопа стало равно N₂=N₀/2^k .
По условию задачи, $begin{displaymath} n_{1} = mathchoice{displaystylefrac{N_1}{N_1+N_2}}{disp... ...ystylefrac{N_2}{N_1+N_2}}{displaystylefrac{N_2}{N_1+N_2}}. end{displaymath}$       Отсюда
$begin{displaymath} mathchoice{displaystylefrac{n_2}{n_1}}{displaystylefra... ...tylefrac{2^n}{2^k}}{displaystylefrac{2^n}{2^k}} = 2^{n-k}. end{displaymath}$

Учитывая, что t=nT₁+kT₂ ,
получаем систему из двух уравнений относительно неизвестных и
.
Решая её, найдём, например, :

$begin{displaymath} k = mathchoice{displaystylefrac{lg(n_2/n_1)}{lg 2}}{d... ...ystylefrac{T_1}{T_2-T_1}}{displaystylefrac{T_1}{T_2-T_1}}. end{displaymath}$

Значит, искомое
время равно
$begin{displaymath} t = kT_{2} = mathchoice{displaystylefrac{lg (n_2/n_1)}... ...frac{T_1 T_2}{T_2-T_1}} approx 6 cdot 10^{9} mbox{лет}. end{displaymath}$

№ 5. Конечным продуктом радиоактивного распада
является свинец Период полураспада составляет 4,5•109 лет. Определите возраст
минерала, в котором число атомов урана и свинца одинаково.

Дано:

Решение:

По закону
убывания числа радиоактивных атомов со временем:

значит,

Реши
самостоятельно

№1. . Радиоактивный фосфор, использующийся для диагностики
болезней кровообращения, имеет период полураспада 14,3 дня. Найдите активность
образца с числом атомов N = 5 • 1016.

№.2. Определить какая часть начального количества начального
количества ядер радиоактивного изотопа распадется за время t, равное
двум периодам полураспада.

№ 3 .Образец радиоактивного радия находится в
закрытом сосуде. Ядра радия испытывают распад с
периодом полураспада 11,4 суток. Определите число атомов радия, которые
останутся нераспавшимися через 34,2 суток, если образец в момент помещения его
в сосуд содержал атомов радия.

№4.Имеется 8 кг
радиоактивного цезия. Определите массу нераспавшегося цезия после 135 лет
распада, если период полураспада 27 лет. (m= 0,25
кг).

№ 5.Имелось некоторое
количество радиоактивного серебра. Масса серебра уменьшилась в 8 раз за 810
суток. Определите период полураспада. (Т= 270 суток).

№ 6.
Сколько процентов ядер радиоактивного йода–131 с периодом
полураспада 8 суток останется 16 сут?

Элементарные частицы.

Задача
1.

Ядро покоящегося нейтрального атома, находясь в однородном
магнитном поле индукцией В, испытывает α-распад.
При этом рождается α-частица и тяжёлый ион нового элемента. Трек
тяжёлого иона находится в плоскости, перпендикулярной направлению магнитного
поля. Начальная часть трека напоминает дугу окружности радиусом
.Выделившаяся при α-распаде энергия ΔЕ целиком
переходит в кинетическую энергию продуктов распада. Масса α-частицы
равна m_a, её заряд 2е.
Найти модуль отношения заряда к массе │q/М│ для тяжёлого иона.

Решение.
1. На
основании закона сохранения зарядов модули зарядов продуктов распада будут
равны q_и = q_а = q.

2.
Так как нейтральный атом в начале покоился, то его импульс равен нулю,
следовательно, и суммарный импульс продуктов распада тоже равен нулю (основание
– закон сохранения импульса). Отсюда следует, что модули импульсов продуктов
распада будут равными. m_aυ_a= M υ_и.

3.
Ион под действием силы Лоренца начинает двигаться по дуге радиусом R. Сила Лоренца сообщает иону
центростремительное ускорение: q_иBυ =Mυ²/R, q_и BR = M υ_и.

4. А
также по условию имеем ΔЕ = Е_а + Е_и , 2 ΔЕ = m_aυ_a²+ M υ_и²

Решая
систему уравнений (выделены красным), получим: υ_a = M υ_и/m_a, υ_и = q_и BR/ M, υ_a = q_и BR/m_a_. Подставляя значение
скоростей продуктов распада в 4-е уравнение, получим
2 ΔЕ = m_a(q_и BR/m_a)²+ M(q_и BR/ M) ²,

2 ΔЕ = q²B²R²/m_a+
q²B²R²/ M, q/ M = (2 ΔЕ — q²B²R²/m_a)
/ qB²R². Умножив числитель и знаменатель на q и, выполнив ряд алгебраических
преобразований, получим q/ M =(q/m_а) ( (2 ΔЕ m_а / q²B²R²) -1) ,

q/ M =(2е/m_а) ( (2 ΔЕ m_а / 4е²B²R²)
-1)

№ 3. Свободный пион (π⁰-мезон) с энергией
покоя 135 МэВ движется со скоростью V, которая значительно меньше
скорости света.
В результате его распада образовались два γ-кванта, причём один из
них распространяется в направлении движения пиона, а другой – в
противоположном направлении.
Энергия одного кванта на 10% больше, чем другого.
Чему равна скорость пиона до распада?

Решение.

Пион, движущийся со скоростью V, имеет импульс p = mV и энергию , где m – масса пиона.

Энергия γ-кванта E_γ и его импульс р_γ
связаны соотношением:

При распаде пиона на два кванта энергия системы и её импульс сохраняются:
Разделив второе уравнение на первое, получим: .

По условию задачи E₁ =1,1⋅ E₂ , так что

Ответ: V ≈1,43⋅10⁷ м/с .

Реши самостоятельно

№1.π₀-мезон массой 2,4•10^-28
кг распадается на два γ-кванта. Найдите модуль импульса одного из
образовавшихся γ-квантов в системе отсчета, где первичный π₀-мезон
покоится.

№ 2. Атом мюония состоит из
неподвижного протона и отрицательно заряженного мюона массой m = 206m_e,
где m_e — масса электрона, и зарядом, равным заряду
электрона e. Для ближайшей к протону орбиты мюона выполняется условие
квантования 2π rp = h, где r — радиус орбиты, р —
импульс мюона, h — постоянная Планка. Найдите радиус этой орбиты.

№.3. Рассматриваемая
реакция идёт с поглощением энергии 1,3 МэВ. При какой пороговой
(минимальной) скорости α-частиц,
бомбардирующих неподвижную мишень, такая реакция могла пойти? Масса α-частицы $m_{He} = 6,6 cdot 10^{ - 27} ,!$ 6,6·10 ^-27кг.

Ядерные реакции.

№1. Вычислите энергию связи ядра атома
дейтерия.

Дано:

____________________

Решение:

Энергия связи ядра равна

где Δm – разность суммы масс
свободных частиц, входящих в состав ядра, и массы ядра, с – скорость
света в вакууме. Для нахождения разности масс отыскиваем в справочнике по
физике сведения о массах протона ,
нейтрона , электрона
и атома дейтерия .
Для нахождения массы ядра дейтерия необходимо
вычесть из массы атома дейтерия массу электрона, находящегося на его
оболочке:

Но ,
поэтому

№ 2. Вычислите энергетический выход
ядерной реакции

Решение:

Для вычисления энергетического выхода ядерной реакции необходимо
найти разность масс частиц, вступающих в реакцию, и частиц – продуктов реакции.
В реакции участвуют атомные ядра, но в справочных таблицах обычно даются
сведения лишь о массах атомов. Можно найти массу каждого атомного ядра
вычитанием массы электронов оболочки из массы атома. Можно поступить иначе.
Если в уравнении ядерной реакции слева и справа пользоваться только массами
атомов (т.е. массой атома водорода, а не массой протона слева, и массой атома
гелия, а не массой альфа-частицы справа), то из-за одинаковости числа
электронов в атомах, вступающих в реакцию, и в продуктах реакции их вычитание
осуществляется автоматически при нахождении разности масс. Таким образом, для
решения задачи можно воспользоваться сведениями из справочника о массах атомов.

_____________________

Вычислим энергетический выход
при изменении массы на 1 а.е.м.:

Выход ядерной реакции равен

Реши самостоятельно.

№ 1.Найти с помощью табличных значений масс атомов:
а) среднюю энергию связи на один нуклон в ядре О¹⁶;
б) энергию связи нейтрона и α-частицы в ядре B¹¹;
в) энергию, необходимую для разделения ядра O¹⁶ на четыре одинаковые
частицы.

№2. Неподвижное ядро
франция Fr с массовым числом А = 221 претерпевает альфа-распад.
Определите энергетический выход данной реакции, если кинетическая энергия
образовавшегося ядра астата At равна Е_At = 0,1184
МэВ, а его атомный номер Z = 85. При расчетах учесть движение
образовавшихся ядер и считать, что скорости частиц много меньше скорости
света.

№3. При реакции синтеза образуется
ядро изотопа гелия и нейтрон и выделяется энергия Е = 3,27 МэВ. Какую
кинетическую энергию уносит ядро изотопа гелия, если суммарный импульс
исходных частиц равен нулю, а их кинетическая энергия пренебрежимо мала по
сравнению с выделившейся?

№4. Ядро покоящегося нейтрального атома,
находясь в однородном магнитном поле индукцией В, испытывает α-распад.
При этом рождаются α-частица и тяжелый ион нового элемента. Масса α-частицы
равна m_α, ее заряд равен 2e, масса тяжелого иона равна
M. Выделившаяся при α-распаде энергия ΔE целиком переходит в
кинетическую энергию продуктов реакции. Трек тяжелого иона находится в
плоскости, перпендикулярной направлению магнитного поля. Начальная часть этого
река напоминает дугу окружности. Найдите радиус этой окружности.

Комбинированные
задачи.

№ 1. Металлическая пластина облучается
светом с частотой 1,6·10¹⁵Гц. Работа выхода из данного металла равна
3,7эВ. Вылетающие из пластины электроны попадают в однородное электрическое
поле напряжённостью 130В/м. Вектор напряжённости направлен перпендикулярно
поверхности пластины. Какова максимальная энергия фотоэлектронов на
расстоянии 10см от пластины?

Решение.
Электрическое поле совершает работу по перемещению электрона А=qU.
Работа поля, с другой стороны, равна изменению кинетической энергии
электрона    А=Е_к2-Е_к1.                                                                                                                                                     Получаем
Е_к2-Е_к1= qU. Тогда Е_к2= Е_к1=+qU.
Из уравнения Эйнштейна для фотоэффекта hv=А_вых+Е_к1 получаем, что Е_к1= hv-А_вых.Окончательно
Е_к2= hv-А_вых+ qU., где U=Ed.                                                                                                  Подставив
данные, получаем Е_к2= 4,8·10^-19Дж.

№2. Электроны, вылетевшие в
положительном направлении оси Ох под действием света с катода фотоэлемента,
попадают в электрическое и магнитное поля. Какой будет работа выхода с
поверхности фотокатода, чтобы в момент попадания самых быстрых электронов в
область полей, действующих на них, сила была направлена вдоль оси Оу в
положительном направлении? Частота света 6,5·10¹⁴Гц, напряжённость
электрического поля 300В/м, индукция магнитного поля 1мТл.

Решение.                                                                                                                                                  hv=А_вых+Е_к .
                                                                      По
правилу левой руки находим, что сила Лоренца направлена влево и равна F_Л=qBv, сила Кулона направлена вправо и равна F_к=qE.                                                                                                       Приравняв
правые части формул и выразив скорость, получим, что v=Е/В.    Из уравнения Эйнштейна   А_вых=
hv-Е_к., где Е_к=mv/2.
Подставив
числовые значения, получим, А_вых=2·10^-20Дж.

Реши самостоятельно.

№ 1. Фотоэлектроны, выбитые рассеянным светом частоты 6,7·10¹⁴Гц
из металла с работой выхода 1,89эВ, попадают в однородное электрическое
поле. Какова напряжённость поля, если длина тормозного пути у фотоэлектронов,
чья начальная скорость максимальна и направлена вдоль силовых линий
электрического поля, составляет 8,75мм?

№2. Фотокатод,
покрытый кальцием ( Ав=4,42·10^-19 Дж), освещается светом, у которого
длина волны 300 нм. Вылетевшие из катода электроны попадают в однородное
магнитное поле индукцией 8,3·10^-4 Тл перпендикулярно линиям индукции
этого поля. Чему равен максимальный радиус окружности, по которой движутся
электроны? Ответ выразить в мм.

№ 3. Фотокатод (работа выхода А = 4,42*10^-19Дж) освещается
светом с частотой ν. Вылетевшие из катода электроны попадают в однородное
магнитное поле индукцией В=4*10^-4 Тл перпендикулярно линиям индукции
и движутся по окружности, у которой максимальный радиус R=10мм. Чему равна
частота падающего света?

Источник

Ядерная реакция – процесс взаимодействия ядра с элементарной частицей или другим ядром, в процессе которого происходит изменение строения и свойств ядра. Например, испускание ядром элементарных частиц, его деление, испускание фотонов с высокой энергией (гамма-квантов). Одним из результатов ядерных реакций является образование изотопов, не существующих в естественных условиях на Земле.

Протекать ядерные реакции могут при бомбардировке атомов быстрыми частицами (протоны, нейтроны, ионы, альфа-частицы).

Больше полезной информации по разным темам – у нас в телеграм.

Ядерные реакции

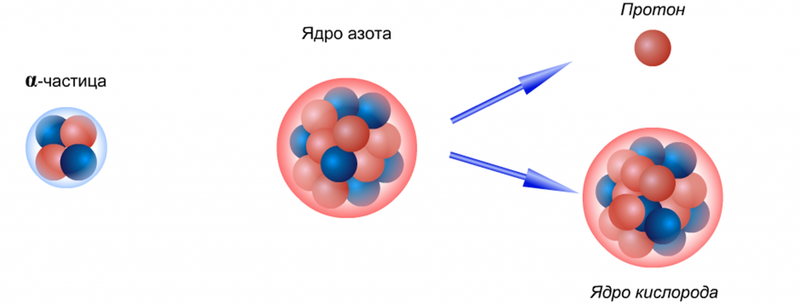
Одна из первых проведенных людьми ядерных реакций была осуществлена Резерфордом в 1919 году с целью обнаружения протона. Тогда еще не было известно, что ядро состоит их нуклонов (протоны и нейтроны). При расщеплении многих элементов была обнаружена частица, являющаяся ядром атома водорода. На основе опытов Резерфорд сделал предположение, что данная частица входит в состав всех ядер.

Эта реакция как раз и описывает один из экспериментов ученого. В опыте выше газ (азот) бомбардируется альфа-частицами (ядра гелия), которые, выбивая из ядер азота протон, превращают его в изотоп кислорода. Запись этой реакции выглядит следующим образом:

При решении задач на ядерные реакции следует помнить, что при их протекании выполняются классические законы сохранения: заряда, момента импульса, импульса и энергии.

Также существует закон сохранения барионного заряда. Это значит, что число нуклонов, участвующих в реакции, остается неизменным. Если мы посмотрим на реакцию, то увидим, что суммы массовых чисел (цифра сверху) и атомных чисел (снизу) в правой и левой частях уравнения совпадают.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.

Удельная энергия связи ядер

Как известно, внутри ядра на расстояниях порядка его размера действует одно из фундаментальных физических взаимодействий – сильное взаимодействие. Чтобы его преодолеть и «развалить» ядро, необходимо большое количество энергии.

Энергия связи ядра – минимальная энергия, необходимая, чтобы расщепить ядро атома на составляющие его элементарные частицы.

Масса любого атомного ядра меньше, чем масса составляющих его частиц. Разность масс ядра и его составляющих нуклонов называется дефектом масс:

Числа Z и N легко определяются при помощи таблицы Менделеева, а почитать о том, как это делается, можно тут. Энергия связи высчитывается по формуле:

Энергия ядерных реакций

Ядерные реакции сопровождаются энергетическими превращениями. Существует величина, называемая энергетическим выходом реакции и определяемая формулой

Дельта M – дефект масс, но в данном случае это разница масс между начальными и конечными продуктами ядерной реакции.

Реакции могут протекать как с выделением энергии, так и с ее поглощением. Такие реакции называются соответственно экзотермическими и эндотермическими.
Чтобы протекала экзотермическая реакция, необходимо выполнение следующего условия: кинетическая энергия начальных продуктов должна быть больше кинетической энергии продуктов, образовавшихся в ходе реакции.

Эндотермическая реакция возможна в случае, когда удельная энергия связи нуклонов в исходных продуктах меньше удельной энергии связи ядер конечных продуктов.

Примеры решения задач по ядерной реакции

А теперь пара практических примеров с решением:

Даже если Вам попалась задачка со звездочкой, стоит помнить – нерешаемых задач не существует. Студенческий сервис поможет выполнить любое задание.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Задачи на Состав атома и ядерные реакции с решениями

Название величины

Обозначение

Единица измерения

Формула

c

м/с

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Краткая теория для решения Задачи на Состав атома и ядерные реакции.

Ядерная физика. Планетарная модель атома. Нуклонная модель ядра. Ядерные реакции.

Ядерные реакции. Энергия связи

Задачи на Состав атома и ядерные реакции с решениями

Название величины

Обозначение

Единица измерения

Формула

c

м/с

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Краткая теория для решения Задачи на Состав атома и ядерные реакции.

Ядерные реакции

Удельная энергия связи ядер

Энергия ядерных реакций

Примеры решения задач по ядерной реакции