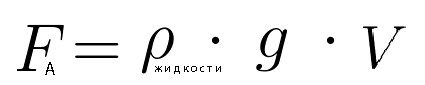Задачи на закон архимеда егэ - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

На графике показана зависимость модуля силы Архимеда F_Арх, действующей на медленно погружаемый в жидкость кубик, от глубины погружения x. Длина ребра кубика равна 10 см, его нижнее основание всё время параллельно поверхности жидкости. Определите плотность жидкости. Ответ приведите в килограммах на кубический метр. Ускорение свободного падения принять равным 10 м/с².

В четыре сосуда, вертикальные сечения которых показаны на рисунке, налита вода. Одна клеточка на рисунке соответствует 10 см.

В одном из этих сосудов гидростатическое давление на дно максимально. Чему оно равно? (Ответ дайте в паскалях.) Ускорение свободного падения принять равным 10 м/с².

Кубик из пробки с ребром 10 см опускают в воду. Каково отношение объёма кубика, находящегося над водой, к объёму кубика, находящегося под водой? Плотность пробки 0,25 г/см³.

Пустой цилиндрический стеклянный стакан плавает в воде, погрузившись на половину своей высоты. Дно стакана при плавании горизонтально, плотность стекла 2500 кг/м³. Чему равно отношение внутреннего объёма стакана к его наружному объёму? Ответ представьте в виде десятичной дроби, округлив до десятых долей.

Пройти тестирование по этим заданиям

Источник

4. Статика и механические колебания

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Гидростатика. Сила Архимеда

Закон Архимеда

На погружённое в жидкость или газ тело действует выталкивающая сила, и равная весу среды, объём которой равен объёму тела.

Выталкивающая сила (сила Архимеда) равна

[F_A=rho_text{ж} g V_text{пчт}] где (displaystyle V_text{пчт}) — объём погружённой части тела, (displaystyle rho_text{ж}) — плотность жидкости.

Плавание тел

Рассмотрим тело плотности (rho) и жидкость плотности (rho_0). Допустим, тело полностью погрузили в жидкость и отпустили. Сразу после отпускания на тело действуют лишь сила тяжести (mg) и архимедова сила (F_A). Если объём тела равен V, то

[mg=rho g V,] [F_A=rho_0 g V]

Имеются три возможности дальнейшего движения тела.

Сила тяжести больше архимедовой силы: (displaystyle mg > F_A), или (displaystyle rho>rho_0). В этом случае тело тонет.

Сила тяжести равна архимедовой силе: (displaystyle mg = F_A), или (displaystyle rho=rho_0). В этом случае тело остаётся неподвижным в состоянии безразличного равновесия.

Сила тяжести меньше архимедовой силы: (displaystyle mg < F_A), или (displaystyle rho<rho_0). В этом случае тело всплывает, достигая поверхности жидкости.

Таким образом, условие плавания тела можно записать в виде неравенства (displaystyle rholeq rho_0).

Два жестко связанные друг с другом одинаковых бруска, имеющие толщину (h=5) см, плавают в воде так, что уровень воды приходится на границу между ними (см. рисунок). Насколько изменится глубина погружения, если на два бруска положить ещё пять таких же? (Ответ дайте в сантиметрах.)

Два одинаковых связанных бруска погрузились наполовину в воду (из условия). Пусть
(displaystylerho_1) – плотность материала, из которого изготовлены бруски, а (displaystyle V) – объем двух брусков. Тогда масса этих брусков будет равна [displaystyle m=rho_1V] Сила, с которой льдинки действуют на воду, равна силе тяжести [displaystyle F=mg=rho_1Vg] Сила, с которой бруски выталкиваются из воды, равна силе Архимеда [F_text{Арх}=rho gfrac{V}2,] где (displaystyle rho) – плотность воды, (displaystyle frac{V}2) – объем погруженного в воду тела (бруски погружены только
наполовину). Так как они плавают на поверхности воды, то эти силы уравновешивают друг друга, значит, имеем: [rho_1Vg=rho gfrac{V}2,] откуда (displaystyle rho_1=dfrac{rho}2,) то есть плотность материала, из которого сделаны бруски в 2 раза меньше плотности воды. Это говорит о том, что если взять семь брусков, то они также будут погружены наполовину, то есть на величину [frac72h=3,5cdot5text{ см}=17,5 text{ см}.] Глубина увеличится на (displaystyle 17,5 -5=12,5) см.

Ответ: 12,5

Подвешенный на нити алюминиевый кубик целиком погружен в воду и не касается дна сосуда. Плотность алюминия равна (displaystyle rho_text{ ал}=2700 text{ кг}/text{м}^3. ) Какова длина ребра куба, если выталкивающая сила равна (displaystyle F_text{Арх}=33,75text{ Н}?) (Ответ дайте в сантиметрах.)

Выталкивающая сила равна по определению [F_text{Арх}=rho_text{в} gV,] где (displaystyle rho_text{в}) – плотность жидкости, в которую погружен кубик, (displaystyle V) – объем погруженной части тела. Так как куб погружен целиком, то (displaystyle V=a^3), получим: [F_text{Арх}=rho_text{в} ga^3] Выразив из этой формулы сторону (displaystyle a), получаем [a=sqrt[3]{frac{F_text{Арх}}{rho_text{в}g }}] Подставив значения в формулу, получим: [a=sqrt[3]{frac{33,75text{ Н}}{10text{ м}/{c^2}cdot1000text{ кг}/text{м}^3}}=0,15text{ м}=15text{ cм }]

Ответ: 15

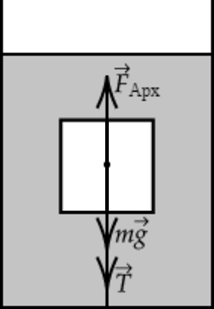
Однородный цилиндр, изготовленный из материала плотностью (displaystyle rho=600) кг/м(^3), с радиусом основания (displaystyle R=25) см и высотой (displaystyle H=20) см привязан нитью ко дну сосуда, наполненного водой. Найдите силу натяжения нити. (Ответ дайте в ньютонах.)

Сделаем рисунок с указанием сил, действующих в системе. Можем записать II закон Ньютона в векторной форме: [vec T+vec F_text{Арх}+mvec g=mvec a,] так как цилиндр покоится, то ускорение равно нулю, в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: [T- F_text{Арх}+mg=0, quad(1)] массу цилиндра можно рассчитать, исходя из формулы (displaystyle rho=frac {m}{V} Rightarrow m=rho V,) где V – объем цилиндра, который можно вычислить по формуле [V=pi R^2 H] Из формулы (1) выразим силу натяжения нити T:[T=F_text{Арх}-mg=rho_text{в}gV-rho gV=Vg(rho_text{в}-rho)=pi R^2 Hg(rho_text{в}-rho),] где (displaystyle rho_text{в}) – плотность воды, подставим в получившееся выражение численные значения:[T=3,14cdot0,25^2text{ м}cdot0,2text{ м}cdot 10text{ м}/text{с}^2 cdot (1000text{ кг}/text{м}^3-600text{ кг}/text{м}^3)=157text{ Н }]

Ответ: 157

Однородный кубический предмет с ребром (displaystyle a=18) см опускают в эфир. На сколько сантиметров длина части стороны, находящейся под жидкостью отличается от длины части над эфиром? Плотность вещества, из которого изготовлен куб равна (displaystyle rho_text{др}=340) кг/м(^3), плотность эфира (displaystyle rho_text{э}=720) кг/м(^3). (Ответ дайте в сантиметрах.)

Запишем условие равновесия кубика на поверхности эфира: [F_text{ Арх}=mg, quad(1)] где (F_text{ Арх}) – выталкивающая сила, действующая на брусок, (displaystyle m) – масса кубика, которую можно рассчитать, исходя из формулы (displaystyle rho_text{др}=frac {m}{V} Rightarrow m=rho_text{др} V,) где V – объем кубика, который можно вычислить по формуле [V=a^3.] Выталкивающая сила равна: [F_text{ Арх}=rho_text{э}gV_text{пчт},] где (displaystyle V_text{пчт}) – объем погруженной части кубика,[V_text{пчт}=xa^2,] где (displaystyle x) – длина части стороны, находящейся под эфиром, значит, выражение (1) можно записать в следующем виде: [rho_text{э}gxa^2=rho_text{др}a^3] [rho_text{э}x=rho_text{др}a, text{ выразим } x=frac{rho_text{др}a}{rho_text{э}}.] Пусть (displaystyle y) – длина части стороны, находящейся над эфиром, можем записать: [y=a-x,] искомая разница длин (displaystyle delta=y-x=a-2x=a-2cdot dfrac{rho_text{др}a}{rho_text{э}}=a(1-2cdot dfrac{rho_text{др}}{rho_text{э}})) подставим в получившееся выражение численные значения: [displaystyle delta=0,18text{ м}(1-2cdot dfrac{340text{ кг}/text{м}^3}{720text{ кг}/text{м}^3})=0,01text{ м}=1text{ см}]

Ответ: 1

В некий резервуар было налито 1000 литров жидкости плотностью (displaystyle rho_1=1500) кг/м(^3). В этой жидкости в равновесии плавает кубик, погруженный в воду на (displaystyle x=130) см. Длина стороны кубика равна (displaystyle a=200) см. В сосуд доливают ещё 1000 литров жидкости плотностью (displaystyle rho_2=1100) кг/м(^3) и перемешивают. Чему после этого будет равна длина погруженной части кубика при плавании в равновесии? Обе жидкости хорошо смешиваются, и при смешивании суммарный объём сохраняется. (Ответ дайте в метрах.)

В условии сказано, что жидкости хорошо перемешиваются. Из этого следует, что при смешивании получается новая жидкость, плотность которой является средним арифметическим изначальных, так как взятые объемы одинаковы. [rho_text{нов}=dfrac{rho_1+rho_2}{2}] Так как кубик плавает на поверхности, то можно записать: [mg=F_text{Арх},] сила тяжести, действующая на тело не изменяется, значит, выталкивающая сила тоже остается постоянной. Сначала сила Архимеда равна:[F_text{Арх1}=rho_1 g V_text{пчт1},] где (displaystyle V_text{пчт1}=a^2x) – объем погруженной части куба до смешивания. После смешения жидкостей в сосуде: [F_text{Арх2}=rho_text{нов} g V_text{пчт2}=dfrac{rho_1+rho_2}{2}g V_text{пчт2},]где (displaystyle V_text{пчт2}=a^2y) – объем погруженной части куба до смешивания, (displaystyle y) – длина погруженной части стороны куба после смешивания жидкостей. Можем приравнять получившиеся выражения, получим [rho_1 g a^2x=dfrac{rho_1+rho_2}{2} g a^2y] [rho_1x=dfrac{rho_1+rho_2}{2}y,] выразим отсюда y: [y=frac{2rho_1 x}{rho_1+rho_2},] подставим в получившееся выражение численные значения: [y=frac{2cdot1500text{ кг}/text{м}^3 cdot1,3text{ м}}{1500text{ кг}/text{м}^3+1100text{ кг}/text{м}^3}=1,5text{ м}]

Ответ: 1,5

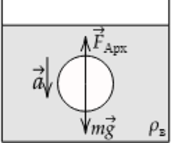
Стеклянный шарик опускается в воде с ускорением (displaystyle a=6) м/с(^2). Найти плотность стекла. Плотность воды (displaystyle rho_text{в}=1000) кг/м(^3). Силами вязкого трения пренебречь. (Ответ дайте в кг/м(^3).)

При движении шарика в воде на него действует сила тяжести (displaystyle mvec g) и сила Архимеда (displaystyle F_text{Арх}). Сделаем рисунок с указанием сил, действующих в системе. Можем записать 2 закон Ньютона в векторной форме: [vec F_text{Арх}+mvec g=mvec a,] в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: [mg- F_text{Арх}=ma,] Отсюда с учетом выражения для силы Архимеда (displaystyle F_text{Арх}=rho_text{в} g V), где V – объем шарика, а
(displaystyle rho_text{в}) – плотность воды, получим: [mg- rho_text{в} g V=ma,] Выразим массу шарика:[m=frac{rho_text{в} g V}{g-a}.] Исходя из формулы, плотность стекла равна [displaystyle rho_text{ст}=frac {m}{V}=frac{rho_text{в} g V}{(g-a)V}=frac{rho_text{в} g }{g-a},] подставим в получившееся выражение численные значения: [rho_text{ст}=frac{1000 text{ кг}/text{м}^3cdot 10text{ м}/text{с}^2 }{10text{ м}/text{с}^2-6text{ м}/text{с}^2}=2500text{ кг}/text{м}^3]

Ответ: 2500

Однородный шарик, изготовленный из материала плотностью (displaystyle rho=2000) кг/м(^3) погружен в воду. Чему равен радиус шара, если выталкивающая сила равна
(displaystyle F_text{Арх}=100) Н? (Ответ дайте в сантиметрах и округлите до целых.)

Выталкивающая сила равна по определению [F_text{Арх}=rho_text{в} gV_text{пчт},] где (displaystyle rho_text{в}) – плотность воды, (displaystyle V_text{пчт}) – объем погруженной части тела. Так как шар полностью опущен в воду, то [V_text{пчт}=frac43pi R^3,] где (displaystyle R) – радиус шара, получим: [F_text{Арх}=rho_text{в} gfrac43pi R^3, (1)] выразим из формулы R: [R=sqrt[3]{frac{3F_text{Арх}}{4rho_text{в}gpi}}] Подставив значения в формулу, получим: [R=sqrt[3]{frac{3 cdot100text{ Н}} {4 cdot1000 text{ кг}/text{м}^3cdot10text{ м}/{c^2}cdot3,14}} approx0,13text{ м}=13text{ см }]

Ответ: 13

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

В этой статье представляю задачи, связанные с плаванием тел и силой Архимеда. Как обычно, сначала пытаемся решить задачи простые, а затем перейдем к более сложным, которые вы найдете в следующей статье.

Задача 1. В воду погружен стеклянный кубик с ребром 10 см. Нижняя его грань находится на глубине 30 см. Рассчитайте силу давления жидкости, действующую: а) на верхнюю грань кубика; б) на нижнюю грань кубика; в) на правую грань; г) на левую грань; д) на переднюю и заднюю грани. Найдите равнодействующую всех этих сил.

Давление на грани кубика

Давление столба жидкости может быть вычислено по формуле , а сила давления может быть найдена из формулы , из которой находим: .

Не забываем, что очень важно помнить про перевод всех данных задачи в систему СИ, поэтому все расстояния и глубины из сантиметров переводим в метры.

Тогда сила давления на грань: , где — длина ребра кубика в метрах, — глубина, причем для боковых граней возьмем среднее значение () так как давление у верхнего края боковых граней и у нижнего – разное.

Сила давления на верхнюю грань, Н:

Сила давления на нижнюю грань, Н:

Сила давления на боковые грани, заднюю и переднюю, Н:

Понятно, что все силы, действующие на боковые, заднюю и переднюю грани друг друга компенсируют, а равнодействующая всех сил будет в итоге суммой сил давления на нижнюю и верхнюю грани:

Так как сила давления на нижнюю грань больше, чем на верхнюю, то равнодействующая направлена вверх.

Задача 2. Определите объем куска алюминия, на который в керосине действует архимедова сила величиной 120 Н.

Сила Архимеда может быть вычислена как , где — плотность жидкости, а — объем самого тела. То есть сила Архимеда не зависит от того, из чего сделано тело, а только от его объема. Вы спросите: почему тогда одинаковые по объему тела, например, шарики равных радиусов, сделанные из дерева и какого-либо металла, по-разному себя ведут в воде: один плавает, второй – тонет? Да просто есть ведь и сила тяжести, которая зависит как раз от массы тела, и в случае деревянного шарика сила Архимеда достаточна, чтобы компенсировать силу тяжести, а в случае с металлическим шариком – нет.

Рассчитаем объем: м

Задача 3. Плавающий деревянный брусок вытесняет 0,5 л воды. Сколько весит брусок?

Так как брусок плавает, то сила Архимеда равна силе тяжести. Нас спрашивают в задаче про вес бруска. Так как система в покое и ускорения нет, то вес бруска равен силе тяжести:

Можно эту задачу решить иначе: вес тела равен весу воды, вытесняемой им. Брусок вытеснил 0,5 литра воды. Воспользовавшись формулой плотности вещества, определяем, что масса такого количества воды равна 0,5 кг, а вес, значит, 5Н.

Задача 4. Тела изготовлены из дерева, пробки и стали. Они имеют объем 100 см каждое. Найдите архимедову силу, действующую на каждое тело, если его погрузить в воду.

Как было показано в одной из предыдущих задач, неважно, из чего изготовлено тело, а важен его объем, поэтому, раз тела обладают одним и тем же объемом, то и сила Архимеда на них действует одинаковая:

Ответ: 1 Н

Задача 5.Тело при погружении в воду становится легче в 5 раз, чем в воздухе. Определите плотность этого тела.

Мы с вами помним, конечно, что на всякое тело, погруженное как в жидкость, так и в газ, действует сила Архимеда. Поэтому в воздухе она также будет действовать на тело. Однако плотность воздуха так мала по сравнению с плотностью воды, что, я думаю, мы этой силой пренебрежем, и примем вес тела в воздухе равным силе тяжести.

Тогда вес тела — на воздухе, а вес тела в воде . А уменьшился вес этого тела в воде благодаря силе Архимеда: , откуда получаем, что

Масса тела равна произведению его плотности на объем:

Подставим:

Откуда и найдем плотность тела:

Ответ: плотность тела 1250 кг/м

Задача 6. На предмет, целиком погруженный в керосин, действует выталкивающая сила величиной 2 кН. Какой будет архимедова сила, действующая на него в воде? А в спирте?

Чтобы узнать, какой будет Архимедова сила, нужно знать объем предмета. Определим его, зная Архимедову силу в керосине: , откуда получаем, что .

Зная объем, определяем Архимедову силу в воде, Н:

Так как плотность спирта равна плотности керосина, то и Архимедовы силы в этих жидкостях будут одинаковы.

Задача 7.Цинковый шар имеет массу 360 г. При погружении в воду его вес становится равным 2,8 Н. Сплошной этот шар или полый?

Определим объем шара в предположении, что полости в нем нет, по формуле плотности (то есть найдем объем куска цинка массой 360 г):

Плотность цинка равна кг/м, объем получается м

Теперь определим реальный объем шара, то есть тот, который он вытесняет, по известному весу в жидкости. Вес шара Н, вес в жидкости равен , откуда объем вытесняемой жидкости (и объем шара)

мы получили больший объем, чем в первом случае, то есть шар имеет полость внутри, которая и влияет на его внешний объем.

Задача 8. Камень имеет объем 7,5 дм и массу 18,7 кг. Какую силу придется приложить, чтобы удерживать его в воздухе и в воде?

Чтобы удержать такой камень в воздухе, нужно преодолеть силу тяжести, то есть Н.

Теперь определим, какую силу достаточно будет приложить в воде, ведь там нам поможет сила Архимеда!

Тогда сила, которую нужно приложить в воде для удержания камня (или, проще, вес этого камня в воде) равна Н

Задача 9. Сплошное однородное тело, будучи погруженным в воду, весит 170 мН, а в глицерин – 144 мН. Каким будет вес этого тела, если его погрузить в четыреххлористый углерод?

Запишем систему уравнений по тем условиям, что описаны в задаче. Вес тела в воде равен весу тела на воздухе, уменьшенному на силу Архимеда:

Вес тела в глицерине равен весу тела на воздухе, уменьшенному на силу Архимеда – только в глицерине сила Архимеда отличается от той, что действовала на тело в воде:

Из этих двух уравнений, объединив их в систему, можно найти объем тела. Вычтем второе уравнение из первого:

Подставляем числа:

Теперь, когда мы знаем объем тела и плотность четыреххлористого углерода, можно найти силу Архимеда в нем:

Ответ: 110 мН

Задача 10. Кусок парафина толщиной 5 см плавает в воде. Он имеет форму прямоугольного параллелепипеда. Какая часть куска выступает над водой?

Если кусок парафина плавает, а не тонет, значит, сила Архимеда достаточна для того, чтобы компенсировать силу тяжести. Тогда можно записать:

Представим массу куска через его объем и плотность:

Здесь — объем всего куска, а — объем погруженной части.

Тогда:

Так как объем – это произведение площади основания на высоту, то можно сократить площадь:

Откуда делаем вывод, что , то есть из пяти см выступает 0,5 см.

Задача 11. Прямоугольная баржа после приема груза осела на 0,5 м. Принимая длину баржи 5 м, а ширину – 3 м, рассчитать вес принятого ею груза.

Рассчитаем объем воды, который был вытеснен баржей после осадки:

Такой объем воды весит 7,5 тонн – это легко понять, помня величину плотности воды.

То есть вес груза, принятого баржей, равен , или 75 кН.

Задача 12. Плот состоит из 12 бревен, каждое из которых имеет объем 0,8 м. Бревна сосновые. Можно ли на этом плоту переправить на другой берег автомобиль массой 1,5 тонны?

Рассчитаем вес плота: Н

К этому весу будет еще добавлен вес автомобиля: Н

Определим силу Архимеда. Если она окажется больше, чем суммарный вес плота и автомобиля, то плот выдержит (не будет затоплен при переправе), а если меньше, то переправлять автомобиль нельзя. Предположим, весь объем плота оказывается в воде при погрузке автомобиля. Тогда сила Архимеда: Н.

Так как , то делаем вывод, что плот может переправить автомобиль и даже не погрузится при переправе целиком в воду, то есть колеса не намокнут.

Задача 13. Теплоход, вес которого вместе с оборудованием составляет 20 МН, имеет объем подводной части при погружении до ватерлинии 6000 м. Как велика грузоподъемность теплохода?

Сразу вычислим силу Архимеда, так как знаем водоизмещение судна:

Н.

Часть этой силы пойдет на компенсацию веса самого судна с оборудованием:

, или 40 МН – такого веса груз можно нагрузить на теплоход.

Задача 14. В сообщающиеся сосуды диаметром каждый налита жидкость плотностью . В один сосуд опустили тело массой , которое стало плавать в жидкости. Как и на сколько изменится уровень жидкости в сосудах?

Тело в одном из двух сосудов

Так как тело плавает, то заключаем, что сила Архимеда достаточна, чтобы скомпенсировать вес тела. Тогда запишем это формулой:

Так как сосудов два, и по закону уровень воды в них одинаков, то, если общий объем воды увеличивается на благодаря телу, то в каждом сосуде он поднимется на .

Высота подъема воды равна

Или

Источник

Данная тема посвящена разбору
решений задач с использованием закона Архимеда и условий плавания тел.

Задача 1. Три шарика одинаковых размеров погружены в воду и
удерживаются нитями на разной глубине. Сравните выталкивающие силы, действующие
на каждый шарик.

РЕШЕНИЕ

И так, как видно из рисунка,
все три шарика полностью находятся под водой. Известно, что на любое тело,
погруженное в жидкость или газ действует выталкивающая сила, которая, согласно
закону Архимеда, равна весу жидкости в объеме погруженной части тела,
направленная вертикально вверх и приложенная в центре давления.

Эта сила пропорциональна
объёму погружённой в жидкость части тела. Согласно условию задачи, все три
шарики имеют одинаковый объём. Значит можно заключить, что на все шарики
действует одинаковая выталкивающая сила.

ОТВЕТ: на все шарики действует одинаковая архимедова сила.

Задача 2. На графике показана зависимость модуля силы Архимеда,
действующей на медленно погружаемый в жидкость кубик, от глубины погружения.
Длина ребра кубика равна 10 см, его нижнее основание все время параллельно
поверхности жидкости. Определите плотность жидкости.

РЕШЕНИЕ

На погружаемый в жидкость
кубик действует выталкивающая сила, которая, согласно закону Архимеда, прямо
пропорциональна плотности жидкости и объему погруженной части тела.

Задача 3. Тело плавает на границе раздела двух жидкостей с
плотностями ρ₁ и ρ₂, погрузившись во вторую
жидкость на 0,6 своего объема. Определите выталкивающую силу, действующую на
тело, если ρ₁ < ρ₂.

Задача 4. Аэростат, объем шара которого 6000 м³,
начинает равноускоренно подниматься вертикально вверх. Масса водорода,
заполняющего шар, оболочки шара, команды и оборудования аэростата 500 кг.
На какую высоту поднимется аэростат за 10 с движения, если плотность
воздуха 0,15 кг/м³, а сопротивление воздуха пренебрежимо мало?

Задача 5. Какую работу необходимо совершить, чтобы плоскую
льдину, толщина которой 0,2 м, полностью погрузить в воду, если площадь
основания льдины равна 1,2 м²? Плотность льда и воды соответственно
равны 900 и 1000 кг/м³.

«Если вы хотите, чтобы
другие верили в вас,

вы должны сначала
убедить их, что верите в них»

Архимед

Источник

В результате выполнения задания 4 ЕГЭ по физике проверяются следующие требования/умения:

Условие равновесия твердого тела, закон Паскаля, сила Архимеда, математический и пружинный маятники, механические волны, звук

Коды проверяемых требований к уровню подготовки (по кодификатору):

1 Знать/ Понимать:

2.1 описывать и объяснять:

2.2 описывать фундаментальные опыты, оказавшие существенное влияние на развитие физики

2.3 приводить примеры практического применения физических знаний, законов физики

2.4 определять характер физического процесса по графику, таблице, формуле; продукты ядерных реакций на основе законов сохранения электрического заряда и массового числа

Читать подробнее…

Коды проверяемых элементов содержания (по кодификатору):

1.3.1 Момент силы относительно оси вращения, где l – плечо силы F относительно оси, проходящей через точку перпендикулярно рисунку

1.3.2 Условия равновесия твердого тела в ИСО

1.3.3 Закон Паскаля

1.3.4 Давление в жидкости, покоящейся в ИСО

1.3.5 Закон Архимеда: если тело и жидкость покоятся в ИСО. Условие плавания тел

1.5.1 Гармонические колебания. Амплитуда и фаза колебаний. Кинематическое описание. Динамическое описание. Энергетическое описание (закон сохранения механической энергии). Связь амплитуды колебаний исходной величины с амплитудами колебаний её скорости и ускорения

1.5.2 Период и частота колебаний. Период малых свободных колебаний математического маятника. Период свободных колебаний пружинного маятника:

1.5.4 Поперечные и продольные волны. Скорость распространения и длина волны. Интерференция и дифракция волн

1.5.5 Звук. Скорость звука

Уровень сложности задания:

Базовый

Максимальный балл за выполнение задания:

Примерное время выполнения задания выпускником, изучавшим предмет:

3-5

Бутылку с подсолнечным маслом, закрытую пробкой, перевернули. Каково расстояние от уровня масла в сосуде до пробки, если сила, с которой действует масло на пробку площадью 10 см², равна 3,6 Н?

Период собственных малых вертикальных колебаний пружинного маятника равен 1,2 с. Каким станет период колебаний, если массу груза пружинного маятника увеличить в 4 раза?

Объём воздушного шара-гиганта 8500 м³. Чему равен вес этого шара вместе с наполняющим его тёплым воздухом и кабиной, если он поднялся и неподвижно висит над землёй? Плотность воздуха 1,2 кг/м³.

Чему равно давление на человека, нырнувшего в море на глубину 10 м при нормальном атмосферном давлении? Плотность морской воды 1030 кг/м³.

Бутылку с подсолнечным маслом, закрытую пробкой, перевернули. Определите силу, с которой действует масло на пробку площадью 5 см², если расстояние от уровня масла в сосуде до пробки равно 20 см. Плотность масла 930кг/м³

Чему равна сила Архимеда, действующая на человека объёмом 50 дм³, полностью погрузившегося в чистую без примесей воду? Ускорение свободного падения принять равным 9,8 м/с².

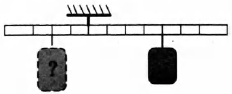
Тело массой 0,1 кг подвесили к четвертому делению правого плеча невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?

При свободных колебаниях на пружине груз массой m проходит положение равновесия со скоростью v. Через четверть периода колебаний он достигает положения максимального удаления от положения равновесия. Чему равен модуль изменения полной механической энергии груза за это время?

Чему равен вес человека в воздухе с учётом действия силы Архимеда? Объём человека V = 50 дм³, плотность тела человека 1036 кг/м³. Плотность воздуха 1,2 кг/м³.

Растянутая на 2 см стальная пружина обладает потенциальной энергией упругой деформации 4 Дж. Насколько увеличится потенциальная энергия упругой деформации этой пружины при её растяжении ещё на 2 см?

Источник

Сила Архимеда .

На тело, погруженное в жидкость действует вверх сила, равная весу вытесненной жидкости.
(rho) это плотность жидкости или газа, то есть той среды, в которой находится тело

Силу Архимеда еще называют выталкивающей силой.

0. Аня уронила в речку мячик объёмом 0,8 л какая сила архимеда действует на мячик,если он погружен в воду только наполовину?
Показать ответ
Показать решение
Видеорешение

Репетитор по физике

8 916 478 10 32

1. Найти силу Архимеда, действующую на тело объемом (V=150 см^3), целиком погруженное в воду .Плотность воды: (rho=1000dfrac{кг}{м^3}).
Показать ответ
Показать решение
Видеорешение

2. Найти силу Архимеда, действующую на тело объемом (V=850 см^3), целиком погруженное в керосин .Плотность керосина (rho=800dfrac{кг}{м^3})
Показать ответ
Показать решение
Видеорешение

3. Найти силу Архимеда, действующую на тело объемом (V=2 м^3), половина объема которого погружено в воду .Плотность воды: (rho=1000dfrac{кг}{м^3})
Показать ответ
Показать решение
Видеорешение

4. Найти силу Архимеда, действующую на тело объемом (V=2 м^3), четверть объема которого погружено в воду .Плотность воды: (rho=1000dfrac{кг}{м^3})

Показать ответ
Показать решение
Видеорешение

5. Найти объем тела, полностью погруженного в воду, если действующая на него сила Архимеда (F_A=20) Н , а плотность воды (rho=1000 ) (dfrac{КГ}{М^3})

Показать ответ
Показать решение
Видеорешение

6. На тело, объемом (V=0,5м^3) полностью погруженное в жидкость, действуюет сила Архимеда (F_A=5000Н). Найти плотность этой жидкости.

Показать ответ
Показать решение
Видеорешение

7. Стальной шар объемом (V=50см^3), полностью погружен в воду. Какая сила Архимеда действует на шар? Плотность воды (rho=1000dfrac{кг}{м^3})

Показать ответ
Показать решение
Видеорешение

8. Чему равна выталкивающая сила (сила Архимеда), действующая в воде на полностью погруженный железный шар массой 0,78 кг? Плотность воды (rho_в=1000dfrac{кг}{м^3})
, Плотность железа (rho_ж=7800dfrac{кг}{м^3})
Показать ответ
Показать решение
Видеорешение

9. Чему равна выталкивающая сила, действующая в воде на полностью погруженный деревянный брусок размером 60x10x15см? Плотность воды (rho_в=1000dfrac{кг}{м^3})

Показать ответ
Показать решение
Видеорешение

10. Чему равна сила Архимеда, действующая в бензине на полностью погруженный медный брусок размером 6x1x2см? Плотность бензина (rho_в=710dfrac{кг}{м^3})

Показать ответ
Показать решение
Видеорешение

11. Чему равна архимедова сила, действующая в воздухе на шарик объемом (V=3000 см^3)? Плотность воздуха (rho_в=1,29dfrac{кг}{м^3})

Показать ответ
Показать решение
Видеорешение

12. Какую силу нужно приложить к камню, находящемуся под водой, чтобы не дать ему пойти ко дну, если на него действует сила тяжести
(F_Т=10Н) и сила Архимеда (F_A=4Н)?
Куда направлена эта сила?

Показать ответ
Показать решение
Видеорешение

13. Какую силу нужно приложить к стальному предмету, находящемуся под водой, чтобы не дать ему пойти ко дну, если на него действует сила тяжести
(F_Т=780Н) и сила Архимеда (F_A=100Н)?
Куда направлена эта сила?

Показать ответ
Показать решение
Видеорешение

14. Какую силу нужно приложить к деревянному предмету, находящемуся под водой, чтобы не дать ему всплывать, если на него действует сила тяжести
(F_Т=50Н) и сила Архимеда (F_A=125Н)?
Куда направлена эта сила?

Показать ответ
Показать решение
Видеорешение

15. Какую силу нужно приложить к деревянному бруску, объемом (V= 0,1 м^3), находящемуся под водой, чтобы не давать ему всплывать ?
Плотность воды (rho_в=1000dfrac{кг}{м^3}). Плотность дерева (rho_д=400dfrac{кг}{м^3})

Показать ответ
Показать решение
Видеорешение

16. Какую силу нужно приложить к деревянной доске, объемом (V= 300 см^3), находящейся под водой, чтобы не давать ей всплывать ?
Плотность воды (rho_в=1000dfrac{кг}{м^3}). Плотность дерева (rho_д=400dfrac{кг}{м^3})

Показать ответ
Показать решение
Видеорешение

17. Какую силу нужно приложить к стальному листу, массой (m= 780 г), находящемуся под водой, чтобы не давать ему утонуть ?
Плотность воды (rho_в=1000dfrac{кг}{м^3}). Плотность стали (rho_с=7800dfrac{кг}{м^3})

Показать ответ
Показать решение
Видеорешение

19. Какую силу нужно приложить к сплошному деревянному кубу, массой (m= 3 кг), находящемуся под водой, чтобы не давать ему всплывать ?
Плотность воды (rho_в=1000dfrac{кг}{м^3}). Плотность дерева (rho_д=400dfrac{кг}{м^3})
Показать ответ
Показать решение
Видеорешение

20. Полый алюминиевый куб, массой (m= 3 кг) и объемом (V= 0,01 м^3) бросили в воду.
Плотность воды (rho_в=1000dfrac{кг}{м^3}). Куб утонет или будет плавать на поверхности?
Показать ответ
Показать решение
Видеорешение

21. Полый алюминиевый куб, массой (m_к= 3 кг) и объемом (V= 0,01 м^3) бросили в воду, но едва он коснулся поверхности воды, как на него села птичка массой (m_п= 2 кг).
Плотность воды (rho_в=1000dfrac{кг}{м^3}). Удастся ли птичке поплавать на нем?
Показать ответ
Показать решение
Видеорешение

22. Каким должен быть минимальный объем надувной лодки массой 50 кг, чтобы взять на борт груз массой 500 кг?
Плотность воды (rho_в=1000dfrac{кг}{м^3}). Удастся ли птичке поплавать на нем?
Показать ответ
Показать решение
Видеорешение

23. какая сила архимеда действует шар объемом (1 м^3 ) и массой 0,5 кг плавающего на поверхности воды ?

Показать ответ
Показать решение
Видеорешение

Источник

Скачать материал

Сейчас обучается 461 человек из 73 регионов

Сейчас обучается 140 человек из 50 регионов

Сейчас обучается 46 человек из 28 регионов

Описание презентации по отдельным слайдам:

1 слайд

Задание ЕГЭ №4 1 части (базового уровня сложности): условие равновесия твердого тела, закон Паскаля, сила Архимеда, математический и пружинный маятники, механические волны, звук.

Материал разработала учитель физики МБОУ «СШ пос. Борское» Бондарева Наталья Петровна
2 слайд

Тематика вопросов для проверки уровня знаний учащихся:
10 слайд

Задача 1
Ответ: 4
Обращаем внимание на единицы измерения времени: 4∙10-3с = 4 мс
11 слайд

Задача 2
Обращаем внимание на то, что период колебаний равен 2 с, а время колебаний – 4с. Значит, маятник совершит 2 полных колебания. Учитывая, что за 1 полное колебание потенциальная энергия имеет максимальные значения 2 раза, то за 2 колебания – 4.
Ответ: 4
12 слайд

Задача 3
F = p ∙ S, p = ρgh = 900 кг/м3∙ 10 м/с2 ∙ 0,2м =1800 Па, F = 1800 Па∙ 0,0005 м2 =0,9 Н
Ответ: 0,9
13 слайд

Задача 4
Т = 4 с, ν = 1/Т = ¼ = 0,25 Гц
Ответ: 0,25
15 слайд

Задача 6
Т.к. период колебаний не зависит от массы, а зависит в данном случае от длины нити, то при уменьшении длины нити в 4 раза, период уменьшается в 2 раза, а частота увеличивается в 2 раза.
Ответ: 2
16 слайд

Задача 7
Т.к. вес вытесненной яхтой жидкости равен весу яхты в воздухе, то вес яхты в воздухе: Р = mg = 2400кг∙10м/с2 = 24000Н, с другой стороны вес вытесненной жидкости Р= 24000Н = ρgV,

Ответ: 2,4
17 слайд

Задача 8
т.к. нам нужна длина рычага l = l1+l2 = 9+3=12 см
Ответ: 12
18 слайд

Задача 9
где l-плечо (перпендикуляр, проведенный из точки опоры на прямую, вдоль которой действует сила, линия, выделенная зеленым цветом), т.о.
М1 = 10Н ∙ 0,1м = 1Нм, М2 = 2Н ∙ 0,2м = 0,4Нм, М3 = 3Н ∙ 0,3м = 0,9 Нм
Ответ:10
19 слайд

Задача 10
где l-плечо (перпендикуляр, проведенный из точки опоры на прямую, вдоль которой действует сила, линия, выделенная зеленым цветом), т.о.
F= 40кг∙10м/с2 = 400Н
М = 400Н∙ АС

М = 400Н∙ 0,5м = 200Нм
Ответ: 200
20 слайд

Задача 11
Т.к плечо силы F в 3 раза больше, то сила в 3 раза меньше: 3Н : 3=1Н
Ответ: 1
21 слайд

Задача 12
FA= ρgV , FA= 800кг/м3 ∙ 10м/с2 ∙0,000003м3 = 0,024Н =24мН
Ответ: 24
22 слайд

Задача 13
S = vt = 330м/с∙3с=990м
Ответ: 990
23 слайд

Задача 14
В начальный момент времени тело должно быть выведено из положения равновесия
Ответ: 3
24 слайд

Задача 15
В широкую U-образную трубку с вертикальными прямыми коленами налиты неизвестная жидкость плотностью ρ1 и вода плотностью ρ2=1000кг/м3 (см. рисунок). На рисунке b=10 см, h=24 см, H=30 см. Какова плотность жидкости ρ1? (Ответ дайте в кг/м3.)

По закону Паскаля р1 = р2; ρ1g(Н-b)+ρ1gb= ρ2gh.
ρ1∙10∙0,2+1000∙10∙0,1=1000∙10∙0,24; ρ1=700кг/м3
Ответ: 700
25 слайд

Задача 16
На графике показана зависимость модуля силы Архимеда FАрх, действующей на медленно погружаемый в жидкость кубик, от глубины погружения x. Длина ребра кубика равна 10 см, его нижнее основание всё время параллельно поверхности жидкости. Определите плотность жидкости. Ответ приведите в кг/м3. Ускорение свободного падения принять равным 10 м/с2.

Сила Архимеда, действующая на кубик равна FA = ρgV, где V — объём погруженной части кубика, ρ — плотность жидкости. Учитывая, что нижнее основание кубика всё время параллельно поверхности жидкости, можем записать: FA = ρga2x, где a — длина стороны кубика, откуда

Ответ: 2700.
26 слайд

Задача 17
В четыре сосуда, вертикальные сечения которых показаны на рисунке, налита вода. Одна клеточка на рисунке соответствует 10 см. В одном из этих сосудов гидростатическое давление на дно максимально. Чему оно равно? (Ответ дайте в паскалях.) Ускорение свободного падения принять равным 10 м/с2.

Учитывая, что р= ρgh, имеем, что давление на дно сосуда зависит от плотности жидкости (во всех сосудах одинаковая) и от уровня жидкости (наибольший в сосуде 3).
р = 1000кг/м3 ∙10м/с2 ∙4∙0,1м = 4000 Па
Ответ:4000
27 слайд

Задача 18
Чтобы частота колебаний увеличилась, период должен во столько же раз уменьшиться, в нашем случае период должен уменьшиться в 2 раза, значит, жесткость должна увеличиться в 4 раза (т.к. жесткость находится в знаменателе радикала). 400Н/м∙4 = 1600Н/м
Ответ: 1600
28 слайд

Список использованных источников:
https://phys-ege.sdamgia.ru/

Краткое описание документа:

В методической разработке для подготовки к ЕГЭ по физике рассматривается решение задач части 1 №4

Задание ЕГЭ №4 1 части (базового уровня сложности): условие равновесия твердого тела, закон Паскаля, сила Архимеда, математический и пружинный маятники, механические волны, звук.

Сообщающимися называют сосуды, имеющие между собой канал, заполненный жидкостью. Наблюдения показывают, что в сообщающихся сосудах любой формы однородная жидкость всегда устанавливается на одном уровне. задачи на сообщающиеся сосуды очень распространены в гидростатике.

Иначе ведут себя разнородные жидкости даже в одинаковых по форме и размерам сообщающихся сосудах. Дело в том, что в сообщающихся сосудах должно устанавливаться одинаковое давление на одной и той же высоте во всех частях сосуда. Но если жидкости различные, то и высота столбов этих жидкостей должна быть различной, чтобы создать одинаковое давление. Поэтому, разнородные жидкости в сообщающихся сосудах могут и не устанавливаться на одном уровне.

Алгоритм решения задач по гидростатике на сообщающиеся сосуды:

Сделать рисунок.
Выбрать горизонтальный уровень, ниже которого во всех сосудах находится одинаковая жидкость. Если такого уровня нет, то, естественно, за нулевой уровень выбираем дно сосудов.
Записать давления относительно этого уровня во всех сосудах и приравнять.
При необходимости использовать свойство несжимаемости жидкости (объем жидкости, вытекающей из одного сосуда, равен объему жидкости, втекающей в другой сосуд).
Решить математически полученную систему уравнений.
(материал сайта https://educon.by/index.php/materials/phys/gidrostatika)

Примеры задач:

В широкую U-образную трубку с вертикальными прямыми коленами налиты неизвестная жидкость плотностью ρ₁ и вода плотностью ρ₂=1000кг/м³ (см. рисунок). На рисунке b=10 см, h=24 см, H=30 см. Какова плотность жидкости ρ₁? (Ответ дайте в кг/м³.)

Ответ: 700

На графике показана зависимость модуля силы Архимеда F_Арх, действующей на медленно погружаемый в жидкость кубик, от глубины погружения x. Длина ребра кубика равна 10 см, его нижнее основание всё время параллельно поверхности жидкости. Определите плотность жидкости. Ответ приведите в кг/м³. Ускорение свободного падения принять равным 10 м/с².

Ответ: 2700.

В четыре сосуда, вертикальные сечения которых показаны на рисунке, налита вода. Одна клеточка на рисунке соответствует 10 см. В одном из этих сосудов гидростатическое давление на дно максимально. Чему оно равно? (Ответ дайте в паскалях.) Ускорение свободного падения принять равным 10 м/с².

Учитывая, что р= ρgh, имеем, что давление на дно сосуда зависит от плотности жидкости (во всех сосудах одинаковая) и от уровня жидкости (наибольший в сосуде 3).

р = 1000кг/м³ ∙10м/с² ∙4∙0,1м = 4000 Па

Ответ:4000

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 153 784 материала в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

Другие материалы

28.03.2018
797
5

28.03.2018
1476
8

Вам будут интересны эти курсы:

Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
Курс повышения квалификации «Формирование компетенций межкультурной коммуникации в условиях реализации ФГОС»
Курс повышения квалификации «Основы управления проектами в условиях реализации ФГОС»
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС технических направлений подготовки»
Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
Курс повышения квалификации «Экономика: инструменты контроллинга»
Курс повышения квалификации «Финансы: управление структурой капитала»
Курс повышения квалификации «ЕГЭ по физике: методика решения задач»
Курс профессиональной переподготовки «Организация технической поддержки клиентов при установке и эксплуатации информационно-коммуникационных систем»
Курс повышения квалификации «Мировая экономика и международные экономические отношения»
Курс профессиональной переподготовки «Организация деятельности по водоотведению и очистке сточных вод»
Курс профессиональной переподготовки «Теория и методика музейного дела и охраны исторических памятников»

Источник