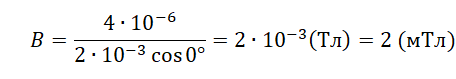Задачи на закон электромагнитной индукции егэ - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Задания Д9 B15 № 1504

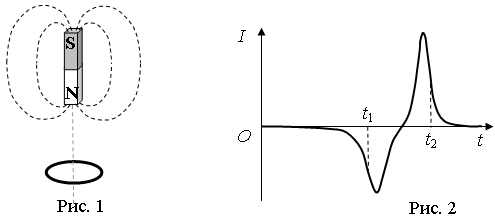
На рисунке приведен график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн.

Определите модуль среднего значения ЭДС самоиндукции в интервале времени от 10 до 15 с.

1)  2 мкВ

2)  3 мкВ

3)  5 мкВ

4)  0

Задания Д9 B15 № 1506

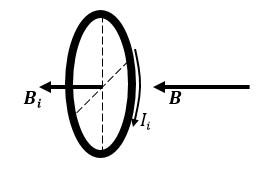
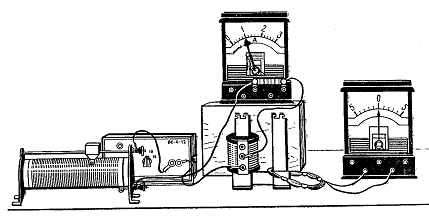
На рисунке изображен момент демонстрационного эксперимента по проверке правила Ленца, когда все предметы неподвижны. Южный полюс магнита находится внутри сплошного металлического кольца, но не касается его. Коромысло с металлическими кольцами может свободно вращаться вокруг вертикальной опоры. При выдвижении магнита из кольца влево кольцо будет

1)  оставаться неподвижным

2)  перемещаться вправо

3)  совершать колебания

4)  перемещаться вслед за магнитом

Задания Д9 B15 № 1516

На рисунке приведена демонстрация опыта по проверке правила Ленца. Опыт проводится со сплошным кольцом, а не разрезанным, потому что

1)  сплошное кольцо сделано из стали, а разрезанное  — из алюминия

2)  в разрезанном кольце возникает вихревое электрическое поле, а в сплошном  — нет

3)  в сплошном кольце возникает индукционный ток, а в разрезанном  — нет

4)  в сплошном кольце возникает ЭДС индукции, а в разрезанном  — нет

Задания Д9 B15 № 1612

В опыте по исследованию ЭДС электромагнитной индукции квадратная рамка из тонкого провода со стороной квадрата b находится в однородном магнитном поле, перпендикулярном плоскости рамки. Индукция поля возрастает за время t по линейному закону от 0 до максимального значения B_max. Как изменится ЭДС индукции, возникающая в рамке, если b увеличить в 2 раза?

1)  не изменится

2)  увеличится в 2 раза

3)  уменьшится в 2 раза

4)  увеличится в 4 раза

Задания Д9 B15 № 1613

1)  увеличится в 2 раза

2)  увеличится в 4 раза

3)  не изменится

4)  уменьшится в 2 раза

Пройти тестирование по этим заданиям

Источник

Закон электромагнитной индукции, или закон Фарадея – основной закон электродинамики. В сегодняшней статье разберем решение нескольких задач на применение закона электромагнитной индукции.

Подписывайтесь на наш телеграм – там есть не только задачи, но и много интересного для учащихся всех специальностей. А еще, не пропустите приятные скидки и акции на нашем втором канале!

Электромагнитная индукция: задачи с решением

Прежде чем решать задачи на электромагнитную индукцию, вспомните теорию и держите под рукой полезные формулы.

Не знаете, как подступиться к задаче? Держите универсальную памятку по решению абсолютно любых физических задач.

Задача №1 на закон электромагнитной индукции

Условие

Проводник, свитый в 5 витков, находится в магнитном поле. Магнитный поток через поверхность витка изменяется по закону Фt=50-3t (Вб) . Определить направление и силу индукционного тока в проводнике, если его сопротивление равно 5 Ом.

Решение

Согласно основному закону электромагнитной индукции в проводнике возникает ЭДС индукции, величина которой определяется скоростью изменения магнитного потока, пронизывающего контур:

ε=-NdФdt

Индукционный ток в проводнике можно найти по закону Ома:

I=εR

Вычислим производную и найдем ток:

dФdt=d50-3tdt=-3

Тогда:

I=3NR=3·55=3 А

Уменьшение потока вызывает увеличение ЭДС, то есть направления потока и поля индукционного тока совпадают:

Ответ: 3 А.

Задача №2 на закон электромагнитной индукции

Условие

По катушке индуктивностью L=8 мкГн течет ток I=6 А. Определить среднее значение ЭДС самоиндукции, возникающей в контуре, если сила тока изменяется практически до нуля за время ∆t=5 мс.

Решение

По определению, магнитный поток равен:

Ф=L·I

ЭДС самоиндукции определим по закону Фарадея:

<ε>=∆Ф∆t=-L∆I∆t

Учитывая, что индуктивность неизменна, и магнитный поток изменяется только за счёт изменения силы тока до нуля (ΔI = I), можно записать:

<ε>=-LI∆t

Подставим числа и вычислим:

<ε>=-8·10-6·65·10-3=-9,6·10-3 В

Ответ: -9,6 мВ.

Задача №3 на закон электромагнитной индукции

Условие

Магнитный поток через контур проводника сопротивлением 0,04 Ом за 3 секунды изменился на 0,013 Вб. Найдите силу тока в проводнике, если изменение потока происходило равномерно.

Решение

В данном случае силу тока можно выразить через закон Ома с учетом закона электромагнитной индукции:

Ii=εiR=-∆Ф∆t1R

Подставляем значения и вычисляем:

Ii=0,0133·0,04=0,11 А.

Ответ: 0,11 А.

Задача №4 на закон электромагнитной индукции

Условие

Прямой проводящий стержень длиной 40 см находится в однородном магнитном поле с индукцией 0,1 Тл. Концы стержня замкнуты гибким проводом, находящимся вне поля. Сопротивление всей цепи 0,5 Ом. Какая мощность потребуется для равномерного перемещения стержня перпендикулярно линиям магнитной индукции со скоростью 10 м/с?

Решение

Если стержень будет двигаться равномерно, магнитный поток через площадь, «заметаемую» стержнем за некоторое время, будет равен:

Ф=ВS=Blvt

При этом разность потенциалов на стержне будет равна ЭДС и, согласно закону электромагнитной индукции Фарадея:

U=dФdt=Blv

Искомая мощность будет равна мощности, выделяемой на сопротивлении:

P=U2R=Blv2R=0,1·0,4·1020,5=0,32 Вт

Ответ: 0,32 Вт.

Нужно больше задач на мощность? Читайте наш блог!

Задача №5 на закон электромагнитной индукции

Условие

В проволочное кольцо, присоединенное к баллистическому гальванометру, вставили прямой магнит. При этом по цепи прошел заряд q=50мкКл. Определить изменение магнитного потока через кольцо, если сопротивление цепи гальванометра R=10 Oм.

Решение

По закону Фарадея, ЭДС находится как отношения изменения магнитного потока ко времени, за которое оно произошло:

εi=∆Ф∆t∆Ф=εi·t

C другой стороны, по закону Ома, можно записать:

εi=IR

Ток, в свою очередь, равен отношению проходящего заряда ко времени:

I=∆Q∆t

C учетом всего этого выражения для ЭДС и потока можно переписать:

εi=R·∆Q∆t∆Ф= R∆Q∆t∆t=R∆Q∆Ф=10·50·10-6=5·10-4 Вб

Ответ: 0,5 мВб.

Вопросы на тему «Электромагнитная индукция»

Вопрос 1. Что такое электромагнитная индукция?

Ответ. Электромагнитная индукция — это явление, когда в замкнутом проводнике (контур, рамка) возникает ток, при помещении этого проводника в изменяющееся магнитное поле.

Вопрос 2. Что такое магнитный поток?

Ответ. Магнитный поток, или поток магнитной индукции через какую-то поверхность – это скалярная физическая величина, равна произведению модуля магнитной индукции на площадь данной поверхности и косинус угла между вектором индукции и нормалью к поверхности.

Ф=BScosα

Магнитный поток характеризует густоту силовых линий магнитного поля, пронизывающих поверхность. Единица измерения – Вебер.

Вопрос 3. Сформулируйте закон Фарадея

Ответ. Закон электромагнитной индукции Фарадея гласит:

ЭДС индукции в замкнутом контуре равна скорости изменения магнитного потока, пронизывающего контур, взятой с противоположным знаком.

εi=-dФdt

Вопрос 4. Что означает знак «-» в формуле для закона электромагнитной индукции.

Ответ. Направление индукционного тока определяется по правилу Ленца: индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток. В соответствии с правилом Ленца ток направлен так, что созданный им магнитный поток противодействует изменению внешнего магнитного потока. Именно поэтому в формуле присутствует знак «-».

Вопрос 5. Как закон Фарадея применяется на практике?

Ответ. Закон электромагнитной индукции Фарадея нашел широчайшее применение. В качестве самого распространенного примера можно привести такое устройство, как электродвигатель, принцип действия которого основан именно на этом законе.

Нужна помощь в решении задач и других заданий по учебе? Профессиональный сервис для студентов всегда поспособствует качественному выполнению всех работ.

Источник

31. Электродинамика (расчетная задача)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Электромагнитная индукция

Квадратная проволочная рамка со стороной (l = 10) см находится в однородном магнитном поле с индукцией (vec{B}) На рисунке изображена зависимость проекции вектора на перпендикуляр к плоскости рамки от времени. Какое количество теплоты выделится в рамке за время (t = 10) с, если сопротивление рамки (R = 0,2) Ом? Ответ дайте в мДж

“Демоверсия 2020”

При изменении магнитного поля изменяется поток вектора магнитной индукции (text{ Ф}(t)=B(t)S) через рамку площадью (S=l^2) что создаёт в ней ЭДС индукции В соответствии с законом индукции Фарадея: [varepsilon=-frac{Delta Phi}{Delta t}=-frac{Delta B_{n}}{Delta t} cdot S] Эта ЭДС вызывает в рамке ток, сила которого определяется законом Ома для замкнутой цепи [I=frac{varepsilon}{R}=-frac{1}{R} cdot frac{Delta Phi}{Delta t}=-frac{S}{R} cdot frac{Delta B_{n}}{Delta t}] Согласно закону Джоуля – Ленца за время (Delta t) в рамке выделится количество теплоты [Q=I^{2} R Delta t=frac{S^{2}}{R} cdot frac{left(Delta B_{n}right)^{2}}{Delta t}=frac{l^{4}}{R} cdot frac{left(Delta B_{n}right)^{2}}{Delta t}] На первом участке графика (Delta t = t_1=4) с и (Delta B =B_1-B_0=-1) Тл на втором участке (Delta t_2=t_2-t_1=6) с и (Delta B=B_2-B_1=0,6) Тл, поэтому суммарное количество выделившейся теплоты [Q=Q_{1}+Q_{2}=frac{l^{4}}{R}left[frac{left(Delta B_{1}right)^{2}}{Delta t_{1}}+frac{left(Delta B_{2}right)^{2}}{Delta t_{2}}right]] Подставляя сюда значения физических величин, получим: [Q=frac{(0,1 text{ м}^{4}}{0,2 text{ Ом}} cdotleft[frac{1 text{ Тл}^{2}}{4 text{ с}}+frac{0,36 text{ Тл}^{2}}{6 text{ с}}right]=0,155 cdot 10^{-3} text{ Дж}]

Ответ: 0,155

По параллельным проводникам (bc) и (ad), находящимся в магнитном поле с индукцией (В), со скоростью (v = 1) м/с скользит проводящий стержень (MN), который находится в контакте с проводниками (см. рисунок). Магнитное поле перпендикулярно плоскости проводников. Расстояние между проводниками (l = 30) см. Между проводниками подключен резистор с сопротивлением (R = 2) Ом. Сопротивление стержня и проводников пренебрежимо мало. При движении стержня по резистору (R) течет ток (I = 60) мА. Какова индукция магнитного поля?

“Основная волна 2020 Вариант 3”

ЭДС: [xi = IR quad (1)] Кроме того ЭДС равна [xi =left|dfrac{Delta text{ Ф}}{Delta t}right|=dfrac{BDelta S }{Delta t}=Bvlquad (2)] где (Delta S) – изменение площади контура за время (Delta t).
Приравняем (1) к (2) [Bvl=IR Rightarrow B=dfrac{IR}{Bv}=dfrac{60text{ мА}cdot 2text{ Ом}}{1text{ м/с}cdot 300text{ мм}}=0,4text{ Тл}]

Ответ: 0,4

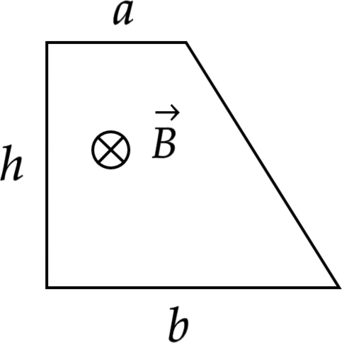
Замкнутый проводник в виде прямоугольной трапеции находится в магнитном поле с индукцией (B = 6 cdot10^{-2}) Тл, направленной перпендикулярно плоскости трапеции от нас. Сопротивление единицы длины проводника (rho = 0,023) Ом/м. Найти величину тока (I), текущего в проводнике при равномерном уменьшении поля до нуля в течение (tau=3) с. Размеры отрезков проводника (a=0,2) м, (b=0,5) м, (h=0,4) м.

При изменении магнитного потока в контуре будет появляться ЭДС индукции, следовательно, по контуру будет идти ток.
Направим вектор нормали контура (перпендикуляр) от нас сонаправленно с вектором магнитной индукции.
Магнитное поле уменьшается, следовательно: (Deltatext{Ф}<0)
Закон Фарадея: [xi_i=-frac{Delta text{Ф}}{Delta t}] где (Delta text{ Ф}) – изменение магнитного потока, (Delta t) – время. Значит, ЭДС индукции положительна. По правилу правого винта (правой руки) ЭДС индукции направлена по часовой стрелке и ток направлен в этом же направлении. [xi=frac{S(B-0)}{tau}] По закону Ома: [I=dfrac{xi_i}{R}=frac{SB}{Rtau}] Сопротивление проводника: [R=rho P] где (P) – периметр трапеции [P=a+b+h+sqrt{(b-a)^2+h^2}] [S=frac{a+b}{2}h] Следовательно, сила тока равна [I=frac{(a+b)hB}{2(a+b+h+sqrt{(b-a)^2+h^2})rhotau}=76 text{ мА}] (I=76 мА), ток течет по часовой стрелке.

Ответ: 76 мА

Катушка, имеющая 100 витков и расположенная перпендикулярно магнитному полю с индукцией 6 Тл, поворачивается за 1 с на угол (90^{circ}). За это время в катушке наводится ЭДС со средним значением 0,6 В. Определите площадь (в см(^2)) поперечного сечения катушки.

ЭДС индукции: [xi_i=-frac{Delta text{Ф}}{Delta t}=dfrac{ N Delta S B}{Delta t},quad(1)] где (Delta text{ Ф}) – изменение магнитного потока, (Delta t) – время, (B) – модуль вектора магнитной индукции, (Delta S) – изменение площади. [xi=frac{NBS(cosalpha_1-cosalpha_2)}{Delta t}=frac{NBS(1-0)}{Delta t}=frac{NBS}{Delta t}] (N) – количество витков , (B) – модуль вектора магнитной индукции, (S) – площадь. Из предыдущего уравнения площадь равна: [S=frac{xi Delta t}{NB}=frac{0,6text{ В}cdot1text{ с}}{100cdot6text{ Тл}}=10 text{ см$^2$}]

Ответ: 10

Плоский виток провода расположен перпендикулярно однородному магнитному полю. Когда виток повернули на (180^{circ}), по нему прошел заряд 7,2 мкКл. На какой угол (в градусах) надо повернуть виток, чтобы по нему прошел заряд 1,8 мкКл?

ЭДС индукции: [xi_i=-frac{Delta text{Ф}}{Delta t},] где (Delta text{ Ф}) – изменение магнитного потока, (Delta t) – время.
По закону Ома: [xi_i=IR=frac{Delta q}{Delta t}R] (I) – сила тока, (R) – сопротивление, (Delta q) – заряд, протекший за время (Delta t). [frac{Delta q}{Delta t}R=-frac{Delta text{Ф}}{Delta t}] Для изменения заряда в первом и во втором случае имеем [Delta q_1=Big|frac{Delta text{Ф}}{R}Big|=Big|frac{BScosalpha_2-BScosalpha_1}{R}Big|] [Delta q_2=Big|frac{Delta text{Ф}}{R}Big|=Big|frac{BScosalpha_3-BScosalpha_1}{R}Big|] (B) – модуль вектора магнитной индукции, (S) – площадь контура, (alpha_1, alpha_2, alpha_3 ) – угол между нормалью к поверхности и вектором (vec{B}) вначале опыта, в конце первого опыта и в конце второго опыта (alpha_1=0^{circ}), (alpha_2=180^{circ}), (alpha_3) – неизвестный угол [frac{Delta q_2}{Delta q_1}=frac{|cosalpha_3-cosalpha_1|}{|cosalpha_2-cosalpha_1|}=frac{cosalpha_3-1}{|-1-1|}=frac{1-cosalpha_3}{2}] [frac{1}{4}=frac{1-cosalpha_3}{2}] [frac{1}{2}=1-cosalpha_3] [cosalpha_3=frac{1}{2}] [alpha_3=60^{circ}]

Ответ: 60

Катушку с индуктивностью 2 Гн, содержащей 200 витков площадью 50 см(^2), помещают в однородное магнитное поле с индукцией 60 мТл, параллельной оси катушки. Обмотку катушки охлаждают до сверхпроводящего состояния, а затем поворачивают катушку на (60^{circ}). Какой силы ток (в мА) возникнет в катушке?

В проводниках, находящихся в сверхпроводящем состоянии, суммарный магнитный поток через сверхпроводящий контур сохраняется [text{Ф}_{text{внешн}}+LI=const] (L) – индуктивность контура, ( I) – сила тока, (text{Ф}_{text{внешн}}) – магнитный поток по внешней цепи [text{Ф}_1+0=text{Ф}_2+LI] Отсюда сила тока с учетом того, что (text{ Ф}=NBS cos alpha), где (B) – модуль вектора магнитной индукции, (S) – площадь рамки,(alpha) – угол между нормалью к поверхности и вектором (vec{B}). [I=frac{text{Ф}_1+0-text{Ф}_2}{L}=frac{NBS-NBS cosalpha}{L}=frac{200cdot60cdot10^{-3}text{ Тл}cdot0,005text{ м$^2$}(1-0,5)}{2text{ Гн}}=15 text{ мА}]

Ответ: 15

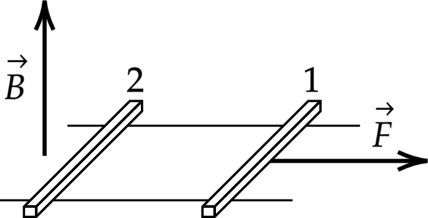
Два стержня массой (m=100) г и сопротивлением (R=0,5) Ом каждый скользят поступательно и равномерно по горизонтальным рельсам с коэффициентом трения (mu=0,2). Расстояние между рельсами (l=15) см, а стержни с рельсами находятся в однородном вертикальном магнитном поле с индукцией (B=2) Тл (см. рисунок). Какова скорость движения первого стержня относительно второго? Самоиндукцией контура пренебречь. Ответ выразите в м/с и округлите до десятых.

ЭДС индукции, возникающее в контуре, при движении стержней равно [|xi| = dfrac{Delta text{ Ф}}{Delta t}=dfrac{B Delta S}{Delta t}=Bvl, quad (1)] где (Delta) Ф – изменение потока за время (Delta t), (v) – скорость движения первого стержня, относительно второго, (S) – площадь контура.
При этом возникает сила тока равная [I=dfrac{|xi|}{2R}quad (2)] На проводники будет действовать сила Ампера и сила трения, а на первый проводник еще и сила (F).
Для первого же проводника, с учетом равномерности движения, имеем [IBl=mu mg Rightarrow I=dfrac{mu mg}{Bl}quad (3)] Приравняем (2) и (3) с учетом (1) и выразим относительную скорость движения [v=dfrac{2mu mgR}{(Bl)^2}=dfrac{2cdot 0,2 cdot 0,1text{ кг}cdot 0,5 text{ Ом} }{(2text{ Тл}cdot 0,15text{ м})^2}approx 2text{ м/с}]

Ответ: 2

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Разбор задач с решением

по теме : «Электромагнитная индукция» .

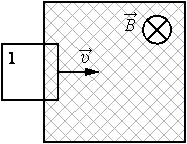
А25-1. В заштрихованной области на рисунке действует однородное магнитное поле, направленное перпендикулярно плоскости рисунка, В = 0,1 Тл. Проволочную квадратную рамку сопротивлением R = 10 Ом и стороной l = 10 см перемещают в плоскости рисунка поступательно со скоростью υ = 1 м/с. Чему равен индукционный ток в рамке в состоянии 1?

А25-2. В заштрихованной области на рисунке действует однородное магнитное поле, перпендикулярное плоскости рисунка с индукцией В = 0,1 Тл. Квадратную проволочную рамку, сопротивление которой 10 Ом и длина стороны 10 см, перемещают в этом поле в плоскости рисунка поступательно равномерно с некоторой скоростью v. При попадании рамки в магнитное поле в положении 1 в ней возникает индукционный ток, равный 1 мА. Какова скорость движения рамки?

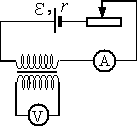
С1-1. На рисунке приведена электрическая цепь, состоящая из гальванического элемента, реостата, трансформатора, амперметра и вольтметра. В начальный момент времени ползунок реостата установлен посередине и неподвижен. Опираясь на законы электродинамики, объясните, как будут изменяться показания приборов в процессе перемещения ползунка реостата влево. ЭДС самоиндукции пренебречь по сравнению с ε.

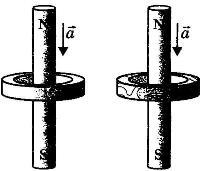
С1-3. Сквозь металлическое и деревянное кольца, не касаясь их, падают одинаковые намагниченные стержни, как показано на рисунке. По-разному ли влияют кольца на ускорение а стержней, и если да, то в чем состоит это различие? Рассмотрите две стадии падения стержня: стержень сближается с кольцом; стержень удаляется от кольца. Ответ поясните, указав, какие физические закономерности вы использовали для объяснения.

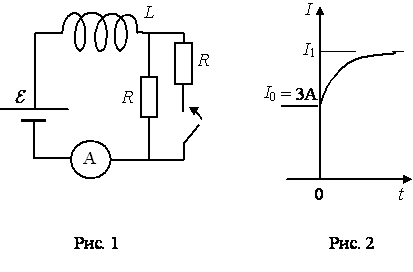
С5-6. Катушка, обладающая индуктивностью L, соединена с источником питания с ЭДС ε и двумя одинаковыми резисторами R. Электрическая схема соединения показана на рис. 1. В начальный момент ключ в цепи разомкнут. В момент времени t = 0 ключ замыкают, что приводит к изменениям силы тока, регистрируемым амперметром, как показано на рис. 2. Основываясь на известных физических законах, объясните, почему при замыкании ключа сила тока плавно увеличивается до некоторого нового значения – I₁. Определите значение силы тока I₁. Внутренним сопротивлением источника тока пренебречь.

С5-7. Намагниченный стальной стержень начинает свободное падение с нулевой начальной скоростью из положения, изображённого на рис. 1. Пролетая сквозь закреплённое проволочное кольцо, стержень создаёт в нём электрический ток, сила которого изменяется со временем так, как показано на рис. 2.

С5-8. Медное кольцо, диаметр которого — 20 см, а диаметр провода кольца 2 мм, расположено в однородном магнитном поле. Плоскость кольца перпендикулярна вектору магнитной индукции. Определите модуль скорости изменения магнитной индукции поля со временем, если при этом в кольце возникает индукционный ток 10 А. Удельное сопротивление меди ρ_С_u = 1,72 • 10^-8 Ом·м.

С5-9. Медное кольцо из провода диаметром 2 мм расположено в однородном магнитном поле, магнитная индукция которого меняется по модулю со скоростью 1,09 Тл/с. Плоскость кольца перпендикулярна вектору магнитной индукции. Каков диаметр кольца, если возникающий в нём индукционный ток равен 10 А? Удельное сопротивление меди ρ_Cu = 1,72·10^-8 Ом

С5-10. Медное кольцо, диаметр которого 20 см, а диаметр провода кольца 2 мм, расположено в однородном магнитном поле. Плоскость кольца перпендикулярна вектору магнитной индукции. Определите модуль скорости изменения магнитной индукции поля со временем, если при этом в кольце возникает индукционный ток 10 А. Удельное сопротивление меди r_Cu = 1,72•10^–8 Ом•м.

С5-11. Плоская рамка из провода сопротивлением 5 Ом находится в однородном магнитном поле. Проекция магнитной индукции поля на ось Ох, перпендикулярную плоскости рамки, меняется от В_1х = 3 Тл до В_2х = -1 Тл. За время изменения поля по рамке протекает заряд 1,6 Кл. Определите площадь рамки.

С5-12. Плоская рамка из провода сопротивлением 5 Ом находится в однородном магнитном поле. Проекция магнитной индукции поля на ось Ох, перпендикулярную плоскости рамки, меняется от В_1х = 3 Тл до В_2х = -1 Тл. Площадь рамки 2 м². Какой заряд пройдет по рамке за время изменения поля?

С5-13. Плоская горизонтальная фигура площадью 0,1 м², ограниченная проводящим контуром с сопротивлением 5 Ом, находится в однородном магнитном поле. Пока проекция вектора магнитной индукции на вертикальную ось Oz медленно и равномерно возрастает от В_1Z = – 0,15 Тл до некоторого конечного значения В_2Z, по контуру протекает заряд 0,008 Кл. Найдите В_2Z.

С5-14. Замкнутый контур из тонкой проволоки помещён в магнитное поле. Плоскость контура перпендикулярна вектору магнитной индукции поля. Площадь контура S = 2•10^–3 м². В контуре возникают колебания тока с амплитудой i_м = 35 мА, если магнитная индукция поля меняется с течением времени в соответствии с формулой B = acos(bt), где а = 6•10^–3 Тл, b = 3500 с^–1. Чему равно электрическое сопротивление контура R?

С5-16. Проводник длиной 1 м движется равноускоренно в однородном магнитном поле, индукция которого равна0,5 Тл и направлена перпендикулярно проводнику и скорости его движения (см. рисунок). Начальная скорость движения проводника 4 м/с. Значение ЭДС индукции в этом проводнике в конце перемещения на расстояние 1 мравно 3 В. Чему равно ускорение, с которым движется проводник в магнитном поле?

С5-17. Горизонтально расположенный проводник движется равноускоренно в вертикальном однородном магнитном поле, индукция которого равна 1 Тл и направлена перпендикулярно проводнику и скорости его движения (см. рисунок). При начальной скорости проводника, равной нулю, и ускорении 8 м/с², проводник переместился на 1 м. ЭДС индукции на концах проводника в конце перемещения равна 6 В. Какова длина проводника?

С5-18. Горизонтально расположенный проводник длиной 1 м движется равноускоренно в вертикальном однородном магнитном поле, индукция которого равна 0,5 Тл и направлена перпендикулярно проводнику и скорости его движения (см. рисунок). При начальной скорости проводника, равной нулю, проводник переместился на 1 м. ЭДС индукции на концах проводника в конце перемещения равна 2 В. Каково ускорение проводника?

С5-19. Прямоугольный контур, образованный двумя рельсами и двумя перемычками, находится в однородном магнитном поле, перпендикулярном плоскости контура. Правая перемычка скользит по рельсам, сохраняя надежный контакт с ними. Известны величины: индукция магнитного поля В = 0,1 Tл, расстояние между рельсами l = 10 см, скорость движения перемычки v = 2 м/c, сопротивление контура R = 2 Ом. Какова сила индукционного тока в контуре? Ответ выразите в миллиамперах (мА)

С5-20. Два параллельных друг другу рельса, лежащих в горизонтальной плоскости, находятся в однородном магнитном поле, индукция B которого направлена вертикально вниз (см. рисунок – вид сверху). На рельсах перпендикулярно им лежат два одинаковых проводника, способных скользить по рельсам без нарушения электрического контакта. Левый проводник движется вправо со скоростью V, а правый покоится. С какой скоростью v надо перемещать правый проводник, чтобы в три раза уменьшить силу Ампера, действующую на левый проводник? (Сопротивлением рельсов пренебречь.)

С5-21. По параллельным проводникам bc и ad, находящимся в магнитном поле с индукцией В, со скоростью v = 1 м/с скользит проводящий стержень MN, который находится в контакте с проводниками (см. рисунок). Расстояние между проводниками l = 20 см. Между проводниками подключен резистор cсопротивлением R = 2 Ом. Сопротивление стержня и проводников пренебрежимо мало. При движении стержня по резистору R течет ток I = 40 мА. Какова индукция магнитного поля?

С5-22. По П-образному проводнику abcd постоянного сечения скользит со скоростью v медная перемычка abдлиной l из того же материала и такого же сечения. Проводники, образующие контур, помещены в постоянное однородное магнитное поле, вектор индукции которого направлен перпендикулярно плоскости проводников (см. рисунок). Какова индукция магнитного поля B, если в тот момент, когда ab = ac, разность потенциалов между точками a и b равна U? Сопротивление между проводниками в точках контакта пренебрежимо мало, а сопротивление проводов велико.

С5-23. Тонкий алюминиевый брусок прямоугольного сечения, имеющий длину L = 0,5 м, соскальзывает из состояния покоя по гладкой наклонной плоскости из диэлектрика в вертикальном магнитном поле индукцией В = 0,1 Тл (см. рисунок). Плоскость наклонена к горизонту под углом α = 30°. Продольная ось бруска при движении сохраняет горизонтальное направление. Найдите величину ЭДС индукции на концах бруска в момент, когда брусок пройдет по наклонной плоскости расстояние I = 1,6 м.

С5-24. Горизонтальный проводящий стержень прямоугольного сечения поступательно движется с ускорением вверх по гладкой наклонной плоскости в вертикальном однородном магнитном поле (см. рисунок). По стержню протекает ток I. Угол наклона плоскости α = 30°. Отношение массы стержня к его длине m/l = 0,1 кг/м. Модуль индукции магнитного поля В = 0,2Тл. Ускорение стержня a = 1,9 м/с². Чему равна сила тока в стержне?

Источник

К однородному медному цилиндрическому проводнику длиной 40 м приложили разность потенциалов 10 В. Каким будет изменение температуры проводника DT через 15 с? Изменением сопротивления проводника и рассеянием тепла при его нагревании пренебречь. (Удельное сопротивление меди 1,7´10–8 Ом´м.)

На рисунке показана схема устройства для предварительного отбора заряженных частиц для последующего детального исследования. Устройство представляет собой конденсатор, пластины которого изогнуты дугой радиусом см. Предположим, что в промежуток между обкладками конденсатора из источника заряженных частиц (и. ч.) влетают ионы, как показано на рисунке. Напряжённость электрического поля в конденсаторе по модулю равна 5 кВ/м. Скорость ионов равна 10⁵ м/с. При каком значении отношения заряда к массе ионы пролетят сквозь конденсатор, не коснувшись его пластин? Считать, что расстояние между обкладками конденсатора мало, напряжённость электрического поля в конденсаторе всюду одинакова по модулю, а вне конденсатора электрическое поле отсутствует. Влиянием силы тяжести пренебречь.

По прямому горизонтальному проводнику длиной 1 м с площадью поперечного сечения подвешенному с помощью двух одинаковых невесомых пружинок жёсткостью 100 Н/м, течёт ток (см. рисунок).

Какой угол составляют оси пружинок с вертикалью после включения вертикального магнитного поля с индукцией если абсолютное удлинение каждой из пружинок при этом составляет ? (Плотность материала проводника )

В электрической цепи, показанной на рисунке, ЭДС источника тока равна 12 В, емкость конденсатора 2 мФ, индуктивность катушки 5 мГн, сопротивление лампы 5 Ом и сопротивление резистора 3 Ом.

В начальный момент времени ключ К замкнут. Какая энергия выделится в лампе после размыкания ключа? Внутренним сопротивлением источника тока, и проводов пренебречь.

Пылинка, имеющая массу и заряд влетает в электрическое поле вертикального высокого конденсатора в точке, находящейся посередине между его пластинами (см. рисунок, вид сверху).

Чему должна быть равна минимальная скорость, с которой пылинка влетает в конденсатор, чтобы она смогла пролететь его насквозь? Длина пластин конденсатора 10 см, расстояние между пластинами 1 см, напряжение на пластинах конденсатора 5 000 В. Система находится в вакууме.

Плоская горизонтальная фигура площадью 0,1 м², ограниченная проводящим контуром, имеющим сопротивление 5 Ом, находится в однородном магнитном поле. Проекция вектора магнитной индукции на вертикальную ось О_z медленно и равномерно возрастает от некоторого начального значения B_1z до конечного значения B_2z = 4,7 Тл. За это время по контуру протекает заряд Δq= 0,08 Кл. Найдите B_1z.

В электрической схеме, показанной на рисунке, ключ К замкнут.

Заряд конденсатора ЭДС батарейки её внутреннее сопротивление сопротивление резистора Найдите количество теплоты, которое выделяется на резисторе после размыкания ключа К в результате разряда конденсатора. Потерями на излучение пренебречь.

Тонкий алюминиевый брусок прямоугольного сечения, имеющий длину L = 0,5 м, соскальзывает из состояния покоя по гладкой наклонной плоскости из диэлектрика в вертикальном магнитном поле индукцией В = 0,1 Тл (см. рисунок). Плоскость наклонена к горизонту под углом a = 30°. Продольная ось бруска при движении сохраняет горизонтальное направление. Найдите величину ЭДС индукции на концах бруска в момент, когда брусок пройдёт по наклонной плоскости расстояние l = 1,6 м.

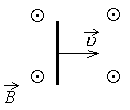
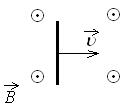
Проводящий стержень длиной l = 20 см движется поступательно в однородном магнитном поле со скоростью v = 1 м/с так, что угол между стержнем и вектором скорости = 30° (см. рисунок). ЭДС индукции в стержне равна 0,05 В. Какова индукция магнитного поля?

Как и во сколько раз изменится мощность, выделяющаяся на резисторе в цепи, схема которой изображена на рисунке, если перевести ключ К из положения 1 в положение 2? Параметры цепи:

На уроке физики школьник собрал схему, изображенную на рисунке. Ему было известно, что сопротивления резисторов равны и Токи, измеренные школьником при помощи идеального амперметра А при последовательном подключении ключа К к контактам 1, 2 и 3, оказались равными, соответственно, Чему было равно сопротивление резистора ?

В цепи, схема которой изображена на рисунке, вначале замыкают ключ а затем, спустя длительное время, ключ Известно, что после этого через ключ протек заряд, равный по модулю Чему равна ЭДС источника тока, если ? Источник считайте идеальным.

В цепи, изображённой на рисунке, сопротивление диода в прямом направлении пренебрежимо мало, а в обратном многократно превышает сопротивление резисторов. При подключении к точке А положительного полюса, а к точке В отрицательного полюса батареи с ЭДС 12 В и пренебрежимо малым внутренним сопротивлением потребляемая мощность равна 14,4 Вт. При изменении полярности подключения батареи потребляемая мощность оказалась равной 21,6 Вт. Укажите, как течёт ток через диод и резисторы в обоих случаях, и определите сопротивления резисторов в этой цепи.

В цепи, изображённой на рисунке, сопротивления резисторов равны между собой: R₁= R₂ = R₃ = R. При разомкнутом ключе К через резистор R₃ течёт ток I₀ =1,4 А. Загорится ли лампа после замыкания ключа, если она загорается при силе тока I = 0,5 А? Сопротивление лампы в этом режиме R_л = 3R. Внутренним сопротивлением источника пренебречь, диод считать идеальным.

Решение

1. Из рисунка видно, что диод включен противоположно направлению тока. Так как диод идеальный, то ток через него и резистор не потечёт.

2. При разомкнутом ключе резисторы и подключены последовательно, а значит, сила тока в этом случае по закону Ома равна

3. Когда ключ замыкают, лампа включается параллельно резистору а значит, сопротивление участка с параллельным соединением проводов будет:

Ток в цепи в этом случае:

Напряжение на параллельных участках одинаково и равно

Тогда через лампу будет проходить ток:

что меньше величины необходимого тока, а значит, лампа не загорится.

Задача 16

Одни и те же элементы соединены в электрическую цепь сначала по схеме 1, а затем по схеме 2 (см. рисунок). Сопротивление резистора равно R, сопротивление амперметра сопротивление вольтметра Найдите отношение мощностей выделяемых на резисторах в этих схемах. Внутренним сопротивлением источника и сопротивлением проводов пренебречь.

Решение

Пусть — сопротивление амперметра, — сопротивление вольтметра, — ЭДС источника. В схеме 1 напряжение на резисторе определяется с помощью закона Ома для замкнутой цепи: где — сопротивление участка цепи, содержащего резистор и вольтметр. Отсюда:

В схеме 2 с помощью закона Ома найдём силу тока через резистор:

Отношение мощностей

Задача 17

Маленький шарик с зарядом и массой 3 г, подвешенный на невесомой нити с коэффициентом упругости 100 Н/м, находится между вертикальными пластинами плоского воздушного конденсатора. Расстояние между обкладками конденсатора 5 см. Какова разность потенциалов между обкладками конденсатора, если удлинение нити 0,5 мм?

Решение

Условия равновесия: Возведем оба равенства в квадрат и сложим их: откуда

Напряженность электрического поля в конденсаторе:

Таким образом,

Задача 18

По П-образному проводнику постоянного сечения скользит со скоростью медная перемычка длиной из того же материала и такого же сечения.

Проводники, образующие контур, помещены в постоянное однородное магнитное поле, вектор индукции которого направлен перпендикулярно плоскости проводников (см. рисунок). Какова индукция магнитного поля если в тот момент, когда разность потенциалов между точками и равна ? Сопротивление между проводниками в точках контакта пренебрежимо мало, а сопротивление проводов велико.

Решение

При движении перемычки в ней возникает ЭДС

Закон Ома для замкнутой цепи :

где — сопротивление перемычки Следовательно,

Задача 19

Два плоских конденсатора ёмкостью С и 2С соединили параллельно и зарядили до напряжения U. Затем ключ К разомкнули, отключив конденсаторы от источника (см. рисунок). Пространство между их обкладками заполнено жидким диэлектриком с диэлектрической проницаемостью ε. Какой будет разность потенциалов между обкладками, если из правого конденсатора диэлектрик вытечет?

Решение

В соответствии с определением понятия «ёмкость» для суммарного заряда конденсаторов имеем:

где 3С — суммарная ёмкость конденсаторов, когда оба они заполнены жидким диэлектриком. После вытекания диэлектрика из правого конденсатора суммарный заряд останется прежним. Так как для плоского конденсатора C~ε, то суммарная ёмкость станет равной (С + 2С/ε), а напряжение будет равно U₁, так что

Решая систему уравнений (1) и (2), получим ответ:

Задача 20

Катод фотоэлемента с работой выхода освещается светом частотой Вылетевшие из катода электроны попадают в однородное магнитное поле с индукцией перпендикулярно линиям индукции этого поля. Чему равен максимальный радиус окружности R, по которой движутся электроны?

Решение

№ этапа	Содержание этапа решения	Чертёж, график, формула	Оценка этапа в баллах
1	Записано уравнение Эйнштейна для фотоэффекта:		1
2	Записано уравнение, связывающее силу Лоренца, действующую на электрон, с величиной центростремительного ускорения: Уравнение преобразовано к виду, устанавливающему связь между кинетической энергией электрона и радиусом орбиты:		1
3	Решена система уравнений и получен ответ в алгебраической форме: Подставлены значения констант и параметров и получен ответ в числовой форме:		1
Максимальный балл	3

Задача 21

В однородном магнитном поле, индукция которого протон движется перпендикулярно вектору магнитной индукции В по окружности радиусом 5 м. Определите скорость протона.

Решение

Из уравнения, связывающего на основе второго закона Ньютона силу Лоренца, действующую на протон, с модулем центростремительного ускорения: . Откуда выражаем искомую скорость.

Задача 22

К одному концу лёгкой пружины жёсткостью k = 100 Н/м прикреплён массивный груз, лежащий на горизонтальной плоскости, другой конец пружины закреплён неподвижно (см. рисунок). Коэффициент трения груза по плоскости Груз смещают по горизонтали, растягивая пружину, затем отпускают с начальной скоростью, равной нулю. Груз движется в одном направлении и затем останавливается в положении, в котором пружина уже сжата. Максимальное растяжение пружины, при котором груз движется таким образом, равно d = 15 см. Найдите массу m груза.

Решение

1. Начальная энергия системы равна потенциальной энергии растянутой пружины: После того, как пружину отпустили, она остановится в положении, при котором она сжата на величину Тогда конечная энергия системы равна потенциальной энергии сжатой пружины:

Приращение полной энергии системы равно работе силы трения

где — модуль силы реакции опоры.

2. В момент, когда груз остановился, по второму закону Ньютона равнодействующая всех сил стала равна нулю. Пружина сжата, поэтому сила упругости пружины направлена вправо. Её уравновешивает сила трения покоя, которая направлена против возможного движения, причём эта сила максимальна, т. к. по условию начальное положение пружины соответствует максимальному растяжению пружины, при котором груз движется таким образом.

Запишем закон Ньютона для вертикальной и горизонтальной оси:

3. Подставим полученное выражение для в равенство из пункта 1:

После подстановки получим

Задача 23

Хорошо проводящая рамка площадью вращается в однородном магнитном поле с индукцией перпендикулярной оси вращения рамки, с частотой Скользящие контакты от рамки присоединены к цепи, состоящей из резистора сопротивлением к которому последовательно присоединены два параллельно соединенных резистора сопротивлениями и (см. рис.). Найти максимальную силу тока, текущего через резистор в процессе вращения рамки. Индуктивностью цепи можно пренебречь.

Решение

При вращении рамки в магнитном поле в ней возникает ЭДС индукции, равная, по закону электромагнитной индукции Фарадея,

(здесь — угловая частота вращения рамки).

В цепи из резисторов, присоединенной к рамке, под действием этой ЭДС возникает ток, равный, согласно закону Ома для полной цепи, где согласно формулам для сопротивления цепи, состоящей из последовательно и, параллельно соединенных резисторов,

Поскольку падение напряжения на параллельно соединенных резисторах и одинаково, по закону Ома для участка цепи причем в точке разветвления тока Из всех записанных уравнений следует, что

откуда искомая максимальная сила тока равна, очевидно,

Подставляя числовые данные и проверяя размерность, получаем:

Задача 24

На двух вертикальных лёгких проводах длиной l каждый подвешен в горизонтальном положении массивный проводящий стержень длиной L. Верхние концы проводов присоединены к обкладкам конденсатора ёмкостью С. Система находится в вертикальном однородном магнитном поле с индукцией В (см. рисунок). Стержень отклоняют от положения равновесия параллельно самому себе на небольшое расстояние и отпускают с нулевой начальной скоростью. Найдите зависимость от времени t заряда q конденсатора, считая, что в начальный момент, при конденсатор был не заряжен. Трением, сопротивлением всех проводников и контактов между ними, а также силами взаимодействия токов в проводниках с магнитным полем пренебречь.

Решение

Согласно условию задачи, взаимодействие токов в проводниках с магнитным полем пренебрежимо мало. Поэтому после отпускания стержень будет совершать свободные колебания, как математический маятник, с круговой частотой по закону где x — текущее отклонение стержня от положения равновесия.

Поток вектора магнитной индукции через замкнутый контур, содержащий все проводники и конденсатор, равен

По закону электромагнитной индукции Фарадея при колебаниях стержня в данном контуре будет возникать ЭДС индукции, равная

Поскольку сопротивлением проводников мы также пренебрегаем, то по закону Ома для полной цепи эта ЭДС равняется напряжению между обкладками конденсатора: откуда

Задача 25

В однородном магнитном поле с индукцией протон движется перпендикулярно вектору индукции со скоростью Определите радиус траектории протона.

Задача 26

Ядро изотопа водорода — дейтерия — движется в однородном магнитном поле индукцией перпендикулярно вектору В индукции по окружности радиусом 10 м. Определите скорость ядра.

Задача 27

В однородном магнитном поле с индукцией B, направленной вертикально вниз, равномерно вращается в горизонтальной плоскости против часовой стрелки положительно заряженный шарик массой m, подвешенный на нити длиной l (конический маятник). Угол отклонения нити от вертикали равен скорость движения шарика равна v. Найдите заряд шарика q.

Решение

Задача 28

На непроводящей горизонтальной поверхности стола проводящая жёсткая рамка массой m из однородной тонкой проволоки, согнутая в виде квадрата ACDE со стороной (см. рисунок). Рамка находится в однородном горизонтальном магнитном поле, вектор индукции которого перпендикулярен сторонам АЕ и CD и равен по модулю В. По рамке течёт ток в направлении, указанном стрелками (см. рисунок). При какой минимальной силе тока рамка начнет поворачиваться вокруг стороны CD?

Решение

Для того, чтобы рамка начала поворачиваться вокруг оси CD, вращательный момент сил, действующих на рамку и направленных вверх, должен быть не меньше суммарного момента сил, направленных вниз.

На проводник с током в магнитном поле действует сила Ампера Если направление тока и магнитного поля параллельны, то сила Ампера не действует. В данном случае на сторону АЕ действует сила Ампера которая по правилу буравчика направлена вверх (на рисунке — на нас). На каждую из сторон действует сила тяжести т. к. масса всего квадрата равна

Запишем условие моментов: где и — плечи сил относительно оси CD.

Отсюда находим минимальную силу тока

Задача 29

Ион ускоряется в электрическом поле с разностью потенциалов кВ и попадает в однородное магнитное поле перпендикулярно к вектору его индукции (см. рисунок). Радиус траектории движения иона в магнитном поле м, модуль индукции магнитного поля равен 0,5 Тл. Определите отношение массы иона к его электрическому заряду Кинетической энергией иона при его вылете из источника пренебрегите.

Решение

Разность потенциалов сообщает иону кинетическую энергию

В магнитном поле, на движущийся ион действует сила Лоренца, которая сообщает ему центростремительное ускорение:

Приравнивая правые части полученных равенств, имеем

Задача 30

Горизонтальный проводящий стержень прямоугольного сечения поступательно движется с ускорением вверх по гладкой наклонной плоскости в вертикальном однородном магнитном поле (см. рисунок).

По стержню протекает ток I. Угол наклона плоскости Отношение массы стержня к его длине Модуль индукции магнитного поля Ускорение стержня Чему равна сила тока в стержне?

Решение

1) На рисунке показаны силы, действующие на стержень с током:

— сила тяжести направленная вертикально вниз;

— сила реакции опоры направленная перпендикулярно к наклонной плоскости;

— сила Ампера направленная горизонтально вправо, что вытекает из условия задачи.

2) Модуль силы Ампера

3) Систему отсчёта, связанную с наклонной плоскостью, считаем инерциальной. Для решения задачи достаточно записать второй закон Ньютона в проекциях на ось х (см. рисунок):

Отсюда находим

Задача 31

В зазоре между полюсами электромагнита вращается с угловой скоростью ω = 100 с^–1проволочная рамка в форме полуокружности радиусом r = 5 см, содержащая N = 20 витков провода. Ось вращения рамки проходит вдоль оси О рамки и находится вблизи края области с постоянным однородным магнитным полем с индукцией В = 1 Тл (см. рисунок), линии которого перпендикулярны плоскости рамки. Концы обмотки рамки замкнуты через скользящие контакты на резистор с сопротивлением R = 25 Ом. Пренебрегая сопротивлением рамки, найдите тепловую мощность, выделяющуюся в резисторе.

Решение

При вращении рамки в магнитном поле в ней возникает ЭДС индукции, равная по модулю

За малое время рамка поворачивается на угол и её площадь, находящаяся в магнитном, поле увеличивается на так что

Так происходит до тех пор, пока площадь рамки в поле увеличивается. После того как вся рамка окажется в поле, эта площадь начнёт уменьшаться с такой же скоростью, так что ЭДС поменяет знак, но сохранит своё значение.

Таким образом, согласно закону Ома для замкнутой цепи, в рамке всё время будет течь ток с одинаковым значением периодически изменяя своё направление на противоположное.

По закону Джоуля — Ленца тепловая мощность, выделяющаяся при этом процессе в резисторе, не зависит от направления тока и равняется

Задача 32

На шероховатой плоскости, наклонённой под углом к горизонту, находится однородный цилиндрический проводник массой от г и длиной см (см. рисунок). По проводнику пропускают ток в направлении «от нас», за плоскость рисунка, и вся система находится в однородном магнитном поле с индукцией направленной вертикально вниз. При какой силе тока цилиндр будет оставаться на месте, не скатываясь с плоскости и не накатываясь на неё?

РешениеНарисуем силы, действующие на проводник с током: силу тяжести направленную вертикально вниз, силу нормального давления перпендикулярную плоскости, и силу Ампера равную по модулю и направленную в данном случае, согласно правилу левой руки, горизонтально влево (см. рисунок). Заметим, что все эти три силы приложены таким образом, что они не создают моментов сил относительно оси цилиндра. Поэтому в равновесии сила сухого трения цилиндра о шероховатую наклонную плоскость децствительно должна равняться нулю — иначе он бы покатился.

Спроецируем эти силы на направление вдоль плоскости и на перпендикуляр к ней. Условия равновесия имеют вид

Из первого уравнения находим искомую величину силы тока при равновесии цилиндра: Подставляя это значение во второе уравнение, находим (хотя эту величину находить по условию не требовалось).

Задача 33

Проводник движется равноускоренно в однородном вертикальном магнитном поле. Направление скорости перпендикулярно проводнику. Длина проводника — 2 м. Индукция перпендикулярна проводнику и скорости его движения. Проводник перемещается на 3 м за некоторое время. При этом начальная скорость проводника равна нулю, а ускорение 5 м/с². Найдите индукцию магнитного поля, зная, что ЭДС индукции на концах проводника в конце движения равна 2 В.

Решение

При движении проводника в магнитном поле на электроны в проводнике действует сила Лоренца. Сила Лоренца равна Напряжённость поля внутри проводника можно рассчитать по формуле Напряжение на концах проводника равно Движение равноускоренное, поэтому путь, пройденный проводником рассчитывается по формуле откуда Следовательно, откуда

Задача 34

Решение

Выражение для модуля ЭДС индукции в случае однородного поля: где S — площадь фигуры;

Закон Ома: E = IR, где R — сопротивление контура; — ток в контуре за время Δt изменения магнитного поля.

Выражение для заряда, протекающего по цепи:

Задача 35

К конденсатору С1 через диод и катушку индуктивности L подключён конденсатор ёмкостью С2 = 2 мкФ. До замыкания ключа К конденсатор С1 был заряжен до напряжения U = 50 В, а конденсатор С2 не заряжен. После замыкания ключа система перешла в новое состояние равновесия, в котором напряжение на конденсаторе С2 оказалось равным U2 = 20 В. Какова ёмкость конденсатора С1? (Активное сопротивление цепи пренебрежимо мало.)

Решение

Энергия заряженного конденсатора С1 до замыкания ключа К:Заряд конденсатора С1:

q = C1U.

Суммарная энергия заряженных конденсаторов после замыкания ключа К:

Так как процесс зарядки конденсатора С2 происходит медленно, нет потерь энергии на излучение, а следовательно, после замыкания ключа К первоначальная энергия заряженного конденсатора С1 в новом состоянии равновесия распределяется между конденсаторами:

Wэ = Wэ1 + Wэ2.

Кроме того, выполняется закон сохранения заряда: q = q1 + q2 = C1U1 + C2U2. Объединяя соотношения, получаем систему уравнений

Решая эту систему, получаем

Задача 36

Математический маятник, грузик которого имеет массу m = 8 г, совершает малые колебания в поле силы тяжести с периодом T₁ = 0,7 с. Грузик зарядили и включили направленное вниз однородное вертикальное электрическое поле, модуль напряжённости которого равен E = 3 кВ/м. В результате этого период колебаний маятника стал равным T₂ = 0,5 с. Найдите заряд q грузика.

Решение

1. В первом случае период колебаний математического маятника равен где l — длина нити подвеса маятника.

2. Во втором случае период колебаний шарика в электрическом поле, направленном вниз, уменьшился, значит, сила натяжения нити подвеса увеличилась и заряд шарика — положительный.

3. При малых колебаниях математического маятника с грузиком массой m и с зарядом q в поле тяготения модуль F силы натяжения нити близок к mg + qE. Уравнение движения грузика в проекции на горизонтальную ось Х имеет вид: где — угол отклонения нити от вертикали, x — смещение грузика. Отсюда получаем уравнение гармонических колебаний: или где Период этих колебаний равен

4. Из последнего уравнения находим заряд шарика маятника:

мкКл.

Задача 37

По горизонтально расположенным шероховатым рельсам с пренебрежимо малым сопротивлением могут скользить два одинаковых стержня массой и сопротивлением каждый. Расстояние между рельсами а коэффициент трения между стержнями и рельсами Рельсы со стержнями находятся в однородном вертикальном магнитном поле с индукцией (см. рисунок). Под действием горизонтальной силы, действующей на первый стержень вдоль рельс, оба стержня движутся поступательно равномерно с разными скоростями. Какова скорость движения первого стержня относительно второго? Самоиндукцией контура пренебречь.

Решение

Задача 38

Два параллельных друг другу рельса, лежащих в горизонтальной плоскости, находятся в однородном магнитном поле, индукция B которого направлена вертикально вниз (см. рисунок, вид сверху). На рельсах находятся два одинаковых проводника. Левый проводник движется вправо со скоростью V, а правый — покоится. С какой скоростью v надо перемещать правый проводник направо, чтобы в три раза уменьшить силу Ампера, действующую на левый проводник? (Сопротивлением рельсов пренебречь.)

Решение

Источник

Подготовка к ЕГЭ по Физике. Решение задач по теме: электромагнитная индукция

З.М.Кенжаев

Основные формулы

Магнитный поток Ф через плоский контур площадью S :

а) в случае однородного поля

Ф = BS cos  = B n S , где  — угол между вектором нормали к плоскости контура и вектором магнитной индукции; B n – проекция вектора В на нормаль n ( B n = B cos  );

Потокосцепление, т.е. полный магнитный поток

 = NФ , где Ф – магнитный поток через один виток; N – число витков.

Работа по перемещению замкнутого контура с током I в магнитном поле определяется соотношением

A = I  Ф ,

где  Ф – изменение магнитного потока, пронизывающего поверхность, ограниченную контуром.

Основной закон электромагнитной индукции (закон Фарадея-Максвелла)

где  i – ЭДС индукции, возникающая в контуре; dФ / dt – скорость изменения магнитного потока, N – число витков контура;  — потокосцепление (  = NФ ).

Разность потенциалов U на концах проводника длиной l , движущегося со скоростью υ в однородном магнитном поле с индукцией В , выражается формулой

U = Blυ sin  , где  — угол между направлениями векторов v и B .

Заряд, протекающий по замкнутому контуру при изменении на величину   потокосцепления, пронизывающего все витки контура, выражается формулой

q =   / R ,

где R – сопротивление контура.

Индуктивность контура

L =  / I .

ЭДС самоиндукции

где — скорость изменения силы тока.

Индуктивность соленоида

L =  0  n 2 l S , где l – длина соленоида, S – площадь его поперечного сечения; n – число витков на единицу его длины.

ЭДС взаимной индукции

где — коэффициент взаимной индукции.

Магнитная энергия W контура с током I

W = LI 2 /2, где L – индуктивность контура.

Объемная плотность энергии w 0 однородного магнитного поля

w 0 = BH/2 =  0  H 2 /2 = B 2 /(2  0  ).

Примеры решения задач

Пример 1. Магнитный момент соленоида 2 А∙м 2 . Найти поток магнитной индукции сквозь соленоид. Длина соленоида равна 30 см.

Дано:

p m = 2 А ×м 2 ; m = 1 ;

l = 30 см = 0,3 м

Ф = ?

Решение

Магнитный момент соленоида складывается из магнитных моментов каждого витка p i = I S, где I — сила тока в обмотке, S — площадь поперечного сечения соленоида:

p m = N I S (1)

Из определения потока Ф вектора магнитной индукции В

Ф =B S = m 0 mI S N. (2)

Используя (1) и (2), получаем:

Ф = m 0 p m / l =4p 10 -7 ×2/0,3 = 8,37×10 -6 Вб.

Ответ: Ф = 8,37 мВб.

Пример 2. Сила тока в соленоиде изменяется по закону I = 20 t – t 3 . Индуктивность соленоида 5 Гн. Какая ЭДС самоиндукции будет в соленоиде через 2 с?

Дано:

I = 20 t – t 3 ;

t = 2 c; L = 5 Гн

e инд = ?

Решение

Согласно закону электромагнитной индукции Фарадея

e инд = — dФ/dt

Из определения индуктивности магнитного контура Ф = L I, где I– сила тока в контуре, а L – его индуктивность. Тогда

e инд = — L dI/dt = L (20 – 3 t 2 ) = 5(20 — 3∙2 2 ) = 40 B.

Ответ: e инд = 40 В.

Пример 3. Скат плывет горизонтально со скоростью 2 м/с. Определить разность потенциалов, возникающую между концами боковых плавников рыбы, если вертикальная составляющая индукции магнитного поля Земли равна 5  10 –5 Тл. Ширина рыбы 30 см.

Дано:

v = 2 м/с;

l = 30 см = 0,3 м;

B ^ = 5 ×10 -5 Тл

U = ?

Решение

При движении ската пересекаются силовые линии магнитного поля Земли; при этом за время dt рыба проходит путь dx и происходит изменение магнитного потока

d Ф = B ^ d S = B ^ l dx = B ^ l v dt

На концах боковых плавников возникает разность потенциалов согласно закону электромагнитной индукции:

U = |e инд | = dФ/dt = B ^ l v = 5 ×10 -5 ×0,3 ×2 = 30 мкВ.

Ответ: U = 30 мкВ .

Пример 4. При индукции магнитного поля 0,1 Тл плотность энергии магнитного поля в железе 10 Дж/м 3 . Какова относительная магнитная проницаемость железа при этих условиях и величина напряженности магнитного поля?

Дано:

B = 0,1 Тл;

w = 10 Дж/м 3 ;

m 0 =4 p 10 -7 Гн /м

m = ? H = ?

Решение

Плотность энергии магнитного поля в магнетике

w = BH/2 = B 2 /(2  0  )

Отсюда находим

H = 2w/B;

m = B 2 /(2m 0 w)

Подставив численные данные, получим

Ответ: m = 398 @ 400; H =200 А/м .

Пример 5. Для магнитной обработки виноматериалов и питьевой воды используют установку на электромагнитах (рис.19), потребляющих мощность 2,4 кВт. Индукция магнитного поля в рабочем зазоре 15,1× 10 -2 Тл. Определить КПД установки, если ее производительность 100 м 3 / час.

Дано:

N потр = 2,4 ×10 3 Вт;

B = 15,1× 10 -2 Тл;

m = 1 ;

Q = 200 м 3 /час =1/18 м 3 /с

h = ?

Решение

По определению коэффициента полезного действия

h = А полезн /А затр (1)

Затраченная работа равна потребляемой из сети энергии

А затр = N потр Dt, (2)

где Dt – отрезок времени.

Полезная работа состоит в намагничивании протекающей жидкости в объеме

V = Q Dt.

Эта работа равна энергии магнитного поля, создаваемого в зазоре:

А полезн = W м = w V = B 2 V/(2  0  ) = B 2 Q Dt /2  0 . (3)

Подставив (3) и (2) в (1), получаем КПД:

h = B 2 Q /(2  0 N потр ) = 1,5 2 /(18 ×2 ×12,56 ×10 -7 × 2,4 ×10 3 ) = 0,104.

Ответ: КПД составляет 10,4 % .

Источник

В задании №15 ЕГЭ по физике нас ждут задачи по теме электромагнитная индукция и оптика.

Задание EF18285

Линии индукции однородного магнитного поля пронизывают рамку площадью 0,5 м² под углом 30° к её поверхности, создавая магнитный поток, равный 0,2 Вб. Чему равен модуль вектора индукции магнитного поля?

Ответ:

а) 0,2 Тл

б) 0,4 Тл

в) 0,8 Тл

г) 0,16 Тл

Алгоритм решения

1.Записать исходные данные.

2.Записать формулу для определения потока магнитной индукции.

3.Выразить искомую величину.

4.Подставить исходные данные и выполнить вычисления.

Решение

Запишем исходные данные:

• Магнитный поток, пронизывающий рамку: Φ = 0,2 Вб.

• Площадь рамки, находящейся в однородном магнитном поле: S = 0,5 м².

• Угол между вектором магнитной индукции и плоскостью, ограниченной контуром рамки: β = 30^о.

Запишем формулу для определения потока магнитной индукции:

Φ=BScosα

Так как в условиях задачи указан угол между вектором магнитной индукции и плоскостью рамки, то угол между нормалью и плоскостью рамки будет равен α=90°−β.

Выразим модуль вектора индукции магнитного поля:

B=ΦScos(90−β)=0,20,5·cos(90°−30°)=0,40,5=0,8 (Тл)

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF19000

Проволочная рамка площадью 2×10^–3м²вращается в однородном магнитном поле вокруг оси, перпендикулярной вектору магнитной индукции. Магнитный поток, пронизывающий площадь рамки, изменяется по закону Ф=4×10^–6cos10πt, где все величины выражены в СИ. Чему равен модуль магнитной индукции? Ответ выразите в мТл.

Алгоритм решения

1.Записать исходные данные.

2.Записать формулу для определения потока магнитной индукции.

3.Выразить искомую величину.

4.Подставить исходные данные и выполнить вычисления.

Решение

Запишем исходные данные:

• Магнитный поток, пронизывающий рамку: Φ = 4∙10^–6cos10πt Вб.

• Площадь рамки, находящейся в однородном магнитном поле: S = 2∙10^–3 м².

Запишем формулу для определения потока магнитной индукции:

Φ=BScosα

Выразим модуль вектора индукции магнитного поля:

B=ΦScosα

Так как рамка вращается в однородном магнитном поле, угол между нормалью, проведенной к ее плоскости, и вектором магнитной индукции постоянно меняется. Если мы примем этот угол за 0 градусов, то косинус этого угла будет равен 1. Тогда мы получим максимальное значение магнитного потока, пронизывающего рамку, и сможем вычислить модуль вектора магнитной индукции.

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18621

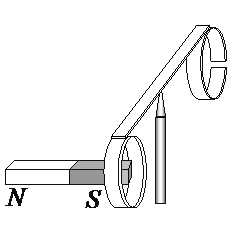
На рисунке запечатлён тот момент демонстрации по проверке правила Ленца, когда все предметы неподвижны. Южный полюс магнита находится вблизи сплошного металлического кольца. Если магнит выдвигать из алюминиевого кольца, то кольцо перемещается вслед за магнитом. Это движение кольца – результат действия

Ответ:

а) силы гравитационного взаимодействия между кольцом и магнитом

б) силы Ампера, действующей со стороны магнитного поля магнита на кольцо, по которому идёт индукционный ток

в) кулоновских (электростатических) сил, которые возникают при движении магнита относительно кольца

г) воздушных потоков, вызванных движением руки и магнита

Алгоритм решения

Проанализировать предложенные варианты ответа.
Установить природу взаимодействия магнита и кольца.
Выбрать верный ответ.

Решение

Гравитационные силы между магнитом и кольцом ничтожно малы при данных массах и расстояниях, поэтому они не могли вызвать притяжения кольца к магниту.

Кулоновские силы характеризуют силу электростатического взаимодействия зарядов. Поскольку магнит не имеет заряда, между ним и кольцом такие силы не возникают.

Металлическое кольцо достаточно тяжелое для того, чтобы заставить его стремительно двигаться вслед за магнитом.

Но вариант с силой Ампера подходит, так как сила Ампера — это сила, с которой действует магнитное поле на проводник с током. В момент, когда магнит двигают в стороны от кольца, магнитный поток, пронизывающий его, меняется. Это вызывает образование в кольце индукционного тока, который также порождает магнитное поле, противодействующее магнитному полю постоянного магнита.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17970

При вращении в однородном магнитном поле плоскости металлического кольца из тонкой проволоки вокруг оси, перпендикулярной линиям поля, максимальная сила индукционного тока, возникающего в кольце, равна I₁. Чему будет равна максимальная сила индукционного тока I₂ в этом кольце при уменьшении скорости вращения кольца в 2 раза?

Ответ:

а) I₂ = 2I₁

б) I₂ = I₁

в) I₂ = 0,5I₁

г) I₂ = 4I₁

Алгоритм решения

1.Записать закон электромагнитной индукции.

2.Установить зависимость между величиной индукционного тока и скоростью вращения рамки.

3.Определить, как изменится величина индукционного тока в кольце при уменьшении скорости ее вращения.

Решение

Запишем формулу закона электромагнитной индукции:

εi=∣∣∣ΔΦΔt∣∣∣

Известно, что отношение изменения магнитного потока ко времени его изменения — это величина, характеризующая скорость этого изменения. Если кольцо в однородном магнитном поле вращать медленнее, то и магнитный поток начнет менять медленнее. Так как ЭДС индукции прямо пропорционально зависит от скорости изменения магнитного потока, то при уменьшении скорости вращения кольца в 2 раза она также уменьшится вдвое.

Также известно, что индукционный ток в рамке определяется формулой:

Ii=εiR

Видно, что индукционный ток и ЭДС индукции — прямо пропорциональные величины. Следовательно, при уменьшении ЭДС индукции вдвое сила индукционного тока тоже уменьшится в 2 раза. Отсюда следует, что I₂ = 0,5I₁.

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18180

Плоская рамка помещена в однородное магнитное поле, линии магнитной индукции которого перпендикулярны её плоскости. Если площадь рамки увеличить в 3 раза, а индукцию магнитного поля уменьшить в 3 раза, то магнитный поток через рамку

Ответ:

а) увеличится в 9 раз

б) не изменится

в) уменьшится в 3 раза

г) уменьшится в 9 раз

Алгоритм решения

1.Записать формулу, раскрывающую зависимость магнитным потоком, площадью рамки, помещенной в магнитное поле и индукции этого поля.

2.Установить, как изменится магнитной поток при изменении указанных в задаче величин.

Решение

Магнитный поток, пронизывающий площадь, ограниченную рамкой, определяется формулой:

Φ=BScosα

По условию задачи площадь рамки увеличивают в 3 раза, а индукцию магнитного поля уменьшают во столько же раз. Следовательно:

S1=3S

B1=B3

Следовательно:

Φ1=B1S1cosα=3S·B3cosα=BScosα=Φ

Следовательно, магнитный поток не изменится.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17636

Катушка индуктивности подключена к источнику постоянного тока. Как изменится энергия магнитного поля катушки при увеличении силы тока через катушку в 3 раза?

Ответ:

а) уменьшится в 3 раза

б) увеличится в 9 раз

в) увеличится в 3 раза

г) уменьшится в 9 раз

Алгоритм решения

1.Записать формулу, определяющую энергию магнитного поля тока.

2.Установить, как изменится энергия магнитного поля тока при увеличении силы тока через катушку в 3 раза.

Решение

Энергия магнитного поля тока определяется формулой:

WМ=LI22

Видно, что энергия магнитного поля тока прямо пропорционально зависит от квадрата силы тока в катушке. Следовательно, если сила тока увеличится втрое, то энергия магнитного поля увеличится в 3², то есть в 9 раз.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF22688

Энергия магнитного поля катушки с током равна 0,64 Дж. Индуктивность катушки равна 20 мГн. Какова сила тока в катушке?

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения в СИ.

2.Записать формулу, определяющую энергию магнитного поля тока.

3.Выполнить решение задачи в общем виде.

4.Подставить неизвестные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

Индуктивность катушки: L = 20 мГн.
Энергия магнитного поля катушки с током: W_M = 0,64 Дж.

20 мГн = 0,02 Гн

Формула для нахождения энергии магнитного поля тока:

WМ=LI22

Отсюда сила тока равна:

I=√2WМL=√2·0,640,02=8 ⎛⎝А⎞⎠

Ответ: 8

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17496

В электромагнитной волне, распространяющейся со скоростью →v, происходят колебания векторов напряжённости электрического поля →E и индукции магнитного поля →B. При этих колебаниях векторы →v, →E, →B. имеют взаимную ориентацию:

Ответ:

а) →B∥∥→E, →B∥∥→v, →E∥∥→v

б) →B⊥→E, →B∥∥→v, →E⊥→v

в) →B⊥→E, →B⊥→v, →E∥∥→v

г) →B⊥→E, →B⊥→v, →E⊥→v

Алгоритм решения

1.Вспомнить, какие величины периодически изменяются при распространении электромагнитной волны.

2.Вспомнить, какое взаимное расположение имеют векторы меняющихся величин электромагнитной волны.

3.Вспомнить, какой является электромагнитная волна — продольной или поперечной.

Решение

Электромагнитная волна представляет собой распространяющиеся с течением времени в пространстве электромагнитные колебания, характеризующиеся периодическим изменением в точках пространства вектора напряженности →E и вектора магнитной индукции →B. Эти векторы лежат и изменяются во взаимно перпендикулярных плоскостях. Поэтому вектора напряженности →E и вектор магнитной индукции →B перпендикулярны (→B⊥→E).

Электромагнитная волна — поперечная волна. Это значит, что векторы периодически меняющихся величин расположены перпендикулярно направлению распространения волны. Направление волны определяется направлением вектора ее скорости. Следовательно, вектор напряженности →E и вектор магнитной индукции →B перпендикулярны вектору скорости распространения волны (→B⊥→v, →E∥∥→v).

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17601

Какой объект, согласно классической электродинамике, не излучает электромагнитных волн?

Ответ:

а) ускоренно движущийся заряд

б) электромагнит, подключённый к генератору переменного тока

в) линия электропередачи

г) покоящийся электромагнит, подключённый к аккумулятору

Алгоритм решения

Вспомнить основное условие возникновения электромагнитных волн.
Проанализировать возможные источники электромагнитных волн и установить, в каком из них необходимое условие не выполняется.

Решение

Главное условие возникновения электромагнитных волн — наличие у движущегося заряда ускорения. Следовательно, ускоренно движущийся заряд излучает электромагнитные волны.

По линиям электропередачи протекает переменный ток, который периодически меняет свое направление. Следовательно, заряды внутри проводников движутся ускоренно, ведь для того, чтобы поменялась скорость (по модулю и направлению), необходимо наличие ускорения. Следовательно, линии электропередач тоже излучают электромагнитные волны. По этой же причине электромагнит, подключённый к генератору переменного тока, также излучает волны.

Покоящийся электромагнит, подключённый к аккумулятору, не может излучать электромагнитные волны. Аккумулятор — источник постоянного тока. Поэтому заряды движутся с постоянной скоростью (без ускорения), и сам электромагнит покоится (не имеет ускорения).

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17566

Выберите среди приведённых примеров электромагнитное излучение с минимальной длиной волны.

Ответ:

а) рентгеновское

б) ультрафиолетовое

в) видимое

г) инфракрасное

Алгоритм решения

Вспомнить расположение видов волн на шкале.
Определить тип волн, имеющих самую короткую длину волны из перечисленных вариантов.

Решение

Шкала электромагнитных волн классифицирует волны по длине или частоте волн. Чем меньше длина волны, тем выше ее частота. Наибольшей длиной волны обладают радиоволны, затем идем инфракрасное, видимое и ультрафиолетовое излучение. После — ионизирующее излучение (рентгеновское и гамма-излучение). Следовательно, наименьшей длиной волн из перечисленных вариантов обладает рентгеновское излучение.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17740

Как изменится период собственных электромагнитных колебаний в контуре (см. рисунок), если ключ К перевести из положения 1 в положение 2?

Ответ:

а) уменьшится в 4 раза

б) уменьшится в 2 раза

в) увеличится в 2 раза

г) увеличится в 4 раза

Алгоритм решения

1.Определить, что изменится при переключении ключа.

2.Записать формулу Томсона.

3.Выяснить, как при этом изменится период собственных электромагнитных колебаний в контуре.

Решение

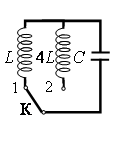
При переключении ключа из положения 1 в положение 2 увеличится индуктивность катушки (в 4 раза). Запишем формулу Томсона:

T=2π√LC

Видно, что если индуктивность возрастет в 4 раза, то период увеличится вдвое. Это можно доказать, приняв, что L₁ = L, а L₂ = 4L. Тогда:

T1=2π√LC

T2=2π√4LC=2π2√LC=4π√LC

Найдем отношение второго периода к первому:

T2T1=4π√LC2π√LC=2

Отсюда:

T2=2T1

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF22720

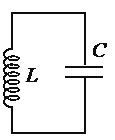
В идеальном колебательном контуре (см. рисунок) напряжение между обкладками конденсатора меняется по закону U_C = U₀cos ωt, где U₀ = 5 В, ω = 1000π с^–1. Определите период колебаний напряжения на конденсаторе.

Алгоритм решения

1.Записать исходные данные.

2.Записать формулу Томсона.

3.Вычислить искомую величину, подставив известные данные.

Решение

Запишем исходные данные:

• Закон изменения напряжения между обкладками конденсатора: UC=U0cosωt.

• Амплитуда напряжения: U0=5 В.

• Циклическая частота колебаний: ω = 1000π с^–1.

Запишем формулу Томсона:

T=2πω=2π1000π=21000=0,002 (с)

Ответ: 0,002

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18656

На рисунке приведён график зависимости силы тока i от времени t при свободных гармонических колебаниях в колебательном контуре. Каким станет период свободных колебаний в контуре, если конденсатор в этом контуре заменить на другой конденсатор, ёмкость которого в 4 раза меньше? Ответ запишите в мкс.

Алгоритм решения

1.Записать исходные данные (определить по графику начальный период колебаний).

2.Перевести единицы измерения величин в СИ.

3.Записать формулу Томсона.

4.Выполнить решение в общем виде.

5.Установить, каким станет период колебаний после уменьшения емкости конденсатора.

Решение

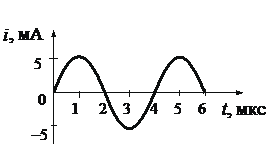
Запишем исходные данные:

• Период колебаний (определяем по графику): T = 4 мкс.

• Емкость конденсатора в первом опыте: C₁ = 4C.

• Емкость конденсатора во втором опыте: C₂ = C.

4 мкс = 4∙10^–6 с

Запишем формулу Томсона:

T=2π√LC

Применим формулу для обоих опытов и получим:

T1=2π√L4C=4π√LC

T2=2π√LC

Поделим первый период на второй:

T1T2=4π√LC2π√LC=2

Отсюда:

T2=T12=4·10−62=2·10−6 (с)=2 (мкс)

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18041

На рисунке показан ход двух лучей от точечного источника света А через тонкую линзу. Какова приблизительно оптическая сила этой линзы?

Ответ:

а) 14 дптр

б) 20 дптр

в) 17 дптр

г) 33 дптр

Алгоритм решения

1.Записать формулу для нахождения оптической силы линзы.

3.Найти точку на главной оптической оси точку главного фокуса линзы.

4.Вычислить фокусное расстояние и перевести его в СИ.

5.Вычислить оптическую силу линзы.

Решение

Оптическая сила линзы определяется формулой:

D=1F

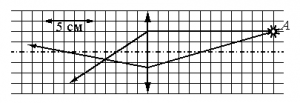
На рисунке видно, что 5 клеток = 5 см. Следовательно, 1 клетка = 1 см. После прохождения сквозь линзу лучи света, параллельные главной оптической оси, фокусируются в главном фокусе, который лежит на этой оси. Значит, фокус находится в точке пересечения этой оси и луча. От него до линзы 3 клетки. Следовательно, фокусное расстояние равно 3 см, или 0,03 м.

Отсюда:

D=10,03≈33 (дптр)

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор | оценить

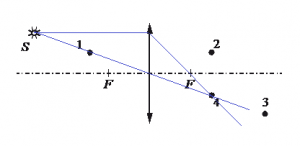
Задание EF18876

Какая точка является изображением точки S (см. рисунок), создаваемым тонкой собирающей линзой с фокусным расстоянием F?

Алгоритм решения

1.Построить изображение точки.

Решение

Построим изображение точки с учетом того, что линза собирающая. Для этого пустим из этой точки луч света, параллельный главной оптической оси. После прохождения через линзу луч преломится и пройдет через фокус. Затем пустим луч от этой точки через оптический центр линзы. Точка, в которой оба луча пересекутся, будет искомой. В данном случае это точка 4.

Ответ: 4

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18181

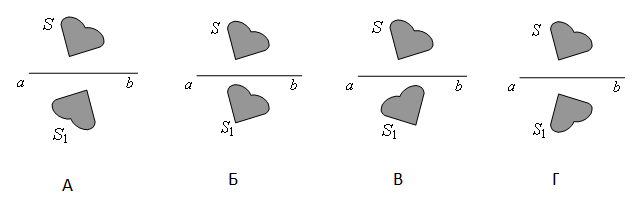
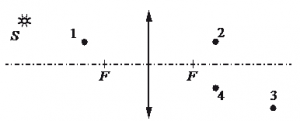
Предмет S отражается в плоском зеркале ab. На каком рисунке верно показано изображение S1 этого предмета?

Ответ:

Алгоритм решения

Записать, какое изображение дает плоское зеркало.
Выбрать изображение, которое соответствует типу описанного изображения.

Решение

Зеркало дает мнимое изображение предмета без увеличения в зеркальном отражении. Это значит, что предмет и его изображение должны быть симметричны относительно плоскости зеркала. Симметричными являются только предмет и его изображение на последнем рисунке — Г.

Ответ: Г

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18076

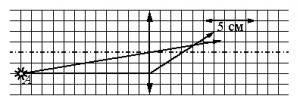
На рисунке показан ход лучей от точечного источника света А через тонкую линзу.

Какова приблизительно оптическая сила этой линзы?

Ответ:

а) –33,3 дптр

б) 7,7 дптр

в) 25,0 дптр

г) 33,3 дптр

Алгоритм решения

1.Записать формулу для нахождения оптической силы линзы.

2.Рассчитать длину 1 клетки.

3.Найти точку на главной оптической оси точку главного фокуса линзы.

4.Вычислить фокусное расстояние и перевести его в СИ.

5.Вычислить оптическую силу линзы.

Решение

Оптическая сила линзы находится по формуле:

D=1F

На рисунке видно, что 5 соответствуют 5 см. Следовательно, 1 клетка равна 1 см. После прохождения сквозь линзу лучи света, параллельные главной оптической оси, фокусируются в фокусе, который лежит на этой оси. Из рисунка видно, фокус находится в точке пересечения этой оси и луча, параллельного ей. Эту точку и линзу разделяют 3 клетки. Следовательно, фокусное расстояние равно 3 см, или 0,03 м.

Отсюда:

D=10,03≈33,3 (дптр)

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17706

Стеклянную линзу (показатель преломления стекла n_стекла = 1,54), показанную на рисунке, перенесли из воздуха (n_{воздуха} = 1) в воду (n_воды = 1,33). Как изменились при этом фокусное расстояние и оптическая сила линзы?

Ответ:

а) Фокусное расстояние уменьшилось, оптическая сила увеличилась.

б) Фокусное расстояние увеличилось, оптическая сила уменьшилась.

в) Фокусное расстояние и оптическая сила увеличились.

г) Фокусное расстояние и оптическая сила уменьшились.

Алгоритм решения

1.Установить характер преломления лучей линзой при ее перемещении из воздуха в воду.

2.Выяснить, как от этого зависят фокусное расстояние и оптическая сила линзы.

Решение

Чтобы узнать, что произойдет с лучами света при прохождении их сквозь линзу, погруженную воду, найдем относительные показатели преломления:

nвоздух−стекло=nстеклоnвоздух=1,541=1,54

nвода−стекло=nстеклоnвода=1,541,33≈1,16

Видно, что относительный показатель преломления уменьшился. Значит, преломленный линзой луч будет менее отклоняться от нормали, проведенной в точке падения на линзу. Следовательно, чтобы достигнуть главной оптической оси, ему придется пройти большее расстояние. Это говорит о том, что фокусное расстояние линзы увеличится.

Оптическая сила линзы — величина, обратная ее фокусному расстоянию. Если оно увеличится, то оптическая сила уменьшится.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор | оценить

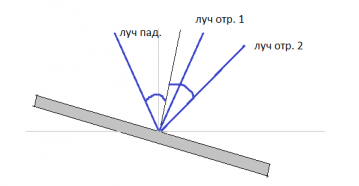
Задание EF18593

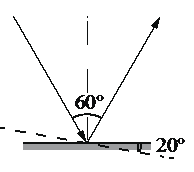
Свет падает на горизонтальное плоское зеркало. Угол между падающим и отражённым лучами равен 60°. Каким станет угол между этими лучами, если повернуть зеркало на 20°, как показано на рисунке?

Алгоритм решения

1.Записать известные данные.

2.Зарисовать рисунок после поворота зеркала.

3.Представить решение задачи в общем виде.

4.Подставить неизвестные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Угол между падающим и отраженным углом: γ1 = 60^о.

• Угол поворота угла: φ = 20^о.

Построим рисунок с учетом того, что зеркало повернули:

Поскольку угол падения, равен углу отражения, то:

α1+β1=60°

α1=β1

2α1=60°

α1=60°2=30°

На рисунке видно, что после переворачивания зеркала угол падения α увеличился на угол переворота:

α=α1+φ=30°+20°=50°

Так как угол падения равен углу отражения, то:

α=β=50°

Отсюда угол между лучом падающим и лучом отраженным равен:

γ=α+β=50°+50°=100°

Ответ: 100

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF22497

Дисперсия проявляется в следующих явлениях:

А. изменение видимого цвета белой ткани при разглядывании её через цветное стекло.

Б. образование радуги при прохождении света через мелкие капли воды.

Верно(-ы) утверждение(-я):

Ответ:

Только А
Только Б
И А, и Б
Ни А, ни Б

Алгоритм решения

Записать определение явления дисперсии света.
Установить, какие из представленных явлений могут быть объяснены дисперсией света.

Решение

Дисперсия — зависимость показателя преломления среды от частоты световой волны. Когда мы рассматриваем белую ткань через цветное стекло, до нас доходят только те лучи, цвет которых соответствует цвету стекла. При этом все лучи преломляются одинаково, так как они имеют примерно одинаковую частоту. Но радуга — это следствие дисперсии света. Когда лучи белого света проходят сквозь капельки воды, лучи разного цвета преломляются по-разному. Поэтому на выходе лучи разлагаются в спектр — радугу.

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18112

Узкий пучок белого света после прохождения через стеклянную призму даёт на экране спектр. Укажите правильную последовательность цветов в спектре.

Ответ:

а) красный – жёлтый – оранжевый – синий

б) оранжевый – синий – жёлтый – зелёный

в) красный – оранжевый – жёлтый – зелёный

г) красный – жёлтый – оранжевый – зелёный

Алгоритм решения

Вспомнить последовательность расположения цветов в спектре.
Выбрать строку, в которой цвета располагаются в соответствующей последовательности.

Решение

Цвета в спектре легко запомнить с помощью фразы: «Каждый охотник желает знать, где сидит фазан». Первая буква слова указывает на первую буква цвета. Следовательно, цвета в спектре располагаются так: красный – оранжевый – желтый – зеленый – голубой – синий – фиолетовый. Этому расположению соответствует строка «в».

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17533

На поверхность тонкой прозрачной плёнки падает по нормали пучок белого света. В отражённом свете плёнка окрашена в зелёный цвет. При использовании плёнки такой же толщины, но с несколько меньшим показателем преломления, её окраска будет

Ответ:

а) только зелёной

б) находиться ближе к красной области спектра

в) находиться ближе к синей области спектра

г) только полностью чёрной

Алгоритм решения

1.Описать наблюдаемое явление.

2.Записать условие наблюдения интерференционного максимума.

3.Выполнить решение в общем виде.

4.Установить, в какой цвет будет окрашена пленка.

Решение

При освещении тонкой плёнки можно наблюдать интерференцию световых волн, отражённых от передней и задней поверхностей плёнки. Условием интерференционного максимума для излучения с длиной волны λ является:

kλ=2dn+Δ

Δ — либо 0, либо λ2 (это зависит от соотношения показателей преломления на границе двуз сред). Тогда при малом изменении значения показателя преломления в меньшую сторону и сохранении порядка k (как в нашем случае и есть), длина волны света будет уменьшаться. Это значит, что из зеленой части спектра она сдвинется в синюю часть.

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17707

На две щели в экране слева падает плоская монохроматическая световая волна перпендикулярно экрану. Длина световой волны λ. Свет от щелей S1 и S2, которые можно считать когерентными синфазными источниками, достигает экрана Э. На нём наблюдается интерференционная картина. Тёмная полоса в точке А наблюдается, если

Ответ:

а) S₂А – S₁А = 2k⋅λ/2, где k– любое целое число

б) S₂А – S₁А = (2k + 1) ⋅λ/2, где k– любое целое число

в) S₂А – S₁А = λ/3k, где k– любое целое число

г) S₂А – S₁А = λ/(2k+1), где k– любое целое число

Алгоритм решения

1.Записать условие наблюдения интерференционного минимума.

2.Выбрать выражение, удовлетворяющее этому условию.

Решение

В точке А будет наблюдаться темное пятно, если волны, достигающие этой точки, будут гасить друг друга. Это возможно при соблюдении условия минимума:

Δd=(2k+1)λ2

Разность хода в данном случае равна:

Δd=S2A−S1A

Следовательно:

S2A−S1A=(2k+1)λ2

где k — целое число.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17972

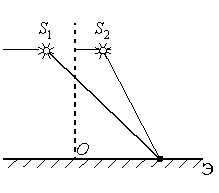
Точечные источники света S1 и S2 находятся близко друг от друга и создают на удалённом экране Э устойчивую интерференционную картину (см. рисунок). Это возможно, если S1 и S2 – малые отверстия в непрозрачном экране, освещённые

Ответ:

а) каждое своей лампочкой накаливания

б) каждое своей горящей свечой

в) одно зелёным лазером, другое красным

г) светом одной лампочки накаливания

Алгоритм решения

Записать условие наблюдения интерференционной картины.
Проанализировать источники и выбрать подходящий под условие.

Решение

Четкая интерференционная картина наблюдается только при освещении щелей когерентными лучами света, имеющими постоянную разность фаз. Когерентные — значит волнами одной частоты. Поэтому лазер зеленый и красный сразу не подходят — они имеют разные частоты.

Одна и та же частота и постоянная разность фаз будет только при условии, что щели освещаются одним источником света. В данном случае — одной и той же лампой накаливания.

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17638

На плоскую непрозрачную пластину с узкими параллельными щелями падает по нормали плоская монохроматическая волна из красной части видимого спектра. За пластиной на параллельном ей экране наблюдается интерференционная картина, содержащая большое число полос. При переходе на монохроматический свет из синей части видимого спектра

Ответ:

а) расстояние между интерференционными полосами увеличится

б) расстояние между интерференционными полосами уменьшится

в) расстояние между интерференционными полосами не изменится

г) интерференционная картина станет невидимой для глаза

Алгоритм решения

Записать, как зависит расстояние между интерференционными полосами от частоты световых лучей.
Выбрать ответ, удовлетворяющий установленной зависимости.

Решение

Зависимость расстояния между интерференционными полосами от частоты световых лучей удалось установить экспериментально. Было выяснено, что чем выше частота, тем меньше расстояние между ними. Частота света из синего части спектра больше частоты из красной части спектра. Поэтому при переходе из красной части спектра в синюю часть расстояние между полосами интерференционной картины уменьшится.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18348

На рисунке приведены спектр поглощения неизвестного газа и спектры поглощения атомарных паров известных элементов. По виду спектров можно утверждать, что неизвестный газ содержит атомы

Ответ:

а) азота (N), магния (Mg) и другого неизвестного вещества

б) только азота (N)

в) только магния (Mg)

г) только магния (Mg) и азота (N)

Алгоритм решения

Определить, при каком условии можно считать, что данный химический элемент входит в состав неизвестного газа.
Сравнить спектр поглощения неизвестного газа и магния. Сделать вывод о том, присутствует ли магний в газе.
Сравнить спектр поглощения неизвестного газа и азота. Сделать вывод о том, присутствует ли азот в газе.
Установить, содержит ли неизвестный газ какие-либо еще элементы.

Решение

Если спектр поглощения неизвестного газа содержит все линии, которые есть на спектре известного элемента, то этот газ содержит этот элемент.

Видно, что спектр поглощения неизвестного газа включает в себя все линии, которые есть в спектре поглощения магния. Следовательно, этот газ содержит магний.

Видно, что спектр поглощения неизвестного газа включает в себя все линии, которые есть в спектре поглощения азота. Следовательно, этот газ также содержит азот.

Но кроме линий, соответствующих азоту и магнию, на спектре поглощения газа наблюдаются другие линии. Следовательно, газ содержит как минимум еще один элемент.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18254

На рисунке приведены спектр поглощения разреженных атомарных паров неизвестного вещества (в середине) и спектры поглощения паров известных элементов (вверху и внизу). По анализу спектров можно утверждать, что неизвестное вещество содержит

Ответ:

а) только натрий (Na) и водород (Н)

б) только водород (Н) и гелий (Не)

в) водород (Н), гелий (Не) и натрий (Na)

г) натрий (Na), водород (H) и другие элементы, но не гелий (He)

Алгоритм решения

Определить, при каком условии можно считать, что данный химический элемент входит в состав неизвестного газа.
Сравнить спектр поглощения неизвестного вещества и водорода. Сделать вывод о том, присутствует ли водород в веществе.
Сравнить спектр поглощения неизвестного вещества и гелия. Сделать вывод о том, присутствует ли гелий в веществе.
Сравнить спектр поглощения неизвестного вещества и натрия. Сделать вывод о том, присутствует ли натрий в веществе.
Установить, содержит ли неизвестный газ какие-либо еще элементы.

Решение

Если спектр поглощения неизвестного газа содержит все линии, которые есть на спектре известного элемента, то этот газ содержит данный элемент.

Видно, что спектр поглощения неизвестного вещества включает в себя все линии, которые есть в спектре поглощения водорода и натрия. Но линий, соответствующих спектру поглощения гелия, в нем нет. Следовательно, это вещество содержит водород, натрий, но не содержит гелий.

Кроме линий, соответствующих водороду и натрию, на спектре поглощения вещества наблюдаются другие линии. Следовательно, оно содержит как минимум еще один элемент.

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17744

На рисунках А, Б и В приведены спектры излучения паров кальция Ca, стронция Sr и неизвестного образца.

Можно утверждать, что в неизвестном образце

Ответ:

а) не содержится стронция

б) не содержится кальция

в) содержатся кальций и ещё какие-то элементы

г) содержится только кальций

Алгоритм решения

Определить, при каком условии можно считать, что данный химический элемент входит в состав неизвестного образца.
Сравнить спектр излучения неизвестного образца и стронция. Сделать вывод о том, присутствует ли стронций в составе образца.
Сравнить спектр излучения неизвестного образца и кальция. Сделать вывод о том, присутствует ли кальций в составе образца.
Установить, содержит ли неизвестный газ какие-либо еще элементы.
Выбрать подходящее утверждение.

Решение

Если спектр излучения неизвестного образца содержит все линии, которые есть на спектре излучения известного элемента, то этот образец содержит данный элемент.

Видно, что спектр излучения неизвестного образца включает в себя все линии, которые есть в спектре излучения стронция. Но линий, соответствующих спектру излучения кальция, в нем нет. Следовательно, этот образец не содержит кальций.

Кроме линий, соответствующих стронцию, на спектре излучения неизвестного образца наблюдаются другие линии. Следовательно, он содержит как минимум еще один элемент.

Из всех перечисленных утверждений верным является только одно — образец не содержит кальция.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник