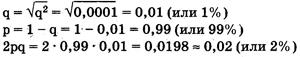МБОУ «Карагайская СОШ № 2»
с. Карагай, Пермский край
Решение задач
по теме «Генетика популяций.
Закон Харди – Вайнберга»
ЕГЭ. Биология, 11 класс.
Решение задач линии 28.
Подготовила:
Трефилова Раиса Поликарповна,
учитель биологии
МБОУ «Карагайская СОШ № 2»
Карагай – 2018
Цель: Дать рекомендации учащимся по выполнению задания линии 28 при подготовке к ЕГЭ.
Задачи:
1. Информировать учащихся 11 класса о требованиях к выполнению заданий линии 28 по биологии.
2. Познакомить с кодификатором, спецификацией и образцами заданий.
3. Мотивировать учащихся к успешной подготовке к ЕГЭ.
Теоретическое обоснование темы
Начальные этапы эволюционных процессов протекают в популяциях на основе закономерностей наследования. Изучение генетической структуры популяции связано с выяснением генотипического состава. В подобных задачах определяется частоты генотипов и аллелей, которые выражаются в % или в долях от единицы. Данная закономерность была выявлена независимо друг от друга двумя исследователями: математиком Г.Харди и врачом В.Вайнбергом.
Формулировка закона:
«Относительные частоты генов в популяции не изменяются из поколения в поколение во времени при следующих условиях:
- Популяция должна быть велика;
- Отсутствует давление отбора на данные признаки;
- Отсутствуют мутации этих генов;
- В популяции особи свободно скрещиваются;
- Нет миграции из соседних популяций».
Предположим некую популяцию с одинаковым соотношением генотипов АА и аа. Частоту генов А (A большое-доминантный признак ) обозначим р, а гена а (а малое – рецессивный признак) – q.
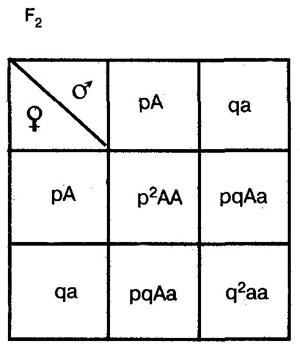
На основании скрещивания составляем решётку Пеннета.
|
♀ |
р(А) |
q(а) |
|
р(А) |
p² (AA) |
pq (Aa) |
|
q(а) |
pq (Aa) |
q² (aa) |
p² (AA) + 2 pq (Aa) + q² (aa) = 1
p + q = 1 (при извлечении квадратного корня)
Сумма частот генов в популяции p + q = 1, следовательно, уравнение можно рассмотреть как: p² + 2 pq + q² = 1
Закон Харди-Вайнберга может быть сформулирован следующим образом:
«В идеальной популяции соотношение частот аллелей генов и генотипов из поколения в поколение является величиной постоянной и соответствует уравнению: p2 +2pq + q2 = 1
где p2 — доля гомозигот по доминантной аллели; p — частота этой аллели; q2 — доля гомозигот по альтернативной аллели; q — частота соответствующей аллели; 2pq — доля гетерозигот.
Закон Харди-Вайнберга при медико-генетических исследованиях, а также при определении частоты генов, генотипов и фенотипов в популяциях в природе, популяций в животноводстве и селекции. В этом его практическое значение.
Рассмотрим решение нескольких вариантов задач по данной теме.
Задача 1. В популяции человека количество индивидуумов с карим цветом глаз составляет 51%, а с голубым – 49%. Определите процент доминантных гомозигот в данной популяции.
Поскольку известно, что карий цвет глаз доминирует над голубым, обозначим аллель, отвечающую за проявление признака кареглазости А, а аллельный ему ген, ответственный за проявление голубых глаз, соответственно, а. Тогда кареглазыми в исследуемой популяции будут люди как с генотипом АА (доминантные гомозиготы, долю которых и надо найти по условию задачи), так и — Аа гетерозиготы), а голубоглазыми – только аа (рецессивные гомозиготы).
По условию задачи нам известно, что количество людей с генотипами АА и Аа составляет 51%, а количество людей с генотипом аа — 49%. Как можно вычислить процент кареглазых людей только с генотипом АА?
Для этого вычислим частоты встречаемости каждого из аллельных генов А и а в данной популяции людей. Обозначив частоту встречаемости аллели А в данной популяции буквой q, имеем частоту встречаемости аллельного ему гена а = 1 – q. (Можно было бы обозначить частоту встречаемости аллельного гена а отдельной буквой, как в тексте выше – это кому как удобнее). Тогда сама формула Харди-Вайнберга для расчета частот генотипов при моногибридном скрещивании при полном доминировании одного аллельного гена над другим будет выглядеть вот так:
q2 AA+ 2q(1 – q)Aa + (1 – q)2aa = 1.
(1 – q)2 = 0,49 – это частота встречаемости людей с голубыми глазами.
Находим значение q: 1 – q = корень квадратный из 0,49 = 0,7; q = 1 – 0,7 = 0,3, тогда q ² = 0,09.
Это значит, что частота кареглазых гомозиготных особей АА в данной популяции будет составлять 0,09 или доля их будет равна 9%.
Ответ: частота кареглазых гомозиготных особей АА равна 9 %.
Задача 2. В популяции озёрной лягушки появилось потомство – 420 лягушат с тёмными пятнами (доминантный признак) и 80 лягушат со светлыми пятнами. Определите частоту встречаемости рецессивного гена и число гетерозигот среди лягушек с тёмными пятнами.
Записываем условие задачи. Тёмный цвет пятен обозначаем А, светлый цвет пятен – а. Необходимо определить генотипы родительских форм.
Признак, фенотип Ген, генотип
Тёмные пятна А
Светлые пятна а
F: 420 лягушат с темн. Пятнами А_
80 лягушат со светл. пятнами аа
Р — ?
Решение задачи
1. Каково количество особей в популяции?
420 + 80 = 500
2. Определяем частоту встречаемости лягушат со светлыми пятнами — q²
q²= 80: 500 = 0, 16 (частота встречаемости аллели равна отношению числа данной аллели к общему числу аллелей в популяции)
3. Определяем частоту встречаемости рецессивного гена «светлое пятно» «а малое», который мы обозначили q:

4. Определяем частоту встречаемости гена «тёмные пятна»(т.е. ), исходя из уравнения р + q = 1, значит, р = 1 – q, следовательно, р = 1 – 0,4 = 0,6
5. Определяем количество гетерозигот Аа :
2рq = 2х0,4 х 0,6 = 0, 48 или 48 %
Объяснение решения задачи: для решения задачи используется закон Харди-Вайнберга.
Ответ:
1) Число особей в популяции – 500.
2) Частота встречаемости рецессивного гена а «светлое пятно» — 0,4.
3) Количество гетерозигот (Аа) носителей гена «светлые пятна» — 0, 48 или 48%.
Задача 3. Популяция состоит из 49 % особей с генотипом АА и 9 % с генотипом аа. Находится ли эта популяция в равновесии?
Признак, фенотип Ген, генотип
р = 49 % или 0,49 АА
q = 9 % или 0, 09 аа
Равновесие — ?
Решение.
1. Если популяция находится в равновесии, то для неё справедливо уравнение Харди – Вайнберга:
p² + 2 pq + q² = 1
2. Для данной популяции частота генотипа АА: p² = 0,49,
частота аллеля А: √0,49 = 0, 7 ; р = 0,7
3. Определяем частоту генотипа аа: q² = 0,09, тогда
частота аллеля а: q =√0,09 = 0,3.
4. Определяем частоту генотипа гетерозиготы Аа: 2 pq = 2 х 0,7 х 0,3 = 0,42
5. Определяем, находится ли популяция в равновесии: если
p² + 2 pq + q² = 1, то 0,49 + 0,42 + 0,09 = 1, следовательно, популяция находится в равновесии.
Ответ:
По уравнению Харди-Вайнберга сумма равна 1, популяция находится в равновесии.
Задачи для самостоятельного решения
1. В Европе на 10 000 человек с нормальным содержанием меланина встречается 1 альбинос. Ген альбинизма наследуется по аутосомно-рецессивному типу. Рассчитать частоту встречаемости носителей гена альбинизма. Носителем называют организм, гетерозиготный по гену, который может вызвать в гомозиготном состоянии нарушение метаболизма.
Ответ: частота встречаемости гетерозигот 2 pq = 0,0198 или почти 2%
2. Предрасположенность к сахарному диабету наследуется по аутосомно-рецессивному типу. Частота встречаемости рецессивного гена предрасположенности к болезни в США приблизительно 22, 5 %. Какова частота встречаемости в США гетерозиготных носителей гена предрасположенности к сахарному диабету.
Ответ: частота встречаемости в США гетерозиготных носителей гена предрасположенности к сахарному диабету равна 0,4982.
3. У человека ген «резус положительный» доминантен по отношению к гену «резус отрицательный». В обследованной по этому показателю популяции 1982 человека были «резус положительными», а 368 – «резус отрицательными». Какова генетическая структура этой популяции?
Ответ: р = 0,5
4. У гречихи ярко-красная окраска растений неполно доминирует над зелёной. Гетерозиготы по данным генам имеют розовую окраску. В панмиктической популяции, состоящей из 840 растений, содержалось 42 красных растения. Какова частота встречаемости гомозиготных растений?
Ответ: частота встречаемости гомозиготных растений = 0,657.
5. Одна из форм глюкозурии наследуется как аутосомно-рецессивный признак и встречается с частотой 7:1000000. Определить частоту встречаемости гетерозигот в популяции.
Ответ: частота встречаемости гетерозиготных особей 2pq в популяции людей = 0,0052775.
Источники информации:
1. Гончаров О.В. Генетика.Задачи. – Саратов: Лицей, 2008.
2. Кириленко А.А. Биология. Сборник задач по генетике. Базовый и повышенный уровень ЕГЭ: учебно-методическое пособие/А.А.Кириленко. – Ростов-на-Дону: Легион, 2009.
3. Кириленко А.А., Колесников С.И. Биология. Подготовка к ЕГЭ-2013: учебно-методическое пособие/А.А.Кириленко, С.И.Колесников. – Ростов-на-Дону: Легион, 2012.
4. http://biology-online.ru/metodichka/konspekty-i-lekcii/obschaja-biologija/zakon-hardi-vainberga-v-reshenii-genetic.html
Закон Харди-Вайнберга
Популяционная генетика занимается генетической структурой популяций.
Понятие «популяция» относится к совокупности свободно скрещивающихся особей одного вида, длительно существующей на определенной территории (части ареала) и относительно обособленной от других совокупностей того же вида.
Важнейший признак популяции — это относительно свободное скрещивание. Если возникают какие-либо изоляционные барьеры, препятствующие свободному скрещиванию, то возникают новые популяции.
У человека, например, помимо территориальной изоляции, достаточно изолированные популяции могут возникать на основе социальных, этнических или религиозных барьеров. Поскольку между популяциями не происходит свободного обмена генами, то они могут существенно различаться по генетическим характеристикам. Для того чтобы описывать генетические свойства популяции, вводится понятие генофонда: совокупности генов, встречающихся в данной популяции. Помимо генофонда важны также частота встречаемости гена или частота встречаемости аллеля.
Знание того, как реализуются законы наследования на уровне популяций, принципиально важно для понимания причин индивидуальной изменчивости. Все закономерности, выявляемые в ходе психогенетических исследований, относятся к конкретным популяциям. В других популяциях, с иным генофондом и другими частотами генов, могут получаться отличающиеся результаты.
Закон Харди-Вайнберга— основа математических построений генетики популяций и современной эволюционной теории. Сформулирован независимо друг от друга математиком Г. Харди (Англия) и врачом В. Вайнбергом (Германия) в 1908 г. Этот закон утверждает, что частоты аллелей и генотипов в данной популяции будут оставаться постоянными из поколения в поколение при выполнении следующих условий:
1) численность особей популяции достаточно велика (в идеале — бесконечно велика),
2) спаривание происходит случайным образом (т. е. осуществляется панмиксия),
3) мутационный процесс отсутствует,
4) отсутствует обмен генами с другими популяциями,
5) естественный отбор отсутствует, т. е. особи с разными генотипами одинаково плодовиты и жизнеспособны.
Иногда этот закон формулируют иначе: в идеальной популяции частоты аллелей и генотипов постоянны. (Поскольку описанные выше условия выполнения данного закона и есть свойства идеальной популяции.)
Математическая модель закона отвечает формуле:
p2+2pq+q2=1
Она выводится на основе следующих рассуждений. В качестве примера возьмем простейший случай — распределение двух аллелей одного гена. Пусть два организма являются основателями новой популяции. Один из них является доминантной гомозиготой (АА), а другой — рецессивной гомозиготой (аа). Естественно, что все их потомство в F1 будет единообразным и будет иметь генотип (Аа). Далее особи F1 будут скрещиваться между собой. Обозначим частоту встречаемости доминантного аллеля (А) буквой p, а рецессивного аллеля (а) — буквой q. Поскольку ген представлен всего двумя аллелями, то сумма их частот равна единице, т. е. р + q = 1. Рассмотрим все яйцеклетки в данной популяции. Доля яйцеклеток, несущих доминантный аллель (А), будет соответствовать частоте этого аллеля в популяции и, следовательно, будет составлять р. Доля яйцеклеток, несущих рецессивный аллель (а), будет соответствовать его частоте и составлять q. Проведя аналогичные рассуждения для всех сперматозоидов популяции, придем к заключению о том, что доля сперматозоидов, несущих аллель (А), будет составлять р, а несущих рецессивный аллель (а) — q. Теперь составим решетку Пеннета, при этом при написании типов гамет будем учитывать не только геномы этих гамет, но и частоты несомых ими аллелей. На пересечении строк и столбцов решетки мы получим генотипы потомков с коэффициентами, соответствующими частотам встречаемости этих генотипов.
Из приведенной решетки видно, что в F2 частота доминантных гомозигот (АА) составляет р, частота гетерозигот (Аа) — 2pq, а рецессивных гомозигот (аа) — q. Поскольку приведенные генотипы представляют собой все возможные варианты генотипов для рассматриваемого нами случая, то сумма их частот должна равняться единице, т. е.
p2+2pq+q2=1
Главное применение закона Харди—Вайнберга в генетике природных популяций — вычисление частот аллелей и генотипов.
Рассмотрим пример использования этого закона в генетических расчетах. Известно, что один человек из 10 тыс. является альбиносом, при этом признак альбинизма у человека определяется одним рецессивным геном. Давайте вычислим, какова доля скрытых носителей этого признака в человеческой популяции. Если один человек из 10 тыс. является альбиносом, то это значит, что частота рецессивных гомозигот составляет 0,0001, т. е. q2 = 0,0001. Зная это, можно определить частоту аллеля альбинизма q, частоту доминантного аллеля нормальной пигментации р и частоту гетерозиготного генотипа (2pq). Люди с таким генотипом как раз и будут скрытыми носителями альбинизма, несмотря на то что фенотипически этот ген не будет у них проявляться и они будут иметь нормальную пигментацию кожи.
Из приведенных простых расчетов видно, что, хотя число альбиносов крайне невелико — всего лишь один человек на 10 тыс., ген альбинизма несет значительное количество людей — около 2% . Иными словами, даже если признак фенотипически проявляется очень редко, то в популяции присутствует значительное количество носителей этого признака, т. е. особей, имеющих этот ген в гетерозиготе.
Благодаря открытию закона Харди—Вайнберга процесс микроэволюции стал доступен непосредственному изучению: о его ходе можно судить по изменениям из поколения в поколение частот генов (или генотипов). Таким образом, несмотря на то что этот закон действителен для идеальной популяции, которой нет и не может быть в природе, он имеет огромное практическое значение, так как дает возможность рассчитать частоты генов, изменяющиеся под влиянием различных факторов микроэволюции.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1.Альбинизм у ржи наследуется как аутосомный рецессивный признак. На участке из 84000 растений 210 оказались альбиносами. Определить частоту гена альбинизма у ржи.
Решение
В связи с тем, что альбинизм у ржи наследуется как аутосомный рецессивный признак, все растения альбиносы будут гомозиготны по рецессивному гену — аа. Частота их в популяции (q2) равна 210/84000 = 0,0025. Частота рецессивного гена а будет равна 0,0025. Следовательно, q = 0,05.
Ответ:0,05
2.У крупного рогатого скота красная масть неполностью доминирует над белой (гибриды имеют чалую окраску). В районе обнаружены: 4169 красных, 756 белых и 3708 чалых животных. Какова частота генов окраски скота в этом районе?
Решение.
Если ген красной масти животных обозначить через А,
а ген белой — а, то у красных животных генотип будет АА (4169), у чалых Аа (3780), у белых — аа (756). Всего зарегистрировано животных 8705. Можно рассчитать частоту гомозиготных красных и белых животных в долях единицы. Частота белых животных будет 756 : 8705 = 0.09. Следовательно q2 =0.09 . Частота рецессивного гена q = 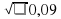
Ответ: р = 0,7, гена q = 0,3.
3.У человека альбинизм – аутосомный рецессивный признак. Заболевание встречается с частотой 1 / 20 000. Определите частоту гетерозиготных носителей заболевания в районе.
Решение.
Альбинизм наследуется рецессивно. Величина 1/20000 —
это q2. Следовательно, частота гена а будет: q = 1/20000 =
= 1/141. Частота гена р будет: р = 1 — q; р = 1 — 1/141 = 140/141.
Количество гетерозигот в популяции равно 2pq = 2 х (140/141) х (1/141) = 1/70. Т.к. в популяции 20000 человек то число гетерозигот в ней 1/ 70 х 20000 = 286 человек.
Ответ: 286 человек
4.Врожденный вывих бедра у человека наследуется как сутосомный доминантный признак с пенетрантностью 25%. Болезнь встречается с частотой 6:10 000. Определите число гетерозиготных носителей гена врожденного вывиха бедра в популяции.
Решение.
Генотипы лиц, имеющих врожденный вывих бедра, АА и Аа (доминантное наследование). Здоровые лица имеют генотип аа. Из формулы р2 + 2pq +. q2=1 ясно, что число особей несущих доминантный ген равно (р2+2рq). Однако приведенное в задаче число больных 6/10000 представляет собой лишь одну четвертую (25%) носителей гена А в популяции. Следовательно, р2 + 2pq = (4 х 6)/10 000 = 24/10000. Тогда q2 (число гомозиготных по рецессивному гену особей) равно 1 — (24/10000) = 9976/10000 или 9976 человек.
Ответ: 9976 человек
4.В популяции известны частоты аллелей p = 0,8 и g = 0,2. Определите частоты генотипов.
|
Дано: |
Решение: |
|
|
p = 0,8 |
p2 = 0,64 |
Ответ: частота генотипа АА – 0,64; генотипа аа – 0,04; генотипа Аа – 0,32.
5.Популяция имеет следующий состав: 0,2 АА, 0,3 Аа и 0,50 аа. Найдите частоты аллелей А и а.
|
Дано: |
Решение: |
|
|
p2 = 0,2 |
p = 0,45 |
Ответ: частота аллеля А – 0,45; аллеля а – 0,55.
6.В стаде крупного рогатого скота 49% животных рыжей масти (рецессив) и 51% черной масти (доминанта). Сколько процентов гомо- и гетерозиготных животных в этом стаде?
|
Дано: |
Решение: |
|
|
g2 = 0,49 |
g = 0,7 |
Ответ: гетерозигот 42%; гомозигот по рецессиву – 49%; гомозигот по доминанте – 9%.
7. Вычислите частоты генотипов АА, Аа и аа (в%), если особи аа составляют в популяции 1%.
|
Дано: |
Решение: |
|
|
g2 = 0,01 |
g = 0,1 |
Ответ: в популяции 81% особей с генотипом АА, 18% с генотпом Аа и 1% с генотипом аа.
8. При обследовании популяции каракульских овец было выявлено 729 длинноухих особей (АА), 111 короткоухих (Аа) и 4 безухих (аа). Вычислите наблюдаемые частоты фенотипов, частоты аллелей, ожидаемые частоты генотипов по формуле Харди-Вайнберга.
Это задача по неполному доминированию, поэтому, распределение частот генотипов и фенотипов совпадают и их можно было бы определить, исходя из имеющихся данных.
Для этого надо просто найти сумму всех особей популяции (она равна 844), найти долю длинноухих, короткоухих и безухих сначала в процентах (86.37, 13.15 и 0.47, соответственно) и в долях частот (0.8637, 0.1315 и 0.00474).
Но в задании сказано применить для расчетов генотипов и фенотипов формулу Харди-Вайнберга и, к тому же, рассчитать частоты аллелей генов А и а. Так вот для расчета самих частот аллелей генов без формулы Харди-Вайнберга не обойтись.
Обозначим частоту встречаемости аллеля А во всех гаметах популяции овец буквой р, а частоту встречаемости аллеля а — буквой q. Сумма частот аллельных генов p + q = 1.
Так как по формуле Харди-Вайнберга p2AA + 2pqAa + q2aa = 1 имеем, что частота встречаемости безухих q2 равна 0.00474, то извлекая квадратный корень из числа 0.00474 мы находим частоту встречаемости рецессивного аллеля а. Она равна 0.06884.
Отсюда можем найти частоту встречаемости и доминантного аллеля А. Она равна 1 – 0.06884 = 0.93116.
Теперь по формуле можем вычислить снова частоты встречаемости длинноухих (АА), безухих (аа) и короткоухих (Аа) особей. Длинноухих с генотипом АА будет р2 = 0.931162 = 0.86706, безухих с генотипом аа будет q2 = 0.00474 и короткоухих с генотипом Аа будет 2pq = 0,12820. (Вновь полученные числа, рассчитанные по формуле, почти совпадают с вычисленными изначально, что говорит о справедливости закона Харди-Вайнберга).
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Одна из форм глюкозурии наследуется как аутосомно-рецессивный признак и встречается с частотой 7:1000000. Определить частоту встречаемости гетерозигот в популяции.
2. Альбинизм общий (молочно-белая окраска кожи, отсутствие меланина в коже, волосяных луковицах и эпителии сетчатки) наследуется как рецессивный аутосомный признак. Заболевание встречается с частотой 1 : 20 000 (К. Штерн, 1965). Определите процент гетерозиготных носителей гена.
3. У кроликов окраска волосяного покрова “шиншилла” (ген Cch) доминирует над альбинизмом (ген Ca). Гетерозиготы CchCa имеют светло-серую окраску. На кролиководческой ферме среди молодняка кроликов шиншилл появились альбиносы. Из 5400 крольчат 17 оказались альбиносами. Пользуясь формулой Харди-Вайнберга, определите, сколько было получено гомозиготных крольчат с окраской шиншилла.
4. Популяция европейцев по системе групп крови резус содержит 85% резус положительных индивидуумов. Определите насыщенность популяции рецессивным аллелем.
5. Подагра встречается у 2% людей и обусловлена аутосомным доминантным геном. У женщин ген подагры не проявляется, у мужчин пенетрантность его равна 20% (В.П. Эфроимсон, 1968). Определите генетическую структуру популяции по анализируемому признаку, исходя из этих данных.
Решение 1. Обозначим аллельный ген, отвечающий за проявление глюкозурии а, так как сказано, что это заболевание наследуется как рецессивный признак. Тогда аллельный ему доминантный ген, отвечающий за отсутствие болезни обозначим А.
Здоровые особи в популяции людей имеют генотипы АА и Аа; больные особи имеют генотип только аа.
Обозначим частоту встречаемости рецессивного аллеля а буквой q, а доминантного аллеля А – буквой р.
Поскольку нам известно, что частота встречаемости больных людей с генотипом аа (а это значит q2) равна 0,000007, то q = 0,00264575
Так как p + q = 1, то р = 1 — q = 0,9973543, и p2 = 0,9947155
Теперь подставив значения р и q в формулу: p2AA + 2pqAa + q2aa = 1,
найдем частоту встречаемости гетерозиготных особей 2pq в популяции людей: 2pq = 1 — p2 — q2 = 1 – 0,9947155 – 0,000007 = 0,0052775.
Решение 2. Так как этот признак рецессивный, то больные организмы будут иметь генотип аа — это их частота равна 1 : 20 000 или 0,00005.
Частота аллеля а составит корень квадратный из этого числа, то есть 0,0071. Частота аллеля А составит 1 — 0,0071 = 0,9929, а частота здоровых гомозигот АА будет 0,9859. Частота всех гетерозигот 2Аа = 1 — (АА + аа) = 0,014 или 1,4%.
Решение 3. Примем 5400 штук всех кроликов за 100%, тогда 5383 кролика (сумма генотипов АА и Аа) составит 99,685% или в частях это будет 0,99685.
q2 + 2q(1 – q) = 0,99685 – это частота встречаемости всех шиншилл и гомозиготных (АА), и гетерозиготных (Аа).
Тогда из уравнения Харди-Вайнберга: q2 AA+ 2q(1 – q)Aa + (1 – q)2aa = 1 , находим (1 – q)2 = 1 – 0,99685 = 0,00315 — это частота встречаемости альбиносных кроликов с генотипом аа. Находим чему равна величина 1 – q. Это корень квадратный из 0,00315 = 0,056. А q тогда равняется 0,944.
q2 равняется 0,891, а это и есть доля гомозиготных шиншил с генотипом АА. Так как эта величина в % составит 89,1% от 5400 особей, то количество гомозиготных шиншилл будет 4811 шт.
Решение 4. Нам известно, что аллельный ген, отвечающий за проявление резус положительной крови является доминантным R (обозначим частоту его встречаемости буквой p), а резус отрицательный – рецессивным r (обозначим частоту встречаемости его буквой q).
Поскольку в задаче сказано, что на долю p2RR + 2pqRr приходится 85% людей, значит на долю резус-отрицательных фенотипов q2rr будет приходиться 15% или частота встречаемости их составит 0,15 от всех людей европейской популяции.
Тогда частота встречаемости аллеля r или ”насыщенность популяции рецессивным аллелем” (обозначенная буквой q) составит корень квадратный из 0,15 = 0,39 или 39%.
Решение 5. Подагра встречается у 2% людей и обусловлена аутосомным доминантным геном. У женщин ген подагры не проявляется, у мужчин пенетрантность его равна 20% (В.П. Эфроимсон, 1968). Определите генетическую структуру популяции по анализируемому признаку, исходя из этих данных.
Так как подагра выявляется у 2% мужчин, то есть у 2 человек из 100 с пенетрантностью 20%, то реально носителями генов подагры является в 5 раз больше мужчин, то есть 10 человек из 100.
Но, так как мужчины составляют лишь пол популяции, то всего людей с генотипами АА + 2Аа в популяции будет 5 человек из 100, а, значит, 95 из 100 будут с генотипом аа.
Если частота встречаемости организмов с генотипами аа составляет 0,95, то частота встречаемости рецессивного аллеля а в этой популяции равна корню квадратному из числа 0,95 = 0,975. Тогда частота встречаемости доминантного аллеля ”А” в этой популяции равна 1 – 0,975 = 0,005.
Расчет частот аллелей в популяции и определение генетической структуры популяции
Расчет частоты аллелей в популяции лисиц
Задача 380.
Из 14345 лисиц, изученных Ромашовым и Ильиной, 12 лисиц черные, 678 – промежуточной окраски, а 13655 лисиц – рыжие. Найдите частоты аллелей черной и рыжей окраски меха в популяции лисиц. Соответствуют ли наблюдаемые численности ожидаемым из уравнения Харди-Вайнберга?
Решение:
По условию задачи дается информация об общем количестве фенотипов особей в популяции и по каждому феноипу в отдельности. Промежуточная окраска у лисиц свидетельствует о неполном доминировании рыжей окраски, что указывает на то, что гетерозиготы и являются особями с промежуточной окраской.
Тогда
А — рыжая окраска шерсти;
а — чернафя окраска шерсти;
АА — рыжая лиса;
аа — черная лиса;
Аа — лиса с промежуточной окраской;
Nобщ. = 1445 лисиц;
р2(АА) = 1365 лисиц;
2pq(Aa) = 678 лисиц;
q2(aa) = 12 лисиц.
Найдем фенотипическую структуру популяции, получим:
p2 + 2pq + q2 = 1 = 100%;
р2(АА) = 13655/14345 = 0,9519 или 95,19%;
2pq(Aa) = 678/14345 = 0,04726 или 4,726%;
q2(aa) = 12/14345 = 0,000836 или 0,0836%.
1. Рассчитаем частоты аллелей черной и рыжей окраски меха в популяции лисиц
По формуле из следствия закона Харди_Вайнберга:
p + q = 1, где
p – частота доминантного аллеля А, q — частота рецессивного аллеля а.
Тогда
q2(аа) = 0,000836, q = 0,02898 приблизительно 0,03;
р(А) + q(а) = 1, р(А) = 1 — q(а) = 1 — 0,03 = 0,97.
2. Рассчитаем Соответствуют ли наблюдаемые численности ожидаемым из уравнения Харди-Вайнберга:
p2 + 2pq + q2 = 1 = 100%;
p2(АА) + 2pq(Аа) + q2(аа) = 1 = 100%;
(0,97)2 + 2(0,97 • 0,03) + (0,03)2 = 1 = 100%;
[0,9519 или 95,19%] + [0,04726 или 4,726%] + [0,000836 или 0,0836%] = 1 = 100%.
Значит, наблюдаемые численности лисиц по фенотипам соответствуют ожидаемым из уравнения Харди-Вайнберга.
Определение частот генотипов в потомстве группы особей
Задача 381.
Определите частоты доминантного и рецессивного аллелей в группе особей, состоящей из 60 гомозигот ВВ и 40 гомозигот bb; в группе, состоящей из 160 особей ВВ и 40 особей bb. Определите частоты генотипов в потомстве этих групп при условии панмиксии.
Решение:
1. Первая группа особей
Nобщ. = 60 + 40 = 100
Определим частоты доминантного аллеля, получим:
р2(ВВ) = 60/100 = 0,6, значит р = 0,6;
q2(bb) = 40/100 = 0,4, значит q = 0,4.
Определите частоты генотипов в потомстве при условии панмиксии, получим:
p2 + 2pq + q2 = 1;
p2(ВВ) + 2pq(Bb) + q2(bb) = 1 = 100%;
(0,6)2 + 2(0,6 • 9,4) + (0,4)2 = [0,36 или 36%(ВВ)] + [0,48 или 48%(Bb)] + [0,16 или 16%(bb)] = 1 = 100%.
Тогда
р2(ВВ) = 0,36 или 36%;
2pq(Bb) = 0,48 или 48%;
q2(bb) = 0,16 или 16%.
2. Вторая группа особей
Nобщ. = 160 + 40 = 200
Определим частоты доминантного аллеля, получим:
р2(ВВ) = 160/200 = 0,8, значит р = 0,8;
q2(bb) = 40/200 = 0,2, значит q = 0,2.
Определяем частоты генотипов в потомстве при условии панмиксии, получим:
p2 + 2pq + q2 = 1;
p2(ВВ) + 2pq(Bb) + q2(bb) = 1 = 100%;
(0,8)2 + 2(0,8 • 0,2) + (0,2)2 = [0,36 или 36%(ВВ)] + [0,48 или 48%(Bb)] + [0,16 или 16%(bb)] = 1 = 100%.
Тогда
р2(ВВ) = 0,64 или 64%;
2pq(Bb) = 0,32 или 32%;
q2(bb) = 0,04 или 4%.
Как правильно рассчитать структуру популяции по генотипам
Задача 382.
Доля особей, имеющих генотип (аа), в большой естественной популяции равна 0,16. Рассчитайте структуру данной популяции по генотипам.
Решение:
q2(aa) = 0,16 = 16%;
p2(AA) = ?
2pq(Aa) = ?
Зная частоту встречаемости рецессивных гомозигот (аа), рассчитаем частоту встречаемости рецессивного аллеля (а), получим:
q2(aa) = 0,16.
Тогда
q(a) = √0,16 = 0,4.
Согласно первому следствию из закона Харди-Вайнберга рассчитаем частоту встречаемости аллеля гена (А), получим:
p + q = 1 = 100%, где
р – частота доминантного аллеля в популяции;
q — частота рецессивного аллеля в популяции.
Тогда
p + q = 1; p(A) + q(a) = 1; p(A) = 1 – q(a);
p(A) = 1 – 0,4 = 0,6.
Используя второе следствие из закона Харди-Вайнберга рассчитаем структуру данной популяции по генотипам, получим:
p2 + 2pq + q2 = 1 = 100%, где
p2 – частота встречаемости доминантных генотипов в популяции;
2pq — частота встречаемости гетерозигот в популяции;
q2 — частота встречаемости рецессивных генотипов в популяции.
Тогда
р2(АА) + 2pq(Aa) = q2(aa) = 1 = 100%;
(0,6)2 + 2(0,6 • 0,4) + (0,4)2 = 1 = 100%;
0,36 или 36%(АА) + 0,48 или 48%(Аа) + 0,16 или 16%(аа) = 1 = 100%.
Ответ:
р2(АА) = 36%;
q2(aa) = 16%;
2pq(Aa) = 48%.
Частота встречаемости гомозиготных растений у гречихи
Задача 383.
У гречихи ярко-красная окраска растений неполно доминирует над зеленой. Гетерозиготы по данным генам имеют розовую краску. В панмиктической популяции, состоящей из 840 растений, содержалось 42 красных растения. Какова частота встречаемости гомозиготных растений?
Решение:
А – ярко-красная окраска растения;
а – зеленая окраска растения;
Аа – розовая окраска растения;
Nобщ. = 840 растений;
N(AA) = 42 ярко-красных растения;
р2 = ?
q2 = ?
1. Рассчитаем долю (частоту) встречаемости доминантных гомозигот (А) в популяции гречихи из условия задачи, получим:
р2(АА) = N(AA)/Nобщ. = 42/840 = 0,05 или 5%.
2. Зная частоту встречаемости доминантных гомозигот (АА) в популяции рассчитаем частоту аллели гена (А), получим:
р2(АА) = 0,05.
Тогда
р(А) = √0,05 = 0,2236.
3. Согласно первому следствию из закона Харди-Вайнберга рассчитаем частоту рецессивного аллеля (а) в популяции гречихи, получим:
p + q = 1; p(A) + q(a) = 1;
q(a) = 1 – р(А) = 1 – 0,22326 = 0,7764.
4. Используя формулу Харди-Вайнберга: p2 + 2pq + q2 = 1 = 100%, рассчитаем частоту встречаемости рецессивных гомозигот (аа) в популяции гречихи, получим:
p2(AA) + 2pq(Aa) + q2(aa) = 1 = 100%;
q2(aa) = (0,7764)2 = 0,6028 или 60,28%.
Ответ:
р2(АА) = 0,05 или 5%;
q2(aa) = 0,6028 или 60,28%.
Использование формулы Харди-Вайнберга для расчета фенотипов у кроликов
Задача 384.
У кроликов окраска волосяного покрова “шиншилла” доминирует над альбинизмом. Гетерозиготы имеют светло-серую окраску. На кролиководческой ферме среди молодняка кроликов шиншилл появились альбиносы. Из 8100 крольчат 25 оказались альбиносами. Пользуясь формулой Харди-Вайнберга, определите, сколько было получено гетерозиготных крольчат, имеющих светло-серую окраску и сколько гомозиготных крольчат, имеющих окраску “шиншилла”.
Решение:
А — окраска волосяного покрова “шиншилла”;
а — альбинизм;
Аа — гетерозигота — светло-серая окраса шерсти;
Nобщ. = 8100 крольчат;
крольчата-альбиносы = 25 шт.;
p2(AA) = ?
2pq(Aa) = ?
q2(aa) = 25/8100 = 0,003086.
Зная частоту встречаемостигомозигот (аа) рассчитаем частоту аллеля (а)
q(а) = √0,003086 = 0,056.
Согласно первому следствию закона Харди-Вайнберга рассчитаем частоту встречаемости гена (А), получим:
р + q = 1, р(А) = 1 — q(а) = 1 — 0,0556 = 0,9444.
Используя формулу Харди-Вайнберга: р2 + 2рq + q2 = 1, рассчитаем фенотипическую структуру данной популяции кроликов, получим:
р2(АА) + 2рq(Аа) + q2(аа) = 1 = 100%;
(0,9444)2 + (2 • 0,9444 • 0,0556) + ( 0,0556)2 = 1 = 100%;
0,89189 или 89,2%(АА) + 0,1050 или 10,5%(Аа) + 0,00309 или 0,3%(аа) = 1 или 100%.
Рассчитаем число светло-серых крольчат, получим:
N(светло-серые крольчата) = 8100 • 0,105 = 850,5 примерно 850 шт.
Рассчитаем число крольчат с окраской «шиншила», получим:
N(«шиншиловые» крольчата) = 8100 • 0,892 = 7225,2 примерно 7225 шт.
Ответ:
N(светло-серые крольчата) = 850 шт;
N(«шиншиловые» крольчата) = 7225 шт.
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 564 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Выберите положения, подтверждающие, что популяция является «единицей эволюции».
1) мутационный процесс начинается в популяции
2) свободное скрещивание возможно только в неизолированных популяциях
3) разные популяции обладают разными генофондами
4) вид не может быть единицей эволюции, так как его ареал, как правило, разорван на составные части
5) различия между видами такие же, как различия между изолированными популяциями одного вида
6) изолированная от других популяция не подвержена действию естественного отбора
Найдите ошибки в приведённом тексте. Укажите номера предложений, в которых сделаны ошибки, исправьте их.
1. Популяция представляет собой совокупность свободно скрещивающихся видов, длительное время населяющих общую территорию. 2. Основными характеристиками популяции являются численность, плотность, возрастная, половая, пространственная структура. 3. Популяция является структурной единицей биосферы. 4. Популяция — это элементарная единица эволюции. 5. Личинки разных насекомых, живущие в пресном водоёме, представляют собой популяцию.
Источник: ЕГЭ по биологии 30.05.2013. Основная волна. Дальний Восток. Вариант 1.
Найдите ошибки в приведённом тексте. Укажите номера предложений, в которых они допущены. Исправьте ошибки.
1. Популяция представляет собой совокупность свободно скрещивающихся особей разных видов, длительное время населяющих общую территорию. 2. Основными характеристиками популяции являются численность, плотность, возрастная, половая и пространственная структуры. 3. Популяция является структурной единицей живой природы. 4. Совокупность всех генов популяции называется её генофондом. 5. Численность популяции всегда стабильна. 6. Популяции одного вида генетически неоднородны, т. е. обладают различными генофондами.
Установите соответствие между примерами и возможными способами видообразования, которые иллюстрируются данными примерами.
ПРИМЕРЫ
А) ранне- и позднецветущие популяции погремка на одном лугу
Б) подвиды тигров — амурский и бенгальский
В) популяции форели в озере Севан, различающиеся сроками нереста
Г) возникшие в результате пищевой специализации виды синиц
Д) популяции обыкновенной белки в Центральной России и на Кавказе
СПОСОБЫ
ВИДООБРАЗОВАНИЯ
1) географическое
2) экологическое
Запишите в таблицу выбранные цифры под соответствующими буквами.
| А | Б | В | Г | Д |
Установите соответствие между событием и процессом, в соответствии с законом Харди-Вайнберга.
СОБЫТИЕ
А) мутационный процесс отсутствует
Б) отсутствуют миграции и эмиграция
В) число доминантных аллелей намного превышает число рецессивных аллелей
Г) высокая гомозиготность популяций
Д) отсутствует давление естественного отбора
Е) идёт обмен генами с другими популяциями
ПРОЦЕСС ЭВОЛЮЦИИ
1) популяция эволюционирует
2) популяция считается «идеальной»
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| A | Б | В | Г | Д | Е |
Генофонд популяции — это совокупность всех состав ляющих популяцию
Элементарной единицей эволюции считают
Источник: ЕГЭ по биологии 30.05.2013. Основная волна. Дальний Восток. Вариант 4.
Определите последовательность географического видообразования.
1) формирование популяции с новым генофондом
2) появление географической преграды между популяциями
3) естественный отбор особей с приспособительными к данным условиям признаками
4) появление особей с новыми признаками в изолированной популяции
Раздел: Основы эволюционного учения
Источник: ЕГЭ по биологии 30.05.2013. Основная волна. Центр, Урал. Вариант 2.
Установите соответствие между примером и способом видообразования, который этот пример иллюстрирует.
ПРИМЕР
А) обитание двух популяций обыкновенного окуня в прибрежной зоне и на большой глубине озера
Б) обитание разных популяций чёрного
дрозда в глухих лесах и вблизи жилья человека
В) распад ареала ландыша майского на изолированные участки в связи с оледенением
Г) образование разных видов синиц на основе пищевой специализации
Д) формирование лиственницы даурской в результате расширения ареала лиственницы сибирской на восток
1) географическое
2) экологическое
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| A | Б | В | Г | Д |
Источник: ЕГЭ по биологии 05.05.2014. Досрочная волна. Вариант 2.
Закон Харди – Вайнберга описывает
1) эволюционирующую популяцию
2) идеальную популяцию
3) малочисленную популяцию
4) популяцию неограниченной численности
Почему даже длительное воздействие стабилизирующего отбора не приводит к полному фенотипическому единообразию в популяции?
Источник: ЕГЭ- 2017
Установите соответствие между характеристиками и способами видообразования: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
ХАРАКТЕРИСТИКА
А. разделение ареала исходного вида
непреодолимыми преградами
Б. различные пищевые специализации
в популяциях исходного вида
В. освоение популяциями новых территорий
Г. стабильность и неразрывность исходного
ареала
Д. различные сроки размножения в
популяциях исходного вида
СПОСОБ
1. экологический
2. географическое
Запишите в таблицу выбранные цифры под соответствующими буквами.
| А | Б | В | Г | Д |
Установите соответствие между указанными условиями и их влиянием на выполнимость закона Харди–Вайнберга: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
УСЛОВИЯ
А) популяция полностью изолирована от других популяций данного вида
Б) половой отбор по исследуемым генам
В) мутирование исследуемых генов
Г) размер популяции очень большой
Д) исследуемые гены влияют на выживаемость особей
ВЛИЯНИЕ
1) соблюдение закона Харди–Вайнберга
2) нарушение закона Харди–Вайнберга
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г | Д | Е |
Пространственная структура вида в природе представлена
Источник: ЕГЭ по биологии 30.05.2013. Основная волна. Дальний Восток. Вариант 3.
Основным критерием возникновения нового вида является
1) появление внешних различий у особей популяции
2) экологическая изоляция популяций
3) географическая изоляция популяций
4) возникновение репродуктивной изоляции между популяциями
Установите соответствие между эволюционными процессами и уровнями, на которых эти процессы начинаются: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
ЭВОЛЮЦИОННЫЕ ПРОЦЕССЫ
А) формируются новые виды
Б) возникновение насекомых
В) изменяет генофонд популяции
Г) прогресс достигается путём идиоадаптаций особей популяции
Д) прогресс достигается путём ароморфозов или дегенерации
Е) развитие плавательных перепонок у уток
1) микроэволюционный
2) макроэволюционный
Запишите в таблицу выбранные цифры под соответствующими буквами.
| А | Б | В | Г | Д | Е |
Установите соответствие между процессами и уровнями организации жизни, на которых эти процессы происходят: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
ПРОЦЕСС
А) формируются новые виды
Б) формируются классы, отряды
В) изменяется генофонд популяции
Г) адаптивные признаки развиваются и распространяются в популяции
Д) прогресс достигается путём ароморфозов
или дегенерации
УРОВЕНЬ
1) микроэволюционный
2) макроэволюционный
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| A | Б | В | Г | Д |
Популяцию считают элементарной единицей эволюции, так как
1) она обладает целостным генофондом, способным изменяться
2) особи популяций имеют сходный обмен веществ
3) особи популяции отличаются размерами
4) она не способна изменяться во времени
Приспособленность вида к жизни в разных условиях в пределах своего ареала обеспечивает его существование в форме
Укажите процессы, относящиеся к микроэволюции.
1) возникновение мутаций и рекомбинаций
2) ароморфоз
3) обмен генами между популяциями
4) биологический регресс
5) идиоадаптация
6) колебания численности популяций
Всего: 564 1–20 | 21–40 | 41–60 | 61–80 …
Е. Н. Маслак
Решение задач по молекулярной биологии и генетике
Элективный курс
Окончание. См. №
6,
7,
8,
9,
10/2009
Задачи по генетике популяций
Закон Харди–Вайнберга
Мы будем рассматривать менделевские популяции:
– особи диплоидны;
– размножаются половым путем;
численность популяции бесконечно большая; а также панмиктические популяции, где случайное свободное скрещивание особей протекает при отсутствии отбора.
Рассмотрим в популяции один аутосомный ген, представленный двумя аллелями А и а.
Введем обозначения:
N – общее число особей популяции
D – число доминантных гомозигот (АА)
H – число гетерозигот (Аа)
R – число рецессивных гомозигот (аa)
Тогда: D + H + R = N.
Так как особи диплоидны, то число всех аллелей по рассматриваемому гену будет 2N.
Суммарное число аллелей А и а:
А = 2D + Н;
а = Н + 2R.
Обозначим долю (или частоту) аллеля А через p, а аллеля а – через g, тогда:
Поскольку ген может быть представлен аллелями А или а и никакими другими, то p + g = 1.
Состояние популяционного равновесия математической формулой описали в 1908 г. независимо друг от друга математик Дж.Харди в Англии и врач В.Вайнберг в Германии (закон Харди–Вайнберга).
Если p – частота гена A, а g – частота гена а, с помощью решетки Пеннета можно представить в обобщенном виде характер распределения аллелей в популяции:
Соотношение генотипов в описанной популяции:
p2АА : 2pgАа : g2аа.
Закон Харди–Вайнберга в простейшем виде:
p2АА + 2pgАа + g2аа = 1.
Задача № 36
Популяция содержит 400 особей, из них с генотипами АА – 20, Аа – 120 и аа – 260 особей. Определите частоты генов А и а.
|
Дано: |
Решение: |
|
| N = 400 D = 20 H = 120 R = 260 p – ? g – ? |
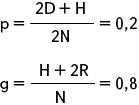 |
Ответ: частота гена А – 0,2; гена а – 0,8.
Задача № 37
У крупного рогатого скота породы шортгорн рыжая масть доминирует над белой. Гибриды от скрещивания рыжих и белых – чалой масти. В районе, специализирующемся на разведении шортгорнов, зарегистрировано 4169 рыжих животных, 3780 чалых и 756 белых. Определите частоту генов рыжей и белой окраски скота в данном раойне.
| Дано: | Решение: | |
| АА – рыжая аа – белая Аа – чалая D = 4169 H = 3780 R = 756 p – ? g – ? |
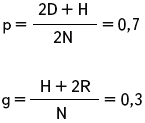 |
Ответ: частота гена рыжей окраски – 0,7; белой – 0, 3.
Задача № 38
В выборке, состоящей из 84 000 растений ржи,
210 растений оказались альбиносами, т.к. у них рецессивные гены находятся в гомозиготном состоянии. Определите частоты аллелей А и а, а также частоту гетерозиготных растений.
| Дано: | Решение: | |
| N = 84000 R = 210 p – ? g – ? 2pg – ? |
g2 = 210 : 8400 = 0,0025 g = 0,05 p = 1 – g = 0,95 2pg = 0,095 |
Ответ: частота аллеля а – 0,05; частота аллеля А – 0,95; частота генотипа Аа – 0,095.
Задача № 39
Группа особей состоит из 30 гетерозигот. Вычислите частоты генов А и а.
| Дано: | Решение: | |
| N = H = 30 p – ? g – ? |
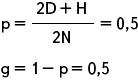 |
Ответ: частота генов А и а – 0,5.
Задача № 40
В популяции известны частоты аллелей p = 0,8 и g = 0,2. Определите частоты генотипов.
| Дано: | Решение: | |
| p = 0,8 g = 0,2 p2 – ? g2 – ? 2pg – ? |
p2 = 0,64 g2 = 0,04 2pg = 0,32 |
Ответ: частота генотипа АА – 0,64; генотипа аа – 0,04; генотипа Аа – 0,32.
Задача № 41
Популяция имеет следующий состав: 0,2 АА, 0,3 Аа и 0,50 аа. Найдите частоты аллелей А и а.
| Дано: | Решение: | |
| p2 = 0,2 g2 = 0,3 2pg = 0,50 p – ? g – ? |
p = 0,45 g = 0,55 |
Ответ: частота аллеля А – 0,45; аллеля а – 0,55.
Задача № 42
В стаде крупного рогатого скота 49% животных рыжей масти (рецессив) и 51% черной масти (доминанта). Сколько процентов гомо- и гетерозиготных животных в этом стаде?
| Дано: | Решение: | |
| g2 = 0,49 p2 + 2pg = 0,51 p – ? 2pg – ? |
g = 0,7 p = 1 – g = 0,3 p2 = 0,09 2pg = 0,42 |
Ответ: гетерозигот 42%; гомозигот по рецессиву – 49%; гомозигот по доминанте – 9%.
Задача № 43
Вычислите частоты генотипов АА, Аа и аа (в %), если особи аа составляют в популяции 1%.
| Дано: | Решение: | |
| g2 = 0,01 p2 – ? 2pg – ? |
g = 0,1 p = 1 – g = 0,9 2pg = 0,18 p2 = 0,81 |
Ответ: в популяции 81% особей с генотипом АА, 18% с генотпом Аа и 1% с генотипом аа.
Занимательные генетические задачи
Задача № 44. «Сказка про драконов»
У исследователя было 4 дракона: огнедышащая и неогнедышащая самки, огнедышащий и неогнедышащий самцы. Для определения способности к огнедышанию у этих драконов были проведены всевозможные скрещивания.
1. Огнедышащие родители – все потомство огнедашащее.
2. Неогнедышащие родители – все потомство неогнедышащее.
3. Огнедышащий самец и неогнедышащая самка – в потомстве примерно поровну огнедышащих и неогнедышащих дракончиков.
4. Неогнедышащий самец и огнедышащая самка – все потомство неогнедышащее.
Считая, что признак определяется аутосомным геном, установите доминантный аллель и запишите генотипы родителей.
Решение:
• по скрещиванию № 4 определяем: А – неогнедышащие, а – огнедышащащие; огнедышащие – ♀ аа и ♂ аа; неогнедышащий самец – ♂ АА;
• по скрещиванию № 3: неогнедышащая самка – ♀ Аа.
Задача № 45. «Консультант фирмы «Коктейль».
Представьте себе, что вы – консультант небольшой фирмы «Коктейль», что в буквальном переводе с английского означает «петушиный хвост». Фирма разводит экзотические породы петухов ради хвостовых перьев, которые охотно закупают владельцы шляпных магазинов во всем мире. Длина перьев определяется геном А (длинные) и а (короткие), цвет: В – черные, b – красные, ширина: С – широкие, с – узкие. Гены не сцеплены. На ферме много разных петухов и кур со всеми возможными генотипами, данные о которых занесены в компьютер. В будущем году ожидается повышенный спрос на шляпки с длинными черными узкими перьями. Какие скрещивания нужно провести, чтобы получить в потомстве максимальное количество птиц с модными перьями? Скрещивать пары с абсолютно одинаковыми генотипами и фенотипами не стоит.
Решение:
F1 : А*В*cc
1. Р: ♀ ААВВсс × ♂ ааbbсс
2. Р: ♀ ААВВсс × ♂ ААbbсс
3. Р: ♀ ААbbсс × ♂ aaВВсс и т.д.
Задача № 46. «Контрабандист».
В маленьком государстве Лисляндия вот уже несколько столетий разводят лис. Мех идет на экспорт, а деньги от его продажи составляют основу экономики страны. Особенно ценятся серебристые лисы. Они считаются национальным достоянием, и перевозить их через границу строжайше запрещено. Хитроумный контрабандист, хорошо учившийся в школе, хочет обмануть таможню. Он знает азы генетики и предполагает, что серебристая окраска лис определяется двумя рецессивными аллелями гена окраски шерсти. Лисы с хотя бы одним доминантным аллелем – рыжие. Что нужно сделать, чтобы получить серебристых лис на родине контрабандиста, не нарушив законов Лисляндии?
Решение:
• провести анализирующее скрещивание и выяснить, какие рыжие лисы гетерозиготны по аллелям окраски, перевезти их через границу;
• на родине контрабандиста скрестить их друг с другом, и 1/4 потомков будет серебристой окраски.
Задача № 47. «Расстроится ли свадьба принца Уно?»
Единственный наследный принц Уно собирается вступить в брак с прекрасной принцессой Беатрис. Родители Уно узнали, что в роду Беатрис были случаи гемофилии. Братьев и сестер у Беатрис нет. У тети Беатрис растут два сына – здоровые крепыши. Дядя Беатрис целыми днями пропадает на охоте и чувствует себя прекрасно. Второй же дядя умер еще мальчиком от потери крови, причиной которой стала глубокая царапина. Дяди, тетя и мама Беатрис –
дети одних родителей. С какой вероятностью болезнь может передаться через Беатрис королевскому роду ее жениха?
Решение:
Построив предполагаемое генеалогическое древо, можно доказать, что ген гемофилии был в одной из X-хромосом бабушки Беатрис; мать Беатрис могла получить его с вероятностью 0,5; сама Беатрис – с вероятностью 0,25.
Задача № 48. «Царские династии».
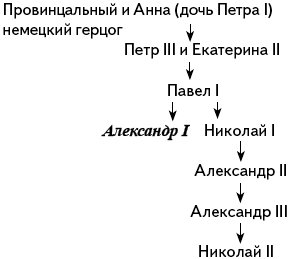
Предположим, что у императора Александра I в Y-хромосоме была редкая мутация. Могла ли эта мутация быть у:
а) Ивана Грозного;
б) Петра I;
в) Екатерины II;
г) Николая II?
Решение:
Сразу же вычеркнем Екатерину II, ввиду ее принадлежности к женскому полу.
Ивана Грозного вычеркнем тоже – он представитель рода Рюриковичей и к династии Романовых не принадлежал.
Ответ: мутация могла быть у Николая II.
Задача № 49. «Листая роман «Война и мир».
Предположим, что в Х-хромосоме у князя Николая Андреевича Болконского была редкая мутация. Такая же мутация была и у Пьера Безухова. С какой вероятностью эта мутация могла быть у:
а) Наташи Ростовой;
б) сына Наташи Ростовой;
в) сына Николая Ростова;
г) автора «Войны и мира»?
Ответ:
• Андрей Болконский не получил от отца Х-хромосому. Его жена не была родственницей ни Болконских, ни Безуховых. Следовательно, у сына князя Андрея мутации нет.
• Наташа Ростова вышла замуж за Пьера Безухова. Пьер передал X-хромосому своим дочерям, но не сыновьям. Следовательно, дочери Наташи Ростовой получили мутацию, а сыновья – нет.
• Сын Николая Ростова получил свою Х-хромосому от матери – дочери старого князя Болконского (из 2 хромосом княжны Марьи мутация была только в одной, следовательно, она передала Х-хромосому своему сыну с вероятностью 50%).
• Лев Николаевич: действие романа заканчивается за несколько лет до рождения Толстого, на страницах романа сам автор не появляется. Но отцом писателя был отставной офицер граф Николай Ильич Толстой, а мать – урожденная Волконская, т.е. родители писателя были прототипами Николая Ростова и его жены, урожденной Марии Болконской. Их будущий сын Лев получит мутацию с вероятностью 50%.
Задача № 50. «Спор Бендера и Паниковского».
Возник у Бендера с Паниковским спор: как наследуется окраска у волнистых попугайчиков? Бендер считает, что цвет попугайчиков определяется одним геном, имеющим 3 аллеля: Со – рецессивен по отношению к двум другим, Сг и Сж кодоминантны, поэтому у попугайчиков с генотипом СоСо – белый цвет, СгСг и СгСо – голубой, СжСж и СжСо – желтый и СгСж – зеленый цвет. А Паниковский считает, что окраска формируется под действием двух взаимодействующих генов А и В. Поэтому попугайчики с генотипом А*В* – зеленые, А*bb – голубые, ааВ* –-
желтые, ааbb – белые.
Они составили 3 родословные:
|
1. P : З × Б |
F1 : З, Б F1 : Б F1 : Г, Ж, Г, Г, Ж, Ж, Ж, Г, Ж |
Какие родословные могли быть составлены Бендером, какие – Паниковским?
Ответ: родословные 1 и 2 могли быть составлены Паниковским, а родословная 3 – Бендером.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ:
1. Багоцкий С.В. «Крутые» задачи по генетике // Биология для школьников. 2005. № 4.
2. Гуляев Г.В. Задачник по генетике. – М.: Колос, 1980.
3. Жданов Н.В. Решение задач при изучении темы: «Генетика популяций». – Киров: изд-во Пед. института, 1995.
4. Задачи по генетике для поступающих в вузы. – Волгоград: Учитель, 1995.
5. Кочергин Б.Н., Кочергина Н.А. Задачи по молекулярной биологии и генетике. – Минск: Народна асвета, 1982.
6. Краткий сборник генетических задач. – Ижевск, 1993.
7. Методическая разработка для учащихся биологического отделения ВЗМШ при МГУ «Законы Менделя». – М., 1981.
8. Методические указания для самостоятельной подготовки к практическим занятиям по общей генетике. – Пермь: изд-во Мед. института, 1986.
9. Муртазин Г.М. Задачи и упражнения по общей биологии. – М.: Просвещение, 1981.
10. Орлова Н.Н. Малый практикум по общей генетике (сборник задач). – М.: изд-во МГУ, 1985.
11. Сборник задач по биологии (учебно-методическое посо-бие). – Киров, 1998.
12. Соколовская Б.Х. Сто задач по молекулярной биологии и генетике. – Новосибирск: Наука, 1971.
13. Фридман М.В. Задачи по генетике на школьной олимпиаде МГУ // Биология для школьников. 2003. № 2.
14. Щеглов Н.И. Сборник задач и упражнений по генетике. – М.: Экоинвест, 1991.
Решение задач по теме «Генетика популяций. Закон Харди-Вайнберга»
материал для подготовки к егэ (гиа) по биологии (11 класс) на тему
В линии 28 на ЕГЭ по биологии учащимся предлагаются различные биологические задачи по генетике, образцов решения которых нет в учебниках, в том числе, и на закон Харди-Вайберга. В работе представлены 3 задачи с анализом ответов и 5 задач для самостоятельного решения.
Скачать:
| Вложение | Размер |
|---|---|
| genetika_populyatsiy.docx | 27.76 КБ |
Предварительный просмотр:
МБОУ «Карагайская СОШ № 2»
с. Карагай, Пермский край
по теме «Генетика популяций.
Закон Харди – Вайнберга»
ЕГЭ. Биология, 11 класс.
Решение задач линии 28.
Трефилова Раиса Поликарповна,
МБОУ «Карагайская СОШ № 2»
Цель: Дать рекомендации учащимся по выполнению задания линии 28 при подготовке к ЕГЭ.
1. Информировать учащихся 11 класса о требованиях к выполнению заданий линии 28 по биологии.
2. Познакомить с кодификатором, спецификацией и образцами заданий.
3. Мотивировать учащихся к успешной подготовке к ЕГЭ.
Теоретическое обоснование темы
Начальные этапы эволюционных процессов протекают в популяциях на основе закономерностей наследования. Изучение генетической структуры популяции связано с выяснением генотипического состава. В подобных задачах определяется частоты генотипов и аллелей, которые выражаются в % или в долях от единицы. Данная закономерность была выявлена независимо друг от друга двумя исследователями: математиком Г.Харди и врачом В.Вайнбергом.
«Относительные частоты генов в популяции не изменяются из поколения в поколение во времени при следующих условиях:
- Популяция должна быть велика;
- Отсутствует давление отбора на данные признаки;
- Отсутствуют мутации этих генов;
- В популяции особи свободно скрещиваются;
- Нет миграции из соседних популяций».
Предположим некую популяцию с одинаковым соотношением генотипов АА и аа. Частоту генов А (A большое-доминантный признак ) обозначим р, а гена а (а малое – рецессивный признак) – q.
На основании скрещивания составляем решётку Пеннета.
♂
p² (AA) + 2 pq (Aa) + q² (aa) = 1
p + q = 1 (при извлечении квадратного корня)
Сумма частот генов в популяции p + q = 1, следовательно, уравнение можно рассмотреть как: p² + 2 pq + q² = 1
Закон Харди-Вайнберга может быть сформулирован следующим образом:
«В идеальной популяции соотношение частот аллелей генов и генотипов из поколения в поколение является величиной постоянной и соответствует уравнению: p 2 +2pq + q 2 = 1
где p 2 — доля гомозигот по доминантной аллели; p — частота этой аллели; q 2 — доля гомозигот по альтернативной аллели; q — частота соответствующей аллели; 2pq — доля гетерозигот.
Закон Харди-Вайнберга при медико-генетических исследованиях, а также при определении частоты генов, генотипов и фенотипов в популяциях в природе, популяций в животноводстве и селекции. В этом его практическое значение.
Рассмотрим решение нескольких вариантов задач по данной теме.
Задача 1. В популяции человека количество индивидуумов с карим цветом глаз составляет 51%, а с голубым – 49%. Определите процент доминантных гомозигот в данной популяции.
Поскольку известно, что карий цвет глаз доминирует над голубым, обозначим аллель, отвечающую за проявление признака кареглазости А, а аллельный ему ген, ответственный за проявление голубых глаз, соответственно, а. Тогда кареглазыми в исследуемой популяции будут люди как с генотипом АА (доминантные гомозиготы, долю которых и надо найти по условию задачи), так и — Аа гетерозиготы), а голубоглазыми – только аа (рецессивные гомозиготы).
По условию задачи нам известно, что количество людей с генотипами АА и Аа составляет 51%, а количество людей с генотипом аа — 49%. Как можно вычислить процент кареглазых людей только с генотипом АА?
Для этого вычислим частоты встречаемости каждого из аллельных генов А и а в данной популяции людей. Обозначив частоту встречаемости аллели А в данной популяции буквой q, имеем частоту встречаемости аллельного ему гена а = 1 – q. (Можно было бы обозначить частоту встречаемости аллельного гена а отдельной буквой, как в тексте выше – это кому как удобнее). Тогда сама формула Харди-Вайнберга для расчета частот генотипов при моногибридном скрещивании при полном доминировании одного аллельного гена над другим будет выглядеть вот так:
q 2 AA+ 2q(1 – q)Aa + (1 – q) 2 aa = 1.
(1 – q) 2 = 0,49 – это частота встречаемости людей с голубыми глазами.
Находим значение q: 1 – q = корень квадратный из 0,49 = 0,7; q = 1 – 0,7 = 0,3, тогда q ² = 0,09.
Это значит, что частота кареглазых гомозиготных особей АА в данной популяции будет составлять 0,09 или доля их будет равна 9%.
Ответ: частота кареглазых гомозиготных особей АА равна 9 %.
Задача 2. В популяции озёрной лягушки появилось потомство – 420 лягушат с тёмными пятнами (доминантный признак) и 80 лягушат со светлыми пятнами. Определите частоту встречаемости рецессивного гена и число гетерозигот среди лягушек с тёмными пятнами.
Записываем условие задачи. Тёмный цвет пятен обозначаем А, светлый цвет пятен – а. Необходимо определить генотипы родительских форм.
Признак, фенотип Ген, генотип
Светлые пятна а
F: 420 лягушат с темн. Пятнами А_
80 лягушат со светл. пятнами аа
1. Каково количество особей в популяции?
2. Определяем частоту встречаемости лягушат со светлыми пятнами — q²
q²= 80: 500 = 0, 16 (частота встречаемости аллели равна отношению числа данной аллели к общему числу аллелей в популяции)
3. Определяем частоту встречаемости рецессивного гена «светлое пятно» «а малое», который мы обозначили q:
q = √ q² = √ 0,16 = 0,4
4. Определяем частоту встречаемости гена «тёмные пятна»(т.е. ), исходя из уравнения р + q = 1, значит, р = 1 – q, следовательно, р = 1 – 0,4 = 0,6
5. Определяем количество гетерозигот Аа :
2рq = 2х0,4 х 0,6 = 0, 48 или 48 %
Объяснение решения задачи: для решения задачи используется закон Харди-Вайнберга.
1) Число особей в популяции – 500.
2) Частота встречаемости рецессивного гена а «светлое пятно» — 0,4.
3) Количество гетерозигот (Аа) носителей гена «светлые пятна» — 0, 48 или 48%.
Задача 3. Популяция состоит из 49 % особей с генотипом АА и 9 % с генотипом аа. Находится ли эта популяция в равновесии?
Признак, фенотип Ген, генотип
р = 49 % или 0,49 АА
q = 9 % или 0, 09 аа
1. Если популяция находится в равновесии, то для неё справедливо уравнение Харди – Вайнберга:
2. Для данной популяции частота генотипа АА : p² = 0,49,
частота аллеля А : √ 0,49 = 0, 7 ; р = 0,7
3. Определяем частоту генотипа аа : q² = 0,09, тогда
частота аллеля а : q =√ 0,09 = 0,3.
4. Определяем частоту генотипа гетерозиготы Аа: 2 pq = 2 х 0,7 х 0,3 = 0,42
5. Определяем, находится ли популяция в равновесии: если
p² + 2 pq + q² = 1, то 0,49 + 0,42 + 0,09 = 1, следовательно, популяция находится в равновесии.
По уравнению Харди-Вайнберга сумма равна 1, популяция находится в равновесии.
Задачи для самостоятельного решения
1. В Европе на 10 000 человек с нормальным содержанием меланина встречается 1 альбинос. Ген альбинизма наследуется по аутосомно-рецессивному типу. Рассчитать частоту встречаемости носителей гена альбинизма. Носителем называют организм, гетерозиготный по гену, который может вызвать в гомозиготном состоянии нарушение метаболизма.
Ответ: частота встречаемости гетерозигот 2 pq = 0,0198 или почти 2%
2. Предрасположенность к сахарному диабету наследуется по аутосомно-рецессивному типу. Частота встречаемости рецессивного гена предрасположенности к болезни в США приблизительно 22, 5 %. Какова частота встречаемости в США гетерозиготных носителей гена предрасположенности к сахарному диабету.
Ответ: частота встречаемости в США гетерозиготных носителей гена предрасположенности к сахарному диабету равна 0,4982.
3. У человека ген «резус положительный» доминантен по отношению к гену «резус отрицательный». В обследованной по этому показателю популяции 1982 человека были «резус положительными», а 368 – «резус отрицательными». Какова генетическая структура этой популяции?
4. У гречихи ярко-красная окраска растений неполно доминирует над зелёной. Гетерозиготы по данным генам имеют розовую окраску. В панмиктической популяции, состоящей из 840 растений, содержалось 42 красных растения. Какова частота встречаемости гомозиготных растений?
Ответ: частота встречаемости гомозиготных растений = 0,657.
5. Одна из форм глюкозурии наследуется как аутосомно-рецессивный признак и встречается с частотой 7:1000000. Определить частоту встречаемости гетерозигот в популяции.
Ответ: частота встречаемости гетерозиготных особей 2pq в популяции людей = 0,0052775.
1. Гончаров О.В. Генетика.Задачи. – Саратов: Лицей, 2008.
2. Кириленко А.А. Биология. Сборник задач по генетике. Базовый и повышенный уровень ЕГЭ: учебно-методическое пособие/А.А.Кириленко. – Ростов-на-Дону: Легион, 2009.
3. Кириленко А.А., Колесников С.И. Биология. Подготовка к ЕГЭ-2013: учебно-методическое пособие/А.А.Кириленко, С.И.Колесников. – Ростов-на-Дону: Легион, 2012.
По теме: методические разработки, презентации и конспекты
Урок физики в 9 классе: «Решение задач по теме «Импульс. Закон сохранения импульса»
Урок повторения и закрепления знаний по теме «Импульс. Закон сохранения импульса» Учащимся после повторения и самопроверки предлагаются задачи разного типа и уровня сложности, алгоритм решения типовых.
Решение задач по теме «Первый закон термодинамики».
Данный материал создан на основе программы Notebook 10 для интерактивной доски. Содержание включает пять задач разной степени сложности с решениями.Используется на уроках в 10 классе базового уро.
разработка урока «Закон Харди-Вайнберга»
Разработка урока может быть использована при изучении темы «Популяционная генетика» для изучении биологии на углубленном уровне и на дополнительных занятиях при подготовке детей к ЕГЭ на базовом уровн.
Решение задач по теме «Второй закон Ньютона». Составление практического задания к компьютерной модели «Движение тел на легком блоке».
Решение задач по теме «Второй закон Ньютона».Составление практического задания к компьютерной модели «Движение тел на легком блоке».(Использование компьютерных технологий на уроках ф.
Разработка урока: Решение задач по теме «Газовые законы»
В разработке урока присутствует повторение темы «Газовые законы». Рассматривается решение качественных и экспериментальных задач. экспериментальные задачи сопровождаются проведением простых опытов с и.
презентация Закон Харди-Вайнберга
Презентация «Генетическое равновесие в популяциях и его нарушение» знакомит учащихся с понятием «популяционная генетика», законом Харди-Вайнберга. Помогает научиться решать разные типы зад.
Решение задач по теме «Генетика популяций. Закон Харди – Вайнберга»
Начальные этапы эволюционных процессов протекают в популяциях на основе закономерностей наследования. Изучение генетической структуры популяции связано с выяснением генотипического состава. В подобных.
Уравнение харди вайнберга в егэ
Установите соответствие между событием и процессом, в соответствии с законом Харди-Вайнберга.
А) мутационный процесс отсутствует
Б) отсутствуют миграции и эмиграция
В) число доминантных аллелей намного превышает число рецессивных аллелей
Г) высокая гомозиготность популяций
Д) отсутствует давление естественного отбора
Е) идёт обмен генами с другими популяциями
1) популяция эволюционирует
2) популяция считается «идеальной»
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| A | Б | В | Г | Д | Е |
Закон Харди — Вайнберга — это закон популяционной генетики — в популяции бесконечно большого размера, в которой не действует отбор, не идет мутационный процесс, отсутствует обмен особями с другими популяциями, не происходит дрейф генов, все скрещивания случайны — частоты генотипов по какому-либо гену (в случае если в популяции есть два аллеля этого гена) будут поддерживаться постоянными из поколения в поколение и соответствовать уравнению: p 2 + 2pq + q 2 = 1, где p 2 — доля гомозигот по одному из аллелей; p — частота этого аллеля; q 2 — доля гомозигот по альтернативному аллелю; q — частота соответствующего аллеля; 2pq — доля гетерозигот.
Расчет частот аллелей в популяции и определение генетической структуры популяции
Расчет частоты аллелей в популяции лисиц
Задача 380.
Из 14345 лисиц, изученных Ромашовым и Ильиной, 12 лисиц черные, 678 – промежуточной окраски, а 13655 лисиц – рыжие. Найдите частоты аллелей черной и рыжей окраски меха в популяции лисиц. Соответствуют ли наблюдаемые численности ожидаемым из уравнения Харди-Вайнберга?
Решение:
По условию задачи дается информация об общем количестве фенотипов особей в популяции и по каждому феноипу в отдельности. Промежуточная окраска у лисиц свидетельствует о неполном доминировании рыжей окраски, что указывает на то, что гетерозиготы и являются особями с промежуточной окраской.
Тогда
А — рыжая окраска шерсти;
а — чернафя окраска шерсти;
АА — рыжая лиса;
аа — черная лиса;
Аа — лиса с промежуточной окраской;
Nобщ. = 1445 лисиц;
р 2 (АА) = 1365 лисиц;
2pq(Aa) = 678 лисиц;
q 2 (aa) = 12 лисиц.
Найдем фенотипическую структуру популяции, получим:
p 2 + 2pq + q 2 = 1 = 100%;
р 2 (АА) = 13655/14345 = 0,9519 или 95,19%;
2pq(Aa) = 678/14345 = 0,04726 или 4,726%;
q 2 (aa) = 12/14345 = 0,000836 или 0,0836%.
1. Рассчитаем частоты аллелей черной и рыжей окраски меха в популяции лисиц
По формуле из следствия закона Харди_Вайнберга:
p – частота доминантного аллеля А, q — частота рецессивного аллеля а.
q 2( аа) = 0,000836, q = 0,02898 приблизительно 0,03;
р(А) + q(а) = 1, р(А) = 1 — q(а) = 1 — 0,03 = 0,97.
2. Рассчитаем Соответствуют ли наблюдаемые численности ожидаемым из уравнения Харди-Вайнберга:
p 2 + 2pq + q 2 = 1 = 100%;
p 2 (АА) + 2pq(Аа) + q 2 (аа) = 1 = 100%;
( 0,97) 2 + 2(0,97 • 0,03 ) + ( 0,03 ) 2 = 1 = 100%;
[0,9519 или 95,19%] + [0,04726 или 4,726%] + [0,000836 или 0,0836%] = 1 = 100%.
Значит, наблюдаемые численности лисиц по фенотипам соответствуют ожидаемым из уравнения Харди-Вайнберга.
Определение частот генотипов в потомстве группы особей
Задача 381.
Определите частоты доминантного и рецессивного аллелей в группе особей, состоящей из 60 гомозигот ВВ и 40 гомозигот bb; в группе, состоящей из 160 особей ВВ и 40 особей bb. Определите частоты генотипов в потомстве этих групп при условии панмиксии.
Решение:
1. Первая группа особей
Nобщ. = 60 + 40 = 100
Определим частоты доминантного аллеля, получим:
р 2 (ВВ) = 60/100 = 0,6, значит р = 0,6;
q 2 (bb) = 40/100 = 0,4, значит q = 0,4.
Определите частоты генотипов в потомстве при условии панмиксии, получим:
p 2 + 2pq + q 2 = 1;
p 2 (ВВ) + 2pq(Bb) + q 2 (bb) = 1 = 100%;
(0,6) 2 + 2(0,6 • 9,4) + (0,4) 2 = [0,36 или 36%(ВВ)] + [0,48 или 48%(Bb)] + [0,16 или 16%(bb)] = 1 = 100%.
р 2 (ВВ) = 0,36 или 36%;
2pq(Bb) = 0,48 или 48%;
q 2 (bb) = 0,16 или 16%.
2. Вторая группа особей
Nобщ. = 160 + 40 = 200
Определим частоты доминантного аллеля, получим:
р 2 (ВВ) = 160/200 = 0,8, значит р = 0,8;
q 2 (bb) = 40/200 = 0,2, значит q = 0,2.
Определяем частоты генотипов в потомстве при условии панмиксии, получим:
p 2 + 2pq + q 2 = 1;
p 2 (ВВ) + 2pq(Bb) + q 2 (bb) = 1 = 100%;
(0,8) 2 + 2(0,8 • 0,2) + (0,2) 2 = [0,36 или 36%(ВВ)] + [0,48 или 48%(Bb)] + [0,16 или 16%(bb)] = 1 = 100%.
р 2 (ВВ) = 0,64 или 64%;
2pq(Bb) = 0,32 или 32%;
q 2 (bb) = 0,04 или 4%.
Как правильно рассчитать структуру популяции по генотипам
Задача 382.
Доля особей, имеющих генотип (аа), в большой естественной популяции равна 0,16. Рассчитайте структуру данной популяции по генотипам.
Решение:
q 2 (aa) = 0,16 = 16%;
p 2 (AA) = ?
2pq(Aa) = ?
Зная частоту встречаемости рецессивных гомозигот (аа), рассчитаем частоту встречаемости рецессивного аллеля (а), получим:
Согласно первому следствию из закона Харди-Вайнберга рассчитаем частоту встречаемости аллеля гена (А), получим:
p + q = 1 = 100%, где
р – частота доминантного аллеля в популяции;
q — частота рецессивного аллеля в популяции.
p + q = 1; p(A) + q(a) = 1; p(A) = 1 – q(a);
p(A) = 1 – 0,4 = 0,6.
Используя второе следствие из закона Харди-Вайнберга рассчитаем структуру данной популяции по генотипам, получим:
p 2 + 2pq + q 2 = 1 = 100%, где
p 2 – частота встречаемости доминантных генотипов в популяции;
2pq — частота встречаемости гетерозигот в популяции;
q 2 — частота встречаемости рецессивных генотипов в популяции.
р 2 (АА) + 2pq(Aa) = q 2 (aa) = 1 = 100%;
(0,6) 2 + 2(0,6 • 0,4) + (0,4) 2 = 1 = 100%;
0,36 или 36%(АА) + 0,48 или 48%(Аа) + 0,16 или 16%(аа) = 1 = 100%.
Ответ:
р 2 (АА) = 36%;
q 2 (aa) = 16%;
2pq(Aa) = 48%.
Частота встречаемости гомозиготных растений у гречихи
Задача 383.
У гречихи ярко-красная окраска растений неполно доминирует над зеленой. Гетерозиготы по данным генам имеют розовую краску. В панмиктической популяции, состоящей из 840 растений, содержалось 42 красных растения. Какова частота встречаемости гомозиготных растений?
Решение:
А – ярко-красная окраска растения;
а – зеленая окраска растения;
Аа – розовая окраска растения;
Nобщ. = 840 растений;
N(AA) = 42 ярко-красных растения;
р 2 = ?
q 2 = ?
1. Рассчитаем долю (частоту) встречаемости доминантных гомозигот (А) в популяции гречихи из условия задачи, получим:
р 2 (АА) = N(AA)/Nобщ. = 42/840 = 0,05 или 5%.
2. Зная частоту встречаемости доминантных гомозигот (АА) в популяции рассчитаем частоту аллели гена (А), получим:
3. Согласно первому следствию из закона Харди-Вайнберга рассчитаем частоту рецессивного аллеля (а) в популяции гречихи, получим:
p + q = 1; p(A) + q(a) = 1;
q(a) = 1 – р(А) = 1 – 0,22326 = 0,7764.
4. Используя формулу Харди-Вайнберга: p 2 + 2pq + q 2 = 1 = 100%, рассчитаем частоту встречаемости рецессивных гомозигот (аа) в популяции гречихи, получим:
p 2 (AA) + 2pq(Aa) + q 2 (aa) = 1 = 100%;
q 2 (aa) = (0,7764) 2 = 0,6028 или 60,28%.
Ответ:
р 2 (АА) = 0,05 или 5%;
q 2 (aa) = 0,6028 или 60,28%.
Использование формулы Харди-Вайнберга для расчета фенотипов у кроликов
Задача 384.
У кроликов окраска волосяного покрова “шиншилла” доминирует над альбинизмом. Гетерозиготы имеют светло-серую окраску. На кролиководческой ферме среди молодняка кроликов шиншилл появились альбиносы. Из 8100 крольчат 25 оказались альбиносами. Пользуясь формулой Харди-Вайнберга, определите, сколько было получено гетерозиготных крольчат, имеющих светло-серую окраску и сколько гомозиготных крольчат, имеющих окраску “шиншилла”.
Решение:
А — окраска волосяного покрова “шиншилла”;
а — альбинизм;
Аа — гетерозигота — светло-серая окраса шерсти;
Nобщ. = 8100 крольчат;
крольчата-альбиносы = 25 шт.;
p 2 (AA) = ?
2pq(Aa) = ?
q 2 (aa) = 25/8100 = 0,003086.
Зная частоту встречаемостигомозигот (аа) рассчитаем частоту аллеля (а)
q(а) = √0,003086 = 0,056.
Согласно первому следствию закона Харди-Вайнберга рассчитаем частоту встречаемости гена (А), получим:
р + q = 1, р(А) = 1 — q(а) = 1 — 0,0556 = 0,9444.
Используя формулу Харди-Вайнберга: р 2 + 2рq + q 2 = 1, рассчитаем фенотипическую структуру данной популяции кроликов, получим:
р 2 (АА) + 2рq(Аа) + q 2 (аа) = 1 = 100%;
(0,9444) 2 + (2 • 0,9444 • 0,0556) + ( 0,0556) 2 = 1 = 100%;
0,89189 или 89,2%(АА) + 0,1050 или 10,5%(Аа) + 0,00309 или 0,3%(аа) = 1 или 100%.
Рассчитаем число светло-серых крольчат, получим:
N(светло-серые крольчата) = 8100 • 0,105 = 850,5 примерно 850 шт.
Рассчитаем число крольчат с окраской «шиншила», получим:
N(«шиншиловые» крольчата) = 8100 • 0,892 = 7225,2 примерно 7225 шт.
Ответ:
N(светло-серые крольчата) = 850 шт;
N(«шиншиловые» крольчата) = 7225 шт.
источники:
http://bio-ege.sdamgia.ru/test?pid=17769
http://buzani.ru/zadachi/genetika/1836-zadachi-na-zakony-khardi-vajnberga-zadachi-380-384
МБОУ «Карагайская СОШ № 2»
с. Карагай, Пермский край
Решение задач
по теме «Генетика популяций.
Закон Харди – Вайнберга»
ЕГЭ. Биология, 11 класс.
Решение задач линии 28.
Подготовила:
Трефилова Раиса Поликарповна,
учитель биологии
МБОУ «Карагайская СОШ № 2»
Карагай – 2017
Цель: Дать рекомендации учащимся по выполнению задания линии 28 при
подготовке к ЕГЭ.
Задачи:
1. Информировать учащихся 11 класса о требованиях к выполнению
заданий линии 28 по биологии.
2. Познакомить с кодификатором, спецификацией и образцами заданий.
3. Мотивировать учащихся к успешной подготовке к ЕГЭ.
Теоретическое обоснование темы
Начальные этапы эволюционных процессов протекают в популяциях на
основе закономерностей наследования. Изучение генетической структуры
популяции связано с выяснением генотипического состава. В подобных
задачах определяется частоты генотипов и аллелей, которые выражаются в %
или в долях от единицы. Данная закономерность была выявлена независимо
друг от друга двумя исследователями: математиком Г.Харди и врачом
В.Вайнбергом.
Формулировка закона:
«Относительные частоты генов в популяции не изменяются из
поколения в поколение во времени при следующих условиях:
• Популяция должна быть велика;
• Отсутствует давление отбора на данные признаки;
• Отсутствуют мутации этих генов;
• В популяции особи свободно скрещиваются;
• Нет миграции из соседних популяций».
Предположим некую популяцию с одинаковым соотношением генотипов АА
и аа. Частоту генов А (A большое—доминантный признак ) обозначим р, а гена
а (а малое – рецессивный признак) – q.
На основании скрещивания составляем решётку Пеннета.
p² (AA) + 2 pq (Aa) + q² (aa) = 1
p + q = 1 (при извлечении квадратного корня)
Сумма частот генов в популяции p + q = 1, следовательно, уравнение можно
рассмотреть как: p² + 2 pq + q² = 1
Закон Харди—Вайнберга может быть сформулирован следующим образом:
«В идеальной популяции соотношение частот аллелей генов и генотипов из
поколения в поколение является величиной постоянной и соответствует
уравнению: p
2
+2pq + q
2
= 1
где p
2
— доля гомозигот по доминантной аллели; p — частота этой аллели;
q
2
— доля гомозигот по альтернативной аллели; q — частота
соответствующей аллели; 2pq — доля гетерозигот.
Закон Харди—Вайнберга при медико—генетических исследованиях, а также при
определении частоты генов, генотипов и фенотипов в популяциях в природе,
популяций в животноводстве и селекции. В этом его практическое значение.
Рассмотрим решение нескольких вариантов задач по данной теме.
Задача 1. В популяции человека количество индивидуумов с карим
цветом глаз составляет 51%, а с голубым – 49%. Определите процент
доминантных гомозигот в данной популяции.
Поскольку известно, что карий цвет глаз доминирует над голубым,
обозначим аллель, отвечающую за проявление признака кареглазости А, а
аллельный ему ген, ответственный за проявление голубых глаз,
соответственно, а. Тогда кареглазыми в исследуемой популяции будут люди
как с генотипом АА (доминантные гомозиготы, долю которых и надо найти
по условию задачи), так и — Аа гетерозиготы), а голубоглазыми – только аа
(рецессивные гомозиготы).
По условию задачи нам известно, что количество людей с генотипами АА и
Аа составляет 51%, а количество людей с генотипом аа — 49%. Как можно
вычислить процент кареглазых людей только с генотипом АА?
Для этого вычислим частоты встречаемости каждого из аллельных генов А и
а в данной популяции людей. Обозначив частоту встречаемости аллели А в
данной популяции буквой q, имеем частоту встречаемости аллельного ему
гена а = 1 – q. (Можно было бы обозначить частоту встречаемости аллельного
гена а отдельной буквой, как в тексте выше – это кому как удобнее). Тогда
сама формула Харди—Вайнберга для расчета частот генотипов при
моногибридном скрещивании при полном доминировании одного аллельного
гена над другим будет выглядеть вот так:
q
2
AA+ 2q(1 – q)Aa + (1 – q)
2
aa = 1.
(1 – q)
2
= 0,49 – это частота встречаемости людей с голубыми глазами.
Находим значение q: 1 – q = корень квадратный из 0,49 = 0,7; q = 1 – 0,7 = 0,3,
тогда q ² = 0,09.
Это значит, что частота кареглазых гомозиготных особей АА в данной
популяции будет составлять 0,09 или доля их будет равна 9%.
Ответ: частота кареглазых гомозиготных особей АА равна 9 %.
Задача 2. В популяции озёрной лягушки появилось потомство – 420 лягушат
с тёмными пятнами (доминантный признак) и 80 лягушат со светлыми
пятнами. Определите частоту встречаемости рецессивного гена и число
гетерозигот среди лягушек с тёмными пятнами.
Записываем условие задачи. Тёмный цвет пятен обозначаем А, светлый
цвет пятен – а. Необходимо определить генотипы родительских форм.
Признак, фенотип Ген, генотип
Тёмные пятна А
Светлые пятна а
F: 420 лягушат с темн. Пятнами А_
80 лягушат со светл. пятнами аа
Р — ?
Решение задачи
1. Каково количество особей в популяции?
420 + 80 = 500
2. Определяем частоту встречаемости лягушат со светлыми пятнами — q²
q²= 80: 500 = 0, 16 (частота встречаемости аллели равна отношению числа
данной аллели к общему числу аллелей в популяции)
3. Определяем частоту встречаемости рецессивного гена «светлое пятно» «а
малое», который мы обозначили q:
q = √ q² = √0,16 = 0,4
4. Определяем частоту встречаемости гена «тёмные пятна»(т.е. ), исходя из
уравнения р + q = 1, значит, р = 1 – q, следовательно, р = 1 – 0,4 = 0,6
5. Определяем количество гетерозигот Аа :
2рq = 2х0,4 х 0,6 = 0, 48 или 48 %
Объяснение решения задачи: для решения задачи используется закон Харди—
Вайнберга.
Ответ:
1) Число особей в популяции – 500.
2) Частота встречаемости рецессивного гена а «светлое пятно» — 0,4.
3) Количество гетерозигот (Аа) носителей гена «светлые пятна» — 0, 48 или
48%.
Задача 3. Популяция состоит из 49 % особей с генотипом АА и 9 % с
генотипом аа. Находится ли эта популяция в равновесии?
Признак, фенотип Ген, генотип
р = 49 % или 0,49 АА
q = 9 % или 0, 09 аа
Равновесие — ?
Решение.
1. Если популяция находится в равновесии, то для неё справедливо
уравнение Харди – Вайнберга:
p² + 2 pq + q² = 1
2. Для данной популяции частота генотипа АА: p² = 0,49,
частота аллеля А: √0,49 = 0, 7 ; р = 0,7
3. Определяем частоту генотипа аа: q² = 0,09, тогда
частота аллеля а: q =√0,09 = 0,3.
4. Определяем частоту генотипа гетерозиготы Аа: 2 pq = 2 х 0,7 х 0,3 = 0,42
5. Определяем, находится ли популяция в равновесии: если
p² + 2 pq + q² = 1, то 0,49 + 0,42 + 0,09 = 1, следовательно, популяция
находится в равновесии.
Ответ:
По уравнению Харди—Вайнберга сумма равна 1, популяция находится в
равновесии.
Задачи для самостоятельного решения
1. В Европе на 10 000 человек с нормальным содержанием меланина
встречается 1 альбинос. Ген альбинизма наследуется по аутосомно—
рецессивному типу. Рассчитать частоту встречаемости носителей гена
альбинизма. Носителем называют организм, гетерозиготный по гену,
который может вызвать в гомозиготном состоянии нарушение метаболизма.
Ответ: частота встречаемости гетерозигот 2 pq = 0,0198 или почти 2%
2. Предрасположенность к сахарному диабету наследуется по аутосомно—
рецессивному типу. Частота встречаемости рецессивного гена
предрасположенности к болезни в США приблизительно 22, 5 %. Какова
частота встречаемости в США гетерозиготных носителей гена
предрасположенности к сахарному диабету.
Ответ: частота встречаемости в США гетерозиготных носителей гена
предрасположенности к сахарному диабету равна 0,4982.
3. У человека ген «резус положительный» доминантен по отношению к гену
«резус отрицательный». В обследованной по этому показателю популяции
1982 человека были «резус положительными», а 368 – «резус
отрицательными». Какова генетическая структура этой популяции?
Ответ: р = 0,5
4. У гречихи ярко—красная окраска растений неполно доминирует над
зелёной. Гетерозиготы по данным генам имеют розовую окраску. В
панмиктической популяции, состоящей из 840 растений, содержалось 42
красных растения. Какова частота встречаемости гомозиготных растений?
Ответ: частота встречаемости гомозиготных растений = 0,657.
5. Одна из форм глюкозурии наследуется как аутосомно—рецессивный
признак и встречается с частотой 7:1000000. Определить частоту
встречаемости гетерозигот в популяции.
Ответ: частота встречаемости гетерозиготных особей 2pq в популяции людей
= 0,0052775.
Источники информации:
1. Гончаров О.В. Генетика.Задачи. – Саратов: Лицей, 2008.
2. Кириленко А.А. Биология. Сборник задач по генетике. Базовый и
повышенный уровень ЕГЭ: учебно—методическое пособие/А.А.Кириленко. –
Ростов—на—Дону: Легион, 2009.
3. Кириленко А.А., Колесников С.И. Биология. Подготовка к ЕГЭ-2013:
учебно—методическое пособие/А.А.Кириленко, С.И.Колесников. – Ростов—на—
Дону: Легион, 2012.
4. http://biology-online.ru/metodichka/konspekty-i-lekcii/obschaja-
biologija/zakon-hardi-vainberga-v-reshenii-genetic.html

 ♂
♂