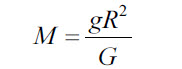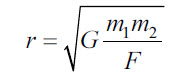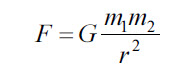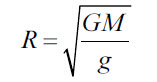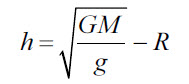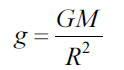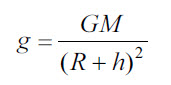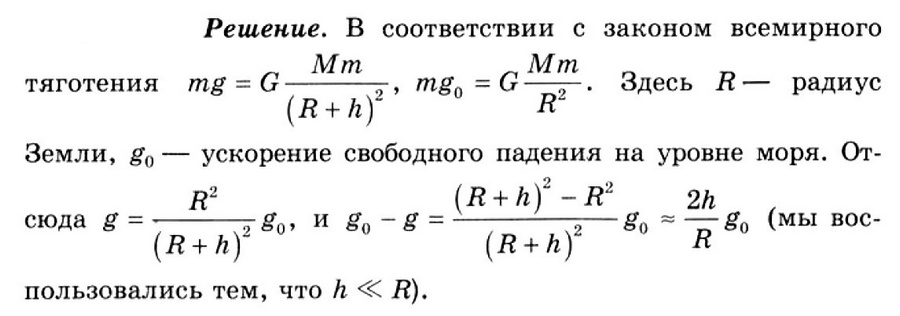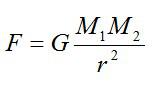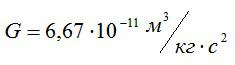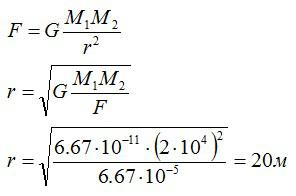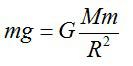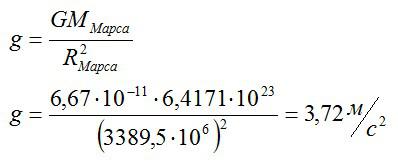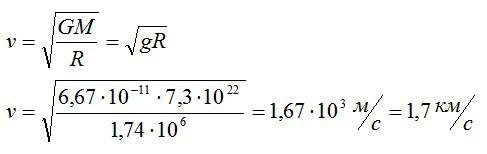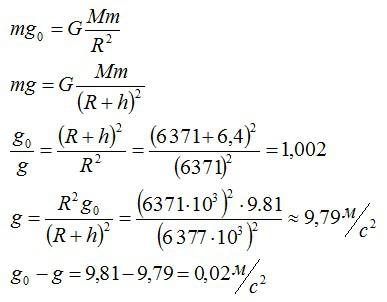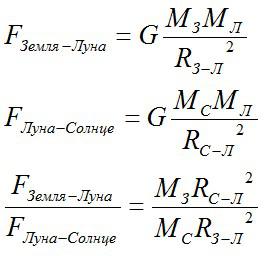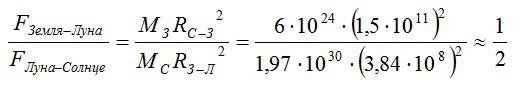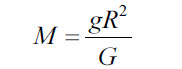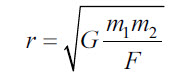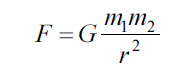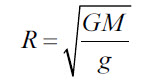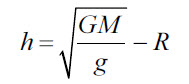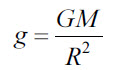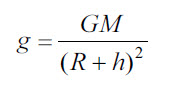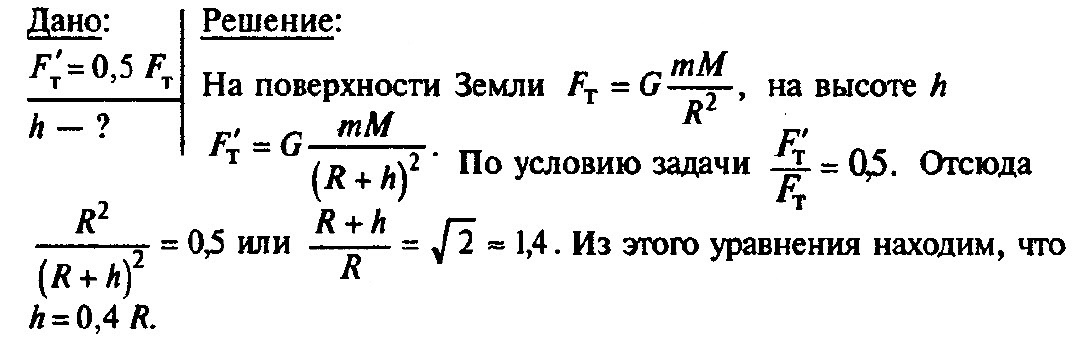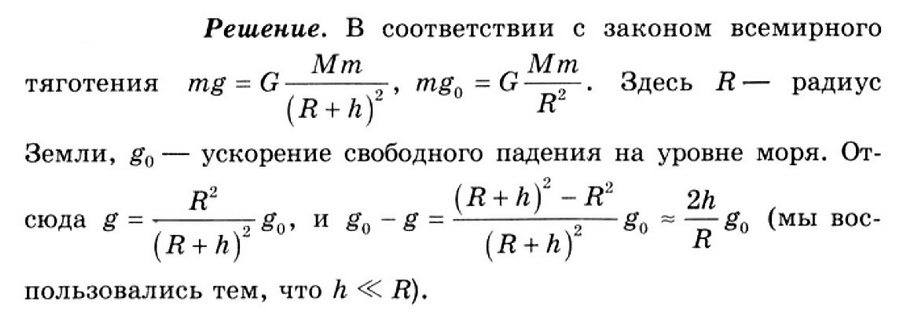Задачи на закон всемирного тяготения егэ - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Земля притягивает к себе подброшенный мяч с силой 5 Н. С какой силой этот мяч притягивает к себе Землю? (Ответ дайте в ньютонах.)

Две планеты с одинаковыми массами обращаются по круговым орбитам вокруг звезды. У первой из них радиус орбиты вдвое больше, чем у второй. Каково отношение сил притяжения первой и второй планет к звезде ?

Две планеты с одинаковыми массами обращаются по круговым орбитам вокруг звезды. Для первой из них сила притяжения к звезде в 4 раза больше, чем для второй. Каково отношение радиусов орбит первой и второй планет?

Две планеты с одинаковыми массами обращаются по круговым орбитам вокруг звезды. Для первой из них сила притяжения к звезде в 4 раза меньше, чем для второй. Каково отношение радиусов орбит первой и второй планет?

У поверхности Земли на космонавта действует сила тяготения 720 Н. Какая сила тяготения действует со стороны Земли на того же космонавта в космическом корабле, движущемся по круговой орбите вокруг Земли на расстоянии трёх земных радиусов от её центра? (Ответ дайте в ньютонах.)

Пройти тестирование по этим заданиям

Источник

Задачи Закон всемирного тяготения с решениями

Формулы, используемые на уроках «Задачи закон всемирного тяготения».

Название величины	Обозначение	Единица измерения	Формула
*Масса планеты*	М	кг
*Расстояние между телами или их центрами*	r	м
*Сила всемирного тяготения*	F	Н
*Постоянная всемирного тяготения*	G	Н•м²/кг²	G = 6,67•10^-11
*Радиус планеты*	R	м
*Высота*	h	м
*Ускорение свободного падения вблизи поверхности планеты*	g	м/с²
*Ускорение свободного падения на большом расстоянии от поверхности планеты*	g	м/с²

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
На каком расстоянии друг от друга находятся два одинаковых шара массами по 20 т, если сила тяготения между ними 6,67•10^-5 Н?

Задача № 2.
Масса Сатурна 5,7•10²⁶ кг, а его радиус— 6•10⁷ м. Определите ускорение свободного падения на Сатурне.

Задача № 3.
Чему равно ускорение свободного падения на высоте над поверхностью Земли, равной двум ее радиусам?

Задача № 4.
На какой высоте над поверхностью Земли сила тяготения в 2 раза меньше, чем на поверхности Земли?

Задача № 5.
С какой силой притягивается к центру Земли тело массой m, находящееся в глубокой шахте, если расстояние от центра Земли до тела равно г? Плотность Земли считайте всюду одинаковой и равной р.

Задача № 6.
Экипаж поднимающегося аэростата периодически проводит измерения ускорения свободного падения. На сколько уменьшилось значение g на высоте h = 6,4 км?

Ответ: на 0,02 м/с²

Задача № 7.
Вычислите ускорение свободного падения и первую космическую скорость у поверхности Луны.

Задача № 8.
Ракета стартует с Луны вертикально вверх с ускорением а = 20 м/с². Сколько весит во время старта космонавт, масса которого m = 90 кг?

Задача № 9. (повышенной сложности)
Во сколько раз сила притяжения между Луной и Солнцем больше, чем сила притяжения между Луной и Землей?

Краткая теория для решения Задачи Закон всемирного тяготения.

Это конспект по теме «ЗАДАЧИ закон всемирного тяготения с решениями». Выберите дальнейшие действия:

Перейти к теме: ЗАДАЧИ на Движение тела по окружности
Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
Вернуться к списку конспектов по Физике.
Проверить свои знания по Физике.

Источник

Закон всемирного тяготения – фундаментальный закон природы, согласно которому все предметы притягиваются между собой. Это проявление гравитационного взаимодействия. Если хотите узнать о гравитации больше – читайте наш отдельный материал.

На своем телеграм-канале мы ежедневно отбираем полезную и интересную информацию. Подписывайтесь!

Закон всемирного тяготения: формулировка, примеры

Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорционально квадрату расстояния между ними.

Примеры действия закона всемирного тяготения:

яблоко, летящее на голову Ньютона;
движение небесных тел;
свет, поглощаемый черной дырой.

Закон всемирного тяготения был сформулирован Ньютоном в 1682 году. Размышляя над законами движения планет, которые ранее были открыты Кеплером, Ньютон хотел узнать, какие силы действуют на небесные тела и заставляют их двигаться определенным образом.

Вопросы на закон всемирного тяготения

Вопрос 1. Если все предметы притягиваются, то почему Луна не падает на Землю, Земля не падает на Солнце и т.д.?

Ответ. Все дело в скорости движения небесных тел. Луна движется вокруг Земли со скоростью равной примерно 1 км/с. Этой скорости недостаточно, чтобы покинуть орбиту, и достаточно, чтобы Луна не упала на Землю. Можно сказать, что Луна падает на Землю, но это падение никогда не заканчивается.

Вопрос 2. Что из этих величин является фундаментальной физической константой: гравитационная постоянная G или ускорение свободного падения g?

Ответ. Гравитационная постоянная G является одинаковой для всех тел в природе и в любой точке Вселенной. Ее значение:

Ускорение свободного падения g в пределах Земли варьируется в зависимости от координат и высоты подъема тела над поверхностью. На других планетах значение g будет совершенно иным, так как оно зависит от массы и размеров небесного тела.

Вопрос 3. Как развивалась теория тяготения после Ньютона и до наших дней?

Ответ. Классическая теория тяготения Ньютона господствовала в физике на протяжении более чем двух веков. В 1915 году Эйнштейн показал, что она является частным случаем общей теории относительности.

Вопрос 4. Что такое первая и вторая космические скорости?

Ответ. Первая космическая скорость – скорость, с которой спутник должен двигаться вокруг Земли или другого космического объекта, чтобы оставаться на орбите и не падать. Для Земли значение первой космической скорости равно 7,91 км/с.
Вторая космическая скорость – скорость, необходимая для того, чтобы покинуть орбиту небесного тела. Значение: 11,2 км/с.

Вопрос 5. С гравитационной постоянной разобрались. Ну а что такое гравитационная неустойчивость?

Ответ. Гравитационная неустойчивость – флуктуации (возмущения, небольшие отклонения) плотности и скорости вещества в пространстве под действием сил тяготения. Гравитационная неустойчивость является причиной возникновения галактик, звезд и звездных скоплений.

Кстати! Для наших читателей действует скидка 10% на любой вид работы.

Задачи на закон всемирного тяготения с решениями

Хотите узнать, как решать задачи на закон всемирного тяготения? Вот памятка по решению любых задач и отдельная статья про задачи на движение тел под действием силы тяжести.

Задача №1. Применение закона всемирного тяготения

Условие

Два одинаковых шара притягиваются друг к другу с силой 6,67*10^-5 Ньютона. Масса каждого шара равна 20 тонн. Найдите расстояние между шарами.

Решение

По закону всемирного тяготения

Ответ: 20 метров.

Задача №2. Расчет ускорения свободного падения на Марсе

Условие

Каково ускорение свободного падения на Марсе?

Решение

Сначала по справочнику найдем значения массы и радиуса Марса:

По закону всемирного тяготения для тела массы m на Марсе:

Сократим m и получим формулу для ускорения свободного падения:

Ответ: 3,72 метра на секунду в квадрате.

Задача №3. Нахождение первой космической скорости на поверхности Луны

Условие

Какова первая космическая скорость на поверхности Луны?

Решение

Первая космическая скорость у поверхности планеты находится по формуле:

Также из этой задачи можно найти ускорение свободного падения на Луне. Оно равно 1,61 м/с2.

Ответ: 1,7 км/с.

Задача №4. Изменение ускорения свободного падения с четом высоты

Условие

Воздушный шар поднимается на высоту 6 километров. Как изменится ускорение свободного падения на этой высоте?

Решение

Запишем закон всемирного тяготения сначала для поверхности Земли, а потом для высоты h. Обозначим ускорение свободного падения на уровне моря как g нулевое.

Ответ: Ускорение свободного падения уменьшится на 0,02 м/с2.

Задача №5. Применение закона всемирного тяготения

Условие

Определите, какая из сил притяжения больше: сила между Землей и Луной или сила между Луной и Солнцем

Решение

Чтобы понять, какая сила больше, нужно их сравнить.

Учитывая, что расстояние между Землей и Луной гораздо меньше, чем расстояние межу Землей и Солнцем, вместо расстояния между Луной и Солнцем можно взять расстояние Земля-Солнце.

Ответ: сила притяжения между Луной и Солнцем примерно в два раза больше.

Нужна помощь в решении задач и других заданий? Обращайтесь в профессиональный студенческий сервис.

Источник

ЕГЭ-11 Физика Задание №2
Закон всемирного тяготения.

№1 Две планеты с одинаковыми массами обращаются по круговым
орбитам вокруг звезды. Для первой из них сила притяжения к звезде в 4 раза
больше, чем для второй. Каково отношение радиусов орбит первой и второй планет?

№2 У
поверхности Земли на космонавта действует сила тяготения 720 Н. Какая сила
тяготения действует со стороны Земли на того же космонавта в космическом
корабле, движущемся по круговой орбите вокруг Земли на расстоянии трёх земных радиусов
от её центра?

№3 Космонавт
на Земле притягивается к ней с силой 700 Н. С какой приблизительно силой
он будет притягиваться к Марсу, находясь на его поверхности, если радиус Марса
в 2 раза меньше, а масса — в 10 раз меньше, чем у Земли?

№4 Сила
притяжения Земли к Солнцу в 22,5 раза больше, чем сила притяжения Марса к
Солнцу. Во сколько раз расстояние между Марсом и Солнцем больше расстояния
между Землёй и Солнцем, если масса Земли в 10 раз больше массы Марса?

№5 Модуль
силы гравитационного взаимодействия двух точечных тел, расположенных на
расстоянии четырёх метров друг от друга, равен 5 Н. Каков будет модуль силы
гравитационного взаимодействия этих тел, если расстояние между ними увеличить
на 1 м?

№6 Две
звезды одинаковой массы притягиваются друг к другу с силами, равными по
модулю F. Во сколько раз уменьшился бы модуль сил притяжения между
звёздами, если бы расстояние между их центрами увеличилось в 1,5 раза, а масса
каждой звезды уменьшилась в 2 раза?

№7 Чему
равен модуль силы тяжести, действующей на тело массой 9 кг, на высоте, равной
половине радиуса Земли?

№8 Модуль
ускорения свободного падения вблизи поверхности астероида равен 0,2 м/с².
Чему будет равен модуль ускорения свободного падения вблизи поверхности другого
астероида, объём которого в 8 раз меньше? Оба астероида однородные, сферические
и состоят из железа. Ответ выразите в м/с².

№9 Сила
гравитационного взаимодействия небольших тел массами m и M,
находящихся на расстоянии R₁ = 100 км друг от
друга, равна по модулю F. Сила гравитационного взаимодействия
небольших тел массами 2m и M, находящихся на
расстоянии R₂ друг от друга, равна по модулю F/50.
На какую величину отличаются расстояния R₁ и R₂?

№10

№11

№12

№13 К
вертикально расположенной пружине динамометра, корпус которого прикреплён к
потолку, подвешен груз массой 8 кг. Каково будет показание динамометра, если
человек, стоящий под грузом, будет пробовать опустить этот груз, действуя на
него направленной вниз силой 50 Н?

Ответы
:

№	1	2	3	4	5	6	7	8	9	10	11	12	13
ответ	0,5	80	280	1,5	3,2	9	40	0,1	1000	0,25	0,5	1	130

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Закон тяготения

Закон всемирного тяготения

Две материальные точки массами (displaystyle m) и (displaystyle M) притягиваются друг к
другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния (displaystyle R) между ними. [F=Gfrac{mM}{R^2}] Гравитационная постоянная — коэффициент пропорциональности

[G=6,67cdot10^{-11} frac{ text{Н}cdot text{м$^2$}}{text{кг$^2$}}]

Сила гравитационного притяжения между двумя шарами равна (F). Во сколько увеличится сила притяжения между шарами, если каждый из них заменить на шар в 4 раза тяжелее, оставив расстояние между шарами неизменным.

По закону всемирного тяготения: [F=Gfrac{M_{1}M_{2}}{R^{2}}] где (M_1) и (M_2) – масса шаров, (R) – радиус между шарами. Так как масса каждого из шаров увеличится в 4, то сила увеличится в 16 раз.

Ответ: 16

Две звезды вращаются вокруг друг друга, сила притяжения между ними равна F. На сколько должно увеличиться расстояние между ними, чтобы сила притяжения осталась неизменной, если масса первой звезды увеличилась в 4 раза?

Сила притяжения между двумя телами равна: [F=Gcdotfrac{M_1M_2}{R^2}] где G – гравитационная постоянная, (M_1), (M_2) – массы тел, R — расстояние между этими телами.
Запишем уравнения до и после того, как изменили массу: [F=
begin{cases}
dfrac{M_1M_2}{R_1^2}\
\
dfrac{4M_1M_2}{R_2^2}
end{cases}
Rightarrow dfrac{M_1M_2}{R_1^2} = dfrac{4M_1M_2}{R_2^2}] [frac{1}{R_1^2}=frac{4}{R_2^2} Rightarrow R_2 =sqrt{R_1^2cdot4} = 2R_1]

Ответ: 2

Сила гравитационного притяжения между двумя шарами равна 200 нН, а расстояние между ними равно 100 м. Какова будет сила притяжения (в нН) между этими шарами, если расстояние между их центрами увеличить в 2 раза

По закону всемирного тяготения: [F=Gfrac{M_{1}M_{2}}{R^{2}}] Составим уравнения для каждого случая, описанного в задаче: [begin{cases}
F_{1}=Gdfrac{M_{1}M_{2}}{R_{1}^2}
\
\
F_{2}=Gdfrac{M_{1}M_{2}}{4R_{1}^2}
end{cases}] Значит сила уменьшится в 4 раза и станет равной 50 нН.

Ответ: 50

Сила гравитационного притяжения между двумя шарами равна (F). Во сколько увеличится сила притяжения между шарами, если один из них заменить на шар в три раза тяжелее, оставив расстояние между шарами неизменным.

По закону всемирного тяготения: [F=Gfrac{M_{1}M_{2}}{R^{2}}] где (M_1) и (M_2) – масса шаров, (R) – радиус между шарами. Так как масса одного из шаров увеличится в три, то и сила увеличится в три раза.

Ответ: 3

Сила гравитационного притяжения между двумя шарами равна (F=100) Н. Какова будет сила притяжения между шарами, если массу каждого из шаров увеличить 2 раза, а расстояние между шарами также увеличить в 2 раза.

По закону всемирного тяготения: [F=Gfrac{M_{1}M_{2}}{R^{2}}] где (M_1) и (M_2) – масса шаров, (R) – радиус между шарами.
Во втором случае сила притяжения равна [F_2=Gfrac{2M_{1}2M_{2}}{4R^{2}}=F=100text{ Н}]

Ответ: 100

Два одинаковых маленьких шарика массой (m) каждый, расстояние между центрами которых равно (r), притягиваются друг к другу с силами, равными по модулю 0,2 пН. Каков модуль сил гравитационного притяжения двух других шариков, если масса каждого из них равна (2m), а расстояние между их центрами равно (2r)? Ответ дайте в пН.

“Демоверсия 2020”

Сила взаимодействия шариков: [F=Gdfrac{mcdot m}{r^2}] Во втором случае: [F=Gdfrac{4m}{4r^2}=Gdfrac{m^2}{r^2}] То есть сила не изменилась

Ответ: 0,2

На Земле на человека действует сила притяжения (F=800) Н. Какая сила будет действовать на этого же человека на Луне, если отношение ускорения свободного падения Луны и Земли равно (dfrac{g_{text{л}}}{g_{text{з}}} = 0,16)? (Ответ дайте в Ньютонах)

Сила приятяжения человека к планете равна: [F = mg] где m – масса человека.
Запишем это уравнение для Земли и Луны соответственно: [F_{text{з}} = mg_{text{з}}] [F_{text{л}} = mg_{text{л}}] Поделив первое уравнение на втрое, получим: [frac{F_{text{з}}}{F_{text{л}}} = frac{g_{text{з}}}{g_{text{л}}} Rightarrow F_{text{л}} = F_{text{з}}cdot frac{g_{text{л}}}{g_{text{з}}}] [F_{text{л}} = 800text{ H}cdot 0,16 = 128text{ H }]

Ответ: 128

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Задачи Закон всемирного тяготения с решениями

Формулы, используемые на уроках «Задачи закон всемирного тяготения».

Название величины	Обозначение	Единица измерения	Формула
*Масса планеты*	М	кг
*Расстояние между телами или их центрами*	r	м
*Сила всемирного тяготения*	F	Н
*Постоянная всемирного тяготения*	G	Н•м²/кг²	G = 6,67•10^-11
*Радиус планеты*	R	м
*Высота*	h	м
*Ускорение свободного падения вблизи поверхности планеты*	g	м/с²
*Ускорение свободного падения на большом расстоянии от поверхности планеты*	g	м/с²

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1. На каком расстоянии друг от друга находятся два одинаковых шара массами по 20 т, если сила тяготения между ними 6,67•10^-5 Н?

Задача № 2. Масса Сатурна 5,7•10²⁶ кг, а его радиус— 6•10⁷ м. Определите ускорение свободного падения на Сатурне.

Задача № 3. Чему равно ускорение свободного падения на высоте над поверхностью Земли, равной двум ее радиусам?

Задача № 4. На какой высоте над поверхностью Земли сила тяготения в 2 раза меньше, чем на поверхности Земли?

Задача № 5. С какой силой притягивается к центру Земли тело массой m, находящееся в глубокой шахте, если расстояние от центра Земли до тела равно г? Плотность Земли считайте всюду одинаковой и равной р.

Задача № 6. Экипаж поднимающегося аэростата периодически проводит измерения ускорения свободного падения. На сколько уменьшилось значение g на высоте h = 6,4 км?

Ответ: на 0,02 м/с²

Задача № 7. Вычислите ускорение свободного падения и первую космическую скорость у поверхности Луны.

Задача № 8. Ракета стартует с Луны вертикально вверх с ускорением а = 20 м/с². Сколько весит во время старта космонавт, масса которого m = 90 кг?

Задача № 9. (повышенной сложности) Во сколько раз сила притяжения между Луной и Солнцем больше, чем сила притяжения между Луной и Землей?

Краткая теория для решения Задачи Закон всемирного тяготения.

Это конспект по теме «ЗАДАЧИ закон всемирного тяготения с решениями». Выберите дальнейшие действия:

Перейти к теме: ЗАДАЧИ на Движение тела по окружности
Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
Вернуться к списку конспектов по Физике.
Проверить свои знания по Физике.

Источник

ЕГЭ—11 Физика Задание №2 Закон всемирного тяготения.

№1 Две планеты с одинаковыми массами обращаются по круговым орбитам вокруг звезды. Для первой

из них сила притяжения к звезде в 4 раза больше, чем для второй. Каково отношение радиусов орбит

первой и второй планет?

№2 У поверхности Земли на космонавта действует сила тяготения 720 Н. Какая сила тяготения

действует со стороны Земли на того же космонавта в космическом корабле, движущемся по круговой

орбите вокруг Земли на расстоянии трёх земных радиусов от её центра?

№3 Космонавт на Земле притягивается к ней с силой 700 Н. С какой приблизительно силой он будет

притягиваться к Марсу, находясь на его поверхности, если радиус Марса в 2 раза меньше, а масса — в

10 раз меньше, чем у Земли?

№4 Сила притяжения Земли к Солнцу в 22,5 раза больше, чем сила притяжения Марса к Солнцу. Во

сколько раз расстояние между Марсом и Солнцем больше расстояния между Землёй и Солнцем, если

масса Земли в 10 раз больше массы Марса?

№5 Модуль силы гравитационного взаимодействия двух точечных тел, расположенных на расстоянии

четырёх метров друг от друга, равен 5 Н. Каков будет модуль силы гравитационного взаимодействия

этих тел, если расстояние между ними увеличить на 1 м?

№6 Две звезды одинаковой массы притягиваются друг к другу с силами, равными по модулю F. Во

сколько раз уменьшился бы модуль сил притяжения между звёздами, если бы расстояние между их

центрами увеличилось в 1,5 раза, а масса каждой звезды уменьшилась в 2 раза?

№7 Чему равен модуль силы тяжести, действующей на тело массой 9 кг, на высоте, равной половине

радиуса Земли?

№8 Модуль ускорения свободного падения вблизи поверхности астероида равен 0,2 м/с

. Чему будет

равен модуль ускорения свободного падения вблизи поверхности другого астероида, объём которого в 8

раз меньше? Оба астероида однородные, сферические и состоят из железа. Ответ выразите в м/с

№9 Сила гравитационного взаимодействия небольших тел массами m и M, находящихся на

расстоянии R

= 100 км друг от друга, равна по модулю F. Сила гравитационного взаимодействия

небольших тел массами 2m и M, находящихся на расстоянии R

друг от друга, равна по модулю F/50. На

какую величину отличаются расстояния R

и R

№10

№11

№12

№13 К вертикально расположенной пружине динамометра, корпус которого прикреплён к потолку,

подвешен груз массой 8 кг. Каково будет показание динамометра, если человек, стоящий под грузом,

будет пробовать опустить этот груз, действуя на него направленной вниз силой 50 Н?

Источник

Задачи Закон всемирного тяготения с решениями

Название величины

Обозначение

Единица измерения

Формула

Масса планеты

М

кг

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://uchitel.pro/wp-content/uploads/2018/10/2018-10-13_19-17-29.jpg" alt width="182" height="69" />

Расстояние между телами или их центрами

r

м

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://uchitel.pro/wp-content/uploads/2018/10/2018-10-13_19-11-33.jpg" alt width="181" height="77" />

Сила всемирного тяготения

F

Н

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://uchitel.pro/wp-content/uploads/2018/10/2018-10-13_19-11-45.jpg" alt width="181" height="68" />

Постоянная всемирного тяготения

G

Н•м2/кг2

G = 6,67•10-11

Радиус планеты

R

м

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://uchitel.pro/wp-content/uploads/2018/10/2018-10-13_19-24-25.jpg" alt width="157" height="82" />

Высота

h

м

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://uchitel.pro/wp-content/uploads/2018/10/2018-10-13_19-24-36.jpg" alt width="189" height="84" />

Ускорение свободного падения вблизи поверхности планеты

g

м/с2

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://uchitel.pro/wp-content/uploads/2018/10/2018-10-13_19-24-48.jpg" alt width="124" height="70" />

Ускорение свободного падения на большом расстоянии от поверхности планеты

g

м/с2

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://uchitel.pro/wp-content/uploads/2018/10/2018-10-13_19-24-58.jpg" alt width="171" height="85" />

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Краткая теория для решения Задачи Закон всемирного тяготения.

Закон всемирного тяготения: формулировка, примеры

Вопросы на закон всемирного тяготения

Задачи на закон всемирного тяготения с решениями

Задача №1. Применение закона всемирного тяготения

Задача №2. Расчет ускорения свободного падения на Марсе

Задача №3. Нахождение первой космической скорости на поверхности Луны

Задача №4. Изменение ускорения свободного падения с четом высоты

Задача №5. Применение закона всемирного тяготения

Закон тяготения

Задачи Закон всемирного тяготения с решениями

Название величины

Обозначение

Единица измерения

Формула

Масса планеты

М

кг

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" src="https://xn--b1agatbqgjneo2i.xn--p1ai/wp-content/uploads/2018/10/2018-10-13_19-17-29.jpg" alt width="182" height="69" />

Расстояние между телами или их центрами

r

м

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" src="https://xn--b1agatbqgjneo2i.xn--p1ai/wp-content/uploads/2018/10/2018-10-13_19-11-33.jpg" alt width="181" height="77" />

Сила всемирного тяготения

F

Н

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" src="https://xn--b1agatbqgjneo2i.xn--p1ai/wp-content/uploads/2018/10/2018-10-13_19-11-45.jpg" alt width="181" height="68" />

Постоянная всемирного тяготения

G

Н•м2/кг2

G = 6,67•10-11

Радиус планеты

R

м

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" src="https://xn--b1agatbqgjneo2i.xn--p1ai/wp-content/uploads/2018/10/2018-10-13_19-24-25.jpg" alt width="157" height="82" />

Высота

h

м

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" src="https://xn--b1agatbqgjneo2i.xn--p1ai/wp-content/uploads/2018/10/2018-10-13_19-24-36.jpg" alt width="189" height="84" />

Ускорение свободного падения вблизи поверхности планеты

g

м/с2

Н•м²/кг²

G = 6,67•10^-11

м/с²

м/с²

Н•м²/кг²

G = 6,67•10^-11

м/с²

м/с²