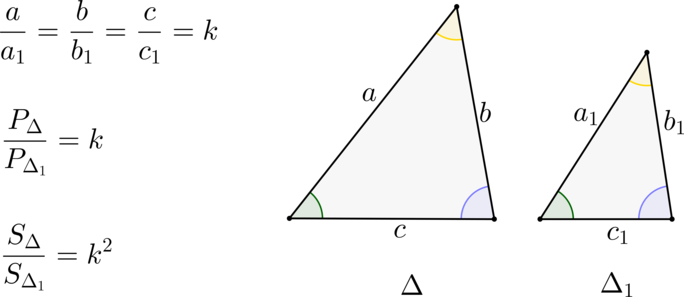3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Треугольник: задачи на подобие
(blacktriangleright) Треугольники подобны, если их углы равны, а сходственные стороны (лежащие напротив равных углов) относятся друг к другу с одним и тем же коэффициентом (k) (пропорциональны).
(blacktriangleright) Признаки подобия:
1. Два угла одного треугольника равны двум углам другого треугольника.
2. Три стороны одного треугольника пропорциональны трем сторонам другого треугольника.
3. Две стороны одного треугольника пропорциональны двум сторонам другого, а углы между этими сторонами равны.
(blacktriangleright) Площади подобных треугольников относятся как (k^2), а периметры – как (k).
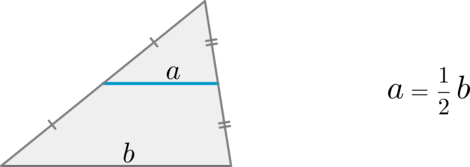
(blacktriangleright) Средняя линия треугольника – отрезок, соединяющий середины двух сторон. Она равна половине третьей стороны.
Задание
1
#3935
Уровень задания: Равен ЕГЭ
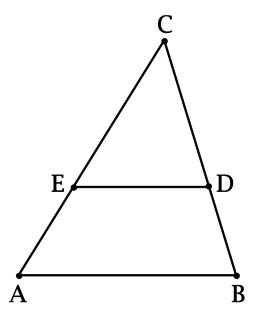
Точка (E) лежит на стороне (AC) треугольника (ABC), причём (dfrac{EC}{AE} = 2). Точка (D) лежит на (BC), причём (EDparallel AB). Найдите (AB), если (ED = dfrac{4}{3}).
Так как (EDparallel AB), то (angle CED = angle CAB), (angle CDE = angle CBA) (как соответственные при параллельных прямых и секущей), тогда треугольники (CED) и (CAB) подобны.
Так как (EC = 2cdot AE), то (AC = 3cdot AE), следовательно, [dfrac{AC}{EC} = dfrac{3cdot AE}{2cdot AE} = dfrac{3}{2}.]
Так как стороны (EC) и (AC) лежат против равных углов (в треугольниках (CED) и (CAB) соответственно), то [dfrac{AB}{ED} = dfrac{AC}{EC} = dfrac{3}{2},] откуда [AB = dfrac{3}{2}cdot ED = dfrac{3}{2}cdotdfrac{4}{3} = 2.]
Ответ:
2
Задание
2
#3937
Уровень задания: Равен ЕГЭ
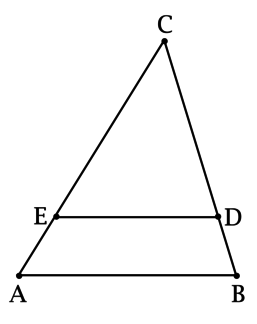
Точка (E) лежит на стороне (AC) треугольника (ABC), причём (dfrac{EC}{AE} = 3). Точка (D) лежит на (BC), причём (dfrac{CD}{CB} = 0,75). Найдите (angle CED — angle CAB). Ответ дайте в градусах.
Рассмотрим треугольники (CAB) и (CED):
(angle C) – общий,
[dfrac{CA}{CE} = dfrac{AE + CE}{CE} = dfrac{AE}{CE} + 1 = dfrac{1}{3} + 1 = dfrac{4}{3} = dfrac{CB}{CD},] тогда треугольники (CAB) и (CED) подобны по пропорциональности двух сторон и равенству углов между ними.
В подобных треугольниках против пропорциональных сторон лежат равные углы, тогда (angle CED = angle CAB), откуда (angle CED — angle CAB = 0^{circ}).
Ответ:
0
Задание
3
#3943
Уровень задания: Равен ЕГЭ
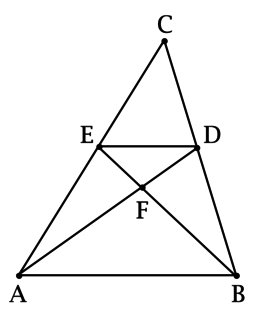
(F) – точка пересечения (AD) и (BE) – медиан треугольника (ABC). Известно, что (S_{ABF} = 1). Найдите (S_{DEF}).
(ED) – средняя линия треугольника (ABC), тогда (ED = 0,5cdot AB), (EDparallel AB).
Так как (EDparallel AB), то (angle DEF = angle ABF), (angle EDF = angle FAB) (как внутренние накрест лежащие при параллельных прямых и секущей), следовательно, треугольники (DEF) и (ABF) подобны (по двум углам). Так как (ED = 0,5cdot AB), причём стороны (ED) и (AB) лежат (в треугольниках (DEF) и (ABF) соответственно) против равных углов, то [dfrac{S_{DEF}}{S_{ABF}} = left(dfrac{ED}{AB}right)^2 = 0,5^2 = 0,25,] откуда с учётом того, что (S_{ABF} = 1) находим (S_{DEF} = 0,25).
Ответ:
0,25
Задание
4
#3936
Уровень задания: Сложнее ЕГЭ
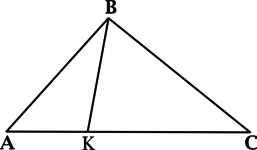
Отрезок (BK) соединяет вершину (B) треугольника (ABC) с точкой на противоположной стороне, причем (angle AKB = angle B). При этом известно, что (BK = 10), (AB = 12), (AC = 18). Найдите (BC).
Рассмотрим треугольники (ABK) и (ACB):
(angle AKB = angle B),
(angle A) – общий, тогда треугольники (ABK) и (ACB) подобны по двум углам.
В подобных треугольниках против равных углов лежат пропорциональные стороны, тогда [dfrac{BK}{BC} = dfrac{AB}{AC},] откуда (dfrac{10}{BC} = dfrac{12}{18}), следовательно (BC = 15).
Ответ:
15
Задание
5
#3938
Уровень задания: Сложнее ЕГЭ
Отрезок (BK) соединяет вершину (B) треугольника (ABC) с точкой на противоположной стороне. При этом известно, что (angle AKB = 105^{circ}), (AB = 12), (AC = 24), (AK = 6). Найдите (angle ABC). Ответ дайте в градусах.
Рассмотрим треугольники (ABK) и (ACB):
(angle A) – общий,
[dfrac{AB}{AC} = dfrac{AK}{AB},] тогда треугольники (ABK) и (ACB) подобны по пропорциональности двух сторон и равенству углов между ними.
В подобных треугольниках против пропорциональных сторон лежат равные углы, тогда (angle ABC = angle AKB = 105^{circ}).
Ответ:
105
Задание
6
#3939
Уровень задания: Сложнее ЕГЭ
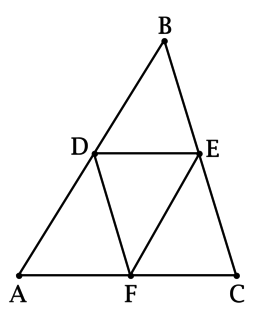
На сторонах (AB), (BC) и (AC) треугольника (ABC) лежат точки (D), (E) и (F) соответственно. Известно, что (dfrac{DF}{BC} = 0,5), (AC = 2cdot DE), (AB-EF=EF) (angle DEF = 61^{circ}), (angle EFD = 55^{circ}). Найдите (angle C). Ответ дайте в градусах.
Так как (angle DEF = 61^{circ}), (angle EFD = 55^{circ}), то (angle EDF = 180^{circ} — 61^{circ} — 55^{circ} = 64^{circ}).
Рассмотрим треугольники (ABC) и (EFD): по условию
[dfrac{DF}{BC} = 0,5 = dfrac{DE}{AC} = dfrac{EF}{AB},] тогда треугольники (ABC) и (EFD) подобны по пропорциональности трех сторон.
В подобных треугольниках против пропорциональных сторон лежат равные углы, тогда (angle C = angle EDF = 64^{circ}).
Ответ:
64
Задание
7
#3940
Уровень задания: Сложнее ЕГЭ
Отрезок (BK) соединяет вершину (B) треугольника (ABC) с точкой на противоположной стороне. При этом известно, что (AB = 12), (AC = 24), (AK = 6), (BK = 10), (BC = 20). Найдите (angle AKB — angle B). Ответ дайте в градусах.
Рассмотрим треугольники (ABK) и (ACB):
[dfrac{AB}{AC} = dfrac{AK}{AB} = dfrac{BK}{BC},] тогда треугольники (ABK) и (ACB) подобны по пропорциональности трех сторон.
В подобных треугольниках против пропорциональных сторон лежат равные углы, тогда (angle B = angle AKB), следовательно (angle AKB — angle B = 0^{circ}).
Ответ:
0
Как показывает статистика, планиметрические задачи вызывают наибольшие сложности у учащихся старших классов. Именно поэтому школьникам будет полезно освежить в памяти основные принципы решения задач с подобными треугольниками при подготовке к ЕГЭ. Причем еще раз повторить эту тему стоит всем ученикам, независимо от того, профильный или базовый уровень планирует сдавать выпускник.
Вместе с образовательным порталом «Школково» вы сможете качественно подготовиться к аттестационному испытанию. Чтобы решение задач ЕГЭ по теме «Подобные треугольники» давалось легко, рекомендуем вспомнить основную теорию. Найти ее вы можете в соответствующем разделе нашего сайта. Здесь представлены основные признаки подобных треугольников (для решения заданий ЕГЭ знать их необходимо), формула отношения их площадей и другая базовая информация. Ее специалисты образовательного портала «Школково» подготовили и изложили в максимально доступной форме.
Отточить навык решения задач ЕГЭ на нахождение сторон и углов подобных треугольников, а также, например, задачи по теореме Пифагора учащиеся также смогут на нашем сайте. В разделе «Каталог» представлен широкий перечень упражнений различной сложности, который постоянно обновляется.
В каждом задании прописано решение и дан правильный ответ. Выполнять задачи с применением признаков подобия площадей подобных треугольников можно в режиме онлайн.
Любое из представленных упражнений при необходимости можно сохранить в разделе «Избранное». Таким образом, к нему возможно будет вернуться в дальнейшем, к примеру, для обсуждения с преподавателем.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
ЕГЭ по математике | профиль — Задание 1 (Задачи на подобные треугольники)
Поддержать сайт:
Похожая статья:

ЕГЭ по информатике — Задание 16 (Чемпионская подготовка)
Мы подошли к 16 заданию из ЕГЭ по информатике. Оно связано с различным…
Категория: ЕГЭ Подкатегория: Информатика
Дата: 19-07-2020 в 10:23:27
2
Оставить коментарий:
Напишите email, чтобы получать сообщения о новых комментариях (необязательно):
Задача против робота. Расположите картинки горизонтально:
|
|
|
|
Подобные треугольники – подробнее
Мы разобрали подробно все, что касается треугольников в общем. Кроме того мы рассмотрели отдельные темы:
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
- Теорема косинусов
- Теорема синусов
- Медиана
- Биссектриса
- Высота
Но что такое подобные треугольники?
Вот, например, такой и такой:
Похожи эти треугольники? Ты скажешь, конечно же нет!
А такой и такой?
Похожи!
А вот такой и такой?
Посмотри внимательно, тоже похожи.
А теперь строго математически!
Треугольники называются подобными, если у них все углы равны и все стороны пропорциональны.
То есть все углы равны и все стороны одного треугольника в ( displaystyle 5), или, в ( displaystyle 7), или в ( displaystyle 8,21) (или и т.д.) больше сторон другого треугольника.
Записываются слова «треугольник ( displaystyle ABC) подобен треугольнику ( displaystyle {{A}_{1}}{{B}_{1}}{{C}_{1}})» с помощью такого значка:
( displaystyle {} Delta ABCsim{ }Delta {{A}_{1}}{{B}_{1}}{{C}_{1}} )
То число раз, в которое отличаются стороны подобных треугольников, называются коэффициентом подобия, обозначается обычно с помощью буквы ( displaystyle k).
То есть, если
( displaystyle Delta ABCsim{ }Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}) с коэффициентом подобия ( displaystyle k), то это означает что
(angle A = angle {A_1},angle B = angle {B_1},angle C = angle {C_1})
и ( displaystyle frac{{AB}}{{{A_1}{B_1}}} = k,frac{{AC}}{{{A_1}{C_1}}} = k,frac{{BC}}{{{B_1}{C_1}}} = k)
Можно было бы все так и оставить, но, как и в случае с равенством треугольников, ленивым математикам стало слишком неохота проверять равенство ВСЕХ трех углов, и пропорциональность ВСЕХ трех сторон.
И они придумали признаки подобия треугольников.
В первую очередь необходимо знать само определение подобных треугольников.
Определение: Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника, т.е. если выполняется:
- ∠А = ∠А1, ∠В = ∠В1, ∠С = ∠С1 (1)
=
=
(2)
K – это отношение сходственных сторон подобных треугольников, называется коэффициентом подобия.
Следует обратить внимание, что сходственные стороны смотрят на равные углы. Подобие треугольников можно установить, проверив только одно из неравенств (1) и (2). Далее будут рассмотрены признаки подобия треугольников и их свойства.
Отношение периметров подобных треугольников равно отношению соответствующих сторон и равно коэффициенту подобия.


Отношение площадей подобных треугольников равно квадрату коэффициента подобия.


Признаки подобия треугольников:
- Если ∠А = ∠А1, ∠В = ∠В1, то
АВС ∾
А1В1С1 (по двум равным углам)
- Если ∠А = ∠А1,
=
, то
АВС ∾
А1В1С1 (по двум пропорциональным сторонам и углу между ними)
- Если
=
=
, то
АВС ∾
А1В1С1 (по трем пропорциональным сторонам)
Далее следует обратить внимание на такие случаи:
- Если A1B1 ∥ A2B2 ∥ A3B3, то АА1 + А1А2 + А2А3 = AB1 + B1B2 + B2B3 (Параллельные отрезки, пересекающие стороны угла отсекают на сторонах угла пропорциональные отрезки. В частности, если АА1 = А1А2 = А2А3, то AB1 = B1B2 = B2B3 – теорема Фалеса. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Подобие прямоугольных треугольников
Остановимся на подобии прямоугольных треугольников.
- Для подобия двух прямоугольных треугольников достаточно, чтобы у них было по одному равному острому углу.








Высота прямоугольного треугольника, проведенная из прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу.
CD2 = AD * DB
CD – биссектриса ∠С. Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам.



Решение задач
- В прямоугольном треугольнике биссектриса острого угла делит катет на отрезки 10 см и 6 см. Найдите периметр треугольника.
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам. АВ — гипотенуза, ВС и АС — катеты, ВК — биссектриса. СК = 6 см, АК = 10 см. ВС : АВ = СК : АВ 6 : 10 = СК : ВС. Тогда ВС = 6х, а АВ = 10х, АС = 16 см. По теореме Пифагора АВ² = ВС² + АС²
100х² = 36х² + 256 64х² = 256
х² = 4 х = 2
Получилось, что АВ = 10х = 20 см, ВС = 6х = 12 см
Периметр Р = АВ + АС + ВС = 20 + 16 + 12 = 48 (см)
- Определить длину AD (x) геометрической фигуры на рисунке.
Треугольники ΔABC и ΔCDE являются подобными так как AB || DE и у них общий верхний угол C. Мы видим, что один треугольник является масштабированной версией другого. Однако нам нужно это доказать математически.
AB || DE, CD || AC и BC || EC
∠BAC = ∠EDC и ∠ABC = ∠DEC (по двум равным углам)
Исходя из вышеизложенного и учитывая наличие общего угла C, мы можем утверждать, что треугольники ΔABC и ΔCDE подобны.
Следовательно,
CA = 
AD = AC — DC = 23.57 — 15 = 8.57
- Диагонали AC и BD трапеции ABCD пересекаются в точке O. Площади треугольников AOD и BOC равны соответственно 16 см2 и 9 см2. Найдите площадь трапеции.
По условию площади треугольников AOD и ВОС не равны, поэтому AD и BC являются не боковыми сторонами, а основаниями трапеции. Тогда треугольники AOD и BOC подобны по двум углам, а отношение их площадей равно квадрату коэффициента подобия k. Поэтому k = 





Площади треугольников ABD и ACD равны, так как эти треугольники имеют общее основание AD и их высоты, проведённые к этому основанию, равны как высоты трапеции, следовательно,





Поэтому и 
- В трапеции ABCD точка пересечения диагоналей делит одну диагональ на отрезки 7 см и 9 см. Средняя линия трапеции равна 12 см. Вычислите длины оснований трапеции.
Решение. Сумма оснований трапеции равна удвоенной средней линии, то есть 24 см. Пусть ВС = х, тогда AD = 24 – x. 

Получаем:
BC = 10,5 и AD = 24 – 10,5 = 13,5
Ответ: BC = 10,5 см и AD = 13,5 см
- Основания трапеции ABCD равны 20 см и 45 см. Одна диагональ AC делит трапецию на два подобных треугольника. Вычислите длину этой диагонали.
Решение. Так как 
Ответ: 30 см.
- Основания трапеции ABCD равны 18 и 32 см. Вычислите длину отрезка, который делит трапецию на две подобные трапеции. Сравните его длину с длиной средней линии MN трапеции.
Решение. Если трапеции AMND и MBCN подобны, то их сходственные стороны пропорциональны. Составим пропорцию:
или
MN2 =
Средняя линия же равна (18 + 32)/2 = 25.
Ответ: 24 см, 24 < 25.
- Боковая сторона трапеции ABCD разделена в отношении 5 : 3, считая от большего основания. Через точку деления параллельно основанию проведена к противоположной боковой стороны прямая EF. Точка K – точка пересечения прямой EF и диагонали BD. Найдите длину этого отрезка, если основания трапеции равны 14 см и 30 см.
Решение: 



EF = EK + KF = 11,25 + 8,75 = 20.
Ответ: 20 см.
- В трапеции ABCD угол ABD равен углу BCD. Основание BC равно 30 см, сторона CD равна 45 см, диагональ BD = 60 см. Вычислите сторону АВ и основание AD.
Решение. Угол ADB равен углу CBD как накрест лежащие углы при параллельных прямых AD и BC и секущей BD. В то же время угол ABD равен углу BCD по условию. Тогда треугольник ABD подобен треугольнику DCB. Составим пропорцию:
Ответ: 90 см, 120 см.
- В трапеции ABCD основания равны 8 см и 6 см. Боковые стороны продолжены до взаимного пересечения в точке M. Вычислите расстояние от точки пересечения боковых сторон до большего основания (AD), если высота трапеции NK = 4 см.
Решение. 

Ответ: 16 см.
- В прямоугольном треугольнике АВС высота, проведенная к гипотенузе, делит ее на части, разность длин которых равна 6 см, а высота СH равна 4. Вычислите длину гипотенузы.
Решение. 

Тогда АВ = 2 + 8 = 10.
Ответ: 10 см.
- Прямая EF, параллельная меньшей стороне AB параллелограмма ABCD, отсекает от него параллелограмм, подобный данному. Стороны большего параллелограмма равны 6 см и 10 см. Вычислите стороны меньшего параллелограмма ABEF.
Решение. Если параллелограммы подобны, то их стороны пропорциональны. Составим пропорцию:
Ответ: 3,6 см и 6 см.
- В равнобедренном треугольнике ABC высота AE, опущенная на боковую сторону, делит ее на отрезки 7 см и 2 см, считая от вершины. Вычислите основания треугольника.
Решение. Проведем высоту треугольника BD. 

Примем AD = DC = x.
Ответ: 6 см.
- Биссектриса AD угла треугольника ABC делит противоположную сторону на отрезки 7 см и 5 см. Периметр треугольника равен 36 см. Вычислите стороны треугольника.
Решение. Известно, что биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.
Следовательно, АВ = 14 см, АС = 10 см.
Ответ: 14 см, 10 см, 12 см.
- В треугольнике АВС высота СН и медиана СМ делят угол С на три равные части. Докажите, что угол С – прямой.
Доказательство. 

Треугольник ACH – прямоугольный, а СМ – биссектриса угла ACH. По свойству биссектрисы угла следует:
То есть СН = 0,5 АС. В прямоугольном треугольнике АСН СН = 0,5 АС. Следовательно, угол А равен 30 градусов, угол АСН равен 60 градусов. Тогда угол С равен 90 градусов, что и требовалось доказать.
Представленный материал по решению задач на подобие помогает результативно решать задачи более высокого уровня сложности по ОГЭ в 9 классе. Задания 23 и 24 часто бывают на подобия.
Автор-составитель – учитель математики высшей категории Кудряшова С.В., 1498 школа г. Москвы.