Задачи по электростатике егэ по физике с решениями - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Какова разность потенциалов между точками поля, если при перемещении заряда 12 мкКл из одной точки в другую электростатическое поле совершает работу 0,36 мДж? (Ответ дать в вольтах.)

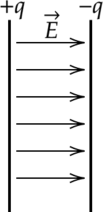
Модуль напряженности однородного электрического поля равен 100 В/м. Каков модуль разности потенциалов между двумя точками, расположенными на одной силовой линии поля на расстоянии 5 см? (Ответ дать в вольтах.)

В электрическую цепь включена медная проволока длиной При напряженности электрического поля 50В/м сила тока в проводнике равна 2 А. Какое приложено напряжение к концам проволоки? (Ответ дать в вольтах.)

Шар радиусом 10 см равномерно заряжен электрическим зарядом. В таблице представлены результаты измерений модуля напряжённости E электрического поля от расстояния r до поверхности этого шара. Чему равен модуль заряда шара? (Ответ дать в нКл.) Коэффициент k принять равным 9·10⁹ Н·м²/Кл².

r, см	10	20	30	40	50
E, В/м	900	400	225	144	100

Шар радиусом 20 см равномерно заряжен электрическим зарядом. В таблице представлены результаты измерений модуля напряжённости E электрического поля от расстояния r до поверхности этого шара. Чему равен модуль заряда шара? (Ответ дать в нКл.) Коэффициент k принять равным 9·10⁹ Н·м²/Кл².

r, см	20	40	60	80	100
E, В/м	225	100	56,25	36	25

Пройти тестирование по этим заданиям

Источник

Задачи по электростатике с решениями

Закон Кулона

6.1.1 В парафине на расстоянии 20 см помещены два точечных заряда. На каком
6.1.2 Два электрических заряда притягиваются друг к другу в керосине с силой 7,8 Н
6.1.3 Два шарика, расположенные на расстоянии 10 см друг от друга, имеют одинаковые
6.1.4 С какой силой ядро атома железа (Fe) притягивает электрон, находящийся
6.1.5 На двух одинаковых капельках воды находится по одному лишнему электрону
6.1.6 Два заряженных шара одинакового радиуса, массой 0,3 кг каждый, расположены
6.1.7 По теории Бора электрон в атоме водорода вращается вокруг ядра
6.1.8 В атоме водорода электрон движется вокруг протона с угловой скоростью
6.1.9 Два одинаковых шара, массы которых 600 г и радиусы – 20 см, имеют
6.1.10 Какое первоначальное ускорение получит капелька жидкости массой 1,6×10^(-5) г
6.1.11 Два точечных заряда 5 и 15 нКл находятся на расстоянии 4 см друг от друга
6.1.12 Два одинаковых металлических шарика с зарядами -15 и 25 мкКл, вследствие притяжения
6.1.13 Два одинаковых маленьких металлических шарика с зарядами 120 и 80 нКл
6.1.14 Во сколько раз изменится сила кулоновского притяжения двух маленьких шариков
6.1.15 Каждый из двух маленьких шариков положительно заряжен так, что их общий заряд
6.1.16 Два одинаковых шарика, заряженные одноименными зарядами и помещенные
6.1.17 Два маленьких одинаковых шарика находятся на расстоянии 0,2 м и притягиваются
6.1.18 Вокруг отрицательного точечного заряда -5 нКл равномерно вращается
6.1.19 Два заряда по 25 нКл каждый, расположенные на расстоянии 0,24 м друг от друга
6.1.20 На нити подвешен заряженный шар массой 300 г. Когда к нему поднесли снизу
6.1.21 На нити подвешен маленький шарик массой 10 г, которому сообщили заряд 1 мкКл
6.1.22 Три одинаковых точечных заряда по -1,7 нКл каждый находятся в вершинах
6.1.23 Две частицы массой 10 г и зарядом 2 мкКл находятся в вершинах равностороннего
6.1.24 В вертикальной трубке, заполненной воздухом, закреплен точечный заряд 5 мкКл
6.1.25 Два одинаковых шарика подвешены на нитях в воздухе так, что их поверхности
6.1.26 Два шарика массой по 1 г подвешены на нитях длиной 0,5 м в одной точке. После
6.1.27 Два маленьких проводящих шарика подвешены на длинных непроводящих нитях
6.1.28 Два одинаковых шарика, имеющих одинаковые заряды 1,6 мкКл, подвешены на одной
6.1.29 Точечные положительные заряды q и 2q закреплены на расстоянии L друг от друга
6.1.30 Точечные положительные заряды q и 2q закреплены на расстоянии L друг
6.1.31 Два маленьких одинаковых металлических шарика заряжены положительным зарядом 5q

Напряженность электростатического поля

6.2.1 Указать размерность единицы напряженности электростатического поля
6.2.2 Определить напряженность электрического поля, если на точечный заряд 1 мкКл
6.2.3 С какой силой действует однородное поле, напряженность которого 2 кВ/м
6.2.4 В некоторой точке поля на заряд 0,1 мкКл действует сила 4 мН. Найти напряженность
6.2.5 Найти заряд, создающий электрическое поле, если на расстоянии 5 см от него
6.2.6 Точечный заряд удалили от точки A на расстояние, в три раза превышающее
6.2.7 Напряженность электрического поля на расстоянии 30 см от точечного заряда 0,1 мкКл
6.2.8 Поле в глицерине образовано точечным зарядом 70 нКл. Какова напряженность поля
6.2.9 Определить напряженность электрического поля на поверхности иона, считая его
6.2.10 Очень маленький заряженный шарик погрузили в керосин. На каком расстоянии
6.2.11 Шарик, несущий заряд 50 нКл, коснулся внутренней поверхности незаряженной
6.2.12 Проводящему шару радиусом 24 см сообщается заряд 6,26 нКл. Определить
6.2.13 Напряженность электрического поля на расстоянии 10 см от поверхности заряженной
6.2.14 Поверхностная плотность заряда на проводящем шаре равна 0,32 мкКл/м2. Определить
6.2.15 Заряд металлического шара, радиус которого 0,5 м, равен 30 мкКл. На сколько
6.2.16 Шар радиусом 5 см зарядили до потенциала 180 В и потом поместили в керосин
6.2.17 Точечные заряды 10 и -20 нКл закреплены на расстоянии 1 м друг от друга в воздухе
6.2.18 Два точечных заряда 4 и 2 нКл находятся друг от друга на расстоянии 50 см. Определить
6.2.19 Два точечных заряда 4 и -2 нКл находятся друг от друга на расстоянии 60 см. Определить
6.2.20 Найти напряженность поля, создаваемого двумя точечными зарядами 2 и -4 нКл
6.2.21 Определить расстояние между двумя точечными зарядами 16 и -6 нКл, если
6.2.22 В однородном электрическом поле напряженностью 40 кВ/м, направленным
6.2.23 Заряды по 0,1 мкКл расположены на расстоянии 6 см друг от друга. Найти
6.2.24 Одинаковые по модулю, но разные по знаку заряды 40 нКл расположены
6.2.25 В серединах всех сторон равностороннего треугольника расположены одинаковые
6.2.26 В двух противоположных вершинах квадрата со стороной 30 см находятся заряды
6.2.27 В трёх вершинах квадрата со стороной 30 см находятся точечные заряды
6.2.28 В трёх вершинах квадрата со стороной 1 м находятся положительные точечные заряды
6.2.29 Четыре одинаковых заряда 40 мкКл расположены в вершинах квадрата со стороной
6.2.30 Шарик массой 1 г подвешен вблизи земли на невесомой и непроводящей нити
6.2.31 На какой угол отклонится бузиновый шарик с зарядом 4,9 нКл и массой 0,40 г
6.2.32 В однородном электрическом поле напряженностью 1 МВ/м, направленном вверх
6.2.33 Поле равномерно заряженной плоскости действует в вакууме на заряд 0,2 нКл
6.2.34 Бесконечная, равномерно заряженная пластина имеет поверхностную плотность
6.2.35 Две бесконечные параллельные пластины равномерно заряжены поверхностной
6.2.36 Две плоские пластинки площадью 200 см2, расстояние между которыми очень мало
6.2.37 Две бесконечные плоскости, заряженные с поверхностной плотностью 2 и 0,6 мкКл/м2
6.2.38 Напряженность электрического поля вблизи земли перед разрядом молнии
6.2.39 Между горизонтальными пластинами заряженного конденсатора, напряженность
6.2.40 Свинцовый шарик радиусом 0,5 см помещён в глицерин. Определить заряд шарика
6.2.41 Капля массой 10^(-10) г, на которой находится заряд, равный 10 зарядам электрона
6.2.42 Капля массой 10^(-13) кг поднимается вертикально вверх с ускорением 2,2 м/с2
6.2.43 Положительно заряженный шарик массой 18 г и плотностью 1800 кг/м3 находится
6.2.44 Для ионизации нейтральной молекулы воздуха электрон должен обладать
6.2.45 Два заряженных шарика с зарядами 300 и 200 нКл, массы которых 0,2 и 0,8 г
6.2.46 Протон движется с ускорением 76 км/с2 в электрическом поле. Определить
6.2.47 Электрон влетает в плоский конденсатор параллельно его пластинам со скоростью
6.2.48 Электрон влетает в однородное электрическое поле напряженностью 200 В/м
6.2.49 Электрон, попадая в однородное электрическое поле, движется вдоль силовых линий
6.2.50 Поток электронов, направленный параллельно обкладкам плоского конденсатора
6.2.51 Электрон, обладающий скоростью 18 км/с, влетает в однородное электрическое поле
6.2.52 Три равных по величине и знаку заряда q расположены в вакууме вдоль одной прямой
6.2.53 Указать направление вектора напряженности электрического поля, созданного в точке
6.2.54 Точечный положительный заряд создаёт на расстоянии 10 см электрическое поле
6.2.55 На каком расстоянии от поверхности шара напряженность электрического поля
6.2.56 Равномерно заряженный проводящий шар радиуса 5 см создаёт на расстоянии 10 см
6.2.57 Проводящий шар радиуса R заряжен зарядом q. Найти напряженность поля в точке
6.2.58 Точечный отрицательный заряд создаёт на расстоянии 10 см поле, напряженность

Потенциал. Разность потенциалов. Работа сил электрического поля

6.3.1 Указать размерность единицы потенциала электростатического поля
6.3.2 Определить электрический потенциал на поверхности сферы радиусом 5 см
6.3.3 При сообщении металлической сфере радиусом 10 см некоторого заряда
6.3.4 Определить напряженность электрического поля в точке, находящейся на расстоянии
6.3.5 На расстоянии 10 м от центра заряженного металлического шара радиусом 3 м
6.3.6 Определить потенциал шара радиусом 10 см, находящегося в вакууме
6.3.7 Металлический шар диаметром 30 см заряжен до потенциала 5400 В. Чему равен
6.3.8 На расстоянии 1 м от центра заряженного металлического шара радиусом 3 м
6.3.9 Найти потенциал электрического поля в точке, лежащей посредине между двумя
6.3.10 Сколько электронов следует передать металлическому шарику радиусом 7,2 см
6.3.11 Определить разность потенциалов (по модулю) между точками, отстоящими
6.3.12 Расстояние между точечными зарядами 10 и -1 нКл равно 1,1 м. Найти
6.3.13 В двух вершинах равностороннего треугольника со стороной 0,5 м находятся
6.3.14 Капля росы в виде шара получилась в результате слияния 216 одинаковых капелек
6.3.15 Электрический пробой воздуха наступает при напряженности поля 3 МВ/м
6.3.16 Два одинаковых точечных заряда по 5 мкКл взаимодействуют с силой 10 Н
6.3.17 Два металлических шара, радиусы которых 5 и 15 см, расположенные далеко друг
6.3.18 Энергия 10^(-17) Дж, выраженная в эВ, составляет
6.3.19 Модуль напряженности однородного электрического поля равен 150 В/м. Какую
6.3.20 На какое расстояние вдоль силовой линии перемещен заряд 1 нКл, если
6.3.21 При лечении статическим душем к электродам электрической машины приложена
6.3.22 Электрическое поле в глицерине образовано точечным зарядом 9 нКл. Какую работу
6.3.23 Два шарика с зарядами 0,8 и 0,5 мкКл находятся на расстоянии 0,4 м. До какого
6.3.24 Какая совершается работа при перенесении точечного заряда 20 нКл из бесконечности
6.3.25 Потенциал заряженного металлического шара 45 В. Какой минимальной скоростью
6.3.26 Две равномерно заряженные проводящие пластины образовали однородное поле
6.3.27 Напряженность поля внутри конденсатора равна E. Найти работу перемещения заряда
6.3.28 На сколько изменится потенциальная энергия взаимодействия зарядов 25 и -4 нКл
6.3.29 Два одинаковых маленьких шарика, имеющих одинаковые заряды 2 мкКл, соединены
6.3.30 На расстоянии 90 см от поверхности шара радиусом 10 см, несущего положительный
6.3.31 Электрон переместился из точки с потенциалом 200 В в точку с потенциалом 300 В
6.3.32 Электрон вылетает из точки, потенциал которой 600 В, со скоростью 12 Мм/с
6.3.33 Электрон с начальной скоростью 2000 км/с, двигаясь в поле плоского конденсатора
6.3.34 В поле неподвижного точечного заряда 1 мкКл по направлению к нему движется
6.3.35 Электрическое поле в вакууме образовано точечным зарядом 1,5 нКл. На каком
6.3.36 Электрическое поле в глицерине образовано точечным зарядом 20 нКл. На каком
6.3.37 Между двумя горизонтально расположенными пластинами, заряженными до 10 кВ
6.3.38 Заряженная частица, пройдя ускоряющую разность потенциалов 600 кВ, приобрела
6.3.39 Электрическое поле образовано двумя параллельными пластинами, находящимися
6.3.40 Пылинка массой 4×10^(-12) кг и зарядом 10^(-16) Кл попадает в поле заряженного
6.3.41 Пылинка массой 10 нг покоится в однородном электростатическом поле между
6.3.42 Электрон с некоторой скоростью влетает в плоский конденсатор параллельно
6.3.43 Какую разность потенциалов должен пройти первоначально покоящийся электрон
6.3.44 Какую скорость может сообщить электрону, находящемуся в состоянии покоя
6.3.45 Заряд 5 нКл находится на расстоянии 0,45 м от поверхности шара диаметром 0,1 м
6.3.46 Два электрона движутся под действием сил электростатического отталкивания
6.3.47 Между катодом и анодом двухэлектродной лампы приложена разность потенциалов
6.3.48 Энергия 100 эВ в системе СИ равна
6.3.49 Найти скорость, которую приобретает электрон, пролетевший в электрическом поле
6.3.50 В углах квадрата со стороной 4 см поместили 4 электрона. Под действием электрических
6.3.51 Электрон, ускоренный разностью потенциалов 5 кВ, влетает в середину зазора между
6.3.52 Маленький металлический шарик массой 1 г и зарядом 100 нКл брошен издалека
6.3.53 В электронно-лучевой трубке поток электронов с кинетической энергией 8 кэВ
6.3.54 В закрепленной металлической сфере радиусом 1 см, имеющей заряд -10 нКл
6.3.55 В зазор между пластинами плоского конденсатора влетает электрон, пройдя перед
6.3.56 Неподвижно закрепленный шарик, заряженный положительно, находится над шариком
6.3.57 Заряды q1=2 мкКл и q2=5 мкКл расположены на расстоянии AB=40 см друг от друга
6.3.58 Шарик массой 10 г с зарядом 100 мкКл подвешен на тонкой нити длиной 50 см
6.3.59 Внутри шарового металлического слоя, внутренний и внешний радиусы которого
6.3.60 По тонкому проволочному кольцу радиуса 3 см равномерно распределен заряд 10^(-9) Кл
6.3.61 Какую работу необходимо совершить, чтобы три одинаковых точечных положительных
6.3.62 В центре закрепленной полусферы радиуса R, заряженной равномерно с поверхностной
6.3.63 В центре закрепленной полусферы радиуса R, заряженной равномерно
6.3.64 На тонком закрепленном кольце радиуса R равномерно распределен заряд q. Какова

Электроемкость. Плоский конденсатор. Соединение конденсаторов. Энергия электростатического поля

6.4.1 Указать размерность единицы электроемкости
6.4.2 Проводник электроемкостью 10 пФ имеет заряд 600 нКл, а проводник электроемкостью
6.4.3 Два металлических шара радиусами 6 и 3 см соединены тонкой проволокой. Шары
6.4.4 Шар радиусом 0,3 м, заряженный до потенциала 1000 В, соединяют проводником
6.4.5 Проводники, заряженные одинаковым зарядом, имеют потенциалы 40 и 60 В
6.4.6 Тысяча одинаковых шарообразных капелек ртути заряжены до одинакового потенциала
6.4.7 Шар радиусом 15 см, заряженный до потенциала 300 В, соединяют проволокой
6.4.8 Шарообразная капля, имеющая потенциал 2,5 В, получена в результате слияния двух
6.4.9 Плоский воздушный конденсатор состоит из двух пластин площадью 100 см2 каждая
6.4.10 Определить площадь пластин плоского воздушного конденсатора электроемкостью 1 мкФ
6.4.11 Плоский конденсатор составлен из двух круглых пластин диаметром 0,54 м каждая
6.4.12 Плоский воздушный конденсатор погрузили в керосин. Во сколько раз изменилась
6.4.13 Плоский конденсатор состоит из двух пластин площадью 50 см2 каждая. Между
6.4.14 Во сколько раз изменится электроемкость плоского конденсатора при уменьшении
6.4.15 Плоский конденсатор, площадь пластин которого 25×25 см2 и расстоянием между ними
6.4.16 Плоский воздушный конденсатор погрузили в воду так, что над водой находится девятая
6.4.17 Между пластинами плоского конденсатора по всей площади проложили слюду (диэлектрик)
6.4.18 Плоский воздушный конденсатор зарядили до 50 В и отключили от источника тока
6.4.19 Плоский воздушный конденсатор, заряженный до напряжения 200 В, отключили
6.4.20 Воздушный конденсатор емкостью 4 мкФ подключен к источнику 10 В. Какой заряд
6.4.21 Какой заряд пройдет по проводам, соединяющим пластины плоского воздушного конденсатора
6.4.22 Во сколько раз увеличится электроемкость плоского конденсатора, пластины которого
6.4.23 Две пластины конденсатора площадью 2 дм2 находятся в керосине на расстоянии 4 мм
6.4.24 Напряжение на батарее из двух последовательно включенных конденсаторов
6.4.25 Батарея из двух последовательно соединенных конденсаторов электроемкостью
6.4.26 Два последовательно соединенных конденсатора с электроемкостью 1 и 3 мкФ подключены
6.4.27 Два плоских конденсатора электроемкостью по 2 мкФ каждый, соединенные последовательно
6.4.28 Два конденсатора электроемкостью 4 и 1 мкФ соединены последовательно и подключены
6.4.29 Два одинаковых плоских воздушных конденсатора соединены последовательно и подключены
6.4.30 Два одинаковых конденсатора соединены последовательно и подключены к источнику
6.4.31 Бумага пробивается при напряженности поля 18 кВ/см. Два плоских конденсатора с изолятором
6.4.32 Три конденсатора электроемкостью 0,1, 0,125 и 0,5 мкФ соединены последовательно
6.4.33 Три воздушных конденсатора емкостью 1 мкФ каждый соединены последовательно
6.4.34 Батарея из 5 последовательно соединенных конденсаторов емкостью 4 мкФ каждый
6.4.35 Определить электроемкость одного конденсатора, если для зарядки батареи, составленной
6.4.36 Конденсаторы электроемкостью 1 и 2 мкФ заряжены до разности потенциалов 20 и 50 В
6.4.37 Незаряженный конденсатор электроемкостью 5 мкФ соединяют параллельно с конденсатором
6.4.38 Плоский заряженный конденсатор соединили параллельно с незаряженным плоским
6.4.39 Шесть конденсаторов электроемкостью 5 нФ каждый соединили параллельно и зарядили
6.4.40 На батарею из трех параллельно соединенных конденсаторов электроемкостью
6.4.41 Конденсатор, заряженный до разности потенциалов 20 В, соединили параллельно разноименными
6.4.42 Найти общую электроемкость соединенных по схеме конденсаторов, если
6.4.43 Определить электроемкость батареи конденсаторов, изображенной на рисунке
6.4.44 Батарея из четырех одинаковых конденсаторов включена один раз по схеме A, другой раз по схеме B
6.4.45 Какое количество теплоты выделяется при замыкании пластин конденсатора электроемкостью
6.4.46 Какое количество теплоты выделяется при заземлении заряженного до потенциала 3000 В
6.4.47 Шар радиусом 25 см заряжен до потенциала 600 В. Какое количество тепла выделится
6.4.48 Плоский воздушный конденсатор после зарядки отключают от источника напряжения
6.4.49 Площадь пластины слюдяного конденсатора 36 см2, толщина слоя диэлектрика 0,14 см
6.4.50 На корпусе конденсатора написано 100 мкФ, 200 В. Какую максимальную энергию можно
6.4.51 При сообщении конденсатору заряда 5 мкКл его энергия оказалось равной 0,01 Дж
6.4.52 Два удаленных друг от друга одинаковых шара емкостью 4,7 мкФ каждый, заряжены
6.4.53 В импульсной фотовспышке лампа питается от конденсатора емкостью 800 мкФ, заряженного
6.4.54 Напряженность электрического поля конденсатора электроемкостью 0,8 мкФ равна 1 кВ/м
6.4.55 Определить работу, которую необходимо совершить, чтобы увеличить расстояние между пластинами
6.4.56 Парафиновая пластинка заполняет все пространство между обкладками плоского конденсатора
6.4.57 Определить количество электрической энергии, перешедшей в тепло при соединении одноименно
6.4.58 Три воздушных конденсатора электроемкостью 1 мкФ каждый соединены параллельно
6.4.59 Плоский конденсатор имеет в качестве изолирующего слоя пластинку из слюды толщиной
6.4.60 Два одинаковых плоских конденсатора электроемкостью 1 мкФ соединены параллельно
6.4.61 Конденсаторы соединены в батарею, причем C1=C2=2 мкФ, C3=C4=C5=6 мкФ
6.4.62 Принимая протон и электрон, из которых состоит атом водорода, за точечные заряды
6.4.63 Плоский воздушный конденсатор, площадь пластин которого равна S, заряжен
6.4.64 Два одинаковых плоских воздушных конденсатора соединены последовательно и подключены
6.4.65 Три одинаковых конденсатора соединены, как показано на рисунке. При разности
6.4.66 Три одинаковых конденсатора соединены, как показано на рисунке. При
6.4.67 Три одинаковых конденсатора соединены, как показано на рисунке. При разности потенциалов
6.4.68 Площадь каждой пластины плоского вакуумного конденсатора S. Конденсатор заряжен

( 42 оценки, среднее 4.55 из 5 )

Источник

Закон сохранения электрического заряда

В замкнутой системе тел алгебраическая сумма зарядов остается неизменной при любых процессах, происходящих с этими телами:

[q_1+q_2+…+q_n=const]

Закон Кулона в вакууме

Сила взаимодействия двух неподвижных точечный зарядов в вакууме прямо пропорциональна произведению абсолютных величин зарядов (q_1) и (q_2) и обратно пропорциональна квадрату расстояния (r) между ними.

[F=kdfrac{q_1q_2}{r^2}]

Где (k=9cdot 10^9) — коэффициент пропорциональности в законе Кулона.

[k=dfrac{1}{4pivarepsilon_0}]

(varepsilon_0=8,85cdot10^{-12} dfrac{text{Ф}}{text{м}}) — электрическая постоянная.

Закон Кулона в диэлектрике

[F=kdfrac{q_1q_2}{varepsilon r^2}]

Напряженность электрического поля — это отношение вектора силы (vec{F}), с которой поле действует на пробный заряд (q), к самому пробному заряду с учетом его знака.

[vec{E}=dfrac{vec{F}}{q}]

Единицы измерения: (displaystyle Big[dfrac{text{В}}{text{м}}Big]) (вольт на метр).

Линии напряженности всегда начинаются на положительных зарядах и заканчиваются на отрицательных.

Напряженность электростатического поля точечного заряда Q в точке A, удаленной на расстояние (r) от заряда (Q), определяется формулой:

[E=dfrac{kcdot |Q|}{r^2}]

Напряженность заряженной бесконечной пластины где (sigma):

[E=frac{sigma}{2varepsilon_0}]

Принцип суперпозиции полей

Пусть заряды (displaystyle q_1, q_2, q_3,… , q_n) по отдельности создают в данной точке поля (vec{E}_1), (vec{E}_2),…,(vec{E}_n). Тогда система этих зарядов создает в данной точке поле (vec{E}), равное векторной сумме напряженностей полей отдельных зарядов.

[vec{E}=vec{E}_1+vec{E}_2+…+vec{E}_n]

Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют (varphi) электрического поля:

[varphi=dfrac{W_p}{q}]

Единицы измерения: (displaystyle [text{В}]) (Вольт).

Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Работа поля по перемещению заряда:

[A_{text{эл}}=q(varphi_1-varphi_2)=qU]

Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется .

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда (q) одного из проводников к разности потенциалов (Delta varphi) между ними:

[C=dfrac{q}{Delta varphi}]

Единицы измерения: (displaystyle [text{Ф}]) (фарад).

Плоский конденсатор — система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика.

Электроемкость плоского конденсатора

[C=dfrac{varepsilon_0S}{d}]

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в (varepsilon) раз:

[C=dfrac{varepsilon_0varepsilon S}{d}]

Последовательное соединение конденсаторов

[U=U_1+U_2]

[q=q_1=q_2]

[dfrac{1}{C}=dfrac{1}{C_1}+dfrac{1}{C_2}]

Параллельное соединение конденсаторов

[U=U_1=U_2]

[q=q_1+q_2]

[C=C_1+C_2]

Энергия заряженного конденсатора

[W=dfrac{q^2}{2C}=dfrac{qU}{2}=dfrac{CU^2}{2}]

Источник

Электростатика и постоянный ток — подготовка к олимпиадам

Еще несколько задач на электростатику и постоянный ток. Здесь даже затронем тему ВАХ.

Задача 1.

Два шарика равной массы , имеющие одинаковые электрические заряды , соединены невесомым непроводящим стержнем длиной , и движутся из бесконечности в направлении закрепленной заряженной сферы по прямой, которая проходит через центр сферы и два небольших отверстия (размер больше диаметра шариков) в ее поверхности (см. рисунок). Сфера непроводящая, заряд распределен по ней равномерно, радиус сферы в 4 раза меньше длины стержня. Диэлектрическая проницаемость стержня равна единице. Сила натяжения стержня в момент, когда его центр совпал с центром сферы, оказалась вдвое больше силы натяжения на бесконечном удалении от сферы.

Чему равен заряд сферы?
Во сколько раз сила натяжения стержня в момент прохождения одним из шариков центра сферы будет превышать значение этой силы на бесконечности?

3. Какой должна быть начальная скорость шариков на бесконечности, чтобы они пролетели сквозь сферу?

К задаче 1

Решение. Первоначально, когда «диполь» на бесконечном удалении от сферы, кулонова сила взаимодействия между шариками равна

А сила взаимодействия между каждым из шариков и сферой в силу большого расстояния практически равна нулю. Также, пренебрегая длиной по сравнению с расстоянием между ближайшим к сфере шариком и сферой, будем считать силы взаимодействия между обоими шариками и сферой одинаковыми.

Тогда сила натяжения стержня будет компенсировать силу Кулона, действующую на шарик, и можно записать

Рассмотрим момент, когда центр сферы и центр диполя совпали.

Первый важный момент

Глядя на рисунок, запишем для обоих шариков уравнения по второму закону Ньютона. Для левого:

Здесь — сила взаимодействия между шариками, — сила взаимодействия шариков со сферой, ведь она тоже заряжена.

Для правого:

Приравнивая, получим:

«Распишем» обе силы:

Откуда .

Теперь изобразим ситуацию, когда один из шариков в центре:

Второй важный момент

И снова запишем уравнения по второму закону Ньютона, правый шарик:

И для левого:

Вычитание уравнений дает:

То есть

На третий вопрос задачи ответим с помощью закона сохранения энергии. Тут важно, чтобы левый шарик оказался внутри сферы.

Третий важный момент

Первоначально диполь имел энергию

А в момент времени, изображенный на рисунке,

Ответ: 1) ; 2) ; 3) .

Задача 2.

Зависимость тока от напряжения на элементе приведена на рис. а). Постройте график зависимости тока от напряжения для схемы, изображённой на рис. б). Схема состоит из резисторов и элементов .

К задаче 2

Решение. Воспользуемся методом вольт-амперных характеристик. По изображенной ВАХ делаем вывод, что имеем в виде элемента — неидеальный диод.

По методу ВАХ при последовательном соединении элементов складываются напряжения при одном и том же токе. При параллельном соединении элементов складываются токи при одном напряжении.

Вольт-амперная характеристика резистора:

ВАХ резистора

Получение ВАХ последовательного соединения резистора с неидеальным диодом:

Последовательное соединение резистора и диода (неидеального)

Получение ВАХ параллельного соединения резистора с неидеальным диодом:

Параллельное соединение резистора с неидеальным диодом

Теперь, так как параллельное соединение резистора с диодом соединено еще и последовательно со вторым диодом, получим ВАХ нижней ветви – снова при одном и том же токе складываем напряжения:

ВАХ нижней ветви

Ну и, наконец, соединяем параллельно верхнюю ветвь с нижней, они соединены параллельно – складываем токи при одном напряжении. Только диод включен обратно, поэтому получится вот что:

Соединяем параллельно верхнюю ветвь с нижней

Задача 3.

Четыре одинаковые пластины площадью расположены параллельно друг другу на одинаковых расстояниях . Вторая и четвертая пластина заряжены зарядами и ( ), первая и третья соединены с источником напряжения ( как показано на рисунке). Найти разность потенциалов между второй и четвертой пластинами . Расстояние много меньше размеров пластин.

К задаче 3

Решение. Предположим, что, будучи подключенными к источнику, пластина 1 зарядилась зарядом , а пластина 3 – зарядом .

Будем помещать пробный положительный заряд в пространство между пластинами, а также над и под ними, чтобы расставить направления векторов напряженностей, создаваемых каждой из пластин.

Рассматриваем область над пластинами. Пластина 1 заряжена отрицательно – вектор направлен к ней, вниз. Пластина 2 заряжена положительно – вектор направлен от нее, вверх. Пластина 3 заряжена положительно – вектор направлен от нее, вверх. Пластина 4 заряжена отрицательно – вектор направлен к ней, вниз.

Знаки мы уже учли, поэтому в уравнении будем писать уже только модули:

Переходим через пластину 1 и оказываемся в пространстве 1-2. Вектор развернется и будет направлен вверх, к пластине 1:

Переходим в пространство 2-3, вектор разворачивается:

И так далее:

Так как нам известно напряжение , используем его:

Перепишем напряженности:

Запишем теперь работы по перемещению заряда между этими пластинами:

Таким образом,

Откуда получим заряд :

Теперь перейдем к вопросу задачи и запишем работу по перемещению заряда между пластинами 2-4:

записано уже выше,

Тогда

Ответ: .

Источник

Эксперт ЕГЭ Н. Л. Точильникова
Задача 31 на ЕГЭ по физике – это расчетная задача из раздела «механические колебания», «электричество» (электростатика, конденсаторы или электрические цепи), «магнетизм», «электромагнитные колебания» или «оптика». Задача может быть и комбинированной: сразу на несколько тем.

Например, вот задача на электростатику и механические колебания:

1. ЕГЭ-2010, вар. 2926

По гладкой горизонтальной направляющей длины скользит бусинка с положительным зарядом Q>0 и массой . На концах направляющей находятся положительные заряды q>0 (см. рисунок). Бусинка совершает малые колебания относительно положения равновесия, период которых равен .

Чему будет равен период колебаний бусинки, если ее заряд увеличить в 2 раза?

Решение:

При небольшом смещении бусинки от положения равновесия

на нее действует возвращающая сила:

$F_x=kgenfrac{}{}{}{0}{qQ}{(l+x)^2}-kgenfrac{}{}{}{0}{qQ}{(l-x)^2}=kqQgenfrac{}{}{}{0}{(l-x)^2-(l+x)^2}{(l+x)^2(l-x)^2}=$

$=-kqQgenfrac{}{}{}{0}{4lx}{(l+x)^2(l-x)^2}approx -kgenfrac{}{}{}{0}{4qQ}{l^3}x,$

пропорциональная смещению . Ускорение бусинки, в соответствии со вторым законом Ньютона, $ma=-kgenfrac{}{}{}{0}{4qQ}{l^3}x,$ , пропорционально смещению.

Отсюда $a=-kgenfrac{}{}{}{0}{4qQ}{ml^3}x$ . С другой стороны при гармонических колебаниях .

Откуда:

$omega^2=kgenfrac{}{}{}{0}{4qQ}{ml^3}$ , а $omega=sqrt {kgenfrac{}{}{}{0}{4qQ}{ml^3}}.$

Так как $T = kgenfrac{}{}{}{0}{2pi}{omega}$ , получаем:

$T = kgenfrac{}{}{}{0}{2pi}{sqrt {kgenfrac{}{}{}{0}{4qQ}{ml^3}}}$

То есть при такой зависимости ускорения от смещения бусинка совершает гармонические колебания, период которых $T=pi sqrt {genfrac{}{}{}{0}{m}{kqQ}l^3}$ .

При увеличении заряда бусинки Q_1=2Q период колебаний уменьшится:

$genfrac{}{}{}{0}{T_1}{T}=sqrt{genfrac{}{}{}{0}{Q}{Q_1}}=genfrac{}{}{}{0}{1}{sqrt{2}}.$

Ответ: $T_1=genfrac{}{}{}{0}{T}{sqrt{2}}$

2. ЕГЭ – 2010, вариант 2926

Горизонтальный проводящий стержень прямоугольного сечения поступательно движется с ускорением вверх по гладкой наклонной плоскости в вертикальном однородном магнитном поле (см. рисунок).

По стержню протекает ток . Угол наклона плоскости $alpha = 30^{circ}$ . Отношение массы стержня к его длине $genfrac{}{}{}{0}{m}{L} = 0,1$ кг/м.

Модуль индукции магнитного поля B=0,2 Тл. Ускорение стержня a=1,9 м/с2 . Чему равна сила тока в стержне?

Решение:

1) На рисунке показаны силы, действующие на стержень с током:

– сила тяжести , направленная вертикально вниз;
– сила реакции опоры , направленная перпендикулярно к наклонной плоскости;
– сила Ампера F_A , направленная горизонтально вправо, что вытекает из условия задачи.

2) Модуль силы Ампера F_A=IBL , (1)
где – длина стержня.

3) Систему отсчета, связанную с наклонной плоскостью, считаем инерциальной.

Для решения задачи достаточно записать второй закон Ньютона в проекциях на ось (см. рисунок): , (2)
где – масса стержня.

Отсюда находим $I=genfrac{}{}{}{0}{m}{L}cdot genfrac{}{}{}{0}{(a_x+g sin alpha)}{B cos alpha}.$ (3)

$I=genfrac{}{}{}{0}{0,1 cdot (1,9 + 10 cdot genfrac{}{}{}{0}{1}{2})}{0,2 cdot genfrac{}{}{}{0}{sqrt{3}}{2}}approx 4 A.$

Ответ: А.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задача 31 на ЕГЭ по физике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Электростатика. Пособие по подготовке к ЕГЭ

«Электростатика»- ещё одно пособие из серии, написанной в качестве минимального по объёму материала, необходимого для решения заданий ЕГЭ.

Задачи по электростатике традиционно относятся к числу самых сложных задач ЕГЭ.

Во-первых, электростатика оперирует с понятиями «электрическое поле», «напряженность», «потенциал», которые очень плохо усвоены на уроках в школе.

Во-вторых, многие задачи из этого раздела требуют умения уверенно выполнять действия с векторами, что уже само по себе создаёт массу трудностей для школьника.

Стоит ещё упомянуть, что сегодняшняя школьная программа выделяет всего два-три месяца при двух-трех часах в неделю на эту часть физики.

Итогом всего этого и является низкий процент решения задач по электростатике на ЕГЭ.

Надеюсь, этот материал поможет вам за сравнительно небольшое время улучшить ваши знания темы «Электростатика» из школьной физики.

Скачать можно здесь Электростатика.pdf.

Успехов вам в освоении физики!

Интересная статья? Поделитесь ею с друзьями:

Источник