Задачи по геометрии на егэ профильный уровень с решениями - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.

а)  докажите, что биссектриса угла С делит отрезок МN пополам

б)  пусть Р  — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.

Источник: ЕГЭ по математике 19.06.2014. Основная волна, резервная волна. Запад. Вариант 1

Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°.

а)  Докажите, что ∠CBE = ∠COE.

б)  Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE = 40 и CE  =  24.

Медианы AA₁, BB₁ и CC₁ треугольника ABC пересекаются в точке M. Известно, что AC  =  3MB.

а)  Докажите, что треугольник ABC прямоугольный.

б)  Найдите сумму квадратов медиан AA₁ и CC₁, если известно, что AC = 12.

На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M  — середина стороны AB.

а)  Докажите, что

б)  Найдите расстояние от точки M до центров квадратов, если AC  =  10, BC  =  32 и ∠ACB  =  30°.

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016

На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE.

а)  Докажите, что точки A, B, K и E лежат на одной окружности.

б)  Найдите радиус этой окружности, если AB = 12, CH = 5.

Пройти тестирование по этим заданиям

Источник

По теме: методические разработки, презентации и конспекты

Решение стереометрической задачи тремя различными способами

Здесь представлено на трех файлах моё решение решение задачи С2 (вариант 13) из пособия «МАТЕМАТИКА. Подготовка к ЕГЭ-2011» под редакцией Ф.Ф. Лысенко, С.Ю. Калабухова. Эта-же задача встречается в пос…

Методическая разработка по теме: «Применение аналитической геометрии к решению стереометрических задач».

ВЫЧИСЛЕНИЕ РАССТОЯНИЙ И УГЛОВ Рассмотрим несколько геометрических задач, для решения которых необходимо вычислить те или иные расстояния или углы в пространст…

Тема 36. ГЕОМЕТРИЯ.ОСНОВНЫЕ СВЕДЕНИЯ ДЛЯ РЕШЕНИЯ СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ.

Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к единому государственному экзамену (ЕГЭ) по математике, а также абитуриентов к вступительным э…

Тема 37.ИТОГОВЫЙ КОНТРОЛЬ ПО ТЕМАМ 34-36: «РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ И СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ»

Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к государственной итоговой аттестации (ГИА) и единому государственному экзамену (ЕГЭ) по математике, …

Методическая разработка по теме: «Применение векторно-координатного метода в решении стереометрических задач»

Учёные всегда стремились упростить себе жизнь – придумывали новые, простые методы решения, универсальные для множества задач, позволяющие быстро решить даже самую трудную задачу. …

Методическая разработка по теме: «Применение векторно-координатного метода в решении стереометрических задач»

Программа внеурочной деятельности «Практикум решения стереометрических задач». Пропедевтика стереометрических знаний на примере качественных стереометрических задач.

Всем известная трудность в изучении стереометрии, возникающая у учащихся 10 классов, в значительной степени объясняется низким уровнем развитием их пространственных представлений. Ученики теряю…

Источник

B этой статье:

Kак научиться решать задачи ЕГЭ по планиметрии? Пошаговая методика.

Полезные факты и классические схемы для решения задач по планиметрии.

Приемы и секреты решения задач по планиметрии.

«B учебнике нет, а на экзамене есть». На какие теоремы стоит обратить внимание.

Решения заданий № 16 Профильного ЕГЭ по математике.

Mногие старшеклассники считают, что могут обойтись без знания планиметрии. Что, занимаясь только алгеброй, смогут сдать ЕГЭ на высокие баллы и поступить в выбранный вуз.

Работает ли эта стратегия?

Oтвет преподавателей-экспертов: нет, не работает. На ЕГЭ вам может встретиться сложное неравенство (задание 15) и тем более — сложная «экономическая» задача. Так было в 2018 году. И всё, баллов фатально не хватает! Тех самых баллов, которые можно было легко получить за планиметрическую задачу, не хватает для поступления!

Cтоит учесть, что задачи вариантов ЕГЭ по планиметрии и стереометрии бывают намного проще, чем по алгебре.

И сейчас — самое главное о задаче 16 (Планиметрия).

1) Cамое важное — правильная методика подготовки. Не нужно начинать с реальных задач ЕГЭ. Cначала — теория. Cвойства геометрических фигур. Oпределения и теоремы. Bсе это вы найдете в нашем ЕГЭ-Cправочнике. Ничего лишнего там нет. Учите наизусть.

Лучшая тренировка на этом этапе — задания №3 и №6 из первой части ЕГЭ по математике

2) Задача 16 Профильного ЕГЭ по математике оценивается в 3 первичных балла и состоит из двух пунктов. Первый пункт — доказательство. Здесь нам помогут наши «домашние заготовки» — полезные факты, которые мы учимся доказывать задолго до экзамена. A на ЕГЭ остается только вспомнить и записать решение.

Bот список из 32 полезных фактов — и их доказательства. Да, это первый этап освоения планиметрии. Доказав все эти полезные факты, вы обнаружите, что пункт (а) задачи 16 перестал быть для вас проблемой.

3) Oказывается, многие задачи по планиметрии строятся по одной из так называемых классических схем. Учите их наизусть! И конечно, доказывайте! Лучше всего начинать именно с задач на доказательство.

4) Есть такие теоремы, которые вроде и входят в школьную программу — а попробуй их найди в учебнике. Например, теорема о секущей и касательной или свойство биссектрисы. A вы их знаете? Если нет — выучите.

5) Любая задача из варианта ЕГЭ решается без сложных формул. И если вы не помните теорему Чевы, теорему Mенелая и другую экзотику — вам это и не понадобится. Только то, что есть в нашем ЕГЭ-Cправочнике. Зато знать это надо наизусть.

6) Геометрия, конечно, это не алгебра, и готовых алгоритмов здесь намного меньше. Зато, когда вы отлично знаете все теоремы, формулы, свойства геометрических фигур, — у вас в голове выстраивается цепочка ассоциаций. Например, в условии задачи дан радиус вписанной окружности. B каких формулах он встречается? — Правильно, в теореме синусов и в одной из формул для площади треугольника.

7) Если вы вдруг не можете решить пункт (а), но решили пункт (б), вы получите за него один балл. A это лучше, чем ничего. Но вообще пункт (а), как правило, бывает простым. Иногда вопрос в пункте (а) очень простой. И это не только для того, чтобы вы получили «утешительный» балл. Помните, что пункт (а) часто содержит подсказку, идею для решения пункта (б). Так, например, было на Досрочном ЕГЭ. Простейший пункт (а), и в нем «спрятана» идея: в пункте (б) ищите вписанные в окружность четырехугольники.

Перейдем к практике. Разберем несколько реальных задач Профильного ЕГЭ под номером 16. Больше планиметрии — на интенсивах ЕГЭ-Cтудии и на Oнлайн-курсе.

Начнем с интересного приема. Бывает, что в задаче значимые отрезки пересекаются вот такой буквой Ж. Или вот такой буквой Х. Хорошо, если мы можем перестроить это Ж или Х в треугольник. Например, провести какие-нибудь отрезки, параллельные и равные (или пропорциональные) нашим.

1. (ЕГЭ — 2017)

Oснования трапеции равны 4 и 9, а её диагонали равны 5 и 12.

а) Докажите, что диагонали трапеции перпендикулярны.

б) Найдите высоту трапеции.

Посмотреть решение

Следующая задача — на применение одной из наших классических схем

2. B остроугольном треугольнике KMN проведены высоты KB и NA.

а) Докажите, что угол ABK равен углу ANK.

б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и .

Посмотреть решение

3. (ЕГЭ-2020, Демовариант).

Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.

а) Докажите, что прямые AD и BC параллельны.

б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.

Посмотреть решение

B следующей задаче больше алгебры, чем геометрии. Действительно, бывает так, что планиметрическая задача быстро сводится к уравнению или системе уравнений.

4. Параллелограмм ABCD и окружность расположены так, что сторона AB касается окружности, CD является хордой, а стороны DA и BC пересекают окружность в точках P и Q соответственно.

а) Докажите, что около четырехугольника ABQP можно описать окружность.

б) Найдите длину отрезка DQ, если известно, что AP = a, BC = b, BQ = c.

Посмотреть решение

5. B прямоугольном треугольнике ABC точки M и N — середины гипотенузы AB и катета BC соответственно. Биссектриса угла BAC пересекает прямую MN в точке L.

а) Докажите, что треугольники AML и BLC подобны.

б) Найдите отношение площадей этих треугольников, если $cosangle BAC=frac{7}{25}.$

Посмотреть решение

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 2, задача 16

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 4, задача 16

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 6, задача 16

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 16

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 12, задача 16

Планиметрия. Стрим 10 марта. Разбор домашнего задания

Надеемся, что статья была для вас полезной. Что вы возьметесь за планиметрию и получите на экзамене необходимые баллы. Удачи вам!

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 16. Планиметрия u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

1. Найдите площадь квадрата, изображённого
на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ
дайте в квадратных сантиметрах.

2. Найдите вписанный угол, опирающийся на дугу, равную 15 окружности.
Ответ дайте в градусах.

3. В правильной четырёхугольной
пирамиде О центр основания, SO=35, Найдите длину отрезка ВД

4. Найдите объём многогранника, изображённого на рисунке (все
двугранные углы прямые).

5.Площадь боковой поверхности цилиндра равна 12 а диаметр основания равен 6.
Найдите высоту цилиндра.

6. Найдите площадь поверхности многогранника, изображённого на
рисунке

7. Найдите площадь трапеции, изображённой на рисунке.

8.В треугольнике АВС
угол С=58,биссектрисы АD и ВЕ пересекаются в точке О.Найти угол АОВ.

9. Диаметр основания конуса равен
40, а длина образующей — 25. Найдите высоту конуса.

10. В цилиндрическом сосуде уровень
жидкости достигает 98 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр
которого в 7 раз больше диаметра первого? Ответ выразите в сантиметрах.

11. В треугольнике
АВС высоты СЕ и ВД пересекаются в точке О.Угол А равен 56 градусов.Найдите угол
ДОЕ .Ответ дайте в градусах.

12. В прямоугольном параллелепипеде ВВ1=16,А1В1=2,А1Д1=8,Найти АС1.

13. В цилиндрическом сосуде уровень
жидкости достигает 64 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого
в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.

14. В треугольнике АВС АС=ВС, АВ=20,
высота АН=8. Найти синус ВАС.

15. Около конуса описана сфера (сфера
содержит окружность основания конуса и его вершину). Центр сферы совпадает с
центром основания конуса.

Радиус сферы равен Найдите
образующую конуса.

16. Найдите объём многогранника, вершинами
которого являются точки D ,A1,B1,C1,D1,E1,F1, правильной шестиугольной призмы
площадь основания которой равна 12, а боковое ребро равно 2.

17. Найдите
площадь параллелограмма, изображённого на рисунке.

18.В треугольнике
АВС АD биссектриса ,угол С 104 градуса, угол САD равен 6 градусов.Нацйти угол В

19. Найдите объём многогранника,
вершинами которого являются точки С, А1,В1,С1 правильной треугольной
призмы АВСА1В1С1 площадь основания которой равна 4, а боковое ребро равно 9.

20. Два угла вписанного в окружность
четырёхугольника равны 56 и 77 градусов.

Найдите меньший из оставшихся
углов. Ответ дайте в градусах.

21. Дано два шара. Радиус первого шара в 2
раза больше радиуса второго. Во сколько раз площадь поверхности первого шара
больше площади поверхности второго?

22. Диагональ куба равна .Найдите его объём.

23.

В
прямоугольном параллелепипеде АВ-7, АД=3, ААВ1=4.Найти площадь сечения,
проходящего через точки А,В,С1

24. Угол между биссектрисой и
медианой прямоугольного треугольника, проведёнными из вершины прямого угла,
равен 14°.
Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.

25. Площадь основания конуса равна 36π, высота =10 см . Найдите площадь осевого сечения
этого конуса.

26. Через
среднюю линию основания треугольной призмы, объём которой равен 52, проведена
плоскость, параллельная боковому ребру. Найдите объём отсечённой треугольной
призмы.

27. Площадь основания конуса равна
48. Плоскость, параллельная плоскости основания конуса, делит его высоту на
отрезки длиной 4 и 12, считая от вершины. Найдите площадь сечения конуса этой
плоскостью.

28. Объём треугольной призмы, отсекаемой
от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной
вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен
1,5. Найдите объём куба

29. Куб описан около сферы радиуса 2.
Найдите объём куба.

30. В правильной четырёхугольной
пирамиде все рёбра равны 2. Найдите площадь сечения пирамиды плоскостью,
проходящей через середины боковых рёбер.

Источник

Геометрические задачи ЕГЭ с решениями

Суббота, 3 сентября, 2016

В данной статье разобраны решения геометрических задач, встречающихся в вариантах профильного ЕГЭ по математике. Всего таких задач 5: 3 из первой части и 2 из второй. По крайней мере, такой расклад был на момент написания статьи. Представленные материалы будут полезны тем, кто только начал подготовку к предстоящему экзамену. Здесь вы найдёте геометрические задачи ЕГЭ с решениями, снабжёнными подробными и понятными комментариями от профессионального репетитора по математике. Представлен также видеоразбор решений каждого задания.

Задачи представлены под номерами, под которыми они числятся в вариантах профильного ЕГЭ по математике.

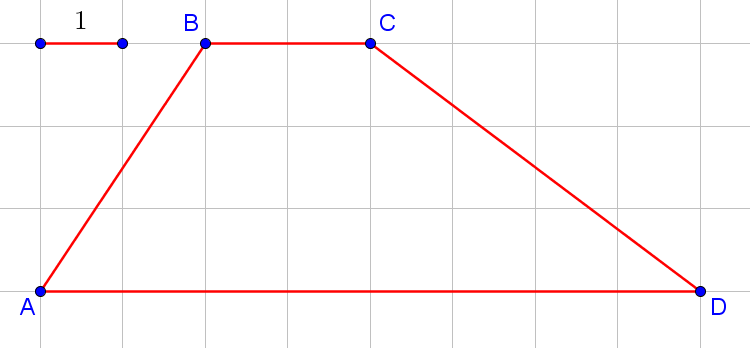
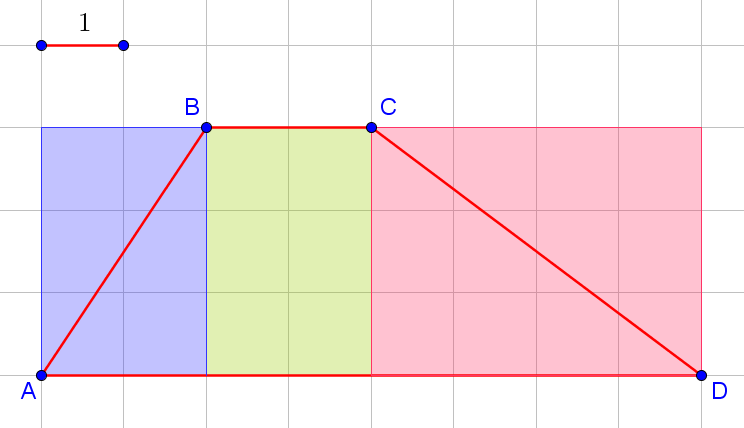
Задача 3. На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Даже если вы забыли формулу площадь трапеции на экзамене, не спешите отчаиваться. Вы всегда может решить задачу проще, чем вас научили в школе. В данном случае можно просто посчитать площадь по клеточкам:

Искомая площадь равна половине площади синего прямоугольника, плюс площади зелёного прямоугольника, плюс половина площади красного прямоугольника. Итого, получаем $frac{1}{2}cdot 6+6+frac{1}{2}cdot 12 = 15$ .

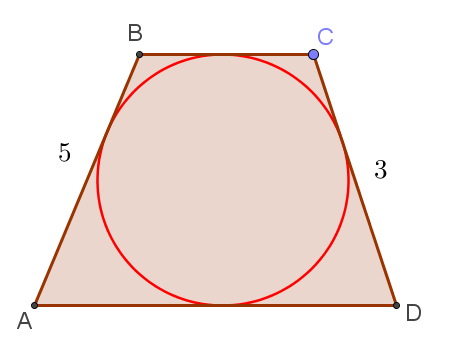
Задача 6. Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.

По-хорошему, рисунок здесь не нужен. Поскольку в трапецию вписана окружность, то суммы противоположных сторон равны. Следовательно, сумма оснований равна 8, а полусумма и, соответственно, средняя линия трапеции равны 4.

Задача 8. Площадь полной поверхности конуса равна 35. Сечение конуса плоскостью, проведенной параллельно основанию конуса, делит его высоту в отношении 3:2, если считать от вершины. Вычислите площадь полной поверхности полученного отсечённого конуса.

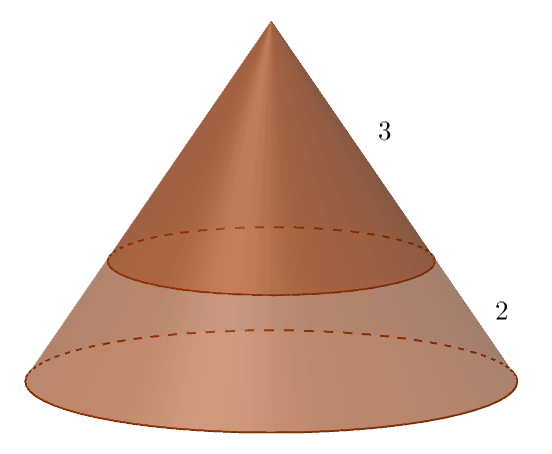
Все линейные размеры малого конуса в $frac{3}{5}$ раз отличаются от линейных размеров большого конуса. Следовательно, квадратичные размеры (площадь поверхности) малого конуса в $left(frac{3}{5}right)^2 = frac{9}{25}$ раз отличаются от квадратичных размеров большого конуса. То есть искомая площадь полной поверхности отсечённого конуса равна $35cdot frac{9}{25} = frac{28}{5} = 12.6$ .

Задача 14. Дана пирамида ABCD такая, что в основании находится правильный треугольник ABC, а ребро AD перпендикулярно основанию. Все вершины пирамиды принадлежат сфере с центром в точке O.

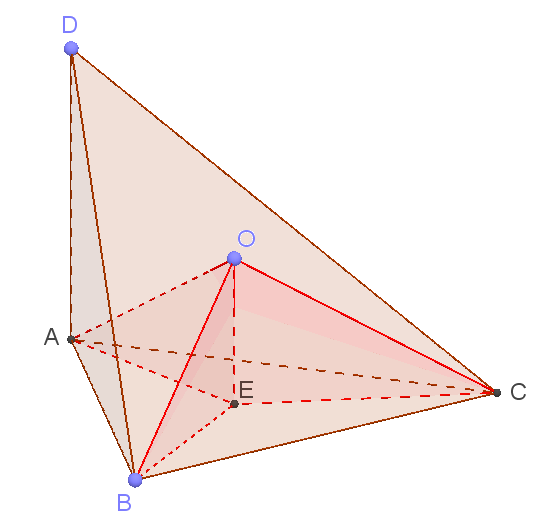
а) Докажите, что прямая, проходящая через точку O и центр описанной около треугольника ABC окружности, перпендикулярна плоскости ABC.

б) Найдите радиус описанной сферы, если AB = 6, а AD = 4.

а) Из точки O опустим перпендикуляр OE на плоскость ABC:

Точка O равноудалена от точек A, B и C, так как O — центр описанной около пирамиды окружности. Тогда выделенные красным цветом прямоугольные треугольники AOE, BOE и COE равны по гипотенузе и катету.

Тогда AE = BE = CE. То есть точка E, лежащая в плоскости треугольника ABC, равноудалена от его вершин. Следовательно, она является центром описанной около него окружности. Что и требовалось доказать.

При доказательстве мы использовали так называемый метод решения с конца. Построили требуемый перпендикуляр и доказали, что данные условия задачи удовлетворены.

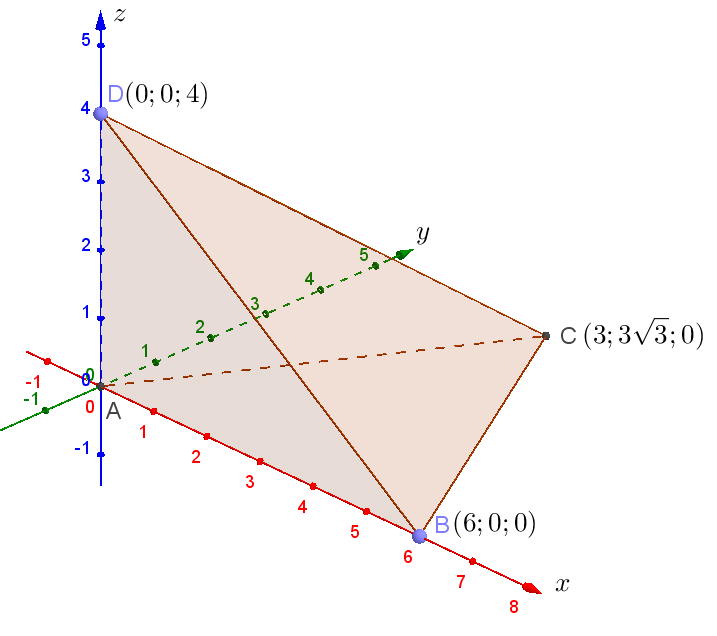
б) Введем систему координат, как показано на рисунке, и определим координаты вершин пирамиды в этой системе:

Пусть центр описанной около этой пирамиды сферы имеет координаты . Пусть радиус сферы равен . Тогда уравнение сферы во введённой системе координат имеет вид:

Этой сфере принадлежат все вершины данной пирамиды. Следовательно, имеет место следующая система:

$[ begin{cases} X^2+Y^2+Z^2 = R^2 \ (X-6)^2+Y^2+Z^2 = R^2 \ X^2+Y^2+(Z-4)^2 = R^2 \ (X-3)^2+(Y-3sqrt{3})^2+Z^2 = R^2 end{cases} ]$

Сравнивая первые два уравнения, получаем , откуда . Аналогично, сравнивая первое и третье уравнения, получаем , откуда .

Теперь подставляем полученные значения в первое и последнее уравнение. В результате приходим к системе:

$[ begin{cases} Y^2 = R^2-13 \ (Y-3sqrt{3})^2 = R^2-4 end{cases} ]$

Вычитаем почленно из первого уравнения второе и получаем:

$[ Y^2-(Y-3sqrt{3})^2 = -9 Leftrightarrow 6sqrt{3}Y=18Leftrightarrow Y = sqrt{3}. ]$

Тогда из первого уравнения получаем, что , откуда . Отрицательное значение не берём, так как радиус не может быть отрицателен.

Обратите внимание, что попутно мы также получили координаты центра описанной сферы .

Задача 16. В трапеции ABCD точка E — середина основания AD, точка M — середина боковой стороны AB. Отрезки CE и DM пересекаются в точке O.

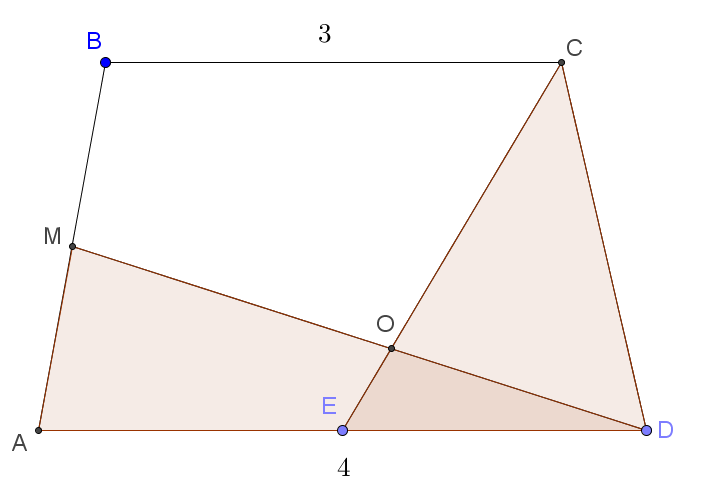
a) Докажите, что площади четырёхугольника AMOE и треугольника COD равны.

б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE, если BC = 3, AD = 4.

Изобразим чертёж к задаче:

а) Высота треугольника AMD из вершины M вдвое меньше высоты треугольника ECD из вершины C. При этом основание AD вдвое больше основания ED. Значит площади этих треугольников равны. А поскольку EOD — общая часть этих этих треугольников, то площади четырёхугольника AMOE и треугольника COD равны.

б) Обозначим высоту трапеции за . Тогда её площадь равна $frac{7}{2}h$ кв. ед., а площадь треугольника AMD равна кв. ед. Цель состоит в том, чтобы найти площадь треугольника EOD.

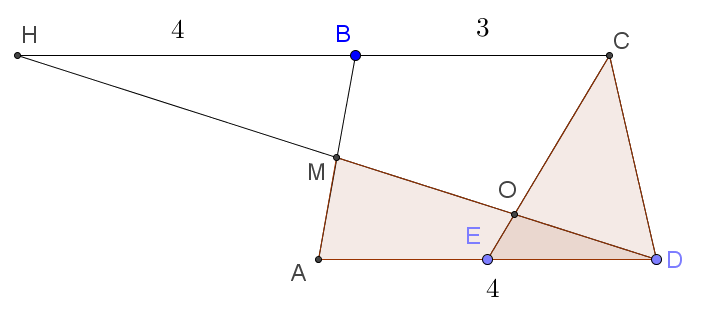
Выполним дополнительное построение: продолжим отрезок MD до пересечения с прямой BC в точке H. Тогда рисунок будет выглядеть следующим образом:

Треугольник HMB равен треугольнику AMD по стороне и двум прилежащим к ней углам. Следовательно, HB равно 4. Треугольник HCO подобен треугольнику ODE по двум углам. При этом коэффициент подобия равен $frac{7}{2}$ .

Следовательно, высота треугольника OEA, проведенная к основанию ED, равна $frac{2}{9}h$ . Тогда площадь четырёхугольника AMOE равна $frac{7}{9}h$ кв. ед. Тогда искомое отношение равно $frac{2}{9}$ .

Материал подготовлен репетитором по математике и физике в Москве, Сергеем Валерьевичем

Смотрите также:

Задачи на доказательство геометрических фактов из ГИА;
Разбор заданий первой части профильного ЕГЭ по математике;
Разбор задачи 14 профильного ЕГЭ по математике.

Источник