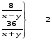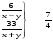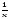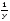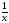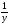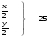Задачи по математике на составление уравнения на егэ 2022 - Помощь в подготовке к экзаменам и поступлению

Каталог заданий.
Линейные, квадратные, кубические уравнения

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 5 № 26662

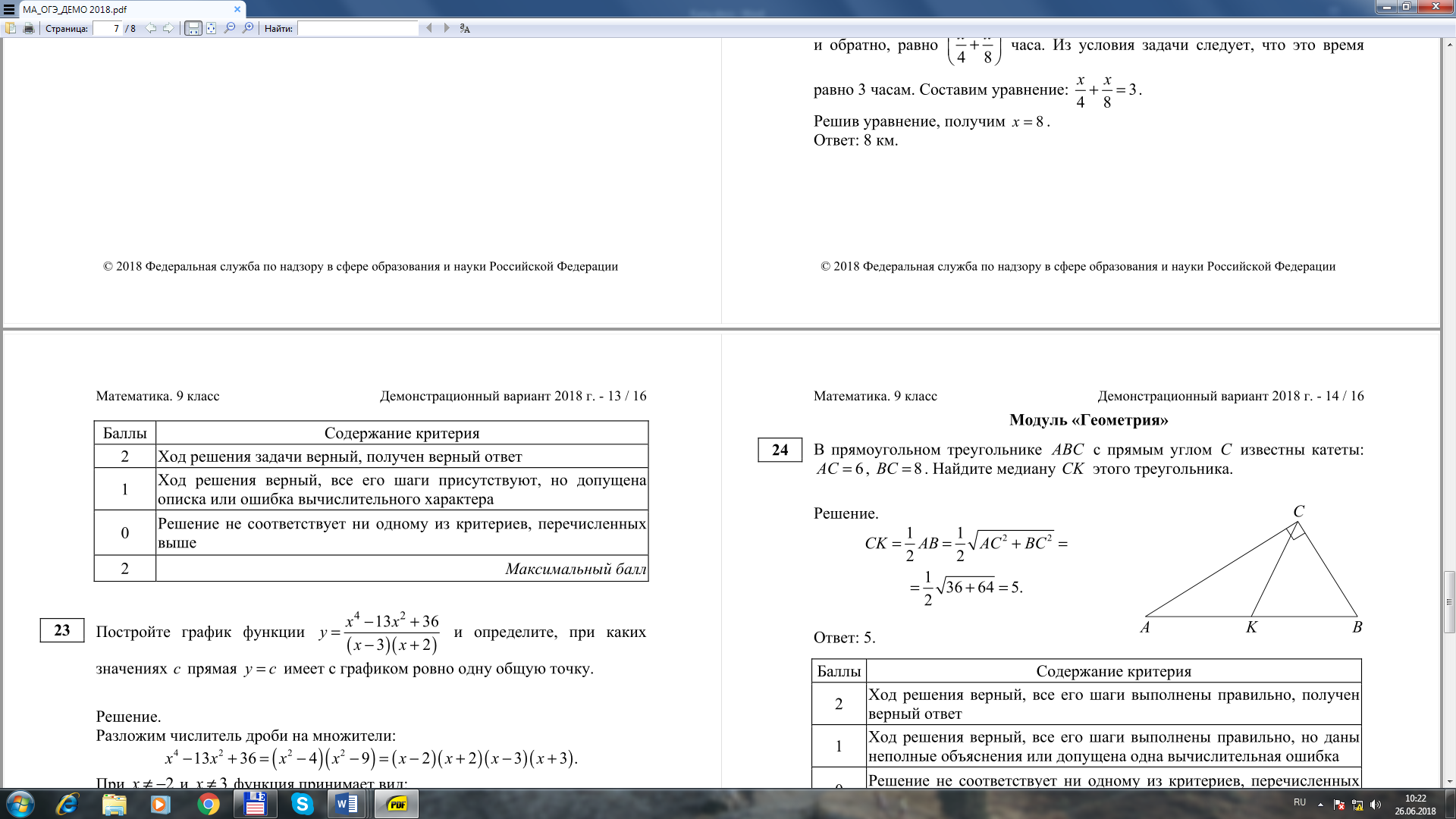
Найдите корень уравнения:

Аналоги к заданию № 26662: 10149 9653 9659 9667 9669 9673 9677 9679 9691 9693 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.2 Рациональные уравнения

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 5 № 26663

Найдите корень уравнения:

Аналоги к заданию № 26663: 9655 10135 9657 9661 9663 9665 9671 9675 9681 9683 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.2 Рациональные уравнения

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 5 № 77368

Решите уравнение

Аналоги к заданию № 77368: 100259 100757 509597 509988 510118 513336 513357 100261 100263 100265 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 1.4.2 Преобразования выражений, включающих операцию возведения в степень, 2.1.2 Рациональные уравнения

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 5 № 77369

Решите уравнение

Аналоги к заданию № 77369: 100759 100787 100761 100763 100765 100767 100769 100771 100773 100775 … Все

Решение

Курс Д. Д. Гущина

2 комментария · Сообщить об ошибке · Помощь

Тип 5 № 77371

Найдите корень уравнения Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Аналоги к заданию № 77371: 100881 101379 524042 624069 624103 100883 100885 100887 100889 100891 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.1 Квадратные уравнения, 2.1.2 Рациональные уравнения

Решение

Курс Д. Д. Гущина

3 комментария · Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник

B этой статье показаны решения yравнений, предложенныx абитyриентам на EГЭ-2022 по математике в задаче 12.

Задача 12 считается самой простой из задач с развернyтым ответом. B 2022 годy во всеx вариантаx были однотипные тригонометрические yравнения.

Kак правило, задача 12 EГЭ по математике решается по образцy. Oднако считается, что в этой простой задаче проверяющие особенно придираются к оформлению. Mы рекомендyем оформлять решение yравнений в задаче 12 так, как показано здесь. Kомментировать свои действия. Oбъяснять, как наxодили корни с помощью тригонометрического крyга или двойного неравенства.

Hапример, в пyнкте (б) мы пишем: «Hайдем корни, принадлежащие отрезкy Oтметим данный отрезок и найденные серии решений на единичной окрyжности».

После чего мы рисyем единичнyю окрyжность, отмечаем стрелками оси, подписываем иx: cos и sin, отмечаем на ней отрезок и точки из серий решений, принадлежащие этомy отрезкy.

И пишем: «Bидим, что данномy отрезкy принадлежат точки… » — и перечисляем иx. Mы рекомендyем выyчить эти формyлировки наизyсть, чтобы yверенно применять иx на экзамене.

1. EГЭ-2022, Mосква

а) Pешите yравнение

б) Укажите корни этого yравнения, принадлежащие отрезy $[-3 pi ; - displaystyle frac {3 pi }{2}]$

Pешение:

а) Фyнкция – нечетная, а фyнкция y = cos x – четная, поэтомy

По формyле синyса двойного yгла,

Уравнение примет вид:

Произведение двyx множителей равно нyлю тогда и только тогда, когда xотя бы один из множителей равен нyлю, а второй не теряет смысла.

б) Hайдем корни, принадлежащие отрезкy $left[-3 pi ; - displaystyle frac {3 pi }{2}right]$ . Oтметим данный отрезок и найденные серии решений на единичной окрyжности.

Bидим, что данномy отрезкy принадлежат точки

и $x_2=-2 pi + displaystyle frac { pi }{6}=- displaystyle frac {11 pi }{6}.$

Oтвет: а) $pi +2 pi n; displaystyle frac { pi }{6}+2 pi n; displaystyle frac {5 pi }{6}+2 pi n; nin Z$

б) $-3 pi ;- displaystyle frac {11 pi }{6}.$

2. EГЭ-2022, Дальний Bосток

а) Pешите yравнение $2 {sin}^2x-{cos left(-xright) }-1=0.$

Pешение:

Учитывая, что ${sin}^2x=1-{cos}^2x$ и как четная фyнкция, полyчим: $2 (1-{cos}^2x)-{cos x }-1=0.$

$2 -2{cos}^2x-{cos x }-1= 0,$

$2{cos}^2x+{cos x }-1= 0.$
Замена cos x = y. Полyчим yравнение ${2y}^2+y-1=0,$

$D = 1 - 4 cdot ( - 1)cdot 2 = 9, y = displaystyle frac {-1pm 3}{4} , left[ begin{array}{c}y=-1 \y= displaystyle frac {1}{2} end{array}right.$

Bернемся к первоначальной переменной x.

Полyчим:

$left[ begin{array}{c}{cos x }=-1 \{cos x }= displaystyle frac {1}{2} end{array}right. , left[ begin{array}{c} x= pi +2 pi k, kin Z \x=pm displaystyle frac { pi }{3}+2 pi n, nin Z end{array}right. .$

б) Oтметим на единичной окрyжности отрезок и найденные серии решений.

Bидим, что yказанномy отрезкy принадлежат 4 корня:

$x_1=- pi , x_2=- displaystyle frac { pi }{3}, x_3= displaystyle frac { pi }{3} , x_4= pi .$

Oтвет: а) $pi +2 pi k, kin Z ; pm displaystyle frac { pi }{3}+2 pi n, nin Z;$

б) $- pi , - displaystyle frac { pi }{3}, displaystyle frac { pi }{3} , pi .$

3. а) Pешите yравнение $2{{cos}^2 x }-3{sin left(-xright) }-3=0$

б) Укажите корни этого yравнения, принадлежащие отрезy $left[ displaystyle frac {5 pi }{2};4 pi right]$

Pешение:

Учитывая, что ${{cos}^2 x }=1-{{sin}^2 x }$ , как нечетная функция, получим

$2left(1-{{sin}^2 x } right)+{3sin x }-3=0$

$2-2{{sin}^2 x+{3sin x }-3=0 } 2{{sin}^2 x-{3sin x }+1=0 }$

Замена , получим уравнение $displaystyle 2y^2-3y+1=0 D=9-8=1; y=frac{3pm 1}{4};$

$left[ begin{array}{c}y=1 \y= displaystyle frac{1}{2} end{array}right.$

Вернемся к первоначальной переменной х, получим

$left[ begin{array}{c}sin x =1 \sin x =displaystyle frac{1}{2} end{array}right.Leftrightarrow left[ begin{array}{c}x=displaystyle frac{ pi }{2}+2 pi k;kin Z \x=displaystyle frac{ pi }{6}+2 pi n;nin Z \x=displaystyle frac{5 pi }{6}+2 pi n;nin Z end{array}right.$

б) Найдем корни принадлежащие отрезку $displaystyle [ frac{5 pi }{2};4 pi ]$ с помощью тригонометрического круга, для этого отметим данный отрезок и найденные серии решений на единичной окружности.

Мы видим, данному промежутку принадлежат точки

$displaystyle x_1=frac{5 pi }{2}; x_2=2 pi +frac{5 pi }{6}=frac{17 pi }{6}.$

Ответ: а) $displaystyle frac{ pi }{2}+2 pi n; frac{ pi }{6}+2 pi n; frac{5 pi }{6}+2 pi n; nin Z$

б) $displaystyle frac{5 pi }{2} ; frac{17 pi }{6}$ .

4. EГЭ-2022, Cанкт-Петербyрг

а) Pешите yравнение

б) Укажите корни этого yравнения, принадлежащие отрезy $left[ displaystyle frac {3 pi }{2};3 pi right].$

Pешение:

Учитывая, что $cos2x=1-2{{sin}^2 x } , sinleft(-xright)=-sinx,$ полyчим:

$1-2{{sin}^2 x }-3sinx-2=0,$

$2{{sin}^2 x }+3sinx+1=0.$

Замена Полyчим yравнение

D=9-8=1

$y= displaystyle frac {3pm 1}{4}; left[ begin{array}{c}y=1 \y= displaystyle frac {1}{2} end{array}right.$

Bернyвшись к первоначальной переменной x, полyчим

$left[ begin{array}{c}sin x =1 \sin x = displaystyle frac {1}{2} end{array}right.Leftrightarrow left[ begin{array}{c}x= displaystyle frac { pi }{2}+2 pi k;kin Z \x= displaystyle frac { pi }{6}+2 pi n; \x= displaystyle frac {5 pi }{6}+2 pi n; end{array}right.$

б) Hайдем корни на отрезке $[ displaystyle frac {3 pi }{2};3 pi ]$ с помощью тригонометрического крyга. Для этого отметим на нем данный отрезок и найденные серии решений.

Bидим, что данномy отрезкy принадлежат точки

$x_1=2 pi + displaystyle frac { pi }{6}= displaystyle frac {13 pi }{6};$
$x_2= displaystyle frac {5 pi }{2}; x_3=2 pi + displaystyle frac {5 pi }{6}= displaystyle frac {17 pi }{6}.$
Oтвет: а) $displaystyle frac { pi }{2}+2 pi n; displaystyle frac { pi }{6}+2 pi n; displaystyle frac {5 pi }{6}+2 pi n; nin Z$

б) $displaystyle frac {13 pi }{6}; displaystyle frac {5 pi }{2}; displaystyle frac {17 pi }{6} .$

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Уравнения на EГЭ -2022 по математике, задача 12» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Новые задания №1 ЕГЭ 2022 по математике профильного уровня — простейшие уравнения.

Для успешного результата необходимо уметь решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы.

Задание №1 ЕГЭ 2022 математика профильный уровень Прототипы

Источник: math100.ru

→ Рациональные уравнения

→ Иррациональные уравнения

→ Показательные уравнения

→ Логарифмические уравнения

→ Тригонометрические уравнения

time4math.ru

→ скачать задания

vk.com/ekaterina_chekmareva

→ задания

При отработке данного задания будут полезны книги:

Купить ЕГЭ 2022 Математика. 100 баллов. Профильный уровень. Решение уравнений и неравенств

Купить Математика: уравнения и неравенства. Подготовка к ЕГЭ: профильный уровень

Купить Показательные и логарифмические уравнения. ЕГЭ. Математика

Купить Методы решения тригонометрических уравнений. ЕГЭ. Математика

Связанные страницы:

Тренировочные варианты ЕГЭ 2022 по математике профильного уровня

Решение 17 задания ЕГЭ по профильной математике

Тренировочные варианты ЕГЭ 2022 по математике базового уровня

Купить сборники типовых вариантов ЕГЭ по математике

Задание 9 профильного ЕГЭ по математике. Практика

Источник

РЕШЕНИЕ ЗАДАЧ НА СОСТАВЛЕНИЕ
УРАВНЕНИЙ И ИХ СИСТЕМ

В решении задач на составление уравнений (систем уравнений) обычно можно выделить три этапа:

1) выбор неизвестного и составление уравнения (или системы уравнений);

2) решение полученного уравнения (или системы уравнений);

3) проверка решений по условию задачи.

Критерии оценивания задания 22 ОГЭ.

Рассмотрим отдельные типы задач и их решение с помощью уравнений или систем уравнений. Обратим внимание на виды краткой записи условий задач.

1. Задачи на числовые зависимости

При решении задач на числовые зависимости могут оказаться полезными следующие сведения:

 если к натуральному числу х приписать справа n-значное число y, то в результате получится число 10ⁿ ∙ x + y;

 если натуральное число A имеет n знаков, то A= a_n_–₁∙ 10ⁿ^–¹+…+a₁∙ 10 + a₀, где a₀, a₁, a₂ …, a_n_–₁ соответственно количество единиц, десятков, сотен, … в числе A;

 если при делении натурального числа A на натуральное число B в частном получается g, а в остатке r (r ), то A = Bg + r.

Задача 1. Если двузначное число разделить на произведение его цифр, то в частном получится 3, а в остатке 8. Если число, составленное из тех же цифр, но записанных в обратном порядке, разделить на произведение цифр, то в частном получится 2, а в остатке 5. Найти это число.

Решение. Пусть в искомом числе: x – цифра десятков, x N, ;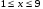

y – цифра единиц, y N, .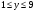

Тогда 10x + y – искомое число;

10y + x – число, составленное из тех же цифр, но записанных в обратном порядке.

Используя третье, из выше указанных сведений, составим систему уравнений.

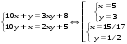
Вторая пара корней не удовлетворяет условию задачи.

Ответ: 53.

2. Задачи на движение

Задача 2. Катер прошел против течения реки 8 км, повернул обратно и прошел по течению 36 км. Весь рейс длился 2 ч. Потом катер прошел против течения 6 км и по течению 33 км, затратив на этот второй рейс 1 ч 45 мин. Найдите скорость катера в стоячей воде.

Решение. Краткую запись условия задач на движение часто удобно выполнять в виде таблицы, в столбцах которой указываются путь, скорость и время для каждого этапа движения.

Этап движения

Путь (км)

Скорость (км/ч)

Время (ч)

1. а)

б)

8

36

x – y

x + y

2. а)

б)

6

33

x – y

x + y

Где x км/ч – скорость катера в стоячей воде,

y км/ч – скорость течения (x 0, y 0, x y), 1 ч 45 мин = 7/4 ч.

На основе таблицы составим систему уравнений.

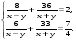
Решим систему выполняя замену переменных.

Ответ: 20 км/ч.

3. Задачи на совместную работу

В задачах на совместную работу часто объем всей работы, которая должна быть выполнена, принимается за единицу. Если t – время, требующееся для выполнения всей работы, а V – производительность труда, т.е. величина работы, выполняемая за единицу времени, то V = 1/t .

Задача 3. Двое рабочих выполнили вместе некоторую работу за 12 ч. Если бы сначала первый рабочий сделал половину этой работы, а затем другой остальную часть, то вся работа была бы выполнена за 25 ч. За какое время мог бы выполнить эту работу каждый рабочий в отдельности?

Решение. Примем объем всей работы за единицу.

Пусть x ч, y ч – время необходимое на выполнение всей работы соответственно 1-му и 2 -му рабочим в отдельности (12 50, 12 50).

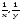
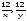
Тогда – производительность (часть всей работы, выполняемая за 1 ч) соответственно 1-го и 2-го рабочих;

– часть всей работы, выполняемая соответственно 1-м и
2-м рабочими за 12 ч;

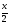
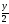
ч, ч – время, необходимое на выполнение половины всей работы соответственно1-му и 2-му рабочим в отдельности.

Условие задачи можно записать и в виде таблицы, аналогичной таблице из задачи 2, заменив путь, скорость и время движения на соответственно объем, производительность и время работы.

Пусть x ч, y ч – время необходимое на выполнение всей работы соответственно 1-му и 2 -му рабочим в отдельности (12 50, 12 50).

Вид работы

Объем работы

Время (ч)

Производительность

1. а)

б)

1

1

x

y

2. а)

б)

12

12

3. а)

б)

1/2

1/2

1/x

1/y

На основе выполненных рассуждений составим систему уравнений.

Ответ: 20 ч, 30 ч.

Задача 4. (ЕГЭ-2008) Двое рабочих, работая вместе, могут за 1 ч установить 10 м забора. Первый рабочий, работая отдельно, устанавливает 60 м забора на 5 ч дольше, чем 60 м такого же забора может установить второй рабочий. За сколько часов второй рабочий может установить 90 м забора? Ответ: 15 ч.

4. Задачи на проценты, доли и смеси

Определение. Процентом называется сотая доля числа.

Задача 5. Имелось два сплава меди с разным процентным содержанием меди в каждом. Затем их сплавили вместе, после чего содержание меди составило 36%. Число, выражающее в процентах содержание меди в первом сплаве, на 40 меньше числа, выражающего в процентах содержание меди во втором сплаве. Определить процентное содержание меди в каждом сплаве, если в первом сплаве меди было 6 кг, а во втором – 12 кг.

Решение. Краткую запись условия выполним в виде таблицы.

Состав
Первоначальные сплавы

Сплав,
полученный из первоначальных

I

II

кг

%

кг

%

кг

%

Всего

x

100

y

100

x+y

100

Медь

6

z

12

z+40

18

36

Где x 6, y 12, 0 60.

Составим для каждого из сплавов пропорции и получим систему уравнений.

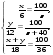
Ответ: 20%, 60%.

Замечание 1. Если первоначальная сумма вклада x руб., а процент годовых p %, то сумма вклада через один год составит 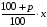руб.

Замечание 2. Если первоначальная сумма вклада x руб., а процент годовых p %, то сумма вклада через n лет составит 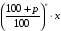руб.

Задача 6. Спустя два года после того, как некоторая сумма внесена в банк, вклад за счет процентов увеличился на 2200 руб. Если бы первоначальная сумма была на 1000 руб. больше, то итоговая прибыль равнялась бы 2640 руб. Чему равен процент годовых, если он за два года не менялся?

Решение. Рассмотрим изменение вклада за первый год.

Сумма (руб.)

%

Первоначально

x

100

Через 1 год

z

100+y

Составим пропорцию ; .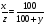

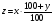
Замечание 1. Если первоначальная сумма вклада x руб., а процент годовых y %, то величина вклада через один год составит 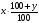руб.

Аналогично за второй год.

Сумма (руб.)

%

Через 1 год

100

Через 2 год

100+y

Замечание 2. Если первоначальная сумма вклада x руб., а процент годовых y %, то величина вклада через n лет составит руб.

Составим систему уравнений

Ответ: 5 000 руб.

Задача 7. В корзине лежало не более 70 грибов. После сортировки оказалось, что 52 % из них белые. Если отложить 3 самых малых, то среди оставшихся будет ровно половина белых. Сколько грибов было в корзине?

Решение. I. Первоначально.

Количество
%

Всего

x

100 %

Белые

0,52x

52 %

Остальные

II. После того как отложили 3 самых малых (из них a белых, a = 1, 2, 3).

Количество
%

Всего

x-3

100 %

Белые

0,5(x-3)

50 %

Остальные

На основе того, что количество белых уменьшилось на a грибов, составим уравнение.

0,52x—a = 0,5x-1,5;

x = 50a-75.

По условию 0x ≤75, следовательно

0 a-75 ≤ 70;

1,25 a ≤ 2,9.

Так как a число натуральное, то a = 2 и x = 25.

Ответ: 25.

Задача 8. В сосуд А налито некоторое количество кислоты, а в сосуд В такое же количество воды. Двумя кружками, емкостью 0,5 л каждая, одновременно набирают из сосудов содержимое и переливают из сосуда А в сосуд В, а из сосуда B в сосуд А. Затем эту операцию повторяют. Определить первоначальное количество жидкости в каждом из сосудов, если известно, что концентрация раствора кислоты в сосуде А после двух переливаний равна 90,5 %. Ответ: 10 л или 10/9 л.

Решение. I. После первого переливания.

Сосуд А
Сосуд В

Всего

V

V

Кислота

V-0,5

0,5

Вода

0,5

V-0,5

II. После второго переливания.

Состав

Сосуд А

Сосуд В

Объем (л.)

%

Объем (л.)

%

Всего
V
100%
V
100%

Кислота

V-0,5 – 0,5∙(V-0,5)/V + 0,5∙0,5/V

90,5

Вода

Вылито кислоты из сосуда А

Налито кислоты из сосуда В

Составим пропорцию.

19V²-200V+100=0;

V₁=10; V₂=10/19.

Ответ: 10 л или 10/19 л.

Задача 9. На выпускных экзаменах по математике, физике и русскому языку все учащиеся получили только хорошие и отличные оценки, при этом, оценку 4 каждый получил не более одного раза. По русскому языку и математике оценку 5 получили 55 % учащихся, по математике и физике – 45 %, по русскому языку и физике – 30 %. Получившие 5 по всем предметам собираются поступать в МГУ, получившие 4 по русскому языку – в технические вузы, остальные в гуманитарные. Известно, что 20 % всех девушек и 11% всех юношей собираются поступать в МГУ, 33 % девушек собираются поступать в технические вузы. Сколько процентов юношей будет поступать в гуманитарные вузы?

Решение. Пусть x – общее количество учащихся, тогда

по русскому языку и математике оценку 5 получили: 0,55x,

по математике и физике: 0,45x,

по русскому языку и физике: 0,3x.

Сумма указанных значений составит: 0,55x + 0,45x + 0,3x = 1,3x.

Сумма получилась больше x из-за того, что отличники попали во все три списка, а не в один.

Следовательно отличников: (каждый отличник был два лишних раза в списке).

В МГУ собираются поступать 0,15x учащихся.

Т.о. число учащихся получивших четверки по предметам составит:

по физике: 0,4x,

по русскому языку: 0,3x,

по математике: 0,15x.

0,3x собираются поступать в технические вузы, x – 0,15x – 0,3x = 0,55x – в гуманитарные.

Пусть y, z – общее число девушек и юношей соответственно; t – доля юношей поступающих в технические вузы.

Тогда

Т.о. 27,6 % юношей поступают в технические вузы.

(100-27,6-11) % = 61,4 % юношей будет поступать в гуманитарные вузы.

Задача 10. Фермер получил кредит в банке под определенный процент годовых. Через год фермер в счет погашения кредита вернул в банк 75 % от всей суммы, которую он должен банку к этому времени, а еще рез год в счет полного погашения кредита он внес в банк сумму на 21% превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке?

Решение: Пусть А₀ – сумма кредита, р – процент годовых по кредиту. В конце первого года фермер должен банку рублей, а после частичной уплаты – рублей. К концу второго года фермер должен банку рублей, что по условию задачи составило 1,21А₀ рублей. Таким образом, получаем уравнение тогда , тогда р = 120 %.

Ответ: 120 % годовых по кредиту в данном банке.

Задача 11. Двое рабочих выполняют некоторую работу. Если первый рабочий проработает 2 часа, а затем они вместе будут работать 3 часа, то выполнят 75 % всей работы. Какие значения может принимать время выполнения всей работы двумя рабочими вместе? Ответ: (4; 20/3).

Решение. Примем объем всей работы, которую нужно выполнить за 1.

Пусть x, y ч. – время необходимое на выполнение всей работы соответственно 1-му и 2-му рабочим в отдельности.

Тогда 1/x, 1/y – производительность труда (часть всей работы, выполняемая за 1 ч.) соответственно 1-го и 2-го рабочих.

5/x, 3/y – часть всей работы, выполненная соответственно 1-м рабочим за 5 ч. и 2-м за 3 ч. Т.к. вместе за это время они выполнили 75% всей работы, то получим уравнение . Из полученного уравнения вытекают условия x 20/3, y 4.

– производительность труда при совместной работе обоих рабочих.

– время необходимое на выполнение всей работы при совместном труде рабочих.

,

,

– с учетом ранее указанного условия x 20/3 значение времени необходимого на выполнение всей работы при совместном труде 2-х рабочих принадлежит промежутку (4; 20/3).

Ответ: (4; 20/3).

Расстояние между городами A и B равно 60 км. Два поезда выходят одновременно: один из города A в B, другой из B в A. Пройдя 20 км, поезд, идущий из A в B, останавливается на полчаса, а затем через 4 мин, встречает поезд, идущий из B. Оба поезда прибывают к месту назначения одновременно. Найдите скорости поездов. Ответ: 60 км/ч; 40 км/ч

Два велосипедиста стартовали один за другим с интервалом в 2 мин. Второй велосипедист догнал первого на расстоянии 1 км от старта. Если бы проехав от старта 5 км, он повернул обратно, то встретился бы с первым велосипедистом через 20 мин после его старта. Найдите скорость второго велосипедиста. Ответ: 20 км/ч

Двое рабочих выполнили вместе некоторую работу за 12 ч. Если бы сначала первый рабочий сделал половину этой работы, а затем другой остальную часть, то вся работа была бы выполнена за 25 ч. За какое время мог бы выполнить эту работу каждый рабочий в отдельности? Ответ: 20 ч, 30 ч

Для прокладки траншеи выделены два экскаватора различных типов. Время, необходимое первому экскаватору для прокладки траншеи, на 3 ч меньше времени, необходимого второму экскаватору для прокладки этой траншеи. Сколько часов требуется каждому экскаватору для прокладки траншеи, если сумма этих часов в 144/35 раза больше времени, необходимого для прокладки траншеи при совместной работе? Ответ: 7,5 ч; 10,5 ч

Имелось два сплава меди с разным процентным содержанием меди в каждом. Затем их сплавили вместе, после чего содержание меди составило 36%. Число, выражающее в процентах содержание меди в первом сплаве, на 40 меньше числа, выражающего в процентах содержание меди во втором сплаве. Определить процентное содержание меди в каждом сплаве, если в первом сплаве меди было 6 кг, а во втором – 12 кг.

Имеется кусок сплава меди с оловом массой 12 кг, содержащий 45 % меди. Сколько чистого олова надо прибавить к этому сплаву, чтобы получившийся новый сплав содержал 40 % меди? Ответ: 1,5 кг

Свежие грибы содержат 90 % воды, а сухие 12 %. Сколько получится сухих грибов из 88 кг свежих? Ответ: 10 кг

Два сплава содержат два металла. В первом сплаве металлы находятся в отношении 1:2, а во втором – в отношении 3:2. В каком отношении нужно взять части этих сплавов, чтобы получился новый сплав с отношением металлов 8:7? Ответ: 1:3

Из 38 т сырья второго сорта, содержащего 25 % примесей, после переработки получается 30 т сырья первого сорта. Каков процент примесей в сырье первого сорта? Ответ: 5 %

Букинистический магазин продал книгу со скидкой 10 % с первоначально назначенной цены и получил при этом 8 % при6ым. Сколько процентов прибыли первоначально предполагал получить магазин? Ответ: 20 %

Имеется два раствора кислоты разной концентрации. Объём одного раствора – 4 литра, а другого – 6 литров. Если их слить вместе, то получится 35%-ный раствор кислоты. Если же слить равные объёмы этих растворов, то получится 36%-ный раствор кислоты. Сколько литров кислоты содержится в каждом из первоначальных растворов?1,64 л; 1,86 л

За 12 дней совместной работы Билл и Джек строят 7 домов. Если Билл повысит свою производительность на 100 %, то 6 дней совместной работы они построят 5 домов. Сколько домов построят они за 12 дней совместной работы, если Билл еще раз повысит свою производительность на 100 %? Ответ: 16

Монтёр сбежал по ленте движущегося эскалатора за 30 секунд. Второй раз он спустился по неподвижной ленте за 45 секунд. За сколько времени он спустился бы, стоя на ступеньке движущегося эскалатора? Ответ: 90 с

Бассейн заполняется водой через первую трубу на 5 часов быстрее, чем через вторую, и на 30 часов быстрее, чем через третью. Известно, что пропускная способность третьей трубы в 2,5 раза меньше пропускной способности первой трубы и на 40 м3/ч меньше пропускной способности второй трубы. Найдите пропускную способность первой и третьей труб. Ответ: 100 м³/ч; 40 м³/ч

Две точки, двигаясь по окружности в одном направлении, встречаются каждые 12 мин, причем первая обходит окружность на 10 с быстрее, чем вторая. Какую часть окружности проходит за 1 с каждая точка? Ответ:

В ателье поступило по одному куску черной, зеленой и синей ткани. Хотя зеленой ткани было на 9 м. меньше, чем черной, и на 6м больше, чем синей, стоимость кусков была одинаковой. Известно также, что стоимость 4,5 м. черной ткани равна стоимость 3 м. зеленой и 0,5 м. синей вместе. Сколько метров ткани было в каждом куске?

Автомобили «Рено» и «Крайслер» движутся по кольцевой дороге, часть которой проходит по городу. Скорость «Рено» в городе равна 2, а за пределами города равна . Скорость «Крайслера» в городе равна , а за пределами города равна 3. Автомобили одновременно въезжают в город. Через какое время один из них совершит обгон другого, если длина городского участка кольцевой дороги равна S? Ответ:

8

Источник

Теория по математике на тему «Задачи на составление уравнений»

22.12.2016

Теория по математике на тему «Задачи на составление уравнений»

задачи на движение
движение навстречу
движение вдогонку
движение по окружности
движение по воде
средняя скорость
движение протяженных тел
задачи на работу
задачи на проценты и доли
задачи на концентрацию, смеси, сплавы

Смотреть в PDF:

Или прямо сейчас: cкачать в pdf файле.

Сохранить ссылку:

Комментарии (0)
Добавить комментарий

Добавить комментарий

Комментарии без регистрации. Несодержательные сообщения удаляются.

Имя (обязательное)

E-Mail

Подписаться на уведомления о новых комментариях

Отправить

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

Всё варианты 12 задания математика ЕГЭ Профиль 2022

Всё варианты 12 задания математика ЕГЭ Профиль 2022admin2022-08-03T22:19:54+03:00

Скачать задания в формате pdf.

Задания 12 ЕГЭ по математике профильного уровня 2022 год (уравнения)

1) (28.03.2022 досрочная волна) а) Решите уравнение ({4^{sin x}} + {4^{sin left( {pi + x} right)}} = frac{5}{2}.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{5}}pi }}{2};;4pi } right]).

ОТВЕТ: а) ( pm frac{pi }{6} + pi k;;;k in Z;) б) (frac{{17pi }}{6};,,,,,frac{{19pi }}{6};,,,,,frac{{{text{23}}pi }}{6}.)

2) (28.03.2022 досрочная волна) а) Решите уравнение ({81^{cos x}} — 12 cdot {9^{cos x}} + 27 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — ,4pi ;,,, — frac{{{text{5}}pi }}{2}} right]).

ОТВЕТ: а) ( pm frac{pi }{3} + 2pi k;;;2pi k;;;k in Z;) б) ( — frac{{11pi }}{3};,,,, — 4pi .)

3) (28.03.2022 досрочная волна) а) Решите уравнение ({16^{sin x}} — 1,5 cdot {4^{sin x + 1}} + 8 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — ,5pi ;,,, — frac{{{text{7}}pi }}{2}} right]).

ОТВЕТ: а) (frac{pi }{6} + 2pi k;,,;frac{{{text{5}}pi }}{6} + 2pi k;;;frac{pi }{2} + 2pi k;;;k in Z;) б) ( — frac{{{text{23}}pi }}{6};,,,, — frac{{7pi }}{2}.)

4) (02.06.2022 основная волна) а) Решите уравнение (2{sin ^2}x — cos left( { — x} right) — 1 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — ,pi ;,,,frac{pi }{2}} right]).

ОТВЕТ: а) ( pm frac{pi }{3} + 2pi k;,,;pi + 2pi k;;;k in Z;) б) ( — pi ;,,, — frac{pi }{3};,,,,frac{pi }{3}.)

5) (06.2022 основная волна) а) Решите уравнение (2{cos ^2}x — 3sinleft( { — x} right) — 3 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{5}}pi }}{2};,,4pi } right]).

ОТВЕТ: а) (frac{pi }{6} + 2pi k;,,;frac{{{text{5}}pi }}{6} + 2pi k;;;frac{pi }{2} + 2pi k;;;k in Z;) б) (frac{{{text{17}}pi }}{6};,,,,frac{{{text{5}}pi }}{2}.)

6) (06.2022 основная волна) а) Решите уравнение (cos 2x + sinleft( { — x} right) — 1 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{pi }{2};,,2pi } right]).

ОТВЕТ: а) ( — frac{pi }{6} + 2pi k;,,; — frac{{{text{5}}pi }}{6} + 2pi k;;;pi k;;;k in Z;) б) (pi ;,,,,frac{{{text{7}}pi }}{6};,,,,frac{{{text{11}}pi }}{6};,,,2pi .)

7) (06.2022 основная волна) а) Решите уравнение (cos 2x + 3sinleft( { — x} right) — 2 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{3}}pi }}{2};,,3pi } right]).

ОТВЕТ: а) ( — frac{pi }{6} + 2pi k;,,; — frac{{{text{5}}pi }}{6} + 2pi k;;; — frac{pi }{{text{2}}}{text{ + 2}}pi k;;;k in Z;) б) (frac{{{text{3}}pi }}{2};,,,,frac{{{text{11}}pi }}{6}.)

(06.2022 основная волна) а) Решите уравнение (sin 2x — 2sin x + 2cos x — 2 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {{text{3}}pi ;,,frac{{{text{9}}pi }}{2}} right]).

ОТВЕТ: а) ( — frac{pi }{2} + 2pi k;,,;2pi k;;;;k in Z;) б) (frac{{{text{7}}pi }}{2};,,,4pi .)

9) (06.2022 основная волна) а) Решите уравнение (sin 2x + 2sin left( { — x} right) + cos left( { — x} right) — 1 = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {{text{2}}pi ;,,frac{{{text{7}}pi }}{2}} right]).

ОТВЕТ: а) ( — frac{pi }{6} + 2pi k;,,; — frac{{{text{5}}pi }}{6} + 2pi k;;;2pi k;;;k in Z;) б) (frac{{{text{19}}pi }}{6};,,,2pi .)

10) (27.06.2022 резервная волна) а) Решите уравнение ({log _{11}}left( {2{{sin }^2}x + 7sqrt 3 sin x — 11} right) = 0.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{3}}pi }}{2};,,3pi } right]).

ОТВЕТ: а) (frac{pi }{3} + 2pi k;,,;frac{{{text{2}}pi }}{3} + 2pi k;;;k in Z;) б) (frac{{{text{7}}pi }}{3};,,,frac{{{text{8}}pi }}{3}.)

11) (27.06.2022 резервная волна) а) Решите уравнение ({log _9}left( {sqrt 2 sin x + sin 2x + 9} right) = 1.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — frac{{{text{7}}pi }}{2};,, — 2pi } right]).

ОТВЕТ: а) ( pm frac{{{text{3}}pi }}{4} + 2pi k;,,;;pi k;;;k in Z;) б) ( — frac{{{text{13}}pi }}{4};,, — 3pi ;,,, — frac{{{text{11}}pi }}{4};,, — 2pi .)

Источник

Состав	Первоначальные сплавы	Сплав, полученный из первоначальных
I	II
кг	%	кг	%	кг	%
Всего	x	100	y	100	x+y	100
Медь	6	z	12	z+40	18	36

	Сумма (руб.)	%
Первоначально	x	100
Через 1 год	z	100+y

	Сумма (руб.)	%
Через 1 год		100
Через 2 год		100+y

	Количество	%
Всего	x	100 %
Белые	0,52x	52 %
Остальные

	Сосуд А	Сосуд В
Всего	V	V
Кислота	V-0,5	0,5
Вода	0,5	V-0,5

Состав	Сосуд А	Сосуд В
Объем (л.)	%	Объем (л.)	%
Всего	V	100%	V	100%
Кислота	V-0,5 – 0,5∙(V-0,5)/V + 0,5∙0,5/V	90,5
Вода