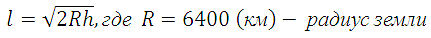Задачи по математике с физическим содержанием на егэ - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Материальная точка движется прямолинейно по закону (где x  — расстояние от точки отсчета в метрах, t  — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t  =  9 с.

Материальная точка движется прямолинейно по закону (где x  — расстояние от точки отсчета в метрах, t  — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t  =  6 с.

Материальная точка движется прямолинейно по закону (где x  — расстояние от точки отсчета в метрах, t  — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 3 м/с?

Пройти тестирование по этим заданиям

Источник

Скачать материал

Сейчас обучается 94 человека из 37 регионов

Сейчас обучается 128 человек из 47 регионов

Описание презентации по отдельным слайдам:

1 слайд

Решение физических задач ЕГЭ по математике.
МОУ «СОШ № 34 с углубленным изучением
художественно-эстетических предметов»
Н.И. Хренникова,
учитель математики
Саратов
2014
2 слайд

Задания с наибольшим количеством аналогов
3 слайд

Задание B12 (№ 28643)
Два тела массой кг каждое движутся с одинаковой скоростью м/с под углом друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении определяется выражением . Под каким наименьшим углом (в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 108 джоулей?
Задание B12 (№ 28613)
Трактор тащит сани с силой кН, направленной под острым углом к горизонту. Работа трактора (в килоджоулях) на участке длиной м вычисляется по формуле . При каком максимальном угле (в градусах) совершeнная работа будет не менее 2800 кДж?
Задание B12 (№ 28053)
Зависимость объeма спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. руб.) задаeтся формулой . Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле . Определите наибольшую цену p, при которой месячная выручка составит не менее 360 тыс. руб. Ответ приведите в тыс. руб.
4 слайд

Задания с наименьшим количеством аналогов
5 слайд

Задание B12 (№ 41991)
Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: , где U — напряжение в вольтах, R — сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 1 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах.
Задание B12 (№ 28083)
В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону , гдеt — время в секундах, прошедшее с момента открытия крана, м — начальная высота столба воды, — отношение площадей поперечных сечений крана и бака, а g — ускорение свободного падения (считайте м/с ). Через сколько секунд после открытия крана в баке останется четверть первоначального объeма воды?
Задание B12 (№ 28393)
Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной l км с постоянным ускорением a км/ч , вычисляется по формуле . Определите, с какой наименьшей скоростью будет двигаться автомобиль на расстоянии 0,4 километра от старта, если по конструктивным особенностям автомобиля приобретаемое им ускорение не меньше 12500 км/ч . Ответ выразите в км/ч.
6 слайд

Шаги решения В12
Решение задач В12 условно можно разделить на несколько шагов:

а) анализ условия и вычленение формулы, описывающей заданную ситуацию, а также значений параметров, констант или начальных условий, которые необходимо подставить в эту формулу;

б) математическая интерпретация задачи — сведение её к уравнению или неравенству и его решение;

в) анализ полученного решения.

Задания В12 отличаются от других тем, что очень высок процент тех, кто даже не приступал к решению.
Основные проблемы — трудности с арифметикой, логические ошибки, невнимательное чтение условия.
7 слайд

линейному уравнению или неравенству

степенному уравнению или неравенству

показательному уравнению или неравенству

логарифмическому уравнению и неравенству

тригонометрическому уравнению или неравенству

Задачи, решение которых сводятся к стандартным уравнениям и неравенствам
8 слайд

При температуре 0oС рельс имеет длину lo= 20 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону l(to) = l0 ( 1+α·to), где α = 1,2·10-5(oC)-1 – коэффициент теплового расширения, to — температура (в градусах Цельсия). При какой температуре рельс удлинится на 9 мм? Ответ выразите в градусах Цельсия.
Задание B12 (№ 28017)
9 слайд

Функция:
Данные:
Получаем уравнение:
Найти:
Ответ: 37,5.
10 слайд

Задание B12 (№ 28027)

Некоторая компания продает свою продукцию по цене p = 600 руб. за единицу, переменные затраты на производство одной единицы продукции составляют ν = 400 руб., постоянные расходы предприятия f = 600000 руб. в месяц. Месячная операционная прибыль (в рублях) вычисляется по формуле π(q) = q( p — ν)- f . Определите наименьший месячный объём производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 500000 руб.
11 слайд

Данные:
Функция:
Найти:
Решаем неравенство:
Ответ:
5500.
12 слайд

Для обогрева помещения, температура в котором Тп = 20°С, через радиатор пропускают горячую воду температурой Т= 60°С. Через радиатор проходит m= 0,3 кг/с воды. Проходя по радиатору расстояние х = 84 м, вода охлаждается до температуры T(°С), причём
где с = 4200 — теплоёмкость воды, γ= 21 — коэффициент теплообмена,
а α = 0,7 — постоянная. До какой температуры (в градусах Цельсия) охладится вода?
Задание B12 (№ 28027)
13 слайд

Данные:
Функция:
Найти:
Получаем уравнение:
Тп = 20°С
Т-?°С
х = 84 м
m= 0,3 кг/с
с = 4200
α = 0,7
Ответ: 30
14 слайд

Находящийся в воде водолазный колокол, содержащий ν= 4 моля воздуха при давлении р1 = 1,2 атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха. Работа (в джоулях), совершаемая водой при сжатии воздуха, определяется выражением
где α = 5,75 — постоянная, Т = 300 К—температура воздуха, P1 (атм) — начальное давление, а р2 (атм) — конечное давление воздуха в колоколе. До какого наибольшего давления р2 (в атм) можно сжать воздух в колоколе, если при сжатии воздуха совершается работа не более чем
20 700 Дж?
Задание B12 (№ 28027)
15 слайд

Функция:
Данные:
Получаем неравенство:
Найти:
Ответ: 9,6
ν= 4
р1 = 1,2
α = 5,75
Т = 300
, при
16 слайд

Трактор тащит сани с силой F = 80 кН, направленной под острым углом а к горизонту. Работа трактора, выраженная в килоджоулях, на участке длиной S = 50 м равна
А = FS cos α.
При каком максимальном угле а (в градусах) совершённая работа будет
не менее 2000 кДж?
,
Задание B12 (№ 28006)
17 слайд

Данные:
Функция:
Найти:
Получаем неравенство:
Ответ: 60
А ≥ 2000
F =80
80•50• cos α ≥ 2000
cos α ≥
0°< α≤ 60
°
А = FS cos α.
S = 50
а (в градусах), при
18 слайд

В ходе распада радиоактивного изотопа его масса уменьшается по закону
m(t) = m0.2-t/T,
где m0 — начальная масса изотопа, t — время, прошедшее от начала распада,
Т — период полураспада в минутах. В лаборатории получили вещество, содержащее m0 = 40 мг изотопа азота-13, период полураспада которого
Т = 10 мин. В течение скольких минут масса изотопа азота-13 будет
не меньше 10 мг?
Задание B12 (№ 27991)
19 слайд

Данные:
Функция:
Найти:
Получаем неравенство:
Ответ: 20
m(t) ≥ 10
m0 = 40 мг
Т = 10 мин
40 *2 -t/10 ≥ 10 ,
2 -t/10 ≥ 2-2 ,
t ≤ 20
m(t) = m0.2-t/T,
t , если
20 слайд

Задачи, решения которых сводятся к квадратным уравнениям и неравенствам.
21 слайд

Мотоциклист, движущийся по городу со скоростью v0 = 57 км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением a = 12 км/ч2. Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением

Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
Задание B12 (№ 28135)
at2
2
v0t
S
+
=
30 км
22 слайд

Решаем неравенство:
Функция:
Данные:
Найти:
Ответ:
30.
23 слайд

Задание B12 (№ 28125)
Лебёдка — механизм, тяговое усилие которого передается посредством каната, цепи, троса
или иного гибкого элемента от приводного барабана.
βt2
2
ωt
φ
+
=
Для сматывания кабеля на заводе используют лебёдку, которая равноускоренно наматывает кабель на катушку. Угол, на который поворачивается катушка, изменяется со
временем по закону , где t — время в
минутах, ω = 750/мин — начальная угловая скорость вращения катушки, а β = 100/мин2 — угловое ускорение, с которым наматывается кабель. Рабочий должен
проверить ход его намотки не позже того момента,
когда угол намотки φ достигнет 22500. Определите время после начала
работы лебёдки, не позже которого
рабочий должен проверить её работу.
Ответ выразите в минутах.
24 слайд

Функция:
Данные:
Найти:
Ответ:
15.
Решаем неравенство:
25 слайд

(m+2M)R2
2
+ M(2Rh + h2).
I
=
Деталью некоторого прибора является вращающаяся катушка. Она состоит из трёх однородных соосных цилиндров: центрального массой m = 8 кг и радиуса R = 5 см, и двух боковых с массами M = 2 кг и с радиусами R + h. При этом момент инерции катушки относительно оси вращения, выражаемый в кг· см2 , даётся формулой
.
При каком максимальном значении h момент инерции катушки не превышает предельного значения 1900 кг· см2 ? Ответ выразите в сантиметрах.
Задание B12 (№ 28165)
26 слайд

Данные:
Функция:
Найти:
Решаем неравенство:
Ответ:
25.
27 слайд

Зависимость объёма спроса q (тыс. руб.) на продукцию предприятия-монополиста от цены p (тыс. руб.) задаётся формулой q = 130 — 10p . Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле r(p) = q · p. Определите наибольшую цену p, при которой месячная выручка составит не менее 360 тыс. руб. Ответ приведите в тыс. руб.
Задание B12 (№ 28053)
28 слайд

Данные:
Функция:
Найти:
Получаем неравенство:
Ответ:
9.
29 слайд

60
-1
a
=
6
7
b
=
Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полёта камня описывается формулой y = ax2 + bx ,
где м-1, — постоянные параметры,
x (м) — смещение камня по горизонтали, y (м) — высота камня над землёй. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 9 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?
Задание B12 (№ 28105)
30 слайд

y = 10
Функция:
Данные:
Найти:

Ответ:
60.
Решаем неравенство:
31 слайд

Задание B12 (№ 28091)
H0
В боковой стенке высокого цилиндрического бака у самого дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём, выраженная в метрах, меняется по закону H(t) = H0 + bt + at2 , где Н0 = 2 м — начальный уровень воды,
м/мин2, м/мин, t — время в минутах,
прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах.
50
1
a
=
5
-2
b
=
32 слайд

Функция:
Данные:
Решаем уравнение:
Найти:
Ответ:
10.
33 слайд

В боковой стенке высокого цилиндрического бака у самого дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём, выраженная в метрах, меняется по закону
, где t — время в секундах,
прошедшее с момента открытия крана, —
отношение площадей поперечных сечений крана и бака, Н0 = 5 м — начальная высота столба воды, а g — ускорение свободного падения (считайте g = 10 м/с2). Через сколько секунд после открытия крана в баке останется четверть первоначального объёма воды?
Задание B12 (№ 28081)
2
gH
2
2
0
0
2
)
(
t
k
g
kt
H
t
H
+
—
=
k
200
1
=
34 слайд

Найти:
H0
4
1
H0
Данные:
Функция:
Решаем уравнение:
Ответ:
100.
35 слайд

Задание B12 (№ 28115)
Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур определяется выражением T(t) = T0 + bt + at2 , где t — время в минутах, T0 = 1450 К, a = — 12,5 К/мин2 , b = 175 К/мин. Известно, что при температуре нагревателя свыше 1750 К прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время после начала работы нужно отключать прибор. Ответ выразите в минутах.
Пирометр — прибор для беcконтактного измерения температуры тел.
36 слайд

Данные:
y = T(t)
y
t
0
1450
Функция:
Найти:
Схематичный график:
1750
tнаиб.
Необходимоотключить
Ответ:
2.
37 слайд

Задачи, в которых необходимо найти длину промежутка.
38 слайд

1,1 с
1,2 с
Задание B12 (№ 28039)
После дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле h = 5t2, где h — расстояние в метрах, t — время падения в секундах. До дождя время падения камешков составляло 1,2 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,1 с?
39 слайд

Найти:
Ответ:
Данные:
Функция:
1,15.
Решение:
40 слайд

Высота над землёй подброшенного вверх мяча меняется по закону h(t) = 1,4 + 9t — 5t2 , где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?
Задание B12 (№ 28059)
41 слайд

Данные:
Функция:
Найти:
Получаем неравенство:
Ответ: 1,4
42 слайд

Задачи, в которых присутствуют несколько переменных
43 слайд

g
L
v
m
P
—
=
2
(
)
Задание B12 (№ 28071)
Если достаточно быстро вращать ведёрко с водой на верёвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведёрка сила давления воды на дно не остаётся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила её давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная
в ньютонах, равна , где m — масса воды в
килограммах, v — скорость движения ведёрка в м/с, L — длина верёвки в метрах, g — ускорение свободного падения (считайте, g = 10 м/с2 ). С какой наименьшей скоростью надо вращать ведёрко, чтобы вода не выливалась, если длина верёвки равна 62,5 cм? Ответ выразите в м/с.
44 слайд

Функция:
Данные:
Решаем неравенство:
Ответ:
2,5
Найти:
45 слайд

В презентации использованы задачи из открытого банка заданий ЕГЭ по математике.

Краткое описание документа:

Презентация «Решение физических задач ЕГЭ по математике « может быть полезна в использована при подготовке учащихся к итоговой аттестации в 10 — 11 классах . Задачи физического содержания всегда вызывают затруднения у выпускников. Работа поможет классифицировать задачи по способам решения задачи, тем самым преодолеть страх перед решением таких задач. Наличие анимации в презентации будет помогать запоминанию разновидностей прототипов задач, подходу к решению различных прототипов задач. Желаю удачи!

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 153 785 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

26.03.2014
942
0

Рейтинг:
5 из 5

26.03.2014
3050
1

26.03.2014
1557
3

26.03.2014
1827
8

26.03.2014
1260
0

26.03.2014
2649
20

26.03.2014
2621
4

Вам будут интересны эти курсы:

Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

Источник

Решение задач с физическим и практическим содержанием ЕГЭ по математике.

Учитель: Васильева Вадия Фаритовна

Тип урока: формирование новых знаний и их применение.

Межпредметные связи: математика, физика.

Методы работы: кейс-технология.

Тип кейса: обучающий

Цели урока:

1. Подготовка к ЕГЭ. Разработка и составление рекомендаций по решению задач физического и практического содержания №10 профильного уровня ЕГЭ по математике.

2.Развитие исследовательских навыков, умения анализировать, систематизировать, интерпретировать полученные результаты.

3.Повышение интереса учащихся к математике. Расширение кругозора через решение задач связанными с жизненными ситуациями.

Задачи урока:

Образовательные: Систематизировать знания и умения учащихся по решению задач физического и практического содержания.

Развивающие: Развивать умение работать с информацией в нестандартной ситуации; развивать логическое мышление, память, наблюдательность, умение представлять решение; развивать самостоятельную, творческую, исследовательскую деятельность; развивать способность к самооценке.
Воспитательные: Воспитывать уважительное отношение к товарищам, умение работать в команде; умение критически относиться к мнению одноклассников.

Метапредметные УУД:

1.Регулятивные:

1)определять цели, включая постановку новых целей, преобразование практической задачи в познавательную;

2)принимать решения в проблемной ситуации на основе переговоров;

2. Познавательные:

1) учиться основам реализации проектно-исследовательской деятельности;

2) осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий.

3.Коммуникативные:

1) учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве;

2)формулировать собственное мнение и позицию, аргументировать и координировать ее с позициями партнеров в сотрудничестве при выработке общего решения в совместной деятельности;

3)работать в группе — устанавливать рабочие отношения, эффективно сотрудничать и способствовать продуктивной кооперации; интегрироваться в группу сверстников и строить продуктивное взаимодействие со сверстниками и взрослыми.

Содержание кейса.

1. Текст «Трудности ЕГЭ»

2. План работы группы.

3. Правила работы с кейсом.

4. Характеристика задания.

5. Задания группам.

6. Лист достижений группы.

7. Домашнее задание.

ХОД УРОКА.

1этап. Постановка проблемы, определение темы и цели урока. (10 мин)

Слово учителя:

-Здравствуйте ребята! Сегодня я хочу начать урок словами Д.Пойа «Если хочешь научиться плавать — смело входи в воду, а если хочешь научиться решать задачи — бери и решай».

-В последнее время вся деятельность на уроке направлена на то, чтобы качественно подготовиться к ЕГЭ. Сегодня мы будем это делать с помощью кейсов, работая в группах. Что это такое вы уже знаете, но я ещё раз напомню. Кейс — это набор документов, направленных на решение задач определённого типа. Работая вместе, вы чётко соблюдаете правила работы в группе (эти правила вы найдёте в кейсе). Чтобы определить тему урока и цель, предлагаю ознакомиться с первым документом кейса.

Один из учеников зачитывает текст из кейса вслух.

Первый документ. Текст «Трудности ЕГЭ»

Усилия практически всех выпускников 11 класса направлены на поступление в любой достаточно престижный ВУЗ. С этой целью они и выбирают сдавать профильный уровень ЕГЭ по математике. В настоящий момент выявилась одна из жестких проблем: как показал обзор источников информации по подготовке к ЕГЭ, зачастую, вместо стандартно сформулированных математических задач, на экзаменах появляются задания, отражающие «какие-то связи» с реальной жизнью. Ситуация усугубляется тем, что встреча с любыми величинами, напоминающими таковые в учебниках физики, приводит некоторых учеников в состояние стойкого оцепенения (ну не получается у них подружиться с физикой). Решая задания с кратким ответом, некоторые ребята сразу узнают своего «противника» — задание №10 с физическим и практическим содержанием. Им сложно оценить величие и различие слов «доход», «прибыль», «выручка», «рейтинг», мелькающих в этих задачах. Более того, там встречаются и худшие монстры: брошенные камни, то вертикально вниз, то вертикально вверх, перегревающиеся приборы, законы излучения звезд и другие не менее «интересные» задачи. Просмотрев учебник математики, мы понимаем, что там нет таких задач. К счастью, у нас много друзей. И почему бы не сосредоточить их интеллектуальные ресурсы во времени и пространстве на выработку каких -то подходов и тактик решения этой проблемы: как одолеть задание №10? Может, кто-то уже его победил? Может у кого-то есть верный способ, как обойти проблему? И как понять, нужно ли вообще волноваться по данному поводу?

Слово учителя:

-Итак, определяем тему урока: (Решение задачи №10 с физическим и прикладным содержанием)

-Какую цель вы сегодня поставите перед собой на уроке? (овладение приёмами решения задачи №10 профильного ЕГЭ по математике, разработка рекомендаций к решению задач этого типа)

-Как вы кратко охарактеризуете эту задачу? (Задачи больше по физике, чем по математике, но необходимые формулы и величины даны в условии. Большинство задач сводится к решению линейного или квадратного уравнения, либо линейного или квадратного неравенства средствами математики).

-Каждой группе нужно разработать и представить на уроке сколько получится, но, желательно, не менее пяти рекомендаций по решению задания № 10 профильного ЕГЭ по математике. Доказать преимущества своих рекомендаций. У каждой группы будет ровно одна задача. На эту работу отводится 10 мин. Если группа справится раньше, представитель сразу выходит на презентацию и защиту решения.

2 этап. Работа над проблемой. (10 мин)

Далее учащиеся сначала самостоятельно изучают содержимое кейса, затем задают уточняющие вопросы, учитель даёт необходимые комментарии.

Второй документ. «План работы группы»

1. Определить руководителя группы, перед которым будет стоять задача координировать работу группы и оценивать работу её участников.

2. Определить секретаря, который будет фиксировать предложенные решения и представителя, который будет защищать эти решения.

3. Внимательно изучить материалы кейса

4. Проанализировать материал и обсудить изученную информацию

5. Обменяться мнениями и составить план работы над задачей

6. Зафиксировать основные и второстепенные проблемы.

7. Работать сообща над проблемой (дискуссия)

8. Выработать решение задачи с оформлением.

9. Представить решение и общие рекомендации по решению задач этого типа.

10. Доказать его оптимальность (чем выгодно это решение).

Третий документ. Правила работы с кейсом в группе.

Этапы	Цель этапа
Знакомство с конкретным случаем	Понимание проблемной ситуации и ситуации принятия решения
Поиск: оценка информации, полученной из материалов задания, и самостоятельно привлеченной информации	Научиться добывать информацию, необходимую для поиска решения и оценивать ее
Обсуждение: обсуждение возможностей альтернативных решений	Развитие альтернативного мышления
Резолюция: нахождение решения в группах	Сопоставление и оценка вариантов решения.
Диспут: отдельные группы защищают свое решение	Аргументированная защита решений
Сопоставление итогов: сравнение решений, принятых в группах	Оценить взаимосвязь интересов, в которых находятся отдельные решения

Четвёртый документ. Характеристика задания.

Задачи с физическим содержанием

Задачи больше по физике, чем по математике, но необходимые формулы и величины даны в условии. Большинство задач сводится к решению линейного или квадратного уравнения, либо линейного или квадратного неравенства.

Поэтому необходимо уметь решать такие уравнения и неравенства, и определять ответ (имеются задачи, в которых нужно выбрать одно из двух решений, имеются и другие нюансы).

Есть задачи которые сводятся к решению показательных, логарифмических, тригонометрических уравнений и неравенств. Ответ в любом случае, должен получиться в виде целого числа или конечной десятичной дроби.

На экзамене с этим заданием успешно справляются около 40%.выпускников. Наибольшая трудность в заданиях такого типа – чтение, понимание условия, применение математических знаний. Около 15% участников экзамена просто не взялись за эту технически простую задачу.

На что необходимо обратить внимание:

1.Если в вопросе прозвучало «определить наибольшее значение», «определить наименьшее значение», то задача в большинстве случаев решается через составление неравенства.

2. Правильно определяйте знак при составлении неравенства. Например: b не менее 21 записывается как b≥21.

3. Если в вопросе задачи прозвучало «сколько», то составляется уравнение.

4. Не забывайте про единицы измерения, если это необходимо (переводим метры в сантиметры, наоборот и пр.) Все величины подставлять в одних единицах измерения.

5. Не упускайте из виду, в каких единицах измерения требуется записать ответ (например, решив задачу, вы получили 0,5 часа, в условии сказано записать ответ в минутах, получается 30 минут; если запишите 0,5 – это ошибка и потерянный бал, хотя задача решена, верно).

Пятый документ Задачи для групп.

1 группа

№10 . Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в К) от времени работы: T(t)=T0 +b t+a t2, где t — время (в мин.), T0 =1380 К, a=− 15 К / мин2, b=165 К / мин. Известно, что при температуре нагревательного элемента свыше 1800 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.

2 группа

№10. Высота над землёй подброшенного вверх мяча меняется по закону h(t)=1,6+13 t−5 t2, где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 6 метров?

3 группа

№10. Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением a=9000 км /ч. Скорость v (в км/ч) вычисляется по формуле v=√2la, где l — пройденный автомобилем путь (в км). Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 120 км/ч.

4 группа

№10. Груз массой 0,38 кг колеблется на пружине. Его скорость v (в м/с) меняется по закону v=v0sin, где t — время с момента начала колебаний
в секундах, T=8 с — период колебаний, v0=2 м /с. Кинетическая
энергия E (в Дж) груза вычисляется по формуле E=(mv2)/2, где m — масса груза (в кг), v — скорость груза (в м/с). Найдите кинетическую энергию груза через 7 секунд после начала колебаний. Ответ дайте в джоулях.

5 группа

№10. Независимое агентство намерено ввести рейтинг R новостных изданий на основе показателей информативности In, оперативности Op и объективности Tr публикаций. Каждый отдельный показатель — целое число от 0 до 3. Составители рейтинга считают, что информативность публикаций ценится втрое, а объективность — вчетверо дороже, чем оперативность, то есть R=(3In+Op+4Tr)/A. Найдите, каким должно быть число A, чтобы издание, у которого все показатели максимальны, получило рейтинг 30.

3 этап. Защита своих идей. (10 мин)

На этом этапе дети в произвольной форме проводят презентацию решений и формулирование рекомендаций. Скорее всего все группы не успеют выступить, поэтому, защита может быть перенесена на следующий урок с последующим фронтальным закреплением.

ПРОЕКТ ПРЕДЛОЖЕНИЙ, как общий вывод, записывается в тетрадь.

4 этап. Подведение итогов (рефлексия) (5 мин)

Подведение итогов проходит в форме пресс-конференции, в ходе которой учащиеся отвечают на вопросы:

• Что общего в представленных заданиях?

• Что отличает группу заданий №10 от других заданий?

• Есть ли такие задачи в наших учебниках?

• Что хотят проверить составители подобных заданий?

• Хватит ли времени решить все задачи открытого банка задач?

• Стоит ли это делать?

• Являются ли задачи с практическим содержанием №10 отражением реальных жизненных ситуаций?

• Можно ли, проанализировав задачу, подготовиться к решению целого набора заданий?

• Можете ли вы сами найти информацию для подготовки к ЕГЭ в сети Интернет, полезные ссылки на on-line тестирование? Все ли они помогут при подготовке к экзаменам?

• Попробуйте понять, для чего лично Вам может пригодиться сегодняшнее занятие?

5 этап. Домашнее задание. (в кейсе)

Задания практического содержания №10из открытого банка задач ФИПИ на карточках с полным оформленным решением в тетради.

Приложение

Лист достижений группы № ______

Руководитель группы _______________________________

Секретарь_________________________________________

Участники группы

_________________________________________

Количество набранных баллов группы

I этап работы в группе ( поиск, обсуждение, нахождение решений) (от 0 до 5 баллов)

II этап работы в группе (составление рекомендаций по решению) (от 0 до 5 баллов)

III этап (защита решений и представление рекомендаций)

Оценивание работы отметкой каждого участника группы.

Источник

Категория: Физические задачи

Расстояние от наблюдателя, находящегося

263802. Расстояние от наблюдателя, находящегося на небольшой высоте h километров над землей до наблюдаемой им линии горизонта вычисляется по формуле: С какой высоты горизонт виден на расстоянии 4 километра? Ответ выразите в километрах.

Дата: 2015-02-02
3535