Задачи по планиметрии для подготовки к егэ профильный уровень - Помощь в подготовке к экзаменам и поступлению

Вариант 1 6. Планиметрия

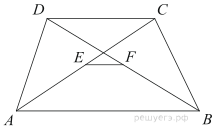
1. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

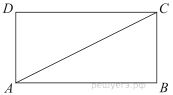
2. Периметр прямоугольника равен 8, а площадь равна 3,5. Найдите диагональ этого прямоугольника.

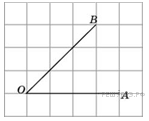
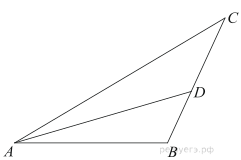
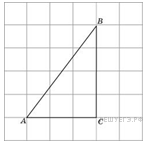
3. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на 2.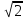

4. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.

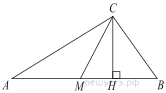
5. Острые углы прямоугольного треугольника равны 53° и 37° . Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

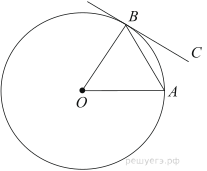
6. Угол между хордой AB и касательной BC к окружности равен 35°. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

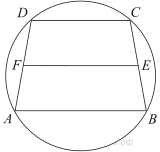
7. Около трапеции описана окружность. Периметр трапеции равен 24, средняя линия равна 11. Найдите боковую сторону трапеции.

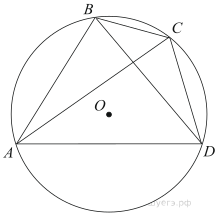
8. Найдите величину угла АВС. Ответ дайте в градусах.

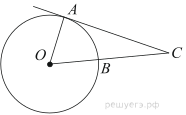
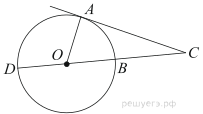
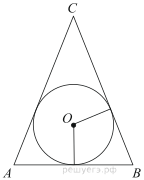
9. Угол ACO равен 35°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.

10. В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах.

Вариант 2 6. Планиметрия

В 1. Сторона правильного треугольника равна 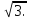Найдите радиус окружности, вписанной в этот треугольник.

2. Две стороны параллелограмма относятся как 9:11, а периметр его равен 40. Найдите большую сторону параллелограмма.

3. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 152°. Ответ дайте в градусах.

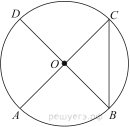
4. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.

5. Радиус окружности, вписанной в правильный треугольник, равен 44. Найдите высоту этого треугольника.

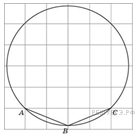
6. Найдите радиус окружности, вписанной в треугольник , считая стороны квадратных клеток равными 1.

7. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 4, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

8. Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.

9. Около трапеции описана окружность. Периметр трапеции равен 52, средняя линия равна 21. Найдите боковую сторону трапеции.

10. Радиус окружности, вписанной в правильный треугольник, равен 31. Найдите высоту этого треугольника.

Вариант 3 6. Планиметрия

1. Четырехугольник ABCD вписан в окружность. Угол ABC равен 110°, угол ABD равен 70°. Найдите угол CAD. Ответ дайте в градусах.

2. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.

3. В треугольнике АВС АС = ВС = 4 , cos ВАС = 0,25. Найдите высоту АН.

4. В ромбе ABCD угол DAB равен 136°. Найдите угол BDC. Ответ дайте в градусах.

5. В треугольнике АВС угол С равен 90°, СН – высота, АС = 3, cos А = . Найдите ВН.

6. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

7. В треугольнике ABC угол C равен 90°, CH — высота, BC = 25, BH = 20. Найдите

8. Найдите площадь ромба, если его диагонали равны 4 и 12.

9. В треугольнике АВС АС = ВС = 4, угол С равен 30°. Найдите высоту АН.

10. В треугольнике ABC угол A равен 30°, угол B равен 86°, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE = CB. Найдите угол BDE. Ответ дайте в градусах

Вариант 4 6. Планиметрия

1. В треугольнике ABC угол C равен 90°, CH — высота, АВ = 15, tg А = . Найдите BH.

2. Угол ACB равен 42°. Градусная величина дуги AB окружности, не содержащей точек D и E, равна 124°. Найдите угол DAE. Ответ дайте в градусах.

3. Сторона ромба равна 20, острый угол равен 30°. Найдите радиус вписанной окружности этого ромба.

4.Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

5. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 20°. Найдите меньший угол прямоугольного треугольника.

6. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.

7. Катеты равнобедренного прямоугольного треугольника равны 82 + 41

Найдите радиус окружности, вписанной в этот треугольник.

8. В остроугольном треугольнике ABC угол A равен 65°. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.

9. В треугольнике АВС угол С равен 90°, СН – высота, ВС = 4, ВН = 4. Найдите

10. Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту этого треугольника.

Вариант 5 6. Планиметрия

1. Найдите косинус угла АОВ. В ответе укажите значение косинуса, умноженное на 2.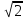

2. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.

3. В треугольнике АВС угол С равен 90°, СН — высота, ВС = 3, sin А = . Найдите АН.

4. Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.

5. Катеты равнобедренного прямоугольного треугольника равны 2+ Найдите радиус окружности, вписанной в этот треугольник.

6. Основания равнобедренной трапеции равны 43 и 7. Высота трапеции равна 27. Найдите тангенс острого угла трапеции.

7. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.

8.Больший угол равнобедренного треугольника равен 98°. Найдите меньший угол. Ответ дайте в градусах.

9. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

10. Стороны параллелограмма равны 38 и 76. Высота, опущенная на первую сторону, равна 57. Найдите высоту, опущенную на вторую сторону параллелограмма.

Вариант 6 6. Планиметрия

1. Сторона АВ треугольника АВС равна 42. Противолежащий ей угол С равен 150° . Найдите радиус окружности, описанной около этого треугольника.

2. Через концы A, B дуги окружности в 114° проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.

3. В треугольнике АВС АС=ВС, АН – высота, АВ=5, sinВАС= . Найдите

4. В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.

5. Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 38°. Найдите угол AOD. Ответ дайте в градусах.

6. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен Найдите высоту трапеции.

7. В треугольнике ABC угол C равен 90°, АС = 8, cos А = Найдите АВ.

8. Периметр треугольника равен 76, а радиус вписанной окружности равен 8. Найдите площадь этого треугольника.

9. Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.

10. В треугольнике ABC угол ACB равен °, угол B равен °, CD — медиана. Найдите угол ACD. Ответ дайте в градусах.

Вариант 7 6. Планиметрия

1. Пусть тупым является угол C, тогда сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

2. Две стороны параллелограмма относятся как 3:17, а периметр его равен 40. Найдите большую сторону параллелограмма.

3. В треугольнике ABC AC = BC, AB = 22, tg А = . Найдите AC.

4. Основания равнобедренной трапеции равны 6 и 12. Боковые стороны равны 5. Найдите синус острого угла трапеции.

5. В треугольнике ABC угол C равен 90°, АС = 17, sin А = . Найдите BC.

6. Найдите площадь треугольника, две стороны которого равны 21 и 2, а угол между ними равен 30°.

7. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 10 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

8. Угол ACO равен 35°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.

9. Угол ACB равен 51°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 144°. Найдите угол DAE. Ответ дайте в градусах.

10.Боковая сторона равнобедренного треугольника равна 5, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.

Вариант 8 6. Планиметрия

1. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.

2. Основания равнобедренной трапеции равны 13 и 25, а ее площадь равна 152. Найдите боковую сторону трапеции.

3. Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.

4. В треугольнике ABC угол C равен 90°, АС = 17, sin А = . Найдите BC.

5. Площадь треугольника ABC равна 136. DE — средняя линия. Найдите площадь треугольника CDE.

6. В треугольнике ABC AC = BC, AB = 8, tg А = . Найдите AC.

7. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 116°. Ответ дайте в градусах.

8. Площадь параллелограмма ABCD равна 176. Точка E — середина стороны CD. Найдите площадь треугольника ADE.

9. Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен 47.

10. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на 2

Вариант 9 6. Планиметрия

1. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.

2. Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.

3. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на

4. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а меньшая дуга окружности AB, заключенная внутри этого угла, равна 37°. Ответ дайте в градусах.

5. Боковые стороны трапеции, описанной около окружности, равны 27 и 4. Найдите среднюю линию трапеции.

6. В треугольнике АВС АС = ВС, АВ = 7 , tg ВАС = , Найдите высоту

7. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 80°. Найдите n.

8. Площадь параллелограмма ABCD равна 189. Точка E — середина стороны AD. Найдите площадь трапеции AECB.

9. Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.

10. Основания равнобедренной трапеции равны 25 и 23. Высота трапеции равна 1. Найдите тангенс острого угла.

Вариант 10 6. Планиметрия

1. Найдите величину угла АВС. Ответ дайте в градусах.

2. В треугольнике ABC угол C равен 76°, AC = BC. Найдите угол A. Ответ дайте в градусах.

3. Площадь треугольника АВС равна 129. ДE – средняя линия, параллельная стороне АВ. Найдите площадь трапеции АВЕД.

4. В треугольнике АВС угол С равен 90°, СН – высота, АН = 12 , cos А = . Найдите АВ.

5. Высота правильного треугольника равна 33. Найдите радиус окружности, описанной около этого треугольника.

6. Основания равнобедренной трапеции равны 5 и 11, а её площадь равна 32. Найдите периметр трапеции.

7. Найдите площадь ромба, если его высота равна 2, а острый угол 30°.

8. Хорда AB делит окружность на две части, градусные величины которых относятся как 3:5. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.

9. В треугольнике известно, что , , угол равен 90°. Найдите радиус вписанной окружности.

10. В треугольнике АВС АС = ВС = 27 , — высота, sin ВАС = . Найдите

6. Планиметрия

Вариант 1

Вариант 2

Вариант 3

40
2
7,5
22
17,5
160
0,6
24
2
56

Вариант 4

Вариант 5

2
122
17,5
46
1
1,5
2
41
30
28,5

Вариант 6

Вариант 7

150
17
22
0,8
34
10,5
24
55
21
10

Вариант 8

Вариант 9

24
9
1
53
15,5
4
18
141,75
36
1

Вариант 10

45
52
96,75
27
22
26
8
112,5
4
30

Источник

16. Задачи по планиметрии

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи по планиметрии

Задание
1

#2436

Уровень задания: Легче ЕГЭ

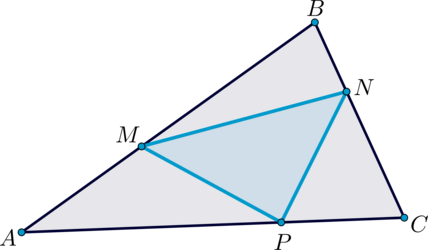
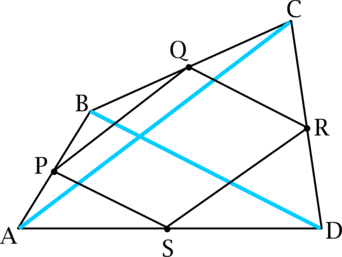
Точки (M, N, P) лежат на сторонах (AB, BC, CA) соответственно треугольника (ABC), причем (AM:AB=BN:BC=CP:CA=1:3). Площадь треугольника (MNP) равна (15). Найдите площадь треугольника (ABC).

(triangle ABC) и (triangle MBN) имеют общий угол (B), при этом (BM=frac23BA), (BN=frac13BC).

Т.к. площади треугольников, имеющих общих угол, относятся как произведения сторон, образующих этот угол, то

[dfrac{S_{MBN}}{S_{ABC}}=dfrac{frac23BAcdot frac13BC}{BAcdot BC}=
dfrac29 quad Rightarrow quad S_{MBN}=dfrac29S_{ABC}]

Аналогично рассуждая, получаем, что

[S_{MAP}=S_{PCN}=dfrac29S_{ABC}]

Следовательно, [15+3cdot dfrac29S_{ABC}=S_{ABC} quad Rightarrow
quad S_{ABC}=3cdot 15=45.]

Ответ: 45

Задание
2

#2444

Уровень задания: Легче ЕГЭ

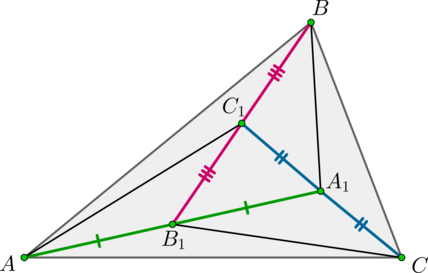
Внутри треугольника (ABC) взяты точки (A_1, B_1, C_1) так, что (B_1) – середина (AA_1), (C_1) – середина (BB_1), (A_1) – середина (CC_1). Найдите отношение площадей треугольников (A_1B_1C_1) и (ABC).

Соединим точки (A) и (C_1), (B) и (A_1), (C) и (B_1).

Т.к. медиана делит треугольник на два равновеликих треугольника, то

[S_{triangle AB_1C}=S_{triangle A_1B_1C}=S_{triangle A_1B_1C_1}.]

Аналогично,

[S_{triangle CA_1B}=S_{triangle C_1A_1B}=S_{triangle AC_1B}=S_{triangle
AC_1B_1}.]

Таким образом, все семь образовавшихся треугольников имеют одинаковые площади. Значит,

[S_{triangle A_1B_1C_1}:S_{triangle ABC}=1:7.]

Ответ:

(1:7)

Задание
3

#1760

Уровень задания: Равен ЕГЭ

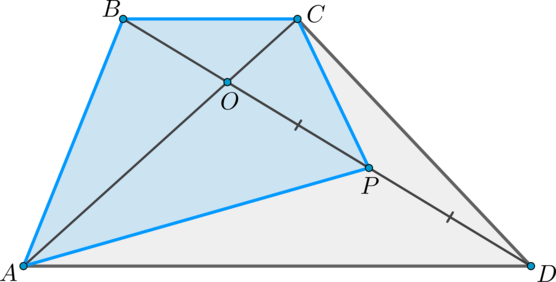
Дана трапеция (ABCD), ее основания (BC) и (AD) равны (2) и (6) соответственно. Диагонали (BD) и (AC) пересекаются в точке (O). Точка (P) – середина (OD). (S_{bigtriangleup ABO}=9). Найдите площадь четырехугольника (ABCP).

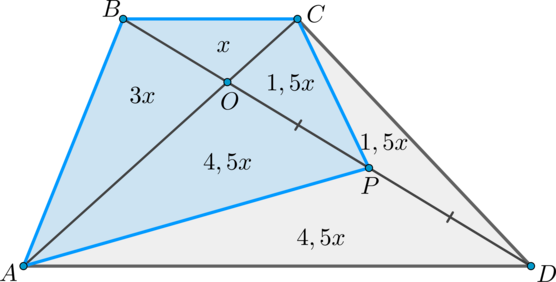
Пусть (S_{bigtriangleup BOC}=x). Заметим, что (bigtriangleup BCO
sim bigtriangleup AOD) по двум углам, так как (BCparallel AD), (angle BCA = angle CAD) как накрест лежащие и (angle BOC = angle
AOD) как вертикальные.

Следовательно, [dfrac{BC}{AD} =dfrac{BO}{OD} =dfrac{CO}{OA}
=dfrac{2}{6} =dfrac{1}{3}.]

(dfrac{S_{bigtriangleup ABO}}{S_{bigtriangleup BCO}}
=dfrac{AO}{OC} =dfrac{3}{1} Rightarrow S_{bigtriangleup
ABO}=3x), аналогично, (S_{bigtriangleup CDO}=3x).

(dfrac{S_{bigtriangleup COP}}{S_{bigtriangleup CPD}}
=dfrac{OP}{PD} =dfrac{1}{1} Rightarrow S_{bigtriangleup
COP}=S_{bigtriangleup CPD}=1,5x).

Площади подобных треугольников относятся как коэффициент подобия в квадрате, следовательно, [dfrac{S_{bigtriangleup BOC}}{S_{bigtriangleup AOD}} =left(
dfrac{1}{3} right)^2 =dfrac{1}{9} Rightarrow
S_{bigtriangleup ADO}=9x Rightarrow S_{bigtriangleup APO}=4,5x
Rightarrowqquad S_{ABCP}=10x.] Так как (3x=9), то (x=3) и, следовательно, (S_{ABCP}=30).

Ответ: 30

Задание
4

#2441

Уровень задания: Равен ЕГЭ

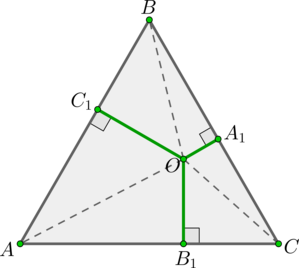
Внутри равностороннего треугольника со стороной (m) движется точка. Докажите, что сумма расстояний от этой точки до сторон треугольника не меняется, и найдите эту сумму.

Рассмотрим равносторонний (triangle ABC), (AB=m), (O) – точка внутри треугольника, (OA_1, OB_1, OC_1) — перпендикуляры на стороны (BC, AC, AB) соответственно.

Рассмотрим (triangle AOB, triangle BOC, triangle COA). Их площади равны (0,5mcdot OC_1; 0,5mcdot OA_1; 0,5mcdot OB_1) соответственно. Тогда сумма их площадей равна площади всего (triangle ABC), следовательно:

[0,5mcdot (OC_1+OA_1+OB_1)=S_{triangle ABC}=dfrac{sqrt3}4m^2 quad
Leftrightarrow quad OC_1+OA_1+OB_1=dfrac{sqrt3}2m.]

Таким образом, мы доказали, что для фиксированного равностороннего треугольника сумма постоянна, а также нашли ее.

Ответ:

(dfrac{sqrt3}2m)

Задание
5

#1287

Уровень задания: Равен ЕГЭ

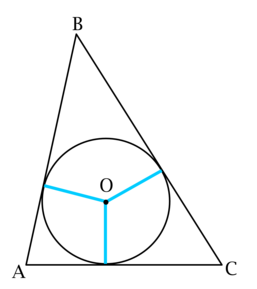
Радиус вписанной в треугольник (ABC) окружности равен трети одной из его высот.

а) Докажите, что одна из сторон треугольника (ABC) равна среднему арифметическому двух других его сторон.

б) Найдите наибольшее возможное значение периметра такого треугольника, если одна из его сторон равна (4), а две другие имеют целые длины.

а) (S_{ABC} = pcdot r), где (p) – полупериметр, а (r) – радиус вписанной в (ABC) окружности.

Пусть (h) – длина той высоты, которая равна (3r), (a) – длина стороны, высота к которой имеет длину (h), (P) – периметр треугольника (ABC).

В итоге имеем: [dfrac{1}{2}hcdot a = S_{ABC} = pcdot r = pcdotdfrac{h}{3},] откуда (a = dfrac{P}{3}), тогда (b + c = dfrac{2P}{3} = 2a), где (b) и (c) длины других сторон треугольника.

б) Длины сторон треугольника (ABC) образуют арифметическую прогрессию: если обозначить (a — c = d), то (a = c + d), (b = c + 2d).

Пусть (d > 0). Тогда (b) наибольшая сторона треугольника (ABC) и существование треугольника (ABC) с длинами сторон (a), (b) и (c) равносильно выполнению неравенства [b < a + cqquadLeftrightarrowqquad c + 2d < 2c + dqquadLeftrightarrowqquad d < c.] Так как длины всех сторон треугольника (ABC) – целые числа, то (d) – целое, следовательно, (dleq c — 1).

Так как (c) – меньшая из сторон, то (cleq 4), тогда (dleq 3), откуда (aleq 7), (bleq 10), тогда [P_{triangle ABC}leq 4 + 7 + 10 = 21.] При этом случай (c = 4), (a = 7), (b = 10) подходит, следовательно, при (d > 0) максимально возможный периметр равен 21.

При (d = 0) треугольник (ABC) равносторонний и (P_{triangle ABC} = 12 < 21).

Случай (d < 0) рассматривается аналогично (меняется только то, что (c > a > b), следовательно, достаточно в рассуждении из случая (d > 0) всюду поменять местами (b) и (c)).

Таким образом, наибольший возможный периметр треугольника (ABC) равен 21.

Ответ:

б) (21).

Задание
6

#1288

Уровень задания: Равен ЕГЭ

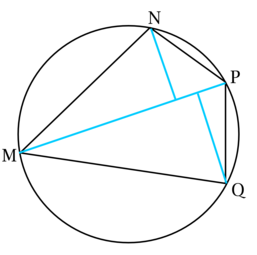
Четырёхугольник (MNPQ) вписан в окружность, причём (dfrac{MN}{PQ} = dfrac{QM}{PN}).

а) Докажите, что точки (N) и (Q) равноудалены от прямой, содержащей (MP).

б) Найдите расстояние от точки (P) до прямой, содержащей (MQ), если (MP = 4), расстояние от (N) до прямой, содержащей (MP) равно (1,5), (MQ = 3).

а) Так как (dfrac{MN}{PQ} = dfrac{QM}{PN}), то (MNcdot PN = QMcdot PQ).

Так как (MNPQ) вписанный, то (angle MNP = 180^circ — angle MQP), следовательно, (sinangle MNP = sinangle MQP).

В итоге [S_{triangle MNP} = 0,5cdot MNcdot PNcdotsinangle MNP = 0,5cdot QMcdot PQcdotsinangle MQP = S_{triangle MQP}.]

С другой стороны, у треугольников (MNP) и (MQP) общее основание, следовательно, их площади относятся как высоты, проведённые к этому основанию, тогда эти высоты равны, значит, точки (N) и (Q) равноудалены от прямой, содержащей (MP).

б) В данном случае (S_{triangle MNP} = 0,5cdot 4cdot 1,5 = 3), но (S_{triangle MNP} = S_{triangle MQP}). Обозначим расстояние от точки (P) до прямой, содержащей (MQ) через (h), тогда [S_{triangle MQP} = 3 = 0,5cdot 3cdot h,] следовательно, (h = 2).

Ответ:

б) (2).

Задание
7

#1289

Уровень задания: Равен ЕГЭ

(ABCD) – выпуклый четырёхугольник, точки (P), (Q), (R) и (S) середины его сторон, причём (PQRS) тоже выпуклый четырёхугольник. (A_1B_1C_1D_1) другой выпуклый четырёхугольник с серединами сторон в точках (P), (Q), (R) и (S).

а) Докажите, что диагонали (PQRS) точкой пересечения делятся пополам.

б) Найдите максимально возможное значение величины (dfrac{S_{A_1B_1C_1D_1}}{S_{ABCD}}).

а) Проведём диагонали (AC) и (BD).

Рассмотрим треугольники (APS) и (ABD): (PS) – средняя линия в треугольнике (ABD), тогда треугольники (APS) и (ABD) подобны, причём (dfrac{PS}{BD} = dfrac{1}{2}).

Аналогично (dfrac{QR}{BD} = dfrac{1}{2}), следовательно, (PS = QR).

Аналогично доказывается равенство (PQ = RS). В итоге в выпуклом четырёхугольнике (PQRS) противоположные стороны равны, тогда (PQRS) – параллелограмм, следовательно, его диагонали точкой пересечения делятся пополам.

б) Докажем, что по взаимному расположению середин сторон выпуклого четырёхугольника его площадь восстанавливается однозначно.

Из подобия (APS) и (ABD) получаем: [dfrac{S_{APS}}{S_{ABD}} = left(dfrac{1}{2}right)^2 = dfrac{1}{4}.]

Аналогично (4S_{QCR} = S_{CBD}), (4S_{PBQ} = S_{ABC}), (4S_{SDR} = S_{ACD}). Тогда [S_{ABCD} = S_{ABD} + S_{CBD} = 4S_{APS} + 4S_{QCR}.] С другой стороны, [S_{ABCD} = S_{ABC} + S_{ACD} = 4S_{PBQ} + 4S_{SDR},] тогда [S_{ABCD} + S_{ABCD} = 4S_{APS} + 4S_{QCR} + 4S_{PBQ} + 4S_{SDR} qquadLeftrightarrow] [S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} = dfrac{1}{2}S_{ABCD}.] Но (S_{ABCD} = S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} + S_{PQRS}), откуда окончательно [S_{PQRS} = dfrac{1}{2}S_{ABCD}.]

Таким образом, по взаимному расположению точек (P), (Q), (R), (S) однозначно восстанавливается площадь параллелограмма (PQRS), а значит и площадь любого выпуклого четырёхугольника с серединами сторон в точках (P), (Q), (R) и (S).

В итоге [dfrac{S_{A_1B_1C_1D_1}}{S_{ABCD}} = 1.]

Ответ:

б) (1).

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.

а)  докажите, что биссектриса угла С делит отрезок МN пополам

б)  пусть Р  — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.

Источник: ЕГЭ по математике 19.06.2014. Основная волна, резервная волна. Запад. Вариант 1

Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°.

а)  Докажите, что ∠CBE = ∠COE.

б)  Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE = 40 и CE  =  24.

Медианы AA₁, BB₁ и CC₁ треугольника ABC пересекаются в точке M. Известно, что AC  =  3MB.

а)  Докажите, что треугольник ABC прямоугольный.

б)  Найдите сумму квадратов медиан AA₁ и CC₁, если известно, что AC = 12.

На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M  — середина стороны AB.

а)  Докажите, что

б)  Найдите расстояние от точки M до центров квадратов, если AC  =  10, BC  =  32 и ∠ACB  =  30°.

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016

На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE.

а)  Докажите, что точки A, B, K и E лежат на одной окружности.

б)  Найдите радиус этой окружности, если AB = 12, CH = 5.

Пройти тестирование по этим заданиям

Источник

Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 1.

В окружности с центром O AC и BD — диаметры. Вписанный угол ACB равен Найдите центральный угол AOD. Ответ дайте в градусах.

Сторона ромба равна 58, острый угол равен Найдите радиус вписанной окружности этого ромба.

Угол ACB равен Градусная величина дуги AB окружности, не содержащей точек D и E, равна Найдите угол DAE. Ответ дайте в градусах.

10.

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 4, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

В треугольнике ABC сторона AB равна 3 угол С равен 135°. Найдите радиус описанной около этого треугольника окружности.

11.

Катеты равнобедренного прямоугольного треугольника равны Найдите радиус окружности, вписанной в этот треугольник.

Хорда AB делит окружность на две части, градусные величины которых относятся как Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.

12.

Основания равнобедренной трапеции равны 240 и 70. Радиус описанной окружности равен 125.

Найдите высоту трапеции.

Касательные CA и CB к окружности образуют угол ACB, равный 34°. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.

13.

Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно , , , Найдите угол B этого четырехугольника. Ответ дайте в градусах.

Угол ACO равен 58°. Его сторона CA касается окружности. Найдите градусную меру дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах.

14.

Радиус окружности, описанной около правильного треугольника, равен Найдите сторону этого треугольника.

Сторона правильного треугольника равна Найдите радиус окружности, вписанной в этот треугольник.

15.

Около трапеции описана окружность. Периметр трапеции равен 48, средняя линия равна 19. Найдите боковую сторону трапеции.

Около окружности, радиус которой равен 1, описан многоугольник, периметр которого равен 8. Найдите его площадь.

16.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 88. Найдите радиус описанной окружности этой трапеции.

Проверочная работа по № 1ЕГЭ «Окружность». ВАРИАНТ – 2.

Сторона ромба равна 100, острый угол равен Найдите радиус вписанной окружности этого ромба.

Угол ACB равен 51°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 144°. Найдите угол DAE. Ответ дайте в градусах.

10.

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 19 и 2, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

В треугольнике ABC сторона AB равна 4 угол С равен 120°. Найдите радиус описанной около этого треугольника окружности.

11.

12.

Основания равнобедренной трапеции равны 72 и 30. Радиус описанной окружности равен 39.

Найдите высоту трапеции.

Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.

13.

Угол ACO равен Его сторона CA касается окружности. Найдите градусную величину дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах.

14.

Радиус окружности, описанной около правильного треугольника, равен Найдите сторону этого треугольника.

Сторона правильного треугольника равна Найдите радиус окружности, вписанной в этот треугольник.

15.

Около трапеции описана окружность. Периметр трапеции равен 76, средняя линия равна 6. Найдите боковую сторону трапеции.

Около окружности, радиус которой равен 7, описан многоугольник, периметр которого равен 30. Найдите его площадь.

16.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен , большее основание равно 36. Найдите радиус описанной окружности этой трапеции.

Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ –3.

Сторона ромба равна 24, острый угол равен Найдите радиус вписанной окружности этого ромба.

10.

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 20 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

В треугольнике ABC сторона AB равна 4 угол С равен 135°. Найдите радиус описанной около этого треугольника окружности.

11.

12.

Основания равнобедренной трапеции равны 144 и 60. Радиус описанной окружности равен 78.

Найдите высоту трапеции.

13.

14.

Радиус окружности, описанной около правильного треугольника, равен Найдите сторону этого треугольника.

Сторона правильного треугольника равна Найдите радиус окружности, вписанной в этот треугольник. ОТВЕТ

15.

Около трапеции описана окружность. Периметр трапеции равен 88, средняя линия равна 12. Найдите боковую сторону трапеции.

Около окружности, радиус которой равен 2, описан многоугольник, периметр которого равен 29. Найдите его площадь.

16.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен , большее основание равно 82. Найдите радиус описанной окружности этой трапеции.

Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 4.

Сторона ромба равна 46, острый угол равен Найдите радиус вписанной окружности этого ромба.

10.

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 15 и 2, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

В треугольнике ABC сторона AB равна 6 угол С равен 120°. Найдите радиус описанной около этого треугольника окружности.

11.

12.

Основания равнобедренной трапеции равны 288 и 84. Радиус описанной окружности равен 150.

Найдите высоту трапеции.

13.

14.

Радиус окружности, описанной около правильного треугольника, равен Найдите сторону этого треугольника.

Сторона правильного треугольника равна Найдите радиус окружности, вписанной в этот треугольник.

15.

Около трапеции описана окружность. Периметр трапеции равен 104, средняя линия равна 20. Найдите боковую сторону трапеции.

Около окружности, радиус которой равен 4, описан многоугольник, периметр которого равен 63. Найдите его площадь.

16.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен , большее основание равно 74. Найдите радиус описанной окружности этой трапеции

Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 5.

Сторона ромба равна 50, острый угол равен Найдите радиус вписанной окружности этого ромба.

10.

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 13 и 2, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

11.

12.

Основания равнобедренной трапеции равны 24 и 10. Радиус описанной окружности равен 13.

Найдите высоту трапеции.

13.

14.

Радиус окружности, описанной около правильного треугольника, равен Найдите сторону этого треугольника.

Сторона правильного треугольника равна Найдите радиус окружности, вписанной в этот треугольник.

15.

Около окружности, радиус которой равен 2, описан многоугольник, периметр которого равен 35. Найдите его площадь.

16.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен , большее основание равно 78. Найдите радиус описанной окружности этой трапеции.

Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 6.

Сторона ромба равна 94, острый угол равен Найдите радиус вписанной окружности этого ромба.

10.

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 15 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

В треугольнике ABC сторона AB равна 3 угол С равен 120°. Найдите радиус описанной около этого треугольника окружности.

11.

12.

Основания равнобедренной трапеции равны 192 и 56. Радиус описанной окружности равен 100.

13.

14.

Радиус окружности, описанной около правильного треугольника, равен Найдите сторону этого треугольника.

Сторона правильного треугольника равна Найдите радиус окружности, вписанной в этот треугольник.

15.

Около трапеции описана окружность. Периметр трапеции равен 100, средняя линия равна 18. Найдите боковую сторону трапеции.

Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 62. Найдите его площадь.

16.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен , большее основание равно 30. Найдите радиус описанной окружности этой трапеции.

Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 7.

Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 38°. Найдите угол AOD. Ответ дайте в градусах.

Сторона ромба равна 20, острый угол равен Найдите радиус вписанной окружности этого ромба.

10.

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 10 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

В треугольнике ABC сторона AB равна 2 угол С равен 120°. Найдите радиус описанной около этого треугольника окружности.

11.

12.

Основания равнобедренной трапеции равны 32 и 24. Радиус описанной окружности равен 20.

Найдите высоту трапеции.

Касательные CA и CB к окружности образуют угол ACB, равный 78°. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.

13.

Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 76°, 101°, 106°, 77°. Найдите угол B этого четырехугольника. Ответ дайте в градусах.

Угол ACO равен Его сторона CA касается окружности с центром в точке O. Сторона CO пересекает окружность в точках B и D (см. рис.). Найдите градусную меру дуги AD окружности, заключённой внутри этого угла. Ответ дайте в градусах.

14.

Радиус окружности, описанной около правильного треугольника, равен Найдите сторону этого треугольника.

Сторона правильного треугольника равна Найдите радиус окружности, вписанной в этот треугольник.

15.

Около трапеции описана окружность. Периметр трапеции равен 52, средняя линия равна 21. Найдите боковую сторону трапеции.

Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 50. Найдите его площадь.

16.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен , большее основание равно 38. Найдите радиус описанной окружности этой трапеции.

Источник

18 июня 2021

В закладки

Обсудить

Жалоба

Тесты по планиметрии

Сборник тестов по всем разделам планиметрии. Проработка этих задач будет служить первым этапом подготовки к успешному решению задачи 16 ЕГЭ. Тесты можно использовать как для работы на спецкурсах по планиметрии, домашней работы, так и итогового контроля.

t1.docx
t2.docx
t3.docx
t4.docx
t5.docx

Автор: Марина Владимировна Авраменко.

Источник

Планиметрия – профильный ЕГЭ по математике (оглавление)

Планиметрия плохо дается многим ученикам. На ЕГЭ эта задача №16 – одна из самых сложных задач и многие даже не пытаются за нее браться.

Весь секрет в том, что понимание планиметрии приходит не постепенно, а сразу. Вчера не получалось, а сегодня уже все понятно. Большинству просто не хватает терпения дойти до этого момента.

Надеемся, что ты не такой и не бросишь занятия на полпути. И вот тебе в помощь все, что нужно знать по планиметрии + несколько вебинаров для отработки навыков!

Планиметрия – часть 1. ЕГЭ №3 (бывшая №6)

Если вы плохо знаете планиметрию, начинайте с этой части и смотрите вебинар за вебинаром, ставьте на паузу и решайте задачи вместе с ведущим вебинаров Алексеем Шевчуком.

Помните, планиметрия требует нарешенности. Чтобы научиться решать любую задачу по планиметрии, нужно решать много задач.

Начните с самого начала.

Планиметрия – прямоугольный треугольник

Итак, прямоугольный треугольник, его свойства, площадь и углы прямоугольного треугольника, теорема Пифагора, тригонометрический функции острых углов, медиана и высота.

Планиметрия – равнобедренный треугольник и произвольный треугольник

В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ.

Очень часто все “проблемы” с решением задач на равнобедренный треугольник решаются построением высоты. Также мы научимся решать и “обычные” треугольники.

Убедимся в достоверности утверждении из прошлого урока о прямоугольных треугольниках – очень часто решение задач сводится к нескольким прямоугольным треугольникам.

Вписанная окружность

В этом видео мы узнаем, что такое вписанная окружность, где находится её центр, и другие ее свойства. В какие фигуры можно, а в какие нельзя вписать окружность.

Научимся решать задачи на вписанную окружность – очень важный навык в понимании планиметрии.

Описанная окружность. Многоугольники

Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства. Около каких фигур можно, а вокруг каких нельзя описать окружность.

Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью.

Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.

Что приблизит нас к умению решать любые задачи по планиметрии.

Теорема косинусов и синусов

Универсальный инструмент при решении треугольников – это теоремы косинусов и синусов.

Они подходят для любых треугольников, а не только для прямых (как теорема Пифагора).

А как мы уже знаем, почти любая задача в планиметрии сводится именно к треугольникам.

На этом уроке мы выучим сами теоремы и научимся применять их при решении задач первой части.

Планиметрия – часть 2. ЕГЭ №16

Эта часть планиметрии – для продвинутых, для тех, кто уже хорошо усвоил планиметрию из первой части.

Принцип тот же – смотрите вебинар за вебинаром и, самое главное, ставьте на паузу и решайте задачи.

Планиметрия. Подобие треугольников. Задачи на доказательство. ЕГЭ №16

Подобие треугольников. Это одна из самых сложных задачи планиметрии в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников!

Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства.

Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.

В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.

Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.

Вы научитесь также применять подобие треугольников не только для доказательств, а и для расчётных задач.

Метод вспомогательной окружности. Из реального ЕГЭ 2016 года

Метод вспомогательной окружности – это очень классный метод, используемый в планиметрии но, к сожалению, он не всегда очевиден. Иногда в задаче нет даже намёка ни на какие окружности, но тем не менее, если догадаться её на рисунке достроить, решение становится в разы проще!

Как минимум, сразу же становятся равными друг другу очень неочевидные углы – те, которые опираются на одну дугу, но без окружности увидеть это было бы нереально сложно. Либо произведения отрезков хорд равны друг другу.

Это очень крутой и удобный метод – но нужно понимать, в каких ситуациях он применяется, ведь далеко не всегда нужно на и без того сложный рисунок лепить ещё и окружность.

Теорема Менелая и Чевы. “Секретный” метод решения самой сложной задачи ЕГЭ по математике

Задача №16. Планиметрия. Одна из самых сложных задач на ЕГЭ. Редко кто (менее 1% учеников!) набирает полные баллы по ней и поэтому грех не воспользоваться шорткатами и лайфхаками, если они есть.

Теорема Менелая и Чевы – один из таких шорткатов. Эти теоремы не входят в стандартную школьную программу, но они невероятно мощный инструмент! Они могут очень-очень упростить решение и сами по себе они красивые и легко запоминаются.

Итак, смотрите видео, учите теорему Менелая и Чевы, используйте ее на ЕГЭ.

Теорема Менелая и Чевы — её уже запретили, наконец, или нет?

Каждый год начинают ходить слухи, что теоремами Менелая и Чевы В ЭТОМ ГОДУ НЕЛЬЗЯ будет пользоваться на ЕГЭ. Правда ли это? Чтобы понять это, достаточно заглянуть в обычный…

Впрочем, смотрите это видео и узнаете, как понять, какими теоремами можно, а какими нельзя пользоваться. А также, на этом вебе мы разберём, что это за теоремы такие, и как ими пользоваться.

Вы узнаете, насколько они крутые и мощные, и насколько экономят нам время в некоторых задачах.

Планиметрия Статград март 2021

Задача №16 из мартовского статграда на планиметрию ничем не удивляет: снова окружность и пропорциональные отрезки в ней, прямоугольные треугольники, вот это всё.

Скучно… Раз-два, и ответ готов!

Но погодите-ка, а почему у нас с вами ответ получился разный? И вроде бы оба делаем всё правильно…

На уроках нашего курса я рассказывал о таких задачах, но их уже давненько не попадалось на ЕГЭ, и все уж думали, что ушла эпоха. Конечно, никакого парадокса в этой задаче нет, нужно всего лишь (ха-ха) быть очень внимательными:)

Смотрите видео, и узнаете, в чём же особенность этой задачи, как её правильно решать и оформлять, а также – как ничего не упустить на экзамене и не потерять баллы!

Планиметрия. Окружности. Задача из олимпиады Физтеха 2020

Планиметрия и окружности! Куда же деться от них в 16 задаче на ЕГЭ?

Те, кто ходил на наш курс подготовки, посвященный 16 задаче, знают, что окружности в задачах на планиметрию попадаются чаще всего.

Иногда вписанные. Иногда описанные. С разными вписанными или описанными фигурами. Иногда одна окружность . Иногда две. Они касаются друг друга или пересекаются друг с другом. Никуда не деться от окружностей – остается только научится их решать и получать удовольствие от красивых задач!

В этом видео мы разберём, что бы вы думали? Задачу 16 из ЕГЭ?

Нет! Пойдём дальше – разберём задачу из олимпиады Физтеха прошлого года.

Стойте, не разбегайтесь! Олимпиады далеко не всегда бывают сложными (особенно, если вы прошли наш курс по 16-й задаче). Эта задача вполне себе ЕГЭ-шного уровня. Про окружности и прямоугольные треугольники.

Готовьтесь и “разминайте” свои теоремы Пифагора, теорему синусов и прочих косинусов.

Разбор задачи №16 (б) из реального варианта ЕГЭ 2021 по профильной математике

Продолжение предыдущего видео. Разбор части (б):

Теперь слово вам…

Как вам наш гид по планиметрии? Что нового вы узнали? Что еще хотите узнать?

Как вам теорема Менелая и Чевы? Один из моих знакомых сказал: “В школе ее от нас утаивали!”. Шутка, в которой есть доля… шутки.

Готовьтесь к планиметрии и забирайте свои 3 балла на ЕГЭ.

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук – ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 – WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org – email для записи

тысячи учеников, поступивших в лучшие ВУЗы страны
автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
закончил МФТИ, преподавал на малом физтехе;
репетиторский стаж – c 2003 года;
в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.

Источник

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Планиметрия»

Открытый банк заданий по теме планиметрия. Задания C4 из ЕГЭ по математике (профильный уровень)

Задание №1208

Условие

Биссектриса острого угла параллелограмма пересекает его сторону в точке K. Окружность радиусом 3 проходит через точку пересечения диагоналей и касается трёх сторон параллелограмма, причём K — одна из точек касания.

а) Докажите, что треугольник ABK равнобедренный.

б) Найдите площадь параллелограмма.

Показать решение

Решение

а) По условию angle BAK=angle KAD, angle KAD=angle AKB как накрест лежащие при BC parallel AD и секущей AK. Следовательно, angle BAK=angle AKB и triangle ABK равнобедренный.

б) Пусть CF=x, FD=y, радиус окружности r, тогда, учитывая, что отрезки касательных, проведённых к окружности из одной точки, равны и треугольник ABK равнобедренный, найдём AD=2x+y, поэтому площадь параллелограмма равна S=2r(2x+y)=6(2x+y).

С другой стороны, площадь параллелограмма равна удвоенной площади прямоугольной трапеции CDNM, так как G — точка пересечения диагоналей, поэтому S= 2cdot frac12cdot P_{CDNM}cdot r= (4r+2x+2y)cdot r= 2r(2r+x+y)= 6(6+x+y).

Приравнивая площади, получим уравнение 2x+y=6+x+y, откуда x=6.

angle COD=90^{circ} как угол, образованный двумя биссектрисами смежных углов. Из triangle COD, OF^2=CFcdot FD, r^2=xcdot y, отсюда y=frac{r^2}x=frac96=frac32.

Теперь найдём площадь параллелограмма ABCD, воспользовавшись одной из формул

S=6(2x+y)=6left( 2cdot 6+frac32 right) =81.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1207

Условие

В окружность вписана трапеция ABCD с основаниями AD и BC, один из углов которой равен 60^{circ}. В трапецию вписана ещё одна окружность.

а) Докажите, что центр описанной окружности трапеции лежит внутри трапеции.

б) Найдите, во сколько раз CD больше радиуса окружности, касающейся сторон AB, AD и вписанной окружности трапеции ABCD, если AD>BC.

Показать решение

Решение

а) План решения.

1. Сделаем чертёж, считая для определённости, что AD>BC (для пункта а) это не имеет значения).

2. Заметим, что трапеция равнобедренная. Обозначим одну из сторон трапеции какой-либо буквой, выразим остальные стороны.

3. Выразим через ту же букву радиус окружности, описанной около трапеции: это можно сделать по теореме синусов для triangle ABD.

4. Обозначим точкой N середину AD, точкой M — середину BC. Найдём CN.

5. Сравним CN с радиусом описанной окружности. Сделаем вывод, учитывая, что радиус описанной окружности лежит на прямой MN.

Решение.

1. Выполним чертёж.

2. Так как трапеция ABCD вписана в окружность, то она равнобедренная, то есть AB=CD=a. angle BAD=60^{circ}. Следовательно, AH =frac12 AB=frac12 a, KD=frac12 a. a. Так как в ABCD вписана окружность, то AB+CD=BC+AD, отсюда BC =frac12 a и AD=frac32 a.

3. Радиус описанной окружности трапеции ABCD равен радиусу описанной окружности triangle ABD. Из triangle ABD по теореме синусов 2R= frac{BD}{sin angle BAD} = frac2{sqrt 3}cdot sqrt {BH^2+HD^2}= frac2{sqrt 3}cdot sqrt {left( frac{asqrt 3}2 right) ^2+a^2}= frac{sqrt 7}{sqrt 3} a, R=frac{sqrt 7}{2sqrt 3} a.

4. Центр O описанной окружности трапеции ABCD лежит на прямой MN, где M и N — середины BC и AD соответственно. CN= sqrt {CK^2+NK^2} = sqrt {left( frac{asqrt 3}2 right)^2+left(frac a4 right)^2}= frac{sqrt {13}}4 a.

5. Сравним CN и R, frac{sqrt {13}}4>frac{sqrt 7}{2sqrt 3,} то есть sqrt {NM^2+MC^2}>sqrt {OM^2+MC^2}, отсюда MN>OM или радиус описанной окружности лежит на прямой MN, а центр описанной окружности лежит внутри отрезка MN.

б) План решения.

1. Сделаем чертёж, обозначив центр вписанной окружности через O_1, а центр второй окружности — через O_2. Построим радиус O_2T perp AD.

2. Из подобных треугольников O_2AT и O_1AN, зная angle O_2AT, вычислим O_2T.

3. Найдём искомое отношение frac{CD}{O_2T}.

Решение.

1. Выполним чертёж.

2. triangle O_2AT sim triangle O_1AN, тогда frac{O_1N}{O_2T}=frac{AO_1}{AO_2}. Обозначим искомый радиус O_2T через x, получим: frac{O_1N}x= frac{AO_1}{AO_1-O_1N-x}. BH=MN, из triangle ABH: BH=ABcdot sin 60^{circ}=frac{asqrt 3}2 , MN =frac{asqrt 3}2.

Центр окружности, вписанной в угол, лежит на биссектрисе этого угла, поэтому angle O_1AN =frac12 angle BAD=30^{circ}. Тогда AO_1=2O_1N (катет, лежащий против угла в 30^{circ}, равен половине гипотенузы). Отсюда frac{O_1N}x=frac{2O_1N}{O_1N-x} , frac1x =frac2{O_1N-x} , O_1N-x=2x, x= frac13 O_1N= frac13cdot frac12 MN= frac16cdot frac {asqrt 3} 2= frac{asqrt 3}{12} , x=frac{asqrt 3}{12} , то есть O_2T=frac{asqrt 3}{12}.

3. frac{CD}{O_2T} = frac a{left( dfrac{asqrt 3}{12} right)} = 4sqrt 3.

Ответ

4sqrt 3.

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1206

Условие

Задан треугольник ABC, каждая сторона которого равна 2. За пределами треугольника дана точка D так, что angle ADC=120^{circ}. Прямая l проходит через точку A и перпендикулярна отрезку, проведённому в A из точки пересечения высот triangle ABC. K — точка пересечения прямых l и BD. Длина отрезка AK равна 1.

а) Докажите, что BKcdot DK=1

б) Найдите длину отрезка AD.

Показать решение

Решение

1. Опишем окружность около треугольника ADC. Так как angle ADC=120^{circ}, то он опирается на дугу этой окружности, градусная мера которой равна 240^{circ}.

Пусть точка M является серединой этой дуги, тогда все дуги AC, AM и CM имеют градусную меру 120^{circ}. Поэтому треугольник AMC является равносторонним, длина каждой его стороны равна длине AC. Значит, точка M совпадает с точкой B треугольника ABC.

Получаем, что указанная окружность описана около треугольника ABC. Её центр O является точкой пересечения биссектрис (высот и медиан). Поэтому отрезок, проведённый из точки A к точке пересечения высот треугольника совпадает с отрезком AO, где AO — радиус описанной окружности. По условию l perp OA.

Так как l perp AO, то l перпендикулярна радиусу, поэтому l является касательной к окружности. По свойству касательной и секущей, проведённых к окружности из одной точки K получаем: AK^2=KBcdot KD. Но AK=1, значит 1=KBcdot KD. Что и требовалось доказать.

б) 1. На рисунке angle KAB=angle KAO+angle OAB. angle KAO=90^{circ} по условию, angle OAB=frac12angle CAB, так как AO — биссектриса angle CAB. Но angle CAB=60^{circ}, значит, angle OAB=30^{circ}, а angle KAB=90^{circ}+30^{circ}=120^{circ}.

2. По теореме косинусов для triangle ABK получаем:

BK^2= AB^2+AK^2-2cdot ABcdot AKcdot cos 120^{circ}= 4+1-2cdot 2cdot 1left( -frac12right) = 7, так как cos 120^{circ}=-frac12, BK=sqrt 7.

В пункте а) установлено, что BKcdot KD=1, поэтому KD=frac1{BK}=frac1{sqrt 7}.

Отсюда BD=BK-KD=sqrt 7-frac1{sqrt 7}=frac6{sqrt 7}.

Заметим, что angle ADB =frac12cdot 120^{circ}=60^{circ} (применили теорему о вписанном угле).

3. Обозначим AD=x.

По теореме косинусов для треугольника ADB получаем: AB^2= AD^2+BD^2-2cdot ADcdot BDcdot cos angle ADB,

4=x^2+frac{36}7-2cdot xcdotfrac6{sqrt 7}cdotcos 60^{circ},

4=x^2+frac{36}7-2cdot xcdot frac6{sqrt 7}cdot frac12,

x^2-frac6{sqrt 7}x+frac87=0.

По теореме Виета x_1 =frac2{sqrt 7}, x_2=frac4{sqrt 7}.

По свойству треугольника DK+AK>AD, поэтому frac1{sqrt 7}+1>AD.

Если AD =frac4{sqrt 7}, то должно выполняться frac1{sqrt 7} +1>frac4{sqrt 7}, frac3{sqrt 7}<1, 3<sqrt 7, что не верно.

Следовательно, AD =frac2{sqrt 7}.

Ответ

frac2{sqrt7}.

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1205

Условие

Две окружности касаются внешним образом в точке P. Прямая MN касается первой окружности в точке M, а второй — в точке N.

а) Докажите, что triangle MNP прямоугольный.

б) Найдите площадь triangle MNP, если известно, что радиусы окружностей равны 4 и 16.

Показать решение

Решение

а) Пусть O_1 и O_2 — центры касающихся окружностей. Через точку P проведём общую касательную заданных окружностей и обозначим через Q точку пересечения этой касательной с прямой MN.

По свойству касательных, проведённых к окружности, будем иметь: QM=QP, QN=QP. Значит, точки M, N и P равноудалены от точки Q, следовательно, angle MPN является вписанным в некоторую окружность с центром в точке Q и радиусом R=MQ. При этом angle MPN опирается на диаметр MN, а значит, angle MPN=90^{circ}. Отсюда triangle MNP является прямоугольным.

б) Пусть O_1 — центр окружности радиуса 4, а O_2 — центр окружности радиуса 16.

Рассмотрим MNO_2O_1: прямая MN — касательная к исходным окружностям, O_1M и

O_2N — радиусы, следовательно, O_1M perp MN и O_2N perp MN. Отсюда O_1M parallel O_2N, а значит MNO_2O_1 — прямоугольная трапеция.

Точка касания двух окружностей лежит на линии их центров, поэтому отрезок

O_1O_2 пересекает касательную PQ в точке P, следовательно, O_1P=O_1M=4, O_2P=O_2N=16, O_1O_2=O_1P+O_2P=4+16=20.

Проведём из точки P перпендикуляр PH к отрезку MN.

Очевидно, что S_{triangle MPH}=S_{MNO_2O_1}-S_{triangle MPO_1}-S_{triangle MPO_2}.

Приведем отрезок O_1Kperp NO_2, Kin NO_2, получим прямоугольник MNKO_1, в котором MN=O_1K и KN=O_1M=4, а также прямоугольный triangle O_1KO_2, в котором KO_2=NO_2-NK=16-4=12.

Следовательно, по теореме Пифагора O_1K= sqrt {O_1O_2^2-KO_2^2}= sqrt {20^2-12^2}= 16, MN-O_1K=16.

По теореме Фалеса frac{MH}{MN}=frac{O_1P}{O_1O_2}, следовательно, MH =frac{MNcdot O_1P}{O_1O_2}=frac{16cdot 4}{20}=frac{16}5, отсюда NH=MN-MH=16-frac{16}5=frac{64}5.

S_{MNO_2O_1}= frac{MO_1+NO_2}{2}cdot MN= frac{4+16}2cdot 16= frac{20}2cdot 16= 160.

MH равна высоте треугольника MPO_1, опущенной на сторону MO_1.

S_{triangle MPO_1}= frac{MHcdot MO_1}2 = frac{dfrac{16}5cdot 4}{2}= 6,4.

NH равна высоте треугольника NPO_2, опущенной на сторону NO_2.

S_{triangle MPO_2}= frac{NHcdot NO_2}2= frac{dfrac{64}5cdot 16}{2}= 102,4.

Значит, S_{triangle MPN}=160-6,4-102,4=51,2.

Ответ

51,2.

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1204

Условие

Биссектриса острого угла A равнобедренной трапеции ABCD пересекает её основание в точке K. В этой трапеции расположены две равные окружности радиусом 2, касающиеся её сторон и друг друга, причём K — одна из точек касания.

а) Докажите, что треугольник ABK равнобедренный.

б) Найдите площадь трапеции.

Показать решение

Решение

а) AK — биссектриса угла angle BAD, значит, angle BAK=angle KAH. Основания AD и BC трапеции параллельны, значит, angle KAH=angle AKB (как накрест лежащие). Поэтому angle BAK=angle AKB, и треугольник ABK равнобедренный.

б) Пусть CF=x, FD=y, радиус окружности r, тогда, учитывая, что отрезки касательных, проведённых к окружности из одной точки, равны и треугольник ABK равнобедренный, BC=2x+y.

С другой стороны, учитывая, что точка M — середина основания BC, получим BC=2x+2r, поэтому y=2r=4.

angle COD=90^{circ} как угол, образованный двумя биссектрисами смежных углов. Из triangle COD, OF^2=CFcdot FD, r^2=xy, но y=2r. Тогда r=2x, x=1.

Найдём основания трапеции BC=2(x+r)=2cdot (1+2)=6, AD=2(y+r)=2cdot (4+2)=12. KH=2r=4

S= frac12(BC+AD)cdot KH= frac12cdot (6+12)cdot 4= 36.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1203

Условие

В треугольнике MNP проведены медианы MM_1 и NN_1. На сторонах MN, MP и NP взяты соответственно точки F, K и E, причём FEparallel MM_1, FKparallel NN_1 и MF:MN=1:3.

а) Докажите, что MK=frac16MP, NE=frac13PN.

б) Найдите площадь треугольника FEK, если площадь треугольника MNP равна 48.

Показать решение

Решение

а) Доказательство.

По условию MF:MN=1:3, то есть MF=frac13MN.

По свойству параллельных линий, отсекающих пропорциональные отрезки на пересекаемых прямых, имеем MK =frac13MN_1, MN_1=N_1P, значит, MN_1 =frac12MP, MK =frac16MP;

NE =frac23NM_1, NM_1=M_1P, NE =frac26PN =frac13PN.

Что и требовалось доказать.

б) S_{FEK}= S_{MNP}-(S_{MKF}+S_{KPE}+S_{FEN}).

S_{MNP}=48; S_{MKF} = frac12MKcdot MF sin angle M= frac12MPcdot MN sin angle Mcdot frac16cdot frac13= S_{MNP}cdot frac1{18}= 48cdot frac1{18} = frac{24}9=frac83.

S_{KPE}= frac12KPcdot PE sin angle P= frac12MPcdot PN sin angle Pcdot frac56cdot frac23= S_{MNP}cdot frac{10}{18}= S_{MNP}cdot frac59= 48cdot frac59= frac{80}3.

S_{FEN}= frac12FNcdot NE sin angle N= frac12MNcdot PN sin angle Ncdot frac23cdot frac13= S_{MNP}cdot frac29= frac{32}{3}.

S_{FEK}=48-left( frac83+frac{80}3+frac{32}3right) =8.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1202

Условие

Две окружности различных радиусов касаются друг друга внешним образом. Их общие касательные, не проходящие через точку касания окружностей, пересекаются в точке O. При этом одна из касательных касается окружностей в точках A и C, считая от точки O, а другая — соответственно в точках B и D.

а) Докажите, что прямая AB перпендикулярна биссектрисе угла, образованного указанными касательными.

б) Найдите расстояние от середины отрезка AB до точки C, если радиусы окружностей равны 2 и 6.

Показать решение

Решение

а) Рассмотрим рисунок.

На нём O_1 и O_2 — центры окружностей (по свойству вписанной в угол окружности точки O_1 и O_2 лежат на биссектрисе angle AOB), K и T — точки пересечения соответственно AB и CD с биссектрисой. O_1A и O_2C — радиусы окружностей, перпендикулярные касательной AC.

triangle O_1AO=triangle O_1BO по общей гипотенузе и острому углу, поэтому AO=BO. Таким образом, треугольник AOB является равнобедренным, и биссектриса OK угла O является высотой и медианой, поэтому точка K является серединой отрезка AB. Это и означает, что прямая AB перпендикулярна биссектрисе angle AOB.

б) Пусть angle AOO_1 равен alpha. Проведём через O_1 прямую O_1L, параллельную AC.

Тогда по свойству соответственных углов при параллельных прямых OC и O_1L и секущей OO_2enspace angle LO_1O_2=alpha. Но O_1O_2=2+6=8, а LO_2=6-2=4. Поэтому sin alpha =frac{LO_2}{O_1O_2}=frac48=frac12. Так как alpha — острый угол, то alpha =30^{circ} , cos alpha =frac{sqrt 3}2, tg alpha =frac1{sqrt 3}.

Заметим, что frac{AO_1}{OA} =tg alpha =frac{1}{sqrt 3}, OA=frac{AO_1}{tgalpha }=frac2{dfrac{1}{sqrt 3}}=2sqrt 3.

OK=OAcdot cos alpha =2sqrt 3cdot frac{sqrt 3}2=3.

Аналогично OC =frac{CO_2}{tgalpha }=frac6{dfrac{1}{sqrt 3}}=6sqrt 3.

В triangle KOC по теореме косинусов KC^2= OK^2 +OC^2 -2cdot OKcdot OCcdot cos alpha = 9+108-2cdot 3cdot 6sqrt 3cdot frac{sqrt 3}2= 63, KC=sqrt {63}=3sqrt 7.

Ответ

3sqrt 7.

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1201

Условие

В трапеции KLMN боковая сторона KL перпендикулярна основаниям. Из точки K на сторону MN опустили перпендикуляр KA. На стороне KL отмечена точка B так, что прямые LA и BN параллельны.

а) Докажите, что прямые BM и MN перпендикулярны.

б) Найдите отношение LA:BN, если угол LMN равен 150^{circ}.

Показать решение

Решение

а) Для доказательства перпендикулярности прямых BM и MN достаточно доказать, что BM parallel KA, а это выполняется в случае, если подобны треугольники SBM и SKA, то есть если справедливо равенство frac{SB}{SK}=frac{SM}{SA}.

Пусть angle SML=alpha , тогда angle SKA=angle ANK=alpha. Из параллельности прямых LA и BN следует, что треугольники SLA и SBN подобны, значит, верно равенство frac{SL}{SB}=frac{SA}{SN}.

В прямоугольном треугольнике SLM, frac{SL}{SM}=sin alpha , откуда SM =frac{SL}{sin alpha }.

В прямоугольном треугольнике SAK, frac{SA}{SK}=sin alpha ,

В прямоугольном треугольнике SKN, frac{SK}{SN}=sin alpha. SK=SN sin alpha.

Перемножая почленно равенства frac{SA}{SK}=sin alpha и frac{SK}{SN}=sin alpha , получим: frac{SA}{SN}=sin ^2 alpha , SA=SN sin ^2 alpha. Учитывая, что frac{SA}{SN}=frac{SL}{SB}, имеем frac{SL}{SB}=sin ^2 alpha , откуда SB =frac{SL}{sin ^2 alpha }.

Тогда frac{SB}{SK}= frac{SL}{sin ^2 alphacdot SNcdot sin alpha }= frac{SL}{sin ^3 alphacdot SN}.

frac{SM}{SA}= frac{SL}{sin alphacdot SN sin ^2 alpha }= frac{SL}{sin ^3 alphacdot SN}. Правые части равенств равны, следовательно, frac{SB}{SK}=frac{SM}{SA}, значит, прямые LA и BN параллельны, и BM и MN перпендикулярны.

б) В силу подобия треугольников SML и SKN, frac{LA}{BN}=frac{SL}{SB}.

Как показано в пункте а), frac{SL}{SB}=sin ^2 alpha. По условию angle LMN=150^{circ}, angle LMN+alpha =180^{circ}, alpha =180^{circ}-150^{circ}=30^{circ}.

frac{SL}{SB}=sin ^2 alpha =sin ^2 30^{circ}=frac14.

Ответ

б) frac14.

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1200

Условие

Точка M — центр окружности, описанной около остроугольного треугольника NPK, Q — центр вписанной в него окружности, W — точка пересечения высот. Известно, что angle PNK=angle MPK+angle MKP.

а) Докажите, что точка Q лежит на окружности, описанной около треугольника PMK.

б) Найдите угол MQW, если angle NPK=47^{circ}.

Показать решение

Решение

а) Чтобы доказать, что точки P, M, Q и K лежат на одной окружности, можно воспользоваться одним из признаков, например доказать, что angle PMK=angle PQK. Найдём эти углы.

M — центр окружности, описанной около треугольника NPK, тогда как центральный и вписанный углы, опирающиеся на одну дугу, angle PMK=2angle PNK.

Запишем сумму углов треугольника PMK и воспользуемся полученным и заданным в условии равенствами.

angle PMK+angle MPK+angle MKP= 2angle PNK+angle PNK= 3angle PNK= 180^{circ},

angle PNK=60^{circ}; angle PMK=120^{circ}.

Q — центр вписанной в треугольник NPK окружности, поэтому Q — точка пересечения биссектрис треугольника.

angle PQK= 180^{circ}-(angle QPK+angle QKP)= 180^{circ}-frac{angle NPK+angle NKP}2.

angle PQK= 180^{circ}-frac{180^{circ}-angle PNK}2= 180^{circ}-frac{180^{circ}-60^{circ}}2= 120^{circ}.

Значит, angle PMK=angle PQK, поэтому точки P, M, Q и K лежат на одной окружности.

б) W — точка пересечения высот треугольника NPK. Найдём угол MQW, для этого

докажем сначала, что и точка W лежит на той же окружности, что и точки P, M, Q и K. Если провести высоту треугольника (например, из вершины P), то образуются прямоугольные треугольники, сумма острых углов каждого такого треугольника равна 90^{circ}. Например, angle WPK+angle PKN=90^{circ}, аналогично можно получить: angle WKP+angle NPK=90^{circ}.

angle PWK= 180^{circ}-angle WPK-angle WKP= 180^{circ}-(90^{circ}-angle PKN)-(90^{circ}-angle NPK)= angle PKN+angle NPK= 120^{circ}, angle PMK=angle PQK=angle PWK, потому точки P, M, Q, W и K лежат на одной окружности.

Так как angle PNK=60^{circ}, angle NPK=47^{circ}, получаем: angle NKP=73^{circ}. В равнобедренном треугольнике PMK, angle MPK=frac{180^{circ}-angle PMK}2=30^{circ}. Учитывая, что PW perp NK, получаем: angle WPK=90^{circ}-angle NKP=17^{circ}. Отсюда angle WPM=angle MPK-angle WPK=13^{circ}.

angle MPK=30^{circ}, angle QPK=frac{angle NPK}2=frac{47^{circ}}2=23, 5^{circ}

angle KPW= 90^{circ}-angle NKP= 90^{circ}-73^{circ}= 17^{circ}, значит, angle MPK>angle QPK>angle KPW, поэтому лучи PW, PQ и PM пересекают дугу окружности в порядке, указанном на рисунке.

Четырёхугольник PMQW вписан в окружность, поэтому сумма его противоположных углов равна 180^{circ} и angle MQW= 180^{circ}-angle WPM= 180^{circ}-13^{circ}= 167^{circ}.

Ответ

б) 167^{circ}.

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1199

Условие

В треугольнике ABC проведены высоты AM и BN. На них из точек M и N опущены перпендикуляры MK и NF соответственно:

а) Докажите, что прямые KF и AB параллельны.

б) Найдите отношение KF:AB, если angle ACB=60^{circ}.

Показать решение

Решение

а) triangle ANO sim triangle BMO по первому признаку подобия (angle ANO=angle BMO=90^{circ}, angle AON=angle BOM как вертикальные). Учитывая, что в подобных треугольниках пропорциональны сходственные стороны и высоты, к ним проведённые, получим frac{AO}{OB}=frac{NF}{KM} (1).

triangle NFO sim triangle MKO по первому признаку подобия

(angle NFO=angle MKO=90^{circ}, angle NOF=angle MOK как вертикальные), отсюда frac{OF}{OK}=frac{NF}{MK}. (2).

Из 1) и 2) следует, что frac{AO}{OB}=frac{OF}{OK}.

Следовательно, triangle AOB sim triangle FOK по второму признаку подобия (angle AOB — общий, frac{AO}{FO}=frac{OB}{OK}).

Из подобия следует angle OAB=angle OFK. Углы OAB и OFK соответственные при прямых AB и KF и секущей AO, следовательно, AB parallel KF по признаку параллельности прямых.

б) В четырёхугольнике NCMO, angle MON= 360^{circ}-(angle N+angle M+angle C)= 120^{circ}.

В triangle MOK, angle MKO=90^{circ}, angle MOK=60^{circ} как смежный с angle MON, тогда angle OMK=30^{circ}. Пусть OK=x, OM=2OK=2x.

В triangle OMB, angle OMB=90^{circ}, angle MOB=60^{circ}, angle MBO=30^{circ}, OB=2OM=4x.

По доказанному в пункте а) triangle FOK sim triangle AOB, значит, сходственные стороны пропорциональны: frac{KF}{AB}=frac{OK}{OB}=frac{x}{4x}=frac14.

Следовательно, KF:AB=1:4.

Ответ

KF:AB=1:4.

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник