Задачи по статике егэ физика

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

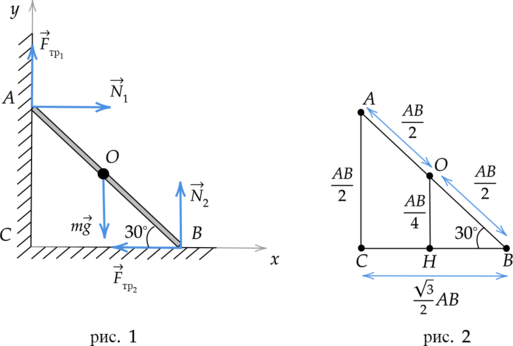
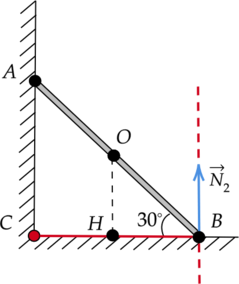
Прут массой 5 кг опирается на две точки горизонтальной и вертикальной поверхностей, образуя с первой угол (30^circ) (см. рисунок). Длина прута (AB = 2sqrt{3}) м. Из приведенного ниже списка выберите два верных утверждения, описывающих эту ситуацию.

1) Модуль силы реакции опоры, действующей на прут со стороны вертикальной поверхности, в два раза больше модуля силы трения, действующей на него со стороны горизонтальной поверхности.
2) Момент силы тяжести относительно оси, проходящей через точку (B) перпендикулярно плоскости рисунка, равен 75 Н(cdot)м.
3) Длина плеча силы трения, действующей на прут со стороны вертикальной поверхности, относительно оси, проходящей через точку (O) перпендикулярно плоскости рисунка, составляет 1 м.
4) Момент силы реакции опоры, действующей на прут со стороны горизонтальной поверхности, относитльно оси, проходящей через точку (B) перпендикулярно плоскости рисунка, равен нулю.
5) Длина прута на 20(%) больше длины плеча действующей на него со стороны горизонтальной поверхности силы реакции опоры относительно точки (C).

1) (color{red}{smalltext{Неверно }})
Укажем все силы, действующие на прут (рис. 1):
(F_text{тр1}), (N_1) — сила трения и сила реакции опоры, действующие на прут со стороны вертикальной поверхности;
(mg) — сила тяжести;
(F_text{тр2}) и (N_2) — сила трения и сила реакции опоры, действующие на прут со стороны горизонтальной поверхности.
Запишем второй закон Ньютона с учетом того, что прут покоится: [vec{F}_text{тр1} + vec{N}_1 + mvec{g} + vec{F}_text{тр2} + vec{N}_2 = 0] Введем оси (Ox) и (Oy) (рис. 1) и спроецируем на них все силы: [begin{cases}
Ox: N_1 — F_text{тр2} = 0\
Oy: F_text{тр1} — mg + N_2 = 0
end{cases}
Rightarrow hspace{3mm}
begin{cases}
N_1 = F_text{тр2}\
F_text{тр1} — mg + N_2 = 0
end{cases}] Таким образом, сила реакции опоры (N_1), действующая на прут со стороны вертикальной поверхности, равна силе трения (F_text{тр2}), действующей на него со стороны горизонтальной поверхности.

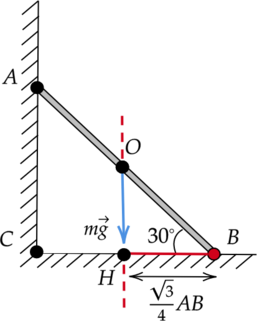
2) (color{green}{smalltext{Верно }})
Момент силы тяжести относитльно оси, проходящей через точку (B) перпендикулярно плоскости рисунка, равен: [M = mgcdot l,] где (l) — плечо силы. Упростим модель (рис. 1) до двух подобных треугольников (Delta ABC) и (Delta OBH) (рис. 2) и, обратившись к геометрии, выразим длины всех отрезков через сторону (AB).

По рисунку видно, что плечом силы тяжести (l) является отрезок (HB), равный (dfrac{sqrt{3}}{4}AB). Таким образом, момент силы тяжести равен: [M = 5text{ кг}cdot 10text{ }dfrac{text{м}}{text{с}^2}cdotdfrac{sqrt{3}}{4}cdot 2sqrt{3}text{ м} = 75 text{ Н}cdottext{м}]

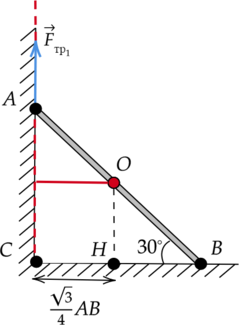
3) (color{red}{smalltext{Неверно }})
Плечо – это кратчайшее расстояние между осью вращения и линией действия силы.

По рисунку видно, что плечом силы трения, действующей на прут со стороны вертикальной поверхности, относительно оси, проходящей через точку (O) перпендикулярно плоскости рисунка, является отрезок, равный по длине отрезку (CH).
Исходя из рис. 2: [CH = dfrac{sqrt{3}}{4}AB] [CH = dfrac{sqrt{3}}{4}cdot 2sqrt{3}text{ м} = 1,5text{ м}]

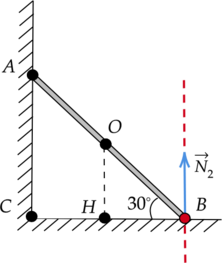
4) (color{green}{smalltext{Верно }})
Момент силы трения (M) равен произведению модуля силы реакции опоры (N_2) на ее плечо (l): [M=N_2cdot l] По рисунку видно, что длина плеча силы трения (l) относительно точки (B) равна нулю (так как ось вращения, проходящая через точку (B), перпендикулярна линии действия силы реакции опоры).

Следовательно, и момент силы реакции (M) так же равен нулю: [M = N_2cdot 0text{ м} = 0text{ H}cdottext{м}]

5) (color{red}{smalltext{Неверно }})
По рисунку видно, что плечом силы реакции опоры (N_2), действующей на прут со стороны горизонтальной поверхности, является отрезок (CB).
Исходя из рис. 2: [CB = dfrac{sqrt{3}}{2} AB hspace{2 mm} Rightarrow hspace{2 mm} AB = dfrac{2}{sqrt{3}}] [AB approx 1,15 hspace{1 mm} CB] Следовательно, длина прута (AB) приблизительно на 15(%) больше длины плеча действующей на него со стороны горизонтальной поверхности силы реакции опоры относительно точки (C).

Ответ: 24

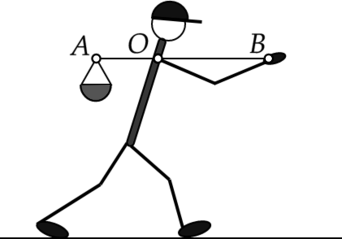
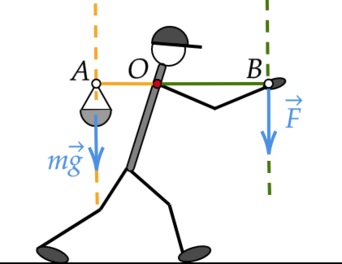
Трудолюбивый Вася собрал в лесу 5 кг ягод. Вася хорошо знал физику, поэтому он нашел палку длиной 1,2 м и решил понести корзину с ягодами так, как показано на рисунке. К концу (B) палки в начале пути Вася прикладывал постоянную вертикальную силу, равную 25 Н. Из приведенного ниже списка выберите два верных утверждения, описывающих эту ситуацию. Массой палки пренебречь.

1) Длина короткого конца палки (относительно точки (O)) составляет 40 см.
2) Момент силы, действующей на конец палки (A), относительно точки (O) равен 25 Н(cdot)м.
3) Плечо вертикальной силы, прикладываемой Васей к концу (B) палки, в два раза больше плеча силы, действующей на конец (A).
4) Момент вертикальной силы, действующей на конец (B) палки относительно точки (O) равен 2 Н(cdot)м.
5) Если Вася устанет и будет прикладывать к концу (B) палки силу на 10 Н меньшую, чем прикладывал в начале пути, то ему нужно будет съесть 3 кг собранных ягод, чтобы палка осталась в равновесии (при неизменных прочих условиях).

1) (color{green}{smalltext{Верно }})
Чтобы рычаг (палка) достиг равновесия, моменты сил, действующих на него справа и слева, должны быть равны: (M_1=M_2). В то же время моменты сил (M_1) и (M_2) по определению равны произведению силы на ее плечо: [M_1 = F_1l_1] [M_2 = F_2l_2] На конец (A) палки действует единственная сила — сила тяжести (Rightarrow) (F_1 = mg).
На конец (B) действует вертикальная сила, которую прикладывает Вася (Rightarrow) (F_2 = F).
По рисунку видно, что плечом силы тяжести относительно точки (O) является отрезок (AO), а плечом силы (F) относительно той же точки — отрезок (OB), причем (OB = AB — AO).
Таким образом: [M_1 = mgcdot AO] [M_2 = Fcdot OB] Приравнивая, получаем: [mgcdot AO = Fcdot OB] [mgcdot AO = Fcdot (AB — AO)] [AO = dfrac{Fcdot AB}{F + mg}] [AO = dfrac{25text{ Н}cdot 1,2text{ м}}{25text{ Н}+5text{ кг}cdot 10text{ }dfrac{text{м}}{text{с}^2}} = 0,4text{ м}] Тогда конец (OB) равен: [OB = AB — AO] [OB = 1,2text{ м} — 0,4text{ м} = 0,8text{ м}] Таким образом, длина короткого конца палки действительно составляет 0,4 м = 40 см.

2) (color{red}{smalltext{Неверно }})
Момент силы, действующей на конец палки (A), относительно точки (O) равен: [M = mgcdot AO] [M = 5text{ кг}cdot10text{ }dfrac{text{м}}{text{с}^2}cdot 0,4text{ м} = 20text{ Н}cdottext{м}]

3) (color{green}{smalltext{Верно }})
Найдем отношение плеч: [dfrac{OB}{AO} = dfrac{AB — AO}{AO} = dfrac{1,2text{ м} — 0,4text{ м}}{0,4text{ м}} = 2]

4) (color{red}{smalltext{Неверно }})
Момент вертикальной силы, действующей на конец (B) палки относительно точки (O) равен: [M = Fcdot OB] [M = 25text{ Н}cdot 0,8text{ м} = 20text{ Н}cdottext{м}]

5) (color{red}{smalltext{Неверно }})
Запишем условие равновесия рычага (палки) для двух случаев — до того, как Вася устал, и после: [Fcdot OB = mgcdot AO] [F’cdot OB = m’gcdot AO] Поделим первое выражение на второе и выразим массу (m’) с учетом того, что (F’ = F — 10text{ H}): [dfrac{Fcdot OB}{F’cdot OB} = dfrac{mgcdot AO}{m’gcdot AO}] [m’ = dfrac{mF’}{F} = dfrac{m(F -10text{ Н})}{F}] [m’ = dfrac{5text{ кг}cdot(25text{ Н}-10text{ Н})}{25text{ Н}} = 3text{ кг}] Таким образом, Васе нужно съесть (Delta m = m-m’ = 5text{ кг} — 3text{ кг} = 2text{ кг}) ягод.

Ответ: 13

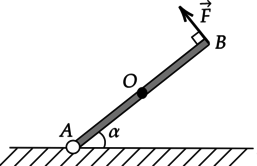
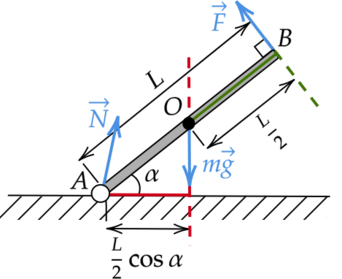
Доску массой 2 кг удерживают с силой, направленной перпендикулярно ее поверхности. Доска образует с горизонтом угол (alpha = 60^circ) (см. рисунок). Длина доски составляет 160 см.
Из приведенного ниже списка выберите два верных утверждения, описывающих эту ситуацию.

1) Длина плеча силы тяжести относительно оси, проходящей через точку (A) перпендикулярно плоскости рисунка, составляет 40 см.
2) На доску действуют с силой (F), равной 50 Н.
3) Длина плеча силы (F) относительно точки (O) в три раза меньше длины доски.
4) Момент силы (F) относительно оси, проходящей через точку (O) перпендикулярно плоскости рисунка, равен 400 мН(cdot)м.
5) Момент силы тяжести относительно оси, проходящей через точку (A) перпендикулярно плоскости рисунка, равен 8 Н(cdot)м.

1) (color{green}{smalltext{Верно }})
По рисунку видно, что длина плеча силы тяжести (mg) относительно оси, проходящей через точку (A) перпендикулярно плоскости рисунка, равна: [l = dfrac{L}{2}cosalpha] [l = dfrac{1,6text{ м}}{2}cos{60}^circ = 0,4text{ м} = 40text{ см}]

2) (color{red}{smalltext{Неверно }})
Чтобы доска находилась в равновесии, алгебраическая сумма моментов сил, действующих на нее, должна равняться нулю.
Мы ничего не знаем о силе реакции опоры (N), поэтому правило моментов удобнее записать относительно точки (A). В этом случае плечо силы реакции опоры (N) равно нулю. Следовательно, и момент этой силы “зануляется”. [FL — mgdfrac{L}{2}cos{alpha} = 0] [FL = mgdfrac{L}{2}cos{alpha}] [F = dfrac{mg}{2}cos{alpha}] [F = dfrac{2text{ кг}cdot10text{ м/с}^2}{2}cos{60}^circ = 5text{ Н}]

3) (color{red}{smalltext{Неверно }})
По рисунку видно, что длина плеча (OB) силы (F) относительно точки (O) в два раза меньше длины доски (AB).

4) (color{red}{smalltext{Неверно }})
Момент силы (F) относительно оси, проходящей через точку (O) перпендикулярно плоскости рисунка, равен: [M = Fcdotdfrac{L}{2}] [M = 5text{ Н}cdotdfrac{1,6text{ м}}{2} = 4text{ Н}cdottext{м} = 4000text{ мН}cdottext{м}]

5) (color{green}{smalltext{Верно }})
Момент силы тяжести относительно оси, проходящей через точку (A) перпендикулярно плоскости рисунка, равен: [M = mgcdotdfrac{L}{2}cos{alpha}] [M = 2text{ кг}cdot10text{ }dfrac{text{м}}{text{с}^2}cdotdfrac{1,6text{ м}}{2}cos{60}^circ = 8text{ Н}cdottext{м}]

Ответ: 15

Очень лёгкая рейка закреплена на горизонтальной оси (O), перпендикулярной плоскости рисунка, и может вращаться вокруг неё без трения. К рейке приложены четыре силы, изображенные на рисунке.

Из приведенного ниже списка выберите два правильных утверждения
1) Относительно оси (O) максимальное плечо имеет сила (F_4)
2) Относительно оси (O) минимальное плечо имеет сила (F_1)
3) Относительно оси (O) минимальным будет момент, создаваемы силой (F_2)
4) Относительно оси (O) максимальным будет момент, создаваемый силой (F_4)
5) Под действием всех изображенных на рисунке рейка будет вращаться

1) Плечо это — кратчайшее расстояние между линией действия силы и связанной с ней точкой (полюсом или осью вращения). В данном случае макисмальное расстояние будет до силы (F_4)
2) Из пункта 1 минимальное плечо будет до силы (F_2)
3) Момент вычисляет по формуле: [M=Flsin alpha,] где (F) – сила, (l) – плечо силы, (alpha) – угол между силой и плечом.
Найдем моменты для каждой из сил, проецируя силы на ось, перпендикулярную оси вращения [M_1=F_1l_1=20text{ см}cdot 1 text{ Н}=20text{ Н $cdot $ см}] [M_2=F_2l_2=10text{ см}cdot 1 text{ Н}=10text{ Н $cdot $ см}] [M_3=F_3l_3=30text{ см}cdot 3 text{ Н}=90text{ Н $cdot $ см}] [M_4=F_4l_4=40text{ см}cdot 2 text{ Н}=80text{ Н $cdot $ см}] Минимальным будет момент (M_2)
4) Из пункта 3) максимальным будет момент (F_3)
5) У нас силы (F_2) и (F_3) будут вращать рейку по часовой стрелке, а силы (F_1) и (F_4) против часовой стрелки, следовательно, чтобы рейка находилась в равновесии должно выполняться условие [M_2+M_3=M_1+M_4 Rightarrow 10text{ Н $cdot $ см}+90text{ Н $cdot $ см}=20text{ Н $cdot $ см}+ 80text{ Н $cdot $ см}] Как мы видим условие равновесия соблюдено, а значит, рейка вращаться не будет.

Ответ: 13

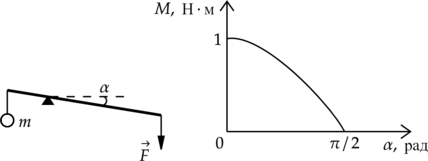
Из лёгкого жёсткого стержня сделан горизонтальный рычаг с длинами плеч 40 см и 100 см. К короткому концу рычага на нити подвешен груз массой (m), а к длинному концу рычага для уравновешивания приложена некоторая сила. Человек начинает медленно опускать длинный конец рычага, прикладывая к нему вертикально вниз силу (см. рисунок). На графике показана зависимость момента (M) силы тяжести груза (m) (относительно точки опоры рычага) от угла (alpha) между рычагом и горизонтом.

Из приведённого ниже списка выберите два правильных утверждения на основании анализа графика.
1) При повороте рычага плечо действующей на груз силы тяжести не изменяется.
2) Когда уравновешенный рычаг горизонтален, модуль приложенной к его длинному концу силы равен 1 Н.
3) Масса груза (m) равна 500 г.
4) При увеличении угла (alpha) момент силы относительно точки опоры рычага уменьшается.
5) Момент силы (F) относительно точки опоры рычага всё время больше 1 Н(cdot)м.

1) При повороте рычага плечо силы тяжести уменьшается.
2) По графику видно, что при уравновешенном в горизонтальном положении рычага, момент силы равен (M=1) Н(cdot) м, откуда сила [F=dfrac{M}{l_2}=dfrac{1text{ Н$cdot$ м}}{1text{ м}}=1text{ Н}] 3) По правилу моментов [M_1=M_2] или [mgl_1=Fl_2] Откуда масса груза [m=dfrac{Fl_2}{gl_1}=dfrac{1text{ Н$cdot$ м}}{10text{ Н/кг}cdot 0,4text{ м}}=250text{ г}] 4) При увеличении угла (alpha) момент силы (F) относительно точки опоры рычага, равный моменту силы тяжести, уменьшается.
5) По графику момент силы (F) все время не превосходит 1 Н(cdot) м

Ответ: 24